On Models for Binomial Data with Random Numbers of Trials

Summary

A binomial outcome is a count s of the number of successes out of the total number of independent trials n = s + f, where f is a count of the failures. The n are random variables not fixed by design in many studies. Joint modeling of (s, f) can provide additional insight into the science and into the probability π of success that cannot be directly incorporated by the logistic regression model. Observations where n = 0 are excluded from the binomial analysis yet may be important to understanding how π is influenced by covariates. Correlation between s and f may exist and be of direct interest. We propose Bayesian multivariate Poisson models for the bivariate response (s, f), correlated through random effects. We extend our models to the analysis of longitudinal and multivariate longitudinal binomial outcomes. Our methodology was motivated by two disparate examples, one from teratology and one from an HIV tertiary intervention study.

1. Introduction

A logistic regression analysis with binomial outcome s_i for observation i conditions on the total number of trials n_i = s_i + f_i, where f_i is the number of failures. In many studies, n_i are not fixed by design but are random. In teratology studies on mice, researchers are interested in the proportion of fetuses with a given deformity (Paul, 1982; Machado et al., 2001). In public health studies on HIV transmission prevention, the proportion of protected sex acts, that is, sex acts using contraceptives, out of the number of total sex acts is a measure of the sexual risk behavior (Posner et al., 2001; Rotheram-Borus et al., 2001; Pinkerton, Chesson, and Layde, 2002; Foss et al., 2003; Rotheram-Borus et al., 2004). The total number of fetuses and sex acts, n_i, are random and not under the control of the investigator.

Choosing to model only successes or failures out of the total is no longer appropriate with random n_i. Teratology researchers expect the proportion of diabetic mice fetuses with a given deformity to increase as maternal mouse blood glucose levels increase. Analyzing the binomial outcome does not tell us if the increasing fraction of deformities is due to more deformities or fewer well-formed fetuses or a combination thereof. The effect of glucose levels on the number of viable fetuses may be uncertain, is also of interest, and is relevant to the proportion of viable fetuses.

A high ratio of protected sex acts out of the total number of sex acts s_i/n_i and low number of unprotected sex acts f_i are both successful outcomes. High ratios s_i/n_i and low f_i might be expected to be correlated across the population. A person with n_i = 0 might, at a later observation, be anticipated to have high s_i/n_i, should they have n_i > 0 at that time. For example, low numbers of sex acts of any kind may be correlated with high fractions of protected acts. Both no sex acts and high fractions of protected acts are successes in HIV transmission prevention studies and the presence of no acts may indicate that a person is likely to have a high probability of protected acts, should any acts occur. This correlation is not included in the logistic regression of s_i successes out of f_i + s_i trials, and the f_i are redundant in the logistic regression.

Several analytic techniques have been proposed to account for the random n_i. A logistic regression may include n_i as a covariate but does not allow s_i and f_i to be simultaneously modeled. Data points where n_i = 0 are still excluded, for example, observations are excluded for people who did not have sex. The multinomial-Poisson model (Terza and Wilson, 1990) models n_i ∼ Poisson (λ_i) and s_i ∣ n_i ∼ binomial (n_i, π_i). Successes s_i ∼ Poisson (λ_iπ_i) and failures f_i ∼ Poisson {λ_i(1 − π_i)} are modeled as independent given covariates. In our two examples, this independence seems a priori implausible. In the multinomial-Poisson model, observations with n_i = 0 contribute to the Poisson likelihood, but not to the binomial likelihood.

We recommend correlated bivariate Poisson models (Kocherlakota and Kocherlakota, 1992; Johnson, Kotz, and Balakrishnan, 1997) for the bivariate response (s_i, f_i). We use random effects to model correlation between s_i and f_i. The bivariate Poisson model offers a number of advantages over analytic techniques that do not model s_i and f_i directly. The bivariate Poisson model may be easier to implement in standard statistical software packages than the multinomial-Poisson model; no transformation is needed to produce parameter estimates for outcomes s_i and f_i. The relationship between s_i and f_i is of interest and can be modeled. For models implemented in a Bayesian framework, regression coefficient and random effect priors are easier to formulate because they are on the same scale for both count responses, unlike for the multinomial-Poisson model.

The bivariate Poisson model is easily extended to longitudinal multivariate binomial responses that are prevalent in public health studies on HIV transmission prevention. For example, the proportion of protected sex acts and proportion of sex partners to whom HIV-positive status is disclosed may be assessed (Rotheram-Borus et al., 2001). A negative correlation between protection and disclosure may be hypothesized; people may feel less of an obligation to disclose their HIV-positive status if protection is used. Models for multivariate binomial responses (Lefkopoulou, Moore, and Ryan, 1989; McCullagh and Nelder, 1989) and longitudinal bivariate discrete responses (Rochon, 1996) capture correlation between proportions but do not model correlation between successes and failures within or between binomial responses. We will show in our example on HIV transmission risk data that the correlation of successes and failures provides useful information.

Notation for cross-sectional and longitudinal multivariate binomial data with random n is introduced in Section 2. We consider several covariance models for the random effects of the successes and failures in Section 3 and discuss model selection using Bayes factors in Section 4. The logistic model priors and posteriors induced by the Poisson model are discussed in Section 5. The Poisson models are applied to univariate binomial data from a teratology study and longitudinal bivariate binomial data from an HIV transmission risk study in Section 6. Discussion follows in Section 7.

2. Model Notation

A random-intercept logistic model (Anderson and Aitkin, 1985; Beitler and Landis, 1985; Wong and Mason, 1985; Zeger and Karim, 1991; Agresti, 2002) with observations on experimental units i = 1, …, N, taken at time point j, with longitudinal K-variate binomial data s_ijk ∼ Binomial (n_ijk, π_ijk), k = 1, …, K, with probability π_ijk of success has linear predictor

$$\text{log}\frac{{\pi }_{\mathit{\text{ijk}}}}{1-{\pi }_{\mathit{\text{ijk}}}}=x_{\mathit{\text{ij}}}^{\prime }{\gamma }_k+{\delta }_{\mathit{\text{ik}}},$$ (1)

where γ_k is a vector of regression coefficients for the k th response and covariate vector x_ij is assumed the same for all responses k for simplicity and random effect vector δ_i = (δ_i1, …, δ_iK)′ ∼ N_K (0, τ). The model and notation applies to cross-sectional data by dropping subscript j. We first consider univariate longitudinal binomial data, K = 1 dropping the subscript k. We jointly model z_ij1 = s_ij and z_ij2 = f_ij, our bivariate response, with a bivariate longitudinal Poisson model

$$z_{\mathit{\text{ijh}}}\sim \text{Poisson}({\lambda }_{\mathit{\text{ijh}}}),$$ (2a)

with means λ_ijh = E(z_ijh), h = 1, 2. For longitudinal multivariate binomial data, z_ijh corresponds to successes for h = 2k − 1 and failures for h = 2k from the k th binomial observation, h = 1, …, H = 2 × K. Using a log link, the linear predictors are

$$\text{log}({\lambda }_{\mathit{\text{ijh}}})=x_{\mathit{\text{ij}}}^{\prime }{\alpha }_h+{\beta }_{\mathit{\text{ih}}},$$ (2b)

where again for simplicity the covariate vector x_ij is assumed the same for all responses h and α_h is a vector of coefficients for x_ij for the hth outcome. We use random effects β_ih to induce correlation between z_ij1 and z_ij2. For H ≥ 2, the vector β_i of random effects for each person β_i = (β_i1, …, β_iH)′ ∼ N_H(0, Σ) with elements β_ih where Σ is an H × H covariance matrix.

3. Covariance Models

We discuss covariance models for H-variate cross-sectional Poisson random effects. The most general covariance model has Σ_uns = (Σ_ab), a, b = 1, …, H, to be the unstructured covariance matrix. Define ${\sigma }_a^2={\sum }_{\mathit{\text{aa}}}$ and ${\rho }_{\mathit{\text{ab}}}={\sum }_{\mathit{\text{ab}}}{\sigma }_a^{-1}{\sigma }_b^{-1}$. Special cases of Σ_uns correspond to interesting models.

For H = 2, we consider five covariance matrices Σ_q, q = 1, …, 5, nested in Σ_uns. Uncorrelated random effects with ρ₁₂ = 0, result in diagonal Σ₁. The random effects account for overdispersion but do not induce correlation between z_ij1 and z_ij2. Covariance matrices Σ₂ and Σ₃ are special cases of Σ_uns and Σ₁, respectively, with diagonal variances equal, ${\sigma }_1^2={\sigma }_2^2$. In some data sets the success and failure counts may share one random effect, β_i1 = ±β_i2 and singular Σ₄ (+) or Σ₅ (−) result. For longitudinal models we consider multivariate random-intercept models. Chen et al. (2003) discusses additional covariance models.

4. Comparing Covariance Models

We fit multivariate Poisson models to binomial data in a Bayesian framework and employ Bayesian model checking techniques to compare different covariance model fits to the data. Bayes factors (Jeffreys, 1961; Kass and Raftery, 1995) are used to test random effect covariance models.

We employ a Bayes factor B₁₀ in favor of model M₁ against M₀ (Bernardo and Smith, 1994, p. 390; Raftery, 1995, p. 165) to compare models M₁ and M₀. Let ω be a parameter or set of parameters from M₁ fixed at ω₀ in M₀ and let θ be the remaining model parameters. We assume prior densities under M₁ and M₀ satisfy p(θ ∣ M₀) = p(θ ∣ ω = ω₀, M₁) and calculate B₁₀ using the Savage–Dickey density ratio (Dickey, 1971; Verdinelli and Wasserman, 1995)

$$B_{10}={\frac{p(\omega )}{p(\omega \mid Y)}\mid }_{\omega ={\omega }_0},$$ (3)

where p(ω) and p(ω ∣ Y) are the prior and posterior densities of ω under M₁ evaluated at ω = ω₀ and Y is the observed data. Nonnested covariance models M₁ and M₂ are also compared using Bayes factors. If model M₂ can be compared to M₀ by B₂₀ then M₂ can be compared to M₁ by a Bayes factor because B₂₁ = B₂₀/B₁₀. Kernel density estimation as implemented in S-PLUS 6.0 (Venables and Ripley, 1999) was used to estimate p(ω) and p(ω ∣ x).

For example, to test M₀ : ρ₁₂ = 0, draws are taken from the prior and posterior densities of the most general covariance matrix Σ_uns. Then β_uns,1 is calculated as the ratio of the prior density over the posterior density of correlation ρ₁₂ estimated at ρ₁₂ = 0 by kernel density estimate for both the prior and the posterior.

5. The Induced Logistic Model

5.1 Model Parameters

Although we model the counts, we maintain interest in the binomial probabilities π_ik. The logistic model parameters are functions of the Poisson model parameters. For K-variate binomial data, π_ik = λ_i(2k−1)/{λ_i(2k−1) + λ_i2k}. Substituting for λ_ih using equation (2b) gives

$${\pi }_{\mathit{\text{ik}}}=\frac{1}{1+\text{exp}\left[-x_i^{\prime }\left\{{\alpha }_{2k-1}-{\alpha }_{2k}\right\}-\left\{{\beta }_{i(2k-1)}-{\beta }_{i2k}\right\}\right]}.$$ (4)

The logistic coefficient vector is γ_k = α_2k−1 − α_2k and random effect is δ_ik = β_i(2k−1) − β_i2k with binomial random effect variance $\tau ={\sigma }_1^2+{\sigma }_2^2-2{\rho }_{12}{\sigma }_1{\sigma }_2$ for K = 1 under Σ_uns. For covariance matrix Σ_q, q = 1, 2, …, 5, variance τ is ${\sigma }_1^2+{\sigma }_2^2$, $2{\sigma }_1^2(1-\rho )$, $2{\mathit{\sigma }}_1^2$, 0, and $4{\mathit{\sigma }}_1^2$, respectively.

For K = 2, Σ_uns is a 4 × 4 matrix and τ = (τ_ab) is a 2 × 2 matrix with elements a, b = 1, 2, where ${\tau }_{11}={\sigma }_1^2+{\sigma }_2^2-2{\sigma }_{12}$, ${\tau }_{22}={\sigma }_3^2+{\sigma }_4^2-2{\sigma }_{34}$, and τ₁₂ = τ₂₁ = σ₁₃ + σ₂₄ − σ₁₄ − σ₂₃. For K ≥ 2 and other covariance models, covariance matrix properties may be utilized to determine τ.

5.2 Priors

We discuss priors for the H-variate Poisson model and the induced priors from the logistic regression coefficients. Priors for p-vector coefficient α_h and random effect vector β_i are set to be N_p(μ_h, ηI) and N_H(0, Σ_uns), respectively, where I is an identity matrix. The prior density for Σ_uns is inverse-Wishart, IW (S, v),

$$\begin{array}{cc}f({\sum }_{\text{uns}}\mid S,v)=\hfill & {\left\{2^{vk/2}{\pi }^{k(k-1)/4}\prod _{i=1}^k\Gamma \left(\frac{v+1-i}{2}\right)\right\}}^{-1}\hfill \\ \hfill & \times {\left|S\right|}^{v/2}{\left|{\sum }_{\text{uns}}\right|}^{-(v+k+1)/2}\text{exp}\left\{-\frac{1}{2}\text{tr}(S{\sum }_{\text{uns}}^{-1})\right\},\hfill \end{array}$$

where tr (A) is the trace of a square matrix A, Γ is the gamma function, S = (S_ab), a, b = 1, …, k, is a known symmetric, positive definite k × k scale matrix and degrees of freedom parameter v. We set S to be diagonal, implying a priori the random effects are equally likely to be positively or negatively correlated. Model Σ₁ has prior $P({\sigma }_1^2,{\sigma }_2^2\mid {\rho }_{12}=0)$ with independent random effects and results in independent prior densities for ${\mathit{\sigma }}_1^2$ ∼ inverse-gamma(1.5, S₁₁/2) and ${\mathit{\sigma }}_2^2$ ∼ inverse-gamma(1.5, S₂₂/2).

In the logistic model, the induced priors for γ_k and δ_i are N_p(μ_2k−1 − μ_k/2, 2ηI) and N_K (0, τ), respectively. We choose invertible H × H matrix C so τ is the upper left K × K submatrix of

$$C{\sum }_{\text{uns}}{C}^{\prime }={\left\{{(C^{\prime })}^{-1}{\sum }_{\text{uns}}^{-1}{C}^{-1}\right\}}^{-1}\sim \text{IW}(CS{C}^{\prime },v).$$ (5)

By properties of the IW distribution τ is also distributed inverse-Wishart (Press, 1982, p. 118). For H = 2,

$$C=\left(\begin{array}{cc}1& -1\\ 1& c_{22}\end{array}\right),$$ (6)

where c₂₂ ≠ −1 is an arbitrary real number. Then

$$\tau \sim \text{inverse-gamma}\left(\frac{v-1}{2},\frac{V}{2}\right),$$ (7)

where V = S₁₁ + S₂₂. For H = 4, C = (r₁, r₂, r₃, r₄)′ with row vectors r₁ = (1, −1, 0, 0), r₂ = (0, 0, 1, −1), and arbitrary row vectors r₃ and r₄, linearly independent of r₁ and r₂. Then

$$\tau \sim \text{IW}(W,v),$$ (8)

where W = (W_ab), a, b = 1, 2, has elements W₁₁ = S₁₁ + S₂₂, W₂₂ = S₃₃ + S₄₄, and W₁₂ = W₂₁ = 0.

6. Examples

We consider teratology data containing a cross-sectional univariate binomial outcome and data from the Healthy Living Project (HLP), a public health study on HIV transmission behaviors containing a longitudinal bivariate binomial outcome. Multivariate Poisson models with random effects covariance matrix Σ_uns are fit to the data. We analyze data sets containing all observations, referred to as complete data sets, and data sets excluding observations whose success and failure counts sum to zero, referred to as nonzero subsets, for closer comparison with logistic models.

Analyses are conducted in WinBUGS version 1.41 software (Spiegelhalter, Thomas, and Best, 2000) and based on a 10³ iteration burn-in followed by 10⁶ iterations. Inspection of time series and lagged autocorrelation plots showed the number of iterations to be satisfactory. Posterior means (M) and standard deviations (SDs) of the parameters are reported in Tables 1 and 2.

Table 1. Posterior means (M) and SDs from bivariate Poisson and univariate logistic models fit to teratology data. Reference splotch allele group has neither parent with splotch allele.

	Bivariate Poisson model				Logistic model
	Complete data		Nonzero subset		Induced		Estimated
Part of model	M	SD	M	SD	M	SD	M	SD
With exencephaly
Intercept	−1.57	0.89	−2.15	0.96	−4.69	1.08	−5.20	1.21
Blood glucose level	0.0012	0.0011	0.0022	0.0012	0.0041	0.0014	0.0046	0.0016
Splotch allele group
Father	0.33	0.43	0.41	0.43	0.39	0.48	0.53	0.52
Mother	0.56	0.51	0.53	0.50	0.73	0.58	0.82	0.62
Without exencephaly
Intercept	2.78	0.46	2.53	0.45
Glucose level	−0.0024	0.00064	−0.0019	0.00063
Splotch allele group
Father	−0.027	0.21	0.013	0.21
Mother	−0.21	0.29	−0.20	0.28
Random effect variances
With exencephaly	0.64	0.31	0.53	0.25	0.81	0.34	0.87	0.48
Without exencephaly	0.24	0.082	0.20	0.063
Correlation	0.040	0.25	−0.12	0.24

Table 2. Posterior means (M) and SDs of parameters from longitudinal bivariate Poisson and univariate logistic models fit to HLP data. Models adjust for age at baseline and risk group.

	Bivariate Poisson model				Univariate Binomial model
	Complete data		Nonzero subset		Induced		Estimated
Part of model	M	SD	M	SD	M	SD	M	SD
Protected acts
Base	1.82	0.28	2.16	0.20	0.43	0.26	−0.023	0.36
Base * Intv	0.31	0.12	0.45	0.091	0.66	0.12	0.87	0.15
Follow	1.69	0.29	2.22	0.21	0.62	0.098	0.73	0.36
Follow * Wks	−0.11	0.014	−0.13	0.014	−0.024	0.018	−0.15	0.026
Follow * Wks2	0.0073	0.0097	0.0097	0.0010	0.0043	0.0013	0.014	0.0019
Follow * Intv	0.033	0.14	0.27	0.12	0.52	0.16	0.053	0.20
Follow * Intv * Wks	0.011	0.027	−0.048	0.029	0.13	0.036	0.23	0.052
Follow * Intv * Wks2	0.00046	0.0020	0.0057	0.0021	−0.0083	0.0027	−0.018	0.0039
Unprotected acts
Base	2.54	0.25	1.74	0.21
Base * Intv	0.37	0.098	−0.21	0.077
Follow	2.22	0.25	1.60	0.21
Follow * Wks	−0.061	0.010	−0.11	0.011
Follow * Wks2	0.00040	0.00076	0.0054	0.00081
Follow * Intv	0.064	0.11	−0.25	0.10
Follow * Intv * Wks	−0.069	0.020	−0.18	0.022
Follow * Intv * Wks2	0.0033	0.0015	0.014	0.0016
Random effect variances
Protected acts	3.38	0.21	2.74	0.17	5.03	0.29	6.28	0.41
Unprotected acts	2.25	0.12	1.86	0.11
Correlation	0.13	0.037	−0.095	0.038

We plot posterior densities for probability π_x given covariate vector x as approximated by the S-PLUS 6.0 kernel density estimator. Comparisons are made between π_x estimated from logistic regression models and indirectly estimated from bivariate Poisson regression models as discussed in Section 5. We use a = 1, …, A draws ${\alpha }_h^{(a)}$ and γ^(a) from the joint posterior of the parameter estimates, with A = 1000; every hundredth iteration out of the total 10⁶ iterations was used. The δ^(a) are sampled from density N(0, τ^(a)). The estimates are

$${\widehat{\pi }}_x=\frac{1}{A}{\sum _{a=1}^A\left[1+\text{exp}\left\{-x^{\prime }{\gamma }^{(a)}-{\delta }^{(a)}\right\}\right]}^{-1}.$$ (9)

6.1 Teratology Data

The teratology data was originally reported on in Machado et al. (2001). It was collected to measure the effects of diabetes in 68 pregnant female C57BL/6J mutant mice on malformations in their litters. Nonzero subset analyses exclude six females with no live births. The binomial outcome is the fraction of live births with exencephaly. We split the binomial n_i into a bivariate count outcome, the number of viable fetuses with and without exencephaly from each litter. Diabetes was chemically induced in the female parents prior to pregnancy and assessed by blood glucose levels in milligrams per deciliter. Some parental mice contained a splotch allele thought to confer added susceptibility to malformations in their offspring. Covariates from the original analysis were used: an intercept; maternal blood glucose level (Glucose level); and a three-category splotch allele indicator, categorized as whether the father had the allele (Father), the mother had the allele (Mother), or neither parent had the allele. The experimental design excluded both parents having the allele. If both parents had the allele a fetus could not form. The linear predictor is parameterized as

$$\begin{array}{ll}\text{log}({\lambda }_{\mathit{\text{ih}}})\hfill & ={\alpha }_{h1}+{\alpha }_{h2}\text{Glucose}{\text{level}}_i+{\alpha }_{h3}{\text{Father}}_i\hfill \\ \hfill & +{\alpha }_4{\text{Mother}}_i+{\beta }_{ih}.\hfill \end{array}$$ (10)

6.1.1 Data priors

Priors on α₁ and α₂ are set to be N₄ (0, 10I), proper but basically uninformative. The prior on Σ is IW(S, v), with degrees of freedom, v = 4 and H = 2. We specify a diagonal scale matrix S so the expectation E(Σ) = (v − H − 1)⁻¹ S = S is a reasonable estimate of the random effect variances.

The mean litter size for the C57BL/6J mouse is listed as 7 on the Laboratory Animal Science Center section of the Boston University Medical campus web site, http://www.bumc.bu.edu. We use this to develop a prior for the random effects variances. We start with a guess that half of the litter is malformed so our prior point estimate of the mean litter size of malformed and nonmalformed fetuses is 3.5. We take 0.001 and 7 as a lower and upper 0.005 and 0.995 probability bounds on the mean for an individual litter. We want the 0.005 and 0.995 percentiles of the random effects distribution on the log scale to give us end points of log(0.001) = −6.9 and log(7) = 1.17. Six SDs span 99% of a normal density. The SD of the random effects is approximately {1.9 − (−6.9)}/6 ≈ 1.5. The random effects variance is 1.5² ≈ 2 and we set S₁₁ = S₂₂ = 2.

Priors on γ and δ_i are then N₄ (0, 20I) and N(0, τ), respectively, and the prior on τ is inverse-gamma(1.5, 1).

6.1.2 Results

Parameter estimates from random-intercept bivariate Poisson and univariate logistic models fit to the cross-sectional teratology data set are shown in Table 1. A higher proportion of malformed births with exencephaly is associated with increased blood glucose levels in the logistic model. The Poisson model shows the association with blood glucose is driven by a negative association between nonmalformed birth counts and increased glucose levels; an association with the number of malformed births is not seen. The association between the number of malformed births and blood glucose levels is close to being significant in the nonzero subset (M = 0.0022 and SD = 0.0012), showing that different conclusions might well be drawn from analyses on the complete data and on the nonzero subset.

For the nonzero subset, we estimate Bayes factors β_uns,1, comparing covariance structures Σ_uns to Σ₁, to be 0.47 and similarly β_uns,2 = 0.60. The first Bayes factor favors independent random effects, ρ₁₂ = 0, and β_uns,2 favors equal random effect variances, ${\sigma }_1^2={\sigma }_2^2$.

6.2 HLP Data

We use data with n = 175 from the Choosing Life: Empowerment, Action, Results study (CLEAR; Rotheram-Borus et al., 2004) to create priors for models fit to HLP data (n = 936; Gore-Felton et al., 2005; Lightfoot et al., 2005). Nonzero subset analyses (n = 852) exclude observations for participants who were sexually inactive during the previous time period; 20%, 794 out of 3918, observations were excluded. The HLP study was modeled on the CLEAR study and bears many similarities. Both studies were designed to reduce HIV-transmission behaviors and improve the quality of life for persons living with HIV. Across studies, participants shared a similar socioeconomic status and were recruited from similar types of social service agencies in several metropolitan areas from 1999 to 2000 in the CLEAR study and from 2000 to 2002 in the HLP study. Sexual behavior, substance use, and quality-of-life measures were assessed at baseline, 3, 6, 9, and 15 months in the CLEAR study and at baseline and 5-month intervals up to 25 months in the HLP study. At baseline, participants in both studies were randomized to an immediate or delayed intervention condition.

There are two main differences across studies. The CLEAR sample is younger, ages 16 to 29 with a median age of 23, compared to the HLP sample, ages 19 to 67 with a median age of 40. Recruitment was based on different HIV-transmission behaviors. Current drug use and sexual activity were required to be recruited into the CLEAR and HLP studies, respectively. Study details may be found on the CHIPTS web site (http://chipts.ucla.edu/projects/chipts).

The bivariate binomial outcome, the proportion of sex partners to whom HIV-positive status is disclosed and the proportion of protected sex acts, is split into a multivariate Poisson outcome for the number of disclosed and undisclosed sex partners and number of protected and unprotected sex acts. We fit multivariate longitudinal Poisson random effects models. Relevant covariates based on analyses from prior studies include time, in units of 10 weeks (Wks); intervention arm (Intv), categorized as 1 = immediate or 0 = delayed; age at baseline (Age); and a four-category HIV risk indicator established by the Centers for Disease Control (CDC, 2001), categorized as men who are injecting drug users (IDU), non-IDU who are having sex with other men (MSM), non-IDU men not having sex with other men (HTM), and women.

Visual inspection of the HLP data suggested a piecewise regression allowing different trajectories for each intervention arm from baseline to 5 months and from 5 months to 25 months. Indicators for baseline (Base) and follow-up (Follow = 1 − Base) allow the trajectories to be modeled. Quadratic terms for time are included to model an observed curvilinear trend from 5 to 25 months. The linear predictor is parameterized as

$$\begin{array}{cc}\text{log}({\lambda }_{\mathit{\text{ijh}}})=\hfill & {\alpha }_{h1}{\text{Age}}_i+{\alpha }_{h2}{\text{MSM}}_i+{\alpha }_{h3}{\text{IDU}}_i+{\alpha }_{h4}{\text{HTM}}_i\hfill \\ \hfill & +{\alpha }_{h5}{\text{Base}}_{\mathit{\text{ij}}}+{\alpha }_{h6}\text{Base}\ast {\text{Intv}}_{\mathit{\text{ij}}}+{\alpha }_{h7}{\mathit{\text{Follow}}}_{\mathit{\text{ij}}}\hfill \\ \hfill & +{\alpha }_{h8}\text{Follow}\ast {\text{Wks}}_{\mathit{\text{ij}}}+{\alpha }_{h9}\text{Follow}\ast {\text{Wks}}_{\mathit{\text{ij}}}^2\hfill \\ \hfill & +{\alpha }_{h10}\text{Follow}\ast {\text{Intv}}_{\mathit{\text{ij}}}+{\alpha }_{h11}\text{Follow}\ast \text{Intv}\ast {\text{Wks}}_{\mathit{\text{ij}}}\hfill \\ \hfill & +{\alpha }_{h12}\text{Follow}\ast \text{Intv}\ast {\text{Wks}}_{\mathit{\text{ij}}}^2+{\beta }_{\mathit{\text{ih}}}.\hfill \end{array}$$ (11)

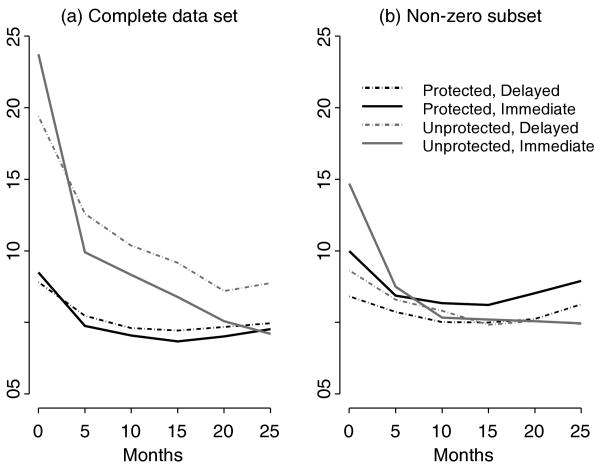
We plot estimated mean counts λ̂_.jh for outcome h at time point j in Figure 1. Outcomes are modeled on the logarithmic scale and transformed back to the original scale prior to plotting. The transformed expectation is of course not the expectation on the transformed scale for nonlinear transformations. A parametric version of the smearing estimate (Duan, 1983) is used to calculate the mean on the transformed scale. We use a = 1, …, A draws ${\alpha }_h^{(a)}$ and ${\beta }_{\mathit{\text{ih}}}^{(a)}$ from the joint posterior of the parameter estimates and random effects, with A = 100; every ten-thousandth iteration out of the total 10⁶ iterations was used. The estimate is

Figure 1.

Estimated mean outcomes over time by intervention condition from longitudinal bivariate Poisson model fit to HLP (a) complete data set and (b) nonzero subset.

$${\widehat{\lambda }}_{.\mathit{\text{jh}}}=\frac{1}{\mathit{\text{AN}}}\sum _{a=1}^A\sum _{i=1}^N\text{exp}\left\{x_{\mathit{\text{ij}}}^{\prime }{\alpha }_h^{(a)}+{\beta }_{\mathit{\text{ih}}}^{(a)}\right\}.$$ (12)

6.2.1 Data priors

Prior distribution parameter values for HLP data analyses were obtained from the CLEAR data set. Separate random-intercept Poisson regression models were fit to each outcome in SAS software, version 8.2, using the GLIMMIX macro (Wolfinger and O'Connell, 1993; Littell et al., 1996) using a pseudolikelihood approach. For the hth outcome and pth coefficient a N(μ_hp, ω_hp) prior was used with μ_hp and ω_hp set to the coefficient and coefficient variance estimate from the CLEAR data analyses.

The prior on Σ was set to be IW (S, v), with v = 6. The diagonal scale matrix, S, was specified so the expectation E(Σ) = (v − H − 1)⁻¹ S = S had diagonal variance elements corresponding to random effect variance estimates from the CLEAR data analysis.

Inferred priors on γ_k and δ_ik are N_p(Θ_k, Λ_k) and N_K(0, τ), respectively, where Θ_k is a vector with elements Θ_kp = μ_2k−1,_p − μ_2k,p and diagonal covariance matrix Λ_k has diagonal elements Λ_kpp = ω_2k−1,_pp + ω_2k,pp. The prior on τ is inferred to be IW(S, v), where diagonal scale matrix S has elements S₁₁ = 5.49 and S₂₂ = 4.47, calculated from CLEAR random effect variance estimates of 0.99, 1.53, 0.74, and 1.50 for the number of partners disclosed to, partners not disclosed to, protected acts, and unprotected acts, respectively.

6.2.2 Analysis results

We fit random-intercept multivariate Poisson and bivariate logistic models to the bivariate binomial outcome for the fraction of protected sex acts and disclosure. Parameter estimates are similar to parameter estimates from random-intercept bivariate Poisson and univariate logistic models fit to each binomial outcome separately. This is not surprising considering the low correlation of −0.085, 95% probability interval = (−0.17, 0.0068), between random effects in the bivariate binomial model, indicating binomial outcomes are nearly independent. We present parameter estimates for one of the binomial outcomes, the fraction of protected sex acts, in Table 2.

The proportion of protected sex acts increases over time more rapidly at first in the immediate condition, compared to the delayed condition. In Figure 1, the Poisson model shows the initial increase in the logistic model to be driven by an initial decrease in the number of unprotected acts in the immediate condition, compared to the delayed condition. The number of protected acts follow a similar trajectory across intervention conditions; inclusion of the zero counts eliminates the level shift in trajectories between intervention conditions at follow-up time points. Inclusion of the zero counts also reverses the direction of the correlation between random effects.

For the nonzero subset, we estimate Bayes factors β_uns,1 to be 1.23, favoring independent random effects, ρ₁₂ = 0, and β_uns,2 to be 105.96, favoring unequal random effect variances, ${\sigma }_1^2\ne {\sigma }_2^2$.

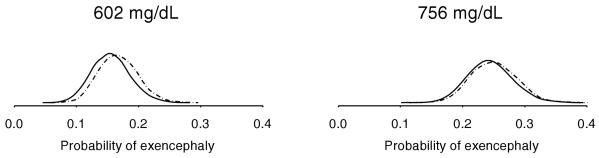
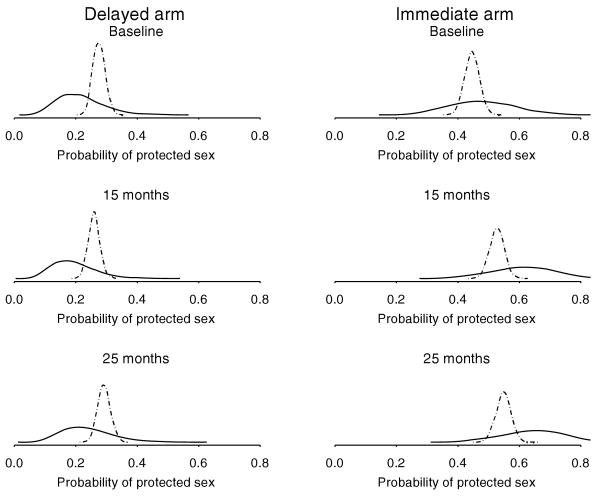
Approximate posterior densities for teratology and HLP outcome probabilities under the logistic and bivariate Poisson models are shown in Figures 2 and 3, respectively. The density shapes from the cross-sectional teratology data are quite similar, whereas the bivariate Poisson densities resulting from the longitudinal HLP data are much narrower compared to the logistic densities. In the HLP data, the bivariate Poisson model produces much smaller confidence intervals compared to the logistic model.

Figure 2.

Approximate marginal posterior density of π, the probability of exencephaly, from bivariate Poisson (- -) and logistic (—) regressions fit to teratology nonzero subset. Densities are shown for 25th and 75th percentiles of sample blood glucose levels.

Figure 3.

Approximate marginal posterior density of π_.j, the probability of protected sex, from longitudinal bivariate Poisson (- -) and longitudinal logistic (—) regressions fit to HLP nonzero subset. Densities are shown for each intervention arm at three time points.

7. Discussion

Our analyses highlight the importance of capturing the complex nature of binomial data with random numbers of trials through the multivariate Poisson model. In both of our examples, the expansion of the binomial outcome to the bivariate Poisson model allowed us to examine the relationship between successes and failures and key covariates, giving a more detailed picture of the data. Biologists may be interested to examine whether teratogenic agents lead to different rates of malformed and normal births. Interventions targeting HIV-transmission behaviors may be very different, depending on whether the goal is to decrease unprotected acts or increase the proportion of protected acts.

More complex random effect models are possible. We could replace the random effects in equations (1) and (2b) with a more complicated random effects structure. For example, we could have a random intercept and slope instead of a random intercept, or more complex random effects. Alternatively, we could induce an autoregressive structure on the random effects over time, so that within-subject random effects were not constant over time (refer to Chen et al., 2003). Another possible covariance model for time-varying random effects is the product correlation model (Weiss, 2005, Chapter 13). For both the autoregressive and product correlation models, there would be additional Poisson variability in addition to the random effect variance.