Improved automated monitoring and new analysis algorithm for circadian phototaxis rhythms in Chlamydomonas

Abstract

Automated monitoring of circadian rhythms is an efficient way of gaining insight into oscillation parameters like period and phase for the underlying pacemaker of the circadian clock. Measurement of the circadian rhythm of phototaxis (swimming towards light) exhibited by the green alga Chlamydomonas reinhardtii has been automated by directing a narrow and dim light beam through a culture at regular intervals and determining the decrease in light transmittance due to the accumulation of cells in the beam. In this study, the monitoring process was optimized by constructing a new computer-controlled measuring machine that limits the test beam to wavelengths reported to be specific for phototaxis and by choosing an algal strain, which does not need background illumination between test light cycles for proper expression of the rhythm. As a result, period and phase of the rhythm are now unaffected by the time a culture is placed into the machine. Analysis of the rhythm data was also optimized through a new algorithm, whose robustness was demonstrated using virtual rhythms with various noises. The algorithm differs in particular from other reported algorithms by maximizing the fit of the data to a sinusoidal curve that dampens exponentially. The algorithm was also used to confirm the reproducibility of rhythm monitoring by the machine. Machine and algorithm can now be used for a multitude of circadian clock studies that require unambiguous period and phase determinations such as light pulse experiments to identify the photoreceptor(s) that reset the circadian clock in C. reinhardtii.

1. Introduction

Circadian rhythms are oscillations in organismal behavior, physiology or biochemistry that continue under constant conditions with a period of about 24 h but that adjust to environmental time cues like the daily changes in light or temperature. The first circadian rhythm described was that of leaf movements in plants. Circadian rhythms are based on an endogenous pacemaker that allows organisms to measure time. Research on these rhythms and their underlying pacemaker usually involves repeated measurements at regular intervals for several days. Efforts were made early on to automate the measurements. For example, automated monitoring of Drosophila rhythms in eclosion [26] and locomoter activity [4] enabled the isolation of the first circadian clock mutants [10]. The measurement of transcriptional rhythms in living organisms could be automated based on the reporter gene luciferase [7, 15]. It allowed for the isolation of circadian clock mutants in Arabidopsis [14] and the cyanobacterium Synechococcus [9]. For Arabidopsis, monitoring of its circadian rhythm in leaf movement has also been automated [3] and served to confirm that the clock mutants were defective in this rhythm as well [14].

Another rhythm that lends itself to automated measurement is that of phototaxis. Phototaxis is a movement of organisms that is oriented with respect to the direction of the light. In positive phototaxis, the movement occurs towards the light source, whereas in negative phototaxis (usually at high light intensities), it occurs away from the light source. For several flagellated algae like Euglena gracilis [19] and Chlamydomonas reinhardtii [1], phototaxis was shown to exhibit a circadian rhythm. Automated monitoring of rhythms in phototaxis has been accomplished based on a narrow, dim test light beam that is directed through the culture at regular intervals [1, 8, 13]. A light sensor records the extent of decrease in transmittance during the duration of the beam due to accumulation of cells in the beam when they undergo phototaxis. As a consequence, the beam serves the two functions of eliciting the behavior and recording it. Analysis of these rhythms for period and phase has been accomplished by determining successive minima. This was either done by hand [13] or by fitting a parabola [8].

When Kondo and coworkers [8] used their phototaxis machine to acquire an action spectrum for the resetting of the rhythm by light in C. reinhardtii, they discovered that the simple act of placing the cultures into the machine could in itself cause a phase shift. Depending on where in the circadian cycle the culture was at this time, the shift could be considerable (up to 9 h). The most likely explanation for this phenomenon is the presence of the white background illumination the authors used between test light cycles in order to allow their particular strain of C. reinhardtii (the cell wall deficient mutant CW15) to exhibit a prolonged rhythm. Additionally, their white test light beam, although narrow and dim, could also have contributed to the phase shift.

We became interested in determining the photoreceptor(s) that are involved in the light-induced resetting of the circadian clock in C. reinhardtii. This organism is a unicellular green alga that serves as a model for research on a number of cellular processes among them the circadian clock [16, 24]. Its value as a model for circadian clock studies was recently enhanced by the development of automated monitoring of circadian transcription rhythms in the chloroplast of living cells based on a luciferase reporter gene [11]. In order to make our measurements of circadian phototaxis rhythms amenable to resetting experiments by light pulses, we constructed and characterized a phototaxis machine that does not cause a measurable phase shift when cultures are placed into it. The machine uses the original basic design of monitoring the decrease in transmittance from a small and dim light beam due to accumulation of cells in the beam. However, the test light beam originates from LEDs with a narrow wavelength spectrum reported to be specific for phototaxis [22]. With this set-up, strain CC124 of C. reinhardtii displays a rhythm of about five cycles even when energy sources in the form of background illumination between test light cycles or organic compounds in the medium are omitted.

We also designed an algorithm for analysis of the rhythm data and tested its robustness. The algorithm takes every single test light cycle into account by fitting the data to a cosine curve that dampens exponentially and shows global parabolic distortion. The algorithm can also analyze rhythms derived from various time points during the test light cycle and therefore allows for the determination of the optimal time point for a particular strain.

2. Results and Discussion

2.1 Algorithm robustness

The rhythm of phototaxis exhibited by strain CC124 of Chlamydomonas reinhardtii in autotrophic medium and with no background light between test light cycles usually ceases after about 5 days (Fig. 1). This is most likely due to an inability of the cells to replenish their energy stores through photosynthesis. Therefore, we decided to test the accuracy of our algorithm in determining period and phase of virtual rhythms with only three cycles that have various degrees of noise added to their amplitude (Fig. 2). Three full cycles represent the minimum any analysis of actual data would be based on. Virtual rhythms with noise were created by sampling a cosine curve with a period of 24 h, a phase of 12 h, and an amplitude of 1 at hourly intervals and then adding random variables to the amplitude with a mean of zero and a standard deviation that is a particular percent of the amplitude. The margin of error for period and phase determinations at the 95% confidence level is depicted in Figure 2D. It is based on 250 random data sets per noise level. Figure 2D shows that noises with standard deviations of 10, 25, and 50% of the amplitude give rise to periods with ±0.170, 0.425, and 0.850 h of error about the correct period of 24 h, respectively, and phases with ±0.213, 0.532, and 1.065 h of error about the correct phase of 12 h, respectively. We repeated the analysis with five full cycles, which represents a more typical data set obtained from the phototaxis machine. The same levels of noise then give rise to periods with ±0.071, 0.178, and 0.356 h of error about the correct period, respectively, and phases with ±0.172, 0.429, and 0.858 h of error about the correct phase, respectively. Interestingly, increasing the cycle number from 3 to 5 will increase the accuracy of period determination considerably but does not increase the accuracy of phase determination to the same extent. In general, our results indicate that noises of perhaps up to 25% will give a reasonably accurate determination of period and phase, but that rhythms with a higher noise level should be avoided. The circadian rhythms of phototaxis actually measured by our machine generally show levels of noise that are much below the 25% (compare Fig. 1 and Fig. 2B). Since the dampening in our original data is accounted for in our algorithm and therefore does not contribute significantly to possible inaccuracies in period and phase determinations, we conclude that our algorithm is very robust towards the noise in our original data.

Fig. 1.

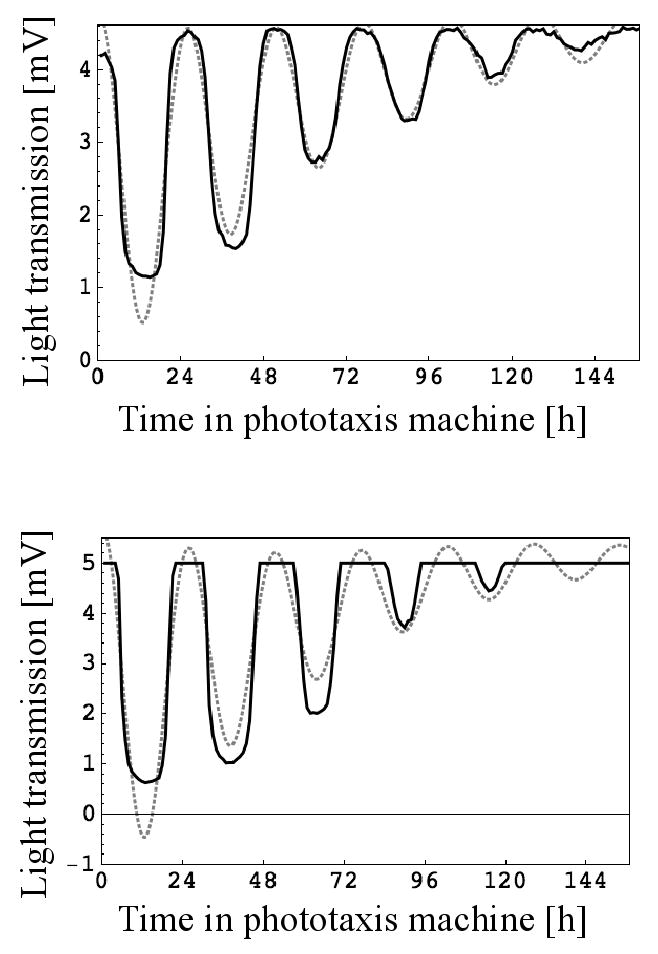
Examples for circadian rhythms of phototaxis as monitored by the machine and their analysis. Every hour a test light beam came on for 15 min and light transmission data were collected every minute. Cultures were kept in photoautotrophic medium with dark conditions between test light cycles. In each graph, the transmission data collected 11 min into the test light cycle are plotted as a solid black line and the model of the data created by the algorithm as a dotted gray line. For each graph, the first seven hours of data collection were omitted for optimal analysis. Upper panel: “Normal” rhythm with the light intensity always within the range of the light sensor. Lower panel: “Cut-off” rhythm because the light intensity is beyond the range of the light sensor during times of low phototactic activity.

Fig. 2.

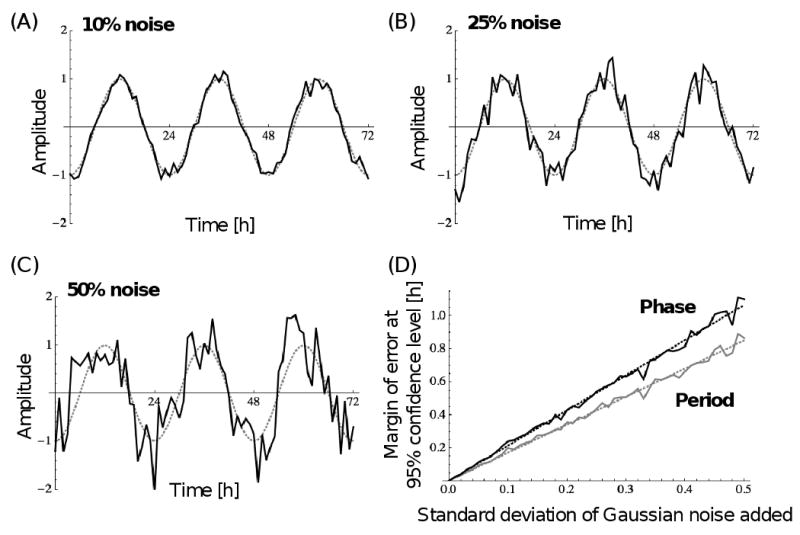
Robustness of the algorithm towards noise. (A) Example graph of an ideal sinusoidal curve with 24 h period and amplitude of 1 (dotted gray line), from which hourly points were sampled and random variables added to the amplitude (solid black line), whose mean is zero and whose standard deviation is 0.1 or 10%. (B) Same as in (A) except that the standard deviation of the random variables is 0.25 or 25%. (C) Same as in (A) except that the standard deviation of the random variables is 0.5 or 50%. (D) Margin of error at the 95% confidence level for the period (gray) and phase (black) for various standard deviations of the random variables. Data were derived from 250 random data sets per standard deviation. Standard deviations were evaluated at 0.01 intervals. Each dotted line represents the linear least-squares fit.

We decided to construct our own algorithm for the analysis of the phototaxis data because none of the existing algorithms met our specific needs. The algorithms developed some time ago for the analysis of circadian phototaxis data [8, 13] only take into account a limited number of the data points collected during each cycle. The algorithms developed for circadian bioluminescence data [17, 18, 21] would have been more appropriate for our data, since they were designed for the analysis of prolonged rhythms. This is not the case for the algorithms to analyze microarray data [5, 12, 20, 23, 25], which were developed for the very limited number of cycles and data points necessarily connected with this technique and whose primary function is to evaluate whether a circadian rhythm is present or not. However, even the algorithms for analysis of bioluminescence data were not optimal for our data, since they do not include the 3 characteristics that together make our algorithm particularly fitting. These 3 characteristics are as follows: (1) Detrending of our data is accomplished with a quadratic polynomial rather than just a linear polynomial to allow for a better fit of the periodic components of the data. (2) Because we are interested in the most accurate period and phase determination from the data, and not in reproducing the general shape of the period components, our model of the data only uses a single sinusoidal component. (3) Because the amplitude of the periodic components of our data gets smaller over time, our model cosine curve includes an exponential decay factor in the amplitude. We find no other algorithm that allows for characteristic 1 and particularly characteristic 3 in its model.

The algorithm we developed can also be used for the analysis of other circadian rhythms such as bioluminescence rhythms of luciferase reporters or RNA and protein rhythms from northern and western blots.

2.2 Effect of data range variability on algorithm

Step (1) in our algorithm for rhythm data analysis is the only step that involves the subjectivity of the experimenter. In this step, the valid data range is set manually. It allows the exclusion of phototaxis data at the start of the measurement if they appear noisy and at its end when the rhythm has ceased. We therefore analyzed the impact that the choice of different ranges has on the calculated period and phase using analysis of variance and Tukey multiple range test (α=0.05).

Based on a data set of 58 replicate samples, we first analyzed various starting times with a fixed ending time of 136 hours or about 5.25 cycles into the measurements (Fig. 3, upper panel). We found that there was a significant difference in period but not phase when the analysis included the first 3 hours of the measurement compared to when they were omitted. This difference indicates that there is a short time after the samples have been placed in the phototaxis machine during which the cultures adjust to the new condition of having their phototaxis tested at regular intervals. There was no significant difference in either period or phase when the starting time for the analysis was varied between 4 and 39 hours into the measurements. Only when the first 46 hours or more were omitted from the analysis was there again a significant difference in period but not phase. The failure to detect a significant difference in phase for the latter conditions is most likely due to the large variability among the replicates, since the standard deviation rose abruptly to ∼5 circadian time (CT) units when the 46 h threshold was reached (see Fig. 3). The phase of a rhythm is commonly expressed in CT units rather than in absolute hours. A CT unit is equivalent to 1/24^th of the free-running period. It generally allows for a better comparison of phases between rhythms that differ in their free-running period. For analysis of the impact of the ending time, we used a fixed starting time of 20 h into the measurements (Fig. 3, lower panel). We found that there was no significant difference in period or phase when the ending time was varied between 97 and 142 hours into the measurements at quarter period intervals. Since a few of the replicates showed a “cut-off” rhythm (see below) and some others might not be considered optimal rhythms, we repeated our analysis by including only the 40 best of the 58 replicates and found the exact same significant and non-significant differences.

Fig. 3.

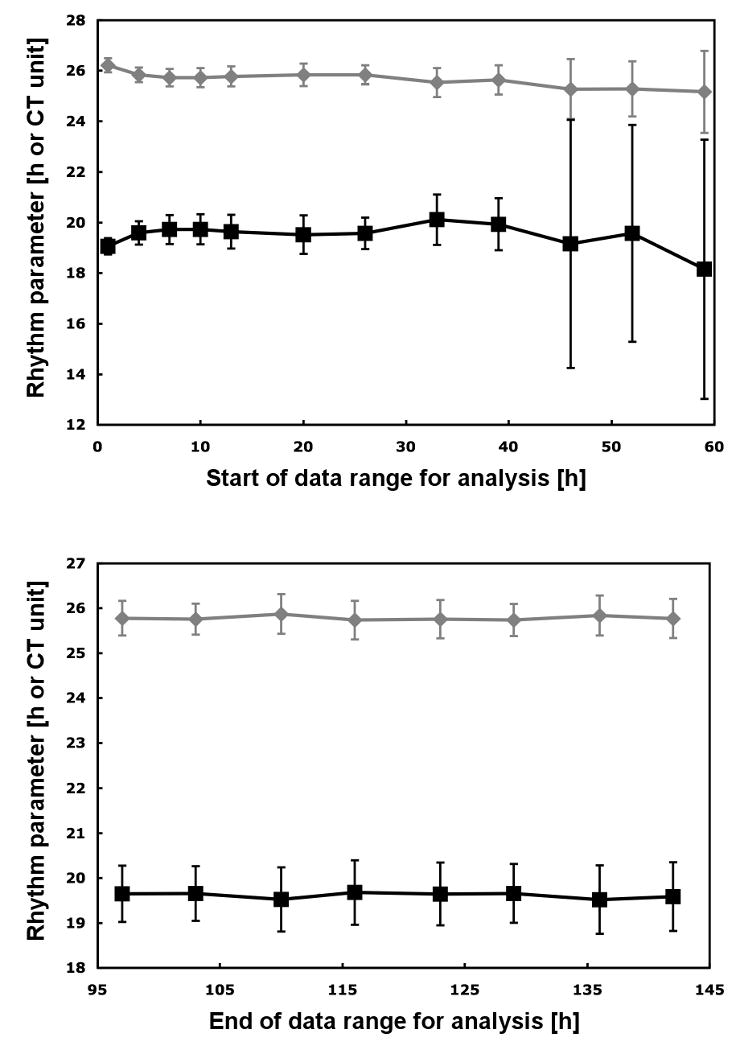
Rhythm parameters calculated by the algorithm based on various ranges of the raw data. The period (in h) is shown in gray with diamond symbols and the phase (in CT units) in black with square symbols. Upper panel: Various starting times with a fixed ending time of 136 hours or about 5.25 cycles into the measurements. Lower panel: Various ending times with a fixed starting time of 20 h into the measurement. All period and phase values represent the average of 58 replicate rhythms. Bars indicate the standard deviation.

We therefore conclude that choosing an appropriate start of the data range for the analysis is crucial but choosing an appropriate end is not. However, there is also quite a broad window at the start of the data range where different starting times yield nearly identical results. For example, for the starting times between 7 and 26 hours into the measurement the difference in period has a mean of only 0.05 ±0.02 h for the 58 replicates. The respective difference in phase has a mean of only 0.07 ±0.04 CT units. The standard deviation for this range of starting times is also nearly identical with a mean of 0.39 ±0.04 h for the period and 0.64 ±0.08 CT units for the phase.

2.3 Effect of channel position on rhythms

We tested whether all channels in the phototaxis machine give rise to rhythms with the same period and phase or whether differences between channels, due to possible differences in environmental conditions, cause detectable differences in these rhythm parameters. We conducted three independent experiments, in which aliquots of the same culture were placed into each of 59 channels. The individual experiments differed slightly from each other. The average period for each experiment was 25.92, 25.80, and 25.77 h with a standard deviation of 0.32, 0.29, and 0.34 h, respectively, and the average phase was 20.35, 20.66, and 20.61 CT units with a standard deviation of 0.45, 0.66, and 0.60 CT units, respectively. However, analysis of variance revealed no significant difference for either the period or the phase between individual channels even when the data were normalized (see materials and methods). This indicates that the conditions in the phototaxis machine are fairly similar between the channels.

2.4 Effect of truncated or “cut-off” rhythms on algorithm performance

Although we optimized the amount of neutral density filter between the test light LEDs and the cultures to bring the intensity of the test light beam into the range of the light sensor, truncated or “cut-off” rhythms may sometimes be measured (Fig. 1, lower panel). These come about when the light intensity of the test beam is saturating the light sensor and reductions in light transmission due to accumulation of cells in the beam during times of low phototactic activity are not recorded. We tested the effect of cut-off truncation on the ability of our algorithm to calculate period and phase for aliquots of the same culture. The analysis is based on three independent experiments with 3, 9, and 13 cut-off rhythms versus 52, 45, and 41 normal rhythms, respectively. The average period and phase calculated for the cut-off versus the normal rhythms differed only slightly. The difference was 0.11, 0.30, and 0.09 h for the period and 0.01, 0.02, and 0.00 CT units for the phase, respectively, in the three independent experiments. The standard deviations of the 6 groups (3 cut-off and 3 normal) were also similar with an average of 0.26 ±0.05 h for the period and 0.51 ±0.12 CT units for the phase. However, when using analysis of variance and Tukey multiple range test (α=0.05), we found a significant difference in period but not phase for the cut-off versus the normal rhythms. In general, our results suggest that cutoff truncation of a rhythm significantly influences its analysis by our algorithm but also that the period and phase values calculated from such a rhythm are still very close to those from a rhythm without cut-off. As a consequence, analysis results from cut-off rhythms should be treated with caution and only used as a first estimate.

2.5 Phase variability based on time cultures are put into phototaxis machine

Kondo and coworkers [8] demonstrated that simply placing the cell wall deficient strain of C. reinhardtii (CW15) into their phototaxis machine could lead to a phase shift. This is obviously problematic when performing experiments designed to determine phase shifts upon light pulses. We tested whether an experimental design could be developed that would prevent phase shifts caused by placing the cultures into the machine. Accordingly, we monitored circadian rhythms of phototaxis without background light between test light cycles. We were able to do this by choosing strain CC124. This strain shows an acceptable circadian rhythm of phototaxis even without background light (Fig. 1), which is not the case for strain CW15. We also avoided as much as possible exciting other photoreceptors besides the ones involved in phototaxis when monitoring the circadian phototaxis rhythm by using narrow wavelength LEDs for the dim test light beams. Sineshchekov and coworkers [22] demonstrated that phototaxis in C. reinhardtii is mediated by the two rhodopsin photoreceptors CSRA and CSRB, which show maximal sensitivity in producing receptor currents at 510 nm and 470 nm, respectively. The dim test light beams in our phototaxis machine originate from LEDs with a maximum at 507 nm and a full width at half maximum of 30 nm.

The upper panel in Figure 4 demonstrates that culture aliquots placed into the phototaxis machine at different times during the 12 h dark phase show period and phase changes of their rhythms that are close to zero. The data are based on three independent experiments with triplicates for each time point per experiment. Analysis of variance revealed that there is no significant difference in period or phase between any of the time points. Furthermore, if compared to cultures that received a 30 min white light pulse of 2.18 μmol photons m^-2 s^-1 at various times during their 12 h dark phase (Fig. 4, lower panel), there is a significant difference in phase change between most of these cultures and the cultures that were placed into the machine at different times (the ones depicted in Fig. 4, upper panel). Statistical significance was evaluated using analysis of variance and Tukey multiple range test (α=0.05). In conclusion, our results suggest that the phase shifts determined after a light pulse are solely due to the light pulse and not a combination of the light pulse and the placement of the culture into the phototaxis machine. Our results also suggest that significant phase shifts can be induced with low intensity light pulses.

Fig. 4.

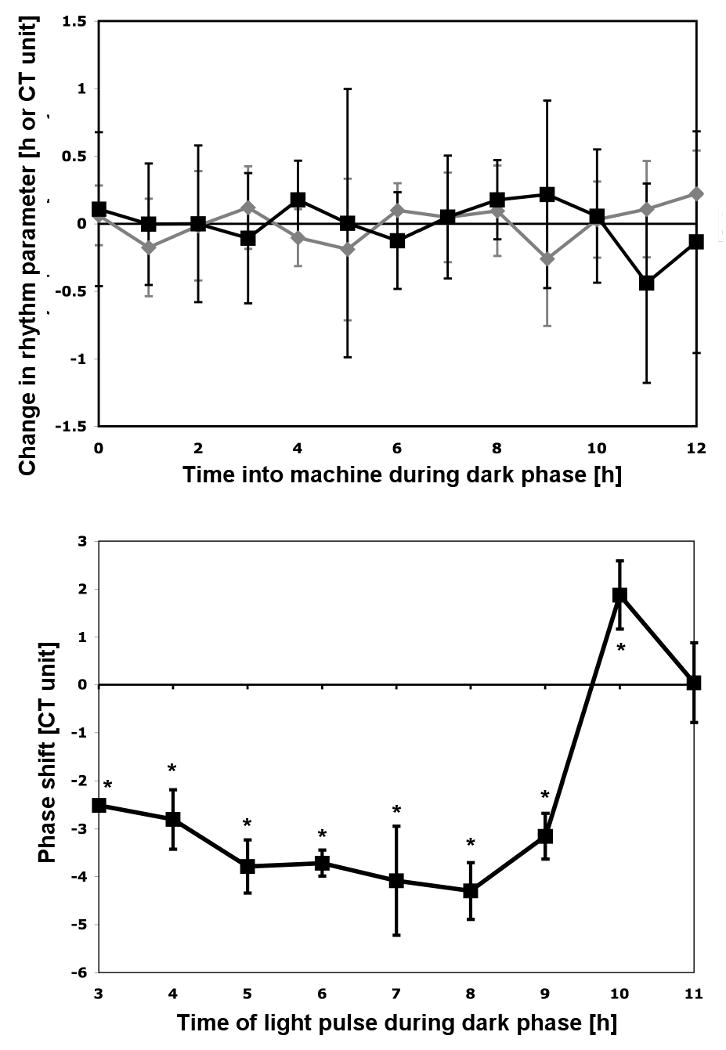
Effect of the time a culture is placed into the monitoring machine on period and phase and the statistical relationship to phase shifts upon light pulses. Upper panel: Aliquots of a culture were put into a dark box at the end of the light phase and placed into the phototaxis machine at the indicated times. Period (gray) and phase (black) changes are plotted with respect to the average of the parameter over all time points. The data in the graph represent the mean of three independent experiments with triplicates for each. Bars indicate the standard deviation derived from all 9 measurements for each time point. Lower panel: Phase response curve for comparison. Aliquoted cultures received a 30 min white light pulse of 2.18 μmol photons m^-2 sec^-1 starting at the indicated times. All cultures were placed into the machine at 12 h into the dark phase. The data in the graph represent the mean and standard deviation of the following number of independent experiments: 4 for 8 h into the dark phase, 3 for 4, 6, 7, and 9 h into the dark phase, 2 for 5, 10, and 11 h into the dark phase, 1 for 3 h into the dark phase. * indicates that these phase shifts are significantly different from the phase changes due to placing the cultures into the machine at various times during the dark phase from the upper panel according to analysis of variance and Tukey multiple range test (α=0.05).

In consequence, our machine and algorithm can now be used for a variety of circadian clock experiments that require unambiguous period and phase determinations. These experiments are not limited to determining phase shifts upon light pulses but may generally involve the study of the pacemaker or the resetting mechanism of the circadian clock through environmental, chemical or genetic manipulations. Similar to the plant model Arabidopsis, the advantage of C. reinhardtii as a model is that automated monitoring has been developed not only for circadian rhythms in bioluminescence based on the reporter gene luciferase [11, 15] but also for a physiological rhythm, which does not require strains that were genetically manipulated to express a reporter gene [2]. This rhythm is that of leaf movement in Arabidopsis [3] and that of phototaxis in C. reinhardtii.

3. Conclusions

We have shown that the machine we constructed is well suited for automated monitoring of circadian phototaxis rhythms exhibited by the model organism Chlamydomonas reinhardtii. We also demonstrated that the algorithm we designed for analyzing the data is robust. There is no difference in rhythm characteristics recorded by different channels of the machine, but if a rhythm shows truncation of its maxima or minima due to sensor limitations, the algorithm is significantly affected. A guideline for optimal analysis under our conditions is to include as many valid cycles of the data as possible but at a minimum 3 full cycles and to set the start of the data range for the analysis anywhere between 7 to 26 h into the phototaxis measurements. This guideline might have to be adjusted, if a different strain or species is analyzed. Most importantly, we succeeded in developing an experimental design based on the phototaxis machine and the algorithm that allows the determination of circadian clock resetting by light pulses without interference from placing the cultures into the machine. This will provide a basis for the analysis of mutant strains defective in the expression of particular photoreceptors and therefore an unambiguous experimental approach for determining the photoreceptor(s) that resets the circadian clock in C. reinhardtii. However, the machine and the algorithm will also enable the study of many other aspects of the circadian clock in C. reinhardtii.

4. Materials and methods

4.1 Strain and growth conditions

Chlamydomonas reinhardtii strain CC124 (137c mt^-) was obtained from Christoph Beck (Albert-Ludwig University, Freiburg, Germany) and used in this study. The strain is also available from the Chlamydomonas Center (Duke University, Durham, NC, USA). Cells were grown photoautotrophically in 0.3 HSM [6] in a light-proof, temperature-controlled incubator (818, Precision). Cells were inoculated from liquid stock into 1 L bottles containing 1 L 0.3 HSM at a concentration of 10⁴ cells/mL. Cultures were aerated with an aquarium pump and grown at 20°C under 12 h light/12 h dark cycles. Light was provided from plant & aquarium fluorescent bulbs (F20T12-PL/AQ wide spectrum, General Electric) from opposite sides with an intensity of 83 μmol photons m^-2 s^-1 per side. For experiments involving the manipulation of cultures during the dark phase, the light/dark cycle was set so that the dark phase coincided with the workday. When cultures reached late log phase of about 1×10⁶ cells/mL after having been exposed to at least 4 light/dark cycles, 3 ml aliquots in 35 mm diameter petri dishes were either placed directly into the phototaxis machine or placed into a dark box at the end of the last light phase. Cell concentrations were determined with a hemacytometer [6] and light-tightness of the incubator and dark box was confirmed with x-ray film.

4.2 Application of light pulses

Light pulses were applied from an Oriel 150 W solar simulator (Spectra-Physics) with a 420-630 nm dichroic cold mirror, which reflected only the visible portion of the light onto the culture sample. Before the collimated light beam reached the culture, it passed through a series of seven beamsplitters (Melles Griot Optics Group) and a 30° diffuser (Edmund Optics) reducing the light intensity to 2.18 μmol photons m^-2 s^-1. Culture samples were removed from the dark box, exposed to the light pulse for 30 min starting at the indicated times, and put back into the dark box. Finally, all cultures including the controls that did not receive a light pulse were placed into the phototaxis machine 12 h after the lights went off. All manipulations before and after the light pulse were carried out in complete darkness.

4.3 Construction of the phototaxis machine

The apparatus for assaying the phototaxis rhythm of C. reinhardtii represents a modification from the one described by Kondo and coworkers [8]. A partial illustration of the set-up is depicted in Figure 5. Two 28 × 38 cm black plastic plates of 1 cm thickness (F in Fig. 5) were each counter bored to securely fit 30 petri dishes of 35 mm diameter and 10 mm height (Corning) containing 3 ml culture aliquots. The counter bored holes (D in Fig. 5) are arranged in six rows of five holes at 5 cm distance from each other. The 0.2 cm thick bottom of each hole contains a 3 mm diameter hole in its center for the test light beam (E in Fig. 5). A 45 × 45 × 20 cm metal test chamber box was constructed for each plate so that the plate can be slid into the box from the front much like a drawer. The boxes are temperature controlled via an external circulating water bath and heat exchanger coils as well as light proof as confirmed with x-ray film. The boxes also contain circuit boards with light sensors, test lights, white background lights, and temperature sensors. When a plate is inserted into its test chamber box, each culture dish aligns with a test light below and light sensor above (Fig. 5). An LED with a maximum at 507 nm and a full width at half maximum of 30 nm (RL5-A7032, Super Bright LEDs, K in Fig. 5) provides the test light from below each culture through the 3 mm diameter hole. The transmission intensity of this light beam is detected by a solid state light sensor (TSL257, Taos, A in Fig. 5) centered above each culture dish. Permanently installed neutral density filters placed in the counter bored holes below the culture dishes bring the maximum intensity of the test light beam into the operating range of the light sensor. Each light sensor produces a DC voltage (0-5vdc) proportional to the intensity of light it receives. These 60 light sensor output voltages are recorded as 60 channels with a data acquisition module (PCI-6225, National Instruments) and are stored in data files on the controlling computer system.

Fig. 5.

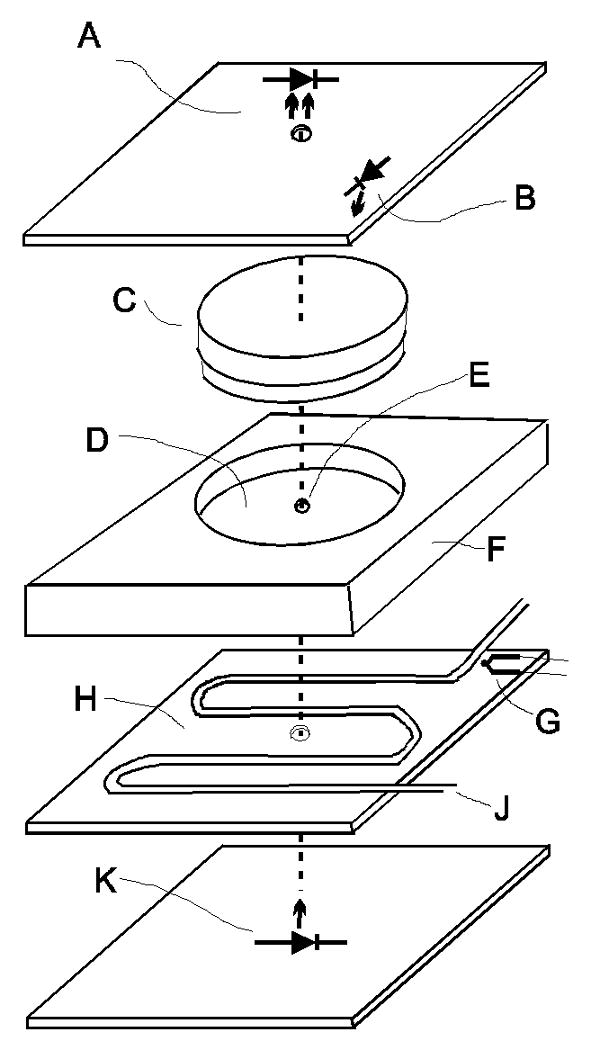
Break-out illustration of the phototaxis machine setup showing one test cell. (A) Light sensor. (B) White LED for background light. (C) Petri dish (35 mm × 10 mm) with culture. (D) Counter bored hole for the petri dish with neutral density filter in the bottom. (E) 3 mm hole for test light beam. (F) Block of black plastic. (G) K-type thermocouple. (H) Heat exchanger consisting of a brass plate with copper coils. (J) Water from a circulating water bath. (K) Blue-green (507 nm) LED for test light.

In each test chamber box, twenty white light LEDs (RL5-W45-360, Super Bright LEDs, B in Fig. 5) are arranged above the culture board at the intersection of four cultures for possible background illumination between test light cycles. The temperature is kept constant by a circulating water bath (Isotemp 3016D, Fisher Scientific) that pumps water through copper coils inside each test chamber box (J in Fig. 5). A temperature sensor (K-type, Omega, G in Fig. 5) contacts the bottom of the sample plates in each test chamber. This allows for automated real time monitoring and recording of the temperature to verify constant conditions. Temperature data are acquired with a thermocouple input module (USB-9211, National Instruments). The two test chamber boxes are stacked on a shaker table (6000, Eberbach). The shaker speed is manually set at a point to maximize redistribution of the sample at the end of each test light cycle but below the point of causing spillage. All of the functions of lighting, timing, shaking, and recording of data is accomplished with a custom designed software program written with LABVIEW that operates under Windows on a dedicated PC. The software controls relays in a custom designed external electronics interface box that in turn controls the on-off status of components such as lights and shaker. The software program menu allows the user great flexibility in the control and timing of test parameters. The software controls the timing of the test light cycles, shaking times and duration, white light timing, monitors temperature, and records data at user-defined intervals.

We confirmed that the background illumination in our machine was not too bright to dampen the phototaxis rhythm by creating a light intensity gradient in one of the two boxes by entirely turning off three of the four rows of background LEDs. This did not increase the duration of the rhythm for strain CC124 nor for strain CW15 (Chlamydomonas Center) when background illumination was supplied for the entire 45 min between each test light cycle.

For all experiments described here, the test light beam was set to come on every hour for 15 min with light transmission readings taken every minute. All analyses of circadian rhythms data reported are based on the light transmission reading obtained 11 min into the test light cycle.

4.4 Algorithm for rhythm data analysis

Period and phase data were generated using an algorithm in Mathematica™ that produces a model of the raw data through the following steps:

1. The experimenter determines the valid data range to give the original data for the analysis. This step allows the exclusion of raw data at the beginning and at the end of the measurement period. The valid data range is determined only once for a particular experiment and applied to all rhythms that were measured simultaneously.

2. The algorithm finds a least-squares quadratic fit to each data set in the form of

   $$f\left(x\right)=a{x}^2+bx+c.$$

3. The algorithm subtracts the quadratic fit from the data so that they oscillate around the horizontal axis.

4. The algorithm takes the discrete Fourier transform of the adjusted data to determine the dominant frequency. This provides an “acceptable” window of periods for a least-square fit to a sinusoid.

5. The algorithm fits the adjusted data to the model

   $$g\left(t\right)=k{e}^{-rt}cos\left[\frac{2\pi }{p}\left(t-n\right)\right]$$

   by solving for k, n, p, and r to minimize

   $$\sum {\left(\text{adjusted data}\left(t\right)-g\left(t\right)\right)}^2.$$

6. The algorithm minimizes a second time by fitting the original data to the model

   $$h\left(t\right)=a{t}^2+bt+c+k{e}^{-rt}cos\left[\frac{2\pi }{p}\left(t-n\right)\right]$$

   while solving for a, b, c, k, n, p, and r within the constrains set in step 2 and 5. The constraints for a, b, c, and r are set to between -0.5 and 2.5 times the previous value, for k to between 0 and 2 times the previous value, for n to between −π and +π of the previous value, and for p to between 0.5 and 1.5 times the previous value. In each cosine equation of step 5 and 6, p represents the period, and the phase is given in absolute hours by $\frac{\mathit{\text{pn}}}{2\pi }$ or in CT units by $\frac{\mathbf{24}\mathit{n}}{2\pi }$.

7. The algorithm generates a table with the period and phase (in CT units) of each data set as determined from the model in step 6 together with the correlation coefficient.

8. The algorithm expresses the phase with respect to a time chosen by the experimenter prior to or after the start of the data range used for the analysis. Thus, the phase can be expressed with respect to the time a light pulse was given. This is important, since a light pulse can change the period as well as the phase of the rhythm in phototaxis.

9. In order to allow the experimenter to visually inspect how well the model fits the original data, the algorithm generates a graph of the model from step 6 together with the original data. In addition, it generates a graph of the original data versus the model data, which if identical will fall on a straight-line diagonal.

The algorithm considers a single data point per test light cycle for the analysis of a rhythm. The phototaxis machine, however, is capable of collecting data points at any time interval during a test light beam. For example, it can be set to collect data points every minute within each test light cycle of 15 min. To obtain rhythm characteristics from different data points, the algorithm can be set to analyze a data point range within a test light cycle. It then executes the analysis for each data point separately as described and compiles the period, phase, and correlation coefficient results in a table. It further calculates the mean of period and phase for each channel with standard deviation and compiles it in a separate table. Since this kind of analysis requires either more time or greater processing capacity, the algorithm has a default setting to execute the analysis in a parallelized fashion, if parallel processing is available.

The Mathematica™ program for the algorithm is available from the corresponding author. Raw data can be imported in form of custom-formatted .lvm files from Labview and visualized through a graphic function of the program.

4.5 Virtual rhythm data with various noises

In order to test our algorithm in handling noisy data, we created virtual rhythms with various degrees of noise. We started with a data set of 73 points sampled from the sinusoidal curve

$$cos\left(\frac{2\pi }{24}t-\pi \right),$$

which has a period of 24 hours and a phase of 12 hours, at the values t = 0, 1,….., 72 hours. This is consistent with the hourly samples typically collected by the phototaxis machine. We then added to the data set random variables that are normally distributed with mean μ= 0 and standard deviation σ, where σ is the decimal equivalent of a percentage of the amplitude of the rhythm, which is 1. Figure 2 shows three example rhythms where the random variable added to the amplitude has a standard deviation of 0.1 or 10%, 0.25 or 25%, and 0.5 or 50%. For each value of σ = 0.01, 0.02,….., 0.5, we generated 250 data sets that were fed into the algorithm to calculate period and phase. These 250 results for period and phase for each value of σ are themselves independently normally distributed, with means roughly 24 and 12 hours, respectively. We calculated the width of a 95% confidence window for both the period and phase by calculating the value k such that

$$\frac{1}{\sqrt{2\pi }s}{\int }_{24-k}^{24+k}{e}^{-\frac{{\left(x-\overline{x}\right)}^2}{2s^2}}dx=0.95,$$

where x̄ is the mean of the answers for the 250 trials and s is the standard deviation of the trial results, calculated separately for both the period and the phase. We also performed the entire procedure by sampling 121 hourly points or five full cycles.

4.6 Statistical analysis

Analysis of variance and the Tukey multiple range tests were performed with the ANOVA package in Mathematica™ at a significance level of α = 0.05. Prior to analysis, the data of each experiment were normalized so that the average was equal to zero for both the period and phase in order to allow for a more valid comparison between experiments.

Abbreviations

CT unit

circadian time unit or 1/24^th of a circadian rhythm's free-running period