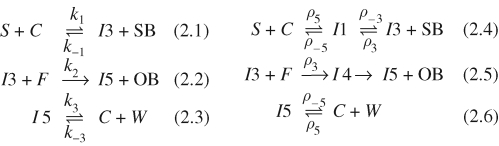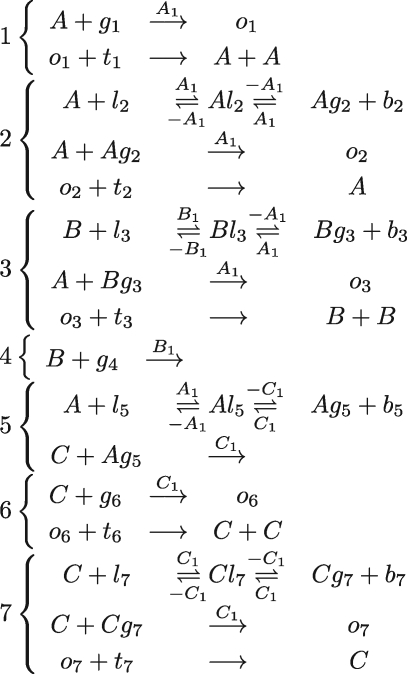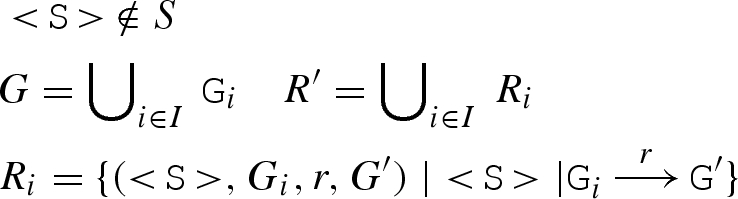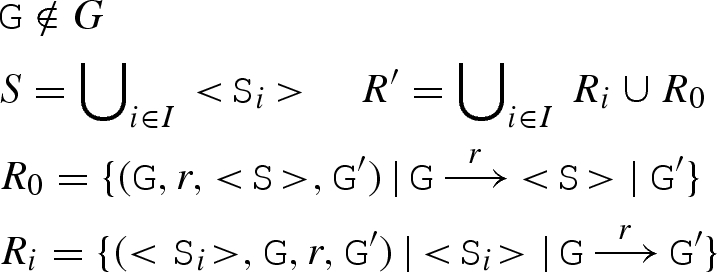A programming language for composable DNA circuits

Abstract

Recently, a range of information-processing circuits have been implemented in DNA by using strand displacement as their main computational mechanism. Examples include digital logic circuits and catalytic signal amplification circuits that function as efficient molecular detectors. As new paradigms for DNA computation emerge, the development of corresponding languages and tools for these paradigms will help to facilitate the design of DNA circuits and their automatic compilation to nucleotide sequences. We present a programming language for designing and simulating DNA circuits in which strand displacement is the main computational mechanism. The language includes basic elements of sequence domains, toeholds and branch migration, and assumes that strands do not possess any secondary structure. The language is used to model and simulate a variety of circuits, including an entropy-driven catalytic gate, a simple gate motif for synthesizing large-scale circuits and a scheme for implementing an arbitrary system of chemical reactions. The language is a first step towards the design of modelling and simulation tools for DNA strand displacement, which complements the emergence of novel implementation strategies for DNA computing.

1. Introduction

Nucleic acids have a number of desirable properties for engineering artificial biochemical circuits. Their sequences can be precisely controlled in order to encode distinct signals while avoiding cross-talk between molecules, and Watson–Crick base pairing can be used to engineer interactions between specific molecules at well-defined rates. Previous efforts in designing biochemical circuits with DNA have tended to make use of additional restriction enzymes (Benenson et al. 2001, 2003), or structural features such as hairpins within the molecules to perform computation (Sakamoto et al. 2000; Benenson et al. 2004; Yin et al. 2008). While this allows the implementation of somewhat ingenious molecular devices (Yurke et al. 2000; Venkataraman et al. 2007), simpler designs have recently been proposed for the construction of large-scale, modular circuits. In particular, a range of information-processing circuits have recently been implemented in DNA by using strand displacement as the main chemical process to perform computation. Examples include various digital logic circuits (Seelig et al. 2006) together with catalytic signal amplification circuits that function as efficient molecular detectors (Zhang et al. 2007). The use of DNA strand displacement to perform computation enables the construction of simple, fast, modular composable and robust circuits, as demonstrated in Zhang et al. (2007).

A range of modelling approaches have also been developed for DNA computation (Paun et al. 1998). One example is sticker systems (Kari et al. 1998; Paun & Rozenberg 1998), which model the sticking together of DNA strands. Such operations can effectively model Adleman's experiment (Adleman 1994), in which DNA was used to compute a Hamiltonian path in a graph. Other examples include Watson–Crick automata, which are the automata counterpart to sticker systems, insertion–deletion systems, which contain operations for inserting and deleting DNA sequences, and splicing systems, which can be physically implemented with the help of restriction enzymes. A more recent review of modelling approaches is presented in Amos (2005), together with their corresponding physical implementations.

So far, however, DNA strand displacement operations have only been represented either by informal notations or by manually constructing a corresponding set of chemical reactions. Here, we investigate whether strand displacement can be used as the basis for a DNA programming language. The execution rules of the language correspond to interactions between physical DNA strands, while the kinetics of these rules correspond to the underlying kinetics of strand displacement.

We first present an overview of a programming language for DNA strand displacement, which includes basic elements of sequence domains, toeholds and branch migration. We also present an algorithm for automatically generating a set of chemical reactions from a given set of DNA molecules. We then use our language to model various practical and theoretical systems, including an entropy-driven catalytic gate (Zhang et al. 2007), a simple gate motif for synthesizing large-scale circuits (Qian & Winfree 2008) and a scheme for implementing an arbitrary system of chemical reactions (Soloveichik et al. 2008). More generally, the algorithm allows a given circuit design to be repeatedly modified and simulated in an iterative cycle, until it exhibits the desired behaviour. Inspired by the work of Yin et al. (2008), in the long term we envisage a language that can be used to program a range of DNA molecules, simulate their behaviour and then automatically generate the corresponding nucleic acid sequences, ready for synthesis.

2. Results

2.1. A language for DNA strand displacement

2.1.1. Simple examples

We present a language for DNA strand displacement by means of simple examples, together with their corresponding graphical representation. The design of the language is motivated by the assumptions outlined in Zhang et al. (2007). Examples of DNA molecules are presented below, where parallel composition (|) denotes the presence of multiple molecules next to each other.

The molecule 1 : 2 represents a lower strand of DNA, where the 3′ end of the strand is assumed to be on the left, as indicated by an arrowhead in the graphical representation. The strand is divided into domains, which correspond to short DNA sequences. The domains are represented by numbers 1 and 2, where each number represents a distinct domain. The DNA sequences of distinct domains are assumed to be sufficiently different that they do not interfere with each other. The red domain 1 represents a toehold domain, while the black domain 2 represents an ordinary specificity domain. The colour is merely an annotation, since the length of the domain sequence is sufficient to determine its type. Toehold domains are very short sequences, generally between 4 and 10 nucleotides in length, that enable one DNA strand to bind to another. Since the sequence is short, the two strands will quickly unbind from each other in the absence of further interaction along neighbouring domains. The molecule <1 2> represents an upper strand of DNA, where the 3′ end of the strand is assumed to be on the right. The strand consists of two domains that are complementary to domains 1 and 2, where two domains are complementary if their respective sequences are Watson–Crick complementary. We denote 1 : 2 as a lower strand and <1 2> as an upper strand in order to emphasize the complementarity between strands. Two complementary strands 1 : 2 and <1 2> can hybridize along their complementary domains to form a double-stranded molecule [1 2]. A molecule can also consist of multiple upper strands bound to a single lower strand. For example, [1 2]:[3 4] consists of upper strands <1 2> and <3 4> bound to a single lower strand 1:2:3:4. There can also be gaps between bound upper strands, as in the molecule [1 2]:3:[4 5], where domain 3 of the lower strand is unoccupied.

Bound upper strands can also overhang to the left or right, as shown below.

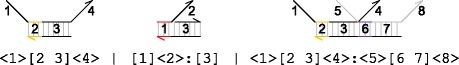The molecule <1>[2 3]<4> consists of an upper strand <1 2 3 4> bound to a lower strand 2:3. The region [2 3] of the molecule is double-stranded, while <1> and <4> represent single-stranded regions overhanging to the left and right. The molecule [1]<2>:[3] consists of an upper strand <1 2> bound to a molecule 1:[3], where the single-stranded region <2> is overhanging the double-stranded region [3]. Multiple overhanging strands can be bound simultaneously along different regions, as in the case of the molecule <1>[2 3]<4>:<5>[6 7]<8 > , which represents two upper strands, <1 2 3 4> and <5 6 7 8 > , bound along regions [2 3] and [6 7], respectively. Notice how the colon is used to separate the two bound upper strands. In general, the DNA molecules are assumed to have no additional secondary structure. This can be achieved by careful selection of appropriate DNA sequences, as discussed, for example, in Zhang et al. (2007).

We give examples of the main types of interactions that are possible between DNA molecules in the strand displacement language. The simplest example is of one strand binding to another, as shown below.

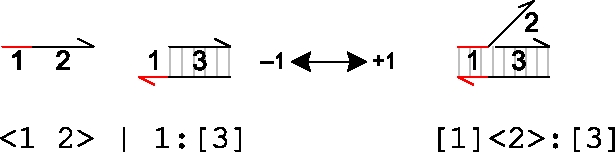An upper strand <1 2> can bind to a molecule 1:[3] on toehold domain 1, and the bound strand can subsequently unbind. The rates of binding and unbinding are determined by the sequence of the toehold domain 1 and are given by ρ₁ and ρ₋₁ which can be abbreviated to +1 and −1, respectively.

A given strand can also be displaced by another strand as a result of binding, as shown below.

Although toehold domains are short enough to unbind rapidly in the absence of additional specificity domains, they are still long enough to greatly accelerate the initiation of strand displacement when additional specificity domains are present. In the above example, when the strand <1 2> becomes bound, it initiates the displacement of its neighbouring strand by a process of branch migration. Although this process involves a random walk of multiple elementary steps, these are relatively fast at experimental concentrations and can be omitted (Zhang et al. 2007). This was previously demonstrated by Green & Tibbetts (1981) and Yurke & Mills (2003), who showed that strand displacement can be modelled as a second-order process over a wide range of experimental conditions. This means that the unbinding reaction on toehold domain 1 can be effectively ignored, and the two consecutive reactions can be approximated by a single displacement reaction with rate ρ₁ as follows.

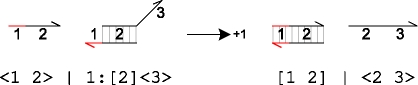Once bound, a given strand can also cause the toehold domain of a neighbouring strand to unbind, as shown below.

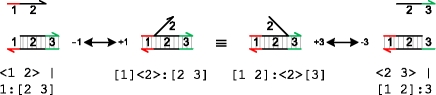A strand <1 2> can bind to a molecule 1:[2 3] on toehold domain 1, and then displace the bound domain 2 of its neighbouring strand by branch migration. This can result in the unbinding of the neighbouring strand on toehold domain 3. The reverse sequence of reactions can also occur. Since branch migration is very fast compared with binding and unbinding reactions, the two molecules [1]<2>:[2 3] and [1 2]:<2>[3] are considered equivalent. This is because the molecule will be constantly migrating back and forth between these two states, such that the states become indistinguishable from the point of view of the slower binding and unbinding reactions.

The strand displacement language also allows parametrized modules to be defined, as shown below.

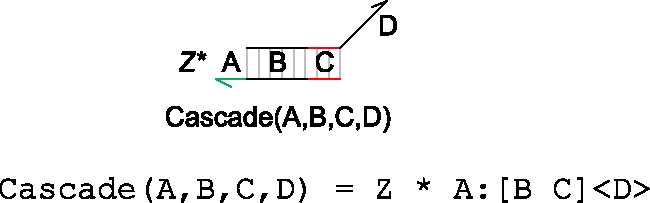A module is represented as a collection of one or more molecules enclosed in a box. In this example, the module consists of a population of molecules Z*A:[B C]<D > , where Z* denotes the number of copies of the molecule. The name of the module Cascade(A,B,C,D) is written along the bottom, where A,B,C,D represent parameters of the module. The parameters allow similar molecules to be constructed using different domains, as shown below.

The molecules represent the result of executing three separate instances of the module Cascade(A,B,C,D) with three different sets of parameters: Cascade(2,3,4,5), Cascade(4,5,6,7) and Cascade(5,6,7,8). In this example, a strand <1 2 3> will be able to displace a strand <3 4 5> from the first stage of the cascade, which will in turn displace a strand <5 6 7> from the second stage, which will then displace a strand <7 8 9> from the third and final stage. In general, modules allow parts of a program to be reused with different parameters, reducing code repetition and enabling more compact programs.

The language also allows local domains to be defined for a particular collection of molecules, as shown below.

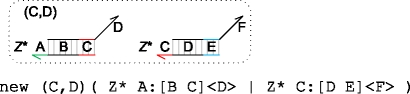Local domains are represented using the new keyword. Graphically, they are represented by placing a dotted line around the molecules, with the local domains in the top left corner. In this example, the domains (C,D) are local to molecules A:[B C]<D> and C:[D E]<F> . This guarantees that there can be no interference on domains C and D from any other molecules in the system, even if those molecules use the same names C or D. In practice, this is enforced by renaming the local domains C, D in the event of any clashes. The renaming is done prior to executing a given system of molecules. Local domains are particularly useful when building large programs from smaller building blocks, since they avoid having to manually check all the domains in a given program to ensure that there are no unintended clashes.

2.1.2. Main syntax and execution rules

In general, there are many possible configurations for individual DNA molecules, and many ways in which these molecules can interact with each other over time. We capture the set of possible molecular configurations and interactions by defining precise syntax and execution rules for the DNA strand displacement language. In this section, we present the main rules, together with their corresponding graphical representation. The complete set of rules is provided in §3.

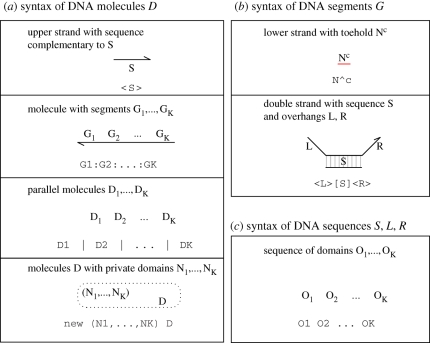
The syntax of the strand displacement language is presented in figure 1, in terms of DNA molecules D, molecule segments G and DNA sequences S, L, R. A sequence S consists of a series of domains O1 … OK, where a domain O can be a specificity domain N or a toehold domain N∧c with degree of matching c. N is a name or number representing a unique DNA sequence, where the sequence of toehold domains is assumed to be between 4 and 10 nucleotides in length. The degree of matching c allows different binding and unbinding rates to be implemented for different molecules that interact on the same toehold domain. The degree c is assumed to be greater than 0 and less than or equal to 1, where a sequence N∧1 with degree 1 is identical to the sequence N. Degrees of matching 1 can usually be omitted, where N∧1 is abbreviated to N. Small mismatches in sequence complementarity can significantly affect toehold binding and unbinding rates, while still avoiding interference with other toehold domains. Thus, the degree of matching can be used to modify the binding and unbinding rates of a given toehold. For example, a toehold <N∧1> will interact with toeholds N∧c1 and N∧c2 at different rates depending on the degrees of matching c1 and c2. If c1 < c2 < 1 then toehold <N∧1> will have a higher binding rate and a lower unbinding rate when interacting with N∧c2, compared with N∧c1. To simplify the syntax, we assume that all toeholds in upper strands have degree of matching 1. This avoids having to record the degree of matching for both upper and lower strands in a double-stranded molecule.

Figure 1.

Syntax of the strand displacement language, in terms of (a) DNA molecules D, (b) molecule segments G and (c) DNA sequences S, L, R. For each construct, the graphical representation at the top is equivalent to the program code at the bottom. Sequences S, L, R are composed of a series of domains O1 … OK, where a domain O can be a specificity domain N or a toehold domain N∧c with degree of matching c. We assume that all toeholds in upper strands have degree of matching 1.

A molecule D can be an upper strand <S> with a sequence complementary to S, or a molecule with segments G1: … :GK. A segment G can be a lower strand with toehold domain N∧c, or a double strand [S] with upper strands <L> and <R> overhanging to the left and right, respectively, written <L>[S]<R > . The syntax ensures that specificity domains on the lower strands are always occupied by an upper strand, such that only toehold domains on the lower strands can be unoccupied. This ensures that two single-stranded molecules can only interact with each other via complementary toehold domains, as described by Zhang et al. (2007).

Multiple DNA molecules can be present in parallel, written D1 | … | DK. We abbreviate K parallel copies of the same molecule D to K*D . Domains N1, … ,NK can also be restricted to molecules D, written new (N1, … , NK) D. This represents the assumption that the domains are not used by any other molecules apart from D. We also allow module definitions of the form X(m) = D, where m are the module parameters and X(n) represents an instance of the module D with parameters m replaced by n. We assume a fixed set of module definitions, which are declared at the start of the program.

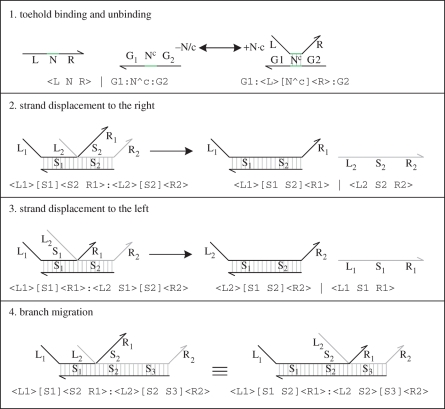
The main reduction and equivalence rules of the language are presented in figure 2. The reduction rules are of the form D → ^r D′, which means that D can reduce to D′ by a reaction with rate r. We write D ^r′ ↔ ^r D′ as an abbreviation for the two reductions D → ^r D′ and D′ → ^r′ D. We also write D → D′ as an abbreviation for a reduction that is effectively immediate.

Figure 2.

Reduction and branch migration rules of the strand displacement language. For each rule, the graphical representation at the top is equivalent to the program code at the bottom.

The first reduction rule models toehold binding and unbinding. Each toehold domain N is associated with corresponding binding and unbinding rates given by ρ_N and ρ_−N, which can be abbreviated to + N and − N, respectively. We multiply the binding rate by the degree of matching c of domain N and we divide the unbinding rate by this degree, since a low degree of matching between toehold sequences will result in slower binding and faster unbinding. In practice, the degree of matching c of a toehold N∧c can be determined by measuring the binding rate of N∧c to <N> and dividing by the binding rate of N∧1 to <N> . The next two rules model a strand being displaced from a molecule to the right and left. The reductions are immediate, since branch migration is considered to be much faster than toehold binding or unbinding. The fourth rule models equivalence of molecules up to branch migration. Since a given DNA molecule can rapidly sample its space of possible configurations by branch migration, the different configurations are considered to represent the same molecule.

We can use the reduction rules of the language to generate the set of all possible reactions for a given set of DNA molecules. Essentially, this is achieved by repeated application of the reduction rules to the molecules, where each application of a rule corresponds to a reaction. The rules are repeatedly applied until no new reactions are generated. The algorithm is presented in more detail in §3. The strand displacement language can be used to construct an initial set of DNA molecules, and then to determine automatically the set of all possible interactions between these molecules over time, together with their corresponding interaction rates. We illustrate the application of the strand displacement language to three main case studies.

2.2. Case study: entropy-driven catalytic gate

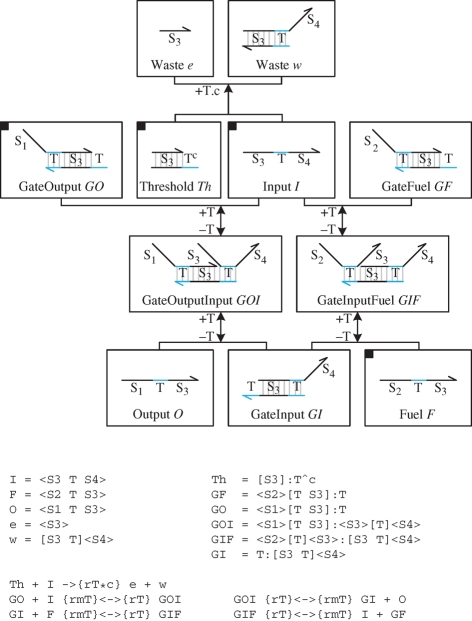
This case study uses the strand displacement language to implement an entropy-driven catalytic gate developed by Zhang et al. (2007). The gate enables key functions of signal amplification and circuit gain, which are essential for implementing large cascaded circuits in DNA. According to Zhang et al. (2007), the gate is substantially simpler, faster, better understood and more modular than previous DNA hybridization designs.

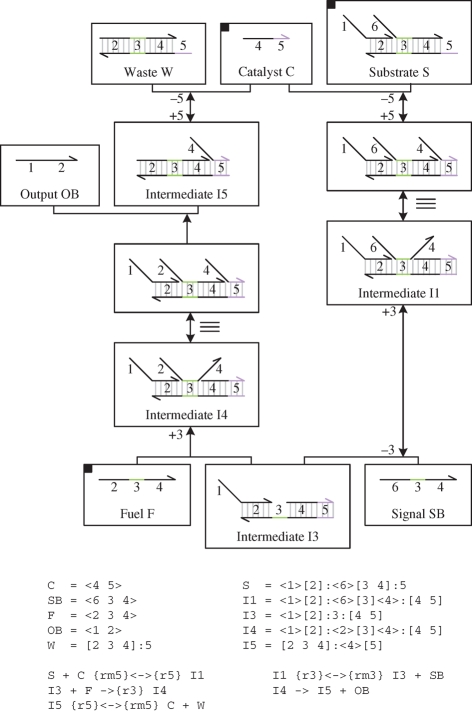
Figure 3 presents an implementation of the entropy-driven catalytic gate of Zhang et al. (2007) in the strand displacement language. The gate consists of initial concentrations of fuel, catalyst and substrate molecules. The full sets of species and reactions for the gate are presented in figure 4. These were compiled from the molecules of figure 3 using the algorithm described in §3. From the compiled reactions, we observe that Catalyst C binds to Substrate S, causing the release of Signal SB and Output OB in the presence of Fuel F. The same catalyst can be reused to drive the release of multiple signal and output strands, provided sufficient substrate and fuel molecules are present. Thus, the compiled reactions serve as an initial validation of the catalytic gate design.

Figure 3.

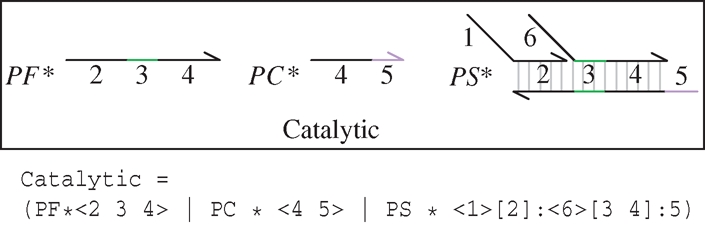
An implementation of the entropy-driven catalytic gate of Zhang et al. (2007) in the strand displacement language. The gate consists of Fuel <2 3 4> , Catalyst <4 5> and Substrate molecules <1>[2]:<6>[3 4]:5, at initial concentrations given by PF, PC and PS, respectively.

Figure 4.

Species and reactions for the entropy-driven catalytic gate of Zhang et al. (2007). Starting from the molecules of figure 3, the full set of species and reactions were compiled using the algorithm described in §3. Species are given unique identifiers to allow a more compact representation of reactions. Here the species identifiers were chosen to be the same as in Zhang et al. (2007).

Note that the compiled reactions of figure 4 differ from the manually defined reactions of Zhang et al. (2007). A comparison between the two sets of reactions is given in figure 5. A non-catalytic reaction 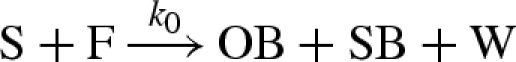as also given in Zhang et al. (2007), but the rate k₀ was considered to be negligible and can be effectively ignored. Both models also assume the presence of excess reporter molecules SR and OR, which detect the signals SB and OB, respectively, as follows:

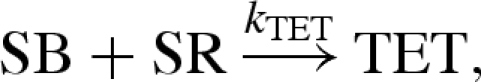2.7

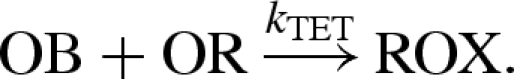2.8

The reporter SR binds to the signal SB causing the release of the green tetrachlorofluorescein (TET) fluorophore, while the reporter OR binds to the output OB causing the release of the red carboxy-Xrhodamine (ROX) fluorophore. Thus, the levels of green and red fluorescence can be used to measure the concentrations of signal and output strands, respectively.

Figure 5.

Comparison between the manually defined reactions of Zhang et al. (2007), shown on the left, and the compiled reactions of figure 4, shown on the right.

The remaining reactions in Zhang et al. (2007) assume that the binding rate for S and C is the same as the binding rate for C and W, since both reactions involve the same toehold sequence 5. Similarly, the binding rate for I3 and SB is assumed to be the same as the binding rate for I3 and F. Thus, k₁ = k₋₃ = ρ₅ and k₋₁ = k₂ = ρ₃. This is consistent with the reduction rules of the strand displacement language, which assume that interactions on the same toehold occur at the same rate.

For reaction (2.5), since strand displacement is assumed to be much faster than toehold unbinding, the unbinding reaction on toehold 3 is effectively ignored, which is consistent with reaction (2.2). This assumption was previously discussed in §2.1. For reaction (2.4), the original reactions ignored the formation of the intermediate complex I1, resulting in the approximation reaction (2.1). The toehold unbinding reaction ρ₋₃ is considered to be quite fast, since toehold 3 is deliberately shortened to accelerate strand unbinding. However, the original reactions do not explicitly take into account the constraints between ρ₋₃ and ρ₋₅. According to our reactions, the rate of unbinding of toehold 3 must be significantly faster than the rate of unbinding of toehold 5, and we can simulate the effects of different unbinding rates for these toeholds.

In figure 6, we simulate the system assuming that toehold 3 unbinds 10 times more quickly than toehold 5, and we compare this with the simulation of the original reactions presented in Zhang et al. (2007). Even with an order of magnitude difference, the effects on the system behaviour are still noticeable. The faster the unbinding rate for toehold 3, the closer the results to the original simulations (not shown). Thus, we can quantify the impact of toehold strengths on the overall system dynamics, prior to implementing the physical system in DNA. Note that the chemical reactions for the system were compiled directly from the DNA molecules themselves by application of the algorithm outlined in §3. This simplifies the process of evaluating new designs before their subsequent implementation. In the original experimental setup, the reaction rate k₃ = ρ₋₅ was difficult to measure, and was fit to the data. Even if we are unable to measure the exact rates experimentally, it is possible to ensure constraints between rates, such as ρ₋₃≫ρ₋₅, by choosing appropriate sequences for the corresponding toehold domains.

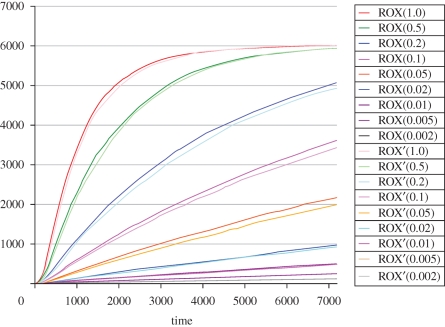
Figure 6.

Simulation results for the entropy-driven catalytic gate of figure 4, using reactions (2.4)–(2.8). The rates are taken from Zhang et al. (2007), with ρ₅ = 6.5 × 10⁵, ρ₃ = 4.2 × 10⁵, k_TET = 8 × 10⁵ and k_ROX = 4 × 10⁵ M⁻¹ s⁻¹, and with ρ₋₅ = 4 × 10⁻³ s⁻¹ and ρ₋₃ = 10 × ρ₋₅. Initial concentrations of S = C = 10 nM, F = 13 nM and OR = SR = 30 nM were used, where the concentration of C was varied by a factor of 1–0.002. The levels of ROX fluorescence (arbitrary units) were plotted over time (s) for different input concentrations of catalyst C. The simulation results for the reactions of Zhang et al. (2007) are represented on the same plot using dark colours, while the results from the reactions of figure 4 are shown in pale colours. The simulation results of both systems differ slightly, where the choice of rate constants is discussed in the main text.

2.3. Case study: gate motif for large-scale circuits

This case study uses the strand displacement language to implement a DNA gate motif developed by Qian & Winfree (2008). The motif was designed as a building block for synthesizing large-scale circuits involving potentially thousands of gates.

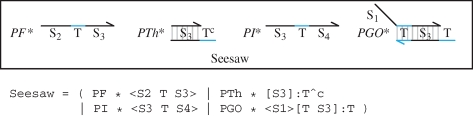
Figure 7 presents an implementation of the seesaw gate of Qian & Winfree (2008) in the strand displacement language. The gate is essentially a simplified version of the catalytic gate developed by Zhang et al. (2007). The main species and reactions for the gate are presented in figure 8. These were compiled from the molecules of figure 7 using the algorithm of §3. The compiled reactions are consistent with the manually defined reactions of Qian & Winfree (2008). From the compiled reactions, we observe that the Input I is neutralized by the Threshold Th. Once all the Threshold molecules are consumed, the Input can bind to the GateOutput GO, causing the release of the Output O. The Fuel F binds to the GateInput GI, causing the release of the Input I, which can be subsequently reused to catalyse the displacement of additional Output molecules.

Figure 7.

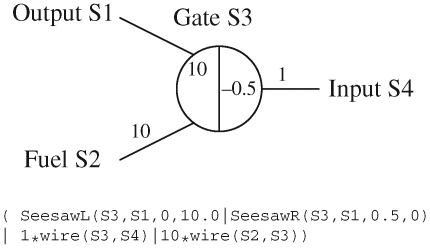
An implementation of the seesaw gate of Qian & Winfree (2008) in the strand displacement language. The gate consists of Fuel <S2 T S3> , Threshold [S3]:T∧c, Input <S3 T S4> and GateOutput molecules <S1>[T S3] : T, at initial concentrations given by PF, PTh, PI and PGO, respectively.

Figure 8.

Species and reactions for the seesaw gate of Qian & Winfree (2008). Starting from the molecules of figure 7, the set of species and reactions were compiled using the algorithm described in §3.

In addition to the reactions shown in figure 7, there are a number of spurious reactions between toehold domains. For example, the Input <S3 T S4> can interact with T:[S3 T]<S4> on toehold T. However, since there is a mismatch in the specificity domains of these molecules, they will immediately unbind. Although these reactions can potentially slow down the system, they will not result in major interferences. This illustrates an important principle when designing large-scale circuits: the same toehold domain can be reused in multiple reactions, provided the specificity domains are chosen accordingly. Toehold domains can bind and unbind repeatedly, but a displacement reaction can only progress if there is a subsequent match between the adjacent specificity domains. In the remainder of the paper we omit such spurious interactions on toehold domains.

An empty seesaw gate T:S3:T consists of a single domain S3 with toehold domains T to the left and right. The Input binds to the right toehold of the gate, while the Output and Fuel bind to the left toehold. The Input, Output and Fuel strands are defined as <S3 T S4 > , <S1 T S3> and <S2 T S3 > , respectively, and are termed wires, since they can each form a link between two gates. For example, the Input wire <S3 T S4> can form a link between gates T:S3:T and T:S4:T. The threshold molecules consume the Input, preventing it from binding to the main gate until all the threshold molecules are depleted. This acts to filter out low levels of input that could have been produced accidentally, such as those produced by a leaky circuit. In order to achieve this, the threshold gate is designed so that it binds to the input at a much faster rate than the main gate. In Qian & Winfree (2008), this is implemented by extending the binding region of the threshold toehold. Here, we implement the increased binding rate by increasing the degree of matching of the threshold toehold, so that it is significantly higher than the degree of matching of other toeholds. Although the maximum degree of matching is 1, in practice we can encode a degree of matching greater than 1 by lowering the degree of matching of all other toeholds.

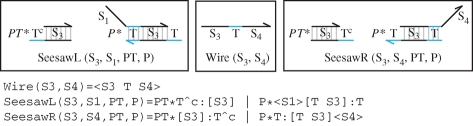
In general, each seesaw gate can interact with multiple wires to the left and right. We can model this by defining two modules, SeesawL and SeesawR, as shown in figure 9. The specificity domains of the gate and interacting wire are passed as parameters, together with the populations of the threshold gate and the initially bound wires. Figure 10 presents an instance of the seesaw gate of figure 7, using the more general modules of figure 9. A more abstract graphical representation of the gate is also given. Initial populations of Fuel, Input and Output wires are given by 10, 1 and 0, respectively. The populations are represented as numbers on the edges connected to the gate, where the absence of a number denotes a population of 0. There is also an initial population of 10 Output wires bound to the left side of the gate, assuming suitable population units. This is indicated by the number 10 inside the left half of the circle, next to the Output wire. There are no Fuel or Input wires bound to the gate, since there are no positive numbers inside the circle next to the Fuel or Input wires. The negative number −0.5 on the inside of the circle next to the Input wire indicates an initial population of 0.5 threshold gates. According to Qian & Winfree (2008), we assume that a given seesaw gate will not have both a population of bound wires and a population of threshold gates. Under these assumptions, a single integer can be used to represent both populations. If the integer is positive, then it represents the population of bound wires, and if it is negative, then its absolute value represents the population of threshold gates. For the program definition of our seesaw modules, rather than using a single integer, we use two positive numbers PT and P, with the additional constraint that both numbers cannot be greater than zero simultaneously.

Figure 9.

Generic modules for the seesaw gate of figure 7.

Figure 10.

An instance of the seesaw gate of figure 7, using the more general modules of figure 9. A more abstract graphical representation of the gate is also given.

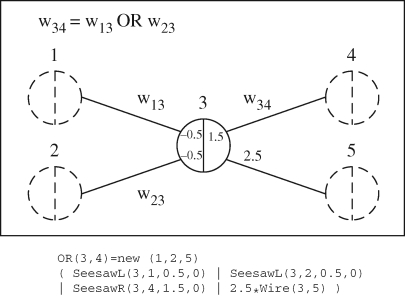
We can use these modules to implement the logical OR gate presented in Qian & Winfree (2008), as shown in figure 11. Gates with a dotted outline have a population of zero, and are not needed. They are mainly included to give a uniform representation. As a result, for the OR gate implementation only domains 3 and 4 need to be passed as parameters. The OR gate takes two wires that bind to the left of domain 3. Once one or both of these wires are present in sufficient numbers to consume all the threshold gates, they will displace the wire <3 T 4> that is bound on the right of domain 3. The fuel <3 T 5> ensures that the bound input wires are freed again from the gate 3. A module for the AND gate can also be defined, though its behaviour is more complicated (see Qian & Winfree 2008 for full details). Here we have shown how seesaw gate modules can be used to construct simple logic gate modules, which can in turn be used to construct complex logical circuits of arbitrary size.

Figure 11.

Example logical OR circuit made of seesaw gates. Signal concentrations below 0.1 are considered OFF, while signal concentrations above 0.9 are considered ON.

2.4. Case study: compiling chemical reactions to DNA

The previous case studies described how physical DNA systems can be represented as molecules in the strand displacement language. The molecules were then systematically translated to chemical reactions for simulation and analysis. This case study addresses the reverse question of how to translate an arbitrary set of chemical reactions to a set of DNA molecules, in order to derive systematically a physical DNA implementation. The question was previously addressed in Soloveichik et al. (2008) by translating a given set of chemical reactions to an extended set of reactions representing the implemented system. Here we present a translation from a set of chemical reactions directly to a set of DNA molecules. The extended set of reactions for these molecules is then derived automatically using the algorithm of §3.

We first illustrate the principle of the translation on a number of simple chemical reactions, using the approach presented in Soloveichik et al. (2008). Essentially, each chemical species X is associated with three distinct domains X1,X2,X3, where X1 and X3 are toeholds. The general form of a species X is given by <H X1 X2 X3> , where <X1 X2 X3> denotes the recognition region of the species, and <H> denotes the history region. We assume that members of the same species must all have the same recognition region, but can have different history regions.

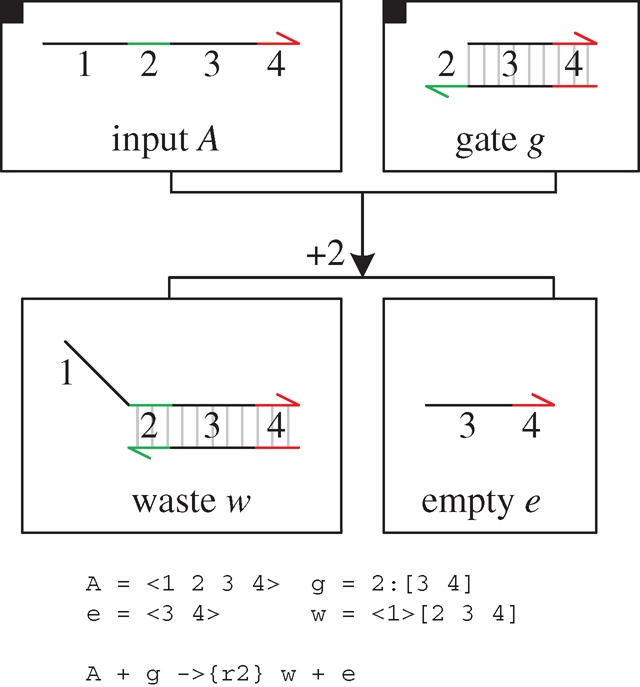
Figure 12 presents a DNA implementation of a degradation reaction 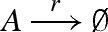, where species A is associated with the recognition region <2 3 4>. The reaction is implemented by a population of gates g, which transform a strand <1 2 3 4> into inert waste. The reaction rate r is obtained by using a constant population Pg of gates g, such that r = ρ₂ · Pg. In order to achieve this, Soloveichik et al. (2008) assume an excess population of gates that is large enough to remain effectively constant. We adopt the same approach for the implementation of constant gate populations, but later discuss a potential alternative.

Figure 12.

DNA implementation of a degradation reaction 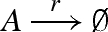. The implementation uses a constant population Pg of gates g, such that r = ρ₂ · Pg.

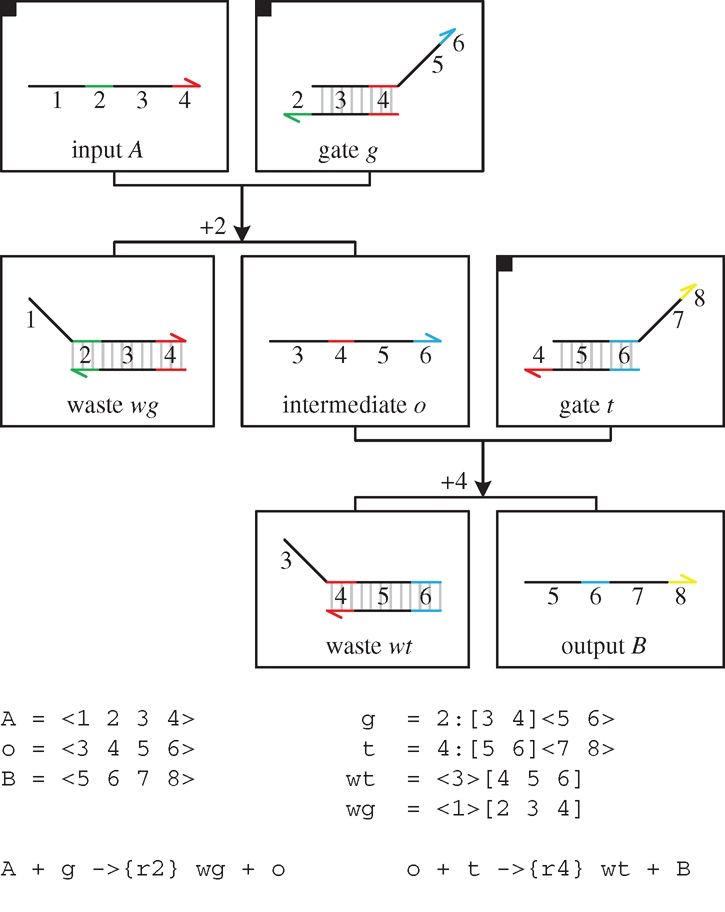
Figure 13 presents a DNA implementation of a transition reaction 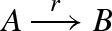. As with degradation, the reaction is implemented by a constant population Pg of gates g, such that r = ρ₂ · Pg. In order to ensure that the domains of species B are completely independent from the domains of species A, an additional translation gate t is needed. Furthermore, in order to ensure that the reaction remains effectively first order, a very large constant population Pt of translation gates t is used, such that ρ₄ · Pt ≫ r.

Figure 13.

DNA implementation of a transition reaction 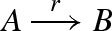. The implementation uses a constant population Pg of gates g, such that r = ρ₂ · Pg, and a very large constant population Pt of translation gates t such that ρ₄ · Pt ≫ r.

Figure 14 presents a DNA implementation of a production reaction 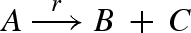. The implementation of the reaction is similar to that in figure 13, except that the intermediate output strand o displaces two strands instead of one from the translation gate t, which correspond to the two output species of the reaction.

Figure 14.

DNA implementation of a production reaction 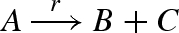. The implementation is similar to that in figure 13, except that the translation gate t produces two output strands instead of one.

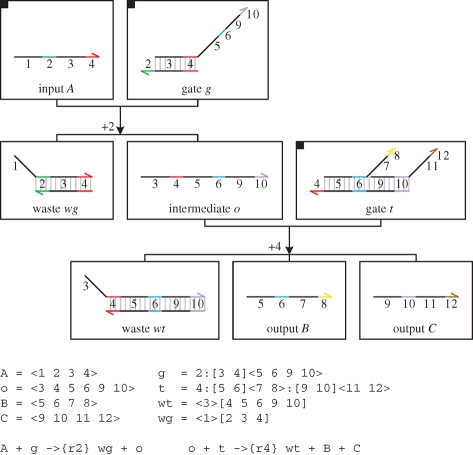
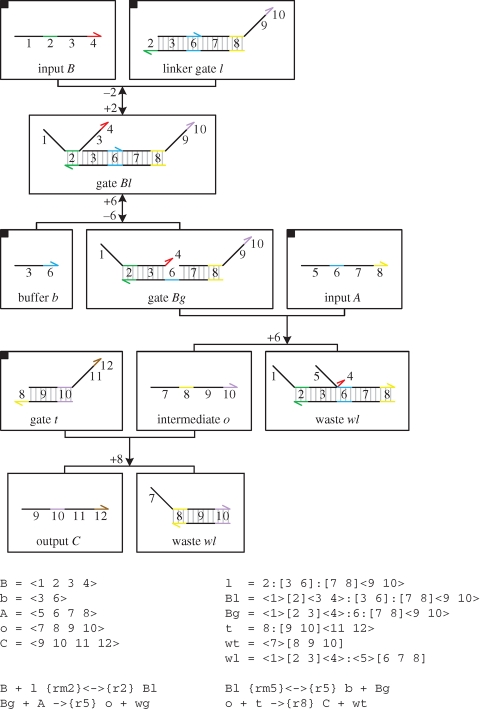
Figure 15 presents a DNA implementation of a binary reaction 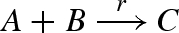. The implementation is less straightforward than in the previous examples, since the output C must only be produced when both inputs A and B are present. The solution, as presented in Soloveichik et al. (2008), is to use a linker gate l that rapidly binds and unbinds the reactant B, such that the bound and free species B are in equilibrium, where f(Bg) denotes the fraction of bound species B. When the species A is present, it can interact with the bound form of species B to complete the reaction. The rates and populations are chosen such that r = f(Bg) · ρ₆.

Figure 15.

DNA implementation of a binary reaction 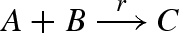. The implementation uses large constant populations Pl and Pb of linker gates l and buffers b, respectively, such that Pl · ρ₂ and Pb · ρ₆ ≫ r. Furthermore, the toehold unbinding rates are chosen such that ρ₋₂ and ρ₋₆ ≫ r. These constraints ensure that an equilibrium can be rapidly established between the population of free linker gates l and bound linker gates Bg. The rates and populations are also chosen such that r = f(Bg) · ρ₆, where f(Bg) denotes the fraction of bound species Bg at equilibrium. As with the unary reactions, we use a very large constant population Pt of gates t such that ρ₈ · Pt ≫ r.

Figure 16 presents a more general translation from chemical reactions to DNA molecules, based on the approach presented in Soloveichik et al. (2008). The translation is defined for unary and binary reactions, but translations for higher order reactions can be defined in a similar fashion. The translation is defined as a collection of modules in the strand displacement language, which take the populations of gates and buffers as parameters. The populations are chosen so as to implement accurately the corresponding reaction rates, using the approach outlined in the previous examples. The populations also take into account the fact that a given species may be involved in multiple binary interactions simultaneously and can therefore bind to multiple different gates, affecting the equilibrium of free and bound species. As an alternative to varying the initial gate populations, we can also vary the degree of complementarity of toeholds for each reaction, as discussed in Soloveichik et al. (2008).

Figure 16.

Translation from chemistry to DNA, based on the approach presented in Soloveichik et al. (2008). The translation is defined as a collection of modules in the strand displacement language, where each chemical species X is associated with three distinct domains (X1,X2,X3). The species module implements an initial population P of the species represented by domains (X1,X2,X3). 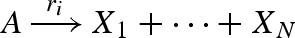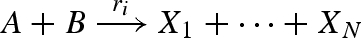The unaryN and binaryN modules implement unary and binary reactions of the form and , respectively. The modules rely on a set of local domains (I1, … ,IN) to limit interference between reactions. We assume that populations Pg, Pl, Pb and Pt are large enough to remain effectively constant, and that Pt is large enough to implement reactions that are effectively immediate. The populations Pg, Pl, Pb are passed as parameters to the modules, and are chosen to implement accurately the corresponding reaction rates as follows. We let f(X) denote the fraction of unbound species X and let f(Xg) denote the fraction of species X bound to a gate g. These populations can be computed beforehand, assuming that an equilibrium between free and bound species is quickly reached. In the unary case, r = ρ_A1 · Pg · f(A) and ρ_A3 · Pt ≫ r. In the binary case, r = ρ_B1 · f(B) · f(Ag) and ρ_B3 · Pt, ρ_A1 · Pl, ρ_B1 · Pb, ρ_−B1, ρ_−A1 ≫ r. The latter constraints ensure that all intermediate reactions are fast enough with respect to r to be effectively ignored.

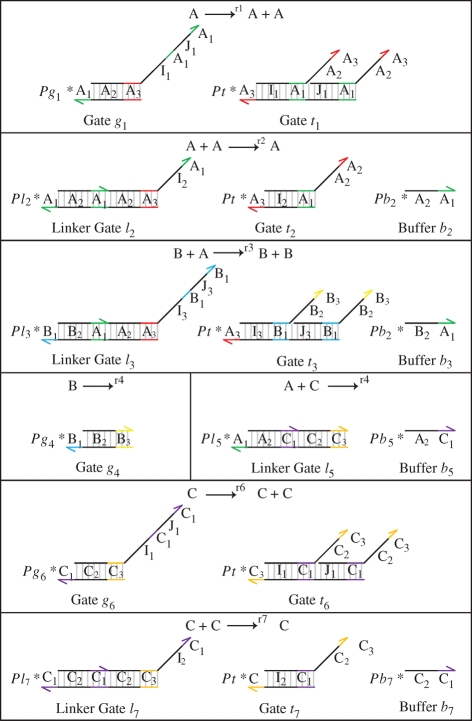
As an example, we consider the coupled chemical reactions for the chaotic system of Willamowsky and Rossle, which was used as a case study in Soloveichik et al. (2008). The reactions for this system are summarized in table 1, together with their translation to DNA molecules. The translation is implemented using a set of modules for unary and binary reactions, which are defined in a similar fashion to the general modules presented in figure 16. The local domains used in each of the modules ensure that the domains of different gates do not interfere with each other. Expanded versions of these modules are shown in figure 17. The expansion is performed automatically by the compiler, as described in §3.

Table 1.

DNA implementation of the chaotic chemical system due to Willamowsky and Rossle, based on the implementation of Soloveichik et al. (2008). The reaction rates are defined as r₁ = 0.03, r₂ = r₇ = 5 × 10⁴, r₃ = r₅ = 10⁵, r₄ = 0.01, r₆ = 0.0165. The implementation uses modules unary0, unary2, binary0, binary1 and binary2, which are defined in a similar fashion to the general modules unaryN and binaryN presented in figure 16. The populations Pg1, … ,Pl7, Pb2, Pb3, Pb, Pb7 and the toehold binding and unbinding rates are chosen to implement accurately the corresponding reaction rates. The populations are passed as parameters to the modules, along with the species A, B, C, where A = (A1,A2,A3), B = (B1,B2,B3) and C = (C1,C2,C3).

no.	chemistry	DNA molecules
1		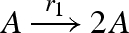unary2(A,Pg1,A,A)
2		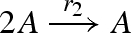binary1(A,A,Pl2,Pb2,A)
3		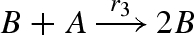binary2(B,A,Pl3,Pb3,B,B)
4		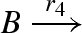unary0(B,Pg4)
5		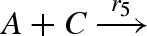binary0(A,C,Pl5,Pb5)
6		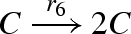unary2(C,Pg6,C,C)
7		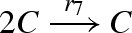binary1(C,C,Pl7,Pb7,C) )

Figure 17.

DNA molecules obtained by expanding the modules of table 1.

The main species and reactions generated from the DNA molecules are presented in figure 18. The reactions are similar to those presented in Soloveichik et al. (2008), except that there are two reversible reactions instead of one for establishing an equilibrium between species, linker gates and buffer strands. The additional reactions will not affect the overall dynamics of the system, provided they are effectively immediate. According to figure 18, this will require the toehold unbinding rates involved in all the equilibrium reactions to be sufficiently rapid. In addition to the reactions represented in figure 18, a number of other reactions are generated, which arise from the fact that the toeholds of some of the intermediate outputs can bind to multiple gates. For example, toehold A3 of the intermediate output <A2 A3 I1 A1 J1 A1> can bind to three distinct gates, even though it can only displace strands from one of these gates. This should not significantly affect the overall dynamics, provided the toehold unbinding rates are also fast. Nevertheless, it is important to take into account these factors when determining toehold rates and gate populations.

Figure 18.

Main species and reactions for the DNA molecules of figure 17. The reactions were compiled using the algorithm of §3.

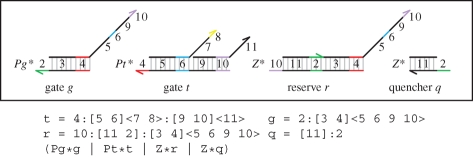
As mentioned previously, the translations assume that reaction gates are present in sufficiently large numbers so as to remain effectively constant over time. Another way of ensuring constant gate populations is to introduce a reservoir of inactive gates that become active each time a gate is used. An example design is presented in figure 19. The advantage of this design is that we have a more precise control over the gate populations, and can use lower population numbers. If needed, we can continually supply new inactive gates to ensure that the active gate population is kept constant indefinitely.

Figure 19.

A possible implementation of a replenishable gate. The gates g and t implement a reaction of the form 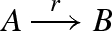. The extra reserve r is in excess, so that whenever a reaction is executed, a new gate with the same function as g is activated to take the place of the gate that was used.

Another issue that needs to be addressed is the fact that buffer strands continually accumulate after each execution of a bimolecular reaction. It should be possible to engineer a more sophisticated collection of molecules that also recycles excess buffer strands from the system, so that the population of buffer strands is kept constant. Finally, in many cases complete sequence independence between strands may not be necessary, allowing various optimizations to be introduced, as discussed in Soloveichik et al. (2008). The use of a concise strand displacement language for describing the interactions between DNA molecules should facilitate the design and analysis of such optimizations.

3. Methods

In this section, we formalize the DNA strand displacement language as a process calculus. We give definitions for the syntax and execution rules of the calculus, together with its translation to chemical reactions. The definitions are given in the style of process calculi such as the pi-calculus (Turner 1996; Milner 1999; Sangiorgi & Walker 2001), with the addition of a stochastic reduction semantics along the lines of Phillips & Cardelli (2007). The formal definitions are used as the basis for an implementation of the strand displacement language, and are also used to reason about basic language properties.

3.1. Syntax of the strand displacement calculus

The syntax of the DNA strand displacement calculus (DSD) is defined in terms of molecules D, molecule segments G and sequences S, L, R, as shown in table 2. A molecule D can be an upper strand <_ S _> with a sequence that is complementary to S. The upper strand is terminated by an empty sequence _ at both ends, to allow for potentially empty left and right overhangs when an upper strand binds to a molecule. The upper strand can also be abbreviated to <S> by omitting the empty sequences. A sequence S is a concatenation of one or more domains N, where a domain is a name or number that represents a specific DNA sequence. A toehold domain is represented as N∧c, where c denotes the degree of matching, such that 0 < c ≤ 1. Toehold sequences are assumed to be between 4 and 10 nucleotides in length. Sequences L and R denote potentially empty sequences that overhang to the left and right of a bound upper strand, respectively. A segment G can be a lower strand with a single toehold domain N∧c, or a double strand <L>[S]<R> consisting of an upper strand <L S R> bound to a lower strand S. The upper and lower strands are bound along the double-stranded region [S], with upper strands <L> and <R> overhanging to the left and right. A segment G can also be a concatenation G1:G2 of two segments G1 and G2. Importantly, when two segments are concatenated they are assumed to be joined along a continuous lower strand. Thus, the syntax only allows a single lower strand per molecule.

Table 2.

Syntax of the DNA strand displacement calculus (DSD), defined in terms of molecules D, molecule segments G and sequences S, L, R. The syntax assumes that 0 < c ≤ 1 and that all toeholds in an upper strand <_ S _> have a degree of matching c = 1.

DSD	syntax	description
D	()	empty molecule
	<_ S _>	upper strand with sequence complementary to S
	G	molecule segment G
	D1 | D2	parallel composition of molecules D1 and D2
	new N D	molecules D with local domain N
	X(n)	instance of a module X with parameters n
G	N∧c	toehold domain N with degree of matching c
	<L>[S]<R>	double strand [S] with left and right overhangs <L>, <R>
	G1:G2	concatenation of G1 and G2
S	N	domain N
	N∧c	toehold domain N with degree of matching c
	S1 S2	concatenation of S1 and S2
L	_	empty sequence
	_ S	left overhanging sequence S
R	_	empty sequence
	S _	right overhanging sequence S

Multiple molecules D1, … , DK can be executed in parallel, written D1 | … | DK. A domain N can also be restricted to molecules D, written new N D. This represents the fact that domain N is unique to molecules D and does not occur in any other molecules. Finally, a molecule can be an instance X(n) of a module X with parameters n. We assume the existence of a fixed environment of module definitions X1(m1) = D1, … ,XK(mK) = DK. The definitions are assumed to be non-recursive, such that a module cannot invoke itself, either directly or indirectly via another module.

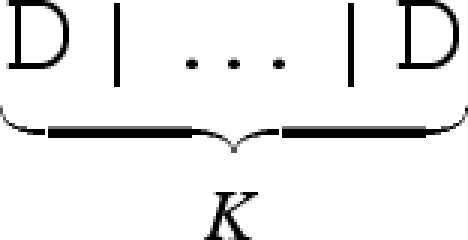
We define a number of syntactic abbreviations for the calculus, as summarized in table 3. We omit terminating empty sequences, where S _ and _ S are abbreviated to S, and we abbreviate a toehold N∧1 with degree of matching 1 to N. We also omit empty overhanging strands, where <_>[S]<R> is abbreviated to [S]<R > , and <L>[S]<_> is abbreviated to <L>[S]. We abbreviate successive restrictions new N1 … new NK D to a single restriction new (N1, … ,NK) D. Finally, we abbreviate K identical copies of a molecule 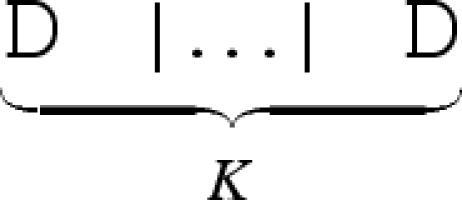to K*D.

Table 3.

Syntax abbreviations for the strand displacement calculus.

syntax	abbreviation
S _	S
_ S	S
N∧1	N
<_>[S]<R>	[S]<R>
<L>[S]<_>	<L>[S]
new N1 … new NK D	new (N1, … ,NK) D
	K*D

3.2. Semantics of the strand displacement calculus

We consider a reduction semantics that explicitly represents toehold binding, toehold unbinding and strand displacement, as defined in table 4. Each toehold N∧c is assigned corresponding binding and unbinding rates given by ρ_N and ρ_−N, respectively. The rule 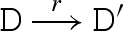means that D can reduce to D′ with rate r. We write 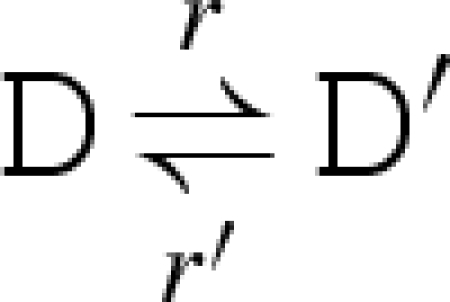as an abbreviation for 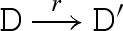and 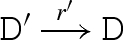. We also write 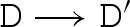as an abbreviation for 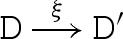, where ξ represents a rate that is significantly faster than any of the toehold unbinding rates.

Table 4.

Reduction rules of the strand displacement calculus.

rule	condition	before	reduce	after
RB		<L N R> | G1:N∧c:G2		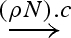G1:<L>[N∧c]<R>:G2
RU		G1:<L>[N∧c]<R>:G2		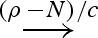<L N R> | G1:N∧c:G2
RDR		<L1>[S1]<S2 R1>:<L2>[S2]<R2>		<L1>[S1 S2]<R1> | <L2 S2 R2>
RDL		<L1>[S1]<R1>:<L2 S1>[S2]<R2>		<L1 S1 R1> | <L2>[S1 S2]<R2>
RGR		G:G2		G′:G2
RGL		G1:G		G1:G′
RP		D1 | D2		D1′ | D2
RN		new N D		new N D′
RE		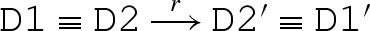D1		D1′

Rules (RB) and (RU) model strand binding and unbinding along a toehold. Analogous rules are also needed to represent toehold binding and unbinding in the absence of G1, G2 or both (not shown). Rules (RDR) and (RDL) model a strand being displaced from a molecule to the right and left, respectively. Rule (RE) allows reduction up to re-ordering of molecules. The re-ordering relation is defined in table 5, where D ≡ D′ means that D and D′ are equivalent up to mixing of molecules and branch migration. We also allow the following approximation to be made: if 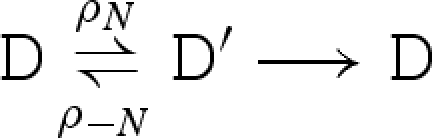then 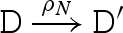, since the reverse reaction at rate ρ_−N will have a negligible rate compared with the alternative forward reaction at rate ξ.

Table 5.

Structural equivalence rules of the strand displacement calculus.

rule	condition	before	equal	after
EZ		D | ()	≡	D
EC		D1 | D2	≡	D2 | D1
EA		D1 | (D2 | D3)	≡	(D1 | D2) | D3
ED	X(m) = D	X(n)	≡	D{m: = n}
ENP	N ∉ fn(D2)	(new N D1) | D2	≡	new N (D1 | D2)
EP	D1 ≡ D1′	D1 | D2	≡	D1′ | D2
EN	D ≡ D′	new N D	≡	new N D′
EM		<L1>[S1]<S2 R1> : <L2>[S2 S3]<R2>	≡	<L1>[S1 S2]<R1> : <L2 S2>[S3]<R2>
EL	G ≡ G′	G1:G	≡	G1:G′
ER	G ≡ G′	G:G2	≡	G′ : G2

As mentioned earlier, a notion of equivalence (≡) is defined in table 5 to allow for mixing and branch migration of molecules. The relation is assumed to be reflexive, symmetric and transitive. Essentially, the rules state that the order of parallel molecules is not important, since molecules are assumed to be well mixed. In addition, since branch migration reactions happen very quickly compared with binding and unbinding reactions, molecules are considered to be equivalent up to branch migration. Rule (ENP) ensures that a domain N that is local to molecules D1 is not used in any parallel molecules D2. If there are any name clashes, the domain N is renamed locally inside D1. The set fn(D) denotes the set of free domain names that are used by molecules D, where new N D acts as a binder for name N in D. Rule (ED) allows an instance of a module to be replaced with its definition, where the parameters m are replaced with n in molecules D, written D{m: = n}.

One of the key assumptions of the language is that two single-stranded molecules can only interact with each other via complementary toehold domains. This is enforced at a syntactic level, by ensuring that a molecule with a lower strand is either a single-stranded toehold domain N∧c or a double-stranded sequence with left and right overhangs. Thus, in order to ensure that single strands can only ever interact on toeholds, it is sufficient to show that the syntax of the language is preserved by reduction. This property is captured by proposition 2.1.

Proposition 3.1. —

then .

Proof. —

By induction on the derivation of reduction, according to table 4. By inspection of the reduction rules, we observe that none of the rules results in the liberation of a single-stranded, non-toehold region of a lower strand. Since reduction is also defined up to structurally equivalent molecules, we prove a similar property for the structural equivalence rules of table 5. ▪

3.3. Compiling DNA molecules to reactions

Given a collection of DNA molecules, we generate a corresponding set of reactions by repeated application of the reduction rules of table 4, where each application of a reduction rule corresponds to a single reaction. The generated reactions can in turn generate new molecular species, where molecules are assumed to be equal up to branch migration, as defined in table 5. This is implemented by defining a standard form for segments, where a segment G is in standard form if all of its branches are migrated as far as possible to the right. In order to show that two segments are equal up to branch migration, it is sufficient to show that they have the same standard form. We also define a standard form for molecules, where molecules D are in standard form if all local domains are at the top-level and all module definitions are expanded with their respective parameters. The standard form is presented in definition 3.1, where all segments and molecules admit a standard form, as stated in proposition 3.2.

Definition 3.1. —

A segment G is in standard form if all of its branches are migrated as far as possible to the right. A collection of molecules D is in standard form if it consists of a set of parallel upper strands and segments, with a top-level set of local domains:

Proposition 3.2. —

All segments G and molecules D admit a standard form.

Proof. —

Any branches in a segment G can be migrated to the right by application of rule (EM). Any local domains new N in molecules D can be moved to the top-level by application of rule (ENP), while any module instances X(n) can be replaced with their corresponding definitions by application of rule (ED). This results in a set of parallel upper strands and segments, with a top-level set of local domains. ▪

We implement a translation from DNA molecules to chemical reactions by defining the syntax and execution rules of a corresponding compiler. The syntax of the DSD compiler is defined in table 6, where a term T of the compiler consists of a set of local domains N, upper strands S, segments G and reactions R. A reaction can be either unary or binary, where a unary reaction (G, r, <S>, G′) consists of a segment G that can reduce with rate r to an upper strand <S> and a segment G′. A binary reaction (<S>, G, r, G′) consists of an upper strand <S> and a segment G that can reduce with rate r to a segment G′.

Table 6.

Syntax of the DSD compiler, where a term T consists of a set of local domains N, upper strands S, segments G and reactions R.

DSDC	syntax	description
T	(N, S, G, R)	local domains N, upper strands S, segments G, reactions R
S	{<S1>, … ,<SN>}	set of N upper strands
G	{G1, … , GN}	set of N segments
R	{θ1, … , θN}	set of N reactions
θ	(<S>, G, r, G′)	reactants <S> and G, rate r, product G′
	(G, r,<S>,G′)	reactant G, rate r, products <S> and G′

The execution rules of the DSD compiler are defined in table 7. The rules are of the form D ⊕ (N,S,G,R), which adds molecules D to a term (N,S,G,R) of the compiler. Initially, molecules D are added to an empty compiler term (ø, ø, ø, ø). Each time a new molecule is added, the set R is augmented with the set of all possible reactions between the new molecule and the existing molecules in the compiler. Each time a new reaction is added, any new molecules generated by the reaction are themselves added to the compiler. This process continues until no new molecules can be generated. The result is a compiler term containing the set of all strands S, segments G and reactions R that are generated from the initial molecules D. The rules of the compiler are summarized as follows.

1. (CR) A set of reactions is added to a term by adding each reaction individually.

2. (CU) A unary reaction (G, r, < S > , G′) is added to a term by adding the products <S> and G′.

3. (CB) A binary reaction (<S>, G, r, G′) is added to a term by adding the product G′.

4. (CN) A local domain is added to the set of local domains of the compiler. Since molecules are assumed to be in standard form, the domain will be globally unique.

5. (CP) Parallel molecules are added one at a time.

6. (CSZ) A strand <S> is discarded if it is already present in the compiler.

7. (CGZ) A segment G is discarded if it is already present in the compiler.

8. (CS) If a strand <S> is not already present, then it is added to the set S. For each segment G_i in the compiler, we compute the set R_i of reactions between <S> and G_i, written 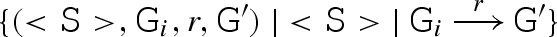. The resulting reactions are then added to the compiler.

9. (CG) If a segment G is not already present, then it is added to the set G. For each strand <S_i> in the compiler, we compute the set R_i of reactions between G and <S_i > , written 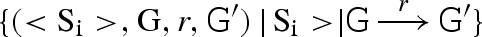. We also compute the set R₀ of reactions involving G alone, written 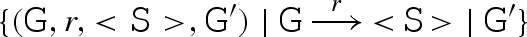. The resulting reactions are then added to the compiler.

Table 7.

Adding molecules to a term of the DSD compiler. We start by adding molecules D to an empty compiler term (ø,ø,ø,ø), written D ⊕ (ø,ø,ø,ø). The result is a compiler term containing the set of all strands S, segments G and reactions R that are generated from the initial molecules D. The rules assume that all molecules D and segments G are in standard form.

rule	conditions	before	def	after
CR		{θ1, … , θN} ⊕T	≜	θ1⊕ … ⊕ θN ⊕T
CU		(G, r,<S>, G′) ⊕ T	≜	<S>⊕G′ ⊕ T
CB		(<S>, G, r, G′) ⊕ T	≜	G′ ⊕ T
CN		(new N D) ⊕ (N, S, G, R)	≜	D ⊕ ({N} ∪ N, S, G, R)
CP		(D1 | D2) ⊕ T	≜	D1 ⊕ D2 ⊕ T
CSZ	<S> ∈ S	<S>⊕T	≜	T
CGZ	G ∈ G	G ⊕ T	≜	T
CS		<S>⊕ (N, S, G, R)	≜	R′ ⊕ (N,{<S>}∪ S, G, R ∪ R′)
CG		G ⊕ (N, S, G, R)	≜	R′ ⊕ (N, S, {G} ∪ G, R ∪ R′)

3.4. Compiling to DNA sequences

One important issue that we have deliberately not addressed is the automatic compilation of domains to nucleotide sequences. This is a challenging problem that requires a detailed theoretical treatment, and is therefore beyond the scope of this paper. Instead, we propose to adopt the semi-automated approach described by Zhang et al. (2007). The approach uses sequences composed of A,C,T and A,G,T for upper and lower strands, respectively, assuming Watson–Crick base pairing between A,T and between G,C. As discussed in Zhang et al. (2007), the restricted alphabet for upper and lower strands reduces potential secondary structure, assuming that specificity domains on the lower strands are never exposed, as stated in proposition 3.1. The approach first chooses random sequences composed of only A,C,T for the domains in the upper strands, and then constructs the complementary domains for the lower strands accordingly. Sub-sequences known to be problematic are altered by hand, such as GGGG, which causes to G-quadruplexing, or AAAAA, which causes synthesis difficulties. The remaining sequences are then concatenated as appropriate to form DNA strands, which are folded using the mFold webserver (Zuker 2003) to check for the presence of undesired interactions. If necessary, some of the domains in the upper strands are changed by hand to G, and the corresponding domains in the lower strands are updated accordingly.

For specificity domains, the sequences are long enough to be chosen to avoid interferences between domains while also avoiding secondary structures. For toehold domains, however, the number of unique sequences is limited, since toeholds are only between 4 and 10 nucleotides in length. As a result, a check on the total number of distinct toeholds will need to be made before attempting to implement a given DNA circuit. This can be achieved by converting the circuit to standard form, according to definition 3.1, and then counting the total number of distinct toehold domains. Circuits where this number exceeds the given limit will not be implementable, which can be signalled by a compilation error.

As a rough estimate, we can use the results presented in Marathe et al. (2001) to obtain approximate upper and lower bounds on the number of distinct toehold domains. For example, if we assume that toehold domains are DNA sequences of length 10 that differ from one another by at least three letters, then the number of distinct sequences that do not interfere with each other on complementary strands, denoted by A₄^R(10,3), is calculated to be between 1184 and 16 912. Note that further work is needed to reduce the gap between the upper and lower bounds, and the estimate does not take into account the constraint that secondary structures should be avoided, which further reduces the number of suitable sequences. Given that a single mismatch along a nucleotide sequence is sufficient to disrupt toehold binding significantly, it may be sufficient for toeholds to differ by only two letters, in which case the number of distinct sequences A₄^R(10,2) is 131 072. As with the previous calculation, this also includes sequences that exhibit secondary structures, which will need to be removed. Note also that there is a trade-off between the number of distinct toeholds and the extent to which the degree of matching of a given toehold can be varied. A more drastic approach for reducing the secondary structure of toeholds is to use sequences composed of only A,C,T for upper strands, as discussed previously. For three-letter sequences of length 10 that differ by at least two letters, this gives a lower bound of A₃(10,2) ≥ 2811.

In spite of these limitations, it is worth noting that we do not need a large number of distinct toeholds in order to implement a large-scale DNA circuit. This is because the toehold is just a starting sequence for a strand displacement reaction: if the toehold binds but the adjacent branch migration region does not, then the branch migration is going to bounce back at the site of the first major disagreement, and the toehold will unbind. Although these reactions will potentially slow down the system, they will not result in major interferences. This allows the same toehold domain to be used in combination with a potentially unlimited number of specificity domains. Thus, a limit on the number of distinct toeholds should not significantly limit the size of a circuit. For example, if we consider the gate motifs in §2.3 for designing large-scale logic circuits, only a single toehold domain T was used.

4. Discussion

This paper presents a programming language and compiler for designing and simulating DNA circuits in which strand displacement is the main computational mechanism. Starting from an initial set of molecules, the compiler computes the set of all possible reactions together with the set of all possible molecules that can be produced. The generated reactions can then be simulated using standard approaches in order to evaluate the circuit design. This greatly simplifies the design and testing of DNA circuits prior to their subsequent implementation. The language was developed to take into account recent experimental and theoretical results on the design of large-scale, efficient, modular DNA circuits. There are a number of areas for future work, as outlined below.

The strand displacement language differs from traditional imperative languages such as Pascal or C in that the main primitives of the language are geared towards an implementation in physical DNA molecules. In particular, the language supports concurrent execution of molecules by means of a parallel composition primitive, and parallel molecules can interact with each other via specific toehold domains. Although the language also features more traditional primitives such as parametrized modules and local variables, it is much closer to concurrent programming languages such as Phillips & Cardelli (2007) than to traditional imperative languages. Furthermore, instead of compiling the program to a sequence of binary digits for execution by a computer, programs will ultimately be compiled to sequences of letters A,C,G,T that code for specific DNA molecules. For testing purposes, programs are compiled to a set of chemical reactions by the compiler of §3, and the resulting reactions are simulated using standard tools.

In this paper, we have presented the core primitives of the strand displacement language, but additional programming constructs can be added as straightforward extensions. For example, conditionals can be used to check whether two domains are equal, while loops can be used to iterate over a collection of molecules. Arithmetic expressions can also be used to express the initial populations of molecules. In all cases, the result of these computations will be a set of DNA molecules, which will then be compiled to physical DNA sequences or to a set of chemical reactions for simulation.

Developing a language that is tailor-made for modelling a particular class of DNA circuits has advantages in terms of the clarity of the models and their close resemblance to physical implementations. From a theoretical perspective, however, it would also be interesting to investigate whether the strand displacement calculus can be encoded using more general calculi such as kappa calculus (Danos et al. 2007) or stochastic pi-calculus (Priami 1995; Phillips & Cardelli 2007). Initial attempts suggest that such encodings are non-trivial and worthy of future investigation.

The design of the strand displacement language is still in its early stages, and there are many ways in which the language can be extended, such as allowing molecules to contain multiple lower strands. There is also scope for defining additional syntactic constraints on molecules, in order to limit interference between molecular domains. Another issue that we have deliberately avoided relates to secondary structures in DNA molecules. We have already mentioned how DNA sequences can be selected in order to eliminate such structures, but in future we may wish to include simple features such as hairpin motifs, as used by Yin et al. (2008).

Rather than translating DNA molecules to chemical reactions and then simulating the reactions in a separate tool, we can use our definition of reduction to implement a simulator that executes the DNA molecules directly. This will allow us to manually progress through the simulation step by step, observing how the molecules interact with each other and change their configurations over time. Such tools would be useful for debugging the design of a particular set of DNA molecules, since we can directly observe how the molecule changes configuration as a result of a particular interaction, and then intervene during the debugging cycle to try new molecular designs.

The last case study illustrated how we can translate a set of chemical reactions to DNA molecules. Each reaction was translated to populations of gate molecules that needed to remain constant over time, which required excess molecules and pre-computation of equilibrium conditions. Rather than translating chemical reactions to DNA, it would be interesting to define an alternative high-level language that still retains an explicit notion of a DNA molecule as a finite resource, while abstracting away from individual domains in the DNA sequence. An example of such a language is described by Cardelli (2009), as a means of simplifying the circuit design process.

As a proof of concept, we have implemented a prototype compiler for the DNA strand displacement language, which will be made available in Phillips (2009). Essentially, the tool can be used to program a collection of DNA molecules and to check whether they conform to the syntax of the language. If not, an error is raised. Otherwise, a text file is produced containing the full set of molecules and reactions that are generated from the initial set of molecules. The generated reactions can then be simulated using standard techniques. In the longer term, we hope to extend our language to automate further the process of designing DNA circuits, by including a compilation step that translates toehold and specificity domains to nucleotide sequences. In this case, the translation would rely on a set of precomputed sequences that are sufficiently distinct from each other, and that do not exhibit secondary structures, using appropriate DNA coding of the regions (Kari et al. 2005; Zhang et al. 2007). The ultimate goal as described by Yin et al. (2008) is to be able to design and simulate arbitrarily complex DNA circuits on a computer, and automatically compile these to a corresponding set of nucleotide sequences, ready for synthesis.