Designing and encoding models for synthetic biology

Abstract

A key component of any synthetic biology effort is the use of quantitative models. These models and their corresponding simulations allow optimization of a system design, as well as guiding their subsequent analysis. Once a domain mostly reserved for experts, dynamical modelling of gene regulatory and reaction networks has been an area of growth over the last decade. There has been a concomitant increase in the number of software tools and standards, thereby facilitating model exchange and reuse. We give here an overview of the model creation and analysis processes as well as some software tools in common use. Using markup language to encode the model and associated annotation, we describe the mining of components, their integration in relational models, formularization and parametrization. Evaluation of simulation results and validation of the model close the systems biology ‘loop’.

1. Introduction

Synthetic biology has seen an explosive development over the last decade (Sprinzak & Elowitz 2005; Andrianantoandro et al. 2006). The engineering of biological systems has been boosted by the availability and improvement of wet-lab techniques. Hand in hand with the development of these experimental approaches, the use of computational tools and methods to model and interpret biological systems has spread and become the mainstream. While at the end of last century, only a few software tools were specifically designed to build and interpret gene regulatory and biochemical reaction networks, today they number in the hundreds.

Biological systems are highly interconnected, and their behaviours most often cannot be derived solely from the properties of single components without the help of computers. While the dynamics of elementary interactions and simple regulatory motifs can sometimes be inferred without the help of mathematical models, the behaviour of more complex reaction networks cannot be unravelled merely by reasoning alone. Therefore, mathematical descriptions of biochemical processes and computational analysis, in combination with experimental results, have become a necessity.

Computer simulations allow the prediction of system behaviour and can help to elucidate the mechanisms underlying biological phenomena. An initial model should be created which is reasonably faithful to the biological structure, and is capable of reproducing known behaviours to an acceptable extent. This can then be used to probe the effects of different environmental conditions, perturbations and variants or different designs. For instance, it is possible to use in silico experiments to screen for possible drug targets (Undrovinas et al. 2006), to optimize certain aspects of a system (e.g. Reijenga et al. 2001), to simulate the behaviour of mutants (e.g. Bray et al. 1993; Novak & Tyson 1997) and to analyse the evolvability and robustness of certain systems (von Dassow et al. 2000). Analyses at this speed and low cost could never be achieved solely using classical experimental methods. Finally, and maybe equally important, models can show us gaps in our understanding of biological processes and suggest which piece of the puzzle or experimental data is missing. The modelling process itself allows one to scrutinize not only the available data, but also the known or assumed mechanisms. This often leads to more questions than answers, and sometimes shows that mechanisms believed to be established do not actually fit into observed phenomena or are insufficient to explain experimental results.

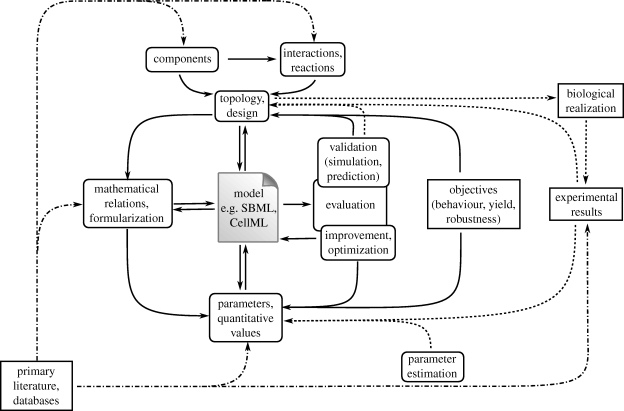
Modelling has been an integral part of the synthetic biology work since its inception (Elowitz & Leibler 2000; Gardner et al. 2000). Synthetic biology, indeed, does not differ from any other engineering activity, where designing and testing of models are as important as the building step. This not only allows economy of time and effort, but also permits optimization of the final product. However, modelling in biology is most often an iterative process; the mathematical model has to be validated by comparison of the model analyses and simulation results with experimental measurements, and to be refined depending on these comparisons. This is especially true for kinetic modelling since a description of the system's final state is required together with its changes over a temporal range. Figure 1 illustrates the model creation process.

Figure 1.

Diagram describing the model creation process, centred around the model file. External inputs come from literature, databases or experiments. Validation and parameter estimation give direct feedbacks on the model, while the predictions can also guide experimental design. The desired objectives for the system to be designed are part of a mostly in silico design cycle, the biological implementation and the fitting and comparison of the model to observations are part of the standard systems biology model development cycle.

Driven by the needs of the research community, the availability of more usable software tools and the existence of community standards, the user population has shifted from dedicated experts in mathematical modelling to scientists with different backgrounds and interests. Computational models have now become another tool for use in parallel to various experimental approaches. Modelling, though, still remains a highly interdisciplinary task. First, it demands a detailed understanding of the biological and biochemical processes to be modelled. This biological knowledge alone is normally not enough, since encoding it into a computer readable form requires some mathematical knowledge and, depending on the tools used, also needs some computer skills. Model manipulation, evaluation and prediction generation, on the other hand, require both computational and biological experience. So while more and more intuitively usable software tools emerge, modelling is still a collaborative effort of experts in different fields or the domain of scientists with a broader overview and training.

2. Formats for model representation

Biochemical or genetic regulatory networks can be represented in various forms and formats, ranging from a crude pathway or an interaction map on a napkin to a system of ordinary differential equations in a computer algebra system (plain text file), or to machine executable code producing integrated time courses of a specific system. Biological reaction networks have many different logical layers. The first layer comprises the interacting molecules, as well as all the state variables. The interactions between the components and the underlying reaction network define the topology of the system and form the next logical layer. The final layer comprises the mathematical expressions for the interactions, and the fluxes in and out of the system.

Synthetic biology activities require the incorporation of as many of these layers as possible in the model. Static network analysis or creation of deletion mutants of a system requires knowledge of the stoichiometry of reactions. This cannot always be readily derived from, for example, ordinary differential equation representations without additional information. Furthermore, in some cases, a system has to be interpreted using different modelling frameworks. For example, in genetic regulatory networks, a continuous deterministic framework might be useful for bifurcation analysis of the qualitative behaviour, while a probabilistic discrete approach could be used to explore robustness and behaviour at low concentrations of some species (Elowitz & Leibler 2000).

As dedicated tools, targeted at different tasks, often use distinct entry formats, their use requires conversion or reimplementation of the original models into compatible formats. Manual conversion of a model from one format to another can be a very tedious and error-prone task, especially for bigger systems. The development of exchange formats for mathematical models facilitated the use of different programs and tools and facilitated their reuse and alteration. Two extensible markup language (XML) formats, the systems biology markup language (SBML) (Hucka et al. 2003) and cellular markup language (CellML; Lloyd et al. 2004), have gained broad support in the modelling community. Both languages store mathematical expressions using content MathML v. 2.0 (Ausbrooks et al. 2003) and use the resource description framework (RDF; Beckett 2004) to incorporate machine-readable metadata.

SBML has been developed as a community effort and consists of hierarchical lists of elements describing the compartments of the model, the pools of reacting entities and the interactions taking place. All elements can be annotated and commented in both human-readable and machine-interpretable forms, allowing extensive documentation and external references to be directly included in the model file. SBML has been widely adopted by the modelling community and is supported by hundreds of tools (see http://sbml.org/SBML_Software_Guide). A key to the success and rapid adoption of SBML by developers has been the availability of a general application programming interface (API) library, libSBML (Bornstein et al. 2008). This allows easy access to all elements of a model and provides unit and semantic checking of the SBML file. Tools can therefore use their own internal representation of a mathematical model, and read and write the actual model file over the standardized interface. As libSBML also features bindings to common scripting languages, a computer-literate modeller can use the API for automatic batch manipulation or simple analysis of SBML files.

Here follows a brief description of the main SBML elements:

1. Compartment. A well-stirred container in which species reside and reactions take place. This may be, for example, a two-dimensional membrane or a cell extending in three dimensions.

2. Species. Entities of a certain type residing in a specific compartment. For example, ATP in the compartment mitochondrion would constitute a different species from ATP in the cytosol.

3. Parameter. This includes all other kinds of named quantities. They can be constant or variable and altered by rules and events. For example, the proton-motive force or a chemical potential could be defined as a parameter in a model.

4. Reaction. A transformation between one or more species with specified stoichiometries. This encompasses not only chemical reactions, but also transport between compartments, in- and out-flux and so on. It can contain an expression for a rate law.

5. Rule. Mathematical expressions to define relations between species and parameters. They come in three different types: assignment rules directly assign the value of an expression to a variable, rate rules to its rate of change with time and algebraic rules define general algebraic equalities between different variables.

6. Function. Definitions of reusable mathematical functions.

7. Event. A discontinuous change taking place when a trigger condition changes from false to true. The change can be in all kinds of variables and apply to more than one.

8. Note. Extensive remarks in extensible hypertext markup language (XHTML), meant to be of human readable form.

9. Annotation. Software-specific metadata and controlled, machine-readable characterizations in an RDF format.

The other widely used XML format, CellML, provides a more modular structure. A model description consists of components and lists of connections between them. This leads to a greater flexibility, especially for multiscale models, and allows for easier reuse of components at the expense of biochemical semantics. The language is mostly developed by the Physiome Project and Bioengineering Institute at the University of Auckland. To date, there have been fewer tools supporting CellML (http://www.cellml.org/tools) than SBML, but tools exist to interconvert between both formats (see http://www.ebi.ac.uk/compneur-srv/sbml/convertors/SBMLConvertors.html; Schilstra et al. 2006), offering users the possibility to choose from a broad range of evaluation software programs.

An important, though often neglected, part of mathematical models is descriptions and characterizations of its components. It can be very valuable to include references and comments directly in the model file, especially for bigger models. Here, entities and relations can become hard to assign to their corresponding biological species and processes, and the original sources can be hard to keep track of. Therefore, extensive documentation of the model, and the references for its components, should always be kept with the model file, especially if more than one person is involved in the modelling process. Traditionally, a model is described by an accompanying text physically separated from the file containing it. While it is essential to have a verbose description of the model, direct annotation of the elements is very useful for exchange and reuse of models, as well as during the creation process itself. A reporting standard for the curation and validation of biological models—MIRIAM or minimal information requested in the annotation of biochemical models (Le Novère et al. 2005)—not only gives rules an encoded model to comply with, but also defines a form for controlled annotations. This scheme for annotations consists of a stable identifier in the form of a uniform resource identifier (URI; Berners-Lee et al. 2005) for each piece of information and a qualifier indicating the relation of this information to the annotated element. A catalogue of resources (such as controlled vocabularies or databases) is provided in MIRIAM resources (Laibe & Le Novère 2007), as well as a set of online services, which include creation and resolution of model annotations in URI form. The ability to include not only the mathematical description, but also reference and biological information in the same file simplifies exchange and reuse of models and eases collaborative work of groups of people on one model. Using a formal modelling language such as SBML, the process of modelling can easily become a collaborative effort, with different people using different tools to insert key players and reactions, annotations, kinetic rate laws, mathematical expressions and parameter values into a common model file.

3. Gathering bits and pieces

Prior to the creation of a detailed kinetic model, one needs to list the main elements. These are the key interacting species and other observables of the system one wants to model (and synthesize afterwards). In addition, one must gather their known regulatory interactions and chemical reactions from the scientific literature and databases. The kind of databases to mine depends very much on the system to be modelled. Apart from the general list given in the yearly nucleic acid research database issue (Galperin & Cochrane 2009), an overview of resources more specific to modelling is given in Ng et al. (2006) and Wierling et al. (2007). For biological pathways and reactions, the Kyoto Encyclopedia of Genes and Genomes (KEGG; Kanehisa et al. 2008), Reactome (Vastrik et al. 2007; Matthews et al. 2008), Panther (Mi et al. 2007) and the Meta- and BioCyc (Caspi et al. 2008) databases are especially useful, as they either directly export in generally used computer-readable formats (such as SBML) or their outputs can be converted to them.

Complementary to searching through databases, text mining tools can help to confine the number of articles to screen and also reveal valuable information on interactions or relationships between components. Among the tools available, iHOP (http://www.ihop-net.org/; Hoffmann & Valencia 2004) and Chilibot (http://www.chilibot.net; Chen & Sharp 2004) have been valuable for us in identifying potential protein and gene-regulatory interactions. A general overview of text mining and some of the available tools is given in Krallinger et al. (2008) and Ananiadou et al. (2006), for example.

Another possibility is to start with existing models that one can access through databases and repositories such as the Biomodel database (Le Novère et al. 2006; figure 2), Java web simulation (JWS) online (Snoep & Olivier 2002) or the CellML model repository (Lloyd et al. 2008). For more specific models, although still quite remote from synthetic biology projects, one can use dedicated repositories such as the database of Quantitative Cellular Signalling (Sivakumaran et al. 2003) and ModelDB (Hines et al. 2004). The models stored in these databases not only give an idea of the interactions and species one may need to model a given biological process, but also provide an overview of the mathematical relations used by other researchers. The models, or parts of them, can then be used as starting points or modules for new modelling efforts. Some of these databases, such as Biomodels database, directly allow creation and retrieval of complete submodels based on user-selected components. Another possibility for creating models from existing ones is to use an online modelling environment such as WebCell (Lee et al. 2006). In addition to offering multiple analysis methods, WebCell also allows import and modification of models from Biomodels database and JWS online. An interesting approach is adopted by SYCAMORE (Weidemann et al. 2008), which merges a database of quantitative enzyme kinetics—SABIO-RK (Wittig et al. 2006)—with the ability to create models via a web front end. These can subsequently be downloaded in the SBML format.

Figure 2.

Biomodels database is a resource offering curated and annotated versions of models published in peer-reviewed literature. The models can be browsed, downloaded or directly simulated online, as shown here for the repressilator.

To keep track of the resources and references used for model components, as mentioned above, they can be stored in a separate text file or as metadata in the XML file directly. SBML offers two possibilities for the latter: (i) the notes and (ii) annotation elements. Both provide further information regarding model elements in human-readable or a machine-friendly format, respectively. Notes are encoded in XHTML, providing flexibility and human readability. Annotations, on the other hand, contain machine-readable metadata in various XML formats, which may be software-specific information or standard pointers, such as MIRIAM annotation in RDF. Many SBML-supporting tools, such as SBML editor (Rodriguez et al. 2007), COmplex Pathway SImulator (COPASI, Hoops et al. 2006) and CellDesigner (Funahashi et al. 2003), allow notes or annotations to be kept.

4. Model creation

Having identified the key components of the system, reacting entities and topology, one needs to design the biochemical structure of the model. While the former steps have dealt with biology, the current one deals with chemistry. This step is still independent of a specific mathematical framework or formulation used. While stoichiometry and qualitative influence of the species can be sketched at this stage, no mathematical expressions and quantitative information are necessary for creating a static model of the system. Still, this kind of a model has already been used to do basic structural analysis, for example for building steady-state models of metabolism (for reviews see Klamt & Stelling 2003; Llaneras & Picó 2008; Planes & Beasley 2008), studying logical networks (Glass & Kauffman 1973; Thomas 1973) or looking for network motifs in regulatory networks (Alon 2007).

SBML supports this stage, especially with the reactions element. This element is not solely destined for simple chemical reactions, but encompasses all forms of transformations between physical entities as well as transport, in- and outflows. Each reaction needs to have at least one reactant or product with a given stoichiometry. Furthermore, it can also contain a species called modifiers, which are not consumed by the reaction, but they influence its rate in some form. To further characterize the role of involved reactants and modifiers, it is helpful to use controlled vocabularies. SBML allows the inclusion of identifiers pointing to terms from the systems biology ontology (SBO; Le Novère et al. 2007) to add a layer of semantics on the components of a model. SBO is a set of six controlled vocabularies that cover, in the context of systems biology, elements such as interactions, mathematical expressions, modelling frameworks and quantitative parameters. In the repressilator model, for e.g., LacIp might be labelled as an inhibitor (SBO:0000020) in the transcription of the tetR gene.

Concerning electrical circuit diagrams, a graphical representation of a biochemical system can be very helpful at this stage. Unlike the engineering disciplines, however, the biological community has yet to adopt a unique and standardized graphical language for the display of biological networks. The Systems Biology Graphical Notation (SBGN) is a recently proposed visual language for the representation of biological networks (Le Novère et al. 2008). It allows unambiguous representation of a process diagram of the reaction network. A number of modelling tools allow one to lay out systems graphically and store them in SBML. CellDesigner (Funahashi et al. 2003), for example, is a platform-independent graphical editor for biological networks, into which existing models in SBML format can be imported and modified. Notes can also be added and mathematical equations entered for the different interactions. Substrates, products and modifiers can be added either directly by drawing and setting the appropriate connections on the canvas or by entering them in the corresponding lists. Information about the graphical layout is stored in a CellDesigner-specific format in the annotation elements of the newly created SBML file. A possible SBGN compliant layout of the repressilator and CellDesigner's interface are shown in figure 3.

Figure 3.

The CellDesigner interface provides an ample selection of graphical elements and editing options to design biochemical and mathematical models. The repressilator is represented in CellDesigner's graphical notation, a derivative of SBGN. The raised window is the editing form for the kinetic law of a single reaction.

While CellDesigner is mainly an editor, it has some built-in deterministic integration capability features, based on a third party ODE Solver, SBMLodeSolver (Machné et al. 2006). For a more thorough analysis, such as stochastic interpretations or structural analysis, the simulation package COPASI (Hoops et al. 2006) and the large group of tools contained in the systems biology workbench (SBW; Sauro et al. 2003) can be used directly from the program. Using SBML as its native format CellDesigner generates models that can be used by the whole family of SBML aware tools.

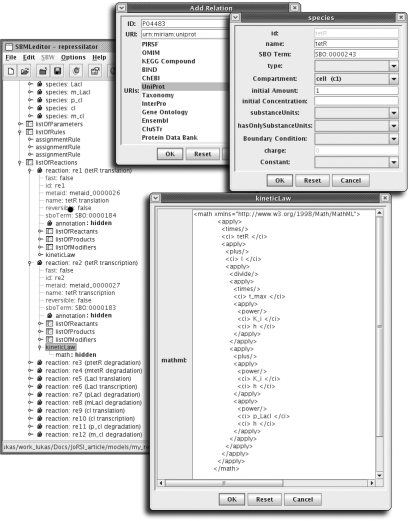
While being intuitive and visually appealing, graphical representations can quickly become cluttered and confusing for large or densely connected networks. Another possibility for creating and editing models in SBML format is purely form-based editors, which provide scalability while retaining precision. We would just wish to mention a few different approaches at this point. For instance, JigCell (Vass et al. 2004), developed at the Virginia Polytechnic Institute & State University, uses a model builder in the form of a spreadsheet. This gives a nice overview even in cases of complex and dense networks. Meanwhile COPASI (Hoops et al. 2006) uses a tree-like representation of the different models elements, spreadsheets to quickly list elements of a given type and more detailed forms to precisely alter each element. While potentially slower than entering reactions in a pure spreadsheet, it facilitates the definition of complex reactions and performs extensive checking in the background. A third approach is taken by SBMLEditor (Rodriguez et al. 2007; figure 4), a low-level SBML editor, currently without any simulation or evaluation capabilities. SBMLEditor is more closely based on the SBML format itself and supports the entire language. It has been up to now one of the few that permit direct entering of MIRIAM and SBO annotations.

Figure 4.

SBMLEditor allows detailed manipulation of all elements of SBML. Here the main overview, the species editing form, a MIRIAM annotation dialogue and the MathML code of the kinetic law shown in figure 2 are displayed.

Lately, some tools specifically aimed for synthetic biology have been created. One approach has been to create gene-regulatory networks from reusable modules similar to those stored in the MIT Registry of Standard Biological Parts (Endy 2005). An effort using quantitative modules in CellML format has been presented at the SysBioSys 2007 conference (Rouilly et al. 2007). Some recent tools have allowed the export in SBML format, such as the command line tool Asmparts (Rodrigo et al. 2007), synthetic biology software suite (Hill et al. 2008), as well as an extension (Marchisio & Stelling 2008) written for the ProMot (Ginkel et al. 2003) suite. These tools and efforts are still in the early stages, but they have already seemed to be quite usable, even if they do not offer the full range of biological parts available in the registry.

5. Entering mathematical relations and numerical values

Once a potential network structure is created, a mathematical framework has to be chosen to develop a kinetic version. As different frameworks allow for complementary analysis and interpretation, it is often useful to keep the model interpretable by more than one formalism. The simultaneous use of alternative frameworks has proved beneficial, especially for gene regulatory networks. This can be seen in one of the landmark papers of synthetic biology describing the repressilator (Elowitz & Leibler 2000). A deterministic approach was used to analyse the qualitative behaviour in dependence of key parameters, while a stochastic version permitted testing of the robustness of the design to transcriptional noise. In this section, we will concentrate on these two frameworks.

As chemical and biological processes are inherently stochastic, it seems natural to take this into account for modelling. However, stochastic simulations are generally computationally much more intensive, and for bigger models or greater numbers of interacting components, this burden quickly becomes limited. For metabolic processes, and in general reactions involving more than a few hundred molecules, the continuous deterministic approach provides a fairly good approximation.

The adequate forms of the mathematical expressions describing interactions and reaction velocities are often difficult to find at first, and sometimes different kinetic laws have to be tried out. In general, one can apply expression derived from first principles or, if the mechanism of reaction is not well defined or completely unknown, resort to generic or empirical rate laws. One of the most general approaches is to employ rate laws derived according to the law of mass action kinetics. In these equations, reaction rates are directly proportional to the activities of the reactants (e.g. concentrations in dilutions and partial pressures in gas phase) to a power, called the order of the reaction for this reactant, which is equal to its stoichiometry. This allows automatic generation of kinetic expressions for bigger reaction networks with only stoichiometric information, by fitting experimental datasets (sometimes leading to reaction orders that differ from stoichiometries). While this approach is widely applied in chemical systems and also has been quite successfully used in signal transduction, it leads to a high number of parameters and intermediary steps, and needs the explicit inclusion of catalysing enzymes. For enzyme-catalysed reactions with a known reaction mechanism, mechanistic rate laws using quasi steady-state or rapid equilibrium assumptions can be applied. The most common rate laws can be looked up in reference books (e.g. Segel (1993) or Cornish-Bowden (2004)) or derived using methods such as the graph-based one derived by King & Altman (King & Altman 1956; Chou 1989). However, for this approach a detailed knowledge of the reaction mechanisms and modifying effectors is essential. Each reaction has also to be treated individually, which might not be feasible for larger models. As an alternative, generic expressions can be used, which show the general behaviour of enzyme-catalysed reactions for varying ranges around reference states of the system. These allow the inclusion of experimentally derived parameters, activators or inhibitors to some extent, even if the exact mechanisms are not known. The simplest forms of these are the irreversible Michaelis–Menten and Hill-like rate laws. However, as many reactions cannot be assumed to be mostly unidirectional (Cornish-Bowden & Cardenas 2001), generic reversible forms for the most commonly used biochemical rate laws have been proposed. Examples are the convenience rate law (Liebermeister & Klipp 2006) and the reversible Hill equation (Rohwer et al. 2007). These rate laws also allow one to include thermodynamic constants, which are easier to measure than kinetic constants, and to easily adopt experimentally determined parameters, while displaying behaviours similar to more detailed mechanisms over a broad range of concentrations.

Some modelling tools offer predefined rate laws. For instance, COPASI and WebCell have a wide range of enzyme and general kinetic laws which can be easily incorporated into the model or used to create more elaborate ones if necessary. Another interesting feature offered by COPASI is the ability to transform all reversible reactions in a model into pairs of irreversible ones. While this of course only works for simple rate laws, it facilitates the use of subsequent stochastic evaluations, as these require the use of probabilities for elementary molecular events.

A convenient way to try out different rate laws for larger models is shown by SBMLsqueezer (Dräger et al. 2008), a plug-in for CellDesigner. It allows one to choose single or groups of reactions, and to apply different kinetic laws from a list of formalisms. In order to assign the adequate rate law and use the correct reactants, products and modifiers, it analyses the diagram created by CellDesigner (a derived form of SBGN) and takes SBO annotations of the species, parameters and reactions into account. While this still needs some user interaction, it is a commendable improvement that greatly facilitates the creation of larger and complex models.

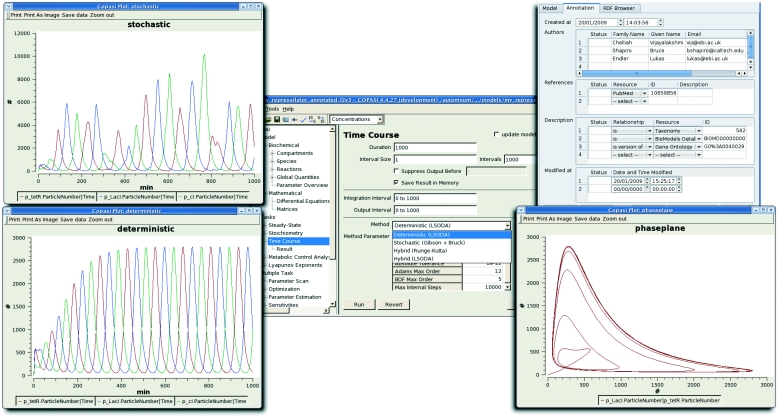
Various mathematical formalisms are employed to model gene-regulatory networks (reviewed in de Jong 2002). While there is evidence for the stochastic nature of transcriptional regulation (Fiering et al. 2000; Elowitz et al. 2002), deterministic approaches are often chosen due to their easier evaluation, and for simplicity of qualitative analysis. In our example, the repressilator, the authors used a Hill-type regulation function to simulate transcriptional repression, and first-order mass action rate laws for modelling translation, transcription and decay. Hill-type functions are often used to model gene expression or signal transduction as they are a subset of logistic functions, and they provide a sigmoid or step-like dose response to modulators, as found in some experimental results (Yagil & Yagil 1971; Rosenfeld et al. 2005; Kaplan et al. 2008). Sometimes, the Hill coefficient can be justified by cooperative binding behaviour—as in the case of the repressilator. In other cases, it can be due to dimensional restriction or more complex mechanisms, subsumed into a single step. Transcription and translation, while actually being composed of multiple reactions, are modelled as single first-order reactions. For the stochastic simulations, repressor binding had to be unravelled into single steps. COPASI allows one to interpret the model using different algorithms. Both a sample stochastic and deterministic time-course evaluation is shown in figure 5.

Figure 5.

COPASI offers various methods for evaluating dynamic models and displaying the results. Time courses of the protein numbers of the repressilator are shown here, calculated using a deterministic (LSODA) and a stochastic (Gibson–Bruck) method. The deterministic solution is also represented as the phase plane of the tetR and the LacI proteins, showing the convergence to a limit cycle. In a separate window, the MIRIAM annotations of the model element are shown.

Some problems cannot be sufficiently described without taking spatial inhomogeneities into account. Although many intracellular processes have been described with the assumption of a well-stirred reaction environment, this approach is insufficient for processes involving intracellular or extracellular gradients or heterogeneous populations of molecules (Kholodenko 2006). While some tools exist to help with the creation and simulation, there are no standard formats for interchange of models involving diffusional processes up to now. An exhaustive survey of the various spatial modelling approaches is beyond the scope of this paper. Different software tools and formalisms commonly employed are reviewed in Lemerle et al. (2005), Takahashi et al. (2005) and Tolle & Le Novère (2006).

Another problem plaguing modelling, in particular of signalling processes, is the combinatorial explosion resulting from alternative non-covalent binding of proteins, and molecular entities existing under different states (conformations, covalent modifications, etc.) One approach to avoid the problem is to use agent-based models of populations. In these methods, interactions between autonomous individuals are simulated. They have been successfully employed to simulate, for instance, bacterial chemo-taxis (Shimizu et al. 2003), tissue formation and developmental processes (reviewed in Thorne et al. 2007) and cancer growth (Wang et al. 2007; Zhang et al. 2009). A related approach is the use of rule-based models, where actual reactions are not described, but only the rules to generate them during simulations (e.g. Blinov et al. 2004; Lok & Brent 2005). As with spatial modelling, there are still few software tools supporting these frameworks, specifically for biology.

6. Finding and fitting parameters

To create a quantitative model, values for the various constants and parameters used in mathematical relations have to be derived. While there exist a vast amount of experimentally derived values in scientific literature, it is often hard to find the relevant ones in the multitude of publications.

For enzyme-catalysed reactions, there exist various databases helping to identify the appropriate values. Two databases providing kinetic parameters are BRENDA (Chang et al. 2008) and the above mentioned SABIO-RK (Wittig et al. 2006). Both offer a wide range of parameters and reactions extracted from primary literature, with powerful search options. SABIO-RK additionally offers the mechanism assumed in the original source and the ability to export reactions in SBML format. Help with directly searching the primary literature is offered by KMedDB (http://sysbio.molgen.mpg.de/KMedDB; Hakenberg et al. 2004). It allows PubMed abstracts to be searched for various kinetic parameters in combination with compound, organism or enzyme reaction identifiers. Further information on the thermodynamics of biological reactions is available at the TECRDB (Goldberg et al. 2004). Another helpful source of general interaction parameters is given by the Kinetik Data of Biomolecular Interaction database (Kumar et al. 2008).

Another common way of finding quantitative information is going through papers describing modelling efforts in the relevant fields. These can be a valuable source of pointers to relevant primary literature, and can also help with deriving or adapting experimental parameters to the form needed for the model. The above-mentioned databases and repositories of models are quite useful in this respect, as they not only give an overview of existing parametrized models, but also offer links to the primary literature.

Most of the parameters derived from the literature can nevertheless be taken only as guideline values for modelling. If measured time courses or steady-state data exist for the system to be described, several algorithms have been implemented for parameter estimation and refinement. For a short overview and comparison of some of these methods see Moles et al. (2003) and Rodriguez Fernandez et al. (2006). An intuitive and useful interface that features numerous global and local estimation methods is offered by COPASI. It allows simultaneous fitting of a subset of parameters to different sets of experimental values. Unfortunately, COPASI up to now has not included support for events. To estimate parameters in models containing events, the tool PET (http://mpf.biol.vt.edu/pet), closely connected with the JigCell suite, offers a convenient graphical interface also allowing multiple time series to be fitted simultaneously. Another tool supporting events is the command line-driven SBML-PET (Zi & Klipp 2006). For users of the commercial Matlab (The MathWorks, MA, USA) environment, SBtoolbox2 (Schmidt & Jirstrand 2006), a free package with SBML support, offers various estimation and optimization methods.

A completely different approach to search for adequate parameters is subsumed under the term optimization. While similar in its methods to parameter estimation, it differs in that it tries to reach a global goal rather than fit a given set of parameters, and is widely used in the engineering of metabolic systems. For a comprehensive review see Banga (2008). Again COPASI offers a range of different algorithms for minimization of a given target objective function.

Another interesting approach is inverse bifurcation analysis (Lu et al. 2006). It can be used to find parameter values exhibiting certain qualitative behaviours. For example, it can help in finding regimes that display certain kinds of switching behaviour, or creating more robust oscillators with a given system. Unfortunately, the tools available for this approach up to now have used Mathematica (Wolfram Research, Inc., IL, USA) or Matlab, and have still required quite some expert knowledge and skill. Hopefully, more user-friendly tools will be developed for this promising approach in the future.

7. Validation and evaluation of the model

Once a model has been created that can be run, it still has to prove its ability to reproduce experimental results up to a required accuracy and predict interesting and non-trivial observables.

Validation of a model can be performed in two stages. Observation of the qualitative behaviour of the model can be very informative in models having multiple steady states and showing switch-like or oscillatory behaviours. The qualitative behaviour can be studied either over small parts of the parameter space, by simply scanning over defined ranges of parameters and initial conditions, or by doing global bifurcation analyses. While the first procedure is easily accessible in many software packages, the second one requires more dedicated tools. CellDesigner offers simple scanning over a range of parameters through SBMLodeSolver, while COPASI offers more sophisticated possibilities. Using loops and combinations of tasks, scans over more than one condition or parameter are possible. For analysing the global qualitative behaviour of a model, numerical bifurcation analysis is one of the most widely used methods. Among the tools available, the free tools XPP-Aut (Ermentrout 2002) and Oscill8 (http://oscill8.sourceforge.net/), both using the Auto continuation library (Doedel 1981), have been used in biological modelling (e.g. Csikász-Nagy et al. 2006). Converters from SBML to the format used by XPP-Aut and Oscill8 are integrated in JigCell, COPASI, SBW, SBtoolbox2 and Biomodels database. Oscill8 can also be integrated into the SBW, allowing to seamlessly analyse models in this framework.

Model checking, originally used in computer science (Clarke & Emerson 1982; Queille & Sifakis 1982), is a different approach to validate the qualitative behaviour of systems. It allows one to test whether the system can fulfil certain objectives, for example reachability of certain states, the consecutive temporal activation of certain species or oscillatory behaviour. While support for quantitative dynamical models is still insufficient, BIOCHAM (Calzone et al. 2006) has limited SBML support and offers model checking capabilities. RoVerGeNe (Batt et al. 2007), a free add-on to the commercial Matlab environment, has been more specifically aimed at the needs of synthetic biology. Using piecewise affine, or for a better fit multi-affine, functions to model transcriptional regulation, it allows users to check whether a genetic regulatory system can exhibit a desired dynamical property or behaviour in a given range of parameters and initial conditions. More relevant to the design of networks, the tool can also be used to find parameters showing a desired behaviour and to test the robustness of the behaviour around these parameter values.

Qualitative analysis can also give hints as to which parameters offer the best success in achieving a desired behaviour or whether a certain design can exhibit the wanted function at all. Identifying the most promising parameters to change, of course, depends not only on the mathematical analysis, but also on the biological feasibility. While some characteristics such as promoter strength, transcript and protein stability are quite variable, enzymatic activities, for example, might be harder to tweak. Also as changes in the characteristics of biological components can at best be qualitative, it is important to find parameter ranges that show behaviour robust to variations. In the repressilator example mentioned above, the qualitative analysis led to the identification of a few key properties important for obtaining stable oscillations—strong promoters with tight cooperative repression and comparable mRNA and protein half-lives, with the protein half-lives mainly determining the period length. Apart from helping to choose the right biological components, these criteria also led the authors of the paper to introduce tags for proteases into the repressor sequences.

Model validity can also be checked by comparison of the results of simulation runs with quantitative experimental data, such as time courses or steady-state concentrations and fluxes. These can sometimes be derived from the literature, or retrieved from databases, for example, quantification of mRNA or metabolites. If the model satisfactorily reproduces experimental results and displays the desired behaviours, it can further be tested by experimental verification of its predicted results and behaviour. JigCell features a dedicated tool, the Comparator (described in Allen et al. 2003), to automatize this comparison. Using user-defined objective functions, it compares a model's results and transformations thereof with given sets of experimental data and assertions on model variables. It also allows different models or versions of a model to be tested to the same data and assertions and then to compare their performance.

8. Conclusion and outlook

The tools already available for model creation are quite sufficient for most applications. Use of inter-convertible formats such as SBML or CellML endows scientists with a rich toolkit supporting nearly all aspects of model evaluation, interpretation and refinement. Most of these tools are freely available for academic users, allowing scientists to try and use more than one program for each task. The ample annotation possibilities of these XML-based formats allow the models to be thoroughly described, which helps in collaborative model building and interpretation, as well as in model exchange and reuse.

Nevertheless, as most of the tools have been designed for systems biology purposes, with a slightly different modelling process in mind, they lack some of the features desirable in synthetic biology. Firstly, they hardly support the modular building process used in some efforts to create synthetic gene regulatory systems. Some tools try to include the available resources targeting synthetic biology—such as the MIT's registry of standard biological parts—as model building resources. While this looks quite promising, they currently offer only a few modules of the available biological elements. Although some of them support general exchange formats and thereby allow for easy export to other tools, they are restricted to only a small number of mathematical formulations, and lack integration of metabolism and signal transduction cascades.

Another feature barely supported up to now is the ability to use qualitative behaviour prediction to guide the design process. Tools that deduce possible behaviours and suggest feasible layouts could be very helpful in the first stages of a synthetic biology project. BIOCHAM offers this facility to some extent, but more tools for deterministic and stochastic kinetic modelling would be desirable. While parameter estimation and optimization are integrated in many programs with intuitive interfaces, qualitative analysis capabilities are mostly found in separate dedicated tools, requiring more mathematical skills and expertise. Efforts to make these tools more accessible to mathematically less proficient scientists would be very useful for both the systems and synthetic biology communities.

A general problem in both systems and synthetic biology is the lack of tools supporting standardized annotation of model elements and biological entities. Some standards have only recently been agreed upon by a broader part of the community, so some time may still be needed until widespread adoption. We believe the use of such a standardized annotation is a necessary development for the interchange and reuse of models and modules by different scientists and tools. One very successful effort in developing a standard, publicly available database of biological parts for synthetic biology has been created in the BioBrick registry of standard biological parts (http://partsregistry.org/). In a recent publication, Canton et al. (2008) proposed a promising way to represent quantitative characteristics of biological devices in the form of a data sheet and demonstrate it on a device composed of BioBrick parts. Mathematical modelling and in silico design of systems would profit very much from the adoption of such standards by the community.

As the vibrant and quickly growing communities of synthetic and systems biology have produced a plethora of tools and algorithms, we are optimistic that the features mentioned above will be implemented soon. The use of open standard formats and community-based development has proved to be of great value in biological modelling and hopefully this successful trend will continue and widen to newly emerging fields.