Partitioning of Functional Data for Understanding Heterogeneity in Psychiatric Conditions

An important goal in medical research is to identify groups of subjects characterized with a particular trait or quality and to distinguish them from other subjects in a clinically relevant way. Measures of biological phenomena, in general, and of psychiatric conditions, in particular, often exhibit symmetric shapes resembling a normal distribution; yet, the statistical approaches predominantly applied have been based on an assumption of underlying categories, whether observed or latent. It is well known that members of homogeneous populations with symmetric (multivariate) unimodal distributions can exhibit very distinct characteristics. Tarpey [2007a] and Tarpey et al. [2008] notice that partitioning of such homogeneous distributions is of importance even if distinct underlying categories are not assumed to underlie the measured phenomenon. For example, guidelines for treatment for depression would require the identification of a cut off on a given depression measure, whether or not the measure exhibits evidence for distinct clusters or mixtures.

The first goal of this paper is to introduce a principled statistical method for studying variation within homogeneous distributions of psychiatric data without the assumption of existing mixtures. The second goal is to obtain clinically relevant partition of the distribution of the trajectories of depressive symptoms during treatment with antidepressants. The method of [Tarpey et al., 2009] based on principal points characterization is applied to partition curves of symptoms of depression over time for the purpose of identifying responders to specific and non-specific treatment effects. Data from one study is used for determining a useful partitioning and an external validation of this partitioning is performed using a second study.

1. Introduction

The issue of “specific” and “non-specific” effects in pharmacotherapy for mental disorders has been a long-standing problem in psychiatry [Quitkin et al., 1987b,a, 2000; Stewart et al., 1998; Ross et al., 2002], and we briefly state it below. Pharmacologic agents are tested in placebo controlled treatment trials and their efficacy is estimated by subtracting the proportion of responders in the placebo group from the proportion of responders in the active drug group. Behind this procedure is the idea that some of the responders in the drug group would have responded to non-specific aspects of the treatment and that the proportion of such subjects is equal to the proportion of responders in the placebo group. Responders in the placebo group are called “non-specific” responders and the reasons for their response have been postulated to include spontaneous remission, life events, the non-specific effect of contact with clinical staff and the non-specific effect of taking a pill. In addition, the responders in the drug group include “specific” responders, those who respond to the specific active chemical component in the drug that is not in the placebo pill. This suggests that the responders in the drug group are a mixture of (at least) two types of individuals: “non-specific” and “specific” responders to the medication. It would be important to be able to distinguish between such responders to drug treatment, since the type of response (“specific” or “non-specific”) might have meaningful implications for the treatment plan and maintenance of the clinical condition. For example, if a patient is not benefiting from the active chemical component in a drug, it is more likely that s/he would relapse while taking the medication than would a subjects who actually benefits from the active chemical in the medication. Conversely, a patient who discontinues the drug too soon after improving might be more likely to relapse if s/he was a specific responder than if s/he was a non-specific responder.

Attempts to identify the non-specific responders to pharmacotherapy by examining the baseline characteristics of responders in the placebo arm and contrasting them to the characteristics of the responders in the drug arm of treatment trials have yielded limited results. Such an approach does not account for the fact that there might be non-specific responders among subjects treated with the drug and therefore it does not allow sufficiently precise differentiation between the specific and non-specific responders among subjects treated with the drug. In psychiatry, in addition to treatment trials for establishing drug efficacy, studies are performed to investigate the necessary duration of drug treatment after response to initial acute treatment for depression. These studies are called discontinuation trials and they offer an opportunity for the development of algorithms for identification of different type of responses to treatment. Discontinuation trials use the following two-phases design: Acute treatment phase: patients are openly treated with the antidepressant under investigation for a specific standard duration of time (say, 12 weeks); and Discontinuation phase: responders to the acute treatment are randomized to double blind continuation on the medication or a switch to placebo. In the discontinuation phase subjects are followed until relapse or end of the study. A variation of this design is to randomize the responders to the acute treatment to more than two groups allowing discontinuation of medication after different durations of the treatment. With respect to the outcome during the discontinuation phase one would hypothesize the following: (I) subjects with “specific” response should relapse when switched to placebo; and (II) subjects with “non-specific” response would relapse with equal frequency whether they remain on the drug or are switched to placebo. Data from such studies, including course of symptoms during acute treatment and baseline covariates, can be used for development and validation of algorithms for identifying specific and non-specific responders.

In the manner this problem has been described so far, it appears that the goal is to identify two different classes of subjects: “specific” and “non-specific” responders. Cluster analysis and finite mixture models for cross sectional data [Titterington et al., 1985] and growth mixture models for longitudinal data are typically used for this purpose [Muthén and Shedden, 1999; James and Sugar, 2003; Elliot et al., 2005]. All of those methods presume the presence of distinct groups and attempt to find them using different approaches. If the distribution is homogeneous, however, they all fail in one way or another, e.g. lack of convergence, lack of unique solution, interpretability (for example, when three clusters are postulated by the theory, but only one is identified by clustering technique). Perhaps the biggest failing though is that the methods may converge to a solution with two or more latent groups that are artificial manifestations of the algorithm because the distribution is homogeneous [e.g. Tarpey et al., 2008].

Yet, even when the (multivariate) distribution of clinical and biological characteristics appears perfectly homogeneous, symmetric and even normal, individuals in the population can still exhibit widely different characteristics. For example, even though the distribution of blood pressure may be perfectly homogeneous symmetric and normal, the blood pressures of hypertensive subjects differ from those of normo-tensive individuals and, what is more important, these differences correspond to differences in a variety of other health outcomes. As another example, consider a bivariate normal distribution with mean (0, 0) and some variance S. Suppose this distribution represents the slope and concavity of curves with the same intercept. In this distribution there will be curves with an overall increasing or decreasing trend, with a concave up or concave down shape, depending on the values of the slope, and curvature. Thus, there are clearly distinct shapes in this distribution, which is perfectly homogeneous symmetric and normal. While it doesn't make sense to look for distinct clusters or mixtures in this case, a coherent question would be to identify shapes that are representative of the distribution.

Symptomathology measures used for identification of types of treatment response (e.g. specific vs. non-specific) such as the longitudinal course of symptoms during acute treatment and baseline characteristics are typically homogeneous and lacking evidence for distinct categories or latent groups. Even though methods such as discriminant analysis, clustering, finite mixture models and latent class models and their variants for longitudinal data, such as growth mixture models, can still be applied to such data, here we take a different approach. We acknowledge explicitly that the distribution of symptom measures can be homogeneous and that distinct clusters may not exist. Never the less, we aim to find a partitioning of this (possibly) homogeneous distribution such that the characteristics of individuals are distinct between partitions.

Recently, cluster analysis methods have been proposed for data consisting of curves [e.g. Heckman and Zamar, 2000; Abraham et al., 2003; Tarpey and Kinateder, 2003; Tarpey, 2007a]. Tarpey et al. [2003] used principal points [Flury, 1990, 1993] which are cluster means for theoretical distributions to identify representative curve profiles in a longitudinal depression study. These cluster and principal point methods can be applied to homogenous distribution. Tarpey et al. [2009] proposed a simple method for estimating principal points for longitudinal mixed effect models that directly models the random effects, can handle missing data and covariates, and can also be applied to growth mixture models. The partitioning based on this approach is a principled statistical method, optimizing criteria appropriate for the data at hand. We apply this method here for the purpose of identifying profiles of symptoms change during treatment that might be associated with type of treatment effect. Two studies are utilized in this investigation. Data from the Study A, serving as training data, is used to describe the distribution of drug-treated individuals with respect to the course of their symptoms severity during acute treatment (phase 1 data) and the partitioning method based on principal points for longitudinal mixed effects model is applied. Data from phase 2 is used for internally validating the clinical importance of the partitioning by examining outcomes during the randomized discontinuation phase of patients within a given section of the selected partition. As test data for external validation we use the data from Study B.

The rest of this paper is organized as follows. Section 2 summarizes the partitioning method developed in Tarpey et al. [2009]; Section 3 describes two discontinuation studies. The selected partition and the validation results are reported in Section 4. In Section 5 we discuss why the approach taken here might be preferable to classical approaches for clustering in the context of mental health. We discuss limitations and extensions as well as implications for psychiatric research.

2. Partitioning of Longitudinal Data

An underlying principle of statistics is to extract the relevant information available in the data, typically through some summarization process, such as fitting a model. Given a random variable X, Tarpey and Flury [1996] defined a random variable Y to be a self-consistent approximation to X if Y is a measurable function of X and

$$E[\mathit{X}|\mathit{Y}]=\mathit{Y}\text{a.s.}$$

Examples of self-consistency are principal components, principal curves [Hastie and Stuetzle, 1989], principal variables [McCabe, 2005], and principal points [Flury, 1990, 1993]. Our focus will be on principal points. Let X denote a random vector. Given a set of k points ξ₁, …, ξ_k, define Y = ξ_j if ‖X − ξ_j‖ < ‖X − ξ_h‖, for h ≠ j. If Y is self-consistent for X, then the points ξ₁, …, ξ_k, are called k self-consistent points of X [Flury, 1993]. If E‖X − Y‖² < E‖X − Y*‖² for any other k point approximation Y* to X, then the k points ξ₁, …, ξ_k are called k principal points of X [Flury, 1990]. Principal points can be regarded as cluster means for theoretical distributions and can be nonparametrically estimated using the k-means algorithm [Hartigan and Wong, 1979].

Let x denote a vector of outcomes for an individual observed over a period of time. Then the standard linear mixed effects model is expressed as:

$$\mathit{x}=\mathit{S}\mathit{\beta }+\mathit{Z}\mathit{b}+\mathit{\epsilon },$$ (1)

where β is a vector of fixed effects, b is a vector of random effects assumed to have mean zero and covariance matrix D, ε is a mean zero vector of random errors with covariance matrix σ²R assumed to be independent of b. S and Z are design matrices.

The shapes of the functional data profiles are determined by the regression relation Sβ + Zb in (1). Here we consider the case of S = Z. The more general case and the case with covariates is examined in [Tarpey et al., 2009]. The goal is to find a self-consistent approximation to Z(β + b) in terms of k principal points, which will be self-consistent for x. The principal “points” in this case correspond to points in function space L² and are actually curves.

Because the regression curves in (1) are determined by β+b, a self-consistent approximation to x; by k curves can be obtained by estimating the k principal points of the N(β, D) distribution, assuming the random effects are normally distributed. The method described here can be adapted to non-normal random effect distributions as well. Maximum likelihood estimators of k principal points of the linear mixed effects model are obtained by first fitting a linear mixed effects model to obtain β̂ and D̂, the maximum likelihood estimates of β and D in (1), and then determining the k principal points of the distribution

$$N(\widehat{\mathit{\beta }},\widehat{\mathit{D}}).$$ (2)

Analytical solutions for the k principal points of the distribution in (2) do not exist except in very simple cases (e.g. small values of k in low dimensions). A very simple computer intensive solution to finding principal points called the parametric k-means algorithm [Tarpey, 2007b] is to apply the k-means algorithm on a very large sample simulated from (2) after the parameters in the linear mixed effects models have been estimated via maximum likelihood estimation (MLE). It then follows that the cluster means from the simulated sample are approximately MLE of the principal points of the linear mixed effects model [Tarpey, 2007b, Section 3].

The parametric k-means algorithm is quite flexible and can be implemented for non-normal random effect distribution such as the skew-normal distribution [Arellano-Valle et al., 2005]. The only requirement is to be able to simulate from the given distribution. In addition, even if a growth mixture model is needed to account for latent categorical predictors, the parametric k-means algorithm can be applied to the estimated finite mixture as well [Tarpey, 2007b, Section 5] to identify different profiles within a mixture.

To associate an observed outcome x_i with a particular principal point ξ_j, [Tarpey et al., 2009] define a posterior probability π_ij as the probability that the ith observation is associated with the jth principal point, j = 1, …, k. Define an indicator variable d_ij which equals one if x_i lies in the area defined by the jth principal point function (or curve) and zero otherwise. That is, d_ij = 1 if x_i(t) is closest to ξ_j(t) using an L² metric. Let β + b_i ∈ ℜ^q denote the q-dimensional regression coefficients (fixed effects plus random effects) for the ith individual. Define a “domain of attraction” D_j for the jth principal point as the subset of the sample space closest to the jth principal point. Then d_ij = 1 if ‖(β + b_i) − ξ_j‖² is less than the squared Euclidean distance between β + b_i and any other principal point coefficient vector ξ_h, h ≠ j. Analogous to the posterior probabilities for finite mixture models, we can classify an observation x_i based on the largest values of E[d_ij|x_i] for j = 1, …, k. From well-known results on the multivariate normal distribution, the conditional distribution of (β + b_i) given x_i is

$$\begin{array}{c}(\mathit{\beta }+{\mathit{b}}_i)|{\mathit{x}}_i\sim N({\mu }_i,{\sum }_i)\hfill \\ {\mu }_i=\mathit{\beta }+{({\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\sigma }^2{\mathit{D}}^{-1})}^{-1}{\mathit{S}}_i^{\prime }({\mathit{x}}_i-{\mathit{S}}_i\mathit{\beta }),\hfill \\ {\sum }_i={({\sigma }^{-2}{\mathit{S}}_i^{\prime }{\mathit{S}}_i+{\mathit{D}}^{-1})}^{-1}.\hfill \end{array}$$ (3)

Therefore the posterior probability π_ij that the ith observation is associated with the jth principal point can be defined as

$$\begin{array}{cc}{\pi }_{ij}\hfill & =E[d_{ij}|{\mathit{x}}_i]\\ \hfill & =\mathit{\text{Pr}}[(\mathit{\beta }+{\mathit{b}}_i)\in D_j|{\mathit{x}}_i]\hfill \\ \hfill & ={\int }_{D_j}N(\mathit{w};{\mu }_i,{\sum }_i)d\mathit{w},\end{array}$$

where w is the integration variable. Typically the q-dimensional regions D_j will be complicated convex subsets of R^q and analytical evaluations of this integral are not possible. However, the posterior probabilities can be estimated via a Monte Carlo simulation. For each observed outcome x_i, simulate a large sample from the conditional distribution (3) with maximum likelihood estimates plugged in for the parameters in (3). Then the estimated posterior probability π̂_ij is computed as the proportion of the simulated sample that is closer to ξ̂_j than to ξ̂_h, h ≠ j. Posterior probabilities can be used to classify new observations.

If the distribution is a finite mixture, the number of mixtures, even if not known, is a fixed number that we determine either correctly or incorrectly. The situation with principal points is different: continuous distributions have k principal points for any k > 0 and these principal points can be estimated. Therefore, k is chosen to produce interpretable results. In a functional data analysis setting, the value of k should be chosen so that the distinct curve shapes in the data are captured by the k principal points. If k is too large, several of the principal point curve profiles might have similar shapes. A value of k can often be chosen that is meaningful for the particular application at hand. In examining the profiles of symptoms change during acute treatment we will use information about subjects' relapse during the double blind discontinuation phase to guide the selection of number of strata in the partition. In addition we will consider the choice of k that explains a high percentage of variability in the underlying distribution. The percentage of variability explained can be based on the usual ANOVA sum of squares: the within group sum of squares is computed by squaring the distance between an observation and the principal point to which it is classified; the total sum of squares is computed by squaring the distance between each observation and the overall mean (which is the principal point for k = 1). Thus, the proportion of variability explained by the k principal points is

$$R^2=1-[\text{SS}\left(\text{within group}\right)/\text{SS}\left(\text{total}\right)].$$ (4)

The within and between sum of squares can be computed from the simulation sample used for the parametric k-means algorithm. As k → ∞, R² → 1. Often values of k as small as 4 or 5 can explain up to 70-80% of the total variability.

3. Two Discontinuation Studies

Here we describe two studies performed with the goal of determining the optimal duration of treatment with fluoxetine for patients with major depression McGrath et al. [2000, 2006]. Depressed patients were treated openly for 12 weeks with a fixed dose of fluoxetine. Symptoms severity was assessed with the Hamilton Depression Rating Scale (HAMD) and Clinicians' Global Impression of improvement scale (CGI) at baseline and at weeks 1, 2, 3, 4, 6, 8, 10, 11 and 12. The HAMD scores are the sum of the severity rating of a number of depression related behaviors and symptoms (such as feeling hopeless, loss of interests, difficulty sleeping) rated on a scale 0 to 3, with high HAMD scores indicating more severe depression. The CGI (improvement) is a scale from 1 to 7 with 1 indicating that the patient has improved very much since baseline, 4 denoting no change, and 7 indicating that the patient has gotten very much worse. At the end of the acute open treatment phase, patients were judged by clinicians to be either responders or non-responders based on CGI: responders were subjects who had scores of 1 (very much improved) or 2 (much improved) at both of the last two assessments (weeks 11 and 12). Responders entered the double blind phase of the study and were randomized to either continue on fluoxetine or to switch to placebo. Subjects were observed for relapse at bi-weekly visits and were called for assessment again in a week if symptoms worsened. Relapse was defined as CGI scores of 3 or more at two consecutive weeks. Study A and Study B had exactly the same inclusion/exclusion criteria and same definition for response to the acute treatment and for relapse in randomized discontinuation phase. Study A enrolled 839 subjects in the acute open label phase; of the responders to acute treatment 395 agreed to be randomized in the double blind discontinuation phase of the study. Study B enrolled 627 subjects in the acute open label phase and 262 of the responders to the acute treatment were randomized in the second phase of the study.

The second phases of these studies and how we use the data to help identify specific and non-specific responders to acute treatment are described below.

3.1 Study A

In the double blind phase of this study responders to the acute treatment were randomized to four discontinuation arms: (i) switch to placebo at randomization (after 12 weeks of active treatment); (ii) switch to placebo 14 weeks after randomization (after 26 weeks of active treatment); (iii) switch to placebo 26 weeks after randomization (after 9 months of active treatment); and (iv) stay on active treatment to the end of the study, which was 52 weeks after randomization (64 weeks of active treatment). Subjects who relapse at any time are taken out of the study and treated openly as appropriate.

The purpose of the study was to establish the optimal treatment duration [McGrath et al., 2000]. To this end three comparisons were made. First, subjects on placebo (arm (i)) are compared to subjects on fluoxetine (arms (ii), (iii) and (iv)) with respect to 14 weeks survival without relapse. This comparison addresses the question whether subjects who are treated for depression with standard course of 12 weeks of antidepressant (here fluoxetine) and respond to the treatment, can safely be taken off the medication. Higher relapse among subjects randomized to placebo than among those randomized to drug after the 12 weeks acute treatment will indicate that patients should continue taking antidepressant. If there is no difference between the relapse rates on drug and placebo, the conclusion would be that when subjects respond to standard acute treatment for depression, continued treatment is not necessary. The second comparison we make addresses the question whether after responding to a standard 12 weeks course for treatment of depression and maintaining remission during an additional 14 weeks of active treatment (i.e. a total of 6 months of treatment), subjects can safely be taken off the medication. For this comparison we use data from subjects in arms (ii), (iii) and (iv), who are still in remission at week 14 after randomization. Twelve weeks survival without relapse is compared between subjects in arm (ii), who were switched to placebo, against subjects in arms (iii) and (iv), who were maintained on drug. The third comparison is between subjects in arm (iii) vs. arm (iv) who are still in remission at the time when subjects in arm (iii) were switched to placebo. This comparison addresses the question whether subjects who have been treated continuously for nine months with an antidepressant and are still in remission can safely be taken off the drug without increased risk for relapse.

Conceptualizing treatment response as “specific” or “non-specific” is relevant to clinical practice — some individuals may require continuous treatment with medication (specific responders), while for others continued drug might not be needed (non-specific responders). In addition, individuals who achieved spontaneous remission might have a low relapse rate both on drug and placebo; such subjects will be different from a group of patients who are equally likely to relapse on placebo and drug, but at a higher rate. The later might be non-specific responders who have temporarily benefited from the pill and/or clinicians attention, but do not have sustained benefit to these effects. These are the subjects properly called “placebo responders” as they respond to non-specific aspects of the treatment; they are distinct from those who experience spontaneous remission irrespective from treatment and are also distinct from those who benefit specifically from the active chemical in the pill.

We use Study A to establish a partitioning of the responders to the acute phase that allows us to identify groups of subjects who might be experiencing specific treatment effect. Using the principal point methodology, we describe these subjects in terms of their course of symptoms decline during the acute treatment.

3.2 Study B

In Study B responders to the acute treatment were randomized to either switching to placebo at randomization, or to continuing the drug until the study's end, which was one year after randomization McGrath et al. [2006]. We use this study to validate the partitioning proposed based on analysis of Study A.

4. Results

The principal points for mixed effects models approach is taken to partition the trajectories of symptoms change during acute treatment. The HAMD ratings at weeks 0, 1, 2, 3, 4, 6, 8, 10, 11, and 12 of acute treatment were modeled with a polynomial of 3^rd degree using the following mixed effect model for longitudinal data:

$$Y_{ij}={\beta }_0+{\beta }_1{t}_j+{\beta }_2{t}_j^2+{\beta }_3{t}_j^3+b_{0i}+b_{1i}{t}_j+b_{2i}{t}_j^2+b_{3i}{t}_j^3+{\epsilon }_{ij},$$ (5)

where Y_ij is the HAMD score for the i^th patient at the j^th assessment occasion; $t_j=(1,t_j,t_j^2,t_j^3)$ and t_j is the time of the j^th assessment; and ε_ij are independent error terms assumed $\mathcal{N}(0,{\sigma }_{\epsilon }^2)$. The distribution of the random coefficients b_i = (b_0i, b_1i, b_2i, b_3i) is assumed 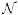(0, D), where D a 4 × 4 covariance matrix. We transformed the time measurements t_j to be centered at 0 to avoid colinearity problems. Data from subjects with at least 3 data points are used which reduced the sample size from 839 to 804. Covariates were also considered allowing interaction between the covariates and time. The results presented here are based on the model without the covariate. The covariates effects on partitioning is examined in Tarpey et al. [2009].

The trajectories of symptoms decline during acute treatment for each subject are now represented by a 4-dimensional parameter β + b_i. We find the principal points for the distribution of these trajectories by utilizing the parametric k-means algorithm from Section 2. Specifically, the classic k-means algorithm (as implemented in R, function kmeans) is applied to 1,000,000 data points sampled from 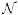(β̂, D̂).

The posterior probability for classifying individual profiles to the closest representative principal point profile is computed as explained in Section 2. Ten thousand data points are simulated from the conditional distribution of the coefficients β + b_i, given the observed outcomes of subject i shown in equation (3)s. We assign a subject to the principal point corresponding to the largest posterior probability.

4.1 Selecting partitioning based on Study A

4.1.1. Partitioning of acute treatment trajectories

Principal points for mixed effects models approach is used to partition the distribution of the trajectories of symptoms during acute treatment of all subjects in the acute treatment phase. Baseline covariates were examined for significant effect in model (5). The only baseline characteristic associated with the course of symptoms change during acute treatment was type of depressive features. Subjects with atypical features had on average a slower rate of change and higher overall levels of depressive symptoms. However, this covariate did not make the distribution of the symptom trajectories appear bi-modal. The distribution of the random coefficients obtained from a mixed effect model without covariates was not meaningfully different from the distribution of coefficients obtained from the model with a type of depression included as a predictor.

Using the parametric k-means algorithm, the distribution is partitioned into 4, 5, 6, and 7 parts. The percent variability explained by the partitioning, assessed as R² from (4) is reported in Table 1.

Table 1. Study A: Percent explained variation (R²) in the trajectories of symptoms severity during the acute treatment using different number of principal points k.

k	7	6	5	4
R2	0.78	0.76	0.72	0.67

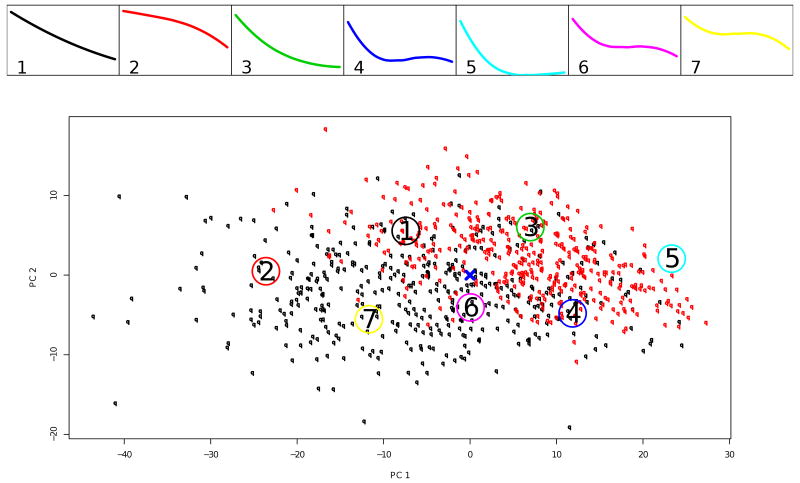
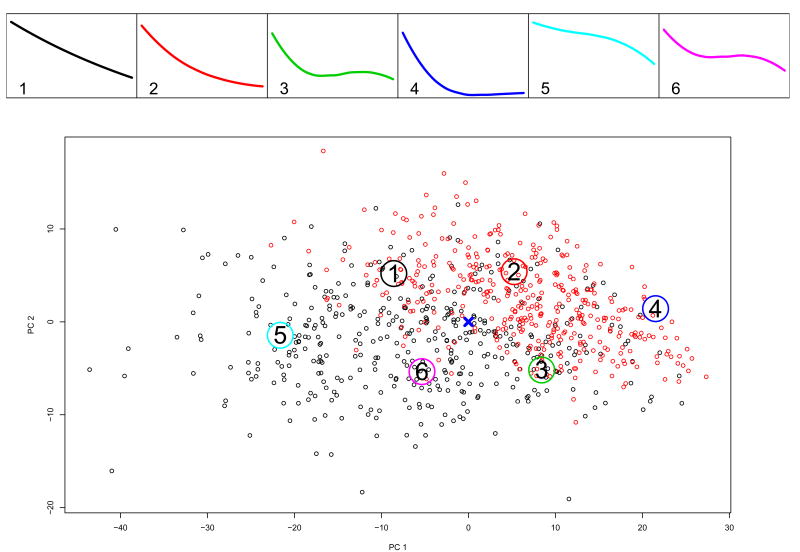
We show the partitioning based on k = 7 and k = 6 principal points on Figures 1 and 2. The trajectories corresponding to the estimated k principal points profiles are in the panels on the top. The bottom panel of each figure shows the individual trajectories for all patients in the acute treatment phase (n=804) represented by their random coefficients from model (5). On this panel for the purposes of graphing, the 4-dimensional vectors of random coefficients are projected onto their first two principal components. Subjects randomized in phase 2 of the study, i.e. the responders to the acute treatment, are plotted in red. The center of the distribution estimated by β is marked with a cross. The large numbered circles indicate the locations of the estimated principal points.

Figure 1.

Study A: k = 7 principal points for the trajectories of symptoms severity during acute treatment. The top panels shows the profiles corresponding to the estimated principal points. The bottom panel shows individual trajectories for the patients in the acute treatment phase represented by their random coefficients from model (5); in red are those who were responders to acute treatment and randomized in the discontinuation phase. For the purposes of graphing, the 4-dimensional vectors of random coefficients are projected onto the first two principal components. The large numbered circles present the estimated principal points.

Figure 2.

Study A: Like Figure 1 for k = 6.

Notice that the principal points of the homogeneous symmetric and normal distribution postulated for the random coefficients from model (5) exhibit quite distinct shapes.

4.1.2. Relapse during treatment discontinuation

Subjects randomized in Phase 2 were categorized as belonging to one of the partitions associated with the principle points based on the largest posterior probability as described in Section 2. Within a partition, a Log-rank test was used to compare the rate of relapse of subjects randomized to drug vs. those randomized to placebo.

First we looked at 14 weeks survival without relapse after standard acute treatment for depression. Of the 395 subjects who entered the double blind discontinuation Phase 2, 96 were in arm (i) and switched to placebo at randomization.

Table 2 summarizes the results for k = 7, 6, 5 and 4. The columns labeled “14 weeks survival after 12 weeks of acute treatment” address the question whether subjects who have been treated acutely for depression and have responded to the treatment can be taken off the drug, or discontinuing the drug after acute response (12 weeks of treatment) would increase their risk for relapse as compared with the continued drug maintenance. For example, when k = 7 of the 395 subjects who responded to acute treatment and entered Phase 2, 77 are in the partition associated with principal point #1 (see Figure 1): 65 of them were randomized to continue on the drug and 12 were switched to placebo. Of those continuing on the drug, 11 relapsed in the first 14 weeks and the remaining either remained in remission or dropped out before week 14 while still in remission and were censored in the survival analysis; of the 12 switched to placebo 7, relapsed in the following 14 weeks. The Log-rank test comparing drug vs. placebo with respect to relapse in the 14 weeks after 12 weeks of acute treatment has p = .0007. Responders to 12 weeks of acute treatment who are associated with this principal point and who are switched to placebo are much more likely to relapse than those who are maintained on the drug for another 14 weeks. Thus, subjects with outcome profiles similar to the one depicted in the first box on the top panel of Figure 1 appear to have experienced the specific effect of the drug. An analogous observation can be made for subjects associated with principal point profile #3.

Table 2. Survival without relapse on drug and placebo for subjects in remission after (a) 12 weeks acute treatment for depression with drug; and (b) 12 weeks acute treatment plus 14 weeks of maintenance with drug, total of 6 months.

pp1	(a) 14 weeks survival after 12 weeks of acute treatment					(b) 12 weeks survival after 6 months of treatment
	Randomized to Drug		Randomized to Placebo		Log-Rank test	Randomized to Drug		Randomized to Placebo		Log-Rank test
	Total	Relapse	Total	Relapse	p	Total	Relapse	Total	Relapse	p
k = 7
1	65	11	12	7	.0007	20	5	13	5	.2912
2	4	1	2	0	.6171	1	0	1	0	1
3	101	29	45	21	.0020	38	5	17	9	.0009
4	69	5	21	9	.0333	24	5	12	2	.9597
5	34	9	9	4	.1385	14	4	4	0	.3614
6	23	5	7	1	.6487	7	2	5	2	.6693
7	3	1	0	0		1	1	0	0
k = 6
1	56	10	10	4	.0325	16	3	12	5	.1108
2	109	31	44	22	.0007	41	8	18	8	.0312
3	56	12	22	8	.1510	19	3	11	2	.8149
4	64	16	15	6	.0779	25	6	10	3	.2843
5	4	1	1	0	1	1	0	1	0	1
6	10	3	4	2	.2924	3	2	0	0
k = 5
1	82	24	32	14	.0524	27	5	14	5	.1741
2	13	2	2	0	.6889	6	1	3	0	.4795
3	18	5	3	2	.0753	5	2	2	2	.3459
4	104	22	36	14	.0138	35	7	17	5	.3892
5	82	19	23	12	.0004	32	7	16	7	.0204
k = 4
1	73	18	18	8	.0286	27	7	13	5	.1514
2	8	1	2	0	.7237	4	1	1	0	.6171
3	71	14	15	8	.0032	20	6	14	5	.6212
4	147	40	61	26	.0021	54	8	24	8	.0239

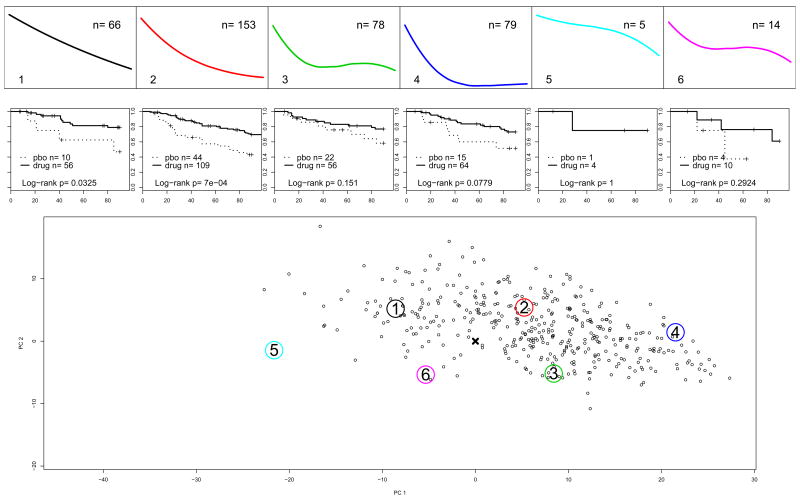
For k = 6, profiles #1 and #2 are very similar to profile #1 and #3 for k = 7 (compare Figures 1 and 2). Consequently, in Table 2 the Log-rank tests for these partitions indicate a strong difference between drug and placebo. Figure 3 presents the results for k = 6 principal points. The top panels show the profiles of the principal points (same as on Figures 2 and the number of subjects from each partition entering phase 2 of the study. Below them are the estimated Kaplan-Meyer survival curves and the p-values from the Log-rank test to compare relapse between continued drug vs. switching to placebo. The bottom panel shows the trajectory coefficients of the 395 subjects who entered phase 2 of the study, i.e. responders to acute treatment only. In contrast, the bottom panel of Figure 2 presents the trajectories of all 804 subjects in the acute treatment phase. Subjects are plotted based on their estimated random coefficients in Phase 1 from model (5) projected onto the 2-dimensional space of the first 2 principal components. Profiles #5 and #6 are clearly not typical for responders to acute treatment, i.e. they are characteristic of non-responders to acute treatment for depression with fluoxetine. Profiles #1 and #2 seem to represent a specific effect of the drug. Profile #3 is associated with a relatively low relapse on placebo, which might indicate a non-specific effect or a spontaneous remission.

Figure 3.

Study A: Survival without relapse in the first 14 weeks after response to acute treatment for subjects in k = 6 partitions. The top panels show profiles of the principal points for the distribution of the trajectories of symptoms change during acute treatment, Phase 1 of the study. The bottom panel shows the Phase 1 trajectories of symptoms decline only for the responders to acute treatment. The large numbered circles present the estimated principal points. The middle panels show Kaplan-Meyer survival curves during the 14 weeks after randomization into Phase 2 and p-values for Log-rank tests.

Next we looked at subjects who have been on the drug for a total of 6 months: 12 weeks acute treatment and 14 weeks of maintenance — these are responders to acute treatment who were randomized to arms (ii), (iii) and (iv) (see Section 3.1) and were still in remission at 6 months when subjects randomized to arm (ii) were switched to placebo. There were 157 such subjects of whom 72 were in arm (ii) and switched to placebo. We compared 12 weeks survival without relapse between those who continued on drug vs. those who switched to placebo. This comparison answers the question whether subjects who have been on an antidepressant for 6 months and are still in remission can be taken off the drug without increasing their risk for relapse. Alternatively, the question is whether there is a group of subjects who still need the drug after 6 months of treatment? The columns labeled “12 weeks survival after 6 months of treatment” in Table 2 summarize the results. For example, for k = 6 subjects with profile #2 who are switched to placebo after being successfully treated for 6 months seem to relapse more than those who are maintained on medication. The conclusion about this profile is confirmed by the results for k = 7 profile #3. Subjects with trajectories of symptoms decline similar to the other profiles appear to not require continuous drug treatment since the relapse rates in the other five partitions are close for drug and placebo.

We also looked at subjects who have been on the drug for a total of 9 months: 12 weeks acute treatment and 26 weeks of maintenance — these are responders to acute treatment who were randomized to arms (iii) and (iv) and were still in remission at 9 months when subjects in arm (iii) were switched to placebo. However, there were only 62 such subjects of whom 34 were in arm (iii) and were switched to placebo. There are too few subjects in each of the partitions to conduct meaningful analyses.

These analyses indicate that steady decline over the course of acute treatment, similar to curves #1 and #2 for k = 6, is associated with increased risk for relapse if the drug is discontinued before 6 months of continuous treatment with antidepressants. Additionally subjects with profiles similar to #2 might even need longer treatment, i.e. 9 months before drug discontinuation. Subjects with non-persistent decline are more likely to have similar probability for relapse whether the drug is discontinued or not at any time after response to acute treatment, indicating a response to non-specific aspects of the treatment.

4.2 Applying partitioning results from Study A to Study B

To validate the partitioning of the trajectories of symptoms change during acute treatment, we applied the partitioning that was selected based on clinical consideration using Study A (training data), to the trajectories from Study B (test data). Based on the results in Table 2 and figures similar to Figure 3 for k = 7, 5 and 4 we selected k = 6.

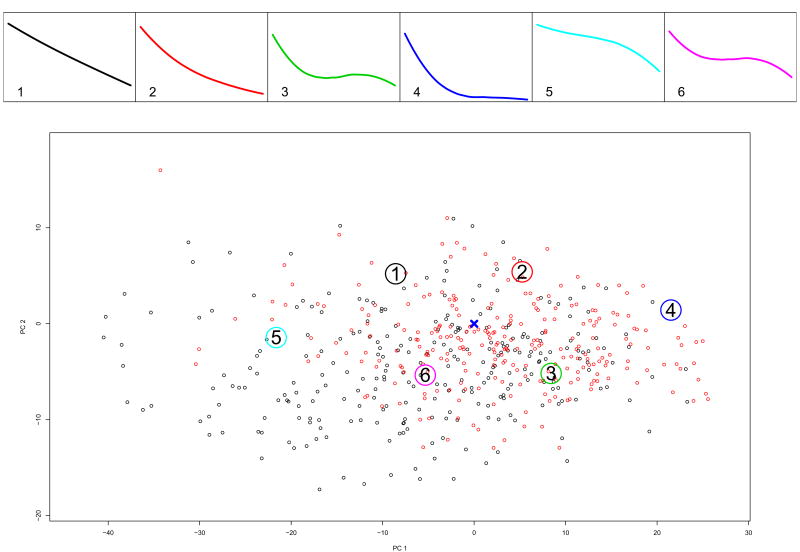
We estimated the conditional density of all subjects in Study B using the regression parameters and the distribution of the random effects from Study A using (3). Based on these conditional distributions we estimated the posterior probability for being in each of the k = 6 partitions and assigned subjects to the partition with highest posterior probability. Figure 4 shows the profiles corresponding to the principal points determined from Study A. The top panels are identical to the top panels of Figure 2. The bottom panel plots the trajectory coefficients of n = 530 of the total 626 in Study B, who had at least 3 assessments during the open phase. The figure shows their trajectories of symptoms change in Phase 1 projected onto the space spanned by the first two principal components of the coefficients from Study A. The locations of the principal points are the same in both figures, but the dots are different (compare with Figure 2). Notice how the distribution of symptom profiles in Study B is shifted towards lower values of the first and second principal components (lower left corner on Figure 4), i.e. the corner of non-responders to acute treatment. However, even though the profiles of non-responders in Study B are not represented very well by the k = 6 partitioning selected from Study A, these six principal points represent the responders adequately. Thus we continue with the k = 6 partition. Alternatively, we could have selected a partition with larger number of strata, k > 6.

Figure 4.

Study B: k = 6 principal points estimated from Study A. The bottom panel shows individual trajectories for patients in the acute treatment phase of Study B projected onto the plane span by the first two principal components of the coefficients from Study A. In red are indicated the trajectories of responders to acute treatment.

Relapse rates on a drug and placebo are compared within each partition, similarly to the analysis for Study A. Figure 5 shows the Kaplan-Meyer curves and the p-value of the Log-rank test. The bottom panel of the figure shows the trajectories of symptoms change during acute treatment for the Study B responders who were randomized in phase 2 (n=262). The results should be compared to those on Figure 3. Note, however, that Figure 3 shows results for 14 weeks survival (time given in days) without relapse after the acute treatment, where as Figure 5 shows 52 weeks survival (time given in weeks). Profiles similar to principal points 2 are associated with a differential relapse between continuation on drug vs. switching to placebo, as observed in Study A. In other words, with a partitioning based on one sample, we identified individuals from another sample who showed similar clinical characteristics, i.e. higher rate of relapse when switched to placebo after response to acute treatment as compared to relapse when continuing drug treatment. Such characteristics are consistent with response to specific drug affect. Principal point #4 in Study A was associated with higher relapse on placebo (although not statistically significant); in Study B this point shows a dramatic differentiation. As in Study A, profiles similar to #3 seem to be consistent with mainly non-specific treatment effect, since the relapse rates on drug and placebo are similar. However, unlike in Study A, here the relapse rate is very high, suggesting a transient placebo effect that wears off. Notice here that there are some differences: subjects in Study A with trajectories similar to principal point #1 have high relapse rates on drug, which was not the case in Study B.

Figure 5.

Study B: 52 weeks survival without relapse for subjects in remission after 6 months of active treatment. k = 6 partitions. The top panels show profiles of the principal points estimated from Study A. Shown also are the numbers of Study B subjects that were classified to belong to each partition. The bottom panel shows the Phase 1 trajectories of symptoms decline of Study B patients who were in remission after 12 weeks of acute treatment. The large numbered circles present the estimated principal points from Study A. The middle panels show Kaplan-Meyer survival curves in 52 weeks after 12 weeks of acute treatment and p-values for Log-rank tests to compare relapse on continued drug vs. switching to placebo.

5. Discussion

Understanding heterogeneity in phenotypical characteristics, symptoms manifestations and response to treatment of subjects with psychiatric illnesses continues to be a challenge in mental health research. As with other questions in psychiatry, the evidence for existence of different types or classes of responders to antidepressant treatment is not empirically evident immediately. Despite decades of research and debate, none of the currently accepted psychiatric disorders or conditions has been conclusively demonstrated to be a discrete entity. For example, many investigators have argued that the boundaries between mild to moderate unipolar depression and the anxiety disorders are arbitrary and that these conditions should be subsumed under the broader rubric of a “general neurotic syndrome”, which is on a continuum with normal functioning. The inability to resolve these fundamental nosological issues is due in large part to the difficulty of demonstrating the existence of distinct boundaries between psychopathalogical conditions.

A number of statistical approaches have been used in an attempt to address this problem. Some of the most frequently used approaches have been discriminant analysis (and examining the distribution of scores derived from it for evidence of bi-modality), cluster analysis, finite mixture models and latent class models. These techniques can be used to test the hypothesis that symptomathology (e.g. clinical and biological features, or family history) in a given sample is best characterized by two or more clusters, classes or distributions. However, the presence or absence of discreteness at the clinical or pathophisiological level does not necessarily correspond to discreteness at the level of etiology. Moreover, numerous factors can contribute to obscuring bi-modality when present (e.g. large variances compared with the difference between the means, or small prevalence of one of the populations). In addition, factors can contribute to the appearance of bi-modality when the distribution is not bi-modal (e.g. biased sampling). To fully resolve the question of discreteness in an etiological sense, it is necessary to have indicators of the underlying causal processes. Because etiology remains unknown for most psychopathological conditions, it is unlikely that any of these techniques, in and of themselves, can produce conclusive results regarding whether particular psychopathological conditions are discrete entities.

In the absence of such causal knowledge, it is not clear if distinct latent classes exist in most cases in psychiatry. Such is the case, considered in this paper: it is conceivable that there exist well-defined sub-populations corresponding to subjects responding to non-specific aspects of the treatment, those that respond to specific aspects of the treatment and those who do not respond to the treatment at all. Alternatively, it is possible that distinct sub-populations do not exist and instead the degree of specific and non-specific response might vary over a continuum with each subject falling along this continuum. Whether or not etiologically distinct classes exist, if the symptomathology data exhibit presence of distinct categories it would be useful to characterize these distinct distributions.

In our experience, most often the real question that mental health researchers have is what cut off points on various (usually) continuous clinical and biological characteristics should they use to help them guide treatment decisions and inform study designs. By tradition, these questions are formulated in terms of identifying distinct clusters. Familiarity with statistical methods for cluster analysis and the lack of widely known methods for describing heterogeneity without assuming different underlying clusters, have lead to the following consequences. On the one hand, questions are formulated in terms of discovering distinct underlying classes and on the other hand, the results from applying cluster-analytic methods, such as latent class, mixture and latent growth models are interpreted as ascertaining the presence of distinct conditions or medical diagnoses. The principal points methodology illustrated here is an alternative to these popular approaches, that might be better suited to the understanding of heterogeneity in some situation.

The principal points methodology is an approach to describing heterogeneity in any distribution including unimodal symmetric distributions like the Gaussian. Tarpey et al. [2009] further developed this methodology to describe the heterogeneity and to partition functions (or curves). In this paper we have shown how their methods can be used to formulate and answer an important question of clinical practice and research. In applications it would be desirable to be able to apply the methodology with more complex models for the sample curves than the cubic polynomial used here as well as to incorporate covariates. Tarpey et al. [2009] show how this can be done using different basis functions, for example B-splines and how covariates can be used to the partitioning.