Finger interaction during maximal radial and ulnar deviation efforts: experimental data and linear neural network modeling

Abstract

The purpose of this study was to characterize finger interactions during radial/ulnar deviation, including interactions with flexion movements. Subjects performed single-finger and multi-finger maximal voluntary contraction (MVC), and maximal forces and various indices of interaction among the fingers were quantified. MVCs in radial/ulnar deviation were 50–80% as strong as in flexion. Along with the ‘master’ fingers (i.e., those explicitly instructed to produce force), substantial force production was also observed in ‘slave’ fingers (i.e., those not explicitly instructed to produce force), a phenomenon termed: force ‘enslaving’. In addition, a drop in MVC during multi-finger tasks as compared to single finger tasks (force ‘deficit’) was also observed. A previously unreported phenomenon that we term: ‘preferred direction enslaving’ was also apparent; both master and slave fingers produced force in the instructed direction with a non-zero perpendicular component. Due to the architectural separation of the involved muscles, preferred direction enslaving provides strong evidence that enslaving results from neural rather than biomechanical factors. A final new phenomenon: ‘negative deficit’, or force ‘facilitation’ was observed in 46.4% of the trials in 21 out of 23 subjects during multi-finger lateral efforts and was further demonstrative of extensive interconnection among neurons serving hand muscles. The data were modeled with high accuracy (~4% mean square error) using a linear neural network with motor ‘commands’ as inputs and finger forces as outputs. The proposed network, equivalent to linear regression, can be used to determine the extent to which finger forces are influenced by peripheral constraints during functional prehensile activities.

Introduction

Hand function relies on fine coordination of digital forces. When grasping an object, the tangential and normal components of the digit forces and the points of force application form synergies related to both necessary grip force and maintenance of rotational equilibrium (Shim et al. 2003; Zatsiorsky et al. 2004a). While extensive experimental and modeling efforts have been made for finger flexion (reviewed in Johansson 2002), comparatively little attention has been paid to radial/ulnar deviation (‘RUdeviation’); the terms ‘radial’ and ‘ulnar’ deviation are adopted herein after Matheson et al. (1970) to refer to unambiguous directions with respect to the forearm. RUdeviation finger strengths have been reported (Matheson et al. 1970), but interaction among fingers during such tasks has not been studied.

It has been demonstrated that purposeful flexion force by one finger is accompanied by involuntary flexion force of other fingers; a phenomenon termed ‘enslaving’ (Li et al. 1998, 2004; Hager-Ross and Schieber 2000). It has also been demonstrated that a finger produces less flexion force during maximal multi-finger task than it does during maximal single-finger task; a phenomenon termed ‘deficit’ (Ohtsuki 1981a, b). Enslaving and deficit are complex phenomena that emerge from both anatomical and neural interconnections among digits (Kilbreath and Gandevia 1994; Schieber and Santello 2004).

These interactions have been modeled using artificial neural networks (Zatsiorsky et al. 1998; Li et al. 2002) and described with inter-finger connection matrices (Gao et al. 2003; Zatsiorsky et al. 2004b). Neural networks (NN), used in several studies of multi-finger synergies (see Latash et al. 2003), allow one to compute hypothetical independent ‘commands’ to individual fingers during multi-finger action (see ‘Neural network modeling’ for a more detailed description of ‘commands’). The term ‘mode’ has also been used instead of ‘command’ (Danion et al. 2003).

The main goals of the current study were: (1) to describe finger interaction during single- and multi-finger force production in RUdeviation, and (2) to model this interaction using a NN approach, similar to the flexion networks used by Zatsiorsky et al. (1998) and Li et al. (2002). We were particularly interested in comparing finger interaction in flexion to that in RUdeviation.

Methods

Subjects

Twelve females (age 23.0 ± 4.0 years, height 168.1 ± 5.9 cm, mass 63.0 ± 8.6 kg, hand length 16.8 ± 1.3 cm) and eleven males (age 25.0 ± 4.6 years, height 176.1 ± 2.6 cm, mass 75.8 ± 4.5 kg, hand length 18.3 ± 1.1 cm) participated. All were right-handed (only right hands were tested) and none reported upper extremity or neural pathology. Prior to participation all subjects gave informed consent according to the policies of the Office for Research Protections of the Pennsylvania State University.

Anthropometric measures of the hand were obtained from photocopies of the subjects' right hands. Average finger widths (measured at the middle of the proximal phalanx; ±standard deviations) for the females were: 18.6 ± 1.5, 17.8 ± 1.6, 17.0 ± 1.0, and 17.1 ± 1.2 mm for the index (I), middle (M), ring (R), and little (L) fingers, respectively. The males' finger widths were: 21.3 ± 1.3, 20.6 ± 0.8, 19.7 ± 1.0, and 18.9 ± 1.4 mm. Average female finger lengths (measured from the MCP joint to the apex of the finger pad) were: 70.8 ± 3.9, 77.2 ± 5.0, 71.4 ± 4.4, and 58.5 ± 4.7 mm, respectively. The male finger lengths were: 75.5 ± 5.6, 82.5 ± 6.1, 77.0 ± 6.1, and 62.7 ± 4.3 mm.

Apparatus

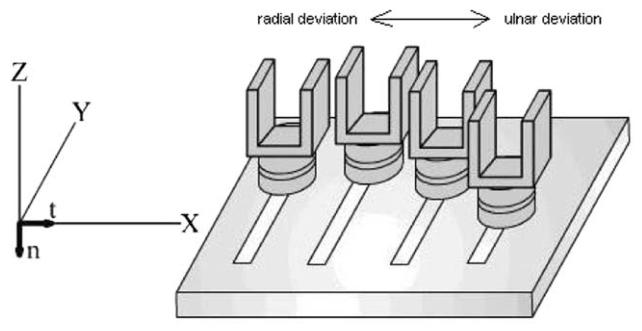
The apparatus design had two main purposes: (1) to allow natural finger action, and (2) to constrain forearm/wrist motion. Four U-shaped aluminum finger ‘slots’ were constructed (Fig. 1). RUdeviation was performed by pressing against the slot walls. The slots were attached to multi-component force/torque transducers (Nano-17; ATI Industrial Automation, Garner, NC, USA), which were in turn attached to an aluminum base. Transducer placement was such that, when the fingers were completely extended, the finger pad apexes were coincident with the center of the transducer faces. Of present interest are normal (F_n) and tangential (F_t) forces, which respectively coincide with the −Z and +X axes (see Fig. 1).

Fig. 1.

Experimental apparatus. The transducers, with 2 × 2 × 2 cm slots attached, were spaced 2 cm apart in the x direction, and their y positioning was determined according to subjects' finger lengths (which were obtained from a photocopy of their right hand)

The apparatus was placed on the surface of a table such that seated subjects had their right elbow resting on the table with forearm perpendicular to the display. Subjects were instructed to not move their elbows from their resting position to minimize forearm/wrist contributions.

The transducer signals were amplified and multiplexed using a custom-constructed conditioning box (ATI Industrial Automation) before being routed to a 12-bit analogue–digital converter (PCI-6031, National Instruments, Austin, TX, USA) and sampled at 50 Hz. Based on the manufacturer's specifications, errors of approximately 0.04 N were expected for the measured forces.

Procedure

The subjects' fingers were wrapped in segments of tensor bandage such that two layers of bandage lay between the skin and the apparatus. The bandage was used to restrict finger movement within the slots, and also as padding for subject comfort.

There were 15 experimental conditions tested (Table 1). Prior to each trial the task direction and the ‘master’ finger(s), i.e., those explicitly instructed to produce force, were displayed on the computer screen. Two repetitions of each of the 15 conditions were conducted. The best of the two repetitions was selected for analysis; there was no tendency for either the first or second to be better, even for repetitions near the end of the session (P = 0.317). Thirty trials were presented randomly.

Table 1.

Experimental conditions

	Master finger(s)	Direction	Conditions
Flexion	I, M, R, L, IMRL	−Z = +n	5
RUdeviation	I, M, R, L, IMRL	±X = ±t	10
		Total	15

The master fingers (index I, middle M, ring R, and little L) were those that were explicitly instructed to produce force. For the flexion and radial/ulnar deviation (RUdeviation) tasks, subjects produced maximal force in either the normal (n) or tangential (t) direction, respectively (see Fig. 1). The five-flexion tasks included four single-finger tasks and two multi-finger tasks. The RUdeviation tasks were the same except that they were performed in +t and −t directions separately. Two repetitions of each of the 15 conditions were performed, yielding 30 trials per subject

For each trial, subjects had up to 5 s to produce an MVC. They were permitted to ramp slowly to MVC, or to generate MVC in a brief thrust; the option was theirs for each trial. Subjects tended to thrust quickly initially, and then to surge later in the trial. The time-history is not considered further herein. The only data analyzed for each trial included a single sample of the four fingers' forces (F_n and F_t), at the instant of the task-defined maximum.

Protocol followed a previous finger MVC study (Li et al. 1998). Subjects were instructed to press as “hard as possible” with the master finger(s) in the given direction. They were also instructed to “focus only on the master finger” and to “ignore the other fingers even if they are producing force”. Feedback for only the master finger(s) and only the task direction (i.e., n or t) was presented on the computer screen. Subjects were required to rest 30 s between trials. Although they were permitted to rest longer if they desired, no subject exercised this option. No subject complained of pain or fatigue at any point during or after the experiment. The entire experimental session lasted approximately 40 min for each subject.

The experimental goal was to investigate interactions among finger forces but not their mechanical and/or neurophysiological origin. We used naïve subjects and followed the experimental design of previous studies with finger pressing (e.g., Zatsiorsky et al. 1998) to study naturally occurring force patterns in situations when only some of the fingers are required to produce force.

Data processing and statistics

Data were not filtered. The following indices were computed based on sets of finger forces measured at the time of maximum master force: (i) forces of all four fingers, (ii) enslaving, defined as force produced by a non-master (‘slave’) finger, and (iii) force deficit, defined as the difference between the force produced by a master finger in a multi-finger task and its peak force during the single-finger MVC test:

$$\text{Force deficit}=\frac{{\left(F_i\right)}_{\mathrm{MVC}}-F_i}{{\left[{\left(F_i\right)}_{\mathrm{MVC}}\right]}_{\text{singlefinger}}}$$ (1)

Standard descriptive statistical methods were used. MANOVA was initially used on all measures to determine whether there was a GENDER (levels male, female) effect, using also TASK (i.e., explicit task or master finger, various levels) and DIRECTION (levels flexion, radial, ulnar) as factors where appropriate. Although there was, as expected, a significant GENDER effect on individual fingers' strength data (P < 0.001), there was no effect on other measures (P = 0.408). We thus pooled all data across genders (except for strength) and analyzed with mixed-effects ANOVA and factors: TASK, DIRECTION, and FINGER (levels I, M, R, L). Two-sided t-tests were performed post-hoc. One-sided t-tests were used in cases where there was an obvious one-sided relation; for example, when comparing master and slave forces, the master finger always produced more than the slave finger. The comparisons using one-sided t-tests are indicated in the text.

Neural network modeling

Neural network modeling was used to quantify the degree of interaction among fingers. Previous networks modeled only normal forces (Zatsiorsky et al. 1998; Li et al. 2002; Danion et al. 2003); the current model also incorporated RUdeviation.

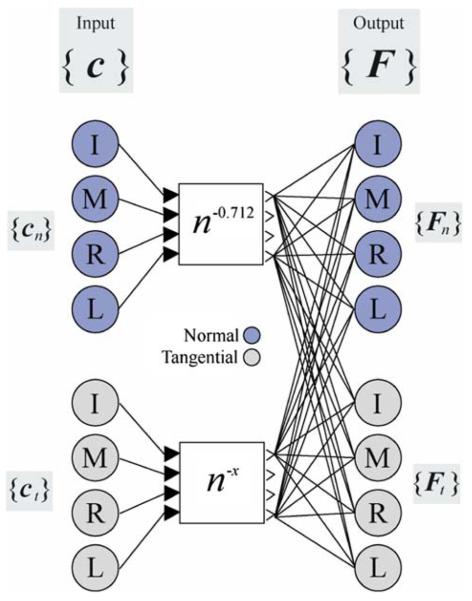
Although different networks were tested (see Preliminary structural analysis), we found that the simplest network that accounted for the interaction behavior was a fully connected eight-input, eight-output network (Fig. 2) that linearly mapped motor ‘commands’ (c) to finger forces (F):

$$\left\{\mathit{F}\right\}=k\left(n\right)\left[\mathit{W}\right]\left\{\mathit{c}\right\}$$ (2)

where k is a scalar function of n, the number of master fingers (n = 1 or 4 in the current experiment). Note that brackets and braces distinguish [matrices] from {vectors}; vectors and matrices are denoted by bold italics and scalars by italics. The coefficient k(n) accounts for force deficit and is addressed further in the following paragraph. The eight-component F vector represents all experimentally observed forces:

$$\left\{\mathit{F}\right\}=\left\{\begin{array}{c}\hfill {\mathit{F}}_{\mathbf{n}}\hfill \\ \hfill {\mathit{F}}_{\mathbf{t}}\hfill \end{array}\right\}$$ (3)

where all F_n elements are positive. The vector c is analogously decomposed as:

$$\left\{\mathit{c}\right\}=\left\{\begin{array}{c}\hfill {\mathit{c}}_{\mathbf{n}}\hfill \\ \hfill {\mathit{c}}_{\mathbf{t}}\hfill \end{array}\right\}$$ (4)

where c_n and c_t are four-element (one element per finger) vectors corresponding to flexion and radial/ulnar ‘commands’, respectively (Table 2). Each component of c can be interpreted as the intensity of neural activation to a given muscle group of a given finger. The model assumes that some neural representation of each finger exists and that the phenomenon of enslaving results from lower-level neural and biomechanical interactions that are not under explicit control. While simple, this type of model has yielded successful behavioral predictions in the past (Zatsiorsky et al. 1998; Li et al. 2002). The c_n elements have range (0, 1), where 1 indicates maximal finger activation (i.e., MVC) and 0 indicates that no voluntary force is produced. The c_t elements have range (−1, +1), since the direction of the tangential forces is not restricted. Maximal inputs (|c_i| = 1) were assumed for all master fingers in only the task direction; all other inputs were assumed to be zero. The inputs and corresponding average outputs for each experimental task are listed in Table 2; the data are experimental F values from the current study, but are presented here rather than in Results to help explain the nature of the network mapping.

Fig. 2.

Neural network architecture. The input commands c are mapped to output forces F. The vectors c and F both contain four normal (n flexion) and four tangential (t RUdeviation) elements, one element for each finger: index (I), middle (M), ring (R), and little (L). The commands have ranges (0, 1) and (−1, 1) for c_n and c_t, respectively. The normal commands c_n are subject to a non-linear gain n^−0.712 (Danion et al. 2003), where n is number of master fingers (see text). The tangential commands c_t are subject to a separate gain n^−x, the value of x was determined experimentally (see Results)

Table 2.

Motor commands c and average forces F (across all subjects; genders pooled) for each experimental task

Task	Master finger(s)	n	c		F
Fn	I	1	[ 1 0 0 0	0 0 0 0]T	[ 44.8	6.63	1.40	2.34	−0.01	−1.75	−0.64	−1.01 ]T
	M	1	[ 0 1 0 0	0 0 0 0] T	[ 11.6	38.9	13.2	1.81	4.71	−3.62	−3.62	−1.25 ]T
	R	1	[ 0 0 1 0	0 0 0 0] T	[ 3.08	15.8	27.5	9.22	0.64	3.64	−4.39	−6.35 ]T
	L	1	[ 0 0 0 1	0 0 0 0] T	[ 2.13	5.41	15.0	24.4	−0.09	1.71	−0.55	−5.84 ]T
	IMRL	4	[ 1 1 1 1	0 0 0 0] T	[ 22.9	28.6	22.1	16.9	4.53	−1.45	−4.30	−6.55 ]T
(Ft)r	I	1	[ 0 0 0 0	−1 0 0 0] T	[ 9.37	2.71	0.77	2.25	−26.7	−5.82	−1.54	−8.01 ]T
	M	1	[ 0 0 0 0	0 −1 0 0] T	[ 1.91	13.4	1.78	1.47	−7.04	−25.4	−8.01	−4.67 ]T
	R	1	[ 0 0 0 0	0 0 −1 0] T	[ 1.13	5.82	7.15	3.48	−2.16	−14.0	−13.3	−9.69 ]T
	L	1	[ 0 0 0 0	0 0 0 −1] T	[ 1.34	3.09	4.14	7.97	−1.75	−7.40	−9.07	−19.5 ]T
	IMRL	4	[ 0 0 0 0	−1 −1 −1 −1] T	[ 9.66	6.94	4.52	5.83	−15.8	−20.9	−11.2	−16.3 ]T
(Ft)u	I	1	[ 0 0 0 0	1 0 0 0] T	[ 12.8	2.69	2.16	2.71	26.9	9.29	2.74	0.92 ]T
	M	1	[ 0 0 0 0	0 1 0 0] T	[ 5.39	9.30	4.66	2.56	11.6	19.0	6.93	2.48 ]T
	R	1	[ 0 0 0 0	0 0 1 0] T	[ 2.81	5.91	4.63	4.86	4.71	13.0	10.1	5.60 ]T
	L	1	[ 0 0 0 0	0 0 0 1] T	[ 2.14	0.97	1.73	10.0	2.77	5.03	4.59	17.1 ]T
	IMRL	4	[ 0 0 0 0	1 1 1 1] T	[ 12.2	8.28	3.80	10.4	19.6	16.0	8.18	9.83 ]T

Radial and ulnar deviation are denoted by (F_t)_r and (F_t)_u, respectively. The number of master fingers is indicated by n, and the master finger(s) force performance is highlighted for each task. The goal of the neural network is to map inputs c to outputs F by minimizing the MSE of the predictions of Eq. 6

T Transpose

The form and value of the deficit coefficient (see Eq. 2) has been reported to be:

$$k\left(n\right)=n^{-0.712}$$ (5)

Equation 5 was derived from a collection of previously published data for one-, two-, three-, and four-finger flexion tasks (Danion et al. 2003). Since the current study only employed one- and four-finger tasks, the Danion denominator was used for the normal commands, but not for the tangential commands. For simplicity, we assumed the same form of k(n) for the tangential commands:

$$\left\{\begin{array}{c}\hfill {\mathit{F}}_{\mathbf{n}}\hfill \\ \hfill {\mathit{F}}_{\mathbf{t}}\hfill \end{array}\right\}=\left[\mathit{W}\right]\left\{\begin{array}{c}\hfill n^{-0.712}\cdot {\mathit{c}}_{\mathbf{n}}\hfill \\ \hfill n^{-x}\cdot {\mathit{c}}_{\mathbf{t}}\hfill \end{array}\right\}$$ (6)

Thus a single extra parameter x, was used to estimate deficit during the tangential tasks. Equation 6 completely describes the network (Fig. 2). The matrix W constitutes an unbiased Jacobian-like linear mapping between inputs c and outputs F. The off-diagonal elements of the 8 × 8 W matrix indicate the behavior of the non-instructed fingers. Thus the two behavioral phenomena of interest: deficit and enslaving, are accounted for by k(n) and the off-diagonal elements of W, respectively (Eq. 2).

It should be noted that no direct connections from inputs to outputs were used (as was done by Zatsiorsky et al. 1998; Li et al. 2002); we thus did not require a hidden layer as in previous studies. The purpose of the direct connections in the previous studies was to estimate a linear component independent of n (which acts only on W). However, since n was not systematically varied in the present experiment, it was impossible to estimate the weights of direct connections uniquely. This does not mean that direct and indirect input–output connections do not exist. It only means that in the present experiment we cannot estimate their individual contributions.

To compensate for inter-subject strength differences only MVC-normalized data were used. The network weights were then multiplied by average forces (Table 2) to be consistent with previous studies by expressing network weights in newtons. By minimizing MSE (mean square error) of the network predictions, the analyses were mathematically equivalent to performing eight (one for each force component) independent linear regression analyses.

Network performance was assessed using both MSE and linear correlation coefficient (r²) between predictions and experimental data. ANOVA was applied to the network predictions, testing for effects of DIRECTION and NUMBER OF FINGERS. All analyses were implemented using MATLAB's neural network toolbox.

Results

Single-finger tasks: general behavior

Maximal flexion and RUdeviation data (Table 3) reveal that radial fingers tended to produce greater flexion MVC than ulnar fingers. Here and elsewhere “radial finger” and “ulnar finger” describe a finger's anatomical location with respect to other fingers; a radial finger is closer to the radius than an ulnar finger. This trend was statistically significant for 78% of the finger pairs (Table 4a, c).

Table 3.

Average maximal flexion (F_n) and RUdeviation (F_t) forces, in newtons (N), for females (n = 12) and males (n = 11) in the single-finger tasks

	Fn				Ft
					Radial				Ulnar
	I	M	R	L	I	M	R	L	I	M	R	L
♀	34.78	28.27	19.88	17.89	20.49	19.25	9.80	16.03	21.37	12.94	7.08	11.80
	(4.52)	(4.43)	(2.64)	(3.46)	(2.58)	(4.46)	(2.22)	(3.01)	(6.51)	(2.76)	(1.58)	(2.06)
♂	55.81	50.53	35.87	31.58	33.53	32.22	17.21	23.37	33.01	25.53	13.41	22.95
	(11.1)	(12.9)	(11.4)	(6.59)	(8.93)	(12.2)	(5.51)	(9.61)	(12.9)	(9.43)	(8.13)	(11.6)

Standard deviations appear in parentheses

Table 4.

Statistical comparisons of single finger MVC performances; P values from one-sided t-tests

(a)	Fn					(b)	± Ft
	I	M	R	L			♀	♂
I	×	0.001	<0.001	0.001		I	−0334	0.458
M	0.157	×	<0.001	<0.001		M	<0.001	0.083
R	<0.001	0.005	×	0.064		R	0.001	0.108
L	<0.001	<0.001	0.146	×		L	<0.001	0.464
(c)	(Ft)r				(Ft)u
	I	M	R	L	I	M	R	L
I	×	0.205	<0.001	<0.001	×	<0.001	<0.001	<0.001
M	0.388	×	<0.001	0.025	0.068	×	<0.001	0.135
R	<0.001	0.001	×	−0.001	<0.001	0.002	×	−<0.001
L	0.009	0.036	−0.040	×	0.034	0.287	−0.019	×

(a) Inter-finger comparisons for the n direction. (b) Intra-finger comparisons between radial and ulnar deviation (±F_t). (c) Inter-finger t comparisons. Female data are shaded gray. The sign of the data indicates the direction of the relation; negative values in (b)indicate that ulnar F_t was greater than radial F_t (see Table 3). Negative values in (c) indicate that the more ulnar finger produced greater MVC on average. Those values that failed to reach significance are highlighted in bold

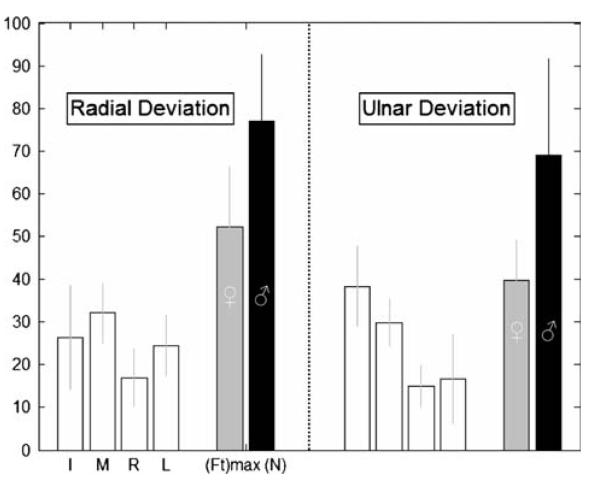
The I and M tended to be the strongest in RUdeviation. This was statistically significant for all finger pairs (P < 0.036; Table 4c) except for the M and L fingers in ulnar deviation (males P = 0.287, females P = 0.135). The R finger was statistically the weakest in RUdevitaion (P < 0.04). Radial forces tended to be larger than ulnar forces, although this could only be confirmed statistically for the M, R, and L fingers in the females (P < 0.001; Table 4b). The males exhibited much larger inter-subject variability (Tables 3, 4b).

Metacarpophalangeal (MCP) joint moments (M_MCP) were computed as the product of F_t and finger length (Table 5). Although the M_MCP data are similar to the F_t data (Table 3), they are reported here because no such data exists in the literature (Matheson et al. 1970 reported only F_t).

Table 5.

MCP joint moments (M_MCP) corresponding to (F_t)_max

	♀		♂
	− MMCP	+MMCP	− MMCP	+MMCP
I	1.45 (0.20)	1.51 (0.47)	2.53 (0.70)	2.48 (0.94)
M	1.48 (0.32)	1.00 (0.24)	2.65 (1.00)	2.11 (0.79)
R	0.70 (0.17)	0.50 (0.10)	1.32 (0.43)	1.04 (0.65)
L	0.94 (0.17)	0.69 (0.14)	1.46 (0.59)	1.43 (0.70)

Negative M_MCP corresponds to radial deviation (i.e., −F_t). Units N m. Standard deviations appear in parentheses

Correlations of the MVC data on three separate anthropometric measures: (1) hand length, (2) finger width, and (3) finger length were quite poor (maximum r² = 0.46). There was no tendency for a specific finger, gender, or force direction to exhibit better correlation with the anthropometric measures.

The F_t data were also normalized by the F_n data, although not presented explicitly in tabular form, results can be inferred from Table 3. RUdeviation strength was on the order of 50–80% of flexion strength. ANOVA revealed a significant effect of both FINGER and DIRECTION (P < 0.001). Linear regression of F_t on F_n found only moderate correlation (r² = 0.57), suggesting that RUdeviation strength is somewhat independent of flexion strength.

Single finger tasks: enslaving

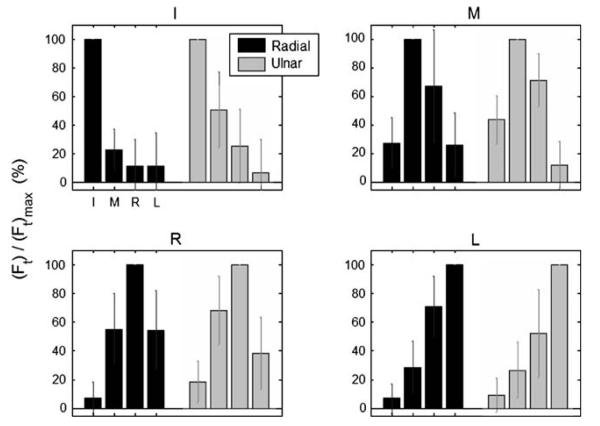
Substantial enslaving, as high as 70% of the single-finger MVC, was observed in the RUdeviation tasks (Fig. 3). Enslaving tended to be greater for fingers adjacent to the master finger (21.9 ± 9.3%) than for non-adjacent fingers (7.7 ± 9.1%). The R finger was largely enslaved, as were other fingers when R was the master finger. The RUdeviation enslaving profiles were similar; ANOVA confirmed significant effects of TASK (i.e., master finger I, M, R, L) and FINGER (P < 0.001), but no significant effect of DIRECTION (P = 0.133).

Fig. 3.

Force enslaving for the single-finger radial and ulnar deviation tasks (dark and light bars, respectively). The four sub-panels represent the four different single-finger tasks (I index, M middle, R ring, L little). Forces are presented as a percentage of each fingers' (F_t)_max. Although enslaving for the master finger is, by definition, zero, it is presented above as 100% for a visual reference. Error bars represent standard deviations across subjects. Note the substantial enslaving, especially for the R finger and for the R task (i.e., when R was the master finger). Neighboring fingers to the master finger tended to be most enslaved

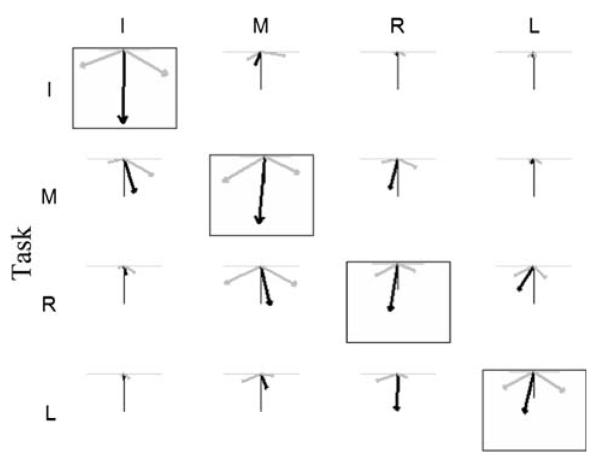
Fingers did not produce force exactly in the required direction (Fig. 4). This is a previously unreported phenomenon that we term: “preferred direction enslaving”. It was observed both in the master fingers and, somewhat surprisingly, in the slave fingers as well. In the master finger, average force directions with respect to the required directions were 23.5 ± 12.7° for the RUdeviation tasks, and 8.1 ± 4.9° for the flexion tasks. ANOVA found a highly significant effect of DIRECTION (P < 0.001), and a mild effect of FINGER (P = 0.057). Preferred direction enslaving in the slave finger was similar for RUdeviation (27.3 ± 20.1°) but was generally higher for the flexion tasks (32.6 ± 20.2°). Like the master fingers, ANOVA found effects of both DIRECTION (P < 0.001) and FINGER (P = 0.014) in slave fingers.

Fig. 4.

Demonstration of non-task direction enslaving in the single finger tasks (males only). The three vectors in each sub panel represent the average forces (N) during the radial deviation (gray-leftward), flexion (black-downward), and ulnar deviation (gray-rightward) trials. Each row represents a different master finger: index (I), middle (M), ring (R), and little (L). Each column indicates separate fingers' behavior during those tasks. The axes indicate the ‘task direction’, or the direction that was explicitly instructed, and also the force magnitude: the length of the axes is 60°N for the boxed panels and 40°N for the non-boxed panels. Preferred direction enslaving is indicated by the angle between the force vector and the neighboring axis of the same color. A quantitative summary is provided in the text

Four-finger tasks: general behavior

Subjects tended to be stronger when producing four-finger radial versus ulnar deviation (Fig. 5). For radial deviation, the M finger tended to contribute most to (F_t)_total, whereas the I finger contributed most in the ulnar direction. Sharing appeared different in radial versus ulnar deviation, and ANOVA confirmed a mild DIRECTION effect (P = 0.09). A separate ANOVA also found a main effect for TASK (i.e., flexion vs RUdeviation) in force sharing (P < 0.001).

Fig. 5.

Radial/ulnar deviation performance for four fingers acting in the same direction. The first four bars of each panel represent F_t sharing (units %) among the fingers; data are pooled across genders. The fifth and sixth exploded bar represents the total F_t (units N); females and males are represented by gray and black bars, respectively. Error bars indicate standard deviations

Four-finger tasks: deficit

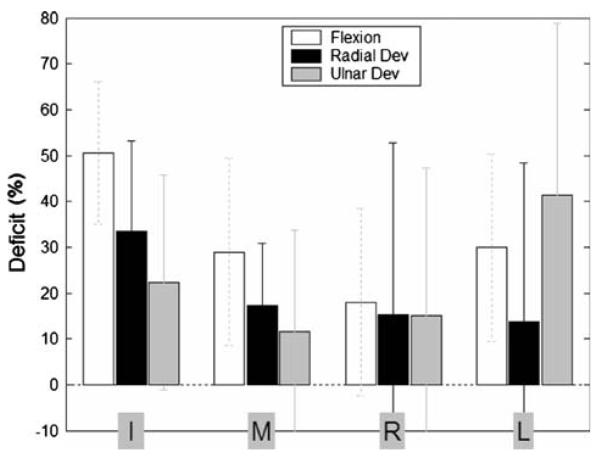
Force deficit was observed in all four-finger tasks (Fig. 6). Single sample t-tests showed that deficit was highly significantly different from zeroin the flexion tasks (P < 0.001). The RUdeviation tasks also generally exhibited highly significant deficit (P < 0.001), but less significant effects were observed for the R and L fingers in radial deviation (P = 0.064, 0.068), and for the M and R fingers in ulnar deviation (P = 0.02, 0.03). Thus, despite rather large variability, especially in RUdeviation force deficit, on average force deficit still dominated.

Fig. 6.

Force deficit for the four-finger tasks. Flexion, radial deviation, and ulnar deviation tasks are indicated by white, black, and gray bars, respectively, and are grouped by fingers. Deficit is expressed as a percentage of the individual fingers' MVCs. Negative deficit values indicate force ‘facilitation’ (see text). Error bars represent standard deviations across all subjects

ANOVA found a significant effect of DIRECTION in all fingers (P < 0.02) except for the R finger (P = 0.94). Post-hoc pair wise t-comparisons revealed that flexion was associated with greater deficit than RUdeviation in the I, M, and L fingers (P < 0.06). The only exception was the L finger whose ulnar deviation deficit tended to be greater than its flexion deficit, but this trend failed to reach significance (P = 0.20). Comparing radial versus ulnar deviation revealed no significant differences in deficit magnitude in the central (M and R) fingers (P > 0.29). The peripheral fingers (I and L), however, showed significant and opposite tendencies: the I finger experienced more deficit in radial deviation (P = 0.08), while R experienced more deficit in ulnar deviation (P = 0.01).

Negative F_t deficit, or force ‘facilitation’ was also observed (i.e., some master fingers produced more force in multi-finger vs single-finger tasks), a phenomenon that has not been previously reported in the literature. Out of 23 subjects, 21 exhibited force facilitation, and for these subjects it was observed in 46.4% of the multi-finger RUdeviation trials. For those trials on which force facilitation was observed, fingers produced an average of 121.3% (±21.1%) of the force magnitude that they did on single finger tasks. Force facilitation was observed quite frequently: 56% of the radial trials and 65% of the ulnar trials were associated with facilitation; flexion trials contrastingly exhibited facilitation in only 4.3% of the trials. Force facilitation occurred least frequently for the I finger (10.9% of the trials), and most frequently for the M and R fingers (26.1%). The L finger exhibited highly frequent facilitation in radial efforts (39.1%), but comparatively infrequent facilitation in ulnar efforts (8.7%).

As an aside, we acknowledge that ‘facilitation’ is dependent on our definition of MVC with respect to single finger tasks (Eq. 1), for now we use this definition to be consistent with previous studies. The issue is addressed further in Discussion.

Neural network results

Preliminary structural analysis

Preliminary analyses were performed to determine the simplest and most encompassing network architecture. We originally modeled the network as a twelve-input, eight-output linear system, separating the radial and ulnar directions into separate commands under the assumption that radial and ulnar deviation would have different enslaving profiles. The network performance (MSE) was only better by approximately 1%. The similarity in results between the two networks was caused by a strong correlation between the trained weights of the radial and ulnar components (r = 0.94). This, coupled with the lack of direction effect found by ANOVA (see single finger task results above), led us to adopt the simplified model (Fig. 2), concluding that enslaving effects were very similar for both radial and ulnar directions.

As described in the Methods, the deficit coefficient for the tangential commands (Eq. 6) was calculated using the form: k(n) = n^−x. Although the current data set included only one- and four-finger tasks, minimizing the network's MSE yielded a gain of x = 0.677. This value was slightly smaller than the flexion deficit coefficient of x = 0.712 that was determined from a large data set (Danion et al. 2003).

Network performance

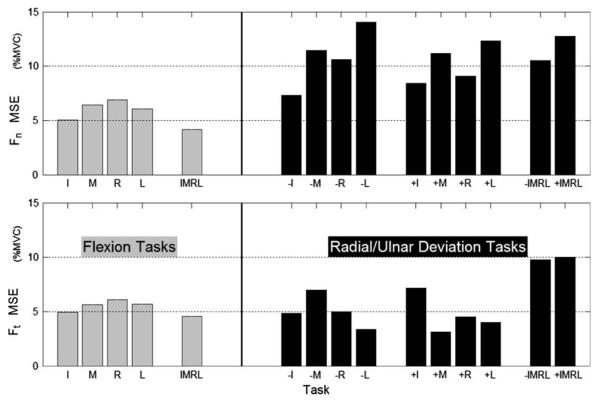
Overall network performance (MSE) was 4.30% MVC (F_n) and 4.21% MVC (F_t), which correspond to correlation coefficients of r² = 0.926 and 0.83, respectively. The magnitude ~1.2 N (4.5% MVC) error is similar to that reported in a previous study (Zatsiorsky et al. 1998), despite the fact that this network fitted twice the number of components as flexion-only networks. Although the testing performance was slightly worse than the training performance, we emphasize that a large proportion of the variance in this data set is explained by our simple linear mapping (Eq. 6).

The distribution of the prediction error across the tasks was generally balanced (Fig. 7). The notable exceptions were that normal forces were generally more poorly predicted for the RUdeviation tasks, and that the tangential predictions were poorest in the four-finger RUdeviation tasks. ANOVA confirmed a weak NUMBER OF FINGERS effect (P = 0.071), but could not confirm a DIRECTION effect (P = 0.575).

Fig. 7.

Network performance, expressed as mean square error (MSE). Flexion tasks are presented in the left panels and radial/ulnar deviation tasks in the right panels. The performances for normal (F_n) and tangential forces (F_t) are presented separately in the top and bottom panels. For each task instructed and non-instructed finger data are pooled. The ‘−’ and ‘+’ signs refer to radial and ulnar deviation, respectively

Network weights

The weight matrix W (Table 6; Eq. 6) constitutes a compact wealth of information regarding the task performance. The diagonal components describe the maximum forces, and the off-diagonal components describe enslaving effects. The matrix elements can be interpreted as the strength of connection between the row and column components; that is, they are the normal (F_n) and tangential (F_t) forces that are induced by the single-finger, single-component commands c_n and c_t of unit intensity (refer to Eqs. 2-6). Alternatively, one may interpret the columns as being similar to the average F for each task (Table 2). Note that the columns of W are not averages, because they are the computed weights of a least-squares fit of (Eq. 6) to the data. For example, the c_n-R column represents the single-finger R finger flexion task; the best fit normal forces for this task were: 1.71, 12.07, 28.13, and 11.05 for the I, M, R, and L fingers, respectively in the column below. The corresponding data from Table 2 are: 3.08, 15.8, 27.5, and 9.22, illustrating the similarity of the measures. Note that all off-diagonal matrix components are non-zero; i.e., enslaving always occurs.

Table 6.

Weight matrix W (Eq. 6)

		cn				ct
		I	M	R	L	I	M	R	L
Fn	I	45.23	9.30	1.71	1.04	0.77	0.69	0.20	0.11
	M	8.72	40.05	12.07	3.57	0.60	−0.98	−0.03	−0.33
	R	2.58	19.58	28.13	14.12	0.88	1.47	−0.53	−1.07
	L	5.73	4.01	11.05	25.51	0.63	0.91	0.59	1.09
Ft	I	1.28	7.79	1.04	0.47	27.83	9.90	2.16	2.18
	M	−3.06	−5.76	5.46	1.64	9.95	25.83	8.34	5.49
	R	−2.82	−11.46	−9.33	−1.26	4.43	17.25	13.25	11.70
	L	−2.93	−2.74	−8.60	−7.31	2.84	5.29	6.47	20.02
Fn %	I	99.8	23.6	6.1	4.2	2.8	2.7	1.5	0.5
	M	19.2	101.7	43.3	14.4	2.2	−3.8	−0.2	−1.7
	R	5.7	49.7	100.9	57.1	3.2	5.7	−4.0	−5.5
	L	12.6	10.2	39.6	103.1	2.4	3.6	4.4	5.5
Ft %	I	2.8	19.8	3.7	1.9	103.0	38.5	16.0	11.1
	M	−6.8	−14.6	19.6	6.6	36.8	100.4	61.7	27.9
	R	−6.2	−29.1	−33.5	−5.1	16.4	67.0	98.1	59.4
	L	−6.5	−6.9	−30.9	−29.6	10.5	20.6	47.9	101.6

W is Jacobian-like in that it maps command inputs c to force outputs F. For convenience, the diagonal elements corresponding to the single-finger tasks are represented in bold, and c and F are decomposed into normal (n), and tangential (t) components for each finger. The top (8 × 12) matrix presents force data and the lower (8 × 12) matrix normalizes each column by the diagonal element represented in bold. Each column represents the predicted (8 × 1) force vector F for a given single-finger task. Each row represents finger performance across tasks

The numerical results are intuitive: (i) the largest terms are found on the main diagonal indicating that a command to a finger yields the largest force response in that finger, and (ii) neighboring fingers, represented by adjacent off-diagonal elements, are evidently enslaved more than non-adjacent fingers. The elements of the off-diagonal quadrants (upper right and lower left panels) confirm the newly observed phenomena of non-task direction enslaving (see Single finger tasks).

The upper right quadrant indicates that some RUdeviation tasks yield predictions of negative F_n, which is impossible using the current apparatus. However, this can be neglected considering that the magnitudes are low with respect both to the diagonal elements and also to the predictions of F_t during the normal tasks (lower left quadrant).

The upper left quadrant of W indicates the F_n that were produced during the flexion tasks and compares very well with the published data of Zatsiorsky et al. (1998), Li et al. (2002), and Danion et al. (2003)—W_D:

$$\left[{\mathit{W}}_{\mathbf{D}}\right]=\left[\begin{array}{cccc}\hfill 49.1\hfill & \hfill 14.0\hfill & \hfill 9.4\hfill & \hfill 7.7\hfill \\ \hfill 10.5\hfill & \hfill 38.0\hfill & \hfill 16.5\hfill & \hfill 6.7\hfill \\ \hfill 5.5\hfill & \hfill 12.9\hfill & \hfill 29.9\hfill & \hfill 15.0\hfill \\ \hfill 2.7\hfill & \hfill 4.1\hfill & \hfill 10.6\hfill & \hfill 24.8\hfill \end{array}\right]$$

Linear regression of the elements of the current F_n−c_n sub-matrix with W_D yielded correlation r² = 0.91. Another important characteristic of W is the existence or lack thereof of sub-matrix symmetry. Symmetry implies, for example, that the M finger is enslaved to the same extent during the I task as the I finger is enslaved during the M task. Sub-matrix symmetry was assessed using linear regressions of the off-diagonal elements [i.e., W(i, j) and W(j, i)]. Symmetry was only mild (r² = 0.48), implying that although there was a small tendency for adjacent fingers to be enslaved similarly, the degree of enslaving depended also to a large extent on which task was being performed.

Discussion

The current data demonstrate that: (a) finger force enslaving and deficit reported previously for flexion, exist also during RUdeviation; (b) flexion and RUdeviation finger force interactions are modeled well by a linear NN that is scaled by the number of master fingers; (c) enslaving effects are highly symmetric between radial and ulnar directions; (d) fingers are enslaved to produce force in directions other than that explicitly instructed; (e) force deficit is greater in flexion than in RUdeviation; (f) although RUdeviation is associated with general force deficit, the opposite, force ‘facilitation’ also frequently occurs; (g) fingers do not share RUdeviation forces evenly during multi-finger efforts; (h) inter-gender and inter-finger strength differences exist in both flexion and RUdeviation; (i) finger strength does not correlate well with anthropometric measures.

Finger RUdeviation strengths have been previously reported (Matheson et al. 1970), but multi-finger data, including the interaction analyses of enslaving and deficit, are new. Peak forces reported by Matheson et al. (1970) were less than half of the current values. The discrepancy is probably due to experimental differences. In particular, Matheson et al. (1970) measured the left hand (only four subjects were left-handed). Also, the authors discarded some subjects from the testing pool because their digits were “too powerful” for the transducer. There are, however, two features of the data sets that agree: (1) the relative strengths of the fingers, and (2) the stronger forces produced in radial versus ulnar deviation.

The RUdeviation force deficit magnitude was somewhat smaller than previously reported for flexion: 34.0, 30.3, 26.1, and 35.1% for the I, M, R, and L fingers, respectively (Zatsiorsky et al. 1998). This could be due to anatomical differences of flexion versus RUdeviation. For example, finger flexion force is achieved primarily by extrinsic muscles whose tendons serve multiple muscles, so deficit is expected to a greater extent in flexors versus ab-/adductors whose muscle bodies are anatomically distinct. Thus deficit (positive or negative) in the ab-/adductors appears to be primarily a neural phenomenon.

Negative force deficit, or force ‘facilitation’, is a phenomenon that been described for postural changes (Li and Yue 2002) but has not been previously reported for constant posture tasks in the hand biomechanics literature. That both deficit and facilitation are frequently observed is an apparent controversy. The current data show that, while the averages indicate that the force deficit prevails, the frequency statistics suggest the existence of the force facilitation for some fingers and in some tasks (Fig. 6). With the current data we can only speculate that the phenomenon is attributable to the high degree of neural interconnectivity between the structures involved in activation of the intrinsic ab-/adductors (e.g., Duque et al. 2005). We acknowledge that this deficit/facilitation controversy is based on a binary distinction that is completely dependent on our definition of MVC in terms of single-finger tasks (Eq. 1). The deficit definition, coupled with our experimental tasks, may not fairly represent the real maximal RUdeviation performance. We nevertheless presently maintain this definition so that our data can be considered in the framework of previous flexion studies. A more deliberate investigation to properly define maximal RUdeviation performance is warranted.

The present interaction results (Table 6) allude to ‘preferred direction enslaving’, which has not been previously reported. For the master finger, the phenomenon is likely rooted in anatomical architecture; muscle tensions do not necessarily transmit forces that correspond, at the endpoint, to externally defined axes. Since flexion was ‘enslaved’ during RUdeviation tasks to a greater degree than was RUdeviation during flexion tasks (Table 6), the data suggest that neural structures involved in RUdeviation are, despite anatomical separation of the involved muscles, strongly connected to neural structures involved in finger flexion. This is functionally intuitive—RUdeviation is kinematically highly coupled with flexion/extension (Li et al. 2005).

An intuitive explanation for the observed ‘preferred direction enslaving’ in the slave fingers is more elusive. Regardless of the neural basis for the phenomena, these types of enslaving provide strong evidence that enslaving results from neural rather than biomechanical factors (because of the architectural separation of the involved muscles).

It is important to realize that the modeled interactions (Table 6) do not constitute obligatory behaviors. For example, subjects can, at will and/or with practice, produce almost any sharing pattern they choose. We view this as higher functionality; the subject must learn to compensate for the lower level connectivity through training. The current data reflect unpracticed behaviors that consistently emerged. Indeed, this is precisely why the data are scientifically interesting; the highly redundant finger force system is channeled toward a relatively small subset of the possible solution space. That is, from an infinite number of experimental enslaving and deficit possibilities, subjects tended to behave very similarly: there were consistent behaviors that emerged that could be predicted well by simple regression.

The NN modeling approach adopted herein leads to multiple insights. Firstly, the eight force-degrees of freedom system are transformed linearly into a more intuitive command space (Eq. 6). This implies that a controller need not be concerned explicitly with force, but rather only with the mode ‘activation’. Secondly, this simple linear connectivity also explains the mechanically unnecessary but consistently observed enslaving behavior.

For future work: since RUdeviation requires friction in everyday tasks, this study would be useful to replicate without finger slots. Such an experiment would certainly lead to different results in the flexion enslaving W sub-matrices for RUdeviation tasks. These particular sub-matrices could be important for understanding performance when RUdeviation is explicitly instructed (for example, when holding a glass of water). It would also be informative to perform the experiment with two- and three-finger tasks to examine the consistency of the W matrix and of the deficit behavior during RUdeviation. Finally, using full thimble-like slots (that allow for finger extension) could affect the W matrix, as some fingers may be naturally enslaved to extend rather than flex.

In summary, the current study extends the work of Zatsiorsky et al. (1998) and Danion et al. (2003). We show that a simple linear network can capture much of the variability in both flexion and RUdeviation tasks. The network weights represent involuntary finger interactions that constitute basic facts regarding both anatomical and functional connections among fingers. Thus the data serve two important purposes with respect to the literature: (1) they expand on the only previous explicit account of RUdeviation strength to include interactions among fingers, and (2) the computed interaction matrix constitutes a constraint to motor redundancy. The former is simply bookkeeping. The latter is less trivial in that information regarding effector interaction is essential for inferring the control schemes that drive redundant systems.