MDL Constrained 3-D Grayscale Skeletonization Algorithm for Automated Extraction of Dendrites and Spines from Fluorescence Confocal Images

Abstract

This paper presents a method for improved automatic delineation of dendrites and spines from three-dimensional (3-D) images of neurons acquired by confocal or multi-photon fluorescence microscopy. The core advance presented here is a direct grayscale skeletonization algorithm that is constrained by a structural complexity penalty using the minimum description length (MDL) principle, and additional neuroanatomy-specific constraints. The 3-D skeleton is extracted directly from the grayscale image data, avoiding errors introduced by image binarization. The MDL method achieves a practical tradeoff between the complexity of the skeleton and its coverage of the fluorescence signal. Additional advances include the use of 3-D spline smoothing of dendrites to improve spine detection, and graph-theoretic algorithms to explore and extract the dendritic structure from the grayscale skeleton using an intensity-weighted minimum spanning tree (IW-MST) algorithm. This algorithm was evaluated on 30 datasets organized in 8 groups from multiple laboratories. Spines were detected with false negative rates less than 10% on most datasets (the average is 7.1%), and the average false positive rate was 11.8%. The software is available in open source form.

Introduction

Since the pioneering work of Ramon y Cajal (1888), there has been a continuing need to develop and improve automated tools for tracing the three-dimensional (3-D) anatomy of individual neurons, and delineating associated microstructures such as dendritic spines (Cajal 1891). The importance of delineating neurons is rooted in the fact that the computational properties of neurons are dependent on their structure (Gulledge et al. 2005; London and Hausser 2005; Costa et al. 2002), in addition to their connectivity (Kalus et al. 2000; Mel 1994). At a finer scale, the microstructure and distribution of dendritic spines are known to be linked to cognitive functions (Lippman and Dunaevsky 2005; Rolston et al. 2007). Furthermore, dynamic changes in their morphology are correlated with synaptic plasticity (Yuste and Bonhoeffer 2001; Matsuzaki 2007).

Building upon a long history of computer-assisted manual tracing methods (Glaser et al. 1983; Capowski 1989), the field has seen the emergence of automated algorithms that operate on 3-D image stacks, and compute digital topological representations, and quantitative measurement data by this group (Cohen et al. 1994; Al-Kofahi et al. 2002, 2008; He et al. 2003; Can et al. 1999; Abdul-Karim et al. 2003, 2005; Tyrrell et al. 2007), and several peer groups (Rodriguez et al. 2003, 2006; Weaver et al. 2004; Schmitt et al. 2004; Wu et al. 2004; Cai et al. 2006; Xiong et al. 2006; Zhang et al. 2007a, b, c; Srinivasan et al. 2007; Losavio et al. 2008). This development has been driven by the advent of 3-D neuroimaging by confocal fluorescence microscopy (Carlsson et al. 1989; Turner et al. 1991, 1994), and more recently, multi-photon microscopy (Potter 1996; Trachtenberg et al. 2002; Pawley 2006). More recently, improvements in imaging resolution have inspired the development of algorithms for automated quantification of dendritic spines (Koh et al. 2002; Wearne et al. 2005; Xu and Wong 2006; Bai et al. 2007; Cheng et al. 2007a, b; Zhang et al. 2007a, b, c). Note that the above comments apply mainly to 3-D methods, although there is some literature on two-dimensional image analysis methods as well (e.g., Al-Kofahi et al. 2003; Dowell-Mesfin et al. 2004).

Despite the prior progress, the performance of automated spine analysis algorithms has remained inadequate compared to the need. Importantly, errors in automated segmentation must be corrected by manual editing, so excessive error rates increase the analysts’ burden and introduce subjectivity. The most common type of error continues to be a high incidence of false positives. One challenge is the small size of these structures compared to the achievable resolution of optical microscopes (Pawley 2006). Often, dendrites and spines are just a few voxels wide. Their boundaries are often blurred, especially along the axial direction, due to the microscope point spread function. A second challenge relates to achievable signal quality with fluorescence imaging. The signal to noise ratio and contrast can be poor, especially when live neurons are being imaged, or when the slices are thick. In addition, the neuronal structure can be discontinuous due to imaging system limitations, and factors such as non-uniform staining and/or fading of fluors. A third challenge relates to the structural complexity of spiny dendrites, especially when they are inter-twined in a complex manner. Adjacent dendrites and spines are often not easy to separate under such conditions. Accurate localization of branch points is difficult when there are complex surrounding dendrites, axons and spines. Some types of spines appear detached from the dendritic branch. When segmenting spines, the presence of background structures at the same spatial scale as the spines make it difficult to isolate spines. This difficulty often increases the false positive rate. Finally, the high degree of natural variability exhibited by neuroanatomic structures (morphological and appearance variability) compounded by imaging system variability make it difficult to model spines robustly, and results in ambiguous detection. It makes the goodness-of-fit values to be low even for valid spines when we fit a mathematical model of a spine to the limited number of voxels available

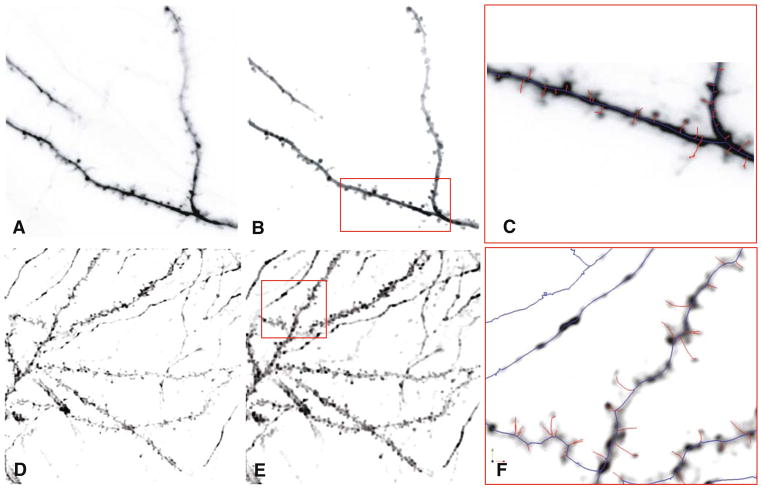
We propose a novel 3-D skeletonization algorithm that addresses many of the challenges noted above. Our algorithm delineates the centerlines of spiny dendrites (often referred to as “dendritic backbones” or simply “backbones” by some authors (Koh et al. 2002; Zhang et al. 2007a, b, c), and the spines (Koh et al. 2002; Wearne et al. 2005). Figure 1 shows sample image stacks from two different laboratories (A,D), and the results of our analysis (C, F) consisting of a delineation of the neurite “backbones” in blue and the spines in red.

Fig. 1.

a, d Sample confocal and 2-photon microscope image stacks from two different laboratories (Trachtenberg and Potter labs, respectively) shown as average-intensity projections and in reverse so hyperfluorescent regions appear dark, and background appears light. b, e Results of image pre-processing. c, f The results of automatic dendritic topology delineation (traces of neurite backbones) and spine detection produced by our algorithms. These are shown enlarged for the selected boxed regions indicated in Panels B & E. The backbone traces are shown in blue and the spines are displayed in red

The rest of this paper describes our method. “Related Literature” reviews the related work. “Specimen Preparation and Imaging” provides image acquisition methods. “Overview of the Image Analysis Approach” describes the main steps of our methodology. In “Experimental Results”, the experimental results are compared and analyzed. Our conclusions and a brief discussion are presented in “Conclusions and Discussion”.

Related Literature

Two main types of algorithm designs have been described in the prior literature for computationally extracting neuroanatomy from images: tracing based methods (e.g., Al-Kofahi et al. 2002); and skeletonization based methods (e.g., Cohen et al. 1994; present paper). A closely related but distinct body of work relates to automated segmentation of vasculature (see Kirbas and Quek 2004 for a partial but useful review).

Tracing-based methods are based on recursive traversal of the image, following an assumed 3-D tube-like local geometry of neurites (Al-Kofahi et al. 2002, 2003). They are most effective when the neurites meet this modeling assumption, although some algorithms are designed to be robust to modeling errors (Tyrrell et al. 2005). Recently developed tracing algorithms (e.g., Tyrrell et al. 2007) have fewer adjustable parameters compared to previous methods, and can adapt to considerable intra-image and inter-image variability. They do not require the neuronal structures to be connected, so can handle partial views. They require no image pre-processing, and are capable of handling low-contrast and noisy data while being fast. Such algorithms have been incorporated into widely-used commercial products (MBF Inc. AutoNeuron and Neurolucida). Finally, recent advances have resulted in enhanced analysis of branch points of neurites from 3-D images (Al-Kofahi et al. 2008).

Skeletonization based methods are based on the notion that the geometric medial axis of the image data captures the neuronal topology. Unlike tracing methods that subsample the image data, these methods process every voxel in the image. In theory, these methods offer the greatest generality since they do not assume that the neurites have a tubular structure. In practice, however, their potential has not yet been fully realized due to limitations of actual algorithms for estimating the medial axis from noisy and blurred microscopy image data. Two main forms of skeletonization algorithms are described in the literature: binarization based algorithms (Cesar and Costa 1999; Falcao et al. 2002; Cornea et al. 2005; Janoos et al. 2008), and grayscale algorithms (Yu and Bajaj 2004). The former are most common—they rely on a binarization step that attempts to separate all the image voxels that constitute the neurite from the background, and then computing the skeleton of the binarized image. Binarization errors directly affect the accuracy of the skeletons. They are also common since the fluorescence intensity varies greatly, and the binarization threshold (cutoff) eliminates some image details irreversibly. The resulting skeletons contain spurious branches (spurs) due to noise-caused irregularities on the binarized surface, and miss many real branches. Some prior efforts (e.g., He et al. 2003; Cohen et al. 1994) attempted to address these limitations using a combination of pre-processing techniques, novel skeletonization algorithms designed to minimize spurious branches, and then performing post-skeletonization cleanup operations. Commonly, short spurs and fragments in the skeleton are pruned, and loops broken. Another kind of post-processing is to reconnect fragments interactively, driven by a cost function designed to minimize angular deviations of the connected trace (He et al. 2003).

Grayscale skeletonization algorithms avoid image binarization altogether, and attempt to estimate the medial axis directly from the grayscale image data (Yu and Bajaj 2004). These algorithms have significant advantages over binarization based methods since they can exploit gradations of voxel intensities to better resolve ambiguities that are lost in a binarized image. They avoid the ambiguities associated with locating surface voxels in a binary image. They are also more robust to image noise. Despite these advantages, a direct application of general-purpose grayscale skeletonization to images of spiny dendrites produces unsatisfactory results. These algorithms lack constraints that are specifically applicable to neuronal images, and the resulting skeletons are far too complex, and spatially imprecise. To overcome these limitations, we propose a 3-D grayscale skeletonization algorithm that incorporates several domain-specific constraints. Mainly, we use the minimum description length (MDL) principle (Rissanen 1978; Leclerc 1989; Barron et al. 1998; Grunwald et al. 2004) to impose a structural complexity constraint, resulting in skeletons that are more concise and accurate. This results in a robust delineation of dendritic backbones.

Once the dendritic backbones are identified, spines are usually modeled as geometric protrusions by most authors. Various boundary tracking and scanning algorithms have been used for spine extraction (Satou et al. 2005). Attached and detached spines are treated differently by most authors (Koh et al. 2002; Xu and Wong 2006). Xu and Wong exploit a dual region growing process for attached spines, searching the tips of spines starting from the backbone and propagating a search process towards the backbone from tentatively marked spine tips. For detached spines, blob analysis is performed with 3-D windows around the dendrite, and the detected blobs are assumed to be spines when they are sufficiently close to the dendrite. Once candidate spines are identified, their shapes and sizes are measured. Using these data, the spines are classified into various types (Xu and Wong 2006). One limitation of current spine segmentation methods is the fact that they do not analyze correlations among adjacent spines, leading to errors in separating closely-situated spines.

The tree-like topology of neurons has been used as a priori information to improve results. One approach is to compute a minimal spanning tree (Cohen et al. 1994). In the method of Herzog et al. (1997), a single dendrite model is initially estimated without any spines or branches. After an initial element is specified interactively, additional elements at the best orientation are sought using an algorithm that attempts to optimize a pre-defined quality measure. This technique proceeds by repeatedly choosing the element with the best quality measure at each step. It terminates when the average intensity of an element’s neighborhood falls below a threshold, or if the element touches an image border. Upon termination, the spines are reconstructed. A model representing the hull of a dendritic backbone is used to detect spines. Spines that are sufficiently long extend beyond the hull model. The local intensity maxima of voxels on the hull surface can indicate the position of outspread spines. The initial spine detection results can be inspected and edited interactively to correct errors. In many situations, it is difficult to detect broken spine necks and closely situated spines. To address this limitation, we propose an intensity-weighted minimal spanning tree (IW-MST) algorithm that can deal with the detached spine and disconnected dendrites in a simple manner.

Our work is focused on 3-D image analysis, but some 2-D methods deserve mention. A 2-D tracing algorithm based on a curvilinear structure detector has been described for dendrite and spine centerline analysis (Zhang et al. 2007a, b, c). The local direction of the centerline is estimated from the second derivatives of the 2D image intensity. A search is conducted based on the current central pixel, and several computed directions. Two boundary points are identified corresponding to each central point. A linear discriminant analysis (LDA) classifier is utilized to separate the spines from other protrusions, based on geometric features such as Zernike moments. These methods share some commonalities with other methods, notably the work of Herzog et al. (1997) in the manner of computing proceeding directions. In addition to the fully automated methods of most interest to us, effective semi-automated 2-D tracing tools have been described in the literature (Meijering et al. 2004). The method consists of two phases: the detection phase assigns a likelihood value to each pixel under consideration to indicate how likely it belongs to a neurite (“neuriteness”) building upon similar work in the vessel segmentation arena (Frangi et al. 1999); the tracing phase links a string of pixels together that represent the most probable centerlines of neurites by means of assigned link cost functions and Dijkstra’s shortest-path algorithm (Cormen et al. 2001). Overall, 2-D methods are computationally faster compared to 3-D methods and can be useful for some in vitro experiments. However, they are inherently limited by the lack of depth information, and cannot analyze spines and dendritic segments that can be oriented along the microscope’s axis.

Specimen Preparation and Imaging

Data for this study were collected at two different laboratories. Images from Dr. Potter were captured with a two-photon excitation laser-scanning microscope in Scott Fraser’s laboratory at Caltech as described in (Potter 2005). Briefly, acute hippocampal slices were cut from juvenile rats at 400 μm, labeled by extracellular microinjection of the lipophilic dye, DiO (16 mg/ml in DMF) and imaged at 830 nm while perfusing with artificial cerebrospinal fluid using a 40×/0.75 NA water-immersion objective lens. Images were collected with 0.125 μm² pixels with Z-steps of 0.5 μm. Some of the images were deconvolved using Huygens software (Scientific Volume Imaging), with a point-spread function created from images of 0.1 μm fluorescent microspheres, about 35 iterations, SNR=50, background 0.5, thresh 0.1% MLE fast.

Images from the Trachtenberg laboratory were acquired at 910 nm using a 40×/0.8 NA Olympus water immersion objective lens. The images were 45 μm on side. The axial step was 1 μm. Images were of GFP expressing neurons in the somatosensory cortex. The apical dendrites of layer 5 pyramidal neurons were imaged.

Overview of the Image Analysis Approach

In this paper, we propose several improvements to 3-D grayscale skeletonization algorithms designed to address the limitations of previous methods, with a specific focus on fluorescence images of spiny neurons, and guided by the minimum description length principle (MDL). We improve spine detection by incorporating additional spine-specific constraints into the MDL estimators. We use available prior knowledge of spines, and correlation analysis to estimate the model complexity and parameters within a Bayesian statistical estimation framework. We describe a one-dimensional graph-theoretic model (Bondy and Murty 1976) of dendrites and spines to represent the topology of the dendritic structure that is initially derived from 3-D grayscale skeletonization based on path-line formation from intensity ridges. The MDL principle enables us to estimate the number of components in this model, and the values of the parameters in a manner that trades off the complexity of the model against its ability to account for the fluorescent signal in the image. We can derive the best-fitted model of a complete dendrite and its spines, based on the observed 3-D image data, instead of detecting each individual spine. The optimal dendrite and spine extraction results are obtained when the model with proper complexity and coverage has maximized the MDL criterion. With a properly chosen weighting factor that trades off complexity and coverage, one can achieve an acceptable trade-off between false negatives and false positives in spine detection for different kinds of images.

Our analysis proceeds along the following main steps. First, the images are deconvolved to correct for the microscope point-spread function, cleaned up to eliminate imaging artifacts, and smoothed. An initial grayscale skeleton is computed from this result. This skeleton may contain loops, and lacks organization. To overcome these two limitations, a minimum spanning tree algorithm based on intensity-weighted edges (IW-MST) is used to extract the neuronal tree structure. This structure must be separated into the main dendritic backbones, spines, and other spurs (for removal). Graph-theoretic erosion operations are then used to compute an initial estimate of the backbones. This estimate is refined using an MDL based spline-fitting algorithm. Using the refined backbone estimates, the spines are detected using a Bayesian estimation algorithm that employs several constraints, including a complexity-based penalty, and prior knowledge of spine structure, including correlations among neighboring spines. This results in the final structural representation that we term the minimum description tree (MDT). From this representation, it is possible to extract measurements and analyze dendrite branching structure, spine density, sizes and shapes, etc.

Image Preprocessing

A commercial image deconvolution package (Autodeblur^™) was used to correct the images from the Trachtenberg laboratory for the microscope point spread function (Holmes et al. 1995). Some of the images from Dr. Potter were deconvolved using Huygens^™ software (Scientific Volume Imaging), with a point-spread function created from images of 0.1 μm fluorescent microspheres, and 35 iterations (SNR= 50, background 0.5, thresh 0.1% MLE fast). In order to avoid unnecessary computations on voxels that are definitely part of the background, a conservative background threshold value of 2–7 grayscale units was used. A 3×3×3 morphological dilation filter was used to smooth out the irregularities in the iso-surfaces of the thresholded image. If the neurites are known to be stained on their surfaces (so they appear like hollow tubes), a flood-filling algorithm can be employed (Rogers 1998). This operation is not necessary if the fluorescent dye fills the neurites. At this stage, connected components of voxels that are too small to be spines (small flecks representing imaging artifacts typically 10 voxels or smaller) were eliminated from further consideration. The results were subjected to iterative smoothing using an anisotropic diffusion algorithm that can smooth images while retaining useful edge structures (Perona and Malik 1990). This algorithm avoids the edge shifting problem of isotropic linear diffusion algorithms, and smooths out unwanted small objects attached to the neurites. Panels (B &E) of Fig. 1 exemplify the results of this pre-processing.

Initial Grayscale Skeletonization

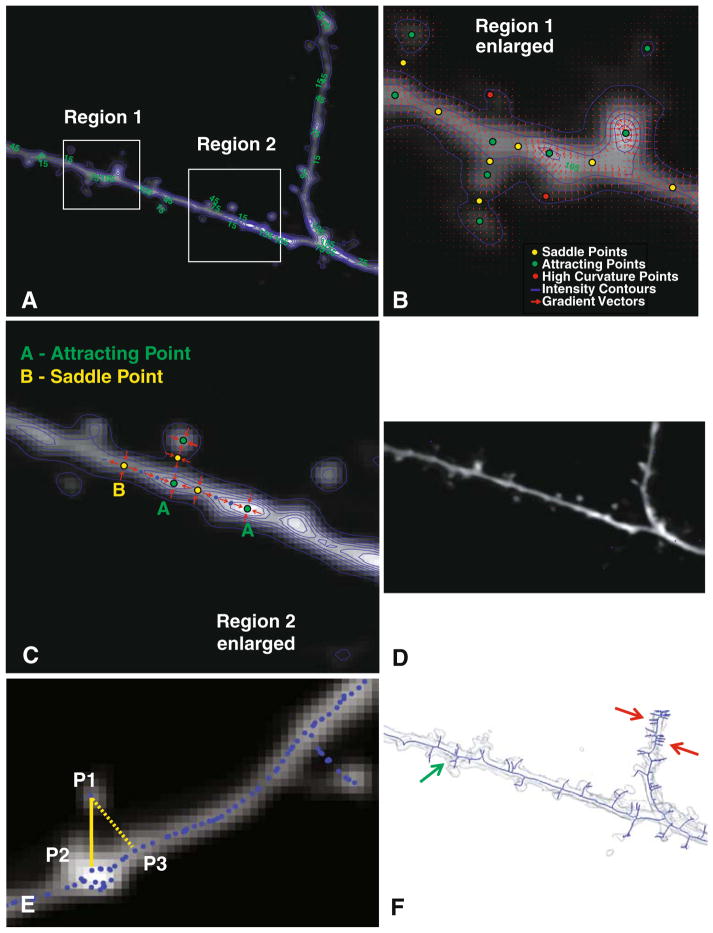
To compute an initial estimate of the grayscale skeleton from the pre-processed image, we proceed as follows (see Fig. 2). First, we compute the gradient vector field denoted I_g(x), where x=(x, y, z) denotes a voxel in the image (Fig. 2b). This field is highly informative, indicating locations of critical points in the image. These are points where the gradient magnitude is zero. There are several types of critical points, as illustrated in Fig. 2b. One type, termed a “saddle point” is typically located at the neck of a spine. Another type, termed an “attracting point” is usually located at the head of a spine. Attracting points are also located at the brightness peaks of dendrites. The nature of a critical point is established by analyzing the eigenvalues of the Jacobian matrix around it (Globus et al. 1991). The gradient vector field is denoted:

$$I_g(x,y,z)=\left(\begin{array}{c}u(x,y,z)\\ v(x,y,z)\\ w(x,y,z)\end{array}\right),$$

Fig. 2.

Illustrating the graph generation procedure. a Average-intensity projection of a 3-D stack overlaid with iso-intensity contours in blue. The numbers in green are intensity values. b Enlarged view of Region 1 showing the iso-intensity contours (blue), and red arrows indicating the intensity gradient vector field. Three types of critical points are also indicated in this panel. c Illustrating the procedure for path-line formation using attracting points and saddle points for an enlarged view of Region 2. Points labeled “A” are attracting points, and points labeled “B” are saddle points of the gradient vector field. Points in blue are skeleton points along paths connecting the attracting and saddle points. d The skeleton points are shown as blue dots over the full average-intensity projection image. e Illustrating the detection of detached spines using the intensity-weighted minimal spanning tree (IW-MST) algorithm. P1 is a point on the skeleton. P2 is closest to P1 in the intensity-weighted sense, whereas P3 is closest to P1 in the simple geometrical sense. f The IW-MST graph for the entire image in Panel A (in blue overlaid on an iso-surface rendering of the image data). These results are processed further

The Jacobian matrix of the vector field has the following form (Theisel and Weinkauf 2002),

$$J_v(x)=\left(\begin{array}{ccc}{u}_x(x)& u_y(x)& u_z(x)\\ v_x(x)& v_y(x)& v_z(x)\\ w_x(x)& w_y(x)& w_z(x)\end{array}\right).$$

The eigenvalues of this matrix for repelling and attracting points have all positive eigenvalues, and all negative eigenvalues, respectively, while saddle points have eigenvalues with mixed signs. The eigenvectors provide important directional information, as described further below. In Fig. 2b, the saddle points (yellow dots) have some gradient vectors (red arrows) pointing towards them, and some others pointing away from them. The attracting points (green dots), on the other hand, only have gradient vectors pointing towards them.

Our algorithm computes an initial skeleton of the neuroanatomy by linking the critical points along paths defined by the eigenvectors of the gradient field using the path-line formation algorithm (Schroeder et al. 1998). This algorithm, illustrated in Fig. 2c, uses the saddle points as initial seed locations for tracing. Starting from each saddle point, we examine its eigenvectors that have positive eigenvalues. These vectors define initial directions for tracing (corresponding to outward-pointing gradient arrows). Our algorithm takes a 1-voxel step along each of these directions, and labels these points as being part of the skeleton (indicated as blue dots in Fig. 2c). This process is repeated until an attracting point is reached.

The above process is largely effective in extracting the skeleton, but has an important drawback—the skeletons of many spines are missed. This is exemplified by the spine on the upper left portion of Fig. 2b. At the point indicated by the red dot, the gradient magnitude is not zero, so a critical point is not detected. This problem can be overcome by locating additional seed points that specifically lie on spines. For this, we utilize points of high curvature in the gradient field—they usually occur at the tips of spines. The procedure for locating these high-curvature points is described next. Consider an iso-gray surface patch denoted dS centered around the point (x, y, z). The principal curvatures k₁ and k₂ (k₁≥k₂) are computed from the eigenvalues of the submatrix of the rotated Hessian matrix (Vliet 1993), as described below. The 3-D Hessian matrix denoted H is rotated to align the x axis with the local gradient direction, denoted g. The resulting matrix H′ can be written as follows:

$$H^{\prime }=\left(\begin{array}{cc}{I}_{gg}& 0\\ 0& |\overline{\begin{array}{cc}{I}_{uu}& I_{uv}\\ I_{vu}& I_{vv}\end{array}}\end{array}\right)=\left(\begin{array}{cc}{I}_{gg}& \\ & {H_t}^{\prime }\end{array}\right),$$ (1)

where I_gg denotes the second derivative of the pre-processed image intensity in the gradient direction, and H′_t is a 2-D Hessian matrix in the tangent plane T perpendicular to g. Let λ₁ and λ₂ denote the eigenvalues of H′_t in that order, i.e. λ₁ ≤ λ₂. As in 2-D space, there exists a relationship between the second derivatives of the 3-D intensity field in the contour direction and the corresponding curvatures. This relationship is expressed as follows:

$$k_1=\frac{-{\lambda }_1}{\left|\right|g\left|\right|},k_2=\frac{-{\lambda }_2}{\left|\right|g\left|\right|},$$ (2)

where ||g|| denotes the magnitude of the 3-D gradient vector. Voxels where k₁ is high (relative to the other voxels in a 3× 3× 3 neighborhood) are chosen as additional seeds (illustrated by the red dot in Fig. 2b). Adding these high-curvature points enables detection of additional spines.

Our approach uses the critical points and the high-curvature points together as seed points for the iterative path-line formation algorithm. This algorithm starts from seed points, and moves through the gradient vector field towards other seed points, thereby tracing paths. Collectively, these traced paths represent the initial grayscale image skeleton. Starting from an initial position x(t₀), the path-line formation algorithm computes a new path location x(t+δt) along the gradient field I_g(x) using the following update equation:

$$\mathbf{x}(t+\delta t)=\mathbf{x}(t)+\int I_g(\mathbf{x}(t))dt.$$ (3)

This is continued until the amount of movement falls below a small pre-set threshold (typ. 0.1 voxel). Common integration schemes for this algorithm include Euler schemes, Runge-Kutta second order (RK-2), or Runge-Kutta fourth order (RK-4). Our work used the Euler scheme.

Using this algorithm, we can detect almost all the spines robustly, and the skeleton of the whole 3-D image is well connected. Even the skeletons of low-contrast objects are located. In Fig. 2d, the initial skeleton points are indicated by blue dots. This initial grayscale skeleton lacks an organization/structure. In order to establish connections among skeleton points and facilitate dendrite and spine analysis, a graph structure of the skeleton points is constructed. This is described next.

Graph Generation & Computation of the Intensity-weighted Minimal Spanning Tree (IW-IMST)

The skeleton points of dendrites and spines can be transformed into a graph-theoretic representation of the topology of the neuron. The vertices of this graph, denoted V_i, i=1,…, N are the 3-D skeleton points (Fig. 2d), and the edges of this graph, link vertices i and j. The edges are defined based on a combination of Euclidean distances between vertices, and image intensity values, as described below. The strengths of the edges are based on the distance between the corresponding vertices and on the image intensity values at the vertices. Specifically, the intensity weighted edge strength E_ij between a pair of vertices i and j is computed as:

$$E_{ij}=\frac{2d(V_i,V_j)}{\mid I(V_i)+I(V_j)\mid },$$ (4)

where d(·) is the Euclidean distance between the vertices, and I(·) is the image intensity at the two vertices. The resulting graph has several limitations. First, it is not concise, since the number of vertices is equal to the large number of points that lie on the skeleton. It does not consolidate a sequence of skeleton points as a segment, for example. Second, it can contain closed “loops” although the neuronal topology is known to not have them. In order to overcome these limitations, we used the minimum spanning tree algorithm. In particular, we use an intensity-weighed algorithm (IW-MST) that identifies the minimal subset of the edges that connect all of the vertices, but in a manner that minimizes the sum of the edge strengths linking the selected subset of vertices. In essence, this procedure is based on the intuitive observation that skeleton points on dendritic ridges are closer to the center of tubular shapes, and also brighter than other points away from the medial axes. The subgraph representing the intensity-weighted minimal spanning tree is denoted G_MST.

The IW-MST algorithm handles detached spines very well. As illustrated in Fig. 2e, P1 represents the center point of a detached spine, and P3 is the geometrically closest point to P1. However, the intensity-weighted closest point is P2, and is the correct root of the spine. Thus, the generated branch P1–P2 is used to represent the spine in the graph structure. In some cases, two detached components of one spine may be close to each other. IW-MST can still perform well in such cases and correctly merge the two components into one if they are not too distant.

Figure 2f shows the result of applying the IW-MST algorithm. This result is still not satisfactory since it contains falsely detected spines (indicated by the red arrows), as well as non-spine branches (green arrows). In the next section, we describe methods to overcome this limitation using the minimum description length principle. “MDL-Based Estimation of Dendritic Backbones” below describes the estimation of the dendritic backbone, and “MDL-based Estimation of Dendritic Spines” describes the process of analyzing spines.

MDL-Based Estimation of Dendritic Backbones

Our method for computing an appropriately concise skeleton is based on an application of the minimum description length (MDL) principle (Rissanen 1978). It enables us to achieve an optimal tradeoff between conciseness of the skeleton, and its accounting (coverage) of the fluorescence intensity in the image data. In this subsection, we describe MDL-based estimation of the dendritic backbones.

The intensity-weighted minimal spanning tree G_MST computed as described above consists of a set of vertices and edges denoted {V_MST, E_MST}. This data structure not only contains the long dendritic backbones, but also short spines and such other secondary structures. The short spines can be eliminated by a graph-theoretic erosion operation that simply eliminates vertices whose degree (the number of connected vertices) is less than or equal to 1. This operation can be described mathematically as follows:

$$\mathit{Erosion}(G_{\mathit{MST}})=G_{\mathit{MST}}-\underset{i}{\cup }\left\{\begin{array}{l}\{e_i,v_i\}\mid deg(v_i)\le 1,e_i\hfill \\ =\mathit{edge}(v_i),(e_i,v_i)\in G_{\mathit{MST}}\hfill \end{array}\right\},$$ (5)

where {e_i, v_i} is a set of a vertex and a edge elements of graph G_MST, and we denote the degree of vertex v_i as deg (v_i). A special case of {e_i, v_i} is {Ø, v_i} when the edge element is empty (the empty set is denoted φ). This corresponds to an isolated vertex.

The graph erosion operation can change the morphology of the graph and removes unwanted trivial leaves of the tree while retaining the primary structure. After a sequence of erosion operations (usually 30–70 operations), just the original backbone structure remains. An unwanted side effect of this operation is a shortening of the backbones. To correct this, we use a graph dilation operation that selectively restores deleted vertices in the reverse order of deletion. Specifically, it only restores voxels that are connected to the tips of the backbone computed by the erosion operations. This restores the length of the backbone. The end result of this operation is denoted G_bb in this paper. The algorithm for performing this operation is described in pseudo-code form below.

for t = 1 to Number of erosion recursion

Erosion(GMST)

Push eroded vertices and edges {ei, vi} into a stack

end

Begin dilation operation

Mark all end vertices if their degrees are one

if the stack is not empty

Pop a vertex and edge {ei, vi} from the stack

if the vertex and edge extends from an end vertex of current graph

Add the vertex and edge back to the graph

Mark new end vertex

else

Discard the vertex and edge

end

end

Obtain the backbone graph, Gbb

The blue dotted lines in Fig. 3(a–d) show example results produced by the above algorithm. It clearly captures the primary structures of neuronal dendritic backbones while rejecting any protrusions, including spines. The connectivity of the main neuronal structures can be clearly visualized and extracted.

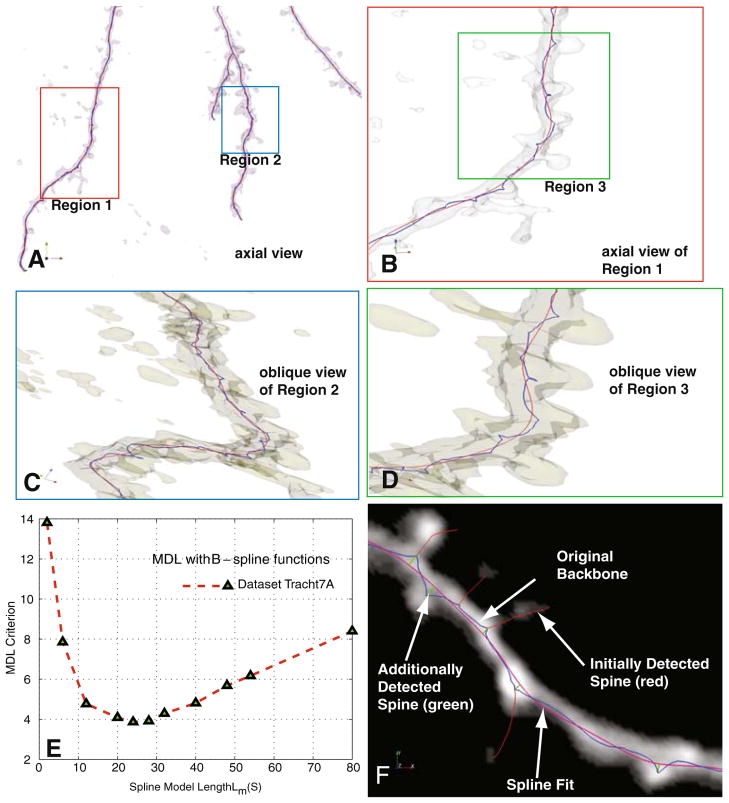
Fig. 3.

Illustrating the procedure for estimating dendritic backbones using B-splines and the minimum-description length (MDL) method. a Iso-surface rending of a sample confocal stack providing an axial view of the data. b Enlarged view of Region 1 in Panel A, showing the initial skeleton (blue) and the B-spline (order k=3) fitted using MDL optimization. c, d Enlarged oblique iso-surface rendering of Region 2 and Region 3 to show fine details of the dendritic backbone estimates. e Shows the MDL criterion plotted as a function of spline model complexity L_m(S). The number of control points in the B-spline curves is set optimally based on the minimum of this curve. f Illustrates the detection of additional spines (green) that are missed in the initial skeleton because of the spline smoothing

However, these lines are subject to influence by spines. Specifically, they deviate from the backbone centerlines near spines. In order to overcome this perturbation, we fit piece-wise polynomial representations known as B-spline curves to the points on the backbone graph G_bb to smooth out these deviations (Schumaker 1981). B-splines offer important advantages including guarantees of smoothness across breaks, efficiency of representation, continuity, banded linear system representations, and good quality of fit. Given n points along the skeleton, the B-spline function defines a set of n “blending functions” (also known as “basis functions”) denoted B_j,k(t). The blending functions are k^th-order polynomials, and t is a parameter that denotes a point along the curve. The coordinates of a point on the curve are denoted S(t)=(x(t), y(t),z(t)). The overall curve is broken into small pieces at points named “knots”, denoted t₀ = 0 ≤ t₁ ≤ … ≤ t_n+k+1. The overall equation for the fitted curve is described as a weighted sum of basis splines of order k, as follows:

$$S(t)=\sum _{j=0}^n{a}_j{B}_{j,k}(t),$$ (6)

where the coefficients {a₀,a₁,…,a_n} are known as the “control points”. One problem that remains is the optimal choice of spline parameters {k, a₀, …, a_n, t₀, …, t_n+k+1}. A number of papers have described optimal criteria and methods to estimate these parameters. In this work, we chose k=3, i.e., cubic B-splines since these splines offer important properties including continuity up to a second derivative, and the fact that they provide the minimum-curvature interpolants to a set of points.

For the remaining parameters, denoted S, we adopted a method based on the minimum description length (MDL) principle (Grunwald et al. 2004), as described below. MDL theory enables a parameter-free estimation of the optimal number of control points. Another method to solve the best fitting problem is iterative fitting (Dierckx 1993; Guéziec and Ayache 1994; Lu and Milios 1994). It involves gradually increasing the number of control points during the fitting process. Generally, the quality of fit is measured as the sum-of-squared-deviations between the sample data (denoted X) and the nearest spline coordinates. The MDL approach seeks out the optimal model parameters denoted S^* that minimize the sum of the description lengths (measured in units of bits) of the B-spline model and the deviations of the fitted curve from the data points X. If the description length (in bits) is denoted |L(·)|, the MDL method can be expressed mathematically as follows:

$${\mathbf{S}}^{\ast }=\underset{S}{argmin}\{\mid L(\mathbf{X}\mid \mathbf{S})\mid +\mid L(\mathbf{S})\mid \}.$$ (7)

We estimate the first term in the argument as the probability distribution of the deviations between the data points and the fitted spline function. Assuming these deviations are Gaussian distributed, our estimate for the first term in Eq. 7 can be written as follows:

$$\mid L(\mathbf{X}\mid \mathbf{S})\mid =\frac{loge}{2}{(\mathbf{X}-{\overline{\mathbf{X}}}_S)}^T{\mathrm{\sum }}_S^{-1}(\mathbf{X}-{\overline{\mathbf{X}}}_S),$$ (8)

where X is the vector of data points and Σ_S is the covariance matrix. To reduce computation, we assumed that the errors of sampling points are independent and identically distributed zero-mean Gaussian variables. Thus the covariance matrix Σ_S is a diagonal matrix with the same variance elements. The number of bits required to encode the spline parameters is estimated as follows, following (Cham 1999):

$$\mid L(\mathbf{S})\mid =(n-k)logM+(n+1)\left(1+log\frac{\beta }{\epsilon }\right).$$ (9)

where n and k are spline parameters as described above, and M is the number of data points in X. Since each knot can be represented by an integer between 0 and M−1, logM bits are necessary to encode it (Lolive et al. 2006). The description lengths of control points are based on a uniformly distributed prior on the interval [−β, β] and with description precision ε. Hence each control point can be represented with $(log\beta +1-log\epsilon )=(1+log\frac{\beta }{\epsilon })$ bits. In practice, the two terms of the description length in Eq. 7 can be weighted differently by the user to adjust the tradeoff between conciseness of the fitted spline and the quality of the fitting (Abdul-Karim et al. 2005). For this, we introduce an additional (optional) parameter α (0,1) for such adjustment. The α-adjusted MDL estimate of the smooth backbone is given by:

$${\mathbf{S}}^{\ast }=\underset{S}{argmin}\{\alpha \mid L(\mathbf{X}\mid \mathbf{S})\mid +(1-\alpha )\mid L(\mathbf{S})\mid \}$$ (10)

Figures 3(a–d) illustrate the process of estimating the optimal B-spline fit using the above approach for the case when α=1/2. In these figures, the initially extracted backbone is shown as blue dots, and the fitted B-spline curves are shown as red lines. Observe that the initially extracted dendritic backbone is not smooth in some places, whereas the B-spline estimate is much more accurate. Figure 3e plots the MDL metric in Eq. 10 when the spline model complexity |L(S)| is varied. The smoothed backbone estimates (red curves) in Figs. 3(a–d) correspond to the minimum point of the plot in Fig. 3e, representing an optimal tradeoff between the model’s conciseness and its quality of fit. Figure 3f illustrates the value of the above procedure. The original estimate of the backbone G_bb (shown in blue) results in several spines being missed, i.e., the skeleton is missing branches. We compute the deviation of the original backbone G_bb from the spline estimate, and identify points that represent local maxima (peaks) in the distance space. We retain only the peaks representing 5 or more voxels of deviation, and treat them as additional spine candidates. These candidates are simply appended to the final list of spines extracted from the IW-MST using the algorithm described next.

MDL-based Estimation of Dendritic Spines

We next describe the process for refining the spine candidates in the IW-MST. As seen in Fig. 2f, the IW-MST contains numerous protrusions. While some of these protrusions correspond to genuine dendritic spines, others are artifacts produced by the grayscale skeletonization step. In order to filter out the artifacts while retaining genuine spines, we again employ the MDL method using mathematical models of spines, as described below.

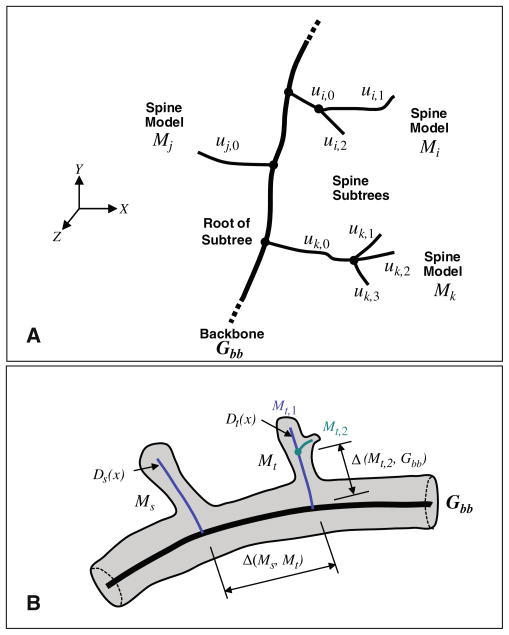
The notation required to facilitate this description is illustrated in Fig. 4. The spines are modeled as subtrees of the IW-MST whose roots are located on the backbone G_bb. These subtrees are denoted M with an appropriate subscript indicating a specific subtree. For instance, M_k in Fig. 4a denotes the k_th subtree. The letter u with appropriate subscripts is used to denote the branches of the subtree. For instance, u_k,0 in Fig. 4a indicates the root branch of the subtree, whereas u_k,2 indicates the second of three sub-branches. We use the symbol Δ to indicate distances between structures. For instance, Δ(M_s, M_t) is the distance between spine models M_s and M_t, respectively. We use the subscript ∂ to denote neighboring structures that lie along the same backbone. For instance, the neighbors of M_s are denoted M_∂s.

Fig. 4.

Illustrating our notation. a The thick line indicates the dendritic backbone G_bb. The letter u with subscripts denotes branches of the spine sub-trees. For instance, u_i,2 denotes a second-level branch in the subtree corresponding to spine model M_i. b Illustrates our notation for distances. The thin blue lines indicate the spine sub-trees detected from the intensity-weighted minimal spanning tree (IW-MST). Two spine models are denoted M_s, and M_t, respectively. The symbol Δ is used to denote distances between a pair of entities

The MDL spine estimation algorithm takes multiple factors into account, including the image data, constraints, and mathematical models describing specific aspects of spines. All of these factors are expressed in Eq. 18 below. The individual terms of this equation are described next. The first term serves to model the spatial distribution of spines along the backbone. The purpose of this term is to penalize multiple estimation of closely situated and redundant structures that actually correspond to a single spine. Instances of such structures can be seen in Fig. 2f. To incorporate this penalty into the estimation, we adapt the Gibbs distribution that is widely used in statistical image processing to express local pattern constraints (Miller et al. 1991; Bouman and Sauer 1993). The Gibbs distribution for the spine models M can be expressed in the following form when considering local groups of spines.

$$g(M)=\frac{1}{Z}exp\left\{-\sum _{c\in C}{V}_c(M)\right\},$$ (11)

where Z is a normalization term, V_c(·) is a cost function defined over a neighboring group c (also known as a clique) of spines, and C is the set of all such groups. The log-likelihood of the above function has the following form:

$$logg(M)=-\sum _{\{s,t\}\in C}{b}_{st}\rho (\mathrm{\Delta }(M_s,M_t))+\mathit{const},$$ (12)

where Δ(M_s, M_t) indicates the distance between M_s and M_t (defined as the total edge length along the backbone), and the coefficient b_st is specified for each pair of M_s and M_t. For the function ρ(·), we used the following formulation suggested by Blake and Zisserman (1987):

$$\rho (\mathrm{\Delta })=-min{\{\mid \mathrm{\Delta }\mid ,T\}}^2+T_0,$$ (13)

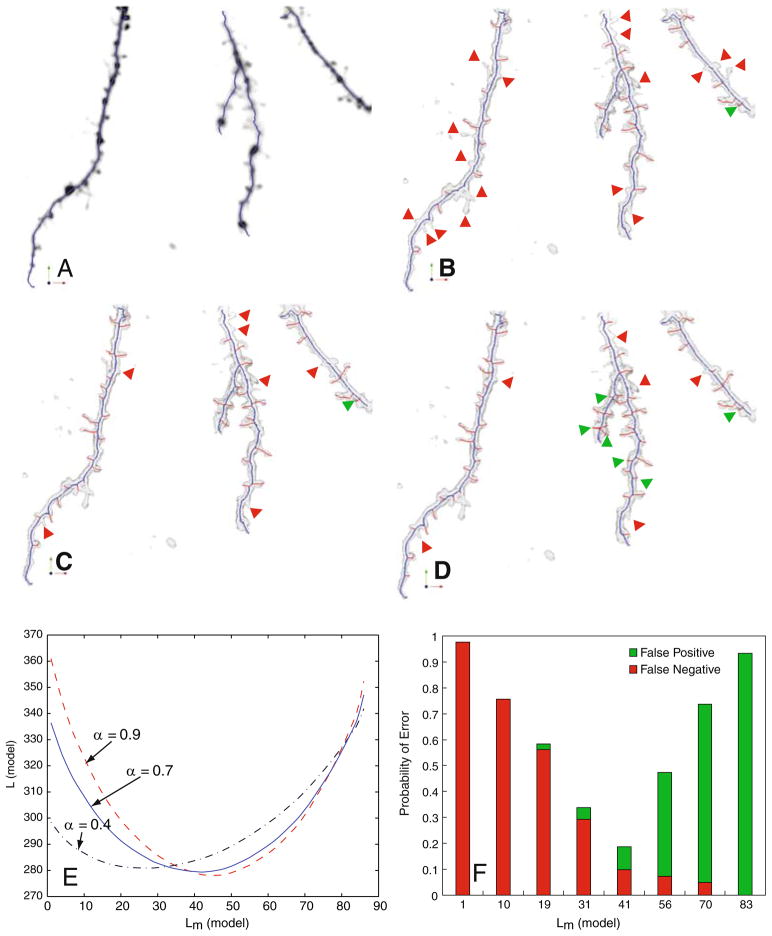
where T is a fixed distance threshold and T₀ is a positive constant (units of squared distance) such that (T₀>T²). This function reflects the expected density of spines, and the above thresholds are set empirically. In our work, we used T=15, and T₀=300 for the sparsely spiny dataset in Fig. 1a, and T=5, and T₀=30 for the densely spiny dataset in Fig. 1b.

To fully model spines, we also need models for the protrusion of spines away from the backbone. For this, we make the reasonable simplifying assumption that probability distributions describing individual spines, denoted h(M_i), are statistically independent of each other. This assumption allows the joint distribution, denoted h(M) for a collection of N_s spine models along a single dendritic backbone to be written simply as the following product:

$$h(M)=\prod _{i=0}^{N_s-1}h(M_i).$$ (14)

To model the distribution h(M_i), we assume that the probability density falls off exponentially as a function of the distance of the spine model to the surface of the dendritic backbone. Under this modeling assumption, if the radius of the dendritic backbone is δ, then the model distribution is given by:

$$h(M_i)=\{\begin{array}{cc}\frac{1}{Z}exp(-\lambda \times \{\mathrm{\Delta }(M_i,G_{bb})-\delta \}),& \text{if}\mathrm{\Delta }(M_i,G_{bb})\ge \delta \\ \frac{1}{Z},& \text{otherwise},\end{array}$$ (15)

where Δ(M_i, G_bb) is the Euclidean distance between the spine model to its nearest point on the backbone G_bb, λ is an empirically chosen constant, and Z is the normalization term for the distribution. The overall model for spines is derived by combining Eqs. 12 and 15, as follows:

$$\mid L_m(M)\mid =-{log}_{2}P(M)=\sum _{i=0}^{N_s-1}{K}_{i}c-{log}_{2}g(M)-{log}_{2}h(M).$$ (16)

where c is a constant representing the description length of each spine, and K_i is the number of spines corresponding to the subtree at location i. This constitutes the model term in our MDL formulation. The data-to-model term is described next below. This term is based on a vector of features denoted D_i(x) that can be extracted from image data for each spine or non-spine object. In the present work, we use the following set of features:

1. Mean fluorescence intensity of the branch;

2. Length of the branch; and

3. Mean vesselness measure (Frangi et al. 1998) over the branch.

The above 3 features for genuine spines differ statistically from those for non-spine protrusions/spurs. We used a learning process for the test datasets. Statistical distributions of these three features were compared for the spine objects and other protrusive non-spine objects. The spine features usually possess higher mean intensities, larger object length and higher mean vesselness values. For instance, for dataset Tracht6A, the mean and standard deviations for these features are listed in Table 1 below.

Table 1.

Sample feature statistics for spine and non-spine protrusions for dataset Tracht6A

Feature	Spines subtree		Non-spine subtree
	Mean	Std. deviation	Mean	Std. deviation
Length	14.4	7.2	9.4	7.9
Mean intensity	44.5	26.8	37.52	25.6
Mean vesselness	0.78	0.2	0.699	0.22

Assuming a multivariate Gaussian model for the feature vectors, we derive the following formulation for the data to model term:

$$\begin{array}{l}\mid L_c(D_i\mid M_i)\mid =-\sum _{x\in M_i}{log}_{2}P(D_i(x)\mid M_i)\\ =N_i·b+a\sum _{x\in M_i}\left({(D_i(x)-{\widehat{u}}_M)}^T{\mathrm{\sum }^{⌢}}_M^{-1}(D_i(x)-{\widehat{u}}_M)\right),\end{array}$$ (17)

where û_M and ${\mathrm{\sum }^{⌢}}_M$ denote the estimated mean and covariance matrix of the feature vector distribution, respectively, the superscript T denotes the matrix transpose, and a, b are constants from the multivariate Gaussian model. The number of sample points on the t^th spine model is denoted N_i. Combining the description lengths from Eqs. 16 and 17, the MDL criterion function L(D, M) for the spine models can be expressed as follows:

$$\begin{array}{l}L(\mathbf{D},\mathbf{M})=\mid L_c(\mathbf{D}\mid \mathbf{M})\mid +\mid L_m(\mathbf{M})\mid \\ =\sum _i{N}_i·b.+a\sum _i\sum _{x\in M_i}\left({(D_i(x)-{\widehat{u}}_M)}^t{\mathrm{\sum }^{⌢}}_M^{-1}(D_i(x)-{\widehat{u}}_M)\right)+\mid L_m(\mathbf{M})\mid \end{array}$$ (18)

The last term defines the cost function of spine models and it acts to force the spine models towards its mostly likely form (Fig. 5). This objective function L(D, M) is minimized with respect to the spine models M_i, given the observed data D. The objective function L(D, M) is minimized with respect to the spine models M_i, given the observed data D to yield the MDL estimate of spines. This can be represented mathematically as follows:

$$M^{\ast }=arg\underset{M}{min}L(\mathbf{D},\mathbf{M}).$$ (19)

Fig. 5.

Illustrating the impact of varying the model complexity L_m(model). a An extreme case of maximum conciseness L_m(model)=0, in which all spines are missed in the skeleton (indicated in blue overlaid on the average-intensity projection of the confocal stack). b A less extreme case L_m(model)=27 (missed spines are indicated by red arrows, false spines are indicated by green arrows). c The case when L_m(model)=42, corresponding the bottom of the solid curve in Panel E, in which fewer spines are missed compared to Panel B, and fewer false detections compared to Panel D. d The case of L_m(model)=53 in which more false spines are detected. Panel E is a plot of the MDL criterion as a function of L_m(model), and different values of the weight factor α. Panel F plots the error rate in detecting spines at varying levels of L_m(model). The results in Panels (B,C,D, F) are all for α =0.7

In summary, we have defined two separate MDL estimation problems in Eqs. 7 and 18 above, to estimate the dendritic backbone and spines, respectively. Alternately, we could have defined a single optimization that simultaneously estimates the backbone and spines to estimate a single minimum description length tree (MDT) as follows:

$$\mathit{MDT}=\{{\mathbf{S}}^{\ast },{\mathbf{M}}^{\ast }\}=arg\underset{\{S,M\}}{min}[L(\mathbf{X},\mathbf{S})+L(\mathbf{D},\mathbf{M})]$$ (20)

Such an approach would be more accurate in principle, but overly complex from a computational standpoint, so was not considered in the present work.

Experimental Results

Our goals in experimentally evaluating the proposed algorithm are threefold. First, we want to ensure that it works on data from multiple neuroscience laboratories to provide a better indication of broader applicability. Second, we want to measure the Type-I and Type-II error rates for a reasonably diverse collection of datasets. Finally, we want to quantify the specific improvement in spine detection performance gained from application of the MDL principle, and get a better understanding of how parameter settings affect performance. To meet the first objective, we tested the proposed algorithm on confocal and 2-photon image data from three laboratories, Trachtenberg Laboratory (UCLA Department of Neurobiology), Potter laboratory (Georgia Tech), and a set of anonymous data sets provided by MBF Bioscience Inc. (Williston, VT). Some of Dr. Potter’s data was collected in Dr. Scott Fraser’s laboratory at Caltech. We also performed experiments with several synthetic (phantom) datasets (not shown here) for verifying algorithm correctness and evaluating the impact of various perturbations, such as morphological variations on spines and various levels of simulated imaging noise.

Table 2 summarizes our measurements of spine detection performance for 30 confocal stacks from the above-mentioned sources. The first 5 rows of the table correspond to time-lapse series from Dr. Trachtenberg’s laboratory. The letters A,B,C,..etc., refer to successive time points. The next 3 rows correspond to datasets from Dr. Potter’s laboratory—these datasets were chosen to evaluate the algorithm’s performance on densely spiny dendrites. The last 3 rows were anonymous datasets (courtesy MBF Biosciences Inc.) that were chosen since they presented a different set of challenges. Overall, this collection of datasets varied greatly in terms of image signal, resolution, dendrite thickness, shapes of spines, and spine density. The accompanying electronic supplement (Supplement 1) to this paper shows average-intensity projections of each of these datasets for the interested reader.

Table 2.

Performance comparison of MDL algorithm and graph morphology method without MDL

All datasets		Number of spines	Number of other protrusions	MDL algorithm			Graph morphology without MDL
				False negative	False negative rate	False positive rate	False negative rate	False positive rate
Tracht6	A	41	45	3	7.3%	6.7%	17.1%	20.0%
	B	51	46	3	5.9%	4.3%	3.9%	78.3%
	C	50	47	2	4.0%	12.7%	14%	44.7%
	D	46	49	2	4.3%	14.3%	4.3%	46.9%
	E	39	44	4	10.3%	2.3%	15.4%	27.3%
	Overall	227	231	14	6.2%	8.1%	10.9%	43.4%
Tracht7	A	25	38	1	4.0%	3.2%	4.0%	29.0%
	B	25	39	1	4.0%	10.6%	76.0%	3.1%
	C	21	31	1	4.8%	6.0%	28.6%	68.0%
	D	24	29	2	8.3%	5.1%	20.8%	28.6%
	E	19	26	2	10.5	11.6%	63.2%	3.8%
	Overall	114	163	7	6.1%	6.5%	38.5%	26.5%
Tracht8	A	29	41	2	6.9%	18.8%	10.3%	48.6%
	B	28	39	2	7.1%	12.8%	7.1%	38.5%
	C	32	46	1	3.1%	17.1%	6.3%	40.0%
	D	32	47	2	6.3%	14.9%	6.3%	34.0%
	E	31	47	2	6.5%	14.9%	6.5%	42.6%
	Overall	152	220	9	5.9%	15.7%	7.3%	40.7%
Tracht11	A	43	49	3	7.0%	18.4%	9.3%	36.8%
	B	41	48	4	9.8%	18.8%	78.0%	2.1%
	C	45	50	3	6.7%	12.0%	8.9%	32.0%
	D	38	46	3	7.9%	13.0%	7.9%	32.6%
	Overall	167	193	13	7.8%	15.6%	20.0%	25.9%
Tracht14	A	27	31	1	3.7%	16.1%	3.7%	74.2%
	B	26	30	1	3.8%	3.3%	3.8%	26.7%
	C	29	33	2	6.9%	18.2%	6.9%	33.3%
	D	27	31	2	7.4%	0.0%	18.5%	6.5%
	E	32	36	3	8.3%	13.9%	40.6%	5.6%
	Overall	141	161	9	6.4%	10.3%	14.7%	29.3%
CalTech20m		81	98	9	11.1%	18.3%	21.0%	26.5%
CalTech100m		89	99	10	11.2%	20.2%	21.3%	35.4%
Pottert330		116	130	8	6.9%	12.3%	21.6%	20.8%
MBFsp5		227	230	17	7.5%	12.2%	17.6%	14.8%
MBFsp6		149	160	13	8.7%	15.0%	10.1%	23.1%
MBFsp8		82	90	11	13.4%	10.1%	26.8%	32.2%
Overall					7.1%	11.8%	18.8%	31.2%

In order to quantify spine detection performance, we used the human eye as the gold standard. We first compiled manually generated data on spine locations, number of spines, and the number of other dendritic protrusions that were not considered to be spines. Electronic Supplement 2 accompanying this paper shows the manual markup data.

In order to understand the value of using the MDL method, we computed false negative, and false positive rates for each of the 30 datasets with and without the MDL principle. Figure 6 shows the qualitative visually appreciable improvement from application of the MDL principle. Overall, the false negative (missed spines) rates for the MDL based algorithm varied in the range of 3.1%–13.4% with an average of 7.1% whereas it varied in the range of 3.9%–40.6% with an average of 18.8% without the MDL application. Application of the MDL algorithm clearly improves the overall false negative rate performance. With a few exceptions, the MDL based algorithm performed significantly better than the non-MDL algorithm for most individual datasets. We next measured the false positive rates for spurious spine detection, and these showed much more variations from one dataset to another. The false positive rates ranged from 0%–19.2% for the MDL based algorithm with an average of 11.4%, whereas they ranged from 2.1%–8.3% without MDL with an average of 31.2%. Again, application of the MDL principle clearly improves performance in the aggregate, as well as for most (not all) individual datasets.

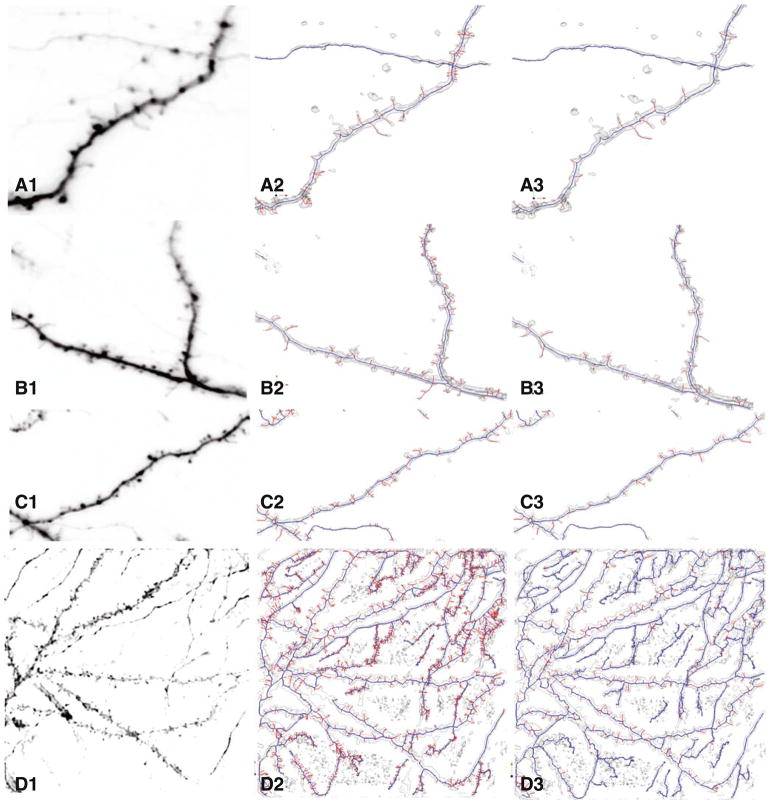
Fig. 6.

Four examples illustrating the qualitative improvement from using the MDL approach over a conventional skeletonization approach. The leftmost column of panels show maximum-intensity projections of the images. The middle column of panels show the results of conventional skeletonization (graph morphology based but without MDL constraint) without the MDL constraint. The rightmost column of panels show the improved results generated by the proposed MDL based method

Our algorithm has a total of 11 adjustable parameters controlling the preprocessing, graph generation, MDL modeling steps. The default choices produced good results, although empirical tuning often improves the results. In practice, these parameters can stay fixed for a batch of images collected using a fixed imaging protocol. The following paragraphs provide additional insight into these parameters, and Electronic Supplement 3 lists all the parameters, provides explanations, and points to specific sections in the paper where they are discussed (Fig. 7).

Fig. 7.

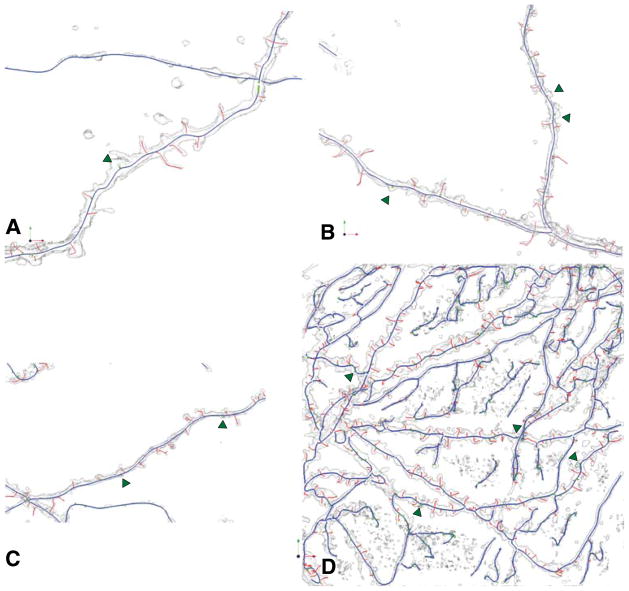
Illustrating the improved spine detection after backbone smoothing on the images in the previous figure. Green arrows indicate the additional spines that were detected that were missed in Fig. 6. These are the final results of our algorithm

In the pre-processing step, the intensity threshold determines the background regions we are not interested in. Typically, we set it conservatively to 2 gray levels. The connected component size can be used to remove objects smaller than a chosen volume. Based on the background noise, we selected 100 voxels for the higher magnification Trachtenberg datasets and 10 voxels for the Potter datasets. Generally, the detached spines have volumes larger than these threshold values, so that they are not removed by mistake. The parameters controlling the anisotropic diffusion smoothing k and t are selected based on the conduction coefficients and the number of iterations of diffusion. Typically, we set k as 800 and t as 2 iterations, so that we achieve a reasonable amount of image smoothing without losing sufficient ridge information in the image that is needed for skeletonization.

In the graph generation step, computation of seed points for skeletonization is controlled by two parameters: critical point gradient vector magnitude threshold, and the high-curvature threshold. They are chosen to obtain the two kinds of seeds according to the gradient vector magnitude and curvature magnitude. Typically, we choose gradient vector magnitude threshold in the range of 0.04 to 0.15. Whenever an interpolated vector in a sub-voxel location has a magnitude below this value, we take it as a critical point. Similarly, if the curvature k₁ at a location has a value above the high-curvature threshold parameter, and it is also a local maximum of curvature values, then we detect it as a high curvature seed point. In the IW-MST algorithm, we described the distance d(V_i, V_j). We set a threshold on this distance to determine the edge range over all 3-D skeleton points. If the distance between 2 points is above this threshold, we assume there is no edge between them in the graph structure before generating the IW-MST. We usually select values in the range 5–15 for various datasets. After the MST is derived, we can prune the tree structure when the trivial branches are shorter than a certain length. For all the datasets, if the outmost branch is shorter than 4, we prune it. Also, the backbone extraction from the MST is a graph morphological method with iterative graph erosion and dilation steps. We set the morphology strength as the number of iterations for graph erosion and dilation. Typically, we choose 30–70 iterations.

Application of the MDL method can be adjusted using the parameter α to adjust the influence of the model description term or the data description term (i.e., tradeoff between coverage and conciseness) (Abdul-Karim 2005). This issue was explored in Fig. 5e. When the weight factor α ∈ [0,1] is selected (it can be estimated from training datasets), the optimization is performed on both terms. The optimizer is the solution to the extreme point of the MDL values, L_min, on the relationship curve of description length L(D, M) and conciseness,

$$\stackrel{⌢}{M}=arg\underset{M}{min}\{\alpha \mid L_c(\mathbf{D}\mid \mathbf{M})\mid +(1-\alpha )\mid L_m(\mathbf{M})\mid \}.$$ (21)

A similar situation exists for error rates in spine detection. When the MDL model description is simple, it does not have high coverage of spines. The false negative rate is high although the false positive rate is low, as shown in Fig. 5f. On the other hand, if the MDL model description is complex, the models cover many objects that include not only spines, but also some non-spine objects. Thus the false negative rate is low but the false positive rate is high. The solution of the best MDL model needs to be found between these two extreme situations.

From the training sets, the model solution M* needs to reduce the false negative and false positive rates. In order to make the MDL optimizer M* coincide with models that produce the minimum total probability of error, P(Error), we need to choose the proper weight α. In Fig. 5e, we can see how different α values may affect the MDL criterion curves. When α is relatively small, e.g., α=0.4, the model description length is over-weighted, therefore, and we tend to have simpler models in the solution. On the other hand, when α is relatively large, e.g., α = 0.9, the model description length is under-weighted, and we tend to have more complex models in the solution. The proper α value should induce the MDL models in the best presentation to reduce the false negative and false positive rates for spine detection. In our experiments, we chose α = 0.70 for almost all the Trachtenberg datasets with sparse spines and α = 0.95 for the Potter datasets with dense spines. The extra spine offset parameter determines the distance threshold above which a skeleton-offset point is detected as the position of a missing spine if the deviated point also has local maximum distance from its backbone. Typically, we set this threshold to 1.5 voxels for all the datasets.

Figure 6 shows an example of spine skeletons with diverse spines shapes and densities. The MDL algorithm result, shown in Fig. 6(b, d, f), is compared with spine detection with the graph morphology method without MDL, shown in Fig. 6(a, c, e).

Table 2 shows the numbers and percentage of spine detection and false detection among all groups of datasets analyzed here.

Data Interchange Methods

The output of the automated tracing can be saved in widely used file formats. Among others, we have used the SWC file format (Scorcioni et al. 2008) that allows us to readily compute morphological measurements using widely available tools such as the L-measure, and use existing trace viewers and editors. The dendritic backbones and spines have different type indices in the SWC outputs.

Conclusions and Discussion

Grayscale skeletonization is a natural approach for reconstructing the 3-D neuroanatomy from images, and provides an improvement over prior methods that required image binarization. However, successful application of this method to real data requires additional modifications and advances that form the central contributions of this work. The MDL principle is a natural methodology for ensuring that the reconstructions represent a concise yet complete (to the extent permitted by the fluorescence signal) description of the neuroanatomy (Abdul-Karim et al. 2005). However, a direct application of the MDL principle via a single global optimization step is intractable. By applying MDL concepts to individual processing stages rather than all steps at once, the methods described in this paper achieve an approachable implementation that nevertheless yields a clear-cut improvement over conventional grayscale skeletonization. Graph theoretic algorithms represent yet another tool with natural applications to neuroanatomy reconstruction. Our use of graph-theoretic morphology operations including erosion, dilation, and intensity-weighted minimum spanning trees, and minimum description trees (MDT) enable us to overcome some of the limitations of grayscale skeletonization results, and improve the detection of spines. When possible, we have used a combination of geometry and image intensity information, as exemplified by the intensity-weighted minimum spanning tree (IW-MST). These results are further improved by smoothing the dendritic backbones.

A particular aspect of this study is the evaluation of the algorithms over data from multiple laboratories. In this regard, we view this study as just the beginning of a much wider study aimed at analyzing data from an even larger cohort of laboratories.

The algorithms described here were implemented partly in MATLAB and mostly in C++. They were not optimized for speed. Typical computing times for various steps for a typical dataset with dimensions 512×512×35 on a desktop computer with a 2.6 GHz Intel Core 2 Duo CPU are approximately as follows: 60 s for the preprocessing, 900 s for the initial grayscale skeletonization, 30 s for the graph generation and computation of IW-MST and 100 s for the MDL-based estimation of dendritic backbones and spines. Thus the total time is about 1,090 secs.

Information Sharing Statement

The source code and executable software described in this work are freely available from the authors to interested colleagues. The methods described continue to be improved for speed and ease of use. Updated implementations of this method are included in the freely available open-source FARSIGHT toolkit whose documentation is available on the worldwide web at address http://www.farsight-toolkit.org. This toolkit also includes open source tools to inspect and edit automated segmentation results overlaid on the images. The above-mentioned website is an open collaborative Wiki page that is open to computationally trained collaborators and neuroscience users worldwide. Interested colleagues should contact the corresponding author (B.R.) for further information.