Abstract
Methods for identifying meaningful growth patterns of longitudinal trial data with both nonignorable intermittent and drop-out missingness are rare. In this study, a combined approach with statistical and data mining techniques is utilized to address the nonignorable missing data issue in growth pattern recognition. First, a parallel mixture model is proposed to model the nonignorable missing information from a real-world patient-oriented study and concurrently to estimate the growth trajectories of participants. Then, based on individual growth parameter estimates and their auxiliary feature attributes, a fuzzy clustering method is incorporated to identify the growth patterns. This case study demonstrates that the combined multi-step approach can achieve both statistical gener ality and computational efficiency for growth pattern recognition in longitudinal studies with nonignorable missing data.
Keywords: Nonmissing at random, intermittent missing, growth pattern recognition, parallel mixture model, fuzzy clustering
1. Introduction
Missing data commonly occur in patient-oriented research and studies with longitudinal designs. For decades, different statistical methods utilizing the missing patterns and mechanisms have been proposed to address missing data, ranging from simple listwise deletion to the currently popular maximum likelihood (ML) or Bayesian model-based multiple imputation (e.g. References 1-8). The missing patterns, such as univariate, monotone, or arbitrary patterns, are used to depict which values are missing or observed in the data. The missing mechanisms express the relation between missingness and the values of variables in the data. These mechanisms are categorized formally as missing completely at random (MCAR), missing at random (MAR), and nonmissing at random (NMAR). In this literature, NMAR is also called nonignorable or informative drop-out, while MCAR and MAR are termed as ignorable or noninformative drop-out.5, 6, 9-11 Historically, the simple listwise or pairwise deletion for an ad hoc complete-case analysis can be applied under MCAR assumption, but this simple procedure results in serious bias when the missing rate is high.
Here, we illustrate an analytic approach that addresses the nonignorable missing data issue using a longitudinal, patient-oriented case study where the purpose is to identify substantive latent growth patterns. This example data set is a prototype of longitudinal data sets where a large proportion of data is missing due to a potentially NMAR mechanism. In other words, the missingness is dependent on the missing values of the variable of our interest, which is nonignorable and informative. In this repeated trial data study, the NMAR missing data are from the dependent variable (i.e. the repeatedly observed response variable), but not from the attributes.12 Also, the missingness includes two types: (a) intermittent missingness (i.e. occasional missing and can relapse) and (b) drop-out missingness (i.e. premature withdrawal and never relapse). To solve this issue, conventional weighting methods may be applied but only when covariate information is limited and sample size is large. 13-16 Weighting methods for use with MAR or NMAR, such as those based on generalized estimating equations (GEE), have recently been developed. However, the semiparametric estimator employed by these methods can be less efficient and less powerful than ML or Bayesian estimation under correctly formulated parametric models (e.g. References 17-21).
Imputation methods also are used to handle missing data, and can be grouped into single, resampling, or multiple imputations. These methods now are utilized primarily under the MAR assumption. Single imputations, such as mean, regression, and hot deck imputation, do not account for imputation uncertainty, and therefore, can cause bias and lose statistical precision.5, 14, 22-24 Both resampling and multiple imputations can estimate the imputation uncertainty. However, resampling imputations, such as bootstrap and jackknife, rely on large samples and are computationally intensive. 25-28 Multiple imputation is less computationally intensive than resampling, and as long as the proportion of missing information is small, multiple imputation results are robust even if MAR fails.6, 29-32 However, under MAR, substantial problems with bias, efficiency, and coverage can arise when missing information exceeds 25% or the correlation between missingness and the dependent variable is greater than 0.4.33
To address the absence of a satisfactory way, we propose a new approach using a parallel mixture model (PMM) to deal with the NMAR problem. The PMM is utilized to generate growth parameter estimates for each subject by considering both observed and NMAR missing values of the repeated measures in parallel, so that each subject has complete growth factors used for depicting their own growth trajectories. However, a purely statistical modeling approach is inadequate as the PMM has a computational disadvantage in growth pattern recognition when a large number of attributes are also considered.
Some have proposed a purely data mining approach, but the most common techniques in the data mining field rely on preprocessing methods, which adopt the same principle of listwise/pairwise deletion and single imputation (e.g. References 34 and 35). Although investigators in a few recent data mining studies (e.g. Reference 36) acknowledge the potential harm of contributing to the appearance of completeness based on these inadequate preprocessing methods, use of these strategies in data mining has not been scrutinized adequately, either empirically or theoretically. Furthermore, missingness under the NMAR mechanism largely has not been addressed in this work. With complete data and especially with a greater number of attributes, data mining techniques are more computationally efficient than PMM to identify growth patterns. Therefore, one of data mining techniques, the fuzzy C-means (FCM) clustering, is incorporated in our study to conduct the cluster identification when more attributes (e.g. covariates) are included, in order to improve computational efficiency.
Thus, the actual motivating rationale of this research is any longitudinal data set used for growth pattern recognition with two characteristics: (1) Informative NMAR missing data on a repeatedly measured response variable, where both intermittent and drop-out missingness coexist and (2) more attributes are used to identify growth patterns along with the subjects' growth profiles. The goal here is to combine the merits of modern statistical methods with the data mining techniques to model the missing data under NMAR mechanism, and effectively identify unique growth patterns in longitudinal designs. This multi-step approach was applied to an observational study, designed to assess stress regulation patterns in the neonatal period (from birth to 1 month of age) among those exposed to tobacco during pregnancy and those not. The study had a high proportion of NMAR missing data. Combining the PMM and FCM along the lines we proposed, the procedure appears to adequately address the NMAR missing problem while achieving accurate growth pattern recognition.
In the next section, the theoretical background of PMM is proposed and compared with the pattern mixture model that is conventionally used under NMAR, and in Sec. 3, the FCM clustering method is discussed. To evaluate the utility of this method, in Sec. 4, the step-wise PMM and FCM clustering method is applied in an empirical case study to identify clusters with post-hoc statistical analyses. The final section includes discussion of these results and conclusions.
2. Parallel Mixture Model
2.1. Conventional NMAR model
To illustrate the PMM model, conventional NMAR models are reviewed briefly in order to understand the development and principles of PMM. Introduced in the early 1980s, pattern mixture and selection models are the two major NMAR models commonly used. Only pattern mixture models are discussed here as they do not require detailed specification of missing mechanism and their likelihood function tends to be more convenient to maximize than selection models.1, 5, 10, 37-41 Pattern mixture models proposed in missing data context have specific implications regarding both (a) the observed patterns of missing data, and (b) the mixture of the distribution of the observed data under different missing patterns and the distribution of the occurrence of missing patterns. The two implications are expressed mathematically via the following expressions.6
Definition 1. Let M denote the categorical variable that identifies the missing patterns, Y denote the complete data that include the observed values Yobs and missing values Ymis, Y = Yobs + Ymis. If the unknown parameters ξ and ω are associated with Y and M, respectively, and assume the observations are modeled independently, then
| (1) |
| (2) |
Equation (1) shows the independence among the observations i; Equation (2) expresses the joint distribution of yi under different missing patterns mi, f(yi|mi, ξ) and the occurrence of the missing patterns, f(mi|ω).
In a longitudinal study, considering the random effects for the repeated measures data and the missing values, the pattern mixture model can be redefined as below.
Definition 2. Let subject i have repeated measures yi = (yi1, …, yit) at time t, and let and denote the observed and missing values of yi, xj, the fixed covariates. Let mi denote the missing indicator, bi denote the random coefficients varying across the subjects, and ξ, ω, and τ denote the unknown parameters associated with Y, M, and b, respectively. Then
| (3) |
The first two terms describe the joint distribution of yi and bi given missing pattern mi; the last term reflects the distribution of missing patterns. There are two kinds of nonignorable missingness in longitudinal studies, according to Little and Rubin.6 One is that M depends on the outcome Y, that is,
| (4) |
The other assumes that the probability of missingness depends on the underlying random coefficients (or latent continuous variable) bi,
| (5) |
To apply the above pattern mixture model in a practical longitudinal study, the first step is to divide the subjects into groups based on the missing patterns. These groups, then, can be used to examine the effect of missing patterns on the outcomes, to evaluate the group-by-time interaction related to the missing patterns, to estimate and compare models of different missing patterns, or even to obtain the overall estimates averaged across the missing patterns. This pattern mixture approach has been utilized in multiple regression, structural equation models, and multilevel models in longitudinal studies.42-44 These analyses can be implemented in current statistical packages such as SAS 9.1 45 and Mplus 5.0.46 The disadvantage of using pattern mixture models is that the missing pattern grouping must be conducted before modeling and the identification of groups in the data processing step is subjective, which can be problematic particularly when sample size in groups is small.43
2.2. Parallel mixture model
Unlike the pattern mixture models, the PMMs empirically identify clusters of subjects (i.e. latent groups) in the modeling process itself. Muthén 47, 48 has proposed a two-part growth mixture model to handle the problem of zero-inflation. We propose PMM to estimate the individual growth parameters using an NMAR missing data set. With PMM, the nonignorable missingness also is assumed to depend on a latent categorical variable ci in addition to the latent continuous variable bi and the outcome yi as discussed above.
Definition 3. Let subject i have repeated measures yi = (yi1, …, yit) at time t, where , , mi, bi are defined as above. Let ci = (ci1, ci2, …, cik) be a latent categorical variable, where cik = 1 if subject i belongs to cluster k and zero otherwise. Then
| (6) |
Assuming mi only depends on ci, byi, and bmi for Y and M part, respectively, and xj are not considered at this stage in this research, Equation (6) can be simplified as
| (7) |
As implied in (7), both the Y and M parts of the model are influenced by ci. In general, ci can be defined for the Y (cyi) and M parts (cmi), respectively. In this case study, ci is defined only by the Y part while the M part only gives the cluster information.
Under the general latent model framework, the growth model for Y part can be expressed as follows:
| (8) |
| (9) |
where yi is a t × 1 vector of repeated measures for subject i; Λyk is a t × q design matrix of the Y part for growth parameter loadings for each subject. For example, Column 1 of Λyk contains intercepts with value of 1; Columns 2 and 3 are parameter vectors associated with slope and quadratic terms, respectively; byi is defined as a q × 1 vector of Y part containing the continuous latent variables. For example, the byi vector can include intercept, slope, and quadratic growth parameters for each subject. ayk is a q×1 matrix containing the growth factor means in the kth cluster. Finally, εi is a t × 1 vector of measurement errors for each i, εi ~ (0, Φk) and ζi is a vector of residuals for subject i in the kth cluster, ζii ~ (0, ψk,), and both εi and ζi are assumed uncorrelated with other variables. As a relatively high portion of NMAR missing values exist in this case study with a medium sample size, the bootstrap standard errors are calculated for the growth parameter estimates and parameter estimates of attributes.49, 50
For the M part, let mi denote is a t × 1 vector of binary categorical outcome for subject I, where t is the number of time points. Given ci and bmi in this study, the conditional independence for ui, in symbol, is
| (10) |
In general, mit can follow an ordered polytomous logistic regression and in this study mit follows binomial logistic regression. Let mi* be a t × 1 logit vector mi, Amk be a t × q design matrix for growth parameter loadings for each subject, κmk be a q × 1 matrix containing the means for the logit coefficients in the kth cluster and bmi be a q × 1 vector of logit coefficients of M part. Given the subject is in cluster cj = k, the model for mi, in symbol, is
| (11) |
| (12) |
Ignoring the residual terms and conditioning on ci, Equations (11) and (12) imply that the logits mi* do not vary across subjects instead across clusters, ci. To implement the PMM, the usual EM algorithm for the regular ML under MAR and ignorability need to be revised to take into account the updated E step information on ci, as the missingness cannot be ignored when conditioning on ci.
To sum up, the rationale for applying PMM to NMAR missing data without the attributes xj is as follows: First, NMAR missing data is common in longitudinal studies, and there is substantial interest in estimating the growth parameters byi rather than using a number of observed repeated measures in growth pattern recognition, because (a) the estimated growth parameters generated from PMM consider nonignorable missing information; (b) an optimal data reduction can be achieved (e.g. 10-dimensional repeatedly measured response variables over time can be reduced to three-dimensional individual growth parameters). Second, after the first step — PMM modeling, all subjects have complete data on their own growth parameters with statistical generality, which will further facilitate the next step, the fuzzy clustering procedure that performs better with high-dimensional but complete data.
3. Fuzzy Clustering
At the first step, the subjects with missing repeated measures were assigned estimated growth parameters using PMM. In other words, with the post-hoc complete data set in which each subject has growth parameters and their original corresponding attributes, we can combine the data mining techniques to efficiently conduct the cluster identification procedure.
For this working example, given five-dimensional covariates xj, and three-dimensional b̂yi = (b̂0i, b̂1i, b̂2i) where b̂0i, b̂1i, b̂2i represent intercepts, slopes, and quadratic estimates, an eight-dimensional data matrix for cluster partition was obtained. Two main clustering methods are available for partition: hard clustering that divides the data set into mutually exclusive subsets and fuzzy clustering that allows the subjects to simultaneously belong to several subsets, but with different degrees of membership. In practice, fuzzy clustering better reflects the real-world circumstance where an individual can have membership in different clusters but with different degrees, and therefore, was selected.
FCM has been proved to be a valid, analytically tractable and computationally efficient clustering method and can solve nonlinear optimization problems using Lagrange multipliers.51, 52 This technique has been frequently used in pattern recognition (e.g. References 53-61) and was therefore applied here. Let X denote the eight-dimensional working data set, X = (b̂0i, b̂1i, b̂2i, x1i, x2i, …, x5i), V denote the cluster centroids, V = (v1, v2, …, vk) and k represent the kth cluster, and U denote the degree of membership for subjects i (i = 1, 2, …, n) in the respective clusters k, U = (μ11, μ12, …, μik), 0 ≤ μik ≤ 1, ∀i, k. Let w denote the weight exponent, and A denote the norm-inducing matrix.51 The objective function to be minimized is
| (13) |
where |xi − vk2| is the Euclidean distance (equivalent to the variance) and μik is constrained as follows:
| (14) |
Using Lagrange multipliers, the stationary points of Equation (13) are identified by combining the constraint (14) to f and setting the gradients of f′ with respect to U, V and λ to zero; that is,
| (15) |
The specific algorithm is well known and is applied as follows: Given the eight-dimensional working data set X, the number of clusters 1 < k < c, the weighting exponent w > 1, the termination tolerance ε < 0 and the norm-inducing matrix A.
Step 1. Initialize U matrix such that U(0).
Step 2. Compute the cluster centroids
| (16) |
Step 3. Compute the distances
| (17) |
Step 4. Update the partition matrix U(0) to U(1) until ∥ U(1) − U(0) ∥ < ε
| (18) |
Step 5. Repeat Steps 2–4 h times.
With the results from above fuzzy clustering, that is, cluster centroids vk, membership degree values μik, and the distances Dik, the fuzzy Sammon mapping technique 62 was applied to map the eight-dimensional data space to the desired two-dimensional plane for visualization. Also, two validation coefficients were used to validate the optimal number of clusters by considering the clustering errors: Classification entropy (CE),63, 64 Xie and Beni's index (XB).65 CE measures the fuzziness of the cluster partition and the larger the value, the closer to optimal the number of clusters. Symbolically,
| (19) |
where n is the number of subjects and μij has the same meaning as above. The drawback of CE is that it increases monotonically with the increase of number of clusters and lacks a direct connection to the data. XB, which quantifies the ratio of the total variation within clusters and the separation of clusters, where the smallest value indicating the optimal number of clusters, is more suitable and hence, a widely used index for fuzzy clustering. The index can be expressed as:
| (20) |
where the symbols have the same meaning as above and the denominator stands for the minimum distance between cluster centroids. Both CE and XB coefficients were used in this study for the cross-validation purposes.
4. Application in a Case Study
The advantages of combining the PMM and FCM techniques are demonstrated in the following case study. As a part of a project funded by the National Institute of Drug Abuse (Espy, Principal Investigator) to delineate the impact of prenatal tobacco exposure on change in neonatal regulation, a systematic assessment, the Neonatal Temperament Assessment (NTA; adapted from Reference 92), was administered to neonates at birth, 2 weeks, and 4 weeks of age. In particular, the NTA Stressor module is designed specifically to evaluate the neonate's regulatory response to a mid-intensity stressor, where a metal disc is immersed in ice water and is applied to the neonate's thigh for a total of five trials. This module was selected for analysis because its requirements for administration and resultant NMAR data. Because this module is administered in a fixed sequence after last feeding, the neonate's initial state before application provides meaningful information regarding his or her regulatory abilities. In this study, multiple measures of prenatal exposure were available for use as attributes in the clustering algorithm. In addition to the basic exposure group membership, maternal self-reported tobacco use and urinary cotinine levels (a metabolic by-product of nicotine, the main psychoactive compound in tobacco) were collected at 16 weeks, 28 weeks, and delivery.
4.1. Outcome and attributes
On the NTA Stressor module, “latency to soothe” (in seconds) is scored on each of the five cold-disc trials. The outcome variable, “latency to soothe” is calculated as the average of these latencies over the five trials to reduce measurement errors. Thus, each neonate has three average latency scores, representing the value at the birth, 2-week, and 4-week age points. The NMAR missing data for these latency scores will be explained in Section 4.2. Although more repeated measures should exhibit the merits of data reduction in the PMM modeling (e.g. from 10 observed repeated measures to 3 latent growth parameters), this case study is intended as an example where the growth parameter estimates can be inferred based on the missing data using the PMM.
Five attributes were added in the fuzzy clustering procedure. “PTE” represented the tobacco exposure group status, coded as 1 for tobacco-exposed and 0 for nonexposed, respectively. The other predictor, “COT,” represented the cotinine level in ng/mL analyzed from maternal urine collected around the 28th week of pregnancy, which biochemically indexed of the amount of tobacco exposure at the cusp of the second and third trimesters. Among the attributes, “ED” was the mothers' educational attainment in years. “ALCHX” indicated mothers' pre-pregnancy drinking history in the month prior to the mothers' last menstrual period, with 1 coded for those who reported drinking and 0 for nondrinkers. “MJ” specified whether the mother reported marijuana use during pregnancy or whose neonate tested positive for marijuana in meconium samples collected at birth (coded as 1) vs those who did not (coded as 0).
4.2. Missingness for the NTA stressor module
4.2.1. Trial level missingness
Several aspects of the stressor module design contributed to the observed missingness in the case study data, resulting in both intermittent and drop-out missingness Within the module at any given age, some neonates were too irritable at the outset of the module that precluded administration of the cold-disc trials. In these cases, each of the trials within the module had missing latency to soothe values. For others, over the course of the stressor module, some neonates were not consoled by the end of the 3-minute trial, and therefore, the stressor module was terminated. In these cases, the remaining trials of the module had missing latency to soothe values. Finally, some neonates did not become irritable to the application of the cold-disc within the allotted time on a given trial. In these cases, the latency to soothe value for that trial was missing. In each of these circumstances, informative missing values were assigned to the subjects for the trial in order to calculate the outcome measure. Since a dependence between missingness and stress regulation ability, the key outcome variable being measured, seems plausible and cannot be ruled out, it is prudent to start the analysis with the presumption that NMAR exists.
4.2.2. Missingness at the module level
As the trial-level descriptions indicate, there are two easily discernable NMAR missing situations that result for the module outcome. The first reflects neonates who were too irritable to be administered the stressor module at all, and thus have a missing average latency value for that module. The other in volves those who did not once respond with irritability to the cold-disc stressor on any of the module trials, and thus never needed to be consoled. The average latency would be missing in this situation as well, though for an entirely different reason than the first. There is a third circumstance, where on at least one trial, the neonate never became irritable to the cold-disc within the allotted time, but on another trial became irritable but could not be consoled within the allotted trial time and then the module was terminated. The end result is a missing latency value for these key trials, but due to both a blend of the “nonirritable” to the stressor missing and the “too irritable/not soothable after the stimulus was removed” missing situations. For the purposes here, the latency to soothe outcome for these cases was treated as though it was missing because of too irritable, as that was the circumstance that precluded further completion of the administration of the stressor module.
4.2.3. Missing rates
The missing values on the repeated measure stress regulation outcome variable are the primary concern. For the 266 cases completed to date, only 12 (4.5%) subjects had nonmissing average latency values for all three assessments. If a listwise deletion method were used, the sample size would drop to 12, which clearly results in a loss of substantial subjects and information about the outcome. A total of 61 (22.9%) subjects had missing values on all trials of only one assessment, and therefore, were missing the average latency outcome score at one age point only. Another 111 (41.7%) subjects were missing average latency value for two assessments. A fair number of subjects (82; 32.8%) were missing an average latency to soothe outcome value for all three assessments. For each assessment, more infants were missing an average latency score than those who were not; that is, 59.8%, 69.9%, and 69.2% of subjects had a missing outcome value at birth, 2 weeks and 4 weeks of age, respectively.
As the missing average latency to soothe values reflect two different missing data circumstances (i.e. “not irritable” or “too irritable/not soothable”), these two categories of missingness must be separated for appropriate treatment in the analyses to follow. The missing trial latency to soothe values for “too irritable/not soothable” subjects were assigned a value of 181 (in seconds) because this designated threshold just exceeded the a priori trial 3-minute time limit and reflected the persistent irritability of the subjects. These values were retained to aid in the estimation procedures of the modeling and clustering demonstration that follows. For “nonirritable” subjects, their missing values were kept as missing in order to distinguish these groups.
4.3. Parallel mixture model vs pattern mixture model for the NTA stressor module
4.3.1. Pattern mixture model for the NTA stressor module
On t repeated measures, there are 2t possible missing patterns over time. In this study, three waves of data collection at birth, 2-, and 4-weeks of age were considered and eight missing patterns were observed with corresponding frequencies displayed in Table 1, where “O” stands for observed values for the Stressor module across data waves and “M” represents missing values. The eight observed missing patterns were used by pattern mixture models. After separation of the two missing conditions as described above, there were 144 subjects with experimental records.
Table 1.
Observed missing patterns and frequency for pattern mixture model in case study.
| Missing pattern | Frequency |
|---|---|
| OOO | 144 |
| MOO | 45 |
| OMO | 26 |
| OOM | 22 |
| MMO | 11 |
| MOM | 10 |
| OMM | 4 |
| MMM | 4 |
Due to the sparseness of four patterns (MMO, MOM, OMM, and MMM), they were grouped into one single group called “Combined Group (CG),” representing subjects who had missing stressor modules for at least two assessments (for detailed grouping criteria and implementation of pattern mixture model, see Reference 43. Based on Definitions 1 and 2 and assuming no covariates at the stage, Equations (3) and (5) can be simplified as
| (21) |
| (22) |
Using a multilevel representation with the dummy-coded grouping variable for the five missing patterns, M, the model could be expressed as:
| (23) |
| (24) |
| (25) |
| (26) |
where yti is the outcome variable, latency to cry and t represents time. Parameters are the random coefficients b0i, b1i, and b2i (the latent continuous variables) for intercepts, slopes, and acceleration/deceleration of the ith subject; β0, β2, and β4 are the mean parameters for b0i, b1i, and b2i when Mi= 0, i.e. subject i belongs to Pattern OOO; β1, β3, and β5 are the mean differences in intercepts, slopes, and acceleration/deceleration among the missing-pattern groups. The level-1 error terms εti are assumed to be independent of level-2 error terms ν, where εti ~ (0, σ2) and ν ~ (0, ψ). The model allows individuals to deviate from the missing-pattern group trend in terms of ν0i (intercepts), ν1i (slopes), and ν2i (acceleration/deceleration). This model could be implemented in Mplus(5.0) using multiple group analysis or SAS(9.2) using PROC MIXED or PROC GLIMMIX.66 As mentioned earlier, the subjects' growth parameters estimates b̂0i, b̂1i, and b̂2i were the primary concern. The partial output of individual growth parameter estimates based on the observed missing patterns from the pattern mixture model was listed in Table 2. The output showed a substantial number of negative estimates for the intercepts, which did not conform to the actual design, where the initial status of the latency to soothe variable should have been at least zero if the subject was not irritable at all.
Table 2.
Partial growth parameter estimates from pattern mixture model and PMM.
| Pattern mixture |
PMM |
|||||
|---|---|---|---|---|---|---|
| ID | IY | SY | QY | IY | SY | QY |
| 20000 | −3.94 | −0.15 | −0.35 | 32.83 | 118.57 | −21.75 |
| 20002 | −20.89 | 12.23 | −1.1 | 90.42 | 100.6 | −28.77 |
| 20006 | −47.51 | 25.84 | −3.46 | 21.86 | 40.05 | −10.94 |
| 20010 | −39.22 | 19.94 | −2.45 | 46.22 | 109.11 | −28.77 |
| 20012 | 31.29 | −16.32 | 2.49 | 180.46 | −6.48 | 0.58 |
| 20020 | −33.22 | 20.2 | −2.52 | 21.5 | −5.83 | 0 |
| 20022 | −14.26 | 5.54 | −0.99 | 26.07 | 123.03 | −22.42 |
| 20024 | −17.67 | 6.77 | −1.34 | 12.58 | 130.04 | −21.9 |
| 20028 | 14.37 | −8.74 | 1.09 | 108.36 | 50.39 | −8.89 |
4.3.2. Parallel mixture model for the NTA stressor module
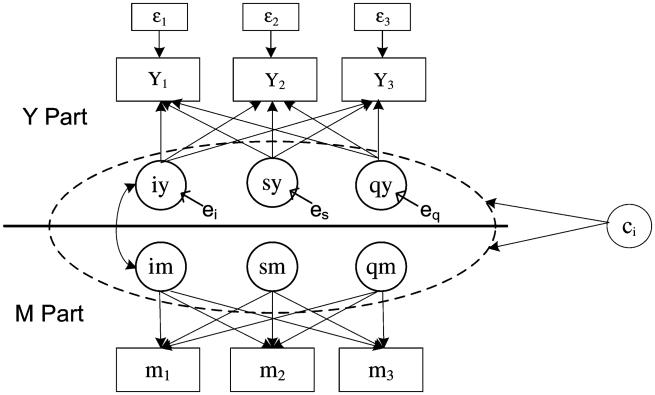
Then, the PMM was applied to the same data. Based on Definition 3, the latent categorical variable ci was introduced into the model, instead of grouping subjects into observed missing pattern categories a priori. To visualize the Y -part and M-part models expressed in Equations (7)-(12), refer to the diagram in Figure 1.
Figure 1.
Parallel mixture model for NTA case study.
As depicted in Figure 1, the Y part and M part of PMM are separated by the black line but associated by the latent variables in the dashed ellipse, where iy, sy, and qy represent the continuous latent variables for each subject (i.e. byi in Equations (7)-(9)), and im, sm, and qm represent bmi in Equations (10)-(12). ei, es, and eq are the bootstrap standard errors associated with the continuous latent variables. Each latent variable in the respective circles has indicators y1–y3 representing the three repeated measures outcomes, or indicator m1–m3 representing missing. Residuals of each measure are represented by ε1–3 in squares; double-arrowed curve lines represent correlation/covariance among latent variable and single-arrowed lines represent estimated path values. The two single-arrowed lines point to byi and bmi from ci, as assumed earlier, represent that ci is defined by the Y part but the M part gives the cluster information.
The PMM for individual growth parameter estimation was implemented in Mplus 5.0. Local maxima often are encountered in mixture modeling, especially with an increasing number of latent clusters. For ci = k ≥ 2, this study used 10,000 random sets of starting values at the initial stage and 1000 optimizations at the final stage, respectively.46, 67 All estimates in this study were obtained avoiding the local maxima and five clusters were found. The growth parameter estimates for each subject were much more reasonable than those from pattern mixture models. For example, the intercepts estimates were not negative, consistent with the experimental design (see Table 2).
4.4. Fuzzy clustering for NTA stressor module
At the second step, fuzzy clustering was conducted by considering individual growth parameters estimated from PMM model and the five attributes: “PTE,” “COT,” “ED,” “ALCHX,” and “MJ” (i.e. eight-dimensional X in Equations (13)-(15)). The FCM algorithm was implemented in Matlab (6.5) to obtain the fuzzy clusters within 15 sec.
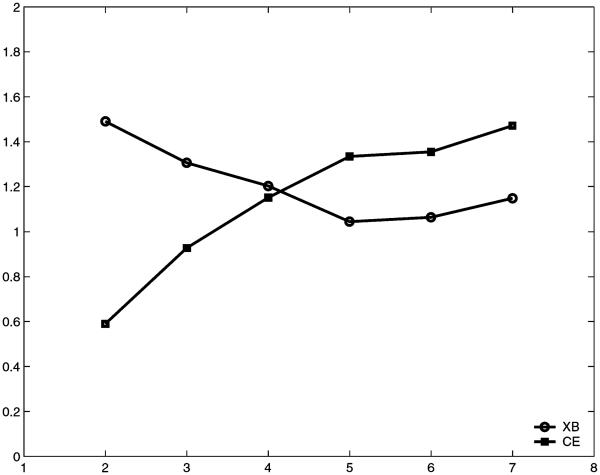
Two coefficients, CE and XB index were used to identify the latent clusters by considering clustering errors. The CE monotonically increased with the number of clusters. However, above five clusters, the value of CE increased slowly (see Figure 2). The XB curve reached its lowest point at five clusters and then increased. Based on these two indexes, five clusters were clearly optimal.
Figure 2.
CE and XB coefficients for fuzzy clustering identification.
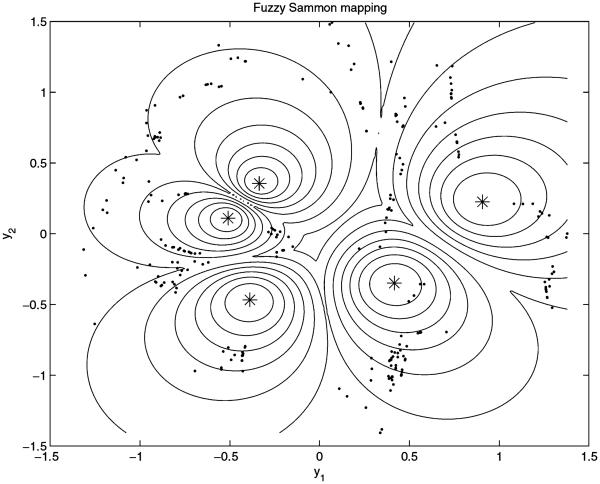
To view the five clusters of the eight-dimensional data space, fuzzy Sammon mapping was applied to obtain the two-dimensional plane shown in Figure 3. As displayed in Figure 3, the asterisk spots represent the projected centroids and the dots representing subjects are clustered within each cluster. The values on the two axes are the projected normalized scores for these subjects.
Figure 3.
Visualization of five latent clusters.
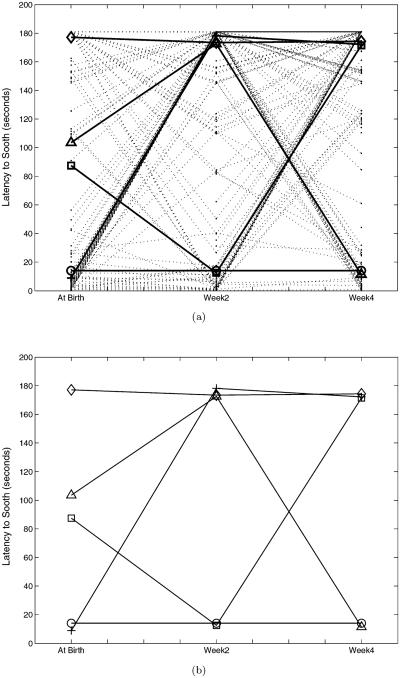
The growth patterns of these five clusters are displayed in Figure 4. The persistently highly irritable, nonsoothable cluster (diamond line) includes those subjects whose average latency to soothe was around 180 sec, consistently across the three assessment age points. At the bottom, persistently nonirritable cluster (circle line) represents those whose values were below 20 sec across the three assessments. Between the two clusters, there were three other patterns which are labeled as declining (triangle line), rising (square line), and rise to plateau (plus line) clusters, respectively.
Figure 4.
Five growth patterns: (a) Estimated growth trends vs observed trends (b) estimated growth trends.
4.5. Post-hoc tests for NTA stressor module
After the identification of five latent clusters, two sets of post-hoc tests were implemented. First, the Chi-square tests were used to examine the proportion of categories of “PTE” (prenatal tobacco-exposed/nonexposed infants), “ALCHX” (before pregnancy maternal drinking/nondrinking), and “MJ” (use of marijuana during pregnancy/nonuse) group within each cluster. The two continuous variables, “COT” and “ED,” were tested across the five clusters. Nonparametric Kruskal Wallis tests were used due to relatively small sample sizes in each cluster. As indicated in Table 3, the proportion of neonates exposed prenatally to tobacco differed from the expected proportion of 0.5 in the persistently irritable, nonsoothable cluster, χ2(1, N = 116) = 5.83, p = 0.02. The maternal cotinine value at 28 weeks, however, did not differ amongst the five clusters, χ2(4, N = 257) = 3.03, p = 0.554. No significant differences were found within each cluster in the proportion of neonates whose mothers reported a history of drinking alcohol in the month prior to the last menstrual period and whose mothers did not. There were also no differences in maternal educational attainment across the five clusters, χ2(4, N = 257) = 2.58, p = 0.631. The proportion of neonates exposed to marijuana during pregnancy differed from the expectation in persistently irritable, nonsoothable, and rising clusters.
Table 3.
Chi-square test within five clusters.
| Persistently highly (N = 116) |
Declining (N = 32) |
Rising (N = 44) |
Rise to plateau (N = 48) |
Persistently nonirritable (N = 17) |
|
|---|---|---|---|---|---|
| Nonexposed | 45 | 20 | 18 | 22 | 8 |
| Prenatal Tobacco | 71 | 12 | 26 | 26 | 9 |
| Exposed | |||||
| χ2(1) | 5.83* | 2.00 | 1.46 | 33 | 0.06 |
| No prior drinking | 28 | 8 | 13 | 16 | 3 |
| Drinking prior to pregnancy | 88 | 24 | 31 | 32 | 14 |
| χ2(1)a | 0.046 | 0.000 | 0.485 | 1.778 | 0.490 |
| No use | 97 | 29 | 36 | 45 | 16 |
| Marijuana use | 19 | 3 | 8 | 3 | 1 |
| χ2(1)b | 7.456** | 0.003 | 4.4* | 0.469 | 0.212 |
| Kruskal–Wallis Tests across Five Clusters c | |||||
| 219.08 | 96.09 | 137.70 | 165.94 | 130.00 | |
| COT d | (473.49) | (225.44) | (387.48) | (388.70) | (278.79) |
| χ2(4) d | 3.025 | ||||
| 13.54 | 13.75 | 13.98 | 13.50 | 14.06 | |
| ED d | (1.71) | (1.63) | (2.02) | (1.62) | (2.22) |
| χ2(4) d | 2.578 | ||||
p < 0.05 ;
p < 0.01 ;
p < 0.001
Exact p-values were used as relatively small sample sizes were used.
the expected proportion for drinking prior to pregnancy is 3/4
the expected proportion for marijuana use is 1/11
the numbers in cells indicate means and standard deviations of each cluster
nonparametric Kruskal–Walls tests due to relatively small sample sizes.
5. Conclusions and Discussions
The identification of growth patterns with nonignorable missing data was addressed in a longitudinal study under the NMAR assumption. A new stepwise approach, combining PMM and FCM techniques, was demonstrated to utilize informative and nonignorable missing information to achieve computational efficiency as well as statistical generality. The step-wise approach was realized by: Step 1, estimating the growth parameters for each subject with bootstrap standard errors using PMM, which models both the observed and NMAR missing values (including intermittent and drop-out missingness); Step 2, using individual growth parameters and attributes to identify the growth patterns through the fuzzy clustering method by considering clustering errors. Importantly, these results show that using PMM to estimate individuals' growth parameters can achieve data reduction, especially when more repeated measures were observed for subjects. Meanwhile, this modeling approach can retain the number of collected subjects with the nonignorable missing values, rather than deleting these cases or imputing uncertain values for these informative missing values. The concept of combining the PMM and fuzzy clustering method is novel and feasible. Currently, different software is required for each step. In the future, an integrated algorithm is expected to be developed to conduct the whole procedure.
In this paper, PMM was illustrated in comparison with pattern mixture models in theoretical discussion and in a case study. The PMM model using latent clusters in our case was demonstrated to outperform the pattern mixture model which uses observed missing patterns. We expect that PMM will demonstrate its superiority in other applications that are similar to this study, assuming different growth patterns indeed exist. As to single-growth-pattern data, we expect the pattern mixture model should still fit well. In the future, a simulation study is planned to systematically compare the results of these two models un der different modeling conditions.
With complete attributes added to the model, fuzzy clustering methods were incorporated because of computational efficiency. The widely applied FCM clustering method performed well in this case study. Substantively, the identified clusters appear to have validity, given the findings in our lab and others 68-70 that link prenatal tobacco exposure to difficulties in self-regulation in the neonatal and early infancy developmental periods. In the future, other existent clustering methods (e.g. References 71-77) will be compared to this FCM technique to evaluate its utility via simulation and case studies. As more novel fuzzy clustering methods emerge in data mining research (e.g. Reference 78), future studies may also consider comparing the FCM method with these methods in order to generalize this hybrid technique for growth pattern recognition.
Acknowledgments
This research was supported in part by R01 DA014661 from the National Institute on Drug Abuse (Espy, PI), R01 MH065668 from the National Institute of Mental Health (Espy, PI), and P01 HD038051 (Washburn, PI) and R01 HD050309 (Taylor, PI) from the National Institute of Child Health and Development. We wish to thank the participating families, project staff, and graduate students who assisted in various tasks associated with these projects.
References
- 1.Allison PD. Multiple imputation for missing data: A cautionary tale. Sociol. Methods Res. 2000;28(3):301–309. [Google Scholar]
- 2.Anderson TW. Maximum likelihood estimates for a multivariate normal distribution when some observations are missing. J. Am. Stat. Assoc. 1957;52(278):200–203. [Google Scholar]
- 3.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J. Royal Stat. Soc. Series B Methodol. 1977;39(1):1–38. [Google Scholar]
- 4.Little RJA, Schluchter MD. Maximum likelihood estimation for mixed continuous and categorical data with missing values. Biometrika. 1985;72(3):497–512. [Google Scholar]
- 5.Little RJA, Rubin DB. Statistical Analysis with Missing Data. John Wiley; New York: 1987. [Google Scholar]
- 6.Little RJA, Rubin DB. Statistical Analysis with Missing Data. John Wiley; New York: 2002. [Google Scholar]
- 7.Meng X-L, Rubin DB. Maximum likelihood estimation via the ECM algorithm: A general framework. Biometrika. 1993;80(2):267–278. [Google Scholar]
- 8.Schafer JL. Multiple imputation: A primer. Stat. Methods Med. Res. 1999;8(1):3–15. doi: 10.1177/096228029900800102. [DOI] [PubMed] [Google Scholar]
- 9.Diggle P, Kenward MG. Informative drop-out in longitudinal data analysis. Appl. Stat. 1994;43(1):49–93. [Google Scholar]
- 10.Little RJA. Modeling the drop-out mechanism in repeated-measures studies. J. Am. Stat. Assoc. 1995;90(431):1112–1121. [Google Scholar]
- 11.Rubin DB. Inference and missing data. Biometrika. 1976;63(3):581–592. [Google Scholar]
- 12.Roy J, Lin X. Missing covariates in longitudinal data with informative dropouts: Bias analysis and inference. Biometrics. 2005;61(3):837–846. doi: 10.1111/j.1541-0420.2005.00340.x. [DOI] [PubMed] [Google Scholar]
- 13.Horvitz DG, Thompson DJ. A generalization of sampling without replacement from a finite universe. J. Am. Stat. Assoc. 1952;47(260):663–685. [Google Scholar]
- 14.Little RJA. Survey nonresponse adjustments for estimates of means. Int. Stat. Rev./Revue Internationale de Statistique. 1986;54(2):139–157. [Google Scholar]
- 15.Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- 16.Rosenbaum PR, Rubin DB. Constructing a control group using multivariate matched sampling methods that incorporate the propensity score. Am. Stat. 1985;39(1):33–38. [Google Scholar]
- 17.Lipsitz SR, Ibrahim JG, Zhao LP. A weighted estimating equation for missing covariate data with properties similar to maximum likelihood. J. Am. Stat. Assoc. 1999;94(448):1147–1160. [Google Scholar]
- 18.Park T. A comparison of the generalized estimating equation approach with the maximum likelihood approach for repeated measurements. Stat. Med. 1993;12(18):1723–1732. doi: 10.1002/sim.4780121807. [DOI] [PubMed] [Google Scholar]
- 19.Robins JM, Rotnitzky A, Zhao LP. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. J. Am. Stat. Assoc. 1995;90(429):106–121. [Google Scholar]
- 20.Zeger SL, Liang K-Y, Albert PS. Models for longitudinal data: A generalized estimating equation approach. Biometrics. 1988;44(4):1049–1060. [PubMed] [Google Scholar]
- 21.Zhao LP, Lipsitz S. Designs and analysis of two-stage studies. Stat. Med. 1992;11(6):769–782. doi: 10.1002/sim.4780110608. [DOI] [PubMed] [Google Scholar]
- 22.Afifi AA, Elashoff RM. Missing observations in multivariate statistics: I. Review of the literature. J. Am. Stat. Assoc. 1966;61(315):595–604. [Google Scholar]
- 23.Buck SF. A method of estimation of missing values in multivariate data suitable for use with an electronic computer. J. Royal Stat. Soc. Series B (Methodological) 1960;22(2):302–306. [Google Scholar]
- 24.Marker DA, Judkins DR, Winglee M. Large-scale imputation for complex surveys. In: Groves RM, Dillman DA, Eltinge JL, Little RJA, editors. Survey Nonresponse. Wiley; New York: 2002. [Google Scholar]
- 25.Efron B. Missing data, imputation, and the bootstrap m. J. Am. Stat. Assoc. 1994;89(426):463–475. [Google Scholar]
- 26.Fay RE. Alternative paradigms for the analysis of imputed survey data. J. Am. Stat. Assoc. 1996;91(434):490–498. [Google Scholar]
- 27.Rao JNK, Shao J. Jackknife variance estimation with survey data under hot deck imputation. Biometrika. 1992;79(4):811–822. [Google Scholar]
- 28.Shao J, Chen Y, Chen Y. Balanced repeated replication for stratified multistage survey data under imputation. J. Am. Stat. Assoc. 1998;93(442):819–831. [Google Scholar]
- 29.Glynn RJ, Laird NM, Rubin DB. Multiple imputation in mixture models for nonignorable nonresponse with follow-ups. J. Am. Stat. Assoc. 1993;88(423):984–993. [Google Scholar]
- 30.Raudenbush SW, Bryk AS. Hierarchical Linear Models: Applications and Data Analysis Methods. London Sage; 2002. [Google Scholar]
- 31.Rubin DB. Multiple imputation after 18+ years. J. Am. Stat. Assoc. 1996;91(434):473–489. [Google Scholar]
- 32.Rubin DB, Schenker N. Multiple imputation for interval estimation from simple random samples with ignorable nonresponse. J. Am. Stat. Assoc. 1986;81(394):366–374. [Google Scholar]
- 33.Collins LM, Schafer JL, Kam C-M. A comparison of inclusive and restrictive strategies in modern missing data procedures. Psychol. Methods. 2001;6(4):330–351. [PubMed] [Google Scholar]
- 34.Parthasarathy S, Aggarwal CC. On the use of conceptual reconstruction for mining massively incomplete data sets. Knowledge Data Eng. IEEE Trans. 2003;15(6):1512–1521. [Google Scholar]
- 35.Tseng S-M, Wang K-H, Lee C-I. A pre-processing method to deal with missing values by integrating clustering and regression techniques. Appl. Artif. Intell. 2003;17(5/6):535. [Google Scholar]
- 36.Zhang S, Qin Z, Ling CX, Sheng S. Missing is useful: Missing values in costsensitive decision trees. IEEE Trans. Knowledge Data Eng. 2005;17(12):1689–1693. [Google Scholar]
- 37.Little RJA. Pattern-mixture models for multivariate incomplete data. J. Am. Stat. Assoc. 1993;88(421):125–134. [Google Scholar]
- 38.Little RJA. A class of pattern-mixture models for normal incomplete data. Biometrika. 1994;81(3):471–483. [Google Scholar]
- 39.Little RJA, Wang Y. Pattern-mixture models for multivariate incomplete data with covariates. Biometrics. 1996;52(1):98–111. [PubMed] [Google Scholar]
- 40.Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychol. Methods. 2002;7(2):147–177. [PubMed] [Google Scholar]
- 41.Verbeke G, Molenberghs G. Linear Mixed Models for Longitudinal Data. Springer-Verlag; New York: 2000. [Google Scholar]
- 42.Duncan SC, Duncan TE. Modeling incomplete longitudinal substance use data using latent variable growth curve methodology. Multivariate Behav. Res. 1994;29(4):313–338. doi: 10.1207/s15327906mbr2904_1. [DOI] [PubMed] [Google Scholar]
- 43.Hedeker D, Gibbons RD. Application of random-effects pattern-mixture models for missing data in longitudinal studies. Psychol. Methods. 1997;2(1):64–78. [Google Scholar]
- 44.Muthén B, Kaplan D, Hollis M. On structural equation modeling with data that are not missing completely at random. Psychometrika. 1987;52(3):431–462. [Google Scholar]
- 45.SAS Institute Inc. SAS/STAT User's Guide, Version 9.1. SAS Institute Inc; Cary, NC: 2003. [Google Scholar]
- 46.Muthén L, Muthén B. Mplus User's Guide. 4th ed. Muthén & Muthén; Los Angeles: 2006. [Google Scholar]
- 47.Muthén B. Latent variable mixture modeling. In: Marcoulides GA, Schumacker RE, editors. New Developments and Techniques in Structural Equation Modeling. Lawrence Erlbaum Associates; Mahwah, NJ: 2001a. pp. 1–33. [Google Scholar]
- 48.Muthén B. Second-generation structural equation modeling with a combination of categorical and continuous latent variables: New opportunities for latent class/latent growth modeling. In: Collins L, Sayer A, editors. New Methods for the Analysis of Change. APA; Washington: 2001b. pp. 291–322. [Google Scholar]
- 49.Efron B, Tibshirani RJ. An Introduction to the Bootstrap. Chapman and Hall; New York: 1993. [Google Scholar]
- 50.Enders CK. Applying the Bollen-Stine bootstrap for goodness-of-fit measures to structural equation models with missing data. Multivariate Behav. Res. 2002;37:359–377. doi: 10.1207/S15327906MBR3703_3. [DOI] [PubMed] [Google Scholar]
- 51.Bezdek JC. Pattern Recognition with Fuzzy Objective Function Algorithms. Kluwer Academic Publishers; Norwell, MA: 1981. [Google Scholar]
- 52.Dunn JC. Some recent investigations of a new fuzzy partition algorithm and its application to pattern classification problems. J. Cybern. 1974;4:1–15. [Google Scholar]
- 53.Hathaway RJ, Bezdek JC, Hu Y. Generalized fuzzy c-means clustering strategies using Lp norm distances. IEEE Trans. Fuzzy Syst. 2000;8(5):576–582. [Google Scholar]
- 54.Muller KR, Mika S, Ratsch G, Tsuda K, Scholkopf B. An introduction to kernel-based learning algorithms. IEEE Trans. Neural Networks. 2001;12(2):181–201. doi: 10.1109/72.914517. [DOI] [PubMed] [Google Scholar]
- 55.Ahmed MN, Yamany SM, Mohamed N, Farag AA. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data. IEEE Trans. Med. Imag. 2002;21(3):193–199. doi: 10.1109/42.996338. [DOI] [PubMed] [Google Scholar]
- 56.Fan J, Zhen W, Xie W. Suppressed fuzzy c-means clustering algorithm. Patt. Recognit. Lett. 2003;24:9–10. 1607–1612. [Google Scholar]
- 57.Wang X, Wang Y, Wang L. Improving fuzzy c-means clustering based on feature-weight learning. Patt. Recognit. Lett. 2004;25(10):1123–1132. [Google Scholar]
- 58.Pianykh OS. Analytically tractable case of fuzzy c-means clustering. Patt. Recognit. 2005;39(1):35–46. [Google Scholar]
- 59.Torres A, Nieto JJ. Fuzzy logic in medicine and bioinformatics. J. Biomed. Biotechnol. 2006;6:1–7. doi: 10.1155/JBB/2006/91908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Cai W, Chen S, Zhang D. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Patt. Recognit. 2007;40(3):825–838. [Google Scholar]
- 61.Chang K, Lin Z, Liu S, Tyan C. Myocardial ischemia detection by pulse signal features and fuzzy clustering. 2008 International Conference on BioMedical Engineering and Informatics. :473–477. [Google Scholar]
- 62.Feil B, Balasko B, Abonyi J. Visualization of fuzzy clusters by fuzzy Sammon mapping projection: application to the analysis of phase space trajectories. Soft Computing. 2002;11(5):479–488. [Google Scholar]
- 63.Cheng HD, Chen J-R, Li J. Threshold selection based on fuzzy c-partition entropy approach. Patt. Recognit. 1998;31(7):857–870. [Google Scholar]
- 64.Cheng HD, Chen Y-H, Sun Y. A novel fuzzy entropy approach to image enhancement and thresholding. Signal Process. 1999;75(3):277–301. [Google Scholar]
- 65.Xie XL, Beni G. A validity measure for fuzzy clustering. IEEE Trans. Patt. Anal. Mach. Intell. 1991;13(8):841–847. [Google Scholar]
- 66.Littell RC, Milliken GA, Stroup WW, Wolfinger RD. SAS System for Mixed Models. 2nd ed. Cary, NC; SAS Institute Inc: 2006. [Google Scholar]
- 67.Muthén B. Latent variable analysis: Growth mixture modeling and related techniques for longitudinal data. In: Kaplan D, editor. Handbook of Quantitative Methodology for the Social Sciences. Sage; Newbury Park, CA: 2004. pp. 345–368. [Google Scholar]
- 68.Law KL, Stroud LR, LaGasse LL, Niaura R, Liu J, Lester BM. Smoking during pregnancy and newborn neurobehavior. Pediatrics. 2003;111(6):1318–1323. doi: 10.1542/peds.111.6.1318. [DOI] [PubMed] [Google Scholar]
- 69.Willoughby M, Greenberg M, Blair C, Stifer C. Neurobehavioral consequences of prenatal exposure to smoking at 6 to 8 months of age. Infancy. 2007;12(3):273–301. [Google Scholar]
- 70.Wakschlag LS, Leventhal BL, Pine DS. Elucidating early mechanisms of developmental psychopathology: The case of prenatal smoking and disruptive behavior. Child Dev. 2006;77(4):893–906. doi: 10.1111/j.1467-8624.2006.00909.x. [DOI] [PubMed] [Google Scholar]
- 71.Shi Y, Wan J, Zhang X, Kou G, Peng Y, Cao Z, Guo Y. Comparison study of two kernel-based learning algorithms for predicting the distance range between antibody interface residues and antigen surface. Int. J. Comput. Math. 2006;84(5):697–707. [Google Scholar]
- 72.Zheng J, Zhuang W, Yan N, Kou G, Peng H, McNally C, Erichsen D, Cheloha A, Herek S, Shi C, Shi Y. Classification of HIV-1 mediated neuronal dendritic and synaptic damage using multiple criteria linear programming. Neuroinformatics. 2004;2(3):303–326. doi: 10.1385/ni:2:3:303. [DOI] [PubMed] [Google Scholar]
- 73.Peng Y, Kou G, Shi Y, Chen Z. Descriptive framework for the field of data mining and knowledge discovery. Int. J. Inform. Technol. Decision Making. 2008;7(4):639–682. [Google Scholar]
- 74.Chen Z. From data mining to behavior mining. Int. J. Inform. Technol. Decision Making. 2006;5(4):703–711. [Google Scholar]
- 75.Huang X. Comparison of interestingness measures for web usage mining: An empirical study. Int. J. Inform. Technol. Decision Making. 2006;6(1):15–41. [Google Scholar]
- 76.Zhang W. YinYang bipolar fuzzy sets and fuzzy equilibrium relations: For clustering, optimization, and global regulation. Int. J. Inform. Technol. Decision Making. 2006;5(1):19–46. [Google Scholar]
- 77.Zhong N. Impending brain informatics research from web intelligence perspective. Int. J. Inform. Technol. Decision Making. 2006;5(4):713–727. [Google Scholar]
- 78.de Castro LN, Timmis J. Artificial immune systems: A novel paradigm to pattern recognition. In: Corchado JM, Alonso L, Fyfe C, editors. Artificial Neural Networks in Pattern Recognition. University of Paisley; UK: 2002. pp. 67–84. [Google Scholar]
- 79.Brown EC, Catalano RF, Fleming CB, Haggerty KP, Abbott RD. Adolescent substance use outcomes in the raising healthy children project: A two-part latent growth curve analysis. J. Consult. Clin. Psychol. 2005;73(4):699–710. doi: 10.1037/0022-006X.73.4.699. [DOI] [PubMed] [Google Scholar]
- 80.Hui L, Powers DA. Growth curve models for zero-inflated count data: An application to smoking behavior. Struct. Equat. Model. 2007;14(2):247–279. [Google Scholar]
- 81.Jennrich RI, Schluchter MD. Unbalanced repeated-measures models with structured covariance matrices. Biometrics. 1986;42(4):805–820. [PubMed] [Google Scholar]
- 82.Kowalski KG, McFadyen L, Hutmacher MM, Frame B, Miller R. A two-part mixture model for longitudinal adverse event severity data. J. Pharmacokinet. Pharmacodyn. 2003;30(5):315–336. doi: 10.1023/b:jopa.0000008157.26321.3c. [DOI] [PubMed] [Google Scholar]
- 83.Muthén B. Beyond SEM: General latent variable modeling. Behaviormetrika. 2002;29:81–117. [Google Scholar]
- 84.Muthén B, Brown CH, Masyn K, Jo B, Khoo S-T, Yang C-C, et al. General growth mixture modeling for randomized preventive interventions. Biostatistics. 2002;3(4):459–475. doi: 10.1093/biostatistics/3.4.459. [DOI] [PubMed] [Google Scholar]
- 85.Muthén B. Two-part growth mixture modeling [Electronic Version] 2001 Accessed April 5, 2007, @ http://www.gseis.ucla.edu/faculty/muthen/articles/Article 095.pdf.
- 86.Muthén B, Brown CH. Non-ignorable missing data in a general latent variable modeling framework [Electronic Version] 2001 Accessed January 15th, 2007, @ http://www.statmodel.com/
- 87.Nagin DS. Analyzing developmental trajectories: A semiparametric, group-based approach. Psychol. Methods. 1999;4:139–157. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]
- 88.Olsen MK, Schafer JL. A two-part random-effects model for semicontinuous longitudinal data. J. Am. Stat. Assoc. 2001;96(454):730–745. [Google Scholar]
- 89.Rubin DB. Statistical matching using file concatenation with adjusted weights and multiple imputations. J. Bus. Econ. Stat. 1986;4(1):87–94. [Google Scholar]
- 90.Rubin DB. Multiple Imputation for Nonresponse in Surveys. Wiley; New York: 1987. [Google Scholar]
- 91.Schafer JL, Schenker N. Inference with imputed conditional means. J. Am. Stat. Assoc. 2000;95(449):144–154. [Google Scholar]
- 92.Riese M. Implications of sex differences in neonatal temperament for early risk and developmental/environmental interactions. Journal of Genetic Psychology. 1986;147:507–513. doi: 10.1080/00221325.1986.9914526. [DOI] [PubMed] [Google Scholar]