Collaborative computational anatomy: An MRI morphometry study of the human brain via diffeomorphic metric mapping

Abstract

This article describes a large multi‐institutional analysis of the shape and structure of the human hippocampus in the aging brain as measured via MRI. The study was conducted on a population of 101 subjects including nondemented control subjects (n = 57) and subjects clinically diagnosed with Alzheimer's Disease (AD, n = 38) or semantic dementia (n = 6) with imaging data collected at Washington University in St. Louis, hippocampal structure annotated at the Massachusetts General Hospital, and anatomical shapes embedded into a metric shape space using large deformation diffeomorphic metric mapping (LDDMM) at the Johns Hopkins University. A global classifier was constructed for discriminating cohorts of nondemented and demented subjects based on linear discriminant analysis of dimensions derived from metric distances between anatomical shapes, demonstrating class conditional structure differences measured via LDDMM metric shape (P < 0.01). Localized analysis of the control and AD subjects only on the coordinates of the population template demonstrates shape changes in the subiculum and the CA1 subfield in AD (P < 0.05). Such large scale collaborative analysis of anatomical shapes has the potential to enhance the understanding of neurodevelopmental and neuropsychiatric disorders. Hum Brain Mapp, 2009. © 2008 Wiley‐Liss, Inc.

INTRODUCTION

Emerging collections of imaging, clinical, and functional data at multiple sites provide an unprecedented opportunity to increase statistical power in detecting disease in the human brain (e.g., Fennema‐Notestine et al., 2007). However, there are several formidable challenges such as portability of software and data developed and collected at individual sites. To address these challenges, the National Institutes of Health created the Biomedical Informatics Research Network (BIRN) [Grethe et al., 2005; Jovicich et al., 2005; Keator et al., 2008]. In addition, a major difficulty confronting BIRN and other neuroscientists is that the human brain is a collection of geometrically complex, interconnected, folded structures. Serious study of the function and structure of the human brain requires computational analysis that considers this complex geometry. Computational Anatomy has emerged as a discipline focused on such issues including the representation of the biological variability of the local coordinate systems of human anatomy studied via morphometric tools [Grenander and Miller, 1998; Miller et al., 2002; Thompson and Toga, 2002]. Computational Anatomy encompasses many forms of neuromorphometric analysis [Thompson et al., 2004]. Focusing on the inference of the statistical representations of shape, studies in the computational anatomy of growth, atrophy, and disease have literally exploded over the past few years.

In particular, applications of Computational Anatomy in normal aging and Alzheimer's Disease (AD) have been studied in both cortex and deep brain structures by several groups [Ballmaier et al., 2004; Buckner et al., 2004; Csernansky et al., 2000; Gee et al., 2003; Good et al., 2001; Miller et al., 2003; Thompson et al., 2003]. AD is characterized by neuronal degeneration associated with the progressive deposition of neurofibrillary tangles and β‐amyloid plaques. Structural MRI has revealed widespread changes with some of the earliest and most robust in the hippocampal formation [Ball, 1977; Fischl et al., 2002; Haller et al., 1996; Head et al., 2005; Kaye et al., 1997; Killiany et al., 2002; Laakso et al., 2000; Lehtovirta et al., 1995; Petersen et al., 2000]. With the advent of large scale multi‐site neuroimaging studies of AD such as the Alzheimer's Disease Neuroimaging Initiative (ADNI) [Jack et al., 2008], an accurate and explicit representation of the shape of the hippocampus is essential for accurately characterizing the nature and exact location of shape changes.

In Computational Anatomy, morphometric studies of shape are carried out by metric comparison of anatomical structures via vector field displacements relating the coordinatized structures [Avants and Gee, 2004; Beg et al., 2005; Miller et al., 2006]. The morphometry study reported here focuses on a large scale mult‐site shape analysis of the hippocampus in a 101‐subject MRI data set consisting of controls and subjects clinically diagnosed with AD and semantic dementia (SD). The processing pipeline described here involves data collection and automated construction and visualization of anatomical manifolds from MRI data collected at Washington University in St. Louis and annotated via FreeSurfer [Fischl et al., 2002, 2004] at the Massachusetts General Hospital; the morphometric comparison was performed at the Johns Hopkins University. Two statistical characterizations of the normal and disease cohorts based on shape change are presented here. First, a localized statistical analysis is performed in the common, extrinsic, template coordinates of the atlas. Local areas of change are encoded via the momentum representation of shape change in the population indexed over the atlas. The second approach is to construct classifiers for discriminating the population directly from the metric distances between anatomical structures as generated via large deformation diffeomorphic metric mapping (LDDMM) [Beg et al., 2005; Miller et al., 2006; Vaillant et al., 2007]. Clustering is performed using discriminant analysis in the dimensions obtained from multidimensional scaling (MDS) of the matrix of interpoint metric distances between anatomies. This provides a method for building classifiers for discriminating between cohorts.

It is demonstrated that a single data analysis pipeline allows for the direct metric analysis of human hippocampus shape going directly from the MR image to quantitative measures of morphometric shape change revealing the class conditional structure associated with cohorts of nondemented and demented subjects. Cohort clustering is reflected by localized changes in the subiculum and CA1 subfield of the hippocampus.

METHODS

Data Acquisition

MRI data from 101 individuals were collected at Washington University in St. Louis as part of ongoing studies of structural brain morphometry associated with the Alzheimer Disease Research Center [Buckner et al., 2004, 2005; Fotenos et al., 2005, 2008; Gold et al., 2005; Head et al., 2005; Salat et al., 2004]. The present study analyzed data from individuals classified as nondemented control subjects (n = 57; mean age = 76 years, range = 60–89; 26 female), clinically diagnosed AD (n = 38; mean age = 74 years, range = 62–84; 15 female) and SD (n = 6; mean age = 69 years, range = 62–80; 2 female). The classification of nondemented controls and AD employed procedures based on the Clinical Dementia Rating (CDR; [Morris, 1993]). The determination of AD or control status was based solely on clinical methods, without reference to psychometric performance. The diagnosis of AD is based on clinical information (derived primarily from a collateral source) that the subject has experienced gradual onset and progression of memory decline and other cognitive domains; see Fotenos et al. [2005] and Marcus et al. [2007] for more details of selection criteria for these subjects. All nondemented control subjects were CDR 0 that excludes any indication of memory impairment. Individuals meeting criteria for MCI would not be included in our CDR 0 group. For AD, 28 were CDR 0.5 (very mild dementia) and 10 were CDR 1 (mild dementia). For SD, 4 were CDR 0.5 and 2 CDR 1 at their nearest assessment to the MRI. The six individuals with SD have been described previously [Gold et al., 2005] and were classified based on a specifically designed battery of neuropsychological tests meeting original [Hodges et al., 1992] and consensus [Neary et al., 1998] inclusion and exclusion criteria for SD. Although a larger number of participants with SD would be desirable, we were only able to recruit six to this specific scanning protocol. Participants were excluded if they had a history of neurologic, psychiatric, or medical illness that contributed to dementia diagnosis. Participants consented to participation in accordance with guidelines of the Washington University Human Studies Committee. The imaging procedures have been described previously [Marcus et al., 2007]. Data from the AD cohort can be obtained freely as part of the OASIS open‐access data release (http://www.oasis-brains.org). Briefly, for each participant, two to four high‐resolution MP‐RAGE scans were motion‐corrected and averaged per participant (four volumes were averaged for all except five participants; Siemens 1.5 T Vision System, resolution 1 × 1 × 1.25 mm, TR = 9.7 ms, TE = 4 ms, FA = 10, TI = 20 ms, TD = 200 ms) to create a single image volume with high contrast‐to‐noise. These acquisition parameters were empirically optimized to increase gray/white and gray/cerebrospinal fluid contrast.

The Morphometry of Hippocampal Manifolds

Left and right hippocampi were segmented using automated whole brain Bayesian segmentation via Freesurfer [Fischl et al., 2002, 2004], labeling each voxel of the MRI volume based on prior probabilistic information compiled from a set of manually labeled training brain volumes and the local intensity distribution of each class. A single connected representation of each hippocampus is based on a combination of geometric constraints, with components removed or added iteratively to minimize the total costs until the segmentation is modified into a single topologically correct connected component [Segonne et al., 2003]. A tessellation was constructed based on eight triangles representing each face at the interface of hippocampus voxels and differently labeled voxel. To ensure smoothness and accuracy of the surface, the surface was refined based on Gaussian curvature measurement to get rid of high‐frequency errors in regions where a string of voxels with similar intensity to the hippocampus is mistakenly labeled because of the partial volume effects of the white matter and the adjacent ventricle.

We model the space of shapes I ∈ as objects indexed over manifolds or subsets of ℝ³, either two‐dimensional surfaces or three‐dimensional subvolumes. The shape space is a Riemmannian manifold with metric structure resulting from the assumption that the shapes are an orbit under a group of diffeomorphisms [Grenander and Miller, 1998] (1‐1 and onto transformations with inverses that are smooth). For any pair I, J ∈ , there exists a flow of diffeomorphisms g _t,t ∈ [0,1] transforming one shape to the other g · I ∼ J. The metric distance between any pair I, J is given by the length of the shortest or geodesic curve through the space of shapes connecting them. The diffeomorphisms are constructed as a flow of ordinary differential equations 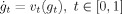with g ₀ = id the identity map, and associated vector fields v_t, t ∈ [0,1]. The metric between two shapes I, J takes the form

(1)

such that g transforms I to J. The norm ∥·∥_V is chosen to ensure that the vector fields are smooth in space (derivatives exist in the squared‐energy sense). To calculate the norm, we use LDDMM for surfaces [Vaillant and Glaunès, 2005; Vaillant et al., 2007] and for volumes [Beg et al., 2005], by introducing a cost function measuring correspondence between mapped anatomical objects C(g · I,J) and then computing the geodesic connection to minimize the cost. The shapes come as segmented volumes or as triangulated meshes associated with the hippocampal subregion. For mapping the triangulated meshes representing the boundary of the hippocampus from Freesurfer, we use the surface matching [Vaillant et al., 2007]; for mapping the volume segmentations, we use the image matching procedure for segmentations [Kirwan et al., 2007; Miller et al., 2005]. In each case, we solve the inexact matching problem forcing one shape to map onto the other, obtaining a matching cost C that is small but not identically zero. In LDDMM, volume mapping correspondence is based on the intensity data at the voxel level whereas in LDDMM surface mapping, it is based on the normals to the triangulated surfaces [Vaillant and Glaunès, 2005]. Reliability has been demonstrated for both methods [Beg et al., 2005; Qiu et al., 2007a, b; Vaillant et al., 2007]; also pose in both cases is removed via rigid landmark alignment prior to the mapping. The LDDMM metric shape space embedding is computationally intensive. The mapping procedures were run on clusters at JHU, the BIRN coordinating center at San Diego, and the Teragrid (http://www.teragrid.org).

Shape Analysis Via Random Momentum Fields

To localize geometric changes in the anatomical structures of the group, statistical shape analysis is performed on the diffeomorphic maps. The geodesic flow 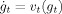between any pair of shapes I, J is encoded by the initial vector field ν₀ [Miller et al., 2006]; along the geodesic there is a conservation law, which implies that the entire flow can be generated from the initial vector field in the tangent space at the identity of the shape. Localized statistical shape analysis is performed on these initial vector fields as first done for landmarked shapes [Vaillant et al., 2004]. It is natural to compute the statistically significant locations of the shape change between the populations characterized by these initial vector fields. Defining the norm ∥v _t∥${}_{\mathit{\text{V}}}^{\text{2}}$ = 〈Av _t, v _t〉, then along the geodesic the momentum is defined as M _t = Av _t, where A is the inverse of the Green's kernel that makes V a reproducing kernel Hilbert space. Assuming that the momentum is smooth enough, it satisfies

(2)

The initial momentum M ₀ completely determines the LDDMM maps from the template onto the target shapes and has the added attractive property that it is normal to the level lines of the template [Miller et al., 2006]. For surface mapping, M ₀ is normal to the template and specified by a scalar field indexed over it according to

(3)

with N(·) the normal field to the surface. Population shape variation is represented by the size of the scalar fields μ(x), x ∈ S ^temp with positive sign pointing the outward motion and negative pointing the inward motion relative to the template coordinates. For statistics we model μ(x), as a Gaussian field in the form of

(4)

where the U _k are Gaussian random variables and ϕ_k(x) are chosen as the k‐th eigenfunction of a complete orthonormal base generated from the Laplace‐Beltrami operator on S ^temp [Qiu et al., 2006].

Template Construction

We assume that the orbit 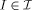of anatomical shapes is generated from an exemplar or template I _temp ∈ , which must be estimated. All elements 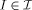are modeled as generated by the flow of diffeomorphisms from the template for some 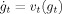with I = g ₁ · I _temp. Our random model assumes that the anatomies 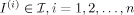are generated via geodesic flows of the diffeomorphism equation with the conservation equation holding, and the flow satisfies the conservation Eq. (2) so that when M ${}_{\text{0}}^{\text{(}\mathit{\text{i}}\text{)}}$, i = 1,2,…,n are considered as hidden variables, our probability law on 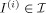is induced via the random law on the initial momenta M ${}_{\text{0}}^{\text{(}\mathit{\text{i}}\text{)}}$. We model this as independent and identically distributed Gaussian random fields with zero mean and fixed covariance matrix. The goal is to estimate I _temp from the set of observations that are taken as conditional Gaussian random fields with mean fields I ⁽ⁱ⁾ = g ${}_{\text{1}}^{\text{(}\mathit{\text{i}}\text{)}}$ · I _temp. An iterative expectation–maximization procedure [Allassonniere et al., 2007; Ma, 2006; Ma et al., 2008] is used to generate the template. An initial manually constructed left and right hippocampus surface was mapped to each of the observations, and transformed via 10 iterations over the entire population.

Classification

Classification is achieved by applying MDS [Cox and Cox, 1994] to the n × n matrix of intersubject metric distances 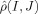obtained for n subjects. MDS aims to detect the finite d‐dimensions that explain the observed distances between the shapes. Clearly, given a population in an n‐dimensional space, having the metric distances between them allows for the categorization of the n‐dimensions upon which they are laid out. If all the anatomies are connected along several axes, then these axes can be discovered via direct examination of the metric distances between every element in the population. The metric distance matrix is expanded as a completely orthonormal basis 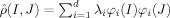, where {φ_i, i = 1,…,d} is generated via singular value decomposition. This finite dimensional Euclidean embedding is then used in statistical tests via linear discriminant analysis.

Denote the embedded feature vector of a shape as X _i ϵ ℝ${}^{\mathit{\text{d}}{}_{\mathit{\text{L}}}\text{+}\mathit{\text{d}}{}_{\mathit{\text{R}}}}$ and its class label as C _i ∈ C. Given labeled training populations with labels (X ₁,C ₁), …, (X _n,C _n) independent and identically distributed, Fisher's linear discriminant involves the selection of a “best” hyperplane for partitioning the feature space into discriminant regions. This involves estimation of class‐conditional prior probabilities π_j = P[C = j], and class‐conditional mean vectors μ_j and covariance matrices Σ_j. Test observation X is classified as belonging to that class that maximizes the class‐conditional posterior probability. These classifiers can be understood as projection into (C − 1)‐dimensional Euclidean space and subsequent piecewise linear partitioning.

Conditioned on training data (X _i,C _i), i = 1,…n, we choose the number of discriminating dimensions d _L, d _R for the MDS by minimizing an empirical estimate of the conditional probability of misclassification (Devroye et al. [1996], page 3) given by

Given m new feature vectors X _j ϵ ℝ${}^{\mathit{\text{d}}{}_{\mathit{\text{L}}}\text{+}\mathit{\text{d}}{}_{\mathit{\text{R}}}}$, j = n + 1, … , n + m, the optimum selection of dimensions minimize the empirical estimator

(5)

where the classifiers are indexed by the MDS embedding dimensions d _L and d _R.

Concerning the model selection criteria, we have considered several involving empirical risk minimization. In particular, Fisher's linear discriminant can be understood as involving estimation of class‐conditional prior probabilities π_j = P[C = j], and class‐conditional mean vectors and covariance matrices. “Linear” implies constant covariance for all classes j; model bias can be reduced by relaxing this constraint, at the expense of increased variance. Test observation X is then classified as belonging to that class, which maximizes the class‐conditional posterior probability. These classifiers can also be understood as projection into (C − 1)‐dimensional Euclidean space and subsequent piecewise linear partitioning. Fisher's procedure, and associated optimality results, can be derived from Bayes theory and from likelihood ratio theory. The approach is perhaps most suitable for applications in which the class‐conditional distributions are unimodal, and can be seen to be optimal for the case of spherically symmetric class‐conditional distributions. General linear discriminant analysis can be more difficult to employ but can be shown to out‐perform Fisher's version [Duda and Hart, 1973].

RESULTS

Localized Shape Analysis in Template Coordinates

Figure 1 provides an intuitive notion of metric distances computed from a flow sequence of diffeomorphisms satisfying dg _t/dt = v _t (g _t), g ₀ = id matching I (control) to J (AD). The numbers at each stage of the sequence are the distances obtained from .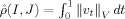

Figure 1.

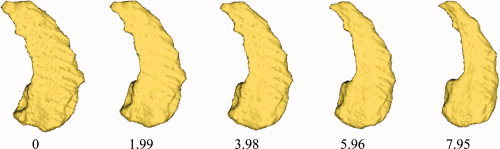
The flow of a sequence of diffeomorphisms generated by LDDMM applied to the shapes I satisfying dg _t/dt = v _t(g _t), g ₀ = id matching I (control) to J (AD). Shown below each is the estimate of the metric 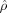given by .

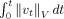Figure 2 shows the template estimation of 3D hippocampus data. To illustrate the template property, the initial and final metric distances (ρ(I ₀,I _k), ρ(I ${}_{\text{0}}^{\text{(10)}}$,I _k)) are shown for 8 of the 101 targets. Clearly, the initial template I ${}_{\text{0}}^{\text{(0)}}$ is further in metric distance than the estimated template I ${}_{\text{0}}^{\text{(10)}}$.

Figure 2.

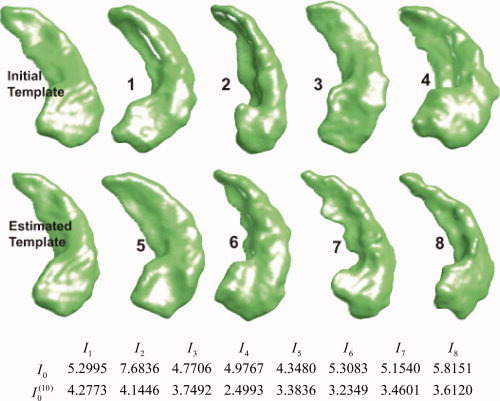
Initial template and the generated BIRN template after iterations of the template estimation algorithm through the collection of shapes (left column); 8 of the 101 shapes are shown. The first row of the table shows the metric distances 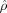between the original template I ₀ and the population; second row shows the distance of the constructed template I ${}_{\text{0}}^{\text{(10)}}$.

Once the template coordinates are constructed, the metadata can be transferred to it using the diffeomorphic mapping procedure. Figure 3 shows a partitioning on the left hippocampus surface in template coordinates S ^temp obtained by diffeomorphic transfer of the Washington University hippocampus atlas [Wang et al., 2006] to the template. The partitioning was based on the intersection of segmentations of the subiculum, subfields (CA1, CA2, CA3, CA4), and gyrus dentate with the hippocampal surface [Duvernoy, 1998; Wang et al., 2006]. The three partitioned zones are inferior medial zone (IMZ) proximal to the subiculum, lateral zone (LZ) proximal to the CA1 subfield, and superior zone (SZ) proximal to the gyrus dentate and the CA2, CA3, and CA4 subfields.

Figure 3.

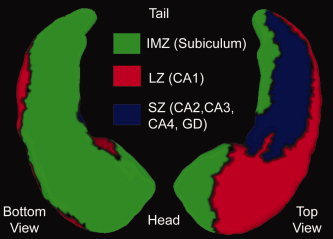
Bottom and top views of the partitioned left hippocampal surface of the template transferred from the Washington University template [Wang et al., 2006]. Partitioning is based on the intersection of the subvolume segmentations with the surface: IMZ (inferior medial zone) contains the subiculum, LZ (lateral zone) contains the CA1 subfield, and SZ (superior zone) contains the CA2, CA3, and CA4 subfields and the gyrus dentate (GD).

Figure 4 compares the averaged shapes of the populations of the demented (purple, n = 38) and nondemented subjects (n = 57), where the SD subjects were excluded. These “average” anatomical structures were generated by finding the average vector field that transfers the template onto the nondemented (vector endpoints) and demented (purple) population groups generated by using the geodesic flow of the average vector field ₀ representing each group. Note that the largest velocity vectors occur in the IMZ and LZ partitions that are proximal to the subiculum and the CA1 subfield.

Figure 4.

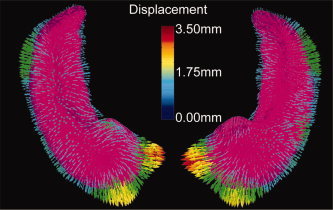
Average shapes of the populations of demented (purple, n = 38) and nondemented adults (vector endpoints, n = 57) generated by shooting the template onto the two populations. The largest velocity vectors occur in the IMZ and LZ partitions (based on Fig. 3) that are proximal to the subiculum and CA1 subfield, respectively.

Hippocampus Shape Analysis Via Random Momentum Fields

To compare the shape difference between the above two populations, two‐sample Student's t‐test was performed on each of the first 20 expansion coefficients U _k. It was found that group difference occurred in the 1st, 5th, 20th components at a significance level of 0.05. Figure 5 shows significant differences in the magnitude of the Jacobian measured on a logarithmic scale and averaged over all the maps between the two populations indexed over the template S ^temp. The warm and cool colors correspond to expansion and compression, respectively. Note that hippocampal atrophy, while not directly measured, is indicated by the location of shape change as inferred from the Jacobian. Note that the greatest expansion occurs in the IMZ and LZ partitions that are proximal to the subiculum and the CA1 subfield.

Figure 5.

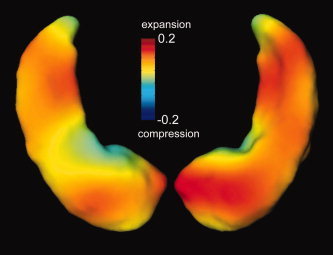
Determinant of Jacobian (measured on a logarithmic scale) shows the difference between demented (n = 38) and nondemented (n = 57) groups. Largest expansion occurs in the LZ and IMZ partitions (based on Fig. 3) that are proximal to the CA1 subfield and subiculum, respectively.

Classification Based on the Metric Distances

To demonstrate the performance of classification of two populations, we consider a training set (n = 45) of nondemented subjects (n _c = 21) as one class corresponding to CDR 0 and group all AD and SD, that is, demented subjects (n _d = 24) as the other class corresponding to CDR 0.5 or CDR 1 and consider the remaining m = 56 subjects as test subjects corresponding to 36 nondemented subjects with CDR 0 and 20 demented subjects with CDR 0.5 or CDR 1. Figure 6 shows the empirical probability of error 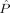from Eq. (5) as a function of MDS embedding dimensions d _L and d _R for the two class version of the problem; the darker the color, the smaller 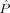is. A region of dimensionality‐space yielding classification performance estimates significantly superior to chance is apparent; at (d ${}_{\mathit{\text{L}}}^{\text{*}}$,d ${}_{\mathit{\text{R}}}^{\text{*}}$) = (4, 5) we obtain .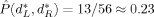

Figure 6.

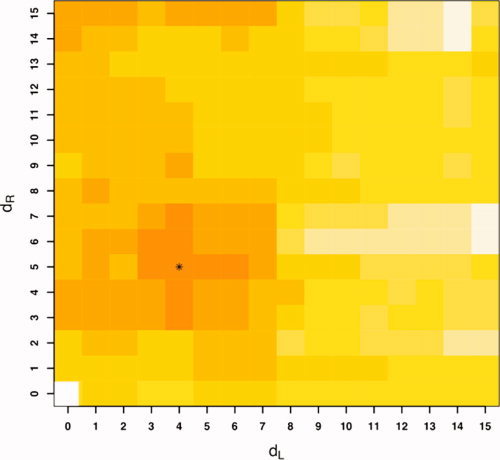
Two class (nondemented CDR 0 vs. demented CDR 0.5 or 1) discriminant classification error 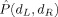as a function of MDS embedding dimensions for left (d _L) and right hippocampus (d _R); darker color represents smaller 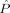. The minimizing dimensions are d ${}_{\mathit{\text{L}}}^{\text{*}}$ = 4, d ${}_{\mathit{\text{R}}}^{\text{*}}$ = 5 (asterisk) with minimizing test set performance estimate .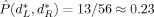

Figure 6 also shows the smoothness of 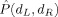, and the regularization inherent in the relatively low‐dimensional model selected suggests that the level of performance obtained here represents a statistically significant improvement (over chance) in classification capability. A permutation test [Good, 2000] puts the estimated P‐value for this result at 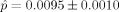. Thus, metric classifier based on LDDMM captures shape information in the MR data that is correlated with clinical diagnoses. Although volume alone does provide some classification signal (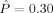), performance using metric distances is superior.

DISCUSSION

This study demonstrates the ability of both CA tools and data to be combined across multiple sites to generate results consistent with clinical findings in normal and abnormal aging in AD. In particular, CA tools based on large deformation diffeomorphic mappings [Csernansky et al., 2000, 2004; Miller, 2004; Wang et al., 2003, 2006] have been useful in discriminating nondemented subjects and those with very mild AD in cross‐sectional and longitudinal studies. Deformations of the hippocampal surface proximal to the CA1 subfield and the subiculum were also observed [Wang et al., 2003, 2006]. More recently, a longitudinal study found that reduced volume and abnormal shape of the hippocampus could predict future cognitive decline in healthy elderly individuals [Csernansky et al., 2005]. The pattern of hippocampal shape variation in these subjects resembled those observed in subjects with very mild AD [Csernansky et al., 2000; Wang et al., 2006].

Although SD is a disease preferentially affecting semantic memory and has a different regional pattern of neuronal loss than in AD, this study demonstrated how embedding anatomical configurations in a metric shape space via metric distances 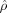between shapes permits classification via clustering. The approach constructs the metric classifier via MDS and linear discrimination analysis. Further, class conditional discrimination between demented (CDR 0.5 or CDR 1) and nondemented (CDR 0) can be performed based on the metric structure of LDDMM.

As with landmark and dense image mappings [Vaillant et al., 2004; Wang et al., 2007], the GRF representation of momentum was shown to provide a compact and efficient representation of anatomical variation. Prominent shape changes were observed in both the IMZ and LZ partitions proximal to the subiculum and CA1 subfield, respectively (Figs. 4 and 5) which is consistent with several histopathological findings [e.g., Rossler et al., 2002; West et al., 1994, 2004]. However, these shape changes do not reflect actual atrophy. It is possible that atrophy in other subregions of the hippocampus could have induced the observed shape changes. Some expansion in the lateral aspect of the subiculum (see Fig. 5) has not been observed in histopathological studies. These observations need to be resolved by either a larger population or longitudinal study that is not the purpose of this study. In addition, it should be emphasized that the observed shape changes take place on the surface of the hippocampus via the momentum along the normal to the boundary defined by the image contrast, and do not reflect the changes within the hippocampus or neighboring structures such as the gyrus dentate. However, as has been demonstrated in our previous work as well as others [e.g., Shi et al., 2007], the surface‐based approach encodes the localized shape changes in the hippocampus in AD or neuropsychiatric diseases.

The methodology demonstrated here goes directly from dense segmented images to metric distances. Originally, LDDMM [Beg et al., 2005] worked directly on the dense MR images, with no segmentations involved requiring the contrast between the images to be modeled so that the image matching is well defined. This contrast modeling is, of course, similar to the segmentation approach. Thus, the efficacy of the segmentation would imply efficacy in the direct matching of MR intensities. Other high‐dimensional diffeomorphic metric shape space embeddings now exist for anatomical shapes measured in other ways, including labeled landmarks [Joshi and Miller, 2000], unlabeled landmarks [Glaunès et al., 2004], and dense image volumes measured as diffusion tensor images [Cao et al., 2005, 2006]. Collaborative analysis of shapes via diffeomorphic metric mappings has the potential to enhance the understanding of disease in large scale studies such as ADNI.