SoDA2: a Hidden Markov Model approach for identification of immunoglobulin rearrangements

Abstract

Motivation: The inference of pre-mutation immunoglobulin (Ig) rearrangements is essential in the study of the antibody repertoires produced in response to infection, in B-cell neoplasms and in autoimmune disease. Often, there are several rearrangements that are nearly equivalent as candidates for a given Ig gene, but have different consequences in an analysis. Our aim in this article is to develop a probabilistic model of the rearrangement process and a Bayesian method for estimating posterior probabilities for the comparison of multiple plausible rearrangements.

Results: We have developed SoDA2, which is based on a Hidden Markov Model and used to compute the posterior probabilities of candidate rearrangements and to find those with the highest values among them. We validated the software on a set of simulated data, a set of clonally related sequences, and a group of randomly selected Ig heavy chains from Genbank. In most tests, SoDA2 performed better than other available software for the task. Furthermore, the output format has been redesigned, in part, to facilitate comparison of multiple solutions.

Availability: SoDA2 is available online at https://hippocrates.duhs.duke.edu/soda. Simulated sequences are available upon request.

Contact: kepler@duke.edu

1 INTRODUCTION

B cells express immunoglobulin (Ig) molecules on their outer surface and secrete them into the extracellular space. Secreted Ig is known as antibody. The genes that encode for antibodies are generated by many diversifying mechanisms including combinatorial rearrangement of gene segments, addition of non-templated (n) nucleotides at the junctions, and somatic hypermutation. This circumstance presents the important challenge of inferring the components of the original rearrangement for any observed Ig gene. Because point mutations cause loss of information regarding the original rearrangement, there may be multiple plausible solutions. In this article, we present a Bayesian statistical method based on a Hidden Markov Model (HMM) that allows a complete statistical treatment of the problem by providing the posterior probability of each possible rearrangement.

Antibodies serve as effector molecules that neutralize microbes by binding to exposed antigens and targeting them to other components of the immune system, such as phagocytic cells and complement, that effect clearance. Ig genes generate diversity in two stages: an antigen-independent and an antigen-dependent stage. Antigen-independent diversity is generated in the bone marrow, where B cells originate, by combinatorial rearrangement of gene segments and junctional diversity. Combinatorial diversity is created in a number of ways. First, each antibody molecule comprises one heavy- and one light-chain protein. Both the light- and heavy-chain genes are encoded by gene segments that are genetically rearranged during a process known as V(D)J recombination (Sakano et al., 1980; Tonegawa, 1983). Heavy chains are made up of three gene segments—variable (VH), diversity (DH) and joining (JH) where as light chains only have a V and J segment. In humans, there are ∼50 known functional VH segments, 27 known functional DH segments, and six known functional JH segments (LeFranc, 2001). This arrangement allows for ∼8100 combinations in the heavy chain alone. Humans also have two light-chain loci, κ (Lorenz et al., 2001) and λ (Frippiat et al., 1995). Only one of these loci is expressed per cell so that each antibody either has a κ light chain or a λ light chain. Humans have 44 functional Vκ, 5 Jκ, 33 Vλ genes and 5 Jλ (LeFranc, 2001) resulting in 220 possible κ chains and 165 possible λ chains. Thus this combinatorial rearrangement alone allows for greater than 3 million antibodies. Junctional diversity is the result of multiple recombination site choices for each recombination event and the addition of n nucleotides. n nucleotides are sometimes added at the junction by terminal deoxynucleotidyl transferase (TdT) between adjoining gene segments (Desiderio et al., 1984). Although TdT is believed to be expressed only in pro-B cells, the stage in which the heavy-chain rearrangement takes place (Desiderio et al., 1984), the presence of n nucleotides in light chains has also been seen in a few studies (Bridges, 1998).

Antigen-dependent diversity is generated by somatic hypermutation in the periphery in a manner dependent on activation-induced cytidine deaminase (AID); during this process, mutations in the Ig genes are accumulated at rate of up to 10⁶ times the normal background rate (Muramatsu et al., 2000). B cells are subsequently selected for enhanced affinity for the eliciting antigen. It is estimated that these processes of diversification can generate ∼10¹² different antibodies making it challenging to correctly identify the underlying germline gene segments and subsequently the sequences of the complementarity determining regions (CDRs).

The inference of the recombination and mutation events that produced a given Ig gene is of great importance in the study of humoral immunity and has been tackled in many different ways. The goal of such inference is to identify each of the component gene segments used as well as the recombination sites, point mutations and n nucleotides. The aligned gene segments usually overlap, which is why alignments of the target gene to the individual gene segments cannot be treated as independent. Somatic mutations, n nucleotide addition and recombination site choice make this task more challenging. The short length of the DH gene segment makes it especially difficult to identify the CDR3 region of the heavy chain, which is the most diverse region in the antibody sequence. This leads to many possible gene segment combinations that can result in a given antibody gene. Hence, it is necessary to report all such rearrangements and assign a probability to each of the combinations, making it easy to compare all possible rearrangements.

Several algorithms have been developed for inferring Ig gene segment composition. IMGT/V-QUEST is one of the first and most complete of these tools and has the ability to analyze both Ig and TCR sequences for a variety of organisms including human and mouse (Guidicelli et al., 2004). V-QUEST, however, is based on the BLAST algorithm; it does not guarantee finding the best alignment of two sequences (Altschul et al., 1990). Additionally, the implementation of the algorithm only allows for running a maximum of 50 sequences at a time. Another tool, JOINSOLVER, is based on the identification of conserved motifs in the target gene (Souto-Carneiro et al., 2004). Both JOINSOLVER and V-QUEST provide multiple gene segment possibilities but the implementation only provides junction analysis for the topmost choice. Somatic diversification analysis (SoDA) (Volpe et al., 2006) uses a 3D alignment algorithm that allows for insertions and deletions. The algorithm uses dynamic programming and is an extension of the Smith–Waterman local alignment algorithm (Smith and Waterman, 1981). The 3D alignment allows for a continuous alignment through all the states of the recombination. SoDA infers only a single highest-scoring alignment, and ignores other solutions that may have equal or nearly equal scores. SoDA's guarantee of optimality in the inferred rearrangement is obtained at the cost of computational effort; SoDA takes more CPU time than either JOINSOLVER or V-QUEST. A major shortcoming for all the programs above is that they do not provide a meaningful comparison of the different possible rearrangements. iHMMune-align (Gaeta et al., 2007) partially solves the problem and provides a probabilistic model using an HMM to infer the rearrangement. iHMMune-align uses the Viterbi algorithm (Rabiner, 1989) to find the most probable path through the alignment matrix, but does not sum over paths or provide results on sub-optimal alignments. This choice becomes an issue when selecting an appropriate DH gene segment for Ig heavy chains. The DH gene is the shortest of all gene segments, and is typically the most difficult to align. We have found Ig genes that present an equally good alignment with different DH genes (see Results section and Figure 5). iHMMune-align or SoDA gives only the solution with the highest score even if the highest score is not significantly better than the second highest score and so on (iHMMune-align does provide the option of viewing the top 10 VH gene alignments, but not DH).

Fig. 5.

The alignment of CDR3H of sequence by 1154693 using IGHD1-21*01 by (a) SoDA2, (b) IMGT/V-QUEST, JOINSOLVER and iHHMune, (c) SoDA. Rearrangements (b) and (c) were also provided by SoDA2 at a slightly lower probability.

Among these four methods, only SoDA allows for gaps when performing alignments, although insertions and deletions are known to occur at non-negligible frequencies during somatic hypermutation (Smith et al., 1996), and alignment without gaps when gaps are present leads to dramatically erroneous inferences.

The method we are introducing here is an update of SoDA—we call it SoDA2. It employs a probability mass function-based alignment for determining gene segments and a probabilistic HMM for the inference of CDR3. The system calculates the posterior probability over all paths using a particular set of gene segments by the forward and backward algorithms. It then provides the alignment path with the highest posterior probability. If the sequence does not hold enough information to unambiguously select a gene segment, SoDA2 reports all alignments that do not differ significantly. We tested this method using a simulated dataset constructed from the statistics of observed rearrangements and compared these results with those obtained using existing methods. We also used two natural datasets, a set of clonally related Ig genes and a random set of sequences from NCBI. Each test indicates that SoDA2 provides the most thorough and accurate results among all programs in addition to providing the most statistically complete results.

2 METHODS

2.1 Determining the type of Ig

The first step consists of aligning the target sequence with a consensus-like sequence of the VH, Vκ and Vλ families to determine if the input sequence is a heavy, kappa or lambda chain. These consensus sequences are pre-created by separate alignments of the VH, Vκ and Vλ segments. We use the AHO numbering scheme (Honegger and Plückthun, 2001) which is based on the spatial alignment of known 3D structures of Ig domains. The gaps are placed to minimize the average deviation from the averaged structure of the aligned domain so that the position of the CDRs remains consistent. The consensus is represented by a probability mass function (pmf), a L × 5 matrix where L is the length of the V genes in this case (Kepler et al., submitted for publication). For each nucleotide position in the gene, we determine the frequency of use for each nucleotide state (including ‘gap’) at that position in the family. For the target antibody, we create a similar pmf using the quality scores of the input sequence. The quality score is proportional to the log probability of the estimated sequencing error and is provided by the user's base-calling software (Ewing and Green, 1998). If quality scores are not provided, we treat the input sequence as well-determined and all mismatches as due to somatic mutation. The pmf at each position of the target sequence depends on the quality score, which varies at each position, and a mutation frequency μ which is assumed to be constant over positions. For each position, we then have the probability of observing the five bases (including a gap) at that position given the quality score and the mutation frequency. We use the pmf of the target antibody gene and the pmf of the VH, Vκ and Vλ sequences as scores to create a local alignment (Kepler et al., submitted for publication; Smith and Waterman, 1981).

2.2 V and J gene pre-alignment

Assume, for example, that our target sequence has been determined to be a heavy chain. We use the trace-back path generated by aligning the pmf of VH to our target and obtain the likelihood for each member of the VH family. The mutation frequency μ is recalculated after observing mismatches in the highest scoring alignment. All VH segments with equally high likelihood alignments are then submitted to the HMM. The position of the invariant cysteine is determined.

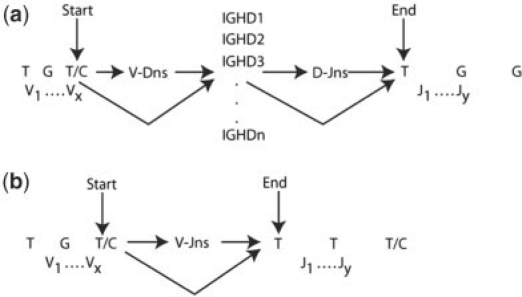
The target sequence is then aligned past the invariant cysteine with all the appropriate JH segments, using the pmf-based alignment mentioned above. The JHs with the highest likelihood are selected for submission to the HMM. The target sequence is further trimmed at the invariant tryptophan/phenylalanine, and only the remaining region, CDR3, is used as our target sequence for the HMM. The 3′ ends (post-invariant cysteine) of all significant VH gene segments and the 5′ ends (before invariant tryptophan/phenylalanine) of all JH segments from the pre-alignment are also chosen for the HMM. Since DH segments are most difficult to identify, we submit all DH segments to the HMM. The mutation frequency of the final trimmed target sequence to be considered for the HMM is set at 1.5 μ since the CDR3 region is subject to higher mutation than the VH region (Cowell et al., 1999; Gaeta et al., 2007). Figure 1 shows the basic set-up of the HMM for heavy chains (Fig. 1a) and light chains (Fig. 1b) with an overview of the states and allowed transitions.

Fig. 1.

The basic topology of the HMM for (a) heavy chains and (b) kappa and lambda chains. The HMM starts at the last base of the invariant cysteine of all high-likelihood V segments, runs through all DH segments in the case of heavy chains, and through all high-likelihood J segments till the first base of the invariant tryptophan or phenylalanine.

2.3 HMM

We implemented a pair HMM with 10 non-silent states—match/mistmatch state in V gene, insertion in V gene (Iv), deletion in V gene (Dv), V–D junction n nucleotides, match/mismatch in DH gene, insertion in the DH gene (Id), deletion in the DH gene (Dd), D–J junction n nucleotides, match/mismatch in the J gene, insertion in the J gene (Ij) and deletion in the J gene (Dj). Our HMM must begin in the match/mismatch state of the V gene since the invariant cysteine is encoded by the V. The end state must be match/mismatch in the J gene at the beginning of the invariant tryptophan/phenylalanine.

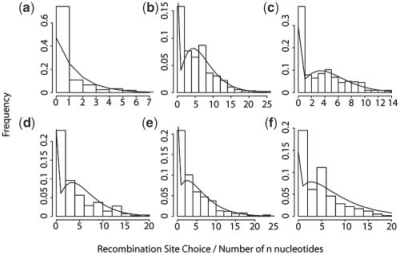
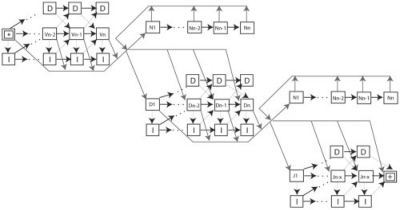
The emission probabilities in every state are determined by the pmf calculated using the quality scores and the mutation rate μ. For target sequences with unknown quality scores, high-quality scores are assumed, making the probability of the observed base depend only on μ. Emission probabilities for the n nucleotide states are determined based on empirical data (Basu et al., 1983). Transition probabilities between states are determined by fitting a negative binomial distribution to the recombination site choice for VH, DH and JH and number of n nucleotides in the junctions as determined in a set of 293 unmutated sequences rearranged sequences (Fig. 2, Jackson et al., 2004). Figure 3 shows a detailed implementation of the HMM with transition probabilities.

Fig. 2.

Distributions for (a) VH gene recombination site choice, (b) n nucleotides in the VD junction, (c) 5^′ DH recombination site choice, (d) 3^′ DH recombination site choice, (e) n nucleotides in the DJ junction, (f) 5^′ JH recombination site choice. All the data is fit to negative binomial distributions with varying parameters derived from Jackson et al. (2004). These parameters are used for transition probabilities in the HMM.

Fig. 3.

Shows a detailed topology of the HMM with all possible transitions. Each nucleotide in the observed sequence is treated as a separate state. The transition probabilities are derived from empirical data (Jackson et al., 2004). The star denotes the start (third position of invariant cystiene) of the HMM and the + denotes the end (first position of invariant tryptophan/phenylalanine). The I and D in every state stand for insertions and deletions, respectively.

2.4 Algorithm

Once we have the appropriately trimmed target and germline sequences, we calculate the log of the total probability of a proposed rearrangement using the forward and backward algorithms (Durbin et al., 1998; Majoras, 2007). We select the gene segments that lead to the highest posterior probabilities, and perform a posterior Viterbi algorithm with traceback (Fariselli et al., 2005) to select the path with the highest posterior probability for each possible rearrangement. We report the probability of the most probable path for each of the equally probable gene segment sets. For a heavy chain, a DH gene alignment of <3 nt is flagged as ‘unreliable D alignment’. The functionality of an antibody gene is determined as follows and reported with the results. A functional Ig chain must have no stop codons and the invariant cysteine at the start of CDR3 must be in-frame and intact. For heavy chains, the invariant tryptophan at the end of CDR3 must be in-frame and intact; for light chains, CDR3 must end with an in-frame and intact phenylalanine. We provide color-coded output in HTML, text and excel formats to allow the user to use the information in ways most convenient to his or her needs.

3 RESULTS

3.1 Simulated datasets

We created simulated datasets of 100 sequences each with mutation frequencies of 2.5, 5, 10 and 20%. Recombination site choice and number of n nucleotides for these simulations were drawn from a negative binomial distribution. To avoid any bias towards our HMM, the parameters for these simulations were estimated using a set of 662 sequences obtained from Genbank. Furthermore, rearrangements for these sequences were determined using IMGT/VQuest (Guidicelli et al., 2004) rather than SoDA or SoDA2. IMGT Junction Analysis was used to determine empirical data for deriving the distributions (Monod et al., 2004). Mutations were introduced such that the average mutation frequency across the gene was 2.5, 5, 10 and 20%, and the mutation frequency in the CDRs was 2 × than that in the framework. Each of these datasets was used to test SoDA2, SoDA, IMGT/VQuest, JOINSOLVER and iHMMune-align. Inverted D segments were omitted from the simulations because IMGT/VQuest and iHMMune-align do not allow for alignments against them. Table 1 shows the results of running our simulated datasets using the various available software. The table shows the number of rearrangements (all VH, DH and JH with alleles) identified correctly at each mutation rate by each program out of the 100 sequences tested in each group. For all our tests, we only compare the highest scoring rearrangement provided by SoDA2 with the highest scoring ones provided by other programs. For our simulated data, we see that SoDA2 performs better in identifying the complete rearrangement (including correct alleles) than other programs under all mutation rates (Table 1). In particular, SoDA2 outperforms all other programs in DH segment identification (Table 2). SoDA2 falls slightly behind IMGT/V-Quest in VH and JH gene identification due to the trade-off between accuracy and efficiency. We employ a computationally efficient alignment algorithm that aligns the target gene to consensus sequences of alleles, which can lead to the identification of the incorrect allele in a very few cases. Aligning the target gene to every allele would decrease this error but increase computation time significantly. Such errors are seen rarely and do not change the overall superior performance of SoDA2 shown in Table 1. If the score for multiple rearrangements is equal for any of the programs, all rearrangements are considered. Although SoDA2s performance falls at the 20% mutation rate, it still performs better than other software. We only report all alignments that are equally probable and leave it up to the user to select and view any number of V, J or complete alignments he or she wants.

Table 1.

Number of correct rearrangements (correct gene and allele for VH, DH and JH segments) identified by each software out of 100 sequences tested at each mutation rate

	2.50%	5%	10%	20%
SoDA2	73	65	47	28
IMGT/V-QUEST	52	47	42	16
JOINSOLVER	59	47	34	11
iHMMune-align	41	31	22	12
SoDA	46	30	31	6

Table 2.

Number of VH, DH and JH genes (with alleles) identified at each mutation rate for the simulated sequences

	2.5%			5%			10%			20%
	V	D	J	V	D	J	V	D	J	V	D	J
SoDA2	97	76	98	94	73	94	87	58	88	85	42	78
JOINSOLVER	90	65	98	83	61	92	81	42	85	72	20	76
IMGT/Vquest	99	52	94	97	49	93	93	45	89	88	23	82
SoDA	79	65	92	77	68	87	76	42	69	69	20	45
iHMMune-align	87	48	90	86	42	87	78	32	86	69	21	61

For sequences where SoDA2 failed to identify the correct rearrangement as the most probable one, we found a median difference of 0.67 in the natural log of the probability between the highest scoring rearrangement and the correct one at the 5% mutation rate. Thus, if allowed to include rearrangements with low differences (<1) in the natural log of the probability from the top scoring alignment, SoDA2 would have identified correct rearrangements for 22 additional sequences at the 5% mutation rate, yielding a possible 87% success rate.

3.2 Clonally related datasets

In order to test real biological data, we used two clonally related datasets that were used to test iHMMune-align (Gaeta et al., 2007) derived from tonsilar IgD class-switched B cells (Zheng et al., 2004). Because they are clonally related, sequences within a given set should have identical rearrangements and differ only by somatic mutation. We analyzed this dataset using VQuest, JOINSOLVER, SoDA and iHMMune-align to determine the number of times each of the programs resulted in the same rearrangement as was done by Gaeta et al. (2007). We ran the sequences through all the programs and found that iHMMune-align selected 47/57 identical rearrangements for the first group of sequences, while SoDA2 selected 34/57 identical rearrangements. IMGT/VQuest, JOINSOLVER and SoDA identified 37, 25 and 18 identical rearrangements, respectively. SoDA2 returned a minority DH gene segment in 17 cases, a minority JH allele in five cases, and a minority VH allele in four cases. In cases where SoDA2 failed to select the majority VH or JH gene segment, all the other programs, including iHMMune-align also failed to select the majority gene segment. It can be seen in these cases that mutation had obliterated the information necessary to make the correct inference. For the 17 cases where SoDA2 did not return the majority DH segment, the DH segment that was returned was typically judged more probable than the majority segment due to the balancing of n-nucleotide use and mutations. An example of this phenomenon is the inference for AF262199 (Fig. 4). In this case, the mutation frequency in the VH gene segment is ∼7%. SoDA2 selects IGHD1∼26*01 requiring three mutations (8.5% mutation frequency in CDR3) and seven n-nucleotides, while IGHD7∼27*01 requires two mutations (5.5% mutation frequency) and 10 n-nucleotides. For the second dataset of 99 sequences, both iHMMune-align and SoDA2 identified 68/99 identical rearrangements while IMGT/VQuest, JOINSOLVER and SoDA identified 56, 41 and 37 identical rearrangements, respectively.

Fig. 4.

(a) Top rearrangement as chosen by SoDA2 with a higher mutation frequency than the alternative, shown in (b). The different rearrangements represent a trade-off between mutation frequency and number of n nucleotides.

3.3 Sequences from Genbank

We tested a set of 662 sequences collected from Genbank and previously used for testing iHMMune-align and SoDA (Genbank accession nos Z68345-487 and Z80363-770). Out of 662 sequences, 113 produced inferences on which all five programs agreed. There was no agreement from any of the programs on 140 sequences. This means that they either could not infer a rearrangement at all or they all differed in their inference. From the rest, SoDA2 agreed with the majority of the programs on 300 rearrangements (Table 3). These did not include those where SoDA and SoDA2 were the only two in agreement and the chosen rearrangement was the majority. SoDA2 performs considerably better than other programs in this test. We closely examined sequences for which SoDA2 failed to agree with two or more programs. We found a median difference of 1.05 between the top scoring rearrangement and the majority rearrangement. We also found that in all cases, SoDA2 selected an alternative rearrangement equally likely as the majority one.Figure 5 shows an example of one such sequence where SoDA2 selected IGHD2∼21*01 to be the best fitting DH alignment with a score of −785.07 (Fig. 5a). On allowing alignments with a slightly higher probability, we found both the rearrangement chosen by the majority of the programs (VQuest, JOINSOLVER and iHMMune-align, Fig. 5b) and also the rearrangement selected by SoDA (Fig. 5c). The difference in the natural log of the probability is 0.63 in the first case and 0.93 in the second. This shows that allowing rearrangements within a reasonable range of probabilities in SoDA2 would give an accurate and thorough picture of the various rearrangements possible for a given Ig sequence. It is important to note that SoDA2 considers factors such as recombination site choices for each gene segment and numbers of n nucleotides at both junctions derived from empirical data in inferring rearrangements while alignment algorithms used by SoDA, VQuest and JOINSOLVER base their results on sequence similarity matrices which may not accurately represent the process of V(D)J recombination.

Table 3.

Results from 662 sequences from Genbank, showing the performance of the five programs

	Number of rearrangements
All programs agree	113
All programs disagree	140
SoDA2 agrees with two or more programs	300
VQuest agrees with two or more programs	255
iHMMune-align agrees with two or more programs	137
JOINSOLVER agrees with two or more programs	272
SoDA agrees with two or more programs	244
SoDA2 agrees only with SoDA (no other programs agree)	11

If two or more programs displayed the same rearrangement (including the alleles), it was believed to be the majority rearrangement.

4 CONCLUSION

The problem of inferring the correct rearrangement for antigen receptors is difficult due to the stochastic nature of the process, but the task is important for an increased understanding of the population somatic genetics of the immune response. In this paper we present a method based on an HMM that provides a statistical basis for identifying rearrangements of Ig genes. In addition to providing the posterior probability of the top rearrangement candidate, SoDA2 also provides the user with an option to see all rearrangements with sufficiently high posterior probabilities, thus giving the user a statistically complete picture of the observed sequence's origins.

We tested SoDA2 against simulated datasets that were created using empirically observed recombination site choices for each of the gene segments and numbers of n nucleotides in the junctions. We also tested it on two clonally-related datasets as well as a set of Ig heavy chains chosen randomly from Genbank. Our software performed as well as or better than available software on two out of three validation tests. The one test where SoDA did not outperform all of the others involved a single rearrangement. On the identical test with a different rearrangement, SoDA did as well as its nearest competitor. It is important to realize that the key feature of this article is to provide a tool based entirely on a probability model, and that therefore returns results interpretable as posterior probabilities rather than arbitrary scores. As with other inferential procedures, it is important to not only identify the optimal solution, but to identify near-optimal solutions and have a method for the absolute comparison among these alternatives. This performance and thorough result reporting leads to a substantially longer computation time. SoDA2 takes ∼15 s of real user time per set of V and J segment for a given heavy target sequence on a 64 bit machine with a 2.19 GHz processor and 4 GB RAM, but the investment of computational effort seems worthwhile.