Fast and SNP-tolerant detection of complex variants and splicing in short reads

Abstract

Motivation: Next-generation sequencing captures sequence differences in reads relative to a reference genome or transcriptome, including splicing events and complex variants involving multiple mismatches and long indels. We present computational methods for fast detection of complex variants and splicing in short reads, based on a successively constrained search process of merging and filtering position lists from a genomic index. Our methods are implemented in GSNAP (Genomic Short-read Nucleotide Alignment Program), which can align both single- and paired-end reads as short as 14 nt and of arbitrarily long length. It can detect short- and long-distance splicing, including interchromosomal splicing, in individual reads, using probabilistic models or a database of known splice sites. Our program also permits SNP-tolerant alignment to a reference space of all possible combinations of major and minor alleles, and can align reads from bisulfite-treated DNA for the study of methylation state.

Results: In comparison testing, GSNAP has speeds comparable to existing programs, especially in reads of ≥70 nt and is fastest in detecting complex variants with four or more mismatches or insertions of 1–9 nt and deletions of 1–30 nt. Although SNP tolerance does not increase alignment yield substantially, it affects alignment results in 7–8% of transcriptional reads, typically by revealing alternate genomic mappings for a read. Simulations of bisulfite-converted DNA show a decrease in identifying genomic positions uniquely in 6% of 36 nt reads and 3% of 70 nt reads.

Availability: Source code in C and utility programs in Perl are freely available for download as part of the GMAP package at http://share.gene.com/gmap.

Contact: twu@gene.com

1 INTRODUCTION

Numerous programs have been developed to date for the alignment of short reads from next-generation sequencing technologies, such as Illumina/Solexa (Hayward, CA, USA) and ABI/SOLiD (Foster City, CA, USA), to a reference genome or transcriptome. Because of the large numbers of short reads that can be produced from a given sample, much emphasis has placed on speed. Accordingly, recent programs, such as Bowtie (Langmead et al., 2009), BWA (Li and Durbin, 2009) and SOAP2 (Li et al., 2009), have shown how suffix arrays (Manber and Myers, 1993), compressed using a Burrows–Wheeler Transform (BWT; Burrows and Wheeler, 1994), can rapidly map reads that are exact matches or have a few mismatches or short insertions or deletions (indels) relative to the reference.

In addition to speed, it is also important to broaden the range of possible variants that can be detected in reads, since interesting biology is likely to be revealed not merely as single nucleotide polymorphisms (SNPs) or mutations from the reference, but also as more complex phenomena, such as multiple mismatches, long indels and combinations thereof. Such complex variants represent a substantial source of genetic diversity. For example, indels represent 7–8% of human polymorphisms, with 25% of coding indels being longer than 3 nt (Bhangale et al., 2005; Weber et al., 2002). Long indels that affect multiple amino acids may have significant biological consequences. Moreover, as reads continue to lengthen, from their original ∼30 nt to their current 75–100 nt, they are more likely to have multiple or complex differences from the reference, making detection of complex variants even more critical.

Other important biological phenomena arise from splicing events, which provide insights into gene structure, alternative splicing, gene fusions and chromosomal rearrangements. Although splicing can be determined readily in long EST and cDNA sequences using general-purpose genomic mapping and alignment programs such as BLAT (Kent, 2002) or GMAP (Wu and Watanabe, 2005), short reads pose a challenge because they often align to numerous places in a genome, and because they often lack insufficient sequence specificity on one or both ends of the exon–exon junction to accurately define the junction.

One solution for detecting splicing in short reads has been to align them to a reference transcriptome, possibly augmented with artificially constructed exon–exon segments (Wang et al., 2008). However, such an approach will identify only known or predicted combinations of exons, and not unexpected exon pairs that occur through exon skipping, cryptic splicing or gene fusions. Another approach, taken by the TopHat program (Trapnell et al., 2009), analyzes an entire dataset of mapped reads to identify splice site junctions between exons in a given neighborhood. However, that approach requires exons to have sufficiently high expression and will miss splicing events that are spanned by individual reads at a low level. A third approach, provided by the QPALMA program (Bona et al., 2008), can align individual reads across exon–exon junctions using Smith–Waterman-type alignments and a specifically trained splice site model. All of these approaches are limited to identifying only local exon–exon junctions and not unanticipated distant or interchromosomal gene fusion events.

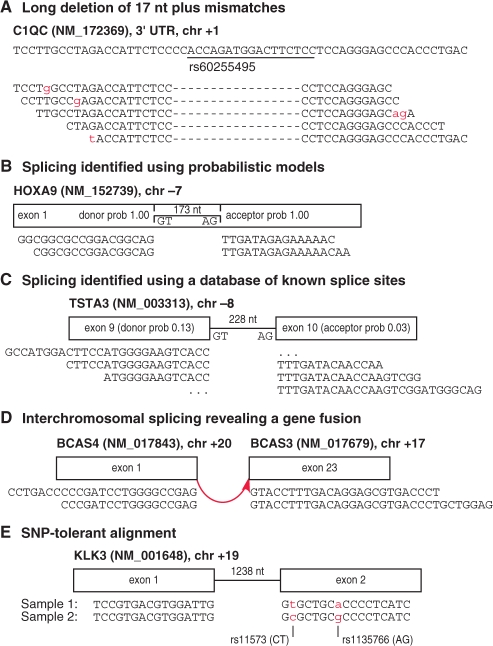
To expand the range of biological phenomena that can be inferred from short reads, we have developed fast and memory-efficient methods for detecting complex variants and splicing in individual reads. Our methods are implemented in GSNAP (Genomic Short-read Nucleotide Alignment Program), which can align single- and paired-end reads as short as 14 nt and as long as desired. Our program can detect splicing, multiple mismatches, long indels and combinations thereof, up to a user-specified point total, limited to a single splice or indel per read, provided the read (or parts of the read on each end of the indel or splice) has a consecutive stretch of 14 nt that match the reference sequence (Fig. 1A). (Future versions of the program may allow multiple indels or possibly multiple splices per read.)

Fig. 1.

Examples of complex variants detected by GSNAP. (A) A 17 nt indel with mismatches in reads (below) relative to a genomic region (above), matching a known polymorphism in dbSNP. (B) Splicing found using probabilistic models reveals an intron within exon 1 of HOXA9, supported experimentally (Dintilhac et al., 2004). (C) Splicing found using known splice sites, despite low probabilistic model scores. Ellipses indicate ‘half intron’ alignments, where reads have insufficient sequence to determine the distal exon. (D) Interchromosomal splicing between BCAS4 and BCAS3 found in the MAQC universal human reference RNA sample and observed in MCF7 cell lines (Hampton et al., 2009). (E) SNP-tolerant alignment near a splice site allows both genotypes to align equally well.

Our program can identify splicing within short reads using two types of evidence. First, it can evaluate the surrounding genomic sequence using probabilistic models of donor and acceptor splice sites (Fig. 1B). Second, it can utilize a user-provided database of known exon–intron boundaries, which avoids false positive and negative results from probabilistic models (Fig. 1C). Known splice sites will reveal most alternative splicing and gene fusion events, which generally occur through exon skipping and crossovers between introns. GSNAP can rely upon either or both of these types of evidence to identify splicing events, including those with mismatches, as well as partial splicing or ‘half intron’ events, where one end has enough sequence to align to one exon, but the other end lacks enough sequence to identify the other exon (Fig. 1C). Splicing events may span not only the short distances seen in normal or alternative splicing, but also long-distance intrachromosomal deletions or inversions, and interchromosomal translocations (Fig. 1D).

Our program also implements the ability to align reads not just to a single reference sequence, but to a reference ‘space’ of all possible combinations of major and minor alleles from databases like dbSNP (Sherry et al., 2001). By aligning to a reference space instead of a single reference sequence, our program avoids treating minor alleles as mismatches and thereby penalizing those genotypes in the alignment process. The utility of SNP-tolerant alignment is illustrated by an example that initially suggested a splice junction specific to one sample, but was actually due to two minor alleles nearby causing the read to fail to align (Fig. 1E). In SNP-tolerant alignment, minor alleles are treated as matches to a reference space, rather than as mismatches to a reference sequence. This idea has been implemented elsewhere (Manske and Kwiatkowski, 2009), but in a way that requires 29 GB of memory for SNP-tolerant alignment to the human genome. In this paper, we show how this feature can be performed instead with a much smaller memory requirement.

Our methods can be generalized for other tasks, such as mapping reads from DNA treated with sodium bisulfite (BS) for the study of methylation state (Lister and Ecker, 2009). BS converts each unmethylated cytosine in genomic DNA to uracil, which appears subsequently as thymine in reads. Reads from BS-converted DNA have a high error rate, which provides additional motivation for efficient detection of multiple mismatches. Although existing alignment programs can be adapted to handle such data, by converting all cytosines to thymines in both the reference sequence and reads (Deng et al., 2009), one subtle problem is that this approach obscures mismatches between reference thymines and read cytosines. The data structures in GSNAP allow it to align BS-seq reads with explicit detection of genomic-T to read-C mismatches, against either a reference sequence or a SNP-tolerant reference space.

2 METHODS

2.1 Overview

We view alignment as a search problem over a space of genomic regions in the reference sequence, or combinations of regions if gaps are allowed. (Although a reference sequence may consist of chromosomes, contigs, transcripts or artificial segments, we simplify our discourse by referring to it as a ‘genome’.) Searching involves the steps of generating, filtering and verifying candidate genomic regions, and its efficiency depends on designing the generation and filtering steps to produce as few candidates as possible. Several alignment programs, including MAQ (Li et al., 2008a), RMAP (Smith et al., 2008), SeqMap (Jiang and Wong, 2008) and RazerS (Weese et al., 2009), preprocess the reads and then generate and filter candidate genomic regions by scanning a read index against the genome.

For large genomes, it is more efficient to pre-process the genome rather than the reads to create genomic index files, which provide genomic positions for a given oligomer. Genomic indexing also permits parts of reads to be aligned to arbitrary genomic regions, needed for long-distance splice detection. Indexing need be done only once for each reference sequence, with the resulting index files usable by each new dataset. Oligomers of all lengths can be indexed using a suffix array or its compressed BWT equivalent, as used in Bowtie, BWA and SOAP2, which can represent a reference sequence compactly, in 2 GB for a human-sized genome of 3 billion nt.

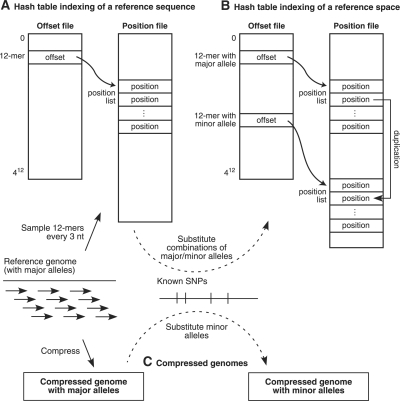
However, when only a single oligomer length q is needed by an algorithm, a simple hash table (Ning et al., 2001) or q-gram index (Rasmussen et al., 2006) applied to the genome will suffice (Fig. 2A). This data structure consists of an offset file (or lookup table) of all possible q-mers, with pointers to a position file (or occurrence table) containing a list of genomic positions for each q-mer. For our search algorithm to work most efficiently, it is important that each position list in the position file be pre-sorted, which allows intersections to be computed quickly among multiple q-mer lookups. The intersection process also requires the positions in each position list to be adjusted at run time for its location in the given read, so they correspond to the diagonals in an alignment matrix between genome and read. Although our alignment algorithm could potentially work with another data structure that provides genomic positions for a given q-mer, a suffix array would require the additional step of sorting each position list at run time.

Fig. 2.

Representing a reference sequence and a reference space for genomic alignment. (A) A hash table consists of an offset file of possible 12mers and a position file containing a sorted list of genomic positions for each 12mer. (B) SNPs in a genomic 12mer are represented by duplicating the position in the lists for all combinations of major and minor alleles within the 12mer. (C) Major alleles are represented in one compressed genome, while minor alleles are represented in another compressed genome.

A set of n sorted lists can be merged in time O(l log n), where l is the sum of list lengths, by using a heap-based multiway merging procedure (Knuth, 1973). A merging procedure can produce not only a list of candidate genomic regions, but also information about the count and read location of the position lists that support each region. This support information can provide evidence about the number of mismatches in the read, and can therefore be used to filter out candidate regions.

To use multiway merging effectively, our algorithm depends on another idea, that of successive score constraints. For a given read, our program is designed to report the ‘best’ alignment or alignments, those with the lowest score based on mismatches plus an opening gap penalty for an indel or a splice. Therefore, our search process is constrained successively by an increasing score level K, starting from K=0 for an exact match, and ending either with a successful alignment at some K or at a maximum score level specified by the user. In addition to finding the best alignment, a constrained search process can also find suboptimal alignments, by continuing the search at successive score levels beyond the first, or optimal, one that yields an alignment. Our algorithm could also find an exhaustive set of alignments up to a given score level by searching at that score level and reporting all results.

Depending on the score constraint K and the read length L, a multiway merging process can be formulated in two different ways to generate and filter genomic regions. For low values of K involving none or a few mismatches relative to L, we apply a merging procedure based on a spanning set of oligomers, which filters genomic regions based on the count of q-mers that support the region. For higher levels of K involving more mismatches, we apply a merging procedure based on a complete set of oligomers, which filters genomic regions based on the pattern of q-mers that support the region. Both the count- and pattern-based criteria provide lower bounds on the number of mismatches present in a read or part of a read. If a lower bound exceeds the given score constraint K of allowed mismatches, the read may be filtered out and need not be verified against the genome to determine the actual number of mismatches.

A hash table is relatively large, requiring 12 GB to represent a human-sized genome if every overlapping oligomer is indexed. Accordingly, SOAP (Li et al., 2008b) requires 14 GB of memory to process a human-sized genome. Although modern computers generally have sufficient physical memory to query such large hash tables, smaller data structures can speed up programs by using memory paging and caching resources more effectively. We can reduce the size of a hash table by sampling the genomic oligomers that are indexed in the table. In our program, we index 12mers every 3 nt in the genome, which reduces the size of a human genomic hash table to 4 GB. As a result, our algorithm is designed to use a hash table sampled every 3 nt and still achieve full sensitivity as if every overlapping oligomer were indexed.

A hash table indexing scheme can be extended to align major and minor alleles equally well in SNP-tolerant alignment. (For ease of discussion, we refer to the alleles in the reference sequence as ‘major’ and their corresponding alternate versions as ‘minor’, regardless of their actual frequencies in a population.) Because a hash table represents the genome in q-mer pieces, it can represent the enormous space of all combinations of major and minor alleles in a relatively straightforward way.

To construct a SNP-tolerant hash table, we scan the genome and process each sampled genomic q-mer that contains one or more SNPs, by generating each possible combination of the major and minor alleles contained within and duplicating this genomic position for each generated q-mer. Finally, we re-sort the position list for each q-mer (Fig. 2B). A lookup in this hash table of any combination of major and minor alleles in a q-mer at a given genomic position will all contain the desired position. Our experience shows that a SNP-tolerant hash table is only slightly larger than the original. When we incorporate the 12 million SNPs from dbSNP version 129 into human genome version 36, the hash table increases in size from 3.8 to 4.0 GB. Our construction algorithm requires that the computer have sufficient memory to store the hash table, thereby requiring 4 GB for a human-sized genome. Verification in a SNP-tolerant manner is discussed in Section 2.4.

2.2 Spanning set generation and filtering

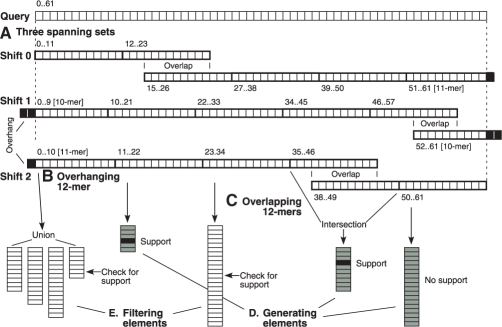
A spanning set is a minimal set of 12mers that covers the read (Fig. 3). This structure exploits the pigeonhole principle that the number of non-supporting 12mers—those that fail to contain a given position in their corresponding position list—provides a lower bound on the number of mismatches in the read. However, implementation of this pigeonhole principle is complicated by our use of sampling in the hash table, which creates uncertainty about the phase of the aligned read relative to the sampled genomic 12mers. Therefore, the program must construct six spanning sets, one for each shift of 0, 1 or 2 nt in both the forward and reverse complement directions (Fig. 3A). In addition, sampled hash tables cause genomic position information to be available only at intervals of 3 nt, thereby causing information to incomplete for 12mers that overhang past read boundaries. To handle such cases, the program computes the position list for a 12mer that overhangs the end of the read by 1 or 2 nt by substituting all possible nucleotides in the overhanging positions and taking the union of the resulting position lists (Fig. 3B).

Fig. 3.

Spanning set method for generating and filtering mismatch candidates. (A) A read of length 62 nt is analyzed at shifts of 0, 1 and 2 nt, with spanning sets each consisting of five elements. Elements at the ends may overhang the ends by 1 or 2 nt. Spanning set elements are shown in detail for the shift of 2 nt. (B) An overhanging 12mer is represented by a union of lists obtained from hash table lookups of all possible substitutions for the overhang. (C) Overlapping 12mers are represented by taking the intersection of their position lists. (D) Elements used for generating candidates (gray). (E) Elements used for filtering candidates (white). A candidate region (black) is supported by two of the generating elements, and is checked for support in the remaining filtering elements.

Another complication is that a spanning set will often contain 12mers that overlap. To address this issue, we consider an overlapping pair of 12mers to be a single ‘element’ in the spanning set, with a position list equal to the intersection of the two constituent position lists (Fig. 3C). The resulting set of elements is non-overlapping, so the pigeonhole principle now holds where k non-supporting elements implies a lower bound of k mismatches, and the region may be filtered out if k>K. There may be several choices for the pair of 12mers that overlap to create a single element; our program heuristically selects the 12mer with the longest position list or union of position lists as the site of the overlap, because the intersection operation on that 12mer is likely to eliminate the largest number of positions from subsequent consideration.

Although we could use all spanning set elements to generate candidates and then proceed to the verification step, we can make our algorithm faster if we designate some elements for generating candidates (Fig. 3D) and reserve others for a separate filtering step (Fig. 3E). This division of labor is intended to reduce the O(l log n) complexity for a heap-based priority queue, which is linear in l. If we check a sorted list of length l_i for the presence of a given position in a filtering step, this can be done in logarithmic time O(log l_i) through a binary search process. Consequently, our method performs a heap-based merge of some position lists (the generating elements), and counts the number of elements that support each of the resulting candidate regions. If this count is high enough to allow the possibility that K or fewer total elements will be non-supporting, then the candidate region undergoes a filtering step that checks each of the filtering elements for support. The algorithm eliminates the candidate if more than K total elements show non-support; otherwise, the region undergoes a verification step to determine the actual number of mismatches.

We have made implementation of our spanning set method efficient in various ways. First, the program selects elements with the shortest position lists as generating elements and the longest ones for filtering elements, because while every position in generating elements must be processed, only some of those in the filtering elements need be. Second, we maintain a pointer on each filtering element and advance that pointer only when we check for support, by using a galloping binary search (Hwang and Lin, 1980). Third, filtering elements that involve unions or intersections of position lists need not have these set operations computed explicitly, but can be represented instead by their constituent position lists, and support checked by performing the appropriate disjunctive or conjunctive searches when needed.

Allocation of N total elements between generating and filtering purposes depends on the constraint score level K of allowed mismatches. At least (K + 1) elements must be generating to guarantee that at least one generating element has support for a candidate region when the K other generating elements do not. We have found empirically that for K > 1, it is more efficient to allocate (K + 2) elements for generating purposes, because the requirement for two supporting elements greatly reduces the number of candidate regions generated.

Because the spanning set method requires at least (K + 2) generating elements [or (K + 1) for the exact and one-mismatch constraints], it can be used to detect only a limited number of mismatches relative to read length L, which limits the total number of elements N. Spanning set elements are non-overlapping in all three shifts when L = 10 (mod 12), so N≤⌊(L + 2)/12⌋. Therefore, (K + 1)<N or (K + 2)<N indicates that the spanning set method can be applied to constraint level K when K = 0 for 14≤L≤21; K≤1 for 22≤L≤33; and K≤⌊(L+2)/12⌋−2 for L≥34.

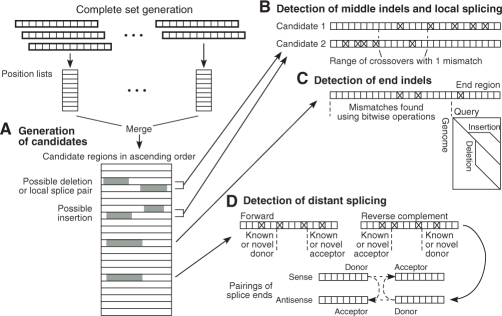
2.3 Complete set generation and filtering

To handle greater numbers of mismatches than those detectable by the spanning set method, we employ a strategy based on the complete set of overlapping 12mers. This complete set method works for any constraint level K of allowed mismatches, as long as the read and candidate region have 14 consecutive matches (a 12mer out of phase by as many as 2 nt). One sufficient condition for 14 consecutive matches is that the number of mismatches be ≤⌊L/14⌋−1. Up to this level of mismatches, GSNAP is an exhaustive algorithm, meaning that it can guarantee to identify and report all available alignments in the genome with that many mismatches.

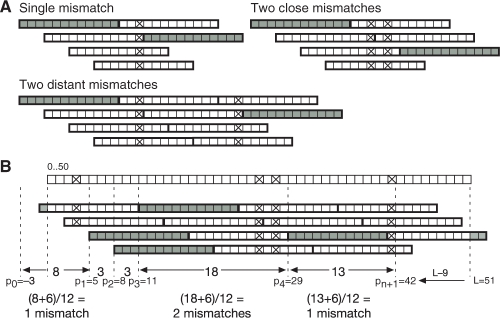
Candidates are generated by performing a multiway merge of position lists for all read locations in a single forward and single reverse complement pass, keeping track of the read location of 12mers that support each candidate region. The pattern of supporting 12mers provides a lower bound on mismatches in the read. If the supporting 12mers have read locations separated by Δp, then the minimum number of mismatches between them is ⌊(Δp+6)/12⌋ (Fig. 4A). Over the entire read, we can sum these lower bounds in a pattern-based lower bound calculation (Fig. 4B). Specifically, if a read of length L has a pattern of supporting 12mers at read locations p_i, i=1,…, n, a lower bound on mismatches is ∑_i=0ⁿ⌊(p_i+1−p_i+6)/12⌋, where p₀=−3 and p_n+1=L−9.

Fig. 4.

Complete set method for generating and filtering mismatch candidates. (A) Patterns of supporting (gray) and non-supporting (white) 12mers induced by a single mismatch, by two close mismatches, and by two distant mismatches (crosses). These patterns indicate a lower bound of ⌊(Δp+6)/12⌋ mismatches, where Δp is the distance between start locations of consecutive supporting 12mers. (B) Pattern-based lower bound calculation for a read of 51 nt, shown on top with actual mismatches. Supporting 12mers (gray) start at read locations 5, 8, 11 and 29, with end locations at −3 and L−9=42. The lower bound formula is summed over successive supporting 12mers to give a total lower bound of four mismatches.

To make the complete set method more efficient, we note that the merging process must process every position from each position list, and can therefore be slowed down by non-specific 12mers with extremely long position lists that do not help localize the read. We can gain efficiency by ignoring these non-specific 12mers, defined currently as those with position lists that are > 10 times the mean position list length. The lower bound formula must be modified accordingly to compensate for the missing 12mers, essentially by assuming that they are supporting. This strategy can potentially fail to align reads or portions of reads if the non-specific or repetitive nucleotide patterns are necessary for mapping the read. To successfully align these reads, the program provides an option for a greedy strategy in which non-specific or repetitive 12mers are initially ignored, and then subsequently included if an alignment is not found.

2.4 Verification of candidate regions

Candidate regions that are generated and survive the filtering process have an established lower bound on their number of mismatches. To determine the actual number of mismatches and verify that it does not exceed the score constraint K, we check these regions by aligning the read against the region. To reduce memory requirements, we store the genome in a compressed format that is created in addition to the hash table during the pre-indexing process (Fig. 2C), and verification is performed against this compressed version of the genome. For indexing of a reference sequence, the compressed genome contains the major alleles. For indexing of a reference space, GSNAP also accesses a second compressed genome that contains the minor alleles. The compressed genome format, as described in our paper on GMAP, stores each nucleotide in 3 bits. Each 32 nt block of the genome is represented by three 32-bit words. The first two words represent the nucleotide using 2 bits each, while the remaining word has 32 bits used as flags. For the major-allele genome, the flags indicate if the genomic position has a unknown or ambiguous nucleotide that cannot be represented as A, C, G or T. For the minor-allele genome, the flags indicate if the genomic position has a SNP.

Verification is performed at the bit level. Instead of decompressing the genome, the program compresses the read and shifts it to match the genome coordinates for a candidate region. The compressed read and genome are then combined bitwise using an exclusive-or function, and adjacent pairs of bits are reduced to yield bit vectors that contain the positions of mismatches. For alignment against a reference space, the read is similarly combined bitwise with the minor-allele genome and the two mismatch results are combined using a logical-and function. Therefore, a mismatch occurs at a SNP only if the read allele differs from both the major and minor alleles. Mismatch results can be further analyzed to count the total number of mismatches, or to report their locations from the left or right of the read. GSNAP will use the built-in bitwise functions popcount, clz (count leading zeroes) and ctz (count trailing zeroes) for these tasks, if they are available on a given machine, or will use its own equivalent bitwise functions if they are not. However, our testing reveals that built-in functions provide only a 1–2% increase in speed, in part because the generation and filtering steps greatly limit the number of regions that must be verified.

2.5 Detecting insertions and deletions

Our program can detect alignments containing a single insertion or deletion, with mismatches up to a user-specified maximum. Indel alignments can be penalized relative to gap-free alignments using a user-defined penalty G. Therefore, as the program imposes progressively stronger constraint levels K of allowed mismatches, it also searches for indel alignments by imposing a constraint level of (K − G) allowed mismatches with an indel.

Indels are detected using two algorithms, one that detects indels in the middle of the short read (between the first and last 14mer), and one that detects indels at the ends (within the first or last 14mer). End indels are constrained to have a distal short fragment that is free of mismatches and sufficiently long (as specified by the user) to determine its alignment reliably. For both methods, the merging step of the complete set method, but not the filtering calculation, is executed to produce all candidate regions having 14 or more consecutive matches with the read.

The method for detecting middle indels seeks a pair of candidate regions that co-localize within the maximum allowed deletion and insertion sizes (Fig. 5A). The position-based lower bound calculation can be applied to both ends of the candidate pair to filter out pairs with too many mismatches. Verification of the remaining candidate pairs at the nucleotide level identifies the location of mismatches in each member of the pair, which can then be analyzed to determine whether an area of possible crossovers exists within the constraint level K of allowed mismatches (Fig. 5B). The middle indel algorithm is efficient even for long indels because the genomic distance between the two ends specifies the gap size and allows efficient verification of mismatches without resorting to a dynamic programming algorithm.

Fig. 5.

Efficient detection of indels and splice pairs. (A) The complete set method generates candidate regions with supporting 12mers (gray). (B) Pairs of candidates within the allowed distance are tested for middle indels and short-distance splice pairs. The constraint on number of mismatches (shown for the value 1) determines a range of crossover points. (C) End indels are tested in the distal 14 nt when the long region of the read has a sufficiently low number of mismatches. (D) Long-distance splicing is detected by identifying known or novel splice sites in single candidate regions within areas defined by constraints on number of mismatches. Candidate regions with donor and acceptor splice sites are then paired to reveal splice junctions.

Detection of end indels also depends upon candidate regions generated by the complete set method, but filters single candidate regions rather than pairs. Candidates are filtered using a variant of the position-based lower bound calculation that ignores the first or last 14mer of the read, which is made non-supporting by an end indel. Candidates that pass this filtering step are verified against the genome to count the number of mismatches in the long part of the read. If the number of mismatches is sufficiently low, the end region is tested across the range of possible end insertion and deletion gap sizes for an indel. For each gap size, the program backtracks from the end until the first mismatch is reached, and then along the main diagonal to count the total number of mismatches near the end (Fig. 5C). An end indel is detected if the distal segment is sufficiently long and if the sum of mismatches in the long and distal regions is sufficiently low.

2.6 Detecting splice junctions

GSNAP can align transcriptional reads that cross exon–exon junctions involving known or novel splice sites. For known splice sites, the program depends upon a user-provided set of splice sites, which belong to one of four categories: donors and acceptors on the plus genomic strand, and donors and acceptors on the minus genomic strand. Identification of novel splice sites is assisted by a probabilistic model, currently implemented as a maximum entropy model (Yeo and Burge, 2004), which uses frequencies of nucleotides neighboring a splice site to discriminate between true and false splice sites.

We use two methods for detecting splice junctions, one for short-distance and one for long-distance splicing. Short-distance splicing involves two splice sites that are on the same chromosomal strand, with the acceptor site being downstream of the donor site, within a user-specified parameter (default 200 000 nt). Short-distance splice junctions can be detected using a method similar to that for middle deletions, except that the distance allowed between candidate regions is much longer (Fig. 5B). As with middle indel detection, the positions of mismatches in the two regions determine whether a crossover area exists with the allowed number of mismatches (K − S), where S is the opening gap penalty for a splice. This crossover area is searched for donor and acceptor splice sites that are either known or supported by a splice site model at a sufficiently high probability. The probability score required is dependent on the length of short read sequence available for alignment in the exon region. When the aligned exon sequence is short, on the order of 12–20 nt, a relatively high probability score is needed. But when the aligned exon sequence is sufficiently long, more than 35 nt, only the expected dinucleotides at the intron end are needed.

For long-distance splicing, probability scores are also used to help find novel splice sites, although the required probability scores are higher for a given length of aligned sequence to compensate for the larger search space over the entire genome. To detect cases of long-distance splicing, the program identifies known or novel splice ends within single candidate regions, in the area delimited by the constraint level K of allowed mismatches (Fig. 5D). Candidate regions with donor and acceptor splice sites are then paired if they have the same breakpoint on the read, and have an acceptable number of total mismatches.

Reads that lie predominantly on one end of a splice junction may have too little sequence at the distant end to identify the other exon. Such alignments can still be reported by our program as partial splicing or ‘half intron’ alignments, if there is sufficient sequence on one end to determine a splice site, but insufficient sequence on the other end for the other site.

2.7 Aligning paired-end reads

GSNAP can align paired-end reads, which are produced when both ends of a nucleotide fragment are sequenced. Paired-end reads can also be generated by circularizing a long fragment of 10 000 or more bases with a short linker, and then cutting outside the linker to give reads at both ends of the long fragment. Our algorithm attempts to find an optimal pair of mapping variants that are concordant, meaning that they are within a user-defined range of expected genomic distances and that their strand directions are consistent. Therefore, GSNAP will favor concordant solutions involving suboptimal alignments on one or both ends, even when better alignments can be found individually for each end.

To consider pairs of alignments together, the program imposes successively stronger constraint levels and attempts to align each end at the given constraint level. For paired-end alignment, both ends of the read contribute toward the overall score, so at a given constraint level K, the program must accumulate alignments for each end up to that level. At each constraint level, the program tries to pair the exhaustive set of alignments found so far at each end to see if any pair is concordant. If so, the best alignment or alignments are those with the lowest total score of mismatches and penalties on the two ends. If suboptimal alignments are desired by the user, the program proceeds to find additional alignments beyond the optimal score level. If the algorithm reaches the maximum user-defined score limit without finding any concordant pair, it reports the best individual alignments for each end.

2.8 BS-converted DNA

An auxiliary program processes an existing reference sequence or reference space hash table to produce two new hash tables, both representing the plus strand of the genome, with one having C–T substitutions and the other having G–A substitutions. The second hash table accommodates reads from the minus strand, whose C–T substitutions appear as G–A substitutions on the plus strand. The auxiliary program combines and sorts the positions for each substituted 12mer into a single position list.

When GSNAP processes a BS read, it performs a C–T substitution of each 12mer in the read to check against the C–T hash table, and a G–A substitution of each 12mer in the reverse complement of the read to check against the G–A hash table. The generation and filtering steps behave as before. The verification step compares the substituted read against the substituted genomic region to identify mismatches. A special check is made in the original read against the original genomic region for mismatches between genomic-T and read-C, which are obscured by a C–T substitution.

3 RESULTS

3.1 Simulated reads

We compared GSNAP with several alignment programs that have been benchmarked in previous studies: MAQ version 0.7.1, SOAP version 1.11, Bowtie version 0.9.9.1, BWA version 0.4.9 and SOAP2 version 2.19. We generated 36, 70, and 100 nt reads that were sampled uniformly from the human genome (NCBI release 36) and generated datasets of different variant types by introducing mismatches or indels at random. Short indels of 1–3 nt were required to be at least 6 nt from the ends, and long indels at least 14 nt. Programs were run on a Linux machine with 8 dual-core AMD 8220 Opteron CPUs at 2.8 GHz and 64 GB of RAM. All programs have a multi-threaded mode, but were run in single-threaded mode in our tests. To study each variant separately and to prevent programs from searching for suboptimal hits, we provided each program with parameters adequate to identify the given variant.

Alignment results (Table 1) show that programs could generally align reads correctly with up to three mismatches, with SOAP2 limited to two mismatches, and with misses observed in 36 nt reads by GSNAP and SOAP and in 70 nt reads by SOAP. Misses of two and three mismatches in 36 nt reads by GSNAP were cases where the number of mismatches exceeded the guarantee condition of ⌊L/14⌋−1 for exhaustiveness, essentially because mismatches were spaced evenly enough to prevent a consecutive stretch of 14 nt to match between the read and genome. Exact alignments were identified most quickly by Bowtie and one-mismatch alignments by SOAP2. Alignments of two and three mismatches in 70 and 100 nt reads were identified at comparable speeds by BWA and GSNAP, and GSNAP was fastest at identifying four or five mismatches. For short indels, GSNAP showed perfect sensitivity, while BWA and SOAP showed a miss rate of up to 5%. SOAP2 was unable to detect indels in the single-end reads in our dataset, although it can detect short indels in paired-end reads. In all but one dataset, GSNAP was fastest at identifying short indels. For long indels, GSNAP was the only program able to detect the alignments, except that long indels in 36 nt reads could also be detected by SOAP at a much slower rate. Detection of long indels by GSNAP occurred at speeds comparable to those for short indels, and showed a miss rate of 0.1%, all due to repetitive regions on one end of the indel, which the program is designed to ignore.

Table 1.

Results of read alignment algorithms on simulated reads

	(Percent misses) Time
Variant	GSNAP	BWA	Bowtie	SOAP2	SOAP	MAQ
36 nt reads
Exact	51	17	9	70	869	2248
1 mm	55	60	33	11	1157	2106
2 mm	(1.0) 304	64	46	39	(2.9) 1470	6008
3 mm	(11.9) 405	551	544	−	(15.6) 1369	19 523
Ins, 1–3	640	(4.9) 767	−	−	(5.1) 5534	−
Del, 1–3	653	(3.3) 1016	−	−	(3.7) 4308	−
Ins, 4–9	(0.1) 507	−	−	−	31420	−
Del, 4–30	(0.1) 887	−	−	−	−	−
70 nt reads
Exact	15	23	9	13	1205	2180
1 mm	23	25	15	12	(0.1) 1564	2120
2 mm	45	33	48	67	(0.9) 2363	6175
3 mm	95	83	542	−	(3.3) 2272	20 316
4 mm	325	373	−	−	(7.8) 2098	(2.4) 20 002
Ins, 1–3	245	(2.0) 323	−	−	(4.3) 15 516	−
Del, 1–3	263	(1.3) 425	−	−	(4.7) 14 645	−
Ins, 4–9	(0.1) 288	−	−	−	−	−
Del, 4–30	(0.1) 292	−	−	−	−	−
100 nt reads
Exact	15	29	11	10	−	2211
1 mm	21	30	16	13	−	2168
2 mm	33	35	56	73	−	6330
3 mm	50	52	620	−	−	20 697
4 mm	82	137	−	−	−	(0.5) 20 503
5 mm	155	543	−	−	−	(2.1) 20 283
Ins, 1–3	269	(1.3) 218	−	−	−	−
Del, 1–3	273	(0.8) 360	−	−	−	−
Ins, 4–9	(0.1) 335	−	−	−	−	−
Del, 4–30	(0.1) 312	−	−	−	−	−

Times (in seconds) are for each set of 100 000 reads. For BWA, times include conversion to genomic coordinates (∼8 s per dataset). For SOAP2, times exclude loading of indices (∼35 s per dataset). Sensitivity was computed over reads that were unique (mapping to one location in the genome) and non-upgradeable (not mapping to another genomic location with a better variant type than the expected alteration). Misses, if any, are represented by percentages in parentheses before the corresponding running time. Dashes indicate variant types that could not be detected by the corresponding program. Variants: mm, mismatch(es); ins, insertion; and del, deletion. Parameter flags used, where n is number of mm in dataset: GSNAP (mm): -t 1 -m n. GSNAP (indel): -t 1 -m 0 -i 0. BWA (mm): aln -o 0 -n n. BWA (indel): aln -n 3 -o 1 -O 1 -E 1. Bowtie: -f -k 10 –quiet -p 1 -v n. SOAP2: -r 2 -v n. SOAP (mm): -s 12 -r 2 -w 10 -v n. SOAP (indel): -s 12 -r 2 -w 10 -v 0 -g 3. MAQ: map -C 10 -e 200 -n n. For the 3-mismatch dataset, Bowtie was also run in its MAQ mode, by removing the -v flag for limiting the number of mismatches and adding ‘-e 200’ to permit more mismatches. In that mode, times for the 36, 70 and 100 nt datasets were 46, 142 and 750 s, but miss rates were 57.2, 13.4 and 6.4%.

We measured the amount of heap memory used by the programs using the Valgrind Massif tool (Nethercote and Steward, 2007). GSNAP used a peak of 86 MB on the exact match datasets, 101 MB on the mismatch datasets and 170 MB on the indel datasets, with memory usage varying from read to read. However, these values do not measure memory used by GSNAP for its hash table position file of size 3.8 GB and the compressed genome of size 1.15 GB, which are accessed using memory mapping when available on the host computer. In memory mapping, our program will run fastest when sufficient physical memory is available to hold relevant parts of the index files. Therefore, for optimum performance on a human-sized genome, GSNAP should have access to 5 GB of physical memory, although the program can still run, albeit more slowly, if less memory is available. One advantage of memory mapping is that multiple instances of GSNAP can run on the same computer simultaneously and share the system memory that is mapped to the index files, without each process having to allocate that memory separately. For comparison, BWA used 2.2 GB on all datasets; Bowtie used 1.1 GB on the exact match datasets and 2.2 GB on the mismatch datasets; MAQ used 302 MB on all datasets; and SOAP used 14 GB on all datasets. Memory usage of SOAP2 could not be determined because source code is not available and the binary program was compiled without the flag necessary for memory profiling.

We also evaluated the ability of GSNAP to detect intragenic and intergenic exon–exon junctions in simulated reads, using either known splice sites from RefSeq or only novel splice site detection (These tests were performed on a earlier version of GSNAP that used absolute probability thresholds, instead of the sliding scale used in the current version). Simulated reads were based upon RefSeq splice sites, and GSNAP achieved perfect sensitivity when it had access to that information, but missed 0.1% of intragenic events and 5% of intergenic events when it relied solely upon probabilistic splice site models. Missed splice events were due to known splice sites with model scores below the default probability threshold of 0.90. Differences in sensitivity between intragenic and intergenic splice detection were due to the different criteria in GSNAP for short-distance splicing, which used a lower probability threshold (default 0.50) for the second splice site. Running times on datasets of 100 000 reads were 48, 114 and 183 s for 36, 70 and 100 nt intragenic reads, and 122, 211 and 287 s for intergenic reads. These running times are faster than those for the benchmarking of mismatches and indels, because the spliced reads were generated from the coding part of the genome, which is less repetitive.

3.2 Transcriptional reads

We measured the impact of complex variant detection and SNP tolerance by GSNAP on actual data taken from universal human reference RNA (UHR, Stratagene catalog number 740 000), used in the MAQC (MicroArray Quality Control) project (Canales et al., 2006) and assayed by Illumina on their Solexa Genome Analyzer. From this dataset, we sampled 100 000 reads uniformly among the dataset of 50 nt reads. Unlike simulated reads, actual reads lack information about their original genomic location, so we determined the performance of programs using alignment yield, which is the percentage of reads that could be aligned by each program with various settings of mismatches, splicing or indels. We tested GSNAP against NCBI human genome version 36 and also against a reference space that covered 12 million SNPs from dbSNP version 129.

Alignment yields were 70% for two mismatches and 74% for three mismatches (Table 2). Alignment yield increased when programs were allowed to identify more complex variants. The addition of splicing involving known splice sites to GSNAP increased alignment yields by 8–9%, and the further addition of novel splice sites increased alignment yields by another 0.3–0.6%. Allowing indels increased alignment yield by a further 1%.

Table 2.

Effect of splicing, indels and SNP tolerance on transcriptional dataset

	Alignment yield (%)		SNP effect on alignment (%)						Time (s)
Variants allowed	Non-SNP	SNP	New	Same	Superset	Subset	Diff	Total	Non-SNP	SNP
≤2 mismatches	69.7	70.2	0.5	1.7	4.9	0.4	0.1	7.5	52	57
Above plus known splicing	78.7	79.1	0.5	1.8	4.8	0.3	0.2	7.6	381	457
Above plus novel splicing	79.0	79.5	0.5	1.9	4.8	0.2	0.3	7.7	457	522
Above plus indels	80.2	80.7	0.5	1.8	4.9	0.2	0.5	8.0	725	905
≤3 mismatches	73.9	74.3	0.4	2.0	5.2	0.4	0.1	8.1	161	214
Above plus known splicing	82.2	82.6	0.4	2.1	5.1	0.3	0.2	8.0	530	668
Above plus novel splicing	82.8	83.1	0.4	2.2	5.1	0.3	0.3	8.3	624	755
Above plus indels	83.8	84.2	0.4	2.1	5.1	0.3	0.6	8.5	949	1262

The introduction of SNP tolerance resulted in only a minor increase in alignment yields. However, 7–8% of alignment results were affected in some way by a SNP. SNP tolerance gave an alignment where none was previously found in only 0.4–0.5% of cases. In 5% of cases, known SNPs revealed additional genomic locations for a given read beyond the original locations, resulting in a superset of the original results. In 0.2–0.4% of cases, SNP tolerance yielded a subset of genomic locations, meaning that some of the mismatches in the original alignments could be resolved in favor of known SNPs. In 1–2% of cases, all mismatches in the original alignments were at known SNP locations, leaving the genomic locations the same, but allowing nucleotide differences to be interpreted as matches to minor alleles rather than as mismatches. In a small fraction of cases, SNP tolerance gave a significantly different set of results compared with the original.

3.3 BS-converted reads

We used the simulated datasets from Section 3.1 with mismatches of 0, 1 and 2 nt, and substituted thymine for cytosine with a probability of 95%, ignoring sequence contexts, such as non-island CG dinucleotides in eukaryotes (Goll and Bestor, 2005) or in CG, CHG and CHH patterns in plants (Cao and Jacobsen, 2002), where methylcytosines occur more often. We aligned the original reads with the standard version of GSNAP and the substituted reads with the methylation flag turned on. Results show that thymine substitution had a minor effect on the ability of GSNAP to identify the original genomic position, due to increased ambiguity in aligning some reads (Table 3). The fraction of additional reads giving non-unique positions in the genome was 5.5% of 36 nt reads, 2.6% of 70 nt reads and 1.3% of 100 nt reads, in the exact match datasets, and slightly higher fractions in the datasets with one or two mismatches.

Table 3.

Effect of simulated BS treatment

		Alignment uniqueness (%)
Length (nt)	Variant	Genomic	BS	Difference
36	Exact	87.1	81.6	5.5
	1 mismatch	86.7	80.6	6.0
	2 mismatches	85.3	78.7	6.5
70	Exact	95.0	92.4	2.6
	1 mismatch	94.9	92.1	2.8
	2 mismatches	94.7	91.7	3.0
100	Exact	96.6	95.3	1.3
	1 mismatch	96.6	95.2	1.4
	2 mismatches	96.5	95.1	1.4

4 DISCUSSION

The methods described in this paper expand the scope of variants that can be detected in reads, and should therefore increase the utility of next-generation sequencing data. The ability to recognize a wide range of variants should also improve mapping accuracy by recognizing the correct genomic origin of variant reads. Likewise, the SNP-tolerance feature implemented in our program should help resolve mappings in certain genomic regions. The utility of this feature should be measured not just by the 7–8% of reads affected, but by its contribution towards making correct biological inferences in the subsequent analysis pipeline. Other researchers (Manske and Kwiatkowski, 2009) have also found cases where SNP-tolerant alignment facilitates the alignment of reads with minor alleles.

We have developed an algorithm to meet the specific needs of short-read sequence analysis for both speed and sensitivity in detecting complex variants and splicing. The strength of our algorithm is its successively constrained search strategy for generating candidate genomic regions by merging position lists from oligomers across the entire read, and filtering them using count- or pattern-based lower bound calculations. Our search procedure operates at the oligomer level, which differs from the nucleotide-level backtracking procedures used in BWT-based programs to identify mismatches and short indels.

By filtering the set of candidate regions, our intersection process represents a significant efficiency improvement over the seed-and-extend strategy, used in BLAT and other seed-based alignment programs, which find genomic regions based on a single q-mer and then test each of those regions in a time-consuming verification step. Some programs, such as ELAND, further restrict the seed to be at the beginning of the short read. The use of seeds can be a highly effective heuristic, and BWA can run faster by using a seeding mode that allows a certain number of mismatches in the initial part of the short read. Our method can be thought of as trying all possible seeds simultaneously over the entire short read, and therefore has the feature of not favoring one part of the read over another.

Our intersection procedure also provides an efficient alternative to the q-gram procedure, used in SHRiMP (Rumble et al., 2009) and RazerS, which scans the entire genome using a sliding window and counts q-mers within bins to find candidate genomic regions (Rasmussen et al., 2006). The q-gram procedure allows for two or more indels in a single read, which is not currently allowed by GSNAP, although our algorithm could be modified to identify them. Another difference is that the q-gram procedure defines alignment differences as an edit distance, where each nucleotide in a gap counts as a difference, so longer indels are considered more distant. In contrast, GSNAP uses only an opening gap penalty in scoring indel alignments, so it can identify long indels more readily.

Our program also differs from several alignment programs, including MAQ, RMAP, SHRiMP, Bowtie, BWA and SOAP2, which have the ability to use quality scores to rank alignments. Although quality scores could be applied in the validation step of our algorithm, it remains unclear to us how best to make tradeoffs between quality scores and alignment results, for example, how to choose between an alignment with one mismatch at a high-quality score or one with two mismatches at lower quality scores. Color space reads produced by ABI SOLiD technology require some extensions to our algorithm, and we are working to implement this capability in our program.

Although our results and experience indicate that our program has practical utility for analyzing next-generation sequencing data, our research is ongoing. In particular, longer reads will entail more flexibility in alignment and may require the enhancement of more general cDNA–genomic alignment programs, such as our GMAP program. Future biological research should benefit from having a diversity of bioinformatics methods and programs to meet the various needs of sequence analysis.