Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2010 Feb 23;26(7):953–959. doi: 10.1093/bioinformatics/btq067

Accelerated similarity searching and clustering of large compound sets by geometric embedding and locality sensitive hashing

Yiqun Cao 1, Tao Jiang 1, Thomas Girke 2,*
PMCID: PMC2844998  PMID: 20179075

Abstract

Motivation: Similarity searching and clustering of chemical compounds by structural similarities are important computational approaches for identifying drug-like small molecules. Most algorithms available for these tasks are limited by their speed and scalability, and cannot handle today's large compound databases with several million entries.

Results: In this article, we introduce a new algorithm for accelerated similarity searching and clustering of very large compound sets using embedding and indexing (EI) techniques. First, we present EI-Search as a general purpose similarity search method for finding objects with similar features in large databases and apply it here to searching and clustering of large compound sets. The method embeds the compounds in a high-dimensional Euclidean space and searches this space using an efficient index-aware nearest neighbor search method based on locality sensitive hashing (LSH). Second, to cluster large compound sets, we introduce the EI-Clustering algorithm that combines the EI-Search method with Jarvis–Patrick clustering. Both methods were tested on three large datasets with sizes ranging from about 260 000 to over 19 million compounds. In comparison to sequential search methods, the EI-Search method was 40–200 times faster, while maintaining comparable recall rates. The EI-Clustering method allowed us to significantly reduce the CPU time required to cluster these large compound libraries from several months to only a few days.

Availability: Software implementations and online services have been developed based on the methods introduced in this study. The online services provide access to the generated clustering results and ultra-fast similarity searching of the PubChem Compound database with subsecond response time.

Contact: thomas.girke@ucr.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Software tools for mining the available small molecule space play an important role in many bioscience and biomedical areas. They are ranging from drug discovery, chemical biology and chemical genomics to medicinal chemistry (Haggarty, 2005; Oprea, 2002; Oprea et al., 2007; Savchuk et al., 2004; Strausberg and Schreiber, 2003). Currently, the structures of over 20 million distinct small molecules are available in open access databases, like PubChem (Austin et al., 2004), ChemBank (Seiler et al., 2008), NCI (Ihlenfeldt et al., 2002), ChemMine (Girke et al., 2005), ChemDB (Chen et al., 2007) and ZINC (Irwin and Shoichet, 2005). To analyze these important data resources, efficient structure similarity search tools are essential for retrieving chemical and bioactivity information from databases (Chen and Reynolds, 2002; Sheridan and Kearsley, 2002). In addition, they are often useful for predicting bioactive small molecules (Cao et al., 2008; Cheng et al., 2007).

A variety of structure similarity search methods are available (reviewed by Willett et al., 1998). Unfortunately, they are often not fast enough forsystematic analyses of very large compound collections with millions of compounds. This is because most of these methods sequentially compare a query structure against all entries in the database and then rank the results by a chosen scoring system, and thus the cost to perform similarity searches grows linearly with the size of the compound database. Therefore, more efficient and sophisticated search methods need to be developed to utilize the available chemical space efficiently.

Clustering of compound sets is essential on practically all stages of the discovery process of bioactive compounds (reviewed by Downs and Barnard, 2002). Commonly, structure similarity-based clustering utilizes the pairwise similarity measures generated by the above compound search methods to partition the data into discrete groups of similar compounds. An example is Jarvis–Patrick clustering, which is among the most widely used clustering methods in cheminformatics (Willett, 1987). Alternatively, they can be used to build hierarchical trees that represent the similarity relationships among all items in a compound dataset. One of the main challenges in this area is the difficulty to cluster the millions of compound structures that are currently available in the public domain. This is because many cluster analysis approaches multiply the complexity of a chosen similarity search method by the number of compounds in the dataset. They often require the calculation of all-against-all similarities for the compounds under investigation and the computational cost grows quadratically with the size of the dataset. Therefore, novel clustering methods need to be developed for exploring this vast chemical space efficiently.

A few methods have been proposed to accelerate the nearest neighbor searching in compound databases. Agrafiotis and Lobanov (1999) reported an algorithm based on k-dimensional (or k-d) trees for diversity analyses. This problem is relevant to clustering (Bentley, 1975) and the method can possibly be adopted to nearest neighbor searching. It works by representing each chemical compound as a multidimensional vector and organizing the compound dataset in a k-d tree structure to speedup diversity analyses. However, the vector representation used is very limited and the k-d tree cannot handle high-dimensional vector data. Later the authors proposed a new data structure called μ-tree to perform guided nearest neighbor search of compounds in general metric space (Xu and Agrafiotis, 2003). A μ-tree organizes the database in recursively partitioned Voronoi regions and represents these partitions as a tree. The method greatly reduces the number of similarity comparisons required for the nearest neighbor search by applying an efficient branch and bound strategy. As a distance-based indexing method, the μ-tree approach does not require the compounds to be represented as multidimensional vectors. However, it requires the similarity measure used to be a metric. Swamidass and Baldi (2007) used upper bounds on similarity measures for structural fingerprints to reduce the number of molecules that need to be considered in the nearest neighbor searches. Later, Baldi et al. (2008) employed tighter bounds to achieve further time savings. These latter two methods have been designed to be used only with fingerprint-based similarity measures.

A variety of data structures and algorithms have been proposed to accelerate the nearest neighbor search in multidimensional Euclidean space (reviewed by Bohm et al., 2001). These methods, often referred to as multidimensional access methods (MAMs), have not been widely used in similarity searching and clustering of chemical compounds. The reason for this may be the popularity of non-Euclidean similarity coefficients in chemical structure similarity searching, which are not immediately compatible with MAMs. Moreover, Fu et al. (2000) reported that the embedding of the generic metric space into multidimensional space can introduce considerable inaccuracy in the nearest neighbor search applications.

In this article, we introduce the embedding and indexing (EI)-Search and EI-Clustering methods for ultra-fast similarity searching and clustering of very large datasets using an EI strategy. First, we introduce an efficient embedding algorithm. Subsequently, we describe the design of EI-Search and EI-Clustering, and test their efficiency and accuracy. Finally, experimental test results for three large compound datasets are presented and discussed.

2 METHOD

2.1 Embedding compounds in Euclidean space

The foundation of our algorithms is the usage of embedding techniques to build multidimensional vector representations of compound structures, which can be used to approximate compound dissimilarities by the inter-vector distances. Embedding objects in Euclidean space offers many benefits, such as the possibility of accelerating the nearest neighbor search. In addition, they are useful for all-pair query approaches used in data visualization, clustering and data mining (Faloutsos and Lin, 1995).

The problem of geometric embedding has previously been studied and applied to the nearest neighbor search in metric space. Three of the most widely used methods in this area are multidimensional scaling (MDS; Kruskal and Wish, 1978), stochastic proximity embedding (SPE; Agrafiotis, 2003; Agrafiotis and Xu, 2002; Smellie et al., 2006) and FastMap (Faloutsos and Lin, 1995). MDS is used to discover structures in datasets by representing the relationships among its objects as spacial distances in a low-dimensional display plane. It is computationally expensive because it depends on the availability of all pairwise dissimilarities among the objects in a dataset. As a result, it becomes quickly infeasible for compound databases with more than a few thousand entries.

Many variances of MDS have been proposed to solve the problem for large datasets. Chang and Lee (1973) selected from the whole dataset a smaller number of representative objects, called pivots, and applied classic MDS to this subset. The remaining objects were then embedded to the same Euclidean space based on their distances to the pivots.

SPE is an alternative to MDS. As a self-organizing algorithm, SPE starts with an initial assignment of data points to coordinates and carries out iterative pairwise refinement steps by adjusting randomly selected pairs of coordinates to better approximate the corresponding dissimilarity values. SPE is very efficient and is reported to scale linearly with the size of the dataset.

FastMap is another fast alternative of MDS with linear-time complexity. It gains its computational efficiency by directly calculating the induced vectors rather than iterative improvement steps used by most MDS implementations. However, the proper choice of the set of pivot objects can be complicated by the presence of large numbers of outlier compounds that are not similar to any other compounds in a compound library.

This study presents an alternative embedding method that is accurate and robust enough to process very large compound datasets. The initial steps of the embedding procedure are similar to the method from Chang and Lee (1973), but it differs significantly in its final optimization steps. The method starts by dividing all compounds into two sets: a small reference compound set and a much larger target compound set. The reference compound set is a user-definable parameter that can be generated by maximum diversity or random selection methods of compounds in a given library. Traditional MDS is applied to obtain the coordinates of the induced reference vectors for the reference compounds. Subsequently, an induced target vector is obtained for each target compound by computing the vector coordinates that can best preserve its dissimilarity to all reference compounds. More specifically, for the i-th target compound oi, the following stress function is minimized:

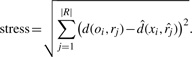graphic file with name btq067m1.jpg (1)

In this equation, d(oi, rj) is the dissimilarity value between target compound oi and reference compound rj. The variable 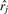Inline graphic is the coordinate of the j-th induced reference vector obtained by applying MDS to the reference compounds. The unknown coordinate of the i-th target vector is xi, and 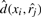Inline graphic gives the Euclidean distance between xi and 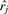Inline graphic. By minimizing the stress function with a global optimization algorithm, the coordinate xi can be computed so that it best preserves the dissimilarities from target compound oi to all reference compounds.

Two very important parameters in our modified version of the MDS algorithm are the number of dimensions D and the reference compound set. Large D values will not increase the minimum value of the stress function, and thus will never negatively impact the embedding quality. To maximize the embedding quality, our method can be used with conservatively large D values of over 100, but at the expense of longer computation times for both the embedding and the downstream similarity searches. Often D values >100 may not be necessary for many types of molecular descriptors (e.g. physicochemical), due to their frequently high redundancy and correlation among each other (Agrafiotis and Xu, 2002). It might also be possible to take advantage of low intrinsic dimensionality of some similarity measures, using methods such as ISOMAP (Tenenbaum et al., 2000) and locally linear embedding (LLE; Roweis and Saul, 2000). However, our tests using ISOMAP with atom pair descriptor also showed that D values >100 may still be necessary for some molecular descriptors to achieve satisfactory accuracy.

The reference compound set is the second important parameter for our approach. The size of the set, R, directly controls the complexity of the stress function. Therefore, the larger the reference compound set, the longer the embedding time. Furthermore, both the size and the composition of the reference set have an influence on the embedding quality. This is because the induced reference vectors serve as similarity landmarks to position each target compound in the embedding space according to its dissimilarity profile to all reference compounds. To minimize ambiguous placements, the reference set should ideally be chosen as diversely as possible and cover the entire chemical space of the target compounds. However, our benchmark tests for structure similarity searching and clustering, have shown that randomly selecting reference compounds is sufficient to obtain robust results (Section 3.5). This is partly because R is usually much larger than the number of D. Due to this redundancy, choosing one or several suboptimal reference compounds will not have a great impact on the embedding quality.

Moreover, it is important to identify the smallest values for R and D, which can achieve satisfactory accuracy. Increasing either value will result in longer processing time. This does not only apply to the embedding of the compound database, but also to every query structure used in similarity searches, because both components have to go through the embedding process. This slightly offsets the time saving gained by the other parts of the algorithm. Agrafiotis et al. (2001) presented a neural network-based method that could reduce the embedding time of our method significantly. However, in our tests we were not able to achieve embedding qualities with this method that were sufficient for similarity search and clustering applications (Supplementary Table S-1).

Compared to the quadratic time complexity of traditional MDS methods, our algorithm offers large time savings. Given similar distributions of pairwise dissimilarities and a fixed number of reference compounds, the running time of the above embedding algorithm is roughly linear to the number of compounds. Because each target compound is processed independently, our method can be easily parallelized on computers with multiple CPU cores or compute clusters. This is a very desirable feature when processing very large compound databases. The related SPE method is in its current form less effective for processing very large datasets because of the challenges involved in implementing a parallelized version of this algorithm. Our tests with a publicly available implementation of the SPE algorithm show that its unparallelized compute times on very large datasets with millions of compounds are too long to obtain embeddings of high enough qualities to perform accurate nearest neighbor searches with acceptable recall rates (Supplementary Table S-2). Nevertheless, SPE is a powerful algorithm that can be easily utilized as an alternative embedding method by our EI-Search and EI-Clustering tools.

2.2 EI-Search

After the compounds are embedded into the D-dimensional Euclidean space, structure similarity searches can be performed by a nearest neighbor search in the embedding space. For this, the query compound is embedded into the same D-dimensional Euclidean space. Subsequently, the corresponding induced vector is used to perform a nearest neighbor search in the embedding space. This search method offers great time savings and flexibility for similarity searches because of two major reasons. First, compared to other similarity measures used for comparing compound structures, Euclidean distances can be calculated very efficiently. Second, many MAMs can be employed in the nearest neighbor search to further improve its time efficiency.

Although many MAMs have been proposed to speedup the nearest neighbor search problem, most of them are affected by the dimensionality problem, often referred to as the curse of dimensionality. This is the phenomenon that for various geometric search problems, including the nearest neighbor search, the best algorithms known have performance trends that degrade exponentially with an increase in dimensionality (Weber et al., 1998). Our tests also confirmed that the SR-tree method (Katayama, 1997) becomes slower than sequential scans of the dataset as soon as D is set to values >100. However, our tests also indicated that the dissimilarities between compound structures can only be preserved reliably with large D values of at least 100. Thus, it is important for our method to combine high-dimensional embedding and an indexing method that are both insensitive to the dimensionality problem.

It has become increasingly popular to use the approximate nearest neighbor search in high-dimensional space to avoid the dimensionality problem. One of these approximation approaches utilizes a spatial index using locality sensitivity hashing (LSH) to perform the fast nearest neighbor search in Euclidean space. LSH uses a family of hashing functions to map database objects into buckets. It is designed to join related items based on a given similarity measure with high probability. Accordingly, many hashing functions vary with respect to their similarity measures. For example, Gionis et al. (1999) introduced in the original LSH paper a bit sampling-based LSH approach that uses the Hamming distance measure. Datar et al. (2004) proposed an LSH scheme for p-stable distributions along with Euclidean distances. However, so far no hashing functions have been developed for the similarity measures that are commonly used for comparing compound structures. This limitation can be addressed by embedding compounds in Euclidean space and building for them a spatial index using induced vectors in embedding space.

Taking advantage of the above embedding and the LSH-based spatial indexing approaches, we designed an efficient approximate compound structure similarity search algorithm. This algorithm is named EI-Search after its two key components: embedding and indexing. The algorithm first preprocesses the compound dataset by embedding it into a high-dimensional Euclidean space and generating a spatial index using LSH. When searching for k compounds that are most similar to a given query compound, a two-step approach is employed to reduce the error introduced in the embedding process and the approximate nearest neighbor search. First, the query compound is embedded in the same Euclidean space. The resulting induced vector is then used in an index-assisted nearest neighbor search of the embedding space to retrieve a candidate set consisting of γ · k vectors that are most similar to it. The relaxation ratio γ is a user-defined parameter that controls the trade-off between processing time and search accuracy. Larger values for γ result in larger candidate sets and possibly higher accuracy, but at the cost of longer search times. Second, a refinement step applies exact structure similarity searches to the candidate set obtained in the first step. This allows the selection of the final k compounds that are most similar to the query structure.

Compared to commonly used structure similarity search methods, EI-Search has several advantages. The most important ones are its time efficiency and compatibility with a wide range of similarity measurements. This makes the method potentially useful for accelerating similarity searches of a variety of data objects that are of relevance to many life science and non-life science areas.

2.3 EI-Clustering

In addition to similarity searching, Euclidean space representations can be used for clustering large datasets very efficiently. For example, spatial join can be used to perform single linkage clustering by finding all vector pairs, which are separated by a distance below a given threshold (Brinkhoff et al., 1993). The nearest neighbor information required for Jarvis–Patrick clustering can also be obtained very efficiently in Euclidean space by using an efficient algorithm for the all-nearest-neighbors problem (Vaidya, 1989).

In this article, we introduce a new clustering method, EI-Clustering, that takes advantage of the accelerated search speed provided by EI-Search to cluster very large sets of chemical compounds under the Jarvis–Patrick clustering framework. Jarvis–Patrick clustering requires a nearest neighbor table, which consists of p nearest neighbors for each compound in the dataset. This information is then used to join compounds into clusters that share at least m nearest neighbors. The values for p and m are user-defined parameters. In case of EI-Clustering, the EI-Search method generates the nearest neighbor information for each compound in the dataset. The resulting nearest neighbor table is then used as direct input for Jarvis–Patrick clustering. When clustering very large datasets, EI-Clustering is particularly efficient due to its fast computation of the nearest neighbor table.

3 EVALUATION

3.1 Implementation

We implemented the EI-Search and EI-Clustering algorithms as C++ programs. Internally, they use the L-BFGS-B library (Zhu et al., 1997) for the global optimization step in the embedding procedure. For the LSH-based spatial indexing, we utilized the lshkit library that implements the MPLSH algorithm, a variant of LSH that requires fewer hash tables and offers large space savings as well as shorter query time (Lv et al., 2007). In addition, we wrote a reusable C++ library for calculating atom pair descriptors. We were particularly interested in testing atom pair descriptors because of their superior performance in structure similarity searching (Chen and Reynolds, 2002). To also include in our tests one of the most widely used fingerprint methods, we employed the fingerprint descriptors used by PubChem and utilized a fingerprint implementation provided by the NIH Chemical Genomics Center (2009). Jarvis–Patrick clustering was performed with a custom program implemented in C++.

3.2 Datasets and testing platform

To test the performance of the proposed methods, benchmark comparisons for similarity searching and clustering were performed using the publicly available compound structures from NCI and PubChem. The NCI dataset consisted of 260 071 compounds. After removing entries that did not generate any usable atom pair descriptors, 260 027 compound structures were used from this collection. From PubChem, we used the structures from the PubChem Compound dataset. From this collection, we selected two sets: one subset consisting of 2.3 million compounds with at least five non-hydrogen bonds (PubChem Subset) as well as the entire PubChem Compound library with over all 19 million compounds (PubChem Compound).

The tests were performed on a Linux computer equipped with Xeon CPUs clocked at 2.4 GHz and 16 GB of RAM. For parallelized computations, a computer cluster was used with the exact same hardware configuration per compute node. Compute times are given as total CPU hours throughout the text.

3.3 Time efficiency of embedding

First, we evaluated the running time of our modified MDS algorithm for different parameters. For this, the compounds from all three datasets were embedded into a high-dimensional Euclidean space.

3.3.1 Time efficiency with respect to the size of the dataset

Our results show that the time required for embedding increases almost linearly with the number of compounds in the library (Table S-3 in Supplementary Materials). The average time to embed one compound varies only slightly across the three datasets and is below 0.3 s using a practical parameter set. Because the embedding algorithm processes each compound independently after applying MDS to the reference compound set, it is trivial to further reduce its computation time by using a compute cluster. In our experiments, it took around 10 min to process the 260 027 compounds of the NCI dataset using 87 CPUs. Similarly, the 19 million compounds of the PubChem Compound library could be processed in less than a day using 80 CPUs.

3.3.2 Time efficiency with respect to the embedding parameters

As discussed above, the number of dimensions D and the number of reference compounds R are the two main factors that will affect the embedding time. To estimate their impact, we randomly selected from the NCI library seven reference compound sets with sizes ranging from 240 to 800 compounds. These reference sets were used in independent test runs of our embedding algorithm where D was set to a fixed value to study the influence of R on the total CPU time. Similarly, to model the impact of D, the value of R was fixed to three times the value of D and the total CPU time was collected using D values ranging from 120 to 260. These ranges were chosen to ensure high-quality embedding, but also to keep the computation within manageable time limits. Our test results (Supplementary Fig. S-1) indicate that the total CPU time of our method grows linearly with R, and exponentially with D. Based on this time behavior, the values for R and D should be chosen as small as possible, but large enough to maintain an embedding quality that is sufficient for the downstream similarity search and clustering steps (see below).

3.3.3 Time efficiency and global optimization parameters

Solving the global optimization problem accounts for most of the embedding time. Therefore, the parameter choice of this step has a great impact on the time efficiency of the embedding step of our method. Using less stringent termination conditions for the L-BFGS-B algorithm, will typically reduce the embedding time, but at a cost of embedding quality. For example, the average time to embed one compound could be easily cut into half with a small loss in accuracy (Supplementary Table S-3). Although the preprocessing of new datasets is time consuming, our method is relatively flexible with respect to adding new entries to an already preprocessed library. Because all entries are embedded independently, one can easily add new ones without repeating this process for the entire dataset. This meets the work flow requirements of many large compound databases, where minor updates occur frequently, but major revisions are rare.

3.4 Quality of embedding

As pointed out by previous studies, embedding metric representations of objects in Euclidean space may reduce the accuracy of the nearest neighbor searches (Fu et al., 2000). However, when the parameters for our embedding method are chosen properly, the method is accurate enough to be used in the prescreening step of EI-Search (as shown in Section 3.5). As a performance test of the embedding step, we randomly selected 10 million compound pairs from the NCI dataset, computed their atom pair-based Tanimoto similarity coefficients and compared them with the corresponding distance values obtained from the induced vectors. The two datasets were highly correlated, as indicated by a Pearson's correlation coefficient of 0.79. Additionally, the agreement among the datasets was evaluated by grouping the Tanimoto coefficients into 10 similarity intervals from 0 to 1 using increments of 0.1. Subsequently, the distributions of the vector distances for each interval were plotted in the form of box plots. In this representation, a low degree of overlap among the boxes from adjacent intervals indicates a strong agreement between the two methods. The box plots obtained from our tests show only a moderate overlap among adjacent intervals, and only minor to no overlap among more distant intervals (Supplementary Fig. S-2). This indicates a strong agreement among the two methods for the majority of the compounds with some inconsistencies at the interval boundaries, but for a much smaller number of cases. For example, for high Tanimoto similarities ranging from 0.8 to 1, the similarities of the corresponding vectors pairs (1−distance) fall all into a very narrow range 0.75–1.0. The two methods also agree very well in the low similarity range. This is indicated by the fact that 98.17% of all compound pairs with a Tanimoto coefficient <0.4 are placed into a very similar range (<0.38) in vector space. Based on these results, our embedding method appears to preserve well-separated ranges of Tanimoto coefficients in a robust manner.

3.5 Accuracy of EI-Search

To further examine the accuracy of the EI-Search method for compound similarity searching, we implemented an EI-Search program and tested it with different parameters. The accuracy of EI-Search is measured by the recall rate. When retrieving the k most similar compounds to a query structure, the recall rate is defined as the percentage of compounds obtained with EI-Search that are also returned by sequential search methods. To evaluate the impact of the different parameters used by EI-Search, the program was run using different values of D, R, k and γ. In each run, the recall rates for 1000 random queries from the NCI dataset were calculated.

First, we compared the recall rates when searching for the k most similar compounds with different R and γ values while the values of k and D were fixed. (Supplementary Fig. S-3a shows the results for constant k and D values of 100 and 140, respectively.) The results indicate that increasing γ from 1 to 50 results in a significant improvement of the recall performance, while this effect starts to plateau off at values of >20. With respect to the number of reference compounds R, the recall rate increases from values 240 to 420. Based on these results, a good empirical choice for R is between two and three times the value of D. Another observation is the fact that the effect of R diminishes for γ values >20. In other words, large enough γ values can compensate a suboptimal choice of R. For example, when γ was set to 20, and k to 100 and D to 140, the best and worst recall rates were 97.87% and 97.35%, respectively. This corresponds to a difference of only 0.52%.

Similarly, we investigated the correlation between the recall rates and the values of D and γ. According to the results from the previous tests, the R values were always set to three times the values of D. When searching for the k most similar compounds the recall rates were collected for different D and γ values while the value of k was fixed. Supplementary Figure S-3b shows the results for a k value of 100. These results indicate that the recall rates consistently improve with the number of dimensions. This effect is much stronger for smaller γ values. For example, when k was set to 100 and γ to 1, then the recall rate could be improved from 58.35% to 65.57% for D values of 120 and 260, respectively. For large γ values above 20 this effect is again much less pronounced. While larger γ values will result in an increase in processing time, their impact is less severe than increasing the value of D. Accordingly, we chose in the subsequent experiments the D values as small as possible and the γ values as large as necessary to maintain both high accuracy and time efficiency of the method.

3.6 Time efficiency of EI-Search

While maintaining high recall rates, EI-Search was able to greatly reduce the time for performing structure similarity searches in large compound databases. To examine the time efficiency of EI-Search, 1000 random queries were performed on each of the three datasets using first the EI-Search program and then exhaustive sequential searches with the atom pair and fingerprint similarity search programs. For each comparison we used for EI-Search the same descriptor type as for the sequential search methods. The query compounds were randomly selected from the dataset. To obtain realistic search results, the 100 most similar compounds with a minimum similarity of 0.5 were retrieved for each query. Atom pair descriptors combined with Tanimoto coefficients were used as similarity measure. For the PubChem Compound library, we also included in the tests the Tanimoto similarities of PubChem's fingerprints. According to the above parameter optimization results, we used in all tests the following settings: R=300, D=120 and γ=30. The obtained search times and recall rates are listed in Table 1.

Table 1.

Performance tests of EI-Search

Dataset
 NCI
 PubChem Subset
 PubChem Compound
Descriptor type Atom pair Atom pair Atom pair Fingerprint
Average search time (s)
 Sequential search 0.800 11.570 93.121 19.658
 EI-Search 0.067 0.170 0.427 0.499
Recall of EI-Search (%)
 Mean 99.95 99.60 97.38 96.32
 SD 0.44 1.82 5.61 11.54
Open in a new tab

Search times and recall rates are listed for searching three large compound sets with EI-Search and the sequential search methods. The same descriptor type was used for each comparison pair. The experiments were performed on the same hardware using the same embedding and relaxation parameters (R = 300, D = 120 and γ = 30). The LSH parameters were supplied by lshkit.

Several conclusions can be drawn from Table 1. First, in comparison to the highly accurate atom pair method, EI-Search achieves in the atom pair descriptor tests very high recall rates ranging from 97.38% to 99.95%. In comparison to the fingerprint method, the recall rate of the corresponding EI-Search is slightly lower with 96.32%. The reason for this reduction may be the fact that fingerprints provide less accurate similarity measures than atom pairs (Chen and Reynolds, 2002). This could result in less robust rankings of the nearest neighbor search results, and therefore a slightly lower recall rate is reasonable. Second, EI-Search provides significant time savings for the nearest neighbor searches. For example, the average time required to search >19 million compounds of the PubChem Compound dataset is reduced for the atom pair approach from >93 to <0.5 s, and for the fingerprint method from >19 to <0.5 s. This corresponds to accelerations by our EI-Search method of over 200 and 40 folds, respectively. Third, while the search time for the exhaustive sequential search methods increases linearly with the size of the databases, this increase is less than linear for the EI-Search method. For instance, searching the PubChem Subset dataset with EI-Search takes on average only 2.5 times longer than searching the NCI dataset, that has one-ninth of the size of PubChem Subset. Finally, another outstanding feature of EI-Search is the fact that its search speed is much less impacted by the complexity of the similarity measure used for database searching than this is the case for the exhaustive methods. For instance, the switch from the fingerprint similarity measure to the more computationally expensive atom pair similarity measure results only in a minor increase of EI-Search's query time, while it is a >4-fold increase for the exhaustive sequential search methods.

3.7 Accuracy and time efficiency of EI-Clustering

To test the performance of our EI-Clustering method for partitioning large compound sets, we clustered all three compound sets with the Jarvis–Patrick algorithm. The required nearest neighbor tables were generated with EI-Search and the exhaustive sequential search methods. EI-Search was run with the same embedding and searching parameters (R=300, D=120 and γ=30) as in the previous section. The LSH parameters were slightly changed to achieve higher accuracy. The process of generating the nearest neighbor tables was parallelized on a computer cluster. For each clustering result, the total search time was calculated for all utilized CPUs. To measure the agreement among the clustering results, we computed the Jaccard partition coefficient for each pair of clustering results (Table 2). Jaccard coefficients close to zero indicate low similarities and values close to one indicate high similarities among the evaluated cluster sets.

Table 2.

Performance tests for EI-Clustering

Dataset
 NCI
 PubChem Subset
 PubChem Compound
Similarity measure Atom pair Atom pair Atom pair Fingerprint
Total clustering time (h)
 Jarvis–Patrick 72.9 7355.6 N/A N/A
 EI-Clustering 3.5 92.2 1517.2 2869.71
Jaccard coefficient 0.9913 0.9887 N/A N/A
Open in a new tab

The table compares the time and accuracy performance of EI-Clustering with Jarvis–Patrick clustering when using exhaustive search methods for generating the required nearest neighbor information. The compute time is given in hours of total CPU time. The agreement among the clustering results is given in the last row in form of Jaccard partition coefficients. Clustering of the PubChem Compound dataset was not possible with the exhaustive search methods due to their insufficient performance on this large dataset.

The results in Table 2 show that the EI-Clustering method can dramatically reduce the processing time of the Jarvis–Patrick clustering approach while maintaining a high level of agreement with the results obtained by Jarvis–Patrick clustering with exhaustive nearest neighbor search methods (Jaccard coefficients >0.98). The total CPU time to process over 2.3 million compounds from the PubChem Subset could be reduced from over 306 days to just 4 days. This is a major improvement, because it makes it feasible to cluster millions of compounds in a few days on a regular workstation or in a few hours when a small computer cluster is available. By running EI-Search on 80 CPUs on a computer cluster, we were able to cluster the entire PubChem Compound library in only a day. Because EI-Clustering spends most of the time running EI-Search, which runs in time sublinear in the size of the dataset, the compute time of EI-Clustering is subquadratic to the size of the dataset. Therefore, EI-Clustering scales much more efficiently to larger datasets than traditional methods. The superior speed of EI-Clustering comes at the cost of a larger memory footprint compared to the other methods. Most of the memory is consumed by its LSH index. For example, when clustering the 19 million PubChem Compound library, the LSH index requires around 13 GB of memory. Considering the performance of today's research workstations, this memory requirement appears to be manageable.

3.8 Availability of the programs and data

The EI-Search and EI-Clustering programs can be downloaded from http://chemmine.ucr.edu/ei/. The same web site features an online service using EI-Search for ultra-fast similarity searching of the PubChem Compound library with subsecond response time. In addition, the site provides access to the EI-Clustering results of the entire PubChem Compound library that are based on atom pair and PubChem fingerprint descriptors.

4 CONCLUSIONS AND FUTURE WORK

In this study, we have presented EI-Search and EI-Clustering as efficient methods for accelerating structure similarity searches and clustering of very large compound datasets. The acceleration is achieved by applying embedding and indexing techniques to represent chemical compounds in a high-dimensional Euclidean space and to employ ultra-fast prescreening of the compound dataset using the LSH-assisted nearest neighbor search in the embedding space. Our tests show that the method can dramatically reduce the search time of large databases, by a factor of 40–200 folds when searching the 100 closest compounds to a query. Recently published acceleration methods achieved only a 5.5-fold reduction in search time when using a Tanimoto threshold of 0.8 and up to 20-fold with a relatively restrictive threshold of 0.9 (Baldi et al., 2008; Swamidass and Baldi, 2007). Another limitation of these methods is their narrow utility spectrum that is currently restricted to fingerprint-based searches. In contrast to this, the EI-Search framework is designed to be useful for a wide spectrum of similarity measures. After embedding, EI-Search will run in most cases with comparable time efficiencies independent of the complexity of the similarity measure. This can be particularly useful for accelerating searches that use much more accurate, but computationally very expensive similarity measures, such as maximum common substructures or 3D approaches (Cao et al., 2008; Raymond et al., 2003; Willett, 2005).

By taking advantage of the fast similarity search speed of EI-Search, we developed EI-Clustering into an effective clustering method for very large datasets. The method accelerated the clustering of the three test datasets used in this study by 20–80 folds. Most importantly, the EI-Clustering made it feasible to cluster datasets of almost 20 million entries within acceptable time limits. Due to its subquadratic running time, the EI-Clustering method should scale well enough to cluster even larger datasets with tens or even hundreds of millions of objects.

In the future, we will expand the performance and utility spectrum of the EI-Search and EI-Clustering methods on several levels. First, several statistical methods will be employed to further improve the embedding algorithm by dynamically optimizing its parameters and the selection of the most effective reference compounds. Second, the EI-Search method will be tested and optimized for the usage of a variety of more complex similarity measures that are available for compound structures. Finally, additional clustering algorithms, besides Jarvis–Patrick clustering, will be incorporated into the EI-Clustering method.

Supplementary Material

[Supplementary Data]
btq067_index.html (740B, html)

ACKNOWLEDGEMENTS

We acknowledge the support from the Bioinformatics Core Facility, the Center for Plant Cell Biology (CEPCEB) and the Institute for Integrative Genome Biology (IIGB) at UC Riverside.

Funding: National Science Foundation (grants IOB-0420033, IOB-0420152, IGERT-0504249 and IIS-0711129).

Conflict of Interest: none declared.

REFERENCES

  1. Agrafiotis D. Stochastic proximity embedding. J. Comput. Chem. 2003;24:1215–1221. doi: 10.1002/jcc.10234. [DOI] [PubMed] [Google Scholar]
  2. Agrafiotis D, Lobanov V. An efficient implementation of distance-based diversity measures based on kd trees. J. Chem. Inf. Comput. Sci. 1999;39:51–58. [Google Scholar]
  3. Agrafiotis D, et al. Multidimensional scaling and visualization of large molecular similarity tables. J. Comput. Chem. 2001;22:488–500. [Google Scholar]
  4. Agrafiotis DK, Xu H. A self-organizing principle for learning nonlinear manifolds. Proc. Natl Acad. Sci. USA. 2002;99:15869–15872. doi: 10.1073/pnas.242424399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Austin CP, et al. NIH molecular libraries initiative. Science. 2004;306:1138–1139. doi: 10.1126/science.1105511. [DOI] [PubMed] [Google Scholar]
  6. Baldi P, et al. Speeding up chemical database searches using a proximity filter based on the logical exclusive OR. J. Chem. Inf. Model. 2008;48:1367–1378. doi: 10.1021/ci800076s. [DOI] [PubMed] [Google Scholar]
  7. Bentley J. Multidimensional binary search trees used for associative searching. Comm. ACM. 1975;18:509–517. [Google Scholar]
  8. Bohm C, et al. Searching in high-dimensional spaces: index structures for improving the performance of multimedia databases. ACM Comput. Surv. 2001;33:322–373. [Google Scholar]
  9. Brinkhoff T, et al. Proceedings of ACM SIGMOD Conference on Management of Data. New York, NY: ACM; 1993. Efficient processing of spatial joins using R-trees; pp. 237–246. [Google Scholar]
  10. Cao Y, et al. A maximum common substructure-based algorithm for searching and predicting drug-like compounds. Bioinformatics. 2008;24:i366. doi: 10.1093/bioinformatics/btn186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chang C, Lee R. A heuristic relaxation method for nonlinear mapping in cluster analysis. IEEE Trans. Syst. Man Cybernet. 1973;3:197200. [Google Scholar]
  12. Chen JH, et al. ChemDB update—full-text search and virtual chemical space. Bioinformatics. 2007;23:2348–2351. doi: 10.1093/bioinformatics/btm341. [DOI] [PubMed] [Google Scholar]
  13. Chen X, Reynolds C. Performance of similarity measures in 2D fragment-based similarity searching: comparison of structural descriptors and similarity coefficients. J. Chem. Inf. Comput. Sci. 2002;42:1407–1414. doi: 10.1021/ci025531g. [DOI] [PubMed] [Google Scholar]
  14. Cheng AC, et al. Structure-based maximal affinity model predicts small-molecule druggability. Nat. Biotechnol. 2007;25:71–75. doi: 10.1038/nbt1273. [DOI] [PubMed] [Google Scholar]
  15. Datar M, et al. Proceedings of the Twentieth Annual Symposium on Computational Geometry. New York, NY: ACM; 2004. Locality-sensitive hashing scheme based on p-stable distributions; pp. 253–262. [Google Scholar]
  16. Downs G, Barnard J. Clustering methods and their uses in computational chemistry. Rev. Comput. Chem. 2002;18:1–40. [Google Scholar]
  17. Faloutsos C, Lin K. Proceedings of the ACM SIGMOD Conference on Management of Data. New York, NY: ACM; 1995. FastMap: a fast algorithm for indexing, data-mining and visualization of traditional and multimedia datasets; pp. 163–174. [Google Scholar]
  18. Fu A, et al. Dynamic vp-tree indexing for n-nearest neighbor search given pair-wise distances. VLDB J. 2000;9:154–173. [Google Scholar]
  19. Gionis A, et al. Proceedings of the International Conference on Very Large Data Bases. San Francisco: Morgan Kaufmann Publishers Inc.; 1999. Similarity search in high dimensions via hashing; pp. 518–529. [Google Scholar]
  20. Girke T, et al. ChemMine. A compound mining database for chemical genomics. Plant Physiol. 2005;138:573–577. doi: 10.1104/pp.105.062687. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Haggarty SJ. The principle of complementarity: chemical versus biological space. Curr. Opin. Chem. Biol. 2005;9:296–303. doi: 10.1016/j.cbpa.2005.04.006. [DOI] [PubMed] [Google Scholar]
  22. Ihlenfeldt WD, et al. Enhanced CACTVS browser of the open NCI database. J. Chem. Inf. Comput. Sci. 2002;42:46–57. doi: 10.1021/ci010056s. [DOI] [PubMed] [Google Scholar]
  23. Irwin JJ, Shoichet BK. ZINC—a free database of commercially available compounds for virtual screening. J. Chem. Inf. Model. 2005;45:177–182. doi: 10.1021/ci049714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Katayama N. Proceedings of the ACM SIGMOD Conference on Management of Data. New York, NY: ACM; 1997. The SR-tree: an index structure for high-dimensional nearest neighbor queries; pp. 369–380. [Google Scholar]
  25. Kruskal J, Wish M. Multidimensional Scaling. Sage Publications; 1978. [Google Scholar]
  26. Lv Q, et al. Proceedings of the International Conference on Very Large Data Bases. VLDB Endowment; 2007. Multi-probe LSH: efficient indexing for high-dimensional similarity search; pp. 950–961. [Google Scholar]
  27. NIH Chemical Genomics Center. PubChem Fingerprint for JChem. 2009 Available at http://ncgc.nih.gov/resources/software.html (last accessed date March 1, 2010) [Google Scholar]
  28. Oprea TI. Chemical space navigation in lead discovery. Curr. Opin. Chem. Biol. 2002;6:384–389. doi: 10.1016/s1367-5931(02)00329-0. [DOI] [PubMed] [Google Scholar]
  29. Oprea TI, et al. Systems chemical biology. Nat. Chem. Biol. 2007;3:447–450. doi: 10.1038/nchembio0807-447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Raymond JW, et al. Comparison of chemical clustering methods using graph- and fingerprint-based similarity measures. J. Mol. Graph Model. 2003;21:421–433. doi: 10.1016/s1093-3263(02)00188-2. [DOI] [PubMed] [Google Scholar]
  31. Roweis S, Saul L. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
  32. Savchuk NP, et al. Exploring the chemogenomic knowledge space with annotated chemical libraries. Curr. Opin. Chem. Biol. 2004;8:412–417. doi: 10.1016/j.cbpa.2004.06.003. [DOI] [PubMed] [Google Scholar]
  33. Seiler KP, et al. ChemBank: a small-molecule screening and cheminformatics resource database. Nucleic Acids. Res. 2008;36(Database issue):351–359. doi: 10.1093/nar/gkm843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Sheridan RP, Kearsley SK. Why do we need so many chemical similarity search methods? Drug Discov. Today. 2002;7:903–911. doi: 10.1016/s1359-6446(02)02411-x. [DOI] [PubMed] [Google Scholar]
  35. Smellie A, et al. Visualization and interpretation of high content screening data. J. Chem. Inf. Model. 2006;46:201–207. doi: 10.1021/ci050404g. [DOI] [PubMed] [Google Scholar]
  36. Strausberg RL, Schreiber SL. From knowing to controlling: a path from genomics to drugs using small molecule probes. Science. 2003;300:294–295. doi: 10.1126/science.1083395. [DOI] [PubMed] [Google Scholar]
  37. Swamidass S, Baldi P. Bounds and algorithms for fast exact searches of chemical fingerprints in linear and sub-linear time. J. Chem. Inf. Model. 2007;47:302. doi: 10.1021/ci600358f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tenenbaum J, et al. A global geometric framework for nonlinear dimensionality reduction. Science. 2000;290:2319. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
  39. Vaidya P. An O (n log n) algorithm for the all-nearest-neighbors problem. Discrete Comput. Geom. 1989;4:101–115. [Google Scholar]
  40. Weber R, et al. Proceedings of the International Conference on Very Large Data Bases. IEEE; 1998. A quantitative analysis and performance study for similarity-search methods in high-dimensional spaces; pp. 194–205. [Google Scholar]
  41. Willett J. Similarity and Clustering in Chemical Information Systems. New York: John Wiley & Sons, Inc.; 1987. [Google Scholar]
  42. Willett P. Searching techniques for databases of two- and three-dimensional chemical structures. J. Med. Chem. 2005;48:4183–4199. doi: 10.1021/jm0582165. [DOI] [PubMed] [Google Scholar]
  43. Willett P. Chemical similarity searching. J. Chem. Inf. Comput. Sci. 1998;38:983–996. [Google Scholar]
  44. Xu H, Agrafiotis D. Nearest neighbor search in general metric spaces using a tree data structure with a simple heuristic. J. Chem. Inf. Comput. Sci. 2003;43:1933–1941. doi: 10.1021/ci034150f. [DOI] [PubMed] [Google Scholar]
  45. Zhu C. L-BFGS-B: Fortran subroutines for large-scale bound constrained optimization. ACM Trans. Math. Softw. 1997;23:550–560. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
btq067_index.html (740B, html)
btq067_1.pdf (438.1KB, pdf)

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES