Abstract
We applied partial least squares (PLS) as a novel multivariate statistical technique to examine neuropsychological correlates of magnetic resonance imaging (MRI) measures of brain volumes in a well studied sample of 15 male patients with chronic schizophrenia. In the current study, because the total number of measures far surpassed the total number of subjects, extant multivariate techniques such as canonical correlation could not be used to examine relationships among simultaneous measures of MRI and neuropsychology. Moreover, because MRI measures were expected to be highly inter-correlated, as would be neuropsychological test scores, extant multivariate statistical techniques would be substantially limited because they typically assume statistical independence among sets of measures. PLS, on the other hand, proved to be especially well suited to examining the relationships among function and anatomy measures in this sample, where statistically significant relationships were demonstrated that were entirely consistent with prior studies using univariate correlation techniques. In particular, statistically significant relationships emerged among sets of MRI temporal lobe measures and neuropsychological tests of verbal memory and categorization as well as among MRI frontal measures and neuropsychological tests of working memory.
Keywords: Partial least squares, Schizophrenia, Magnetic resonance imaging, Neuropsychology
Schizophrenia is almost always associated with marked changes in neuropsychological abilities, including those related to memory, attention, reasoning, and abstraction, all of which are presumed to reflect underlying disturbances in brain structure and/or function. Although these changes are typically viewed as evidence of a generalized neuropsychological impairment (e.g. Blanchard and Neale, 1994, some cognitive abilities have often been thought to be especially compromised by the disease process, including, for example, working memory operations involving the temporary maintenance and manipulation of information (Goldman-Rakic, 1991, 1992), and semantic processes of verbal categorization and mnemonic retrieval (Saykin et al., 1991; Nestor et al., 1993, 1998). These findings have led to what might be viewed as two complementary neuropsychological hypotheses with one positing a frontally mediated working memory impairment in schizophrenia (Goldman-Rakic 1991, 1992) and the other positing to a disease-related disturbance in semantic processing of the left-temporal lobe (Shenton et al., 1992; Nestor et al., 1998).
One of the more direct methods of testing these neuropsychological hypotheses would be to correlate performance on standardized neuropsychology measures with independent magnetic resonance imaging (MRI) of brain anatomy The rationale is that statistical correlational techniques provide an empirical means to capture the relationship of neuropsychological performance on one hand and MRI volumetric measures on the other hand Ideally multivariate correlation would be more statistically rigorous than univariate correlation which can only examine one pair of variables at a time For example canonical correlation might be used to quantify the, associations between sets of neuropsychological test scores and MRI volumetric measures. Alternatively, multiple regression might be used to determine the relationship between a set of MRI volumetric measures and a single neuropsychological test score.
Yet even these multivariate correlational techniques often represent less than optimal statistical models for capturing brain-behavior relationships in schizophrenia. One important limitation is that these techniques assume independence among measures, including those related to brain anatomy and brain function. This assumption becomes potentially problematic especially now that most neuropsychological models view various aspects of cognition as represented by correlated patterns of brain activity that are distributed across functionally and anatomically connected sets of brain structures that form unified neural networks. Such rather dynamic network models suggest that measures derived from either MRI or neuropsychological domains will be highly inter-correlated. In fact, neuropsychological measures are often highly inter-correlated, as are MRI volumetric measures (Nestor et al., 1998). However, in statistical terms, highly correlated measures are generally undesirable, reflecting multicolinearity and statistical redundancy. Thus, for both multiple regression and canonical techniques, multicolinearity poses a considerable obstacle because it reduces statistical power, so that genuine relationships between MRI and neuropsychological performance might go undetected.
The computational demands of these techniques also present significant challenges for studies examining MRI and neuropsychology in schizophrenia. For example, for canonical correlation the computational demands require that there be at least as many subjects as there are variables being measured. This is necessary because the calculation of a canonical correlation involves matrix inversion of the numerical linear weights that are represented in each matrix cell. However both MRI and neuropsychological methods generate relatively large sets of variables that might be statistically redundant but yet potentially theoretically revealing. Unfortunately, for canonical correlation to be applied to these rich sets of data, analysis will have to be limited to either extremely large samples or restricted sets of variables that are fewer than the number of subjects.
Bookstein and colleagues (Streissguth et al., 1993; Bookstein et al., 1996; McIntosh et al., 1997) have developed new statistical methods, collectively referred to as partial least squares (PLS), which can be used to characterize the relationship between two sets of multicolinear measures in relatively small subject samples For example McIntosh et al. (1996) used PLS to test the relationship between a set of measures obtained from brain images (patterns of activation) and measures indexing experimental demands (face encoding). Because PLS operates directly on each correlational coefficient, as opposed to each test score as would be the case for both canonical and regression procedures, it requires neither large samples nor statistical independence among measures. And unlike canonical correlation, which maximizes the correlation between blocks of measures, PLS maximizes the covariance between blocks.
Computationally, PLS carries out a singular value decomposition of a cross-correlational matrix, which is simply a matrix that is generated from two or more lists of ordinary statistical variables (e.g. neuropsychological and MRI). The singular value decomposition produces a series of paired singular vectors or latent variables (LV) The number of LVs produced is equal to the number of measures in the block with the fewest dimensions (measures). PLS computes the covariance between pairs of LVs using the statistic d the first singular value of the cross-correlational matrix. The sum of the squared singular values is equal to the sum of the squared elements of the original cross-correlational matrix. Successive pairs of LVs have the maximum covariance under the constraint that each of the pair is geometrically orthogonal to all LVs extracted previously for its own block. Hence successive pairs of LVs will have smaller covariances (decreasing values of d) Each LV is paired, so that one member of the pair is composed of saliences (or weights) corresponding to each measure in block 1 (e.g. neuropsychological test scores), and the other is composed of saliences for each measure in block 2 (e.g. MRI anatomical regions). Each vector of saliences is exactly proportional to the profile of correlations of the variables of its block, with the LV score corresponding to the other block.
PLS thus provides an economical and efficient statistical test for those studies that seek to model the functional characteristics of highly connected brain structures that form specific neural circuits and systems. Below we present an illustration of PLS analysis as applied to neuropsychological and MRI data generated from a well-studied sample of 15 male chronic SZ, chosen because previous studies had documented univariate correlations (e.g. Shenton et al., 1992; Nestor et al., 1993, 1998).
1. Method
1.1. Subjects and measures
To demonstrate the utility of PLS, we used neuropsychological and MRI data from a previously studied group of 15 chronic male schizophrenics. Neuropsychological measures included tests of various aspects of working memory, namely Hebb's recurring digits (Hebb, 1961), Trail Making Test (Lezak, 1995), and Alternating Semantic Categories (Gotham et al 1988; Downes et al., 1993). Measures of verbal memory and categorization included the similarities subtest of the Wechsler Adult Intelligence Scale-Revised (Wechsler, 1981), immediate and delayed recall versions of the verbal paired associates and the logical memory subtests of the Wechsler Memory Scale-Revised (Wechsler, 1987), and number of categories achieved from the Wisconsin Card Sorting Test (WCST, Heaton, 1981). Relative MRI volumetric measures included white and gray matter of right and left prefontal lobe, as well as right and left volumetric gray matter of superior temporal gyrus, posterior temporal lobe, and parahippocampal gyrus (see Shenton et al., 1992; Nestor et al., 1993, 1998; Wible et al., 1995).
1.2. Cross-correlation matrix
MRI and neuropsychological variables are each represented by a vector or block of ordinary statistical variables that form the cross-correlation matrix. The neuropsychological and MRI measures are referred to as X and Y, respectively. The elements of the X block are numbered from X1 to Xm, each representing a specific neuropsychological test. There are nine neuropsychological tests, X1–X9, so that m, used to denote rows equals 9. The elements of the Y list are numbered from Y1 to Yn, each representing a specific MRI volumetric measures. There are 16 MRI volumetric measures, so that n, used to denote columns, equals 16. We therefore have a matrix of 9 by 16. R will represent this cross-correlation matrix of neuropsychological and MRI measures. The elements of the cross-correlation matrix are Ri; which would be the correlation between a given neuropsychological test score and a specific volumetric MRI measure. PLS is designed to explain the cross-correlation matrix.
1.3. Single vs simultaneous measures
By itself, the cross-correlation matrix does not allow for the simultaneous examination of sets of correlated variables, nor does it provide a systematic method to examine the covariance between distinct sets of neuropsychological measures (e.g. categorization and memory) and MRI measures (e.g. left temporal lobe MRI volumes). The cross-correlation matrix does not provide a direct means to address questions regarding the functional (neuropsychological) characteristics of models of neural circuitry. It explains the variance of only one variable at a time.
1.4. Singular vectors of cross-correlation matrix R
The singular value decomposition of matrix R (neuropsychological test scores and MRI volumetric measures) produces a series of paired singular vectors or latent variables. In the case of the 9 (neuropsychological tests) by 16 (MRI measures) cross-correlation matrix R the singular value decomposition yields nine pairs of singular vectors or latent variables, because the smallest dimension in the cross-correlation matrix is 9. For ease of exposition we will refer to these paired singular vectors as latent variable pairs with latent variable A1 and B1 representing, respectively, the first pair of neuropsychological test scores and MRI volumetric measures. In contrast to the cross correlation matrix, the singular-value decomposition of the cross-correlation matrix provides a means to isolate specific relationships among interrelated sets of neuropsychological and MRI volumetric measures It explains the covariance pattern between neuropsychological and MRI measures.
1.5. Latent variables and saliences
These latent variables are paired, so that latent variable A is composed of m coefficients, one for each X (neuropsychological test score), and latent variable B is composed of n coefficients, one for each Y (MRI volumetric measures). These coefficients are referred to as saliences. The coefficients/saliences of either latent variable, A or B, are scaled so as to have squares that sum to 1. For each latent variable, a salience is weighted or loaded on the basis of its relationship with the other latent variable. For example, the salience of neuropsychological measure WCST is weighed, not solely on the basis of its relationship with the other neuropsychological tests, but also on the basis of its relationship with MRI measures. Thus whereas canonical correlation optimizes the correlation within a block of variables, PLS optimizes the covariance between blocks or pairs of latent variables. Likewise, whereas the interpretation of the coefficients of a canonical correlation will be limited by multicolinearity, the saliences PLS computes have meaning individually or collectively even when (indeed, especially when) the predictor block or the outcome block is intentionally multicolinear.
1.6. Goodness of fit
Does the solution generated from the singular value decomposition fit the original cross-correlation matrix R? Does the solution explain the cross-correlation matrix R? PLS computes the covariance of each pair of latent variables, as represented by the singular value d of the cross-correlation matrix R. The singular value d1 is the covariance between first pair of latent variables (A1, B1). For each of the nine pairs of latent variables, a singular value (d) is computed to reflect the covariance between the pairs of latent variables. The sum of the nine squared singular values is equal to the sum of the squared cross-correlation matrix R. The sum of the total of the squared cross-correlations in matrix R represents the total predictability of either block (e.g. neuropsychological) for the other block (e.g. MRI). To provide the proportion of the sum of the squared cross correlation matrix R explained by the first pair of latent variables, the first singular value (d1) is squared, and then divided by the sum of the square correlations in matrix R. Successive pairs of latent variables will have smaller covariances as measured by ds.
1.7. Test of significance
PLS uses a permutation test to assess the significance of the covariance of the first pair of latent variables (d1). The significance of the covariance of the obtained d1 is compared with the distribution of covariances (ds) arising from random permutations. Data are permuted 10,000 times to determine the likelihood that the obtained covariance (d1) is due to random perturbation.
2. Results
We applied PLS to explain the covariance in the cross-correlation matrix R of 9 neuropsychological tests and 16 MRI measures. The procedure involved four steps: (1) the computation of the cross-correlation between neuropsychological tests and MRI volume measures; (2) the computation of proportion of the sum of the squared cross-correlation matrix explained via singular value decomposition of that matrix; (3) extraction of the nine pairs of latent variables, each pair representing neuropsychological and MRI measures, with each composed of 9 and 16 saliences, respectively; and (4) testing significance of the covariance of the first singular value (d1) by comparing it with the distribution of covariances arising from random permutation tests.
2.1. Cross-correlation matrix R
We previously showed the 9 neuropsychological and 16 MRI cross-correlation matrix R generated from 15 schizophrenic patients produced significant relationships between several of the neuropsychological and MRI volumetric measures (Nestor et al., 1993, 1998). Poor scores on WCST correlated significantly with reduced volumes in left parahippocampal gyrus (r = 0.67, P < 0.01), right parahippocampal gyrus (r = 0.67, P < 0.01), left posterior superior temporal gyrus (r = 0.75 P < 0.01), right posterior superior temporal gyrus (r = 0.68 P < 0.01), and right posterior temporal lobe (r = 0.60 P < 0.05), Poor scores on the WMS-R test of associative memory correlated with reduced volumes in the left posterior superior temporal gyrus for immediate (r = 0.64 P<0.01) and delayed (r = 0.59, P < 0.05) recall. Slower performance on Trails A correlated significantly with reduced volumes in left (r = −0.59, P < 0.05) and right (r = 0.56, P<0.05) posterior superior temporal gyrus and right posterior temporal lobe (r =−0.63, P < 0.05). Slower performance on Trails B correlated significantly with reduced volume in frontal gray matter (r = −0.55, P< 0.05). Poor performance on Alternating Semantic Categories correlated significantly with reduced volumes in left frontal gray matter (r = 0.63, P < 0.05) and left frontal white matter (r = 0.66, P < 0.05), as did poor performance on Hebb's Recurring Digits (r = 0.58, P < 0.05).
2.2. Singular value decomposition
The singular value decomposition (SVD) of the cross-correlation matrix yielded nine pairs of latent variables. The singular value d provides an index of the covariance between each of these pairs. PLS produced the following nine singular values: d1 = 2.959, d2=1.503, d3 = 0.702, d4 = 0.531, d5 = 0.423, d6 = 0.344, d7 = 0.135, d8 = 0.092, and d9 = 0.024. If each of these values are squared, the sum of the squared singular values (12.19) is equivalent to the sum of the squared cross-correlation matrix. The ratio of a squared singular value over this sum provides the percentage of variance explained by the corresponding pairs of latent variables. For the first pair of latent variables this is 0.72% (8.756/12.19) and for the second pair of latent variables this is 0.19% (2.259/12.19). The first two pairs of latent variables account for 91% of the summed squared cross-correlation matrix R.
2.3. Latent variables and saliences
The singular value provides an index of the degree of covariation between a pair of latent variables. The first two pairs of latent variables are of critical importance in that they explained 91% of the summed squared cross-correlational matrix R. To understand the covariation between the first two pairs of latent variables (e.g. A1/neuropsychological, B1/MRI volumes), the saliences within each of the neuropsychological MRI latent variables need to be examined. The neuropsychological latent variables have 9 saliences, and the MRI latent variables have 16 saliences; that is each measurement has a corresponding salience. The saliences within a latent variable (e.g. neuropsychological) indicate which measurements are, in effect, driving the covariation with the corresponding latent variable (e.g. MRI).
Saliences above an arbitrary cutoff of 0.3 are reported (McIntosh et al., 1996). For the first pair of latent variables (i.e. neuropsychological/MRI), PLS computed a singular value (d1) of 2.959. Examination of the individual saliences corresponding to each measure indicated that for first neuropsychological latent variable highest saliences were WCST (s = 0.523), similarities (s = 0.464), Trails A (s = 0.430), Trails B (s = 0.315), and delayed recall for logical memory (s = 0.334). For the MRI latent variable highest saliences were left posterior superior temporal gyrus (s = 0.510), right parahippocampal gyrus (s = 0.436), right posterior superior temporal gyrus (s = 0.388) and left parahippocampal gyrus (s = 0.367). For the second pair of latent of variables, PLS computed a singular value (d2) of 1.503. The second pair of latent variables formed a different pattern of saliences, with high saliences for the neuropsychological latent variable occurring for Alternating Semantic Categories (s = 0.589), Hebb's Recurring Digits (s = 0.535), and Trails B (s = 0.378). For the MRI latent variable high saliences occurred for measures of left frontal gray matter (s = 0.673), right frontal gray matter (s = 0.486), and left frontal white matter (s = 0.474).
Figs. 1 and 2 present the relationship for each of the first two singular value decompositions of the cross-correlation matrix R. The values represent the outer product of the transposed matrix, multiplied by the singular value, which is 2.959 (d1) for Fig. 1 and 1.503 (d2) for Fig. 2. Fig. 1 underscores the strong relationship between categorization and memory and MRI temporal lobe volumes, whereas Fig. 2 shows the relationship of attention and MRI frontal lobe volumes.
Fig. 1.
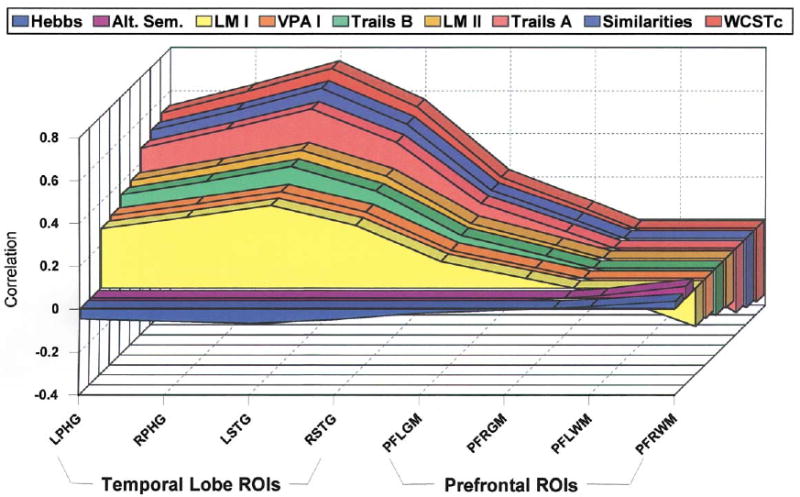
Correlation matrix approximated by first component of singular value decomposition. The values represent the outer product of the transposed matrix, multiplied by the singular value, which is 2.959(d1).
Fig. 2.
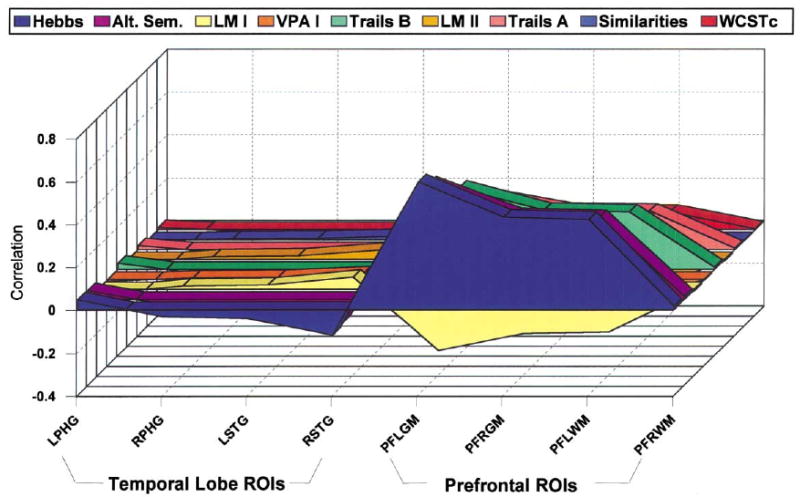
Correlation matrix approximated by second component of singular value decomposition. The values represent the outer product of the transposed matrix, multiplied by the singular value, which is 1.503 (d2).
2.4. Significance testing
The null hypothesis states that the first latent variable pair is ‘ill defined’, meaning that it is without any central tendency when considered as unit vectors in space. If rejected, the null hypothesis gives way to the experimental hypothesis that the first latent variable pair is ‘well-defined’, meaning that two latent variables covary systematically, and that this covariance ‘explains’ the cross-correlation matrix. PLS tests only the first latent variable pair by performing permutation tests. As such, PLS provides an omnibus test of significance, thereby avoiding the problem of multiple comparisons that often encumber other statistical analytic approaches used to determine brain-behavior relations. The permutation tests involve a Monte-Carlo like procedure whereby the cross-correlation matrix is randomly reordered. For each permutation, the first singular value is computed, and after 10,000 permutations, a probability value can be assigned to the obtained d, which will represent like the likelihood that the obtained d is due to random chance. This permutation testing does not rely on distributional assumptions that are typical of most statistical methods. The obtained salience (d1 = 2.959) achieved a high level of significance (P < 0.01).
3. Discussion
The current study illustrated the application of PLS for identifying relationships between MRI structural measures of brain anatomy and neuropsychological test scores in a relatively small subject sample of patients with schizophrenia. Under these circumstances the statistical problem may be viewed as twofold. One is that measures within each of these domains are often highly correlated as would be expected for both brain anatomy and neuropsychological function. Statistically, such interdependence among measures of a domain is often described in terms of redundancy and multicolinearity. The interdependence typically and substantially reduces statistical power of multivariate techniques to reveal genuine relationships between distinct domains. The second statistical problem is the ratio of number of measures to sample size. In MRI and neuropsychological studies, because the number of measures often surpasses the number of subjects, multivariate statistical techniques, such as canonical correlation and factor analysis cannot be computed.
PLS thus addressed both of these statistical problems inherent in the analysis of the neuropsychological MRI data of 15 chronic schizophrenics. It provided a statistically powerful technique to map neuropsychological test scores onto MRI anatomical regions in a small sample of patients with chronic schizophrenia. PLS did so by capitalizing on the intrinsic multicolinearity within each of the neuropsychological and MRI blocks of measures. In the current study, PLS revealed invaluable information that might otherwise had been lost due to the computational limitations and statistical assumptions of extant multivariate techniques, such as factor analysis and canonical correlation.
PLS might be viewed as most analogous to factor analysis, as each provides solutions that is subject to interpretation. Both techniques reduce complex correlational matrices. For factor analysis, the correlational matrix is reduced to a set of factors, each composed of constituent factor loadings, and each explaining a corresponding proportion of statistical variance. For PLS, the cross-correlational matrix is reduced to a set of latent variables, each composed of saliences, and each explaining a corresponding proportion of variance. However, PLS and factor analysis differed not only in that computational procedures allow PLS but not factor analysis to be applied to samples with fewer subjects than measures, but also in terms of methods used to test statistical significance.
Among the more telling criticism of factor analysis is the absence of any objective means to test statistical significance of an obtained factor solution. The extent to which a factor solution might be expected to be found due to chance factors is typically only indirectly addressed. This might be done so, for example, by conducting a so-called confirmatory factor analysis on a second sample of subjects independent of the first sample. If the second factor solution replicates or confirms the first solution then the finding might be viewed as unlikely due to chance. The important point is that the similarity of the two solutions is not computed statistically, rather it is more or less a matter of judgment. By contrast, PLS provides a rigorous permutation test of significance. In the current study, statistical significance underscored that the observed solution to be one that would be highly unlikely due to chance. This clearly represents an additional important advantage of PLS over factor analysis. In addition, by providing a rigorous and objective test of statistical significance, PLS provides a fairly compelling answer to the criticism that it violates two paragons of probability statistics, those being measurement independence and large sample size.
The next question to consider about this new technique speaks to the issue of clinical relevance and theoretical meaning of the obtained, statistically significant PLS findings. In this regard, the current PLS analysis not only demonstrated statistical significant but also pointed to theoretically meaningful relationships between selective sets of neuropsychological test scores and selective sets of corresponding MRI measures of brain anatomy. These relationships conformed closely to those demonstrated by univariate correlation on the same data set (Shenton et al., 1992; Nestor et al., 1993, 1998). In the current PLS analysis, the findings pointed to two important neuropsychological and MRI relationships, each perhaps representative of disease related disturbances in distinct neural networks that support different aspects of higher-order cognition.
First, the strongest relationship emerged for the first latent variable pair of neuropsychological test scores of verbal memory, categorization, and abstraction with the MRI volumetric measures of temporal lobe regions. The first singular pair of latent variables revealed a strong and specific relationship between schizophrenic deficits on tests of memory (e.g. logical memory subtest — II of the WMS-R), executive functions (WCST), and categorization (e.g. similarities subtest of the WAIS-R) and reduced temporal lobe volumes. There is also evidence that some attentional problems (e.g. Trails A and B), are related to reduced temporal lobe volumes. However, by far the strongest contributors as reflected by saliences or weights of greater than 0.45 were neuropsychological measures of categorization and executive functions, on one hand, and left posterior superior temporal gyrus MRI volume on the other hand. In fact, saliences for these measures ranged from 0.464 for WAIS-R similarities, 0.494 for WCST, to 0.510 for left posterior superior temporal gyrus, and these values far exceeded the arbitrary cutoff of 0.30 used by McIntosh et al. (1996) in functional imaging studies.
These saliences therefore suggested that cognitive functions related to neuropsychological test performance on WCST and similarities may be especially important in understanding reduced volume of left superior temporal gyrus in this sample of patients with chronic SZ. While both these tests assess a variety of cognitive functions one common denominator may be related to a fundamental ability to generate and to use verbal categories. For the similarities subtest of the WAIS-R, this is clearly evident in the selection of the test items, as for example the question of how air and water are like. Likewise, even for the WCST, which is typically characterized as a measure of executive functions, an ability to generate and to use categories represent one of the key processing demands. Categorization is generally viewed as a basic information processing operation that is crucial for memory and perception, and which is supported by structures related to superior temporal gyrus, such as superior temporal sulcus (Kolb and Winshaw, 1996). Failure to generate and to use categories might therefore represent an important functional consequence of reduced volumes of the left temporal gyrus in this sample of chronic schizophrenic patients.
The second singular pair of latent variables might be labeled as a frontal lobe factor in contrast to a temporal lobe factor of the first singular pair. As support for this labeling, the only saliences greater than 0.30 were confined to MRI volumetric measures of gray matter of left (s = 0.673) and right (s = 0.486) frontal lobe and white matter of left frontal lobe (s = 0.474). These corresponded to saliences for a selected set of neuropsychological measures, namely Hebb's Recurring Digits (s = 0.589), Alternating Semantic Categories (s= 0.535), and Trails B (s = 0.378). These neuropsychological tasks all impose considerable time pressure demands either through short term memory load of Hebb's Recurring Digits or the speeded response required for Alternating Semantic Categories and Trails B. Moreover, time pressure builds up by the nature of the demands these tasks placed on temporary storage, rehearsal, rapid switching, mental tracking, and inhibition (see Kahneman, 1973). All of these operations represent key operations of working memory (Baddeley, 1992; Cantor and Engle, 1993), and have been linked to frontal lobe activation through recent functional imaging studies (D'Esposito et al., 1998; Jonides et al., 1998). Thus, in the current study, the high saliences for these measures corresponded to those of frontal but not temporal lobe MRI volumes. Such a pattern of covariation would not only be consistent with studies pointing to the importance of frontal lobe to supporting working memory processes, but might also be viewed as evidence of the potential role of failed frontally mediated working memory processes in neuropsychological disturbances of schizophrenia.
To summarize the current study illustrated the applicability and suitability of a novel statistical procedure, known as PLS, to the problem of often statistically redundant, colinear measures of brain anatomy and neuropsychology in schizophrenia. A relatively new technique that has been used in teratology (Streissguth et al., 1993; Bookstein et al., 1996) and more recently in functional brain imaging studies of normal (McIntosh et al., 1996) and schizophrenic subjects (O'Donnell et al., 1999), PLS is eminently suited to problems in which the number of measures exceeds the number of subjects, as is often the case in costly MRI studies of patients with schizophrenia. Rather than losing potentially invaluable information due to the often restrictive statistical assumptions of extant multivariate procedures, PLS capitalize on systematic covariation of simultaneous measures and then provides an objective means to test the statistical significance of the obtained solution. As such, PLS promises to be a highly statistically powerful yet sufficiently rigorous and conservative analytical procedure to test neuropsychological hypotheses of schizophrenia.
Acknowledgments
Supported by MERIT Awards from the Department of Veterans Affairs Medical Research Service (Dr McCarley and Dr Shenton), NIMH grants MH-50740, MH-01110 (Dr Shenton), and MH-40799 (Dr McCarley), and Young Investigator Awards to both Dr Nestor and Dr O'Donnell from the National Alliance for Research on Schizophrenia and Depression.
References
- Baddeley A. Working memory. Science. 1992;225:556–559. doi: 10.1126/science.1736359. [DOI] [PubMed] [Google Scholar]
- Blanchard JJ, Neale JM. The neuropsychological signature of schizophrenia: generalized or differential deficit? Am J Psychiat. 1994;151:41–48. doi: 10.1176/ajp.151.1.40. [DOI] [PubMed] [Google Scholar]
- Bookstein FL, Sampson PD, Streissguth AP, Barr HM. Exploiting redundant measurement of dose and development outcome: new methods from the behavioral teratology of alcohol. Dev Psychol. 1996;32:404–415. [Google Scholar]
- Cantor J, Engle RW. Working-memory capacity as long term memory activation: an individual difference approach. J Exp Psychol: Learn Mem Cogn. 1993;19:1101–1114. doi: 10.1037//0278-7393.19.5.1101. [DOI] [PubMed] [Google Scholar]
- D'Esposito M, Aguirre OK, Zarahan E, Ballard D. Functional MRI studies of spatial and nonspatial working memory. Cognitive Brain Res. 1998;7:1–13. doi: 10.1016/s0926-6410(98)00004-4. [DOI] [PubMed] [Google Scholar]
- Downes JJ, Sharp HM, Costall BM, Sagar HJ, Howes J. Alternating fluency in Parkinson's disease. Brain. 1993;116:887–902. doi: 10.1093/brain/116.4.887. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Prefrontal cortical dysfunction in schizophrenia: the relevance of working memory. In: Carroll BJ, Barrett JE, editors. Psychopathology and the Brain. Raven Press; New York: 1991. [Google Scholar]
- Goldman-Rakic PS. Working memory and the mind. Sci Am. 1992:111–117. doi: 10.1038/scientificamerican0992-110. Special issue. [DOI] [PubMed] [Google Scholar]
- Gotham AM, Brown RG, Marsden CD. Frontal cognitive function in patients with Parkinson's disease on and off levodapa. Brain. 1988;111:299–321. doi: 10.1093/brain/111.2.299. [DOI] [PubMed] [Google Scholar]
- Heaton RK. Odessa. Psychological Assessment Resources; 1981. Wisconsin Card Sorting Test Manual. [Google Scholar]
- Hebb DO. Distinctive features of learning in the higher animal. In: Delafresnage JF, editor. Brain Mechanisms and Learning. Blackwell Scientific Publications; Oxford: 1961. [Google Scholar]
- Jonides J, Smith EE, Marshuetz C, Koeppe RA, Reuter-Lorenz PA. Inhibition of verbal working memory revealed by brain activation. Proceedings of the National Academy of Sciences. 1998;95:8410–8413. doi: 10.1073/pnas.95.14.8410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahneman D. Attention and Effort. Prentice-Hall; Englewood Cliffs, NJ: 1973. [Google Scholar]
- Kolb B, Winshaw IQ. Fundamentals of Human Neuropsychology. 4th. Freeman; New York: 1996. [Google Scholar]
- Lezak MD. Neuropsychological Assessment. Oxford University Press; New York: 1995. [Google Scholar]
- McIntosh AR, Bookstein FL, Haxby JV, Grady CL. Spatial pattern analysis of functional brain images using partial least squares. Neuroimage. 1996;3:143–157. doi: 10.1006/nimg.1996.0016. [DOI] [PubMed] [Google Scholar]
- McIntosh AR, Nyberg L, Bookstein F, Tulving E. Differential connectivity of prefrontal and medial temporal cortices during episodic memory retrieval. Hum Brain Mapping. 1997;5:323–327. doi: 10.1002/(SICI)1097-0193(1997)5:4<323::AID-HBM20>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Nestor PG, Shenton ME, McCarley RW, Haimson J, Smith RS, O'Donnell BF. Neuropsychological correlates of MRI temporal lobe abnormalities in schizophrenia. Am J Psychiat. 1993;150:1849–1855. doi: 10.1176/ajp.150.12.1849. [DOI] [PubMed] [Google Scholar]
- Nestor PG, Shenton ME, Wible CW, Hokama H, O'Donnell BF, Law S, McCarley RW. A neuropsychological analysis of schizophrenic thought disorder. Schizophrenia Res. 1998;29:217–225. doi: 10.1016/s0920-9964(97)00101-1. [DOI] [PubMed] [Google Scholar]
- O'Donnell BF, McCarley RW, Potts GF, Salisbury DF, Nestor PG, Hirayasu Y, Niznikiewicz MA, Barnard J, Shen ZJ, Weinstein DM, Bookstein FL, Shenton ME. Identification of neural circuits underlying P300 abnormalities in schizophrenia. Psychophysiology. 1999;36:388–398. doi: 10.1017/s0048577299971688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saykin AJ, Gur RE, Mozley PD, Mozley LH, Resnick SM, Kester DB, Stafiniak P. Neuropsychological function in schizophrenia. Selective impairment in memory and learning Arch General Psychiat. 1991;48:618–624. doi: 10.1001/archpsyc.1991.01810310036007. [DOI] [PubMed] [Google Scholar]
- Shenton ME, Kikinis R, Jolesz FA, Pollak SD, LeMay M, Wible CG, Hokama H, Martin J, Metcalf D, Coleman M, McCarley RW. Abnormalities of the left temporal lobe and thought disorder in schizophrenia: a quantitative magnetic resonance imaging study. N Engl J Med. 1992;327:604–612. doi: 10.1056/NEJM199208273270905. [DOI] [PubMed] [Google Scholar]
- Streissguth AP, Bookstein FL, Sampson PD, Barr HM. The Enduring Effects of Prenatal Alcohol Exposure on Child Development. University of Michigan Press; Ann Arbor: 1993. [Google Scholar]
- Wechsler D. Wechsler Adult Intelligence Scale - Revised. Harcourt Brace Jovanovich; New York: 1981. [Google Scholar]
- Wechsler D. Wechsler Memory Scale - Revised. Psychological Corporation; New York: 1987. [Google Scholar]
- Wible C, Shenton ME, Hokama H, Kikinis R, Jolesz F, Metcalf D, McCarley RW. Prefrontal cortex and schizophrenia: a quantitative MRI study. Arch Gen Psychiat. 1995;52:279–288. doi: 10.1001/archpsyc.1995.03950160029007. [DOI] [PubMed] [Google Scholar]


