Discrete nonparametric algorithms for outlier detection with genomic data

Abstract

In high-throughput studies involving genetic data such as from gene expression microarrays, differential expression analysis between two or more experimental conditions has been a very common analytical task. Much of the resulting literature on multiple comparisons has paid relatively little attention to the choice of test statistic. In this article, we focus on the issue of choice of test statistic based on a special pattern of differential expression. The approach here is based on recasting multiple comparisons procedures for assessing outlying expression values. A major complication is that the resulting p-values are discrete; some theoretical properties of sequential testing procedures in this context are explored. We propose the use of q-value estimation procedures in this setting. Data from a gene expression profiling experiment in prostate cancer are used to illustrate the methodology.

1 Introduction

Genomic technologies have permeated scientific experimentation, especially in the area of cancer research (Ludwig and Weinstein, 2005). One of the major tasks using these assays is to find genes that are differentially expressed between two experimental conditions. The simplest example is to find genes that are up- or down-regulated in cancerous tissue relative to healthy tissue. Assessing differential expression in this setting leads to a massive multiple comparisons problem that results from performing thousands of univariate tests for each gene. This has led to an explosion of literature on statistical methods for differential expression in genomic studies; see Ge et al. (2003) for a recent review on the topic.

Many authors have advocated for control of the false discovery rate (FDR) (Benjamini and Hochberg, 1995) relative to the traditional familywise type I error (FWER). Less thought has been provided on the choice of test statistic to use. The two most commonly used statistics in the two-sample problem are the t-test and the Wilcoxon rank sum test.

Recently, Tomlins et al. (2005) identified a gene fusion in prostate cancer. They discovered it by making the following observation. For certain genes, only a fraction of samples in one group were overexpressed relative to those in the other group; the remaining samples showed no evidence of differential expression. They used a method called Cancer Outlier Profile Analysis (COPA) to rank such genes using expression data generated by microarrays. Using such a score identified one of the genes involved in the fusion event. Tomlins et al. (2005) proposed a statistic but gave no way of assessing its significance statistically. Recently, Tibshirani and Hastie (2007) and Wu (2007) have proposed modifications of two-sample t-tests to address the same problem. Ghosh and Chinnaiyan (2009) have cast these procedures into a general statistical framework.

In this article we consider discretized versions of the procedures given in Ghosh and Chinnaiyan (2009). They linked outlier detection to the multiple testing problem. While many authors have studied and developed methods for controlling the false discovery rate and related metrics (e.g Efron et al., 2001; Genovese and Wasserman, 2004), they all presume that the test statistics being used come from a continuous distribution. Consequently, under the null hypothesis, the p-values for the test statistics are distributed as a Uniform(0,1) random variable. This fact no longer holds when the test statistics are discrete. One key issue we address here is how to perform multiple testing with discrete test statistics. We review previous work and show that sequential testing procedures are unstable in a particular technical sense. We then describe algorithms that effectively smooth the discrete p-values in order to perform false discovery rate estimation, for which we prove results about asymptotic conrol of the false discovery rate.

We also consider the situation of more than two groups. This was studied by Liu and Wu (2007) using modifications of two-sample testing methodologies. In this article, we address the problem in two different directions. The first is that we will use multiple testing metrics for identification of outliers. As in Ghosh and Chinnaiyan (2009), we cast the relevant statistical problem as one of outlier detection and propose a hypothesis testing framework for outlier detection. Note that while outlier has a very specific statistical interpretation as being aberrant from the usual population, for our purposes, genes with high degrees of ‘outlyingness’ are of great interest. Second, we will again have discrete test statistics, so the multiple testing adjustments proposed by Liu and Wu (2007) do not apply here.

The paper is structured as follows. In section 2, we describe the data setup and formulate the statistical model for outlier detection. We also show how to formulate outlier detection as a hypothesis testing problem, which leads to a natural link with multiple testing procedures. Section 3 reviews previous methods for multiple testing with discrete statistics and discuss a notion of instability for sequential testing procedures. We then propose a false discovery rate estimation procedure in Section 4, along with its extension to multiple groups and a result proving that it asymptotically controls the false discovery rate. In Section 5, the proposed methods are applied to data from a prostate cancer gene expression study. Results from a limited simulation study are given in Section 6. We conclude with some discussion in Section 7.

2 Preliminaries

2.1 Data and outlier detection/multiple testing paradigm

The data consist of (Y_gji), where Y_gji is the gene expression measurement on the gth gene for the ith subject in group j, g = 1, …, G, j = 0, …, (J − 1), i = 1, …, n_j. Let $n={\sum }_{j=0}^{J-1}{n}_j$. The indexing for j is such that we have J groups. We will refer to the group with j = 0 as the baseline group.

For a given gene g, we wish to identify the samples that have outlying values with respect to the gene. We assume that we will use the samples with j = 0 (i.e., the baseline group) as the baseline distribution with which to assess ‘outlyingness.’ Following what was done in Tomlins et al. (2005), we will examine outliers in one direction. This is done because of the idea that biologically, oncogenes might be either overamplified or underamplified but not both. This implies that the tests will be one-sided.

We can phrase this as the following hypothesis testing problem: test the hypothesis $H_0^i$: the ith individual does not have outlying expression values of gene g relative to the baseline population against $H_1^i$: the ith diseased individual does have outlying expression values of gene g relative to the baseline population. For each gene we can perform such a test. We can summarize the results of n_j such tests for the jth group (j = 1, …, J − 1) in Table 1:

Table 1.

Outcomes of n tests of hypotheses regarding outlyingness

	Decide Outlier	Decide Non-outlier	Total
True Non-Outlier	W	V	N0
True Outlier	T	A	N1
	R	Q	nj

Note: The rows represent each sample being a true outlier or a true non-outlier. In the columns, Decide Outlier means that we reject $H_0^i$; Decide Non-outlier means that we fail to reject $H_1^i$. These are the results for a single gene; dependence on gene is suppressed in the notation.

In Table 1 everything is unobserved except for n_j and (R, Q). This is because the rows of the table represent the true status of the samples and are unknown to the data analyst. Table 1 shows a correspondence between outlier detections with testing multiple hypotheses. Based on the table, we can construct appropriate error measures to control. There are two kinds of errors that can be made, corresponding to the off-diagonal elements in Table 1. One error is to declare a sample to be an outlier when it is not an outlier in truth. The second is to not declare a sample as an outlier when in fact it is an outlier. Most error rate measures control the first type of error. Two popular error measures to control are the familywise type I error (FWER) (Shaffer, 1995) and the false discovery rate (FDR) (Benjamini and Hochberg, 1995). In words, the FWER is the probability of making at least one false declaration of a sample being an outlier, while the FDR is the average number of false outliers among the samples declared to be outliers. Using the notation of Table 1, FWER equals Pr(V ≥ 1), while the FDR is E[V/Q|Q > 0]Pr(Q > 0).

We will use multiple testing ideas to develop outlier detection procedures. Everything is done for a fixed gene g. We first estimate F_0g using the empirical cumulative distribution function of Y_gi in the baseline population, i = 1, …, n₀. This yields an estimator ${\widehat{F}}_{0g}(y)={\sum }_{i=1}^{n_0}I(Y_{g0i}\le y)/n_0$. Then we transform the gene expression measurements for the other samples by p̃_gji = 1 − F̂_0g(Y_gji), j = 1, …, (J − 1). We then use the p̃_gji to test $H_0^i$ versus $H_1^i$; in particular smaller values indicate evidence against $H_0^i$ for the gth gene in group j. Note that if F_0g were known and continuous, then 1 − F_0g(Y_gji) would have a uniform(0,1) distribution under $H_0^i$ and a distribution of a stochastically smaller random variable under $H_1^i$.

For a fixed gene, we can use multiple testing ideas to identify outliers. Three popular approaches are Bonferroni’s method, Sidák’s procedure and the Benjamini-Hochberg method. Bonferroni’s procedure declares observation i an outlier if p̃_gji ≤ α/n_j. Sidák’s procedure declares it to be an outlier if p̃_gji ≤ 1 − (1 − α)^1/n_j. Finally the Benjamini-Hochberg procedure proceeds as follows:

1. Set an error rate α.

2. Sort the p̃_gji in increasing order, p̃_gj(1) ≤ p̃_gj(2) ≤ ··· ≤ p̃_gj(_nj).

3. Take as outliers the samples corresponding to p̃_gj(1), …, p̃_gj(k̂), where k̂₌ max{1 ≤ i ≤ n_j: p_gj(i) ≤ iα/n_j}. If no such k̂ exits, conclude that there are no outliers.

Conditional on F̂_0g, all the tests for outliers are independent. This implies that the Bonferroni and Sidák procedure will control the FWER, while the Benjamini-Hochberg procedure will control the FDR exactly for the multiple outlier hypothesis tests for a fixed gene. Observe that the multiplicity being adjusted for in this step of the algorithm is the number of samples in group j.

Suppose we now wish to make gene-specific inferences regarding outlierness. If we use the Bonferroni procedure, we compute for j = 1, …, (J − 1).

$$T_{gj}^B=\sum _{i=1}^{n_j}I\{{\stackrel{\sim }{p}}_{\mathit{gji}}\le \alpha /n_j\}.$$ (1)

For the Sidák procedure, it is

$$T_{gj}^S=\sum _{i=1}^{n_j}I\{{\stackrel{\sim }{p}}_{\mathit{gji}}\le 1-{(1-\alpha )}^{n_j}\},$$ (2)

while for the Benjamini-Hochberg procedure the score would be

$$T_{gj}^{BH}=\widehat{k},$$ (3)

defined in the previous paragraph.

To derive the null distribution of (1), (2) and (3), we adopt a conditional approach in which we permute the labels of the jth group versus the baseline group conditional on the observed row and sum totals corresponding to Table 1. This is analogous to a Fisher’s exact test-type in which a hypergeometric distribution is used to calculate a p-value. To be precise, for gene g in group j (g = 1, …, G; j = 1, …, (J − 1)), we apply a one-sided Fisher’s exact test to the contingency table

$$\left[\begin{array}{cc}{T}_{gj}^M& n_j-T_{gj}^M\\ 0& n_0\end{array}\right],$$

where the superscript M refers to B, S or BH. This leads to p-values $p_{gj}^M$, g = 1, …, G, j = 1, …, (J − 1).

For a fixed j, we now have G p-values for which we need to account for multiple comparisons; the multiplicity is now the number of genes. This is the more familiar domain for differential expression analyses and multiple testing adjustments. There are two notable differences. First, we used the estimated distribution in the group j = 0 to calculate the “p-values” so that a known theoretical distribution is not being used. This is different from much of the previous literature on multiple testing. A second major difference is that the p-values obtained are highly discrete. For example, if n_j = 10 for all j, then the p-value distribution will be discrete and only take one of ten possible values. Examples of discrete p-value distributions can be found in the data analysis done in Section 5. The majority of the recent statistical literature on multiple testing has not dealt with this situation, with some notable exceptions, which we describe next.

3 Multiple testing procedures with discrete data

3.1 Sequential testing procedures

In this section, we assume that J = 2 and thus drop the j subscript from the definitions of $T_{gj}^M$ and $p_{gj}^M$ in the previous section. It is possible to come up with a more powerful testing procedure by exploiting the discrete nature of the test statistics. This was also done by Tarone (1990) and Gilbert (2005) in related settings. To do this, first note that the minimum achievable significance level for a score is

$${\alpha }_g^{\ast }=\left(\begin{array}{c}{n}_1\\ T_g^M\end{array}\right)/\left(\begin{array}{c}n\\ T_g^M\end{array}\right).$$

Note that the significance level is one-sided, as outlyingness is based on extreme expression measurements in one direction.

We now review the modified procedures proposed by Tarone (1990) and Gilbert (2005). The modified Bonferroni procedure would work in the following way. For each g = 1, …, G, let n(g) be the number of tests for which ${\alpha }_g^{\ast }<\alpha /g$, and let N be the smallest value of g such that n(g) ≤ g. Let $R_N=\{1\le i\le G:{\alpha }_i^{\ast }<\alpha /N\}$. For i ∈ R_N, one rejects the ith null hypothesis if $p_i^M<\alpha /N$. By the arguments in Tarone (1990), this procedure will control the FWER. The modified Sidák procedure would work in a similar way, except that we would reject the ith null hypothesis if $p_i^M<1-{(1-\alpha )}^{1/N}$. Both procedures control the FWER and also the FDR. The modified Benjamini-Hochberg procedure (Gilbert, 2005) would proceed in the following way:

• For i ∈ R_N, sort the p-values in increasing order $p_{(1)}^M\le p_{(2)}^M\le \cdots p_{(R)}^M$, where R is the cardinality of R_N.

• Reject the null hypotheses corresponding to $p_{(1)}^M,\dots ,p_{(D)}^M$, where

  $$D=max\{1\le i\le R:p_{(i)}^M\le i\alpha /R\}.$$

  If no such D exists, no hypotheses are rejected.

Assuming the same conditions as in Benjamini and Hochberg (1995), the modified procedure will also control the false discovery rate at level α.

Before describing our proposed multiple testing procedure, we discuss one issue that has not been explored very much in the mutliple testing literature, which we term stability.

3.2 Stability

While we have proposed several multiple testing procedures for gene-specific inference, one issue we have not considered so far is their variability. It is desirable to have testing procedures that have small variability. One comment about the Benjamini-Hochberg procedure is that it is claimed to be more powerful than a single-step procedure like the Bonferroni or Sidák procedure because the former controls the FDR, while the latter controls FWER. However, there is a certain instability in the Benjamini-Hochberg procedure that does not exist for the Sidák or Bonferroni procedure. Assume that R is known. For ease of presentation, we assume that J = 2 and that R = n₁. The multiple testing procedure can be expressed as a function f: [0, 1]^R → Z, where Z is the set {0, 1, 2, …, R}. The function f inputs the n₁ –dimensional vector of p-values and outputs the number of hypotheses rejected. We have the following result:

Proposition

Let ε > 0 be an arbitrary constant (a) For the Bonferroni and Sidák procedures, for all p and all ε > 0,

$$\underset{\epsilon }{max}\mid f(\mathbf{p})-f({\mathbf{p}}_{\epsilon }^i)\mid =1,$$

where ${\mathbf{p}}_{\epsilon }^i=\mathbf{p}$ with the ith component equaling p_i + ε.

(b) For the Bejamini-Hochberg procedure, there exists p such that for all ε > 0,

$$\mid f(\mathbf{p})-f({\mathbf{p}}_{\epsilon }^i)\mid =R.$$

Proof

For (a), perturbing the ith p-value only affects its rejection decision and not that of the other hypotheses. We prove (b) by construction. Define a configuration of p-values whose jth component is p_j ≡ α. Then the Benjamini-Hochberg procedure will reject all hypotheses, since the maximal index k for which p_(k) ≤ kα/R is in fact R. However, if we now consider pⁱ with any ε > 0, then the Benjamini-Hochberg procedure will fail to reject any null hypotheses. This because pⁱ will consist of (R − 1) p-values equalling α and the largest p-value equalling α + ε.

Remark 1

The result of the proposition suggests that there is an inherent stability of sequential multiple testing procedures. In particular, part (b) of the proposition implies the possibility of a slight perturbation in the p-values can lead from rejecting all null hypotheses to rejecting no hypotheses. By contrast, part (a) shows that this will never happen for a single-step testing procedure. This instability will potentially manifest itself in the Benjamini-Hochberg procedure having a greater variance in terms of the number of hypotheses rejected relative to a single-step procedure.

Remark 2

The result of the proposition applies to any multiple testing error metric. In particular, this result applies to FWER and generalized FWER procedures as well.

Remark 3

The proposition makes no assumption about the dependence structure among the p-values. Observe that f itself has a distribution. If we wished to make distributional statements about f (e.g., its mean and variance), then this would require making assumptions on the joint distribution of the p-values.

Remark 4

The proposition is valid for any sample size. An implication of the proposition is that the Benjamini-Hochberg procedure is not ‘continuous’ in a certain sense; it is possible for a small and local perturbation in the p-values to lead to a drastically different result in terms of the number of hypotheses rejected. By contrast, this never happens for the single-step (Bonferroni and Sidák methods) because the local perturbation only affects the decision to reject one p-value. It turns out that the problem does not happen to be with the error rate being controlled (FDR versus FWER) but rather the use of sequential multiple testing methods versus single-step procedures.

Remark 5

If p-values were continuous, then the configuration described in the proof of part (b) of the proposition will have probability zero because ties have zero probability. However, with discrete p-values, the probability of ties is nonzero, which leads to the instability issue.

Remark 6

A referee brought up the interesting issue of whether the stability problem of the Benjamini-Hochberg procedure is because of the discreteness of the test statistics or because of the dependence of the tests. A recent result by Hall and Wang (2009) establishes a result about asymptotic tail independence for joint distributions of test statistics. However, they present a counterexample in their Section 2.1. when their result is not applicable which for our setting corresponds to the p-value equalling one with a positive probability. Since this is possible here due to the discreteness of the tests, it appears that the discreteness of the test statistics would invalidate the Hall and Wang (2009) result.

In particular, the stability argument also applies to the method of outlier detection described in the previous section. This is because in our experience, for the discrete test statistics, we have found that the Benjamini-Hochberg procedure described in Section 2.1 tends to yield much higher variability results than the Bonferroni and Sidák methods, so here and in the sequel, we will use the Bonferroni method for outlier detection.

Other criticisms of the approach of Gilbert were brought up by Pounds and Cheng (2006). We will adapt their approach for false discovery rate estimation to our problem. Unlike Pounds and Cheng (2006), our null distribution is estimated from the data, while they will either use a parametric model or permutation testing to derive their null distribution.

4 Proposed Outlier Detection Methodology

4.1 Two groups

We first consider the case when J = 2, i.e. there are two groups. Then we can apply the algorithm of Pounds and Cheng [18] for multiple testing. The algorithm proceeds as follows.

1. Let p̃₁, …, p̃_d denote the d unique p-values from the original p-values p₁, …, p_G, and let the corresponding number of p-values equal to p̃_i (i = 1, …, d) be denoted as m_i. Note that we expect d to be much less than G due to the discrete nature of the p-values.

2. Define the estimator of the expected proportion of tests with a p-value less than α as

   $$\widehat{F}(\alpha )=G^{-1}\sum _{l=1}^{d}I({\stackrel{\sim }{p}}_l\le \alpha )m_j,$$

   where $G={\sum }_{j=1}^d{m}_j$.

3. Define the estimated proportion of true null hypotheses as π̂ = min(1, 8c), where

   $$c=G^{-1}\sum _{l=1}^{G}2min(p_l,1-p_l),$$

   and min(a, b) denotes the minimum of a and b.

4. Estimate the false discovery proportion as

   $$\widehat{W}(\alpha )=\{\begin{array}{l}\widehat{\pi },\alpha \le 1/2\hfill \\ \widehat{\pi }/2+\widehat{F}(\alpha )-\widehat{F}(1/2),\alpha >1/2.\hfill \end{array}$$

   As described by Pounds and Cheng (2006), what this calculation does is to count every p-value greater than 0.5 as if it were testing a true null hypothesis and count it towards the numerator of the false discovery proportion.

5. Compute t̃_l = Ŵ (p̃_l)/F̂ (p̃_l), l = 1, …, d.

6. Smooth t̃_l using a robust regression algorithm and rank interpolation; details are given in Pounds and Cheng (2006).

7. Construct q-values using the predicted values of t̃_l from the previous step.

This algorithm has been coded by Pounds and Cheng in R and is available at the following URL: www.stjuderesearch.org/depts/biostats/.

What is novel in our problem is that we are using the observed data in the baseline group to calculate the ‘p-values’ p̃_gji. This is identical to what was done in Ghosh and Chinnaiyan (2009). After implementing the algorithm, we can select genes whose q-value is less than a pre-specified threshold. This is referred to as the control paradigm by Pounds and Cheng (2006). They provide extensive simulation evidence to show that the rule of rejecting all genes whose q-value is less than α will control the false discovery rate at level α.

4.2 Asymptotic Error Rate Control: Heuristics

In Pounds and Cheng (2006), no proof of error control in either a finite-sample or an asymptotic setting is given. If the null distribution is known, it turns out that one can use the arguments in Ferreira (2007) to show that the rule described in the previous paragraph will asymptotically control the false discovery rate. However, the null distribution was assumed to be known, whereas in our problem, it is actually estimated from the data. We give a sketch of the proof that the proposed procedure asymptotically controls the FDR under certain assumptions.

Let p̂₁, …, p̂_G denote the G p-values obtained from the Benjamini-Hochberg procedure described in Section 4.1. Let p₁,…, p_G denote the p-values of the G genes if the null distribution were known (i.e., we used F_0g instead of F̂_0g). Of the G genes, we assume that G₀ truly have no evidence of outlying expression and G₁ truly have evidence of outlying expression. Let these two populations have cumulative distribution functions denoted by F₀ and F₁. We define the binary random variable OE_g to denote outlying expression for gene g (i.e., OE_g = 1 if there is evidence of outlying expression, 0 otherwise). We make the following assumptions:

1. Y_gij share common support;

2. For g = 1, …, G, F_0g and F_1g are continuously differentiable, and their density functions f_0g and f_1g are also continuous; furthermore, f_0g is bounded on every compact subset of (0, 1) and is positive on {t: 0 < F_0g(t) < 1}.

3. n₀ and n₁ go to infinity such that n₁/n → λ ∈ (0, 1).

4. Convergence of empirical cdfs:

   $$\begin{array}{l}{G}_0^{-1}\sum _{g=1}^{G}I(p_g\le t,O{E}_g=0)\to F_0(t)\\ G_1^{-1}\sum _{g=1}^{G}I(p_g\le t,O{E}_g=1)\to F_1(t)\end{array}$$

5. uniformly in t.

By assumption D), we can use the result of the main proposition in Ferreira (2007) to show that the Benjamini-Hochberg procedure applied to p₁, …, p_G controls the FDR at the appropriate level. By algebraic manipulation,

$$\begin{array}{l}{G}_0^{-1}\sum _{g=1}^{G}I({\widehat{p}}_g\le t,O{E}_g=0)=G_0^{-1}\sum _{g=1}^G\{I({\widehat{p}}_i\le t,O{E}_g=0)-I(p_g\le t,O{E}_g=0)\}\\ +G_0^{-1}\sum _{i=1}^{G}I(p_g\le t,O{E}_g=0)\end{array}$$

Assumptions A)–C) imply that the first summand on the right-hand side of the equality sign converges almost surely to zero uniformly in t, while by assumption D), the second summand converges almost surely to F₀ uniformly in t. An appeal to the arguments in the proof of the main proposition in Ferreira (2007) can then be used to show that the Benjamini-Hochberg procedure applied to p̂₁, …, p̂_G also asymptotically controls the FDR at the correct level.

4.3 More than two groups

We now consider the situation where we have more than two groups, i.e. J > 2. Outlier detection for the multigroup case has been considered recently by Liu and Wu (2007). Their methodology was primarily based on using F –statistics. As noted by Ghosh and Chinnaiyan (2009), such regression-based statistics only use information on the first two moments, which might lose power in situations where the data are far from normality.

We seek to extend the discrete version of the previous section here. Note that for each gene, we will have a vector of p-values. Again, the p-values are estimated using the distribution of values in the baseline group rather than based on permutation or a theoretical null distribution. Ploner et al. (2006) propose a multivariate density estimation for the local false discovery rate of Efron et al. (2001), while Chi (2008) proposes multivariate extensions of the Benjamini-Hochberg procedure. However, the latter author uses a mixture model for multiple testing that is an extension of that proposed by Genovese and Wasserman (2004). An implication of such a model is that the distribution of p-values is continuous, which is not the case here.

Our approach is the following. First, we convert the multivariate p-values to multivariate q-values applying the Pounds-Cheng algorithm to each component. We now describe two types of hypotheses we might wish to test:

1. Subtype hypothesis: This would be looking for genes that show evidence of outlier expression in at least one group relative to the baseline group.

2. Uniform effect hypothesis: This would correspond to genes that consistently show evidence of outlier expression across all groups relative to baseline.

For the first hypothesis, for each gene, we can simply test if the minimum p-value across the (J − 1) dimensions is less than α/(J − 1), where α is the FDR we wish to control. The procedure would be to then declare all genes for which this condition holds as satisfying the subtype hypothesis.

For the second hypothesis, we can test if the average of the q-values is less than or equal to α for each gene. In the case where the tests are independent across groups, it is easy to show that both procedures will control the FDR. While this will not be exactly true because F̂₀ is used to derive p-values, we can argue that FDR control holds conditional on F̂₀.

Similarly, we can rank genes under the first hypothesis by the smallest q-value across the groups and by the average q-value in the second situation. It is more complicated to adapt the approach of Ploner et al. (2006) for these two hypotheses, as it would require taking their multidimensional FDR estimator and integrating it over the appropriate regions. This is an interesting problem that we leave open for future work.

5 Prostate Cancer Data

The example we use is from a prostate cancer gene expression study, a slightly different version from that considered previously in Ghosh and Chinnaiyan (2009). In this example, there are J = 3 groups, non-cancer, localized prostate cancer and metastatic prostate cancer samples (24, 10, and 6, respectively). While the platform is a two-color gene expression array originally containing 20000 genes, we remove all genes that have any missing measurements, this yields a total of G = 8350 genes.

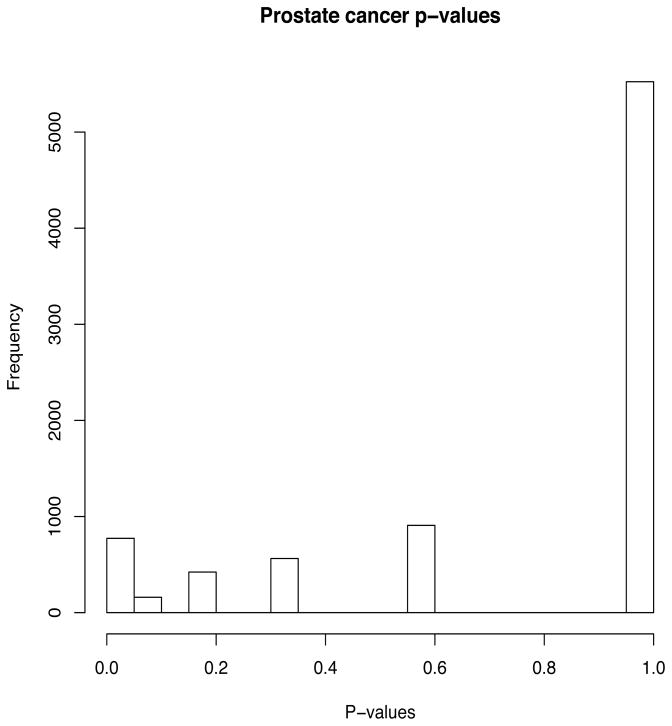
We first begin by collapsing the two types of cancer sample and compare them to the non-cancer samples so that we deal with J = 2 groups. A histogram of the p-values for the Bonferroni statistic $T_g^B$, g = 1, …, 8350 is given in Figure 1. Based on the plot, we see the extremely discrete nature of the p-value distribution. At a significance threshold of 0.05, the method proposed here calls 136 genes significant. The FDR for these genes are given in Table 2.

Figure 1.

Histogram of p-values from prostate cancer data. Even though G = 8350, the number of discrete p-values d = 22.

Table 2.

Estimated FDR (q-value) of 136 genes found significant at the 0.05 threshold for the prostate cancer data

FDR	# Genes
0.0004	3
0.001	1
0.002	2
0.003	4
0.006	5
0.009	7
0.012	12
0.016	21
0.036	29
0.042	31
0.048	21

Based on the genes that were found to have a q-value less than or equal to 0.05, we then searched the Census of Cancer Genes database (Futreal et al., 2004) to determine if there are oncogenes that are found by our analysis. Two genes were found: FANCD2 and TSC2. The first gene, FANCD2, is involved in the disorder Fanconi anemia. Fanconi anemia (FAN) is a genetically heterogeneous recessive disorder characterized by cytogenetic instability, hypersensitivity to DNA crosslinking agents, increased chromosomal breakage, and defective DNA repair. FANCD2 encodes for one of the proteins that makes up a common nuclear protein complex with other proteins encoded by other FAN genes. FANCD2 is known to interact with the BRCA1 and BRCA2 genes (Garcia-Higuera et al., 2001), which are major oncogenes involved in the etiology of breast cancer. Also, in leukemia, FANCD2 is mutated in the germline. The other gene, TSC2 (tuberous sclerosis 2), is a tumor suppressor gene that is a component of membrane microdomains and mediates caveolin-1 localization in post-Golgi transport (Jones et al., 2004). It is mutated in the germline in cancer, primarily in renal cell carcinomas.

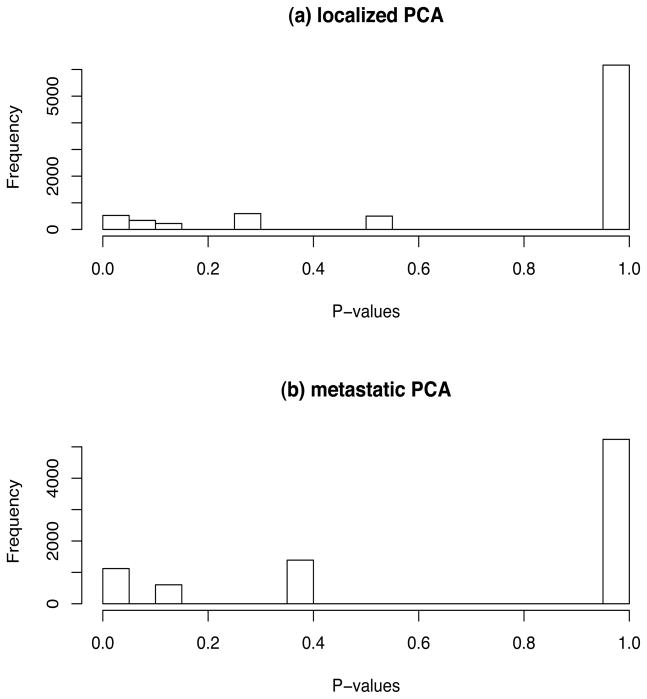
The next step is to do the analysis with J = 3 groups. We will use the non-cancer samples as the baseline distribution. Note that the uniform effect hypothesis is equivalent to the analysis comparing cancer samples to non-cancer samples, so we instead focus on genes that satisfy the subtype hypothesis. The distribution of p-values for the localized and metastatic prostate cancer (PCA) samples are given in Figure 2. The distribution for the metastatic PCA samples is more discrete due to the smaller sample size. After having applied the Pounds-Cheng algorithm to derive multivariate p-values, we select genes based on the rule that the minimum q-value is less than 0.025. Such an analysis leads to selection of 186 genes. Again repeating the Census of Cancer Genes database, another known oncogene, TCL6, is found. The function of TCL6 has not yet been defined; however, this protein may play a role which is similar to or complementary to other T-cell leukemia/lymphoma proteins during early embrogenesis. The association of this gene with T-cell leukemia chromosome translocations implicates this gene as a candidate for leukemogenesis.

Figure 2.

Histogram of p-values from prostate cancer data broken up by cancer subtype: (a) localized prostate cancer (PCA); (b) metastatic prostate cancer. The baseline group is the non-PCA samples.

Notice that while the cancer samples come from subjects with prostate cancer, this analysis has uncovered oncogenes that have been found in other cancers. An implicit assumption is that oncogenes are common across all cancers. This is in keeping with a model for tumorigenesis as posited by Hanahan and Weinberg (2000). They posited that there existed oncogenes that regulated or were dysregulated in the following mechanisms: self-sufficiency in growth signals; insensitivity to anti-growth signals; evading apoptosis (cell death); limitless replicative potential; sustained angiogenesis; tissue invasion and metastasis.

6 Simulation Study

In this section, we assessed the performance of various methods proposed in Sections 3 and 4 in terms of the variability of the testing procedures. All procedures controlled the FDR at the appropriate level. We instead specifically compare the following methods in terms of the variance of the numbers of hypotheses rejected: the methods of Tarone (1990), Gilbert (2005) and the FDR-based estimation procedure outlined in Section 4.1.

Data were generated as correlated multivariate normal measurements with a block correlation structure and positive correlation of ρ = 0.5 and ρ = 0.2. We considered n = 100, 1000 and 10000 genes, made up of 10 blocks of correlated genes. A fraction of the genes were differentially expressed between the two groups; we took the fractions to be 0.1 and 0.30; for these genes, the difference between the two groups was 1.5 units on the standard deviation scale. We considered m = 20 and m = 40, distributed equally between two groups. The test statistics were rounded to the nearest tenth decimal place to simulate discreteness. We considered procedures controlling the false discovery rate at α = 0.05. A total of 1000 simulation samples were generated for each simulation scenario. The results are given in Table 3.

Table 3.

Simulation results for average variance of rejected hypotheses

π0	ρ	m	n	Proposed	Gilbert	Tarone
0.1	0.2	10	100	0.49	0.67	0.72
	0.2	20	100	0.44	0.44	0.46
	0.2	10	1000	1.16	1.95	2.02
	0.2	20	1000	0.51	0.63	0.65
	0.2	10	10000	1.5	4.86	4.97
	0.2	20	10000	0.80	1.79	1.99
	0.5	10	100	0.48	0.86	0.87
	0.5	20	100	0.45	0.69	0.74
	0.5	10	1000	1.35	4.69	6.00
	0.5	20	1000	2.02	8.42	9.47
	0.5	10	10000	5.68	53	60.5
	0.5	20	10000	3.39	54.0	62.58
0.3	0.2	10	100	0.50	0.57	0.60
	0.2	20	100	0.33	0.37	0.39
	0.2	10	1000	0.80	1.27	1.32
	0.2	20	1000	0.55	0.92	0.92
	0.2	10	10000	1.62	4.54	3.70
	0.2	20	10000	0.86	1.65	1.69
	0.5	10	100	0.73	1.8	4.1
	0.5	20	100	0.73	1.46	1.51
	0.5	10	1000	4.3	12.95	13.89
	0.5	20	1000	2.03	11.71	15.09
	0.5	10	10000	4.98	88.8	103.76
	0.5	20	10000	9.5	100.2	146.73

Note: π₀ proportion of true null hypotheses. The number of hypotheses being tested is n, while there are m subjects per group. Proposed represents the procedure outlined in Section 4.1; Gilbert represents the method of Gilbert (2005); Tarone represents the method of Tarone (1990).

Based on the results, we find that the proposed method yields the smallest variability across all scenarios considered. It is clear that the methods of Tarone (1990) and Gilbert (2005) demonstrate much greater variability in terms of the number of hypotheses rejected relative to the proposed method.

7 Discussion

In this article, we have explored the issue of mutliple testing with discrete test statistics in the context of finding genes that have outlying differential expression in one group relative to a baseline group. We have given an argument favoring the so-called direct estimation procedures relative to sequential testing methods. In addition, we have developed nonparametric testing procedures that do not rely on normality. An inspection of previous methods reveals that these methods will be most powerful when a Gaussian assumption can be made; their performance is less clear when there is departure from this distributional assumption. We have focused on one-sided tests, but modifying the methodology to handle two-sided tests is straightforward; in particular, we would take as outliers values whose standardized values in [0, 1] differed from 0.5 in either direction.

For the data example in Section 5, we excluded genes with any missing values. We did this for illustration of the method. In practice, this is not very feasible. In theory, there should be nothing wrong with applying the methodology to the available gene expression measurements and thus having q-values that depend on variable numbers of measurements. Such a complete-case analysis would be valid under an assumption of the data being missing completely at random (Little and Rubin, 2002). One approach that might be practically implementable would be to combine an imputation method such as k-nearest neighbors imputation (Troyanskaya et al., 2001) with the methods proposed in the paper. While the method found 3 genes from the Cancer Census database, it is also possible that many of the other genes found might be undiscovered oncogenes that have never been biologically validated. This illustrates one of the limitations of using a database of known true positives for validation of a method.

While we have described the discreteness in a problem involving gene expression, technologies such as next-generation sequencing platforms and single nucleotide polymorphism arrays offer discrete measurements of molecular activities. Thus, we view the issue of dealing with discrete data in genomics as one that will not go away anytime soon. Further thought is needed on how to develop multiple comparison procedures for this setting.