Adaptive evolution via a major gene effect: Paedomorphosis in the Mexican axolotl

Abstract

Although adaptive evolution is thought to depend primarily on mutations of small effect, major gene effects may underlie many of the important differences observed among species in nature. The Mexican axolotl (Ambystoma mexicanum) has a derived mode of development that is characterized by metamorphic failure (paedomorphosis), an adaptation for an entirely aquatic life cycle. By using an interspecific crossing design and genetic linkage analysis, a major quantitative trait locus for expression of metamorphosis was identified in a local map of amplified fragment length polymorphisms. These data are consistent with a major gene hypothesis for the evolution of paedomorphosis in A. mexicanum.

An unresolved problem in evolutionary genetics concerns the importance of major gene effects in nature. Recent genome mapping experiments suggest a role for major gene effects in the evolution of phenotypic differences between species (1–4). However, it is uncertain if major gene effects play a role in the evolution of traits that are important in adaptation and speciation because little is known about the genetic architecture of natural populations (but see refs. 5 and 6) or about various contingencies (population structure, strength of selection, mode of gene action, and pleiotropy) that might influence the probability that a major mutant allele increases in frequency and becomes fixed in a population (7–14). Although many ecologically important and qualitatively distinct phenotypes have been observed within populations of natural species (15), as well as between closely related species, very few of these examples have been analyzed genetically (11).

The paucity of major mutational examples from nature is not unexpected given that classical genetic approaches, and ultimately linkage analysis with molecular markers, must be applied to nonmodel organisms to test a major gene hypothesis. It is therefore important to study potential, major mutational examples that are of clear adaptive significance in genetically tractable organisms. One of the best known examples involves the evolution of a derived life cycle mode in the Mexican axolotl Ambystoma mexicanum. In this species, a major gene change has been hypothesized to underlie the evolution of paedomorphosis (16, 17), an adaptation for an entirely aquatic life cycle (18–20). Preliminary genetic support for this hypothesis was based on an interspecific cross between A. mexicanum and the obligate metamorph A. tigrinum tigrinum (21). Specifically, an F1 hybrid metamorph (A. mexicanum × A. t. tigrinum) was crossed to an axolotl, and approximately equal proportions of metamorphs and paedomorphs were observed among the offspring. Tompkins (16) concluded that life cycle mode was controlled by alternate alleles at a single locus, with a dominant allele for metamorphosis inherited from A. t. tigrinum and a recessive allele for paedomorphosis inherited from A. mexicanum. By using this same crossing design, Voss (17) made two additional crosses to test the single gene model. Although the segregation ratios from these crosses were not consistent with a strict single gene model, the data were compatible with a major effect locus controlling most of the variation in life cycle mode, with smaller effect loci presumably influencing trait expression under certain environmental conditions.

If the interpretation above is correct, and expression of metamorphosis or paedomorphosis is determined primarily by alternate alleles at a major locus, then it should be possible to identify alleles at a DNA marker locus that cosegregate with the alternate phenotypes. This hypothesis was tested by scoring polymorphic DNA markers for offspring of two interspecific backcrosses in which alternate life cycle modes were segregating. If life cycle mode is controlled by a single gene, F1 individuals of a cross between A. mexicanum and A. t. tigrinum would inherit a dominant allele (MET) from the A. t. tigrinum parent and undergo metamorphosis. In a backcross to A. mexicanum (met), approximately half of the offspring would be heterozygous (MET/met) and undergo metamorphosis, and the other half would be homozygous (met/met) and exhibit paedomorphosis. According to this model, backcross metamorphs would be expected to score for the presence of a dominant A. t. tigrinum-derived DNA marker that is completely linked to MET whereas backcross paedomorphs would be expected to score for an A. mexicanum-derived DNA marker that is completely linked to met.

METHODS

Genetic Crosses.

The crossing strategy and phenotypic segregation analysis have been described (17). In brief, an interspecific cross was made between an obligate metamorphic species (female, A. tigrinum tigrinum) and an obligate paedomorphic species (male, A. mexicanum). Two F1 male hybrids were then backcrossed to a female A. mexicanum (crosses 3 and 4) to produce second generation populations in which alternate life cycle modes were segregating. Approximately 20 second generation offspring from each cross were reared under four different treatment combinations of food and temperature level. Individuals were scored as metamorphs if external gills were completely resorbed within 450 days of hatching.

DNA Marker Loci.

Amplified fragment length polymorphisms (AFLPs) (22) were scored for the P1 adults, P2 adults, and a sample of second generation offspring from crosses 3 and 4. Given that the segregation ratios of metamorphs and paedomorphs within three of the four environmental treatments were statistically consistent with a single gene model (17), the sample of second generation offspring was drawn from all treatments. Modifications of the original AFLP procedure were used to reduce the complexity of the multilocus banding patterns that were generated as a result of the large genome size of Ambystoma. The restriction digestion step using EcorI and MseI, ligation step, and first preselective PCR step followed standard methods (22). Two additional PCR steps then were used to reduce the complexity of the banding patterns: a PCR step using primers E-ACG and M-CAC, followed by a PCR step using primers with an additional selective base (e.g., E-ACGn and M-CACn, where n is one of the four possible bases A, C, G, or T). All 16 combinations of the four base extensions of E-ACGn and M-CACn were used to generate AFLPs; therefore, a total of 16 gels was scored for polymorphic loci. DNA fragments from the P³³ PCR step were size-separated on a DNA sequencing rig (30 × 40 cm) by using 5% polyacrylamide gels (19:1 acryl:bis) and a constant power of 60 W for 2.5 h. Gels were dried and visualized by autoradiography according to standard methods (22).

AFLPs also were generated by using the restriction enzymes NotI and HpaII; the adaptors and primers for these fragments are shown in Table 1. Because NotI is an 8-cutter, the resulting pool of AFLPs was reduced greatly. Accordingly, only one preselective PCR step was necessary before the typical P³³ PCR step using a primer with three selective nucleotides. All combinations of five different NotI (N) primers and four different HpaII (HP) primers, except primer combinations N-ATT/HP-CAC, N-AAT/HP-CAC, and N-AAT/HP-AAC, were scored for a total of 17 gels.

Table 1.

Adaptors and primers for NotI (N) and HpaII (HP) restriction fragments

NotI adaptor ctc  gta  gac  tgc  gta  tt cat  ctg  acg  cat  aac  cgg								HpaII adaptor gac  ggc  gaa  tcc  taa  g cg  ctt  agg  att  c  gc
NotI primers								HpaII primers
N+0	gac	tgc	gta	ttg	gcc	gc		HP+0	ggc	gaa	tcc	taa	gcg	g
N-AAG	gac	tgc	gta	ttg	gcc	gc	aag	HP-ATA	ggc	gaa	tcc	taa	gcg	gat	a
N-AGG	gac	tgc	gta	ttg	gcc	gc	agg	HP-TAC	ggc	gaa	tcc	taa	gcg	gta	c
N-ACA	gac	tgc	gta	ttg	gcc	gc	aca	HP-CAC	ggc	gaa	tcc	taa	gcg	gca	c
N-ATT	gac	tgc	gta	ttg	gcc	gc	att	HP-AAC	ggc	gaa	tcc	taa	gcg	gaa	c
N-AAT	gac	tgc	gta	ttg	gcc	gc	aat

Relative gel mobility scores were determined for informative AFLP marker loci (Table 2). Relative gel mobility refers to the gel position of an AFLP marker locus under the electrophoresis conditions described above. This scale ranges from 0 to 1, with the bottom of the gel equal to 0 and the sample well (which is easily visualized on the autoradiograph) equal to 1.

Table 2.

Primers and relative gel mobilities of informative AFLP marker loci

Primers	AFLP marker	Relative gel mobility
N-AAG/HP-ATA	AFLP11.7	0.57
E-ACGT/M-CACG	AFLP32.17	0.79
E-ACGC/M-CACC	AFLP34.5	0.51

Genetic Linkage Analysis.

AFLPs are primarily dominant and recessive markers, with presence of a marker indicating a heterozygous or homozygous dominant genotype and absence of a marker indicating a homozygous recessive genotype. In the backcross design of this study, the fully informative markers with respect to phase were those deriving from the A. t. tigrinum P1 adult. Accordingly, second generation offspring that were observed to inherit an A. t. tigrinum P1-derived marker were scored as heterozygous for a specific locus, and offspring inheriting no marker at the locus were scored as homozygous recessive. mapmaker 3.0 (23) was used to analyze the 262 dominant AFLP markers (deriving from the A. t. tigrinum P1 adult) that were observed to segregate among cross 3 offspring. First, all of the markers were grouped by using threshold linkage criteria of logarithm of odds (LOD) scores of 3.0, 4.0, and 5.0 (a LOD score of 3.0 corresponds to an odds ratio of 1,000:1 in favor of linkage). Maximum likelihood order and map distance were determined for all linkage groups that were supported at LOD = 4.0. These analyses were conducted to provide general insights about marker linkage relationships and the extent of genome coverage. Second, each of these markers was tested for linkage to a presumptive single locus underlying expression of life cycle mode. Because of multiple marker comparisons, an adjusted (statistically conservative) critical LOD threshold of 3.72 [corresponding to an odds ratio of 5,240:1 in favor of linkage, which approximates the probability of a false-positive: (0.05)/number of 2-point linkage tests (262) = 0.00019] was used to evaluate these 2-point LOD scores. Pairwise comparisons that yielded significant LOD scores were assumed to indicate informative AFLP markers for linkage to major effect genes. A permutation-based method (24, 25) also was used to identify markers associated with major and minor effect genes. In this approach, the phenotypic scores for all of the offspring are randomized with respect to the AFLP genotypic scores, and the data are evaluated for significant pairwise associations between phenotype and markers. The procedure is repeated 1,000 times, and significance is determined as the proportion of times that a pairwise association from the permuted data set is more strongly supported than the most significant pairwise association in the observed data set. After removing the phenotypic effect of the primary locus, the permutation procedure was repeated 1,000 times to analyze the residual phenotypic variation for secondary gene effects.

As a second independent approach to evaluate the significance of primary gene effects that were identified in cross 3, the most informative AFLP markers were scored for cross 4 offspring. Here, a LOD threshold of 3.0 was considered significant because only three pairwise comparisons were tested. The maximum likelihood order for these markers and map distances (Haldane function) between markers were determined by mapmaker 3.0 (23). Life cycle mode was then treated as a complex binary trait and mapped as a quantitative trait locus (QTL) by using a single interval mapping approach. The likelihood functions for this mapping approach were described by Xu and Atchley (26); the likelihood (L₁) of a QTL affecting a binary trait at a particular position is:

where y_i = binary code for life cycle mode (0 = metamorph; 1 = paedomorph), f_i = conditional probability of a QTL genotype given the flanking marker data, p₀ = probability of metamorphosis given a homozygous QTL genotype, and p₁ = probability of metamorphosis given a heterozygous QTL genotype.

L₁ was maximized with respect to p₁ and p₀ by using a generic “hill climbing” algorithm (27) because the iterative solution suggested by Xu and Atchley (26) did not always converge for these data. Values for p₁ and p₀ are estimates of the penetrance of each of the expected QTL genotypes in a backcross design. The expected penetrance values for two fully penetrant, single locus genotypes are 1.0 and 0.0 for the heterozygous and homozygous genotypes, respectively. Deviations from these expected values would indicate incomplete penetrance and thus a possible role for additional factors (genetic and environmental) in the determination of phenotype.

To obtain a likelihood under the null hypothesis of no QTL effect,

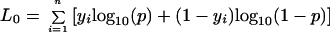was evaluated at

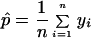LOD scores (L₁ − L₀) were calculated at ≈1-cM map positions to create profiles for estimating QTL effect and position between the informative AFLP marker loci. Given nonadditivity of the recombination fractions defined by each flanking marker and the QTL, the exact map positions of each LOD score determination are 0.01 recombination unit steps relative to the recombination fraction of the left flanking marker and QTL. The map position in centimorgans is given by:

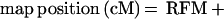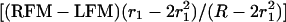where LFM and RFM refer to the cM position of the left and right flanking AFLP markers respectively, R refers to the recombination fraction between LFM and RFM, and r₁ refers to the recombination fraction of the LFM and the QTL.

RESULTS

A total of 33 AFLP primer combinations or gels was screened for 17 paedomorphs and 26 metamorphs of cross 3. These primer combinations yielded 262 AFLP marker loci that were inherited uniquely from the P1 A. t. tigrinum female and thus were informative for linkage. mapmaker 3.0 (23) identified 281 significant pairwise linkages and 48 linkage groups at a LOD threshold of 4.0 (Table 3). The majority of these linkage groups consisted of two markers; however, 23 multi-marker linkage groups also were identified. The total map size was estimated to be 1172.4 cM, with an average interval of 11.61 cM (1172.4/101 intervals) between markers. These loci appeared to provide only partial coverage of the Ambystoma genome because the number of linkage groups did not approximate the chromosome number (n = 14), and there were many unlinked loci. If it is assumed that each of the unlinked markers can support a hypothesis of linkage within an ≈22-cM window, then all of the markers together provide 3658.4 cM of genome coverage. Although it is not possible to known how this estimate compares to the actual genome map size [which may be large given that Ambystoma has a haploid genome size that is an order of magnitude larger than most vertebrates (28)], it seems likely that a majority of the genome was sampled by the AFLP markers.

Table 3.

Linkage relationships among the 262 informative AFLP markers that were scored for cross 3 offspring

Markers in group	LOD threshold
	3.0	4.0	5.0
1	77	113	131
2	17	25	31
3	10	8	10
4	6	6	3
5	5	5	3
6	4	2	2
7	3	2	0
8	2	0	0
9	0	0	0
10	0	0	0
11	1	0	0

Markers were grouped using mapmaker 3.0 and three different LOD thresholds (3.0, 4.0, and 5.0). 

Of the 262 AFLP marker loci that were inherited uniquely from the P1 A. t. tigrinum female, two markers (AFLP11.7, LOD = 1.89; AFLP34.5, LOD = 3.56) were suggestive of linkage to a presumptive single locus underlying expression of life cycle mode, and one (AFLP32.17, LOD = 6.48) was statistically significant (Table 4). The permutation procedure also showed AFLP32.17 to be significantly associated with expression of life cycle mode at P < 0.001; this inference is robust with respect to linkage between markers and the small number of individuals scored. After statistically removing the primary effect of AFLP32.17, the marker contributing the largest effect to the residual phenotypic variation was identified as AFLP30.16 (P = 0.101). However, because AFLP30.16 was only significant at the 10% level, there is no statistical support for additional minor effect QTLs in the determination of life cycle mode.

Table 4.

Segregation ratios of AFLP marker genotypes and life cycle mode phenotypes for offspring of crosses 3 and 4

	AFLP Marker locus
	AFLP11.7		AFLP32.17		AFLP34.5
	Het	Hom	Het	Hom	Het	Hom
Cross 3
Metamorph	19	7	23	3	22	4
Paedomorph	5	12	2	15	5	12
Cross 4
Metamorph	20	3	19	4	19	4
Paedomorph	4	10	3	11	2	12

Het, heterozygous; Hom, homozygous. 

To test the repeatability of the linkage results obtained by using cross 3 offspring, AFLP11.7, AFLP34.5, and AFLP32.17 were scored for the parentals and 14 paedomorphs and 23 metamorphs of cross 4. In this replicate backcross population, the LOD scores for all three markers (LOD = 3.56, 3.34, and 4.24 for AFLP11.7, AFLP34.5, and AFLP32.17, respectively) were statistically significant, providing strong supporting evidence in favor of the hypothesis of linkage between each marker and a hypothesized single gene underlying expression of life cycle mode (Table 4).

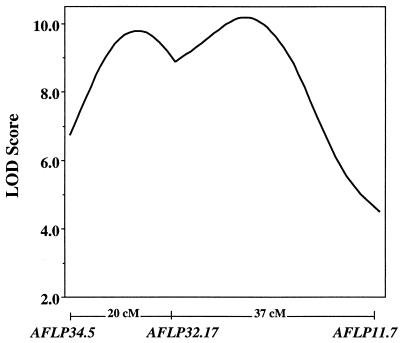
Two-point LOD scores indicated that AFLP34.5 and AFLP32.17 were significantly linked to each other (LOD = 3.00 and 6.62 for crosses 3 and 4, respectively) and that AFLP11.7 was more closely (but not significantly) linked to AFLP32.17 (LOD = 2.33 and 2.44 for crosses 3 and 4, respectively). Given that sample sizes were not sufficient within crosses to support a hypothesis of linkage between distantly spaced markers and that mapmaker 3.0 (23) found the most likely arrangement of AFLP marker loci to be identical between crosses, cross 3 and 4 data were combined to increase the power for mapping. These combined data yielded significant 2-point LOD scores for all pairwise comparisons among these three AFLP marker loci except for the comparison between AFLP34.5 and AFLP11.7 (LOD = 2.86). The most likely arrangement of these AFLP marker loci is shown in Fig. 1.

Figure 1.

LOD score profiles between AFLP34.5 and AFLP32.17 and between AFLP32.17 and AFLP11.7.

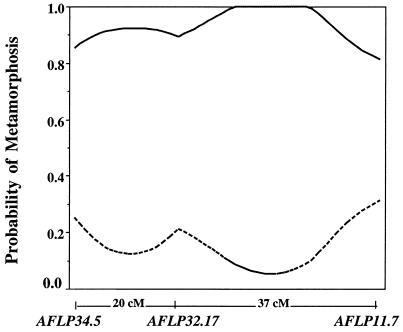
Life cycle mode was then treated as a complex binary trait and mapped as a QTL (Fig. 1). By using a 1-LOD support interval from the maximal LOD peak as an indicator of relative QTL position, the QTL for expression of life cycle mode is located within an ≈30 cM window, with the most likely position near AFLP32.17. For both intervals AFLP34.5-AFLP32.17 and AFLP32.17-AFLP11.5, the probability of metamorphosis given a met/met genotype (p₀) is low whereas the probability of metamorphosis given a MET/met genotype (p₁) is high (Fig. 2). The deviation of p₀ and p₁ from values expected under a single gene model (p₀ = 0.0 and p₁ = 1.0 under a single gene model) indicates that both genotypes are not fully penetrant, suggesting that additional factors influence trait expression. However, because the deviation of penetrance values from simple Mendelian expectation is small (at the maximal LOD peak, p₀ = 0.07 and p₁ = 1.0), these factors appear to contribute a relatively minor effect in comparison to the mapped QTL.

Figure 2.

Plots of probability of metamorphosis as a function of map position. The values of p₀ (probability of metamorphosis given met/met genotype) and p₁ (probability of metamorphosis given MET/met genotype) for a given maximization of L₁ are estimates of the penetrance of the QTL at that position. p₀ = broken line; p₁ = solid line.

DISCUSSION

The genetic linkage data presented here support earlier interpretations of phenotypic segregation in interspecific crosses of A. mexicanum and A. t. tigrinum (16, 17, 21): A major QTL contributes to the expression of alternate life cycle modes. The results therefore are consistent with a major gene hypothesis for the evolution of paedomorphosis in A. mexicanum. The data supporting this hypothesis appear to be robust because the same major gene effect was demonstrated in two replicate backcross families. Given the magnitude of the primary gene effect, relatively small sample sizes and a partial genomic map were sufficient for detecting and mapping the major QTL. On the other hand, these data were less robust with respect to understanding the factors that alter the penetrance of the primary QTL. The finding of no secondary QTL suggests that several loci may make very small contributions to the determination of life cycle mode and/or that environmental factors are important. Although the phenotypic segregation data suggest a role for environmental effects (17), the possibility of a minor effect QTL cannot be discounted in the absence of larger sample sizes and a more complete linkage map (29).

Although there are relatively few examples of adaptive major genes in nature (11), many ecologically relevant and distinct phenotypes have been observed within natural populations (15). That some of these qualitative polymorphisms may have a relatively simple genetic basis (11, 30, 31) suggests a potentially greater role for major effect mutations in evolution than has been suggested previously (refs. 7 and 8 but see ref. 9). Quite simply, natural selection in nature may be sufficiently strong to fix advantageous, major mutations that yield ecologically distinct phenotypes. The evolution of obligate paedomorphosis from a metamorphic or facultative ancestral condition may occur because of ecological opportunity in permanent and productive aquatic habitats (18–20). Indeed, obligate paedomorphosis has evolved independently among several ambystomatid salamanders that inhabit large, stable lakes that were historically devoid of aquatic predators (18, 19).

The fixation of an advantageous recessive allele in a population represents a special problem in population genetic theory because the allele is invisible to selection until homozygotes are formed (10, 11). Theory predicts that the formation of a homozygote will depend on the probability that the recessive allele increases in frequency, which will be higher in a population characterized by inbreeding (10), or if the recessive allele arises in a small population that subsequently undergoes a rapid population increase (ref. 13 but see ref. 14). For the case of salamander paedomorphosis, these conditions often may exist in ancestral populations because ambystomatid populations are often composed of relatively few individuals that show high fidelity for breeding sites and thus a relatively high probability for inbreeding (32). It therefore is conceivable that two carriers of a recessive allele will mate. After the paedomorphic phenotype arises, the recessive allele frequency should increase rapidly because aquatic paedomorphs are more likely to mate with each other than with terrestrial metamorphs that return to the water for a brief time each year. In this respect, the recessive allele can be considered a “speciation gene” because it manifests a morphologically and ecologically differentiated phenotype that is reproductively isolated from the metamorphosing ancestor. Thus, the evolution of obligatorily paedomorphic species via an advantageous recessive allele is consistent with the expected population structure of the founding population and the expected population-level consequences of the paedomorphic phenotype once it is expressed.

It is important to note that, although the genetic linkage results of this study are consistent with a major effect mutational origin for paedomorphosis in A. mexicanum, the historical context of genetic change may be more complex than a perceived single allelic substitution (12). For example, each of several sequential, small effect mutations in the same allele lineage might alter the penetrance of a single locus genotype, from an initially low probability for trait expression to a higher probability. Eventually, sequential small effect mutations during the course of evolution might yield a fully penetrant major gene effect, accounting for all or most of the phenotypic variation in an interspecific cross. Functional analysis of a specific candidate gene (33) is needed to differentiate between a single major mutation vs. several, sequential minor mutations during the course of evolution. Given that most natural species will not be amenable to these rigorous experimental approaches, interspecific crossing designs will probably not contribute definitive answers to our understanding of the number of mutational events that contribute to a major gene effect at a specific locus. However, results from this study indicate that efficient polymorphism detection techniques can be used to identify specific chromosomal regions (loci) that underlie phenotypic differences between natural species.

In summary, results from this study suggest that paedomorphosis in A. mexicanum evolved via a major gene effect. This recessive, major gene yields a phenotype that is clearly adaptive; metamorphic failure or paedomorphosis alters the entire life history of the organism because individuals remain in the aquatic habitat throughout the life cycle (18–20). An adaptive interpretation for the evolution of paedomorphosis also is supported by a convergent pattern of evolution that is observed among other Mexican ambystomatids. During the last few million years, obligate and facultative paedomorphosis has evolved independently a number of times among different Mexican species (34–37). Although it is too early to speculate on the genetic basis of paedomorphosis in these other species, we currently are developing molecular markers and interspecific crosses to determine if the same major QTL locus underlies paedomorphosis in some or all of these independent evolutionary events. These future studies, as well as others that adopt molecular mapping approaches to the study of adaptation in nature, promise to reveal the frequency of major gene effects in evolution.