The Beta-Binomial Distribution for Estimating the Number of False Rejections in Microarray Gene Expression Studies

Abstract

In differential expression analysis of microarray data, it is common to assume independence among null hypotheses (and thus gene expression levels). The independence assumption implies that the number of false rejections V follows a binomial distribution and leads to an estimator of the empirical false discovery rate (eFDR). The number of false rejections V is modeled with the beta-binomial distribution. An estimator of the beta-binomial false discovery rate (bbFDR) is then derived. This approach accounts for how the correlation among non-differentially expressed genes influences the distribution of V. Permutations are used to generate the observed values for V under the null hypotheses and a beta-binomial distribution is fit to the values of V. The bbFDR estimator is compared to the eFDR estimator in simulation studies of correlated non-differentially expressed genes and is found to outperform the eFDR for certain scenarios. As an example, this method is also used to perform an analysis that compares the gene expression of soft tissue sarcoma samples to normal tissue samples.

1 Introduction

Microarrays simultaneously measure the RNA expression of thousands of genes and are widely used in contemporary scientific investigation. Numerous methods have been proposed for the analysis of data from such studies (Mehta et al., 2004). Many of these methods are designed to perform differential expression analysis of gene expression data, i.e., to identify genes with significantly different mean or median expression across one or more distinct biological groups. In such analyses, a hypothesis test is performed for each of m genes. In practice, m is typically greater than 1,000. Thus, it is necessary to address the issue of multiple tests.

Traditional multiple-testing procedures attempt to control the family wise error rate (FWER). The FWER is defined as Pr(V>0), where V is the number of Type I errors incurred in the analysis. Thus, traditional approaches are typically rejection procedures that are developed to ensure that the FWER is kept below a threshold that is pre-specified by the user. It is widely recognized that control of the FWER is too conservative in differential gene expression analysis because m is so large that strict control of the FWER usually does not reject any hypothesis, i.e., does not declare any gene to be significantly differentially expressed.

Subsequently, the false discovery rate (FDR; Benjamini and Hochberg 1995) has been accepted as a more practical way to measure the number of Type I errors than the FWER for differential expression analysis. The FDR is defined as E(Q), i.e., the expected value of ratio Q of the number V of Type I errors (false discoveries) to the total number R of rejections. For R = 0, Q is defined to be equal to 0. The FDR is a more flexible measure of the prevalence of false discoveries incurred in an analysis. Unlike the FWER, which penalizes any Type I error, the FDR allows for some Type I errors to occur so long as they are not overly abundant among the set of results declared to be significant.

Benjamini and Hochberg (1995) introduced a step-down p-value adjustment procedure that controls the FDR at a pre-specified threshold under the assumption that p-values for true null hypotheses are independent uniform (0,1) random variables. They demonstrated that their method of FDR-control is more powerful than several methods to control the FWER. Storey (2002) noted that it can be difficult in practice to pre-specify an appropriate level for the FDR. Thus, he suggested that it may be more practical to estimate an FDR-type measure as a function of the p-value threshold used to determine significance. He developed a method that uses the observed p-values to estimate the positive false discovery rate [pFDR, defined as E(Q|R>0)] as a function of the p-value significance threshold.

Subsequently, numerous additional methods have been proposed to estimate or control the FDR or related measures. Allison et al. (2002) and Pounds and Morris (2003) propose beta-uniform mixture (BUM) models for the p-values and use maximum likelihood techniques to fit these models to the observed p-values. The fitted models then provide estimates of the FDR and other multiple-testing error metrics. Pounds and Cheng (2004) proposed the spacings LOESS histogram as a nonparametric technique to generate estimates of similar error metrics. Cheng et al. (2004) propose a spline-based estimation technique. Pounds (2006) provides a non-technical review of the area, and Cheng and Pounds (2007) give a comprehensive technical review of these and other similar methods.

Each of the reported methods implicitly assumes that the p-values for non-differentially expressed genes are independent uniform (0,1) observations. Some methods additionally assume that all p-values are independent. However, it is well-known that genes operate cooperatively in regulatory and signaling pathways (Storey and Tibshirani 2003). Thus, the expression levels of genes are correlated due to natural biological processes. Therefore, from a biological perspective, the independence of p-values is violated. The methods of Benjamini and Hochberg (1995) and Storey et al. (2004) are robust against certain forms of dependence of the test statistics (and hence the p-values) in terms of conservativeness (Benjamini and Yekutieli 2001; Storey et al. 2004). However, the robustness of existing methods in terms of power remains largely unknown. Consequently, a method that explicitly models the dependence of p-values may give better performance in terms of power than existing methods.

Tsai et al. (2003) proposed to model U, the number of false null hypotheses that are rejected at a specific p-value threshold, with a beta-binomial (BB) distribution. They did this in addition to assuming the binomial distribution for U and compared the results of the two assumptions for several values of the variables of interest in FDR studies. The BB distribution allows for the rejection of individual false null hypotheses to be correlated events. However, for both cases of U, they assumed that rejection of individual true null hypotheses are independent events and thus model V with the binomial distribution. Then the number of rejections R = V + U is what they term the “convolution” of two distributions. They compared the distribution of R and that of the conditional false discovery rate (cFDR) between the two assumptions and found that for the dependence model, the distribution of R has longer and heavier tails than that for the independence model. They also found that the cFDR for the independence model is monotonic, while the cFDR for the dependence model exhibits more of a U-shaped pattern. In the simulation portion of their paper, Tsai et al. used their independence model for R and also a bootstrap-proposed alternative to estimate R. They then compared the performance of the two approaches on data simulated from both the independence and dependence FDR models. They did not assess the performance of the dependence model for R as a method of FDR-estimation.

Here, we propose to account for correlation of p-values testing true nulls by using the BB distribution to model the number V of Type I errors incurred at a specified p-value threshold. The model leads to a beta-binomial false discovery rate (bbFDR) estimator. In Section 2, we describe the proposed model and how to compute the bbFDR estimator. In Section 3, we present simulation studies that compare the performance of the bbFDR estimator to the empirical false discovery rate (eFDR) estimator, which is based on independence of p-values testing true nulls. Section 3 also includes the application of our method to the differential expression analysis of a microarray data set from a gene expression study that compared the expressions of samples of patients with soft tissue sarcoma to normal tissue samples. Section 4 concludes with the discussion of our proposed method and of future research.

2 Methods

The general problem is to simultaneously test m null hypotheses. Let m₀ be the number of true null hypotheses and m₁ be the number of false null hypotheses. Note that these definitions imply m=m₀ +m₁. Furthermore, assume that each test is performed at the same level α. Let V be the number of true null hypotheses that are incorrectly rejected, S be the number of true null hypotheses that are correctly not rejected, U be the number of false nulls that are correctly rejected, and T be the number of false nulls that are incorrectly not rejected. As described in Benjamini and Hochberg (1995), Table 1 summarizes the outcome of the analysis in terms of V, S, U, T, m₀, m₁, and m.

Table 1.

Hypothesis testing outcomes for m hypotheses

	H0 rejected	H0 not rejected	Total
Null H0 true	V	S	m0
Alternative Ha true	U	T	m1
Total	R	W	m

Because each hypothesis test gives one of two outcomes (reject or fail to reject the null hypothesis), we can consider each of the variables V, S, U, and T in Table 1 to be the sum of the number of successes (or failures) in a series of Bernoulli trials. More specifically, if rejection of the null hypothesis is defined as a “success”, then V is the total number of successes in a series of m₀ Bernoulli trials. If the actual level equals the nominal level of each of the m₀ tests of a true null hypothesis, then the expected value of V is m₀α. Under the assumption that p-values testing true null hypotheses are independent uniform (0,1) random variables, V follows a binomial distribution with success probability α and number of trials m₀. As previously mentioned, many methods make these assumptions which ignore the biological reality of intergene correlations. Our approach allows for dependence among the m₀ p-values testing true nulls and similarly for dependence among the m₁ p-values testing false nulls. We assume that each set of p-values has the same structure of dependence, but that each set of p-values is independent of one another.

2.1 The Beta-binomial Distribution

We propose to model V with the BB distribution. That is, V has the following density function:

$$P(V=v)=\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{B(v+a,m_0-v+b)}{B(a,b)},$$ (1)

where B(a, b) = Γ(a)Γ(b)/Γ(a + b), μ =a/(a + b), and φ = (a+b+1)⁻¹, 0< μ <1, 0< φ <1. Here E(V) = m₀μ, the number of Type I errors, or the number of false rejections, is the BB mean (μ is the expected Type I error rate) and φ is the BB positive intra-hypotheses correlation for the m₀ true null hypotheses, i.e., φ = Corr(V_i, V_j), i,j = 1, …, m₀, i ≠ j, where V_i and V_j represent the ith and jth, respectively, indicators of false rejections among the m₀ true null hypotheses.

We can reparameterize equation (1) in terms of only μ and φ to equate to the following density function:

$$P(V=v)=\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{{\displaystyle \prod _{k=0}^{v-1}}\left(\mu +\frac{k\phi }{\phi -1}\right){\displaystyle \prod _{k=0}^{m_0-v-1}}\left(1-\mu +\frac{k\phi }{\phi -1}\right)}{{\displaystyle \prod _{k=0}^{m_0-1}}\left(1+\frac{k\phi }{\phi -1}\right)}.$$ (2)

Equation (2) is a common formulation of the BB density function when one is interested in estimating the mean parameter and the correlation parameter, which in this case are μ and φ, respectively. These parameters are easier to interpret than the original parameters in (1); see Appendix A for the details of the derivation of (2). Now that the density function (2) is in terms of μ and φ (with m₀ assumed to be known), let us assume that we have a BB process in which N realized values of V, say ν₁,…, ν_N, exist. Then the BB log-likelihood function l is given as the follows:

$$l\approx \sum _{i=1}^N\left[\sum _{j=0}^{v_i-1}log\left(\mu +\frac{j\phi }{1-\phi }\right)+\sum _{j=0}^{m_0-v_i-1}log\left(1-\mu +\frac{j\phi }{1-\phi }\right)-\sum _{j=0}^{m_0-1}log\left(1+\frac{j\phi }{1-\phi }\right)\right].$$ (3)

To use equation (3), we first need an estimate for m₀, the number of true null hypotheses, for each set of beta-binomial trials.

2.2 The Mean Differences Method

To estimate m₀, we use the mean differences method proposed by Hsueh et al. (2003). They compared this method to four other methods for m₀ estimation via a simulation study. Their results showed that this method (as well as the least squares method) performed better than the other methods for estimating m₀, whether independence or dependence was the assumed underlying correlation structure among the m hypotheses. In their simulation study, Tsai et al. (2003) used the mean differences method for m₀ estimation under both the independence and dependence assumptions and their results similarly illustrated that this method estimates m₀ very well.

The mean differences method starts with taking the ordered p-values p₍₁₎, …, p_(m), corresponding to the m hypotheses; we obtain these p-values the traditional way by performing m two-group comparisons (t-tests) on the m sets of gene expression levels. Assuming that p₍₀₎ = 0 and p_(m+1) = 1 and that the largest (m+ 1−m₀) p-values come from the true null hypotheses, then define the differences as d_i = p_(i) − p_(i−1) [for i = (m−m₀) + 1_,,…, m+1]. Assuming p_i-independence, then the d_i differences are independent identically distributed beta (1, m₀) with mean E(d_i) = 1/(m₀+1); then

$${\widehat{m}}_0=1/{\overline{d}}_{m_0}-1\approx 1/E(d_i)-1,$$ (4)

where ${\overline{d}}_{m_0}={\displaystyle \sum _{i=m+1-m_0}^{m+1}}{d}_i/(m_0+1)=[1-p_{(m-m_0+1)}]/(m_0+1)$. Starting with j = m+1 and d̄_j = [1− p_(m−j+1)]/j, sequentially, the process stops at the first occurrence of d̄_j−1 ≤ d̄_j. Then the estimate of m₀ (m̂₀) is 1/d̄_j − 1.

2.3 The Permutation Procedure

To maximize (3), we will need realized values for V, the number of false rejections. To accomplish this, we propose the following approach. Given phenotype data that corresponds to expression microarray data for m genes, let E be the gene expression matrix in which the rows represent subjects and the columns represent the various genes. Also, let m̂₀ be the estimated number of true nulls obtained from applying the mean differences method, described in Subsection 2.2, to the data and let r be the observed number of rejections based on some pre-specified α. Then the following steps outline our process for generating realized values for V:

1. Permutation

   Randomly permute the rows of E, keeping the row labels in tact. Call this permuted matrix E^P. This permutation simulates the setting with all m hypotheses being truly null.

2. Hypothesis Testing

   Perform the set of m hypothesis tests on E^P.

3. False Rejections

   Treat the number of observed rejections ν₁ as the number of false rejections. As shown in Table 1, ν ≤ min(r, m̂₀) should be true. ν₁ satisfies this condition, then use the generated value for ν₁; if r<ν₁ ≤ m̂₀, then set ν₁ = r; and if ν₁ > m̂₀, then repeat steps 1 and 2 until ν₁ ≤ m̂₀.

4. Iteration

   Repeat steps 1 through 3 until N values ν₁, …, ν_N are generated.

The set of values v₁, …, ν_N, in addition to m̂₀, can now be used in the log-likelihood function given by equation (3). The next task is to maximize equation (3) to obtain estimates for μ and φ. Once we get the set of values {m̂₀, ν₁, …, ν_N}, then we can use the betabin function from the R version 1.1.8 package aod (Lesnoff and Lancelot, 2005). This function yields estimates for the BB parameters μ and φ. The bbFDR is given by the following formula:

$$\text{bbFDR}=E(V)/r=m_0\mu /r,$$ (5)

where V is the number of false rejections from a BB distribution with parameters μ and φ.

3 Results

We tested the performance of our proposed method on a microarray data set from a study comparing soft-tissue sarcomas and normal tissue samples and also in a simulation study. For the actual data, we estimated the eFDR and applied the methods described in Section 2 to calculate the bbFDR estimate. Then, we compared the two approaches. In the simulation study, we ran various simulations under different conditions to see how well the BB method performed as compared to the empirical approach.

3.1 Example: Soft-Tissue Sarcoma study

We applied the proposed model to an example from a microarray experiment that investigated using the expression of angiogenesis-related genes to classify soft-tissue sarcomas (Yoon et al., 2006). In the experiment, the gene expression patterns of soft-tissue sarcoma tissue samples and those of normal tissue samples were quantified and analyzed using oligonucleotide microarrays. An array consisted of more than 22,000 probe sets representing somewhat more than 14,000 genes. We extracted the data from the GEO database (http://www.ncbi.nlm.nih.gov/projects/geo/), accession number GSE2719. From this database, we found 39 soft-tissue sarcoma sample arrays and 15 normal tissue sample arrays. Hence, our analysis is based on this data set of 54 samples.

In their microarray experiment, Yoon et al. (2006) conducted hierarchical cluster analysis to classify soft-tissue sarcomas and normal tissues into groups on the basis of their gene expression levels. They did this first for both entire set of genes, and then for a subset of angiogenesis-related genes. Their results indicated several clusters for the sarcomas and one cluster for the normal sample, with the normal tissue samples clustering into their own group completely exclusive from any of the sarcoma clusters in both cluster analyses. However, Yoon et al. did not use a statistical approach to estimate FDR. Using their data, we assessed the differential expression by estimating the eFDR and bbFDR and compared the two.

As previously mentioned, the formula for the eFDR is eFDR = E(V)/r = (m₀α)/r. Using this formula, for a pre-determined α, with r being the observed number of rejections, the only task is to estimate m₀. Recall that we used the mean differences method described in Subsection 2.2. Setting α = 0.01, from the set of m = 22,283 probes of the sarcoma data set, the observed number of rejections is r = 3,909, which is about 17.5% of the hypotheses rejected. The mean differences method yields m̂₀ = 18, 935, so the estimated eFDR, i.e., (m̂₀α)/r, is about 0.048.

Assuming the BB distribution for V, we estimated the parameters μ and φ. With the given m̂₀ = 18,935 and r = 3,909, we followed the four permutation steps outlined in Sub-section 2.3 to generate realizations for V based on a sample of N = 1,000 permutations. With V assumed to have the BB density function given by equation (2), for the data set {ν₁, …, v₁₀₀₀} and m̂0 = 18,935 used in place of m₀, we estimated the BB parameters μ and φ by maximizing l in equation (3). Our maximization yielded the following estimates: μ̂ =0.0138 (SE=0.0002) and φ̂ =0.0043 (SE=0.0002). Thus, our approach yields a Type I error estimate (μ̂ =0.0138) that was slightly higher than the nominal α =0.01 and a non-zero estimate of BB correlation. Using (5), the bbFDR estimate was about 0.067. Our BB approach yielded an estimate of the FDR that was about 2% higher than that of the eFDR (0.048).

3.2 Simulation study

As in the application, we did not know the underlying correlation structure; thus, we conducted a simulation study to assess the performance of our BB approach to estimate the FDR and to determine how well the empirical approach maintains its ability to estimate under a stronger correlation structure. We used the following approach to generate correlated gene expression level values.

Assume that the microarray data is organized into an expression matrix E_n×m, where n is the total number of samples and m is the total number of hypotheses, which equates to the total number of genes. The sample size n = n₁+n₂, where n₁ is the size of the control group and n₂ is the size of the threated group. Hence, the jth hypothesis is as follows: H_0j:μ_1j = μ_2j vs. H_aj: μ_1j ≠ μ_2j; j=1, …, m; here, μ_1j and μ_2j are the average jth gene expression values for the control and treated groups, respectively.

As in Hsueh et al. (2003), we generate the same pairwise correlation structure within each set of m₀ true null and m₁ false null hypotheses. Next, we generated the expression values for the matrix E_n×m. For the ijth entry of E, let the expression level be represented by E_ij = Z_i + ε_ij. The following describes how we generated the ij entries of E:

• For i=1, …,n; j=1, …, m₀, let Z_i ~ N(0, ρ) and ε_ij ~ N(0,1 − ρ).

• For i =1, …, n₁; j= m₀ +1, …, m, let Z_i ~ N(0, ρ) and ε_ij ~ N(0,1− ρ).

• For i = n₁ +1, …,n; j= m₀ +1, …, m, let Z_i ~ N(2, ρ) and ε_ij ~ N(0,1 − ρ).

There is no differential gene expression among the first m₀ genes, hence all n samples, whether from the control or treated group, have the same distribution. For the m₁ differentially expressed genes, the n₁ control samples have a N(0, ρ) for Z and the n₂ treated samples have a N(2, ρ) for Z. Based on the described approach, the pairwise correlation for two expression levels, E_ij and E_ij′, is given by ρ = Corr(E_ij, E_ij′), where j and j′ are either both in the set {1, …, m₀} or both in the set {m₀ +1, …, m}. See Appendix B for details on deriving the correlation ρ.

In our simulations, for the set m={1000, 3000} of hypotheses, we assumed the number of true nulls m₀ to be from the set m₀ ={0.8m, 0.9m, 0.95m}. We looked at two different sample-size scenarios: n =20 (n₁ = n₂ = 10) and n=40 (n₁ = n₂ = 20). Within each (m, m₀) combination, we assumed five different underlying correlation structures: ρ =0 (independence), and ρ =0.10, 0.25, 0.50, and 0.75. We set the nominal Type I error rate α =0.01 for all simulations. For each combination presented in this paragraph, we simulated 1,000 microarray representations of E and employed the permutation approach described in Subsection 2.3. We used N=300 permutations to determine the BB estimates at each simulation, and we averaged the estimates over all simulations. We reduced the number of permutations from 1,000 (used in the sarcoma example) to 300 (for these simulations). We had found that our results using 1,000 or 300 permutations were comparable and using the smaller number reduced computing time. Tables 2 through 5 present the results of our simulations.

Table 2.

Simulation sets with sample size n=20 and m=1,000 hypotheses

m	m0	ρ	FDR	eFDR	bbFDR	m̂0	r̂	μ̂	V̄	φ̂
1000	800	0.00	0.0385	0.0424	0.0495	814.3	192.3	0.0117	7.4	0.0023
		0.10	0.0367	0.0427	0.0500	814.5	191.6	0.0117	7.1	0.0039
		0.25	0.0339	0.0432	0.0508	812.5	190.7	0.0118	6.7	0.0100
		0.50	0.0285	0.0437	0.0502	802.3	191.2	0.0121	6.2	0.0344
		0.75	0.0243	0.0543	0.0461	804.2	190.7	0.0111	7.7	0.1025
	900	0.00	0.0827	0.0903	0.0934	910.0	100.9	0.0103	8.4	0.0008
		0.10	0.0783	0.0910	0.0944	909.9	100.4	0.0104	8.0	0.0022
		0.25	0.0706	0.0921	0.0954	907.9	99.9	0.0104	7.6	0.0077
		0.50	0.0619	0.0947	0.0894	893.7	100.0	0.0101	7.9	0.0264
		0.75	0.0444	0.1210	0.0678	892.8	101.9	0.0081	9.4	0.0696
	950	0.00	0.1587	0.1744	0.1708	956.5	55.1	0.0098	8.9	0.0002
		0.10	0.1489	0.1763	0.1729	956.4	54.8	0.0098	8.4	0.0017
		0.25	0.1297	0.1808	0.1721	954.4	54.4	0.0096	8.0	0.0064
		0.50	0.1047	0.1915	0.1439	940.2	55.6	0.0083	9.1	0.0196
		0.75	0.0586	0.2515	0.0972	942.8	52.6	0.0056	6.6	0.0444

Table 5.

Simulation sets with sample size n=40 and m=3,000 hypotheses

m	m0	ρ	FDR	eFDR	bbFDR	m̂0	r̂	μ̂	V̄	φ̂
3000	2400	0.00	0.0377	0.0385	0.0477	2401.6	623.4	0.0124	23.5	0.0020
		0.10	0.0368	0.0386	0.0478	2400.9	622.9	0.0124	23.1	0.0037
		0.25	0.0332	0.0387	0.0480	2397.3	621.3	0.0124	21.5	0.0097
		0.50	0.0322	0.0383	0.0480	2364.3	623.8	0.0132	23.9	0.0330
		0.75	0.0178	0.0390	0.0424	2375.0	615.0	0.0118	15.0	0.1031
	2700	0.00	0.0810	0.0828	0.0907	2701.1	326.4	0.0110	26.5	0.0006
		0.10	0.0804	0.0828	0.0909	2700.1	326.8	0.0110	26.8	0.0022
		0.25	0.0710	0.0836	0.0917	2696.8	324.9	0.0110	25.0	0.0079
		0.50	0.0600	0.0841	0.0850	2665.3	325.7	0.0104	25.8	0.0248
		0.75	0.0420	0.0856	0.0622	2655.7	328.9	0.0088	29.0	0.0720
	2850	0.00	0.1576	0.1601	0.1660	2850.6	178.2	0.0104	28.2	0.0002
		0.10	0.1477	0.1620	0.1677	2850.2	176.8	0.0104	26.8	0.0017
		0.25	0.1395	0.1634	0.1642	2843.7	178.4	0.0101	28.4	0.0065
		0.50	0.1095	0.1684	0.1363	2803.8	181.6	0.0088	31.7	0.0189
		0.75	0.0695	0.1754	0.0879	2783.0	182.2	0.0068	32.2	0.0498

For each simulation scenario, the FDR (the 4^th column in each table) was found by calculating Q (recall Q = 0 for R = 0) for each simulation run, and then averaging over all simulations. Similarly, the eFDR and bbFDR entries were found by calculating the estimates of each simulation run, then averaging over all runs. In Tables 2 through 5 and at the lowest value of m₀, the eFDR is less biased than the bbFDR, except for two cases in which ρ = 0.75 (Tables 2 and 4),. However, as the value of m₀ increases, the bbFDR begins to outperform the eFDR at the lower values of ρ. For example, in Table 2 at m₀ = 800, the bbFDR is less biased for only the highest value of ρ = 0.75; then at m₀ = 900, it is less biased for ρ = 0.50 and 0.75; and finally at m₀ = 950, it is less biased for all five values of ρ. A similar pattern occurs in the other tables. Also, note that the eFDR tends to increase monotonically with ρ and therefore diverges from the FDR. This finding implies that the eFDR breaks down at high gene-expression correlations.

Table 4.

Simulation sets with sample size n=20 and m=3,000 hypotheses

m	m0	ρ	FDR	eFDR	bbFDR	m̂0	r̂	μ̂	V̄	φ̂
3000	2400	0.00	0.0387	0.0425	0.0493	2455.4	577.6	0.0116	22.4	0.0020
		0.10	0.0392	0.0426	0.0496	2452.8	577.2	0.0116	22.8	0.0035
		0.25	0.0376	0.0429	0.0500	2445.7	577.3	0.0117	22.7	0.0089
		0.50	0.0369	0.0437	0.0507	2401.0	579.9	0.0131	26.7	0.0302
		0.75	0.0239	0.0566	0.0458	2397.6	576.0	0.0118	20.5	0.0971
	2700	0.00	0.0828	0.0905	0.0933	2738.9	302.7	0.0103	25.1	0.0007
		0.10	0.0809	0.0909	0.0939	2738.0	302.2	0.0103	24.8	0.0020
		0.25	0.0771	0.0914	0.0942	2730.2	303.6	0.0103	25.5	0.0068
		0.50	0.0590	0.0960	0.0894	2707.3	300.5	0.0099	23.7	0.0220
		0.75	0.0349	0.1110	0.0689	2698.7	292.0	0.0082	18.3	0.0638
	2850	0.00	0.1595	0.1744	0.1703	2876.4	165.1	0.0098	26.4	0.0002
		0.10	0.1548	0.1755	0.1712	2875.0	165.1	0.0098	26.2	0.0015
		0.25	0.1402	0.1792	0.1706	2869.0	165.2	0.0096	26.2	0.0058
		0.50	0.1035	0.1919	0.1459	2836.8	165.7	0.0083	27.3	0.0169
		0.75	0.0674	0.2392	0.0955	2802.5	165.8	0.0067	27.5	0.0462

Tables 2 and 3 represent findings from analyses using the same number of hypotheses (m = 1,000), but with different sample sizes (n = 20 and n = 40, respectively). Both eFDR and bbFDR are less biased for the 40-sample size scenarios as compared to their corresponding 20-sample size scenarios. In comparing Table 4 to Table 2 (and Table 5 to Table 3), we observed a similar pattern. Therefore, increasing the number of hypotheses (genes) from 1,000 to 3,000 resulted in comparable results. We also ran a few scenarios with 5,000 genes and the results were still comparable to their corresponding 1,000-gene and 3,000-gene scenarios. We realized that after a certain value of m is attained, the number of genes m becomes less of a factor, and the proportion of true nulls π₀ (and sample size) that has the greater effect on the results.

Table 3.

Simulation sets with sample size n=40 and m=1,000 hypotheses

m	m0	ρ	FDR	eFDR	bbFDR	m̂0	r̂	μ̂	V̄	φ̂
1000	800	0.00	0.0377	0.0385	0.0477	799.9	207.8	0.0124	7.9	0.0022
		0.10	0.0371	0.0385	0.0478	799.4	207.8	0.0124	7.8	0.0041
		0.25	0.0331	0.0386	0.0481	797.7	207.2	0.0125	7.2	0.0108
		0.50	0.0323	0.0381	0.0477	780.9	208.8	0.0142	8.8	0.0408
		0.75	0.0248	0.0386	0.0416	789.5	208.6	0.0120	8.6	0.1144
	900	0.00	0.0802	0.0828	0.0907	899.9	108.8	0.0110	8.8	0.0007
		0.10	0.0763	0.0831	0.0912	899.5	108.4	0.0110	8.5	0.0024
		0.25	0.0753	0.0830	0.0909	895.8	109.1	0.0110	9.1	0.0083
		0.50	0.0550	0.0844	0.0846	883.6	108.6	0.0109	8.6	0.0298
		0.75	0.0324	0.0868	0.0633	893.7	107.2	0.0081	7.2	0.0737
	950	0.00	0.1541	0.1608	0.1664	949.8	59.2	0.0104	9.3	0.0002
		0.10	0.1510	0.1613	0.1674	949.2	59.3	0.0104	9.3	0.0019
		0.25	0.1266	0.1658	0.1668	946.6	58.6	0.0101	8.7	0.0071
		0.50	0.0944	0.1711	0.1370	934.5	58.4	0.0086	8.4	0.0220
		0.75	0.0528	0.1795	0.0884	941.8	58.0	0.0058	8.0	0.0493

To correlate the simulation study with the sarcoma study, given in Subsection 3.1, we must first recall that m₀ was estimated to be 18,935 in the example. Of the total of 22,283 probe sets from the example, this m₀ corresponds to having about an 85% rate of true null hypotheses; this falls in between the 80% and 90% rates corresponding to the first two (m, m₀) combinations in Tables 2 through 5. Also, recall that the estimate of the BB correlation φ was 0.0044, which according to the tables would correspond to values of ρ between 0.10 and 0.25. This means that for the sarcoma study, these results are in the region of the parameter space where the bbFDR begins to better estimate the FDR, though the bbFDR is slightly more biased than the eFDR. That is, approaching a 90% true null rate and having somewhat low but possibly moderate correlation, the sarcoma study is an example where the bbFDR begins to show improved estimation.

3.3 Figures

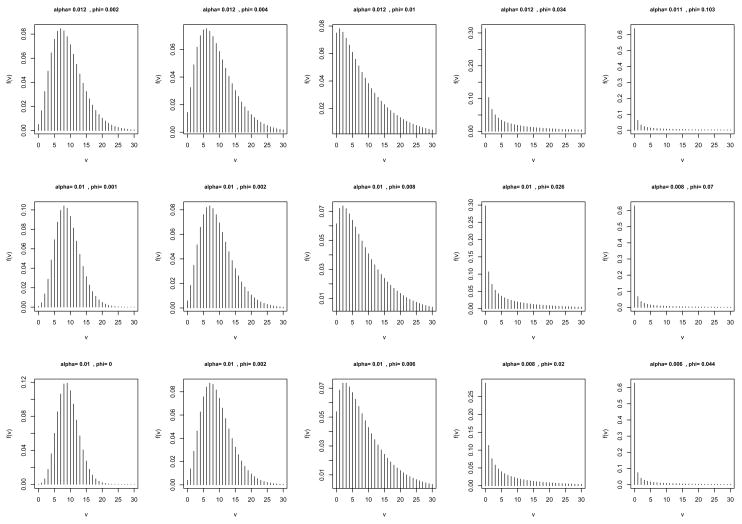
We generated probability mass function (pmf) plots for the sets of simulations in Table 2 to illustrate the change in the distribution of V with the change in the correlation φ. These plots are presented in Figure 1. As can be seen in each row of plots, as φ increases, the distribution of V becomes more right-skewed. The FDR is roughly positively related to E(V). Hence, as the right-skewness increases, E(V) decreases, and because the number of rejections r remains stable for a given m₀, then the FDR also decreases (Table 2).

Figure 1.

Pmf plots of the distribution of false rejections V. Plots, from left to right, correspond to rows of Table 2, i.e., first row of five plots equates to first five rows of Table 2, etc. As the correlation increases in the pmf plots, the distribution of false rejections becomes more right-skewed.

Noticeably from Tables 2 through 5, we see a strong relationship between ρ and φ. This is reasonable, because as the correlation among genes increases, we expect that the corresponding hypotheses, in terms of acceptance and/or rejection, would also increase. In addition to the noticeable relationship between φ and ρ, there also appears to be an inverse relationship between φ and π₀, i.e., the corresponding values of φ are smaller for larger π₀ values. Figure 2 is a plot of the observed relationship between φ and ρ when the π₀ values = 0.8, 0.9, and 0.95, respectively.

Figure 2.

Plots of the observed relationship between φ and ρ when π₀ = 0.8, 0.9, and 0.95.

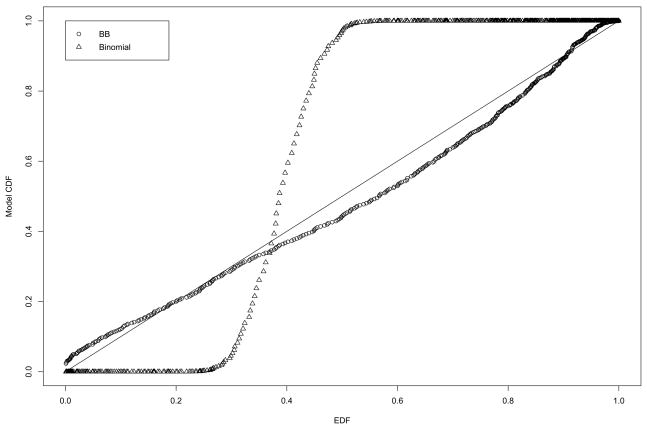
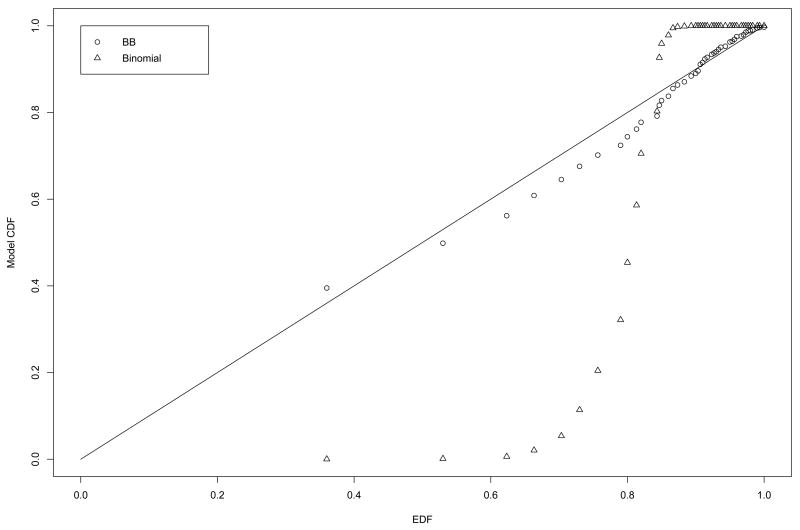
We wanted to assess the validity of the BB model (2) over the binomial model for the distribution of the number of false positives V generated from the permutation algorithm. To accomplish this, we generated probability-probability (P-P) plots of the empirical distribution function (EDF) of the permutation-generated data ν₁, …, ν_N and the cumulative distribution function (CDF) based on (2) and the binomial distribution. Figure 3 are the P-P plots for the permutation-generated data from the sarcoma study; the BB CDF is much closer to the EDF than is the binomial CDF. Figure 4 are the P-P plots for the permutation data for one case of the simulation study: m = 1,000, n = 40, π₀ = 0.90, and ρ =0.50; again, the BB CDF is the closer to the EDF. Note that these two plots represent data from cases of low to moderate gene expression correlations. These results indicate that the BB is a valid assumption for the distribution of V.

Figure 3.

P-P plots for the BB CDF (circles) and the binomial CDF (triangles) of the permutation data (ν₁, …, ν₁₀₀₀) from the sarcoma study.

Figure 4.

P-P plots for the BB CDF (circles) and the binomial CDF (triangles) of the permutation data (ν₁, …, ν₃₀₀) from the simulated data case m = 1,000, n = 40, π₀ = 0.90, and ρ =0.50.

4 Discussion

We have proposed an approach that models the inherent correlation between differential expression analysis p-values that must exist due to the pathway-induced correlation among gene expression levels. Our approach differs from traditional approaches that implicitly assume a binomial distribution for the number of false rejections V. The BB model has the desirable property of including a parameter that directly corresponds to the correlation of whether a p-value is less than a chosen threshold. Therefore, in addition to significance level α, the correlation becomes a factor in FDR estimation. In addition to the BB distribution, we incorporated a permutation-based method into the model to generate pseudo-data to facilitate the model fit. Results from both the application and simulations indicated that this method is reasonable for FDR estimation.

Our simulation studies indicated that the correlation among genes may introduce substantial bias in the traditional FDR estimates that are derived under the assumption of p-value independence. The magnitude of this bias depends on several parameters, including the strength of gene-gene correlation, the number of hypotheses tested, and the proportion of null hypotheses that are true. In general, it appears that traditional methods become more conservatively biased as ρ increases while other parameters fixed. This bias can be very detrimental in terms of statistical power. Although the actual FDR decreases as ρ increases, the expected value of the eFDR estimate remains relatively constant or increases. On the other hand, as ρ increases, the expected value of the bbFDR estimator decreases with the actual FDR. This reduces the conservative bias and improves the power of the bbFDR estimator relative to the eFDR estimator. Additionally, the bbFDR estimator showed conservative bias in most simulation settings. The benefits of the bbFDR are realized even for moderate correlations (between 0.10 and 0.25).

The extent of correlation among gene expression levels in practice and how that correlation translates into correlation among p-values has not been thoroughly examined. Storey and Tibshirani (2003) have suggested that gene-gene correlations are typically negligible in studies that use genome-wide arrays but not so in studies that use specialized arrays that focus on a specific pathway or disease genes. Our example application is consistent with this conjecture: it utilized a genome-wide array and the correlation parameter estimate was small. Correlations can be high (or low) if the important pathways are well (or poorly) represented on the array.

The results from our study indicates that, if there is indeed correlation among gene expression levels in studies of microarray data, then there could be many cases where the FDR estimates are biased. Certain caveats have to be considered, such as the degree of intergene correlation, the number of genes m, and the proportion of true null hypotheses π₀. Although our application to the sarcoma study resulted in a rather low pairwise correlation in terms of the BB distribution, the estimate was significant, and by comparing it to the BB correlation estimates from the simulation study, we found that it may actually be comparable to moderate values for gene expression correlations (between 0.10 and 0.25). In our study, we showed that at moderate correlations under certain conditions, the BB method outperforms the empirical. Even with the low correlation from the actual data, the FDR estimate increased from 5% to about 7%. Given the large number of genes in microarray studies, this seemingly small increase in percentage could be meaningful.

To assess the meaning of the application results and to generally determine the conditions under which our proposed BB modeling approach would best estimate FDR, we conducted a simulation study in which the data structure for many microarray studies was mimicked by using data generated from assumptions of independence and dependence beamong hypotheses. The results indicated that the BB approach obviously outperforms the empirical method at the highest correlations and that at higher values of π₀, it outperforms the empirical one at even lower correlations. We also found that there was similarity in results across values of m, i.e., for a large enough m, the results are more affected by sample size and proportion of true nulls than they are by m itself. This was illustrated by the fact that results from analyses with higher values of m (3,000 and 5,000) were similar to the results for those with m = 1,000.

In our simulations, we generated data with common correlations within the group of m₀ non-differentially expressed genes and the group of m₁ differentially expressed genes. In their simulations under dependence, Hsueh et al. (2003) assumed an equicorrelated model where the pairwise common correlations for both the group of m₀ truly null genes and the group of m₁ differentially expressed genes; we assumed the same correlation structure. Tsai et al. (2003) and Tsai et al. (2005) assumed equicorrelation among the m₁ false null hypotheses. Somerville (2004) assumed a multivariate t-distribution for the m test statistics, with a common correlation ρ. Benjamini et al. (1997) showed that the original Benjamini-Hochberg procedure controls the FDR in the case of equicorrelated test statistics.

In a simulation study designed to assess the ability of the common correlation BB model to estimate sample size in microarray experiments, Tsai et al. (2005) extended the assumption of common correlation among m₁ false nulls to two potential models of correlation that could occur in practice: one where the genes occur in equicorrelated groups and one where there is general correlation structure. They found that the BB assumption can underestimate the desired sample size in these cases. Their BB model differs from ours in multiple ways. Their model assumes R to be BB, while we assume V to be BB. Also, they simulated correlation only among m₁ false nulls, whereas we simulate correlation among the m₀ true nulls as well. The more complex correlation models definitely may have merit; therefore, future research should explore how various methods perform under these more complex correlation structures.

Because intergene expression correlation being an intrinsic feature in studies of microarray data, the BB distribution is a viable option for estimating the FDR. This distribution includes the motivating characteristic of having a correlation parameter to estimate the correlation among the hypotheses in these studies. We have shown that, with the existence of correlation, our method yields an estimate for FDR that is less biased than the empirical estimate, which inherently presumes independence across hypotheses, under certain conditions. Our results illustrate the utility and the conditions under which our BB method outperforms the empirical approach. The method appears to be a legitimate option for estimating the FDR in microarray studies.

Appendix A. Deriving re-parameterized beta-binomial density

Recall from equation (1) that the density function for the beta-binomial distribution is given by the following equation:

$$P(V=v)=\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{B(v+a,m_0-v+b)}{B(a,b)}.$$ (A.1)

Now, given that B(a, b) = Γ(a)Γ(b)/Γ(a + b), then the density function becomes

$$P(V=v)=\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{\mathrm{\Gamma }(v+a)\mathrm{\Gamma }(m_0-v+b)\mathrm{\Gamma }(a+b)}{\mathrm{\Gamma }(m_0+a+b)\mathrm{\Gamma }(a)\mathrm{\Gamma }(b)}.$$ (A.2)

Using the property of the gamma function Γ(·), i.e., for c>1, Γ(c) = (c−1)Γ(c−1) then (A.2) simplifies according to the following steps:

$$\begin{array}{l}P(V=v)=\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{\mathrm{\Gamma }(v+a)\mathrm{\Gamma }(m_0-v+b)\mathrm{\Gamma }(a+b)}{\mathrm{\Gamma }(m_0+a+b)\mathrm{\Gamma }(a)\mathrm{\Gamma }(b)}\\ =\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{(v-1+a)(v-2+a)\cdots (1+a)a\mathrm{\Gamma }(a)·(m_0-v-1+b)(m_0-v-2+b)\cdots (1+b)b\mathrm{\Gamma }(b)\mathrm{\Gamma }(a+b)}{(m_0-1+a+b)(m_0-2+a+b)\cdots (1+a+b)(a+b)\mathrm{\Gamma }(a+b)\mathrm{\Gamma }(a)\mathrm{\Gamma }(b)}\\ =\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{(v-1+a)(v-2+a)\cdots (1+a)a·(m_0-v-1+b)(m_0-v-2+b)\cdots (1+b)b}{(m_0-1+a+b)(m_0-2+a+b)\cdots (1+a+b)(a+b)}.\end{array}$$ (A.3)

Dividing both the numerator and the denominator of (A.3) by (a + b)^m₀, we get

$$\begin{array}{l}=\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{\left(\frac{v-1+a}{a+b}\right)\cdots \left(\frac{1+a}{a+b}\right)\left(\frac{a}{a+b}\right)·\left(\frac{m_0-v-1+b}{a+b}\right)\cdots \left(\frac{1+b}{a+b}\right)\left(\frac{b}{a+b}\right)}{\left(\frac{m_0-1+a+b}{a+b}\right)\cdots \left(\frac{1+a+b}{a+b}\right)\left(\frac{a+b}{a+b}\right)}\\ =\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{\left(\frac{a}{a+b}+\frac{v-1}{a+b}\right)\cdots \left(\frac{a}{a+b}+\frac{1}{a+b}\right)\left(\frac{a}{a+b}\right)·\left(\frac{b}{a+b}+\frac{m_0-v-1}{a+b}\right)\cdots \left(\frac{b}{a+b}+\frac{1}{a+b}\right)\left(\frac{b}{a+b}\right)}{\left(\frac{a+b}{a+b}+\frac{m_0-1}{a+b}\right)\cdots \left(\frac{a+b}{a+b}+\frac{1}{a+b}\right)\left(\frac{a+b}{a+b}\right)}.\end{array}$$ (A.4)

Because a/(a + b) = μ and 1/(a + b) = φ/(φ − 1), when we substitute into (A.4), we get

$$\begin{array}{l}=\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{\left(\mu +\frac{(v-1)\phi }{\phi -1}\right)\cdots \left(\mu +\frac{\phi }{\phi -1}\right)(\mu )·\left(1-\mu +\frac{(m_0-v-1)\phi }{\phi -1}\right)\cdots \left(1-\mu +\frac{\phi }{\phi -1}\right)(1-\mu )}{\left(1+\frac{(m_0-1)\phi }{\phi -1}\right)\cdots \left(1+\frac{\phi }{\phi -1}\right)(1)}\\ =\left(\begin{array}{c}{m}_0\\ v\end{array}\right)\frac{{\displaystyle \prod _{k=0}^{v-1}}\left(\mu +\frac{k\phi }{\phi -1}\right)·{\displaystyle \prod _{k=0}^{m_0}}\left(1-\mu +\frac{k\phi }{\phi -1}\right)}{{\displaystyle \prod _{k=0}^{m_0}}\left(1+\frac{k\phi }{\phi -1}\right)},\end{array}$$ (A.5)

which is the same as equation (2).

Appendix B. Deriving correlation ρ for gene expression values

For sample i, within the set of m₀ genes, the jth and j′th gene expression values are E_ij = Z_i + ε_ij and E_ij′ = Z_i + ε_ij′, where Z_i ~ N(0, ρ) and ε_ij ~ N(0,1 − ρ). Now, the pairwise correlation for these two expression values is

$$\mathit{Corr}(E_{ij},E_{i{j}^{\prime }})=\frac{\mathit{Cov}(E_{ij},E_{i{j}^{\prime }})}{\sqrt{\mathit{Var}(E_{ij})·\mathit{Var}(E_{i{j}^{\prime }})}}.$$ (B.1)

Because E_ij and E_ij′ have the same variance, then equation (B.1) becomes the following:

$$\mathit{Corr}(E_{ij},E_{i{j}^{\prime }})=\frac{\mathit{Cov}(E_{ij},E_{i{j}^{\prime }})}{\mathit{Var}(E_{ij})}.$$ (B.2)

By substituting Z_i + ε_ij and Z_i + ε_ij′ in place of E_ij and E_ij′, respectively, (B.2) becomes

$$\mathit{Corr}(E_{ij},E_{i{j}^{\prime }})=\frac{\mathit{Cov}(Z_i+{\epsilon }_{ij},Z_i+{\epsilon }_{i{j}^{\prime }})}{\mathit{Var}(Z_i+{\epsilon }_{ij})}.$$ (B.3)

Z and ε are independent, and any two ε’s are also independent; thus, equation (B.3) becomes

$$\begin{array}{l}\mathit{Corr}(E_{ij},E_{i{j}^{\prime }})=\frac{\mathit{Var}(Z_i)}{\mathit{Var}(Z_i)+\mathit{Var}({\epsilon }_{ij})}\\ =\frac{\rho }{\rho +(1-\rho )}\\ =\rho .\end{array}$$ (B.4)

In a similar manner, this same correlation ρ can be derived for the set of m₁ genes.