Employing Complier Average Causal Effect Analytic Methods to Examine Effects of Randomized Encouragement Trials

Abstract

Aims

This article details the application of Complier Average Causal Effect (CACE) analysis to the examination of youth outcomes from adaptive substance use prevention trials.

Methods

CACE analysis is illustrated using youth-reports of tobacco-use from ages 11 to 22, from the Adolescent Transitions Program, a family-focused randomized encouragement trial designed for delivery in the school setting

Results

Female gender and early peer deviance predicted family engagement with active intervention components. Further, long-term reductions in youth tobacco use from age 11 to age 22 were found for families that engaged with treatment.

Conclusions

CACE modeling techniques enable researchers to examine factors that predict engagement with core intervention components and to examine intervention effects specifically for youth who engaged with those components.

INTRODUCTION

There has been growing recent interest in identifying multiple pathways of substance use development over adolescence, coupled with a proliferation of newer analytic techniques that permit the identification of heterogeneous trajectories of use, and covariates that discriminate youth following different trajectories (1-3). One overarching theme from this emerging literature is that there are multiple pathways into the initiation and maintenance of substance use behaviors over adolescence, related to distinct profiles of familial (i.e., poor parent management practices, parental substance use/psychopathology, family conflict), and social risks (i.e., peer deviance/peer substance use) (1). Developmental heterogeneity presents a challenge for prevention research, as many prevention programs deliver the same services to all youth, regardless of the risk processes most central to a given individual. In light of this challenge, there is growing interest in “adaptive interventions” (4), which recognize that individual adolescents or families may have different intervention needs, with differing intervention targets and doses likely to be most effective. The core feature of an adaptive intervention is that specific intervention targets and doses are determined individually in light of the needs of the families. Advantages include more efficient use of resources, increased treatment compliance and intervention potency, greater resemblance to real-world clinical practice, and decreased chances of negative effects of intervention components that are inappropriate for a given individual (4).

There are a number of alternative adaptive intervention designs, with different profiles of advantages and disadvantages (5). One flexible example is the randomized encouragement design, in which participants are randomized to either control or intervention conditions (6). Participants in the intervention condition receive the opportunity to engage with intervention services, as they see fit, rather than receiving a standardized intervention sequence. This framework emphasizes the importance of giving families a central role in determining the services best matched to their needs or willingness to engage (14). In line with motivational interviewing principles, participants may receive a baseline assessment with tailored feedback and encouragement to engage with services matched to their needs, in order to maximize treatment engagement. Randomized encouragement trials retain core benefits of traditional randomized clinical trials (RCTs), while offering considerable flexibility to efficiently meet the unique needs of families (6).

Although there are advantages to adaptive intervention designs, there are also limitations, including the difficulty of determining proper analytic strategies to document intervention effects. Typical intent-to-treat (ITT) analyses compare outcomes across all participants in the treatment vs. control groups. In school-based family-focused encouragement trials, however, many low-risk parents may decline services, while high-risk families, who may have difficulties engaging with services in other settings, may find a free school-based intervention particularly attractive. ITT analyses combine outcomes for youth whose families engaged with treatment and those whose families did not, although there should be little effect of intervention for the latter families. Thus, ITT analyses will underestimate the effects of the active intervention components, and the magnitude of this underestimation is related to the proportion of intervention group families who engage with services. Alternative analytic approaches are possible, including per-protocol analysis excluding nonengaging families from the intervention group, or as-treated analysis, grouping individuals by the treatment actually received. However, these approaches break randomization, and have a high potential for bias (7). The central challenge in evaluating the impact of randomized encouragement trials is determining the appropriate comparison group from the control condition. Youth most similar to those from the intervention condition who also engaged with treatment would provide the most accurate picture of development in the absence of treatment engagement.

Fortunately, there have been important developments in statistical techniques for the analysis of RCT outcomes in the face of non-compliance with treatment, referred to as Complier Average Causal Effect (CACE) analyses, that can be applied to adaptive intervention trials (7, 8). CACE analysis builds upon Rubin’s causal modeling framework to yield causal estimates of the effects of intervention for individuals who comply with treatment (9). The core challenge in CACE modeling is illustrated by considering intervention outcomes (μ_i) and proportions of individuals (π_i) in the 4 cells defined by the intersection of treatment assignment, and treatment compliance: compliers (for whom treatment received is the same as the treatment assigned), never-takers (who do not receive treatment, regardless of treatment assignment), always takers (who receive treatment regardless of treatment assignment), and defiers (who always do the opposite of their treatment assignment). Thus, the overall mean of the intervention group can be given as: μ₁ = π_cμ_c1 + π_nμ_n1 + π_aμ_a1 + π_dμ_d1, and the mean of the control group can be given as: μ₀ = π_cμ_c0 + π_nμ_n0 + π_aμ_a0 + π_dμ_d0. In trials that carefully restrict treatment access, individuals in the control group who receive treatment are identified as always-takers (and their absence is assumed when none are identified), and the absence of defiers is assumed (as described below), reducing the number of compliance classes to two, compliers and never-takers. CACE analysis seeks to compare outcomes for individuals in the intervention condition who complied with treatment with individuals in the control group who would have complied with treatment given the opportunity to do so (CACE = μ_c1 – μ_c0).

The challenge for CACE analysis is that while outcomes and sample proportions are observed for compliers and non-compliers in the intervention condition, only the overall outcome mean is observed in the control group. The core insight behind CACE analysis is that we can arrive at an unbiased estimate of the difference in outcomes for compliers in the intervention group with those who would have engaged with treatment in the control group if we make 5 assumptions. First, we assume that potential outcomes for each participant are independent of the outcomes for other participants, known as the Stable Unit Treatment Value assumption (SUTVA). Second, we assume there is a monotonic relationship between treatment assignment and treatment receipt. Consequently, we assume there are no individuals for whom assignment to treatment actually reduces the likelihood of receiving treatment (i.e., no defiers). This assumption reduces the number of compliance types for whom we must derive estimates, permitting a properly identified model. Third, we assume that offering treatment to participants in the intervention condition induces at least some participants to receive treatment, so the compliance rate is not zero. Fourth, we assume that assignment to treatment is random. As such, we can assume that the proportion of compliers should be the same across the intervention and control groups thus allowing us to estimate one of the core unobserved parameters needed to derive a CACE estimate, as π_c1 = π_c0. Fifth, we assume that random assignment to treatment does not affect the outcomes of individuals who do not comply with treatment, an assumption known as the exclusion restriction. For never-takers, for instance, we assume that simply being assigned to treatment does not affect their outcomes, as they do not actually receive the treatment offered to them. In applying these assumptions, an instrumental variable approach to estimating the effect of treatment, accounting for non-compliance can be derived as CACE = (μ₁ – μ₀)/π_c (9).

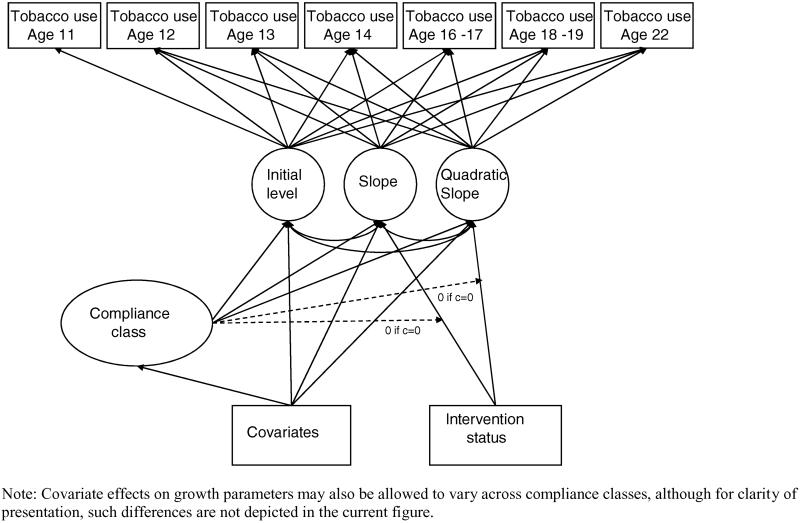
Although the instrumental variable approach marked an important advance in dealing with the problem noncompliance in intervention trials, recent developments in CACE analysis have been driven primarily by the application of more efficient likelihood-based estimation methods, including Two-Stage Least Squares, Bayesian, and maximum likelihood (ML) approaches (8, 10, 11). These likelihood-based approaches yield comparable results (12). The current article focuses on the ML approach, for illustrative purposes, using a mixture modeling framework to identify the optimal comparison group from the control group for observed compliers in the intervention group. This application of mixture modeling permits an examination of two aspects of intervention process—the prediction of intervention engagement and the examination the differential treatment effects on outcome of interest across engaging and non-engaging families. Compliance status is treated as a categorical latent variable, with known values in the treatment condition. Compliance status can be regressed upon covariates to examine pretreatment factors that predict engagement. Importantly, treatment is only allowed to predict substance use outcomes among compliers (as per the exclusion restriction). In longitudinal prevention trials, changes in substance use over time can easily be modeled using latent growth modeling techniques. An example CACE model is shown in Fig. 1.

FIG. 1.

Example CACE model with covariates and categorical outcomes.

CACE analysis can be readily adapted for the analysis of encouragement trails. Participants in the intervention condition who elect not to receive the intervention can be defined as non-compliers. However, this is in name only, as low risk participants (who may not need the intervention) may be less likely to engage with services. In adapting CACE modeling for randomized encouragement trials, we have described families as “engagers” or “non-engagers,” to avoid conveying the implication that “noncompliance” is necessarily a problematic outcome.

METHODS

The current study examines the impact of the Adolescent Transitions Program (ATP) on trajectories of adolescent tobacco use from early adolescence through early adulthood (13). The full sample included 998 youth recruited in two cohorts from three urban public middle schools. Families were ethnically diverse (42.4% Caucasian, 29.2% African American, 6.8% Latino, 21.6% other). Analyses focus on youth reports of the number of times tobacco was used in the prior 30 days, derived from 7 assessment waves when youth were age 11, 12, 13, 14, 16–17, 18–19, and 22. Data collection at age 22 is still ongoing for cohort 2, so the current article only includes data from cohort 1 (original n = 675). Approximately 74% of youth provided data at age 22. Due to space constraints, readers are referred to recent articles for full study details (14).

Stormshak and Dishion (this issue) provide complete details on the ATP, so brief details are presented here (15). The ATP was designed for delivery in public schools, with a model that links universal, selected, and indicated family interventions in a way that titrates intervention intensity to the needs and motivation of the family (13). The universal intervention involves universal screening, and the establishment of a family resource center in the school, providing parent-centered services such as brief parent consultations, and access to videotapes and books. The goal of the resource room was to support positive parenting practices in families of typically developing youth and to engage parents of high-risk youth for the selected intervention with a multistage screening procedure. Students identified with this screening procedure are referred to the selected level of intervention, the Family Check-Up (FCU). The FCU is a brief assessment-driven intervention designed to motivate parenting change when it is needed, as determined by comprehensive assessment, including direct observations and parent and youth reports. An outcome of the FCU is the development of a menu of intervention options for families, including family-management training targets adapted from empirically supported parenting interventions, which represent the indicated level of intervention (13).

Analysis Strategy

We illustrate key analytic steps, including defining engagement status in the intervention group, and the inclusion of covariates in CACE models. All analyses were carried out in Mplus 5.1, using full information maximum likelihood estimation to account for missing data, (16). Trajectories of tobacco use were modeled using intercept, slope, and quadratic slope parameters reflecting the initial level of tobacco use, and the linear and curvilinear rate of change in use over time, respectively. CACE models were implemented as latent growth mixture models, with engagement status included as a training variable for estimating class membership, known in the intervention group, but missing in the control group.

We are reasonably confident of meeting four of the assumptions underlying CACE modeling. First, as the FCU was delivered individually to families, we are reasonably confident in meeting the SUTVA criterion. Assumption two refers to the absence of “defiers.” We can observe that there were no “defiers” in the control group, as treatment records indicate that we did not deliver any intervention components to any control participants. Due to randomization, we assume that the same lack of defiers would be found in the intervention group. The third assumption is that the rate of compliance is not zero, and we can observe a non-zero rate of compliance among participants assigned to treatment, and due to randomization, we assume that the compliance rate is equal across the control and intervention conditions. Finally, the fourth assumption, that treatment assignment is random, was part of the study design. However, the exclusion restriction is the most questionable assumption. Violations of the exclusion restriction may lead to biased CACE estimates, with the magnitude of the bias related to the compliance rate and the effect of random-assignment on families who do not comply with treatment (8). Two types of bias may result from exclusion restriction violations. A demoralization effect, which leads to underestimation of the true CACE effect, occurs if families who are offered treatment but fail to take it show worse outcomes than they would have without random assignment. Conversely, a “moralization” effect, which leads to an overestimate of the CACE effect, occurs if random assignment to treatment has beneficial effects for families regardless of treatment engagement (8). However, the effects of bias due to violations of the exclusion restriction can be ameliorated by the inclusion of covariates predictive of engagement (8).

In order to examine the effect of adding covariates on the CACE estimate of the treatment effect, a series of analyses were conducted. First, a CACE model was examined including only treatment assignment as a predictor, without any additional covariates. In all models, treatment assignment was allowed to predict only the slope in the engager class, but not slope in the non-engager class, the intercept in any class, or class membership. Second, a CACE model including both treatment assignment and covariates was run, with covariates allowed to predict intercept and slope in both classes, along with class membership. Third, the exclusion restriction was relaxed in the presence of covariates, to examine the tenability of this assumption.

RESULTS

Intention-To-Treat Analysis

ITT analyses showed non-significant intervention effects on the slope (estimate = .05, SE = .12, p = n.s.) and quadratic slope (estimate = −.01, SE = .01, p = n.s.)

CACE Analysis: Defining Engagement

The first step in CACE analysis is to define “engagement.” Although all or none engagement may be clear in some trials, the dividing line may be challenging to locate in others. In general, there is a tradeoff, as stringent definitions of engagement may lead to larger CACE estimates, but may also result in the exclusion restriction assumption being less realistic. In the ATP, several definitions of engagement were considered. The most lenient definition of engagement in the intervention condition was simply having at least some contact with the family resource room, and 159 families (47.7%) met this criteria (ranging checking out reading material or films, receiving brief advice, to more formal engagement with the FCU). A more stringent definition of engagement required participants to complete the FCU, regardless of follow-up services, and 85 families (25.5%) assigned to intervention met this criteria. Finally, the most stringent definition of “Engagement” required completing the FCU and receiving individualized parent management training after-wards. Sixty-five families (19.5%) in the intervention condition met this criterion.

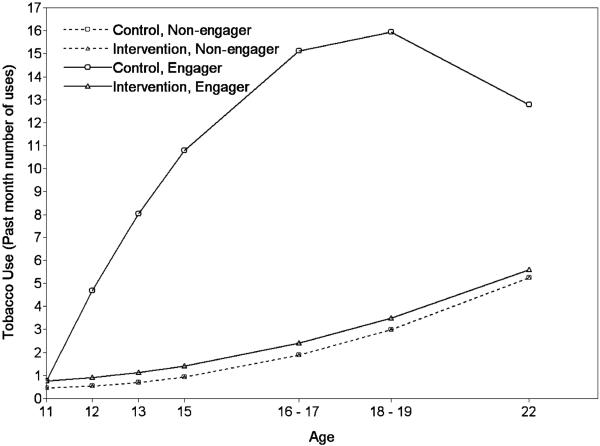
Three CACE models wereexamined, using the increasingly stringent definition of engagement. As expected, more stringent definitions yielded larger CACE estimates. Using the least stringent definition, treatment status was not significantly related to either the linear (estimate = .03, SE = .09, p = n.s.) or curvilinear slope (estimate = −.02, SE = .11, p = n.s.) among engagers. Using the moderately stringent definition, however, the intervention was significantly negatively related to the linear slope for tobacco use (estimate = −4.30, SE = .55, p < .001), but positively related to the curvilinear slope (estimate = .34, SE = .07, p < .001) for engagers. As shown in Fig. 2, treatment predicted significantly less growth in tobacco use, although the intervention effect diminished over time. The effect size for the difference in estimated tobacco use at age 22 for the engagers in the intervention vs. control condition was large (Cohen’s d = 1.27). Using the most stringent definition led to a similar CACE estimate of the impact of treatment on the linear slope (estimate = −4.41, SE = .57, p < .001), and curvilinear slope (estimate .34, SE = .07, p < .001). The effect size for age 22 estimated tobacco use was comparable to the prior effect size (Cohen’s d = 1.18).

FIG. 2.

CACE results of intervention effect on the development of tobacco use.

CACE Analysis: Inclusion of Covariates

The moderately stringent definition of Engagement was adopted for further analyses, because the FCU was conceptualized as the heart of the intervention approach. The next step in CACE analysis was to examine the impact of covariates as predictors of class membership and within-class variation in trajectories. Child gender and ethnicity, and youth-reported peer deviance and family conflict at age 11 were included as covariates. The magnitude of the intervention effect on the slope (estimate = −4.10, SE = .57, p < .001) and quadratic slope parameters (estimate = .33, SE = .07, p < .001) was largely unaffected by addition of these covariates. Engagement was predicted by female gender (estimate = −.52, SE = .22, p < .01) and elevated peer deviance (estimate = −.29, SE = .09, p < .01), while ethnicity (estimate = .14, SE = .22, p = n.s.) and family conflict (estimate = −.15, SE = .10, p = n.s.) not related to engagement.

CACE Analysis: Relaxing the Exclusion Restriction

In the presence of pretreatment covariates, it is possible to relax the exclusion restriction in order to examine its tenability by assuming an additive effect of treatment assignment (17). Relaxing the exclusion restriction assumption only modestly affected the CACE effect for engagers on the slope (estimate = −3.97, SE = .51, p < .001) and quadratic slope (estimate = .31, SE = .06, p < .001). However, in the non-engager class, a small effect of treatment assignment was found for the slope (estimate = .41, SE = .10, p < .001) and quadratic slope (estimate = −.03, SE = .01, p < .001), indicating a small demoralization effect for non-engager families (Cohen’s d = –.23). Although this demoralization effect must be interpreted with a caution in light of possible confounds, similar effects of relaxing the exclusion restriction have been found in other prevention trials (17, 18).

DISCUSSION

The current article examines the application of CACE modeling techniques to examine the effects of adaptive prevention programs on the development of substance use behaviors, focusing on long-term outcomes from a family-focused prevention program on reducing tobacco-use from early adolescence through early adulthood. Current results highlight that engagement with the FCU predicts large long-term reductions in tobacco-use from age 11 through age 22, thereby extending prior analyses of the FCU, which examined treatment effects to age 16–17 (14). Results highlight the advantage of tailoring prevention services to families in such a way as to motivate family engagement with services and maximize resource use. In the current study, families of high-risk youth (indexed by early peer deviance) were most likely to engage with the FCU. In prior analyses with this sample, we identified additional predictors of engagement, including elevated family conflict and the absence of biological fathers from the youth’s primary home (14). Taken together, such results highlight that the parents of high-risk youth were disproportionately likely to engage with the FCU, underscoring the benefit of actively employing methods to target parental motivation to change within the context of randomized encouragement trials. In turn, youth whose parents engaged with the FCU showed significantly less growth in tobacco use over adolescence and into early adulthood when compared with similarly high-risk youth in the control group, and this CACE effect was large in magnitude. Substantively, these results are important in highlighting that parental engagement with the FCU can lead to substantial reductions in early tobacco use, thus pointing to the central role of parents in the early development of tobacco-use behaviors. It is worth highlighting that a relatively small percentage of families in the intervention condition elected to engage with treatment. Work attempting to engage a larger proportion of families into the FCU is ongoing.

These results also illustrate the application of CACE methods to examine treatment outcomes of randomized encouragement trials. The core challenge of these trials is identifying methods to gauge the extent to treatment leads to improved outcomes for participants who elect to engage with core intervention components. CACE modeling techniques enable researchers to examine factors that predict engagement with core intervention components and to examine intervention effects specifically for youth who engaged with those components. In addition to the flexibility of the analytic framework for testing targeted hypotheses regarding intervention effects, CACE modeling has advantages over alternative analytic approaches, as the underlying assumptions are clearly specified and can potentially be examined in the context of specific trials. The current analyses also highlight challenges with respect to the underlying assumptions of CACE modeling, as random assignment to treatment may have had a small demoralization effect on youth whose families did not engage with the FCU. Further analysis is needed to examine this possibility.

It is worth highlighting that CACE analysis is not the only method available for analyses of adaptive prevention trials, and may not be the method of choice, depending upon the trial design. At the trial design stage, researchers should consider multiple-stage randomization procedures to enable the detection of effects of specific intervention components on youth outcomes (27). In the current trial, for instance, we could tease apart the effects of different levels of the prevention program by randomizing youth to the control group, the universal intervention only, the FCU only, or the FCU and parenting services. Alternatively, the benefit of adaptive tailoring could be examined by randomly assigning some youth in the intervention group to receive the 12 week parenting program in uniform fashion, vs. receiving the FCU and an individually tailored parenting program. Outcomes of interest could include intervention effects on youth substance use, as well as rates of family engagement and retention over the course of the trial. These randomization strategies would allow testing of a priori hypotheses regarding more complex intervention effects, rather than relying on post-hoc statistical methods. Even in the context of post-hoc statistical applications, CACE modeling is not the only technique available. For instance, alternative growth mixture-modeling techniques can be used to examine intervention effects for heterogeneous subgroups of youth (1). Alternative propensity core matching approaches could also be used to examine intervention effects for subgroups of youth, although these approaches face issues, such as the number of covariates to include in stratification and handling ambiguous propensity scores (19). CACE modeling has advantages over these alternate approaches, as the statistical assumptions underlying CACE analysis are clearly specified, whereas alternative post-hoc methods are based upon unclear or poorly specified assumptions, and the optimal manner of applying these approaches is not always clear.

Additional Modeling Options

While the current article examined a simple example of CACE modeling for adaptive prevention trials, there are several modeling extensions that may allow testing of additional hypotheses and resolution of modeling issues. First, it is possible to model outcomes of growth processes across engager and non-engager strata. For instance, in the current study, diagnostic data was collected when youth were aged 18–19 years old using structured diagnostic interviews. Prior analyses indicated that family engagement with the FCU predicted significantly decreased likelihood of nicotine dependence/withdrawal diagnosis by late adolescence (odds ratio = .30). We hope to examine the persistence of this diagnostic effect with future analyses. Second, when multiple intervention effects are examined in the same study (i.e., tobacco, alcohol, and other drug use trajectories), it is common to use separate CACE models for each outcome. It is possible that the predictors of engagement may vary across these separate models, as CACE estimates class membership probabilistically (14). In such instances, multiple outcome trajectories can be included in a multivariate CACE model, thereby estimating engagement-class membership only once (20), or a two-stage estimation process may be used, estimating engagement status in step 1, and intervention effects for multiple outcomes across the estimated engagement classes in step 2 analyses (18). Third, when treatment is offered over time, researchers may examine longitudinal changes in engagement related to variations in outcome using a nested latent class modeling approach. For example, Lin and colleagues (21) found that elderly participants in a depression prevention program who complied consistently over the two year course of the trial showed the greatest symptom reductions.

Limitations

Several potential limitations are important to acknowledge. First, in common with other CACE modeling examples, we did not account for the nested structure of the current study, with families nested within schools (8, 14, 18). Nesting may have biasing effects, particularly for group-randomized trials (22). In the current study, we ignored nesting because randomization to treatment occurred at the individual family level, and the active treatment components were delivered individually to families. Thus, school-level influences were expected to be modest for treatment compliance and intervention effects. Indeed, examination of nesting effects by schools for the two cohorts in this study yielded extremely small intraclass correlations for either engagement rates or tobacco use outcomes (all intraclass correlations < = .01).

Second, CACE results are susceptible to bias in the face of violations of the exclusion restriction. Current results highlight that researchers must pay careful attention to the tenability of the underlying assumptions of CACE analysis, and employ appropriate modeling strategies to deal with potential violations when they occur. Identifying predictors of engagement lends confidence to the current results, as do the relatively small differences across CACE models varying covariates and modeling assumptions.

Third, we considered engagement with treatment as a binary variable. It is possible, however, to consider treatment engagement as a continuous variable, which permits more fine-grained examinations of the relation between treatment engagement and youth outcomes. Further, dichotomizing engagement requires sometimes difficult decisions about where to locate the cut-point between non-engagement and engagement. Advanced methods for dealing with continuous compliance, such as dose-response or partial compliance models, are available although further methodological work is needed to clarify modeling assumptions (23, 24).

Future Directions

Research is needed into the mechanisms through which intervention leads to reductions in youth substance use. Earlier ITT analyses of 4-year outcomes of the ATP intervention revealed that reductions in risk for substance use were mediated by increases in observed parental monitoring practices (25). Mediation in CACE models involves potentially challenging statistical assumptions, although work is ongoing to clarify these assumptions (26). We hope to apply such mediation methods in future analyses to examine whether intervention effects for treatment-engagers are mediated by improved family functioning.