Cell Confinement in Patterned Nanoliter Droplets in a Microwell Array by Wiping

Abstract

Cell patterning is useful for a variety of biological applications such as tissue engineering and drug discovery. In particular, the ability to localize cells within distinct fluids is beneficial for a variety of applications ranging from microencapsulation to high-throughput analysis. However, despite much progress, cell immobilization and maintenance within patterned microscale droplets remains a challenge. In particular, no method currently exists to rapidly seed cells into microwell arrays in a controllable and reliable manner. In this study, we present simple wiping technique to localize cells within arrays of polymeric microwells. This robust method produces cell seeding densities that vary consistently with microwell geometry and cell concentration. Moreover, we develop a simple theoretical model to accurately predict cell seeding density and seeding efficiency in terms of the design parameters of the microwell array and the cell density. This short-term cell patterning approach is an enabling tool to develop new high-throughput screening technologies that utilize microwell arrays containing cells for screening applications.

Introduction

A significant fraction of all drug discovery processes (~50%) are performed by using cell-based assays¹. Typically such assays have been performed within multi-well plates. Miniaturizing well dimensions can significantly reduce the cost associated with these studies because of lower consumption of materials and reagents². Thus, the ability to generate patterned cell arrays immobilized within distinct fluids is important for high-throughput screening studies in both tissue engineering and drug discovery applications^3,4. For example, it has been shown that microwells can be used to generate homogeneous embryoid bodies (EBs) in a controlled manner^5,6.

Cell localization and the subsequent deposition of distinct liquids in each microwell can be used to precisely control the presentation of extracellular factors in the cellular microenvironment to study cell fate and function⁴. Typically, cell-ECM interactions are studied by using purified matrix proteins absorbed to cell culture substrates, which requires large amounts of expensive proteins on 96- or 384- well plates⁷. For soluble factors, such as drug candidates, the number of permutations may exceed millions while their quantity can be limited³. In this case, the miniaturization of the assay is necessary because of the high production price and small batch size of the reagents. One potential approach for assay miniaturization is to isolate cell droplets within microwell arrays. For this reason, approaches which could deposit nanoliter cell suspensions into wells could be useful for isolating cells and liquid in a single step. To this end, cell printing methods, such as piezoelectric⁸, inkjet^9,10, acoustic printing^11,12 and optical tweezers¹³ have been previously developed, all requiring specialized equipment. However, despite significant progress, major problems such as clogging, biomolecular denaturization, and low cell viability still exist in nanoliter liquid handling processes^14,15.

In light of these shortcomings, passive confinement of cells offers a simpler approach to cell localization in microwells. Recently, several microfluidic methods were reported in which passive confinement of cells was used to create cell arrays within microwells that contained low shear stress regions^16-18. Although they are attractive approaches due to the shear protection of captured cells and applicability to both adhesive and non-adhesive cells, their applications are limited by the necessity of a microfluidic system and the need to align the microfluidic device with the microwell array.

In this study, we present a method for cell seeding and nanoliter liquid isolation in microwell arrays by using a simple wiping technique. To minimize bubble formation, the surface of the microwell arrays is treated with air plasma to increase its hydrophilicity. The cells are seeded in the microwells by spreading a droplet of cell solution across the microwell array. After seeding, the array is placed in an enclosure with controlled humidity to prevent evaporation.

To generalize our approach, we develop a set of theoretical formulas which accurately predict the cell seeding density and cell seeding efficiency in terms of the design parameters of the microwell array and the concentration of the cell solution. We envision that the ability to generate arrays of segregated nanoliter droplets may be useful for cell-microenvironment interaction studies and other high-throughput screening applications.

Materials and methods

Materials

3-( Trimethoxysilyl ) propyl methacrylate ( TMSPMA ) , 2-hydroxy-2-methyl propiophenone, polyethylene glycol diacrylate (PEGDA), rhodamine B were purchased from Sigma-Aldrich Co., St. Louis, MO. Pluripotent murine embryonic stem (ES) cells, R1 strain¹⁹, were obtained from the Mount Sinai Hospital, Toronto, Canada. Pre-cleaned microscope glass slides were purchased from Fisher Scientific, Waltham, MA. Mouse leukemia inhibitory factor (LIF), ESGRO® was purchased from Chemikon Int. Inc., Eugene, OR. All other tissue culture components were purchased from Gibco-Invitrogen, Carlsbad, CA. All chemicals were used as supplied without further purification.

PEGDA microwell fabrication

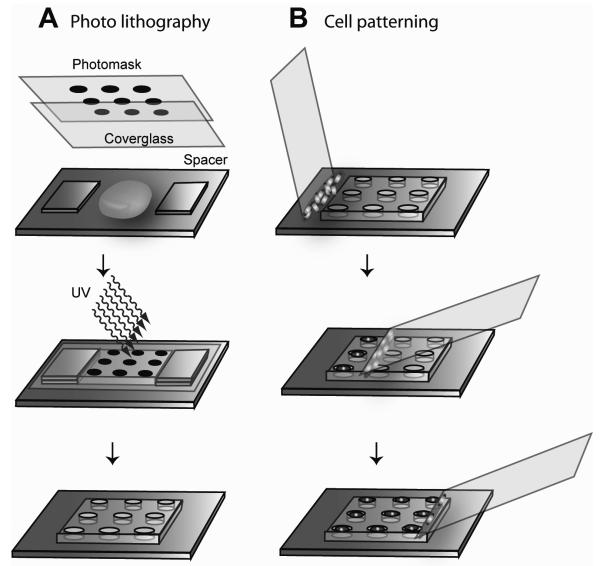
To fabricate microwell arrays, a photolithographic approach was used in which a UV-photocrosslinkable PEGDA (MW = 258) solution containing 0.5 % (w/w) of the photoinitiator 2-hydroxy-2-methyl propiophenone was placed on a TMSPMA treated glass slide. The precursor solution was placed between a coated glass slide and a piece of cover glass with a photomask on top (Figure 1). Microscopy cover slips were used as spacers between the glass support and the cover glass to define the depth of the microwells. The PEG precursor solution was then irradiated through a bright field photomask with UV light of 350-500 nm for 0.4s to 1s, depending on the sizes of the microwells, at an intensity of 100 mW/cm² using the OmniCure® Series 2000 curing station (EXFO Life Sciences & Industrial Division, Canada). The PEG precursor solution did not undergo radical polymerization in the areas shaded by the photomask and remained water soluble. After curing the polymers, the cover glass was carefully removed and the microwells were developed by removing the uncrosslinked macromer with deionized water. The photomask was designed by using the layout editor software CleWin Version 2.8 (WieWeb Software, Hengelo, the Netherlands) and printed on Mylar™ clear films (Fineline Imaging Inc., Colorado Springs, CO). The final microwell arrays contained 400 and 1089 microwells in 20×20 and 33×33 array formats with center-to-center spacings of 500μm and 300μm, respectively. The microwells were all 150 μm deep.

Figure 1.

Microwell fabrication and cell patterning. A) Photolithography. A bright field photomask was placed on top of the stack and the precursor solution was irradiated through the photomask. After UV irradiation, the spacers, cover glass, and the photomask were removed. The PEGDA did not photocrosslink in shaded areas and could be washed away to fabricate microwell patterns. B) Cell patterning. A drop of cell solution was pipetted onto a thin glass slide and placed in contact at an obtuse angle with the microwell slide adjacent to the array. The cover glass was rotated to an angle of 45° and moved across the array, spreading the cell solution into the microwells and removing excess solution from the surface. This process localized cells and isolated liquid in the microwells.

Contact angle measurements

A VCA2000 video contact angle system (AST Products Inc., Billerica, MA) was used to measure the static contact angles of deionized water drops that were 3-4μL in volume on surfaces with and without plasma treatment. To treat the surfaces with oxygen plasma, the whole glass slide was placed in a plasma cleaner for 3 min (Harrick Scientific, model: PDC - 32G, input power 100 W). High-power radio frequency settings (720V DC, 25 mA DC, 18 W) were used to generate the plasma when the chamber was filled with air. For the plasma-treated substrates, the contact angles were measured on flat surfaces (TMSPMA, PEGDA) at 0, 10, 20 and 30 min after plasma treatment.

Cell culture

Pluripotent murine embryonic stem (ES) cells were manipulated under tissue culture hoods and maintained in a humidified incubator at 37°C with a 5 % CO₂ atmosphere. Media components were filtered through 0.22μm pore sized Stericup™ filter units (Millipore, Billerica, MA). Culture media consisted of DMEM knockout medium supplemented with 15 % (v/v) ES qualified fetal bovine serum (FBS), 1 % (v/v) non-essential amino acid solution MEM NEAA, 1 mM L-glutamine, 0.1 mM 2-Mercaptoethanol and 10³ U/ml mouse leukemia inhibitory factor (LIF). Cells were kept undifferentiated by changing media daily and passaging every 2 days with a subculture ratio of 1:4. Tissue culture flasks (T75) were treated with 0.1 % (w/w) gelatin in distilled deionized water and incubated for 24 h immediately prior to use.

Wiping method to seed cells in microwells

To seed the microwells with cells, 15μL of cell media (0.5-2 million cells per ml) was pipetted along the edge of a cover glass which was then slowly wiped across a plasma treated microwell array (Figure 1B). To avoid trapping air in the microwells, the cover glass was first placed to the side of the microwell array, droplet side up (Figure 1B, top), and slowly rotated until the fluid attached to the PEG array. The cover glass was wiped across the array at approximately 1.0 mm/s (Figure 1B, middle). Once the array was traversed (Figure 1B, bottom), the excess fluid outside the array was removed and the array was placed in a humid enclosure to avoid evaporation of the isolated droplets in the microwells.

Cell counting

Prior to seeding, cells were stained using a Live/Dead® stain kit (Invitrogen, Carlsbad, CA). Live cells were stained by a polyanionic dye, calcein, well retained in live cells, producing an intense uniform green fluorescence (ex/em: ~495 nm-blue/~515 nm-green). Dead cells were stained with ethidium homodimer (EthD-1), which enters the damaged cell membranes, undergoes a 40-fold enhancement of fluorescence upon binding to nucleic acids, and produces a bright red fluorescence (ex/em: ~495 nm-green/~635 nm-red). Concentrations of 2 μM and 4 μM were used for the calcein-AM and EthD-1, respectively. Cells were pelletted and suspended in 1 ml of the staining solution for 10 minutes in an incubator. The cells were then re-pelletted and re-suspended in media for cell seeding. After seeding, images were taken using a fluorescent microscope at two wavelengths corresponding to the Live/Dead staining dyes, i.e., green and red. The two images were superimposed for cell counting. The number of cells were counted manually using ImageJ (http://rsbweb.nih.gov/ij/).

Results and discussion

Hydrophilicity of plasma-treated silane and PEGDA surfaces

Microstructures on hydrophilic surfaces are more easily filled than those on hydrophobic surfaces. It is well known that the hydrophilicity of PDMS surfaces decreases over time after plasma treatment^20,21. Similar properties were also reported for some PEGDA polymers²². In this study, the duration of hydrophilicity of PEGDA and TMSPMA after plasma treatment (TMSPMA was present at the bottom of the microwells), was quantified by measuring the static contact angles of deionized water droplets as a function of time. The surfaces of PEGDA and TMSPMA became hydrophilic immediately after plasma treatment. The recovery of hydrophobicity was noted within 10 min after plasma treatment, as quantified by increasing contact angles, with the fastest recovery occurring in the first 10 min following treatment. Based on these results we performed our microwell filling within the first few minutes after plasma treatment.

As the cover glass is wiped across the microwell array, isolated droplets are left in each well. We note that 100% PEGDA258 is not a hydrogel, and although gas may diffuse through the material, soluble factors of even low molecular weight should not travel between wells²³. By maintaining the array in a humid environment, evaporation is minimized and the droplets can be maintained²⁴. Furthermore, provided the contact line of each droplet is inside the well, it cannot escape due to contact line pinning²⁵. Even if the fluid extends beyond the well, due to incomplete wiping or microwell defects, the contact line motion is resisted by contact angle hysteresis. Thus, droplet coalescence and cross-contamination is unlikely.

Cell seeding in microwells by wiping method

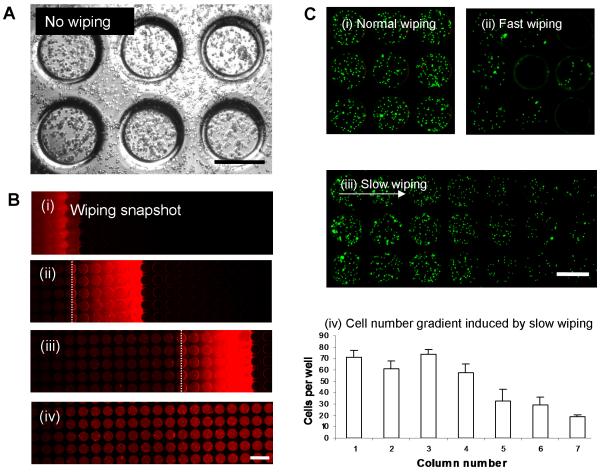
To motivate our wiping technique, we first note that without wiping, cells are randomly placed on the array inside and outside the microwells (Figure 2A). Figure 2B illustrates the progressive wetting of the microwells during the wiping process. A wedge of cell solution is spread across the array at a speed of approximately 0.5 mm/s. To quantify the effects of wiping speed, the cell densities resulting from three different wiping speeds are presented in Figure 2C. The wiping speeds used in most of our experiments were 1.0 mm/s, resulting in cell seeding densities which were approximately uniform across the array (Figure 2C(i)). For speeds above 10 mm/s, the contact line could not keep up with the cover glass and fluid motion, resulting in air being trapped in the microwells (Figure 2C(ii)). For speeds below 0.1 mm/s, a decrease in cell seeding density was observed in the direction of wiping (Figure 2C(iii)-(iv)). This decrease results from reduced cell concentration in the fluid wedge due to cell sedimentation.

Figure 2.

Cell localization in microwells via wiping method. A) Pipetting of cell solution directly onto the array without wiping resulted in many cells remaining on the array surface, outside the microwells. B) Time lapse images (i) to (iv) show the evolution of the wiping process. The bright red strip indicates the wedge of rhodamine/cell solution that is spread over the array, leaving filled wells in its path with no noticeable excess liquid on the array surface. The dotted line indicates where the cover glass contacts the array. The fluid wedge extends across approximately six 229 μm microwells, or 1.8 mm. C) Wiping speed effect on cell distribution in microwells. (i) Normal wiping (1.0 mm/s) produced relatively uniform distribution of cells in the microwells. (ii) Fast wiping (>10 mm/s) resulted in large disparities in cell distribution, leaving many wells without cells and filled with air. (iii), (iv) Slow wiping (< 0.1 mm/s) produced a gradient of cell densities, decreasing in the direction of wiping. In (iv), the bars are the average cell counts of each column of three microwells in (iii). (scale bar = 400μm)

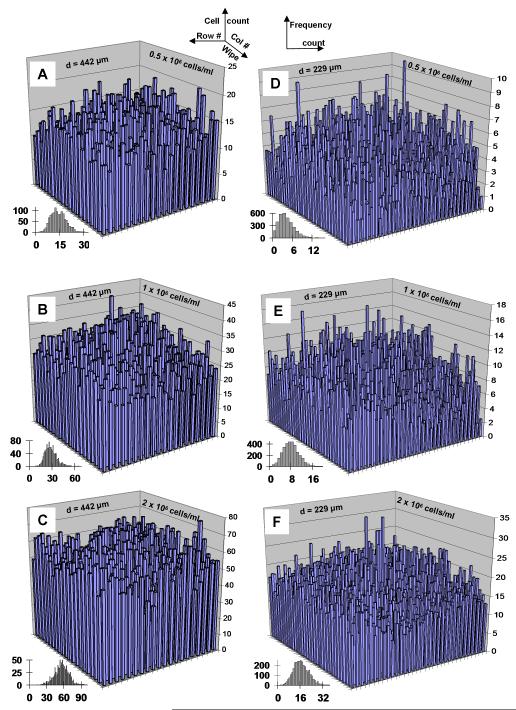
The cell counts from individual microwells are plotted in Figure 3 relative to the microwell position on the array. Column numbers increase in the direction of wiping (back to front). The cell counts peak near the center of the array. In the wiping direction, the cell counts likely increase initially due to aggregate formation on the cover glass and subsequent deposition, and decrease toward the end of the array due to a gradual cell depletion due to deposition (quantified later in the theoretical section). The main sources of variation in the cell counts are outlined later. If the cover glass is similar in width to the microarray (as in our experimental setup), then the spreading fluid wedge causes fluid motion perpendicular to the cover glass and may flush away some seeded cells on the sides of the array (low/high row numbers). Cell counts increase with cell solution concentration, and decrease with the microwell diameter. The dependence of the cell counts on the microwell geometry and cell solution concentration is further quantified in the theoretical section. Histograms of the cell count frequency vs. the cell count per microwell are shown in Figure 3 (insets) to further illustrate the cell count distribution. For easy comparison, a constant bin width of 1 cell is used in each histogram. Since the 20×20 arrays (Figure 3A-3C) have higher cell counts than the 33×33 arrays (Figure 3D-3F), a wider range of cell counts exist, thereby increasing the number of bins. However, the frequencies of cell counts on the 20×20 arrays are much less than those on the 33×33 arrays, leading to smoother histograms for the latter. Lastly, the small cell counts measured on the 33×33 array seeded with a cell solution concentration of 0.5×10⁶ cells/ml (Figure 3D), including several microwells with zero and single counts, skewed the histogram distribution to the left.

Figure 3.

Cell distribution across microwell arrays. Average number of cells per well (n=3) seeded via wiping at 0.5, 1.0, and 2.0 million cells/ml for 442 μm diameter (A, B, C respectively) and 229 μm diameter (D, E, F respectively) were quantified to determine cell seeding densities across the microarray. Insets indicate frequency plots of number of cells per well.

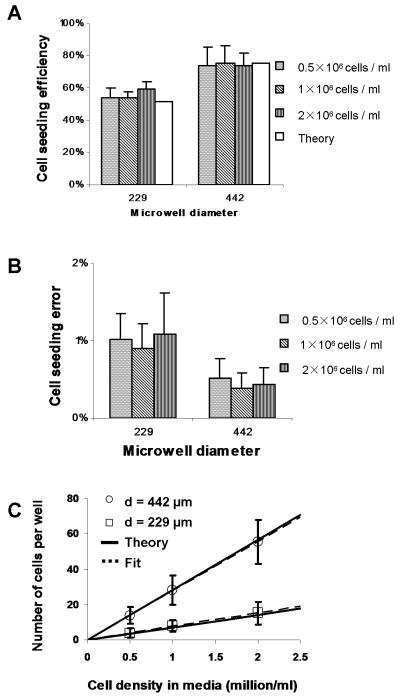
The analysis of the cell count data is summarized in Figure 4. The cell seeding efficiency, defined as the ratio of the number of cells seeded in the microwells to the total number of cells used, is (55.6 ± 3.3)% and (74.4 ± 0.9)% for the 229 μm and 442 μm diameter microwells, respectively, in close agreement with our theoretical values (Figure 4A). The rather low cell seeding efficiencies may be improved by repeatedly collecting the wasted cells and concentrating them for re-seeding. The difference is mainly due to the volume of cell solution held in each array. The ratio of total fluid volume held in the 20×20 array of 442 μm microwells to that in the 33×33 array of 229 μm microwells is 1.5. Since the same volume of cell solution was spread across each array, we would expect a similar ratio of cell seeding efficiencies, in this case 1.3. The difference is due to cell sedimentation, discussed later in the theoretical section. The cell seeding error, defined as the ratio of cells that fall on the array surface outside the microwells to the total number of cells on the array, was measured as (0.8 ± 0.2)% and (0.4 ± 0.1)% for the 229 μm and 442 μm diameter microwells, respectively (Figure 4B). Lastly, the number of cells per well as a function of initial cell solution concentration, for both microwell diameters, is presented in Figure 4C along with the theoretical relation derived next. The linear least-squares fits have slopes 7.62 (R² = 0.9992) for d = 229 μm and 27.8 (R² = 0.9997) for d = 442 μm. For the given cell concentrations and microwell geometries used in our experiments, our simple wiping method seeded microwells with cell counts of (4 ± 3), (8 ± 3), (13 ± 5), (15 ± 6), (28 ± 8) and (55 ± 12).

Figure 4.

A) Cell seeding efficiency, defined as the ratio of the number of cells seeded in the microwells to the total number of cells used, as a function of well diameter and cell density. Theoretical values correspond to equation (4). B) Cell seeding error, defined as the ratio of the number of cells that fall on the array surface outside the microwells to the total number of cells on the array, for all well diameters and cell solution concentrations. C) Number of cells per well as a function of cell density, for both well diameters. Solid and dotted lines correspond to equation (3) and linear least-square fits with slopes 7.03 and 7.62 for d = 229 μm and 28.4 and 27.8 for d = 442 μm, respectively.

In summary, we validated our simple wiping method using three concentrations (0.5, 1 and 2 million cells per ml) in triplicate, resulting in 108 images with 22,000 microwells and more than 500,000 cells. Cells were counted both manually and with cell counting software. The consistent experimental results and the agreement between experiment and theory indicates that the cell seeding density can be easily controlled by varying the initial cell concentration and microwell geometry.

Theoretical model of cell seeding

Physical picture

The physical picture of the cell seeding is as follows (Figure 5). As the cover glass pushes the wedge of fluid, the contact line at the front of the wedge advances on the hydrophilic surface, filling adjoining empty wells with fluid and cells. Cells are also constantly falling toward the wells at their terminal velocity. The cells fall directly into a well or are pushed and scraped into a well by the cover glass. Therefore, two modes of cell seeding exist: initial wetting and deposition / scraping.

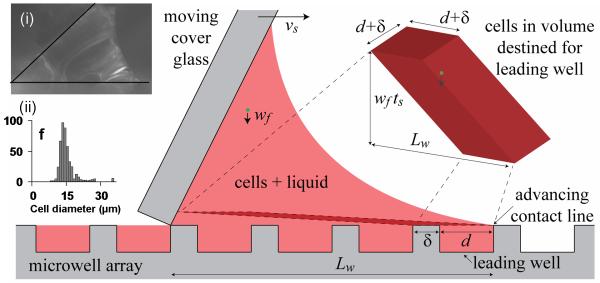
Figure 5.

Schematic of fluid flow and cell seeding during the wiping process. The moving cover glass spreads a wedge of fluid over the microwell array, forcing the leading contact line to advance and draw fluid with cells into empty wells ahead of the wedge. Cells also fall toward the wells and are also pushed and scraped into the wells. The cells destined for the leading well are located in a 3D parallelogram near the array. The height of the slice is exaggerated for clarity. Inset (i) shows actual fluid wedge between the cover glass and the microwell array. Inset (ii) shows the histogram of cell and cell aggregate diameters. The notation is as follows: v_s is the wiping speed of the cover glass, d and δ are the microwell diameter and spacing, t_s is the time over which the cover glass travels the base length L_w of the fluid wedge (~6 microwells), w_f is the terminal fall velocity of the cells (~10 μm/s).

Formula for cell seeding density

By considering the two modes of seeding, we now estimate the number of cells in each well. During the initial wetting stage, the number of cells drawn into a well with the fluid on initial wetting equals the concentration c of cells in the fluid times the microwell volume πd²h/4, where d and h are the microwell diameter and depth. To estimate the number of deposited cells, i.e. those which fall into a well or are pushed and/or scraped in by the cover glass, we first estimate the cells’ terminal velocity and then consider the location of these cells prior to well entry. The terminal velocity of the cells may be estimated from Stokes’ formula²⁶,

$$w_f=\frac{1}{18\mu }{d}_c^2({\rho }_c-\rho )g$$ (1)

where ρ = 1.005 g/ml and μ = 0.0075 g/(cm s) are the density and dynamic viscosity of the cell media²⁷, g = 981 cm/s² is the gravitational acceleration, and ρ_c = 1.07 g/cm³ and d_c are the density²⁸ and mean diameter of the cell and cell aggregates. For the cell/cell aggregate diameter distribution in our experiments (Figure 5 inset(ii)), the mean diameter was d_c = 14.3 μm and the mean fall velocity was w_f = 10.2 μm/s. To estimate the cell location prior to well entry, we note that the cover glass, moving at v_s = 1.0 mm/s, covers the distance L_w = 1.8 mm (i.e. ~ 6 microwells, Figure 2B) between the base of the cover glass and the contact line in a time t_s = L_w / v_s = 1.8s. During this time, the cells have fallen a distance w_f t_s = w_f L_w /v_s = 18.4 μm. Thus, the cells that will fall or will get scraped into the leading well, which we call the deposited cells, are located no more than 18.4 μm from the array surface. Here, the fluid is barely moving due to the no-slip condition and the relatively stagnant fluid in the wells. Thus, away from the cover glass, the horizontal movement of the deposited cells is negligible relative to L_w. The deposited cells effectively fall vertically until they (a) fall into the leading well, (b) hit the surface to the side or preceding the leading well and get scraped into the well by the cover glass, or (c) are hit mid-fall by the moving cover glass and continue to fall until they enter the well. Thus, all the cells that will enter the leading well are located in a fictitious 3D parallelogram extending backward and upward from the leading well and surrounding surface (Fig. 1 and inset (i)). The volume of this 3D parallelogram is (d+δ)²w_f t_s. Combining the estimates for the two modes of seeding, we obtain the total number of cells per well,

$$N=\left(\frac{\pi }{4}{d}^{2}h+{(d+\delta )}^2{w}_f{t}_s\right)c=\left(\frac{\pi }{4}{d}^{2}h+{(d+\delta )}^2\frac{w_f{L}_w}{v_s}\right)c$$ (2)

For a wiping speed of v_s = 1.0 mm/s and a fall velocity w_f = 10.2 μm/s, we obtain

$$N=\left(\frac{\pi }{4}\times {10}^6{d}^{2}h+1836{(d+\delta )}^2\right)n$$ (3)

where d, h, and δ are the well diameter, depth, and spacing and n is the concentration of cells in millions per ml (c = n ×10⁶ cells/ml). Formula (3) may be used to calculate the cell density using our seeding method on microwells of arbitrary dimensions. For the microwells in this study, (d, d + δ, h) = (229.4 μm, 300 μm, 130.2 μm) and (442.3 μm, 500 μm, 154.9 μm), we estimate cell counts per well of N = 7.03n and N = 28.4n, respectively. The slopes of these theoretical relationships is within 7.7% and 2.1% of the fitted slopes corresponding to the experimental data, 7.62 for d = 229.4 μm and 27.8 for d = 442.3 μm (Figure 4C), respectively. The error of our theoretical estimate is well within the experimental variation. Lastly, we note that the terms in the brackets in equations (2) and (3) yields the relative magnitudes of the two modes of cell seeding, initial wetting and sedimentation / scraping. For this study, the cells seeded during initial wetting accounted for the majority of the total seeded cells, 76.5% and 83.8% for d = 229.4 μm and 442.3 μm, respectively. Thus, as we discuss later, the seeding density is largely dependent on cell concentration and well geometry and is less sensitive to the precise wiping speed, cell and fluid properties, contact line motion, and flows within the fluid wedge.

Formula for seeding efficiency

To estimate the seeding efficiency, neglecting cells left unseeded on the array surface, equation (3) can be used to

$$\text{seeding efficiency}=\frac{\#\text{wells}\times N}{\text{volume used}\times c}=\frac{\#\text{wells}}{V_U}(250\pi d^{2}h+1.836{(d+\delta )}^2)$$ (4)

where V_U is the total volume of solution used, in μL. For the values listed above and a 15 μL solution volume used (V_U = 15), equation (4) gives a seeding efficiency of 51.0% and 75.7%, for d = 229.4 μm and 442.3 μm, respectively, within 8% and 2% of the experimental values, 55.6% and 74.4%, respectively (Figure 4A).

Criterion on wiping speed to maintain constant cell seeding density

We now derive a criterion on the wiping speed to maintain a constant (in time) cell concentration and concomitant cell seeding density as the cover glass moves across the array. We have implicitly assumed the cell concentration and seeding density are constant in time to derive equation (4). The cell concentration remains constant provided the total number of deposited cells is small relative to the number of cells in the fluid wedge, or, equivalently, that the volume of the parallelogram is much smaller than that of the fluid wedge. Using our volume estimates above, this criterion can be expressed mathematically as

$$\frac{\#\text{wells}\times {(d+\delta )}^2{L}_w}{\text{volume used}}\frac{w_f}{v_s}<<1$$ (5)

The volume of the parallelogram and the number of deposited cells scale inversely as the wiping speed, and hence we expect that for slow wiping speeds, the cell concentration will decrease as the cover glass wipes across the array. For example, for wiping speeds of v_s = 1.0 mm/s and 0.1 mm/s and a 15 μL solution volume, the left hand side of equation (5) becomes 0.12 and 1.2 for both microwell diameters. Thus, the cell seeding density is expected to decrease significantly along the array for a wiping speed of 0.1 mm/s, as observed in Figure 2C(iv), while that for the 1.0 mm/s wiping speed should decrease only slightly. A mild and gradual decrease in the wiping direction exists in the row averaged cell counts (not reported), though this is small compared to the overall variation in the cell seeding density observed in Figure 3. If a gradient in cell density is desired across the array and a slow wiping speed is used, an estimate can be made of the spatially dependent seeding density by applying equation (2) and updating the concentration c after filling each row of microwells.

Verification and assessment of assumptions in theory

Due to the transient nature of the flows induced by the advancing contact line and cover glass motion, we have made several simplifying assumptions to facilitate the derivation of our estimates. In particular, we have assumed that (i) the cell concentration in the wedge is spatially uniform, (ii) cells remain in the wells once they enter, (iii) cells that fall outside the well are scraped into a well and that (iv) cells that fall into a well appear in the 3D parallelogram.

The first assumption is expected to be valid since a clockwise circulation driven in the fluid wedge by the cover glass motion maintains a spatially uniform cell distribution in the wedge, despite cell sedimentation toward the array. The circulation velocity in the fluid wedge scales as the wiping speed of the cover glass (1.0 mm/s)^29-32, which is much greater than the cell fall velocity (10.2 μm/s). Thus the circulation dominates cell sedimentation and maintains a spatially uniform cell concentration in the fluid wedge.

To support the second assumption, we note that the fluid in the microwells is at rest at all times except initially when the well is filled and later when the cover glass passes overhead. The Reynolds number of these peak flows in the microwells is 0.l5, based on the well depth and cover glass speed (which was chosen similar to the contact line speed to promote complete wetting of the microwells). A mild circulation is induced in the microwells as the cover glass passes³³, but this damps quickly and the fluid returns to rest. It is therefore unlikely that cells leave the wells once they enter, except perhaps near the edges of the cover glass due to flow leakage.

The third assumption is that all cells which fall on the surface of the array are scraped into a well by the cover glass. In practice, cells may pile up on the cover glass between rows of wells, reducing the number of cells that enter the average well and leading to avalanches which dump large numbers of cells into a particular well. This behavior contributes to the variation observed in the measured cell densities and can be avoided by, for example, staggering successive rows of wells by half a diameter, or wiping diagonally across the array.

To assess the last assumption, note that the fictitious parallelogram containing cells destined for the leading well actually extends into the sloping cover glass. However, the overlap is negligible since the parallelogram’s slope is very small, w_f t_s/L_w ~ 0.01.

Cell distribution inside the microwells

The cell distribution within the microwells appears to be random. This is in contrast to a recent study of cell seeding by uniform flow over rectangular trenches, where the cells congregated at the upstream or downstream wall depending on the trench aspect ratio³⁴, which is consistent with experimentally observed and theoretically calculated streamline patterns^29,32. The flow in a steadily driven cylindrical cavity is more complicated^31,33. Thus we did not expect, nor did we observe, regular patterns in cell positioning in our microwells.

Sources of variation in seeded cell counts

The variations in seeded cell counts stem mainly from cell concentration, geometrical variations, avalanching and cell fall velocity. Several factors may affect cell concentration. First, the bright-line haema-cytometer counts varied by approximately 10%, which indicated localized variations in cell concentration. Second, despite periodic agitation of the stock cell solution, some cell aggregation and adherence could occur during pipetting the 15 μl cell solution from the stock to the cover glass.

Geometrical variations in the fabricated microwells, avalanching and variations in cell fall velocity also affect the seeded cell counts. The number of cells that are drawn into a well is proportional to the microwell volume, which varies as the square of the microwell diameter and linearly with depth. Reducing the variation in fabricated microwell geometry is expected to decrease the concomitant variation in cell seeding. In our experiments, the smaller microwell volumes varied by 16%, while the larger microwell volumes varied by only 5%. It is not surprising therefore that larger variations in cell counts were observed for the smaller microwells, even for similar mean seeded cell counts. Avalanching occurs when cells aggregate between the cover glass and the surface of the microarray between microwell rows and then fall into a neighboring microwell when the aggregate becomes too large. This may be overcome by staggering successive rows of microwells by a half wavelength. Lastly, the number of cells that sediment into the wells, accounting for 16-23% of the total cell count, is proportional to the fall velocity which is in turn proportional to the difference between the cell and fluid densities and the square of the cell diameter. Variations in these cell properties could therefore also produce nontrivial variations in cell seeding.

Effects that should not significantly affect the cell seeding density, for wiping speeds near 1.0 mm/s, include variations in the wiping speed, contact line motion, and circulation in the wedge, which has a free surface. The cell seeding is insensitive to these effects because they only affect the sedimentation mode of cell seeding, which accounts for only 16-23% of the cells seeded. For example, a 10% change in the wiping speed could change the sedimented cell density by up to 10%, but would change the total cell seeding density by at most 2.3%. Thus it is unnecessary to precisely control the wiping speed and flow in the wedge for wiping speeds near 1.0 mm/s. This will not be the case if a slow wiping speed (< 0.1 mm/s) is employed to create a gradient in cell density. In that situation, cell sedimentation is a significant seeding mechanism and precise control over cover glass motion is required.

Applications of our wiping technique

Following cell seeding, a non-contact microarrayer may be used to add distinct materials into each microwell³⁵. Combining microarray printing with our seeding technique would be ideal for HTS. Another high-throughput application is to create micro-tissues in the microwell array. These micro-tissues could then be either analyzed inside the microwells or be harvested for in vivo organ regeneration study.

Many traditional microarray techniques involve spraying dotted substances on 2D substrates. Unlike the 2D substrates, microwells provide isolated 3D microenvironments in which to confine cells. Technologies involving microwells aligned in the traditional microarray format are in development, such as a microwell array platform for picoliter membrane protein assays³⁶. Our cell seeding technique would allow the reported method to be extended to cell-based studies. Also, optical microwell arrays allow an entire array to be simultaneously measured yielding a rapid, repetitive, and high-density analysis tool³⁷. When coupled with our cell seeding technique, the simultaneous responses of groups of specific numbers of cells may be obtained.

Conclusions

We have developed a novel robust method for seeding cells in isolated nanoliter droplets in microwell arrays by using a simple wiping technique. The wiping method produces cell seeding densities that vary consistently with microwell geometry and cell concentration. Furthermore, we have derived a simple theoretical model to accurately predict cell seeding density and seeding efficiency. This cell patterning approach is an enabling tool to develop new high-throughput screening technologies for cell-based study.