Abstract
Importance of the field
The advancement in material design and engineering has led to the rapid development of novel materials with increasing complexity and functions. Both non-degradable and degradable polymers have found wide applications in the controlled delivery field. Studies on drug release kinetics provide important information into the function of material systems. To elucidate the detailed transport mechanism and the structure-function relationship of a material system, it is critical to bridge the gap between the macroscopic data and the transport behavior at the molecular level.
Areas covered in this review
The structure and function information of selected non-degradable and degradable polymers have been collected and summarized from literatures published after 1990s. The release kinetics of selected drug compounds from various material systems will be discussed in case studies. Recent progresses in the mathematical models based on different transport mechanisms will be highlighted.
What the reader will gain
This article aims to provide an overview of structure-function relationships of selected non-degradable and degradable polymers as drug delivery matrices.
Take home message
Understanding the structure-function relationship of the material system is key to the successful design of a delivery system for a particular application. Moreover, developing complex polymeric matrices requires more robust mathematical models to elucidate the solute transport mechanisms.
Keywords: degradable polymer, non-degradable polymer, mathematical model, release kinetics
1. Introduction
Drug release has been an important topic in the field of drug delivery for decades. With advancement in material design and engineering, novel materials with increasing complexity and more functions have been introduced into the development of drug delivery devices and systems. Both naturally derived and synthetic macromolecules are extensively used in controlled drug release to maximize bioefficacy, facilitate clinical applicability and improve the quality of life, just to name a few. “Drug release” refers to the process in which drug solutes migrate from the initial position in the polymeric system to the polymer’s outer surface and then to the release medium [1]. This seemingly simple process is affected by multiple complex factors such as the physicochemical properties of the solutes, the structural characteristics of the material system, release environment, and the possible interactions between these factors. A detailed summary of these driving factors is shown in Figure 1.
Figure 1.
Factors influencing drug release kinetics
In general, solute diffusion, polymeric matrix swelling, and material degradation are suggested to be the main driving forces for solute transport from drug containing polymeric matrices [2]. Specifically, Fick’s law of diffusion provides the fundament for the description of solute transport from polymeric matrices. Fickian diffusion refers to the solute transport process in which the polymer relaxation time (tr) is much greater than the characteristic solvent diffusion time (td). When tr ≈ td, the macroscopic drug release becomes anomalous or non-Fickian [3]. The purpose of mathematical modeling is to simplify the complex release process and to gain insight into the release mechanisms of a specific material system. Thus, a mathematical model mainly focuses on one or two dominant driving forces. In literature, well-established models have been developed to describe solute transport based on each of the aforementioned mechanisms. However, disconnects exist between theories and experimental data since there are multiple driving forces involved in a single transport process. Moreover, the existing mathematical models may be insufficient in describing more complex material systems, e.g. delivery systems integrating multiple material components, or stimuli-triggered delivery systems in which the interaction with complex physiological condition is involved. In the following sections, the structure-function relationship of the representative material systems will be discussed. Recent developments in release kinetics and mathematical modeling of selected non-degradable and biodegradable polymer systems will be highlighted.
2. Release kinetics from non-degradable polymeric matrices
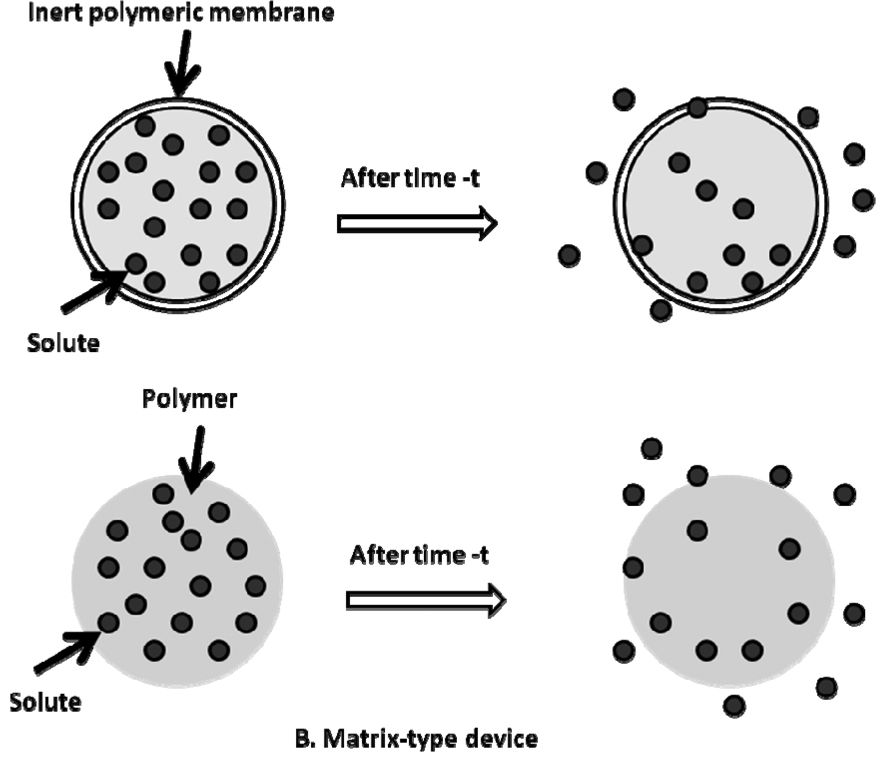
Non-degradable polymers have been widely applied in the fabrication of peroral dosage forms, transdermal films, and implant devices [4]. These polymers include polyurethanes, silicone rubber, poly (ethylene vinyl acetate), just to name a few. Non-degradable polymers used in drug delivery are characterized by tissue/blood compatibility, durability, robust structure and mechanical strength during in vivo application. Materials for long-term use, such as orthopedic and dental implants, have water-repellent surfaces to avoid degradation or erosion processes [5]. Solute transport from non-degradable polymeric systems is mainly considered as diffusion driven. Non-degradable polymers can be fabricated into “reservoir-” and “matrix-” type devices (Figure 2) [6]. By definition, reservoir-type devices refer to those having an inert coating material, which functions as a rate-controlling membrane. The release rate remains relatively constant and is not affected by concentration gradient, but most likely is related to the thickness and permeability of polymeric membrane. In contrast for matrix-type devices, drug release is more likely to be Fickian diffusion driven, which is associated with concentration gradient, diffusion distance, and the degree of swelling [7,8]. In this section, three representative non-degradable polymers are discussed and the release kinetics of selected solutes is reviewed.
Figure 2.
Schematic representation of (A) reservoir- and (B) matrix-type controlled drug delivery devices Adapted from [6]
2.1 Polyurethanes
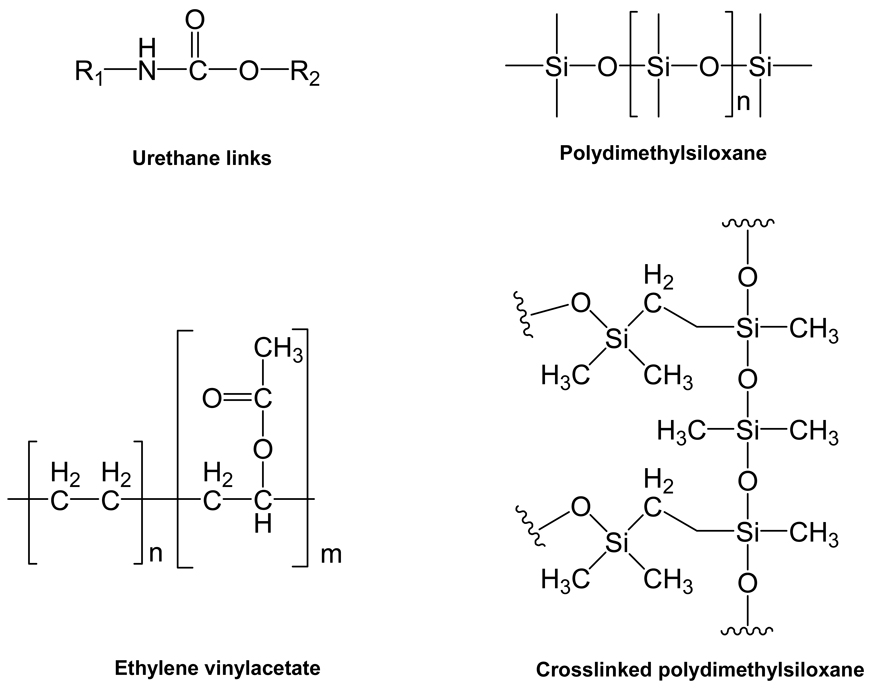
Formed via step-growth polymerization, polyurethanes are characterized by urethane linkages in the backbone (Figure 3). Polyurethane copolymers of (AB)n type consist of alternating “soft segment” and “hard segment”, and the unique physical and mechanical properties of polyurethanes are largely determined by such two-phase domain structures [9]. The phenomenon of phase separation is due to the strong hydrogen bonding between urethane and urea-type hard segments and/or hard segment crystallization [10].
Figure 3.
Structures of representative non-degradable pharmaceutically related polymer
As a class of polymer for drug delivery devices, base polyurethanes are considered non-degradable due to the long duration for complete degradation and the degree of degradation that is negligible relative to the entire release time scale. Base polyurethanes have been well demonstrated to be biocompatible and stable in vivo and therefore have been used in biomedical devices such as insulators for cardiac pacing leads, ventricular assist devices, vascular prostheses, drug delivery implants, tissue adhesives, skin wound dressings, etc [11–14]. For example, Sureskin® II Silver is an FDA approved wound dressing consisting of polyurethane foam that delivers silver-containing agents for treating dermal ulcers, post-operative wounds, superficial wounds, and abrasions [15]. Drug loading into polyurethane based devices can be conducted either prior to polymerization or via equilibrium absorption after polymerization. For polymerization in the presence of drug molecules, mild conditions are generally used to ensure drug stability, such as relatively low temperature and the addition of stabilizing excipients such as heparin to protect protein drugs [16]. Despite the different geometries of the devices, near linear release profile has been observed after the initial burst release and diffusion has been suggested to be the main driving force (Table 1). Thus, polyurethanes have been widely employed in medical implants and other devices in vivo because of the favorable physical mechanical properties and biocompatibility. However, the “non-degradability” also seems to limit the application of polyurethanes in controlled drug delivery, because second interventions are sometimes necessary to remove the device after the treatment. Recently, biodegradable polyurethane derivatives have become the focus of several studies in the field of controlled drug delivery [34–36].
Table 1.
Summary of release kinetics and transport mechanisms of nondegradable polymer based delivery devices
| Type of material | Type of device | Loaded drug | Burst release |
Release kinetics | Transport mechanism |
Ref. |
|---|---|---|---|---|---|---|
| Segmented PU (Cardiomat 610) |
Drug-eluting stent |
1,3-Dipropyl-8- cyclopentyl xanthine |
1 d | Near linear release (~ 20 d) |
Non-Fickian diffusion |
[17] |
| Elast-Eon™ | Drug-eluting stent |
Dexamethasone acetate |
w/ | Biphasic pattern | Fickian diffusion |
[18] |
| Polyurethane (Walopur®) |
Disk-shaped matrices |
Flucloxacillin-Na Fosfomycin Gentamicin-base |
1 d | Near linear (2 ~ 5 d) |
Matrix- controlled |
[19] |
| Poly(urea- urethane) |
Microcapsule | Auramine (Oil-soluble dye) |
w/o | Near linear (~20 min) |
Non-Fickian Diffusion |
[20] |
| PEG modified polyurethane |
Dermal patch | Thiamazole, diclofenac sodium, ibuprofen |
12 h | Biphasic pattern (~ 48 h) |
- | [21] |
| PDMS | Rod (matrix vs. reservoir) |
Ivermectin | w/o | Matrix: first order, 50 d; Reservoir: zero order, 84 d |
Matrix: diffusion Reservoir: case II transport |
[22] |
| PDMS | Intravaginal ring (reservoir) |
TMC120 | 1–2 d | Biphasic; near zero order release for 30 d |
Case II transport |
[23] |
| PDMS | Intravaginal ring (core-type) |
TMC120 | w/o | Zero order, 71 d | Case II transport |
[24] |
| PDMS | Strip (10×20 mm) |
Metronidazole | w/ | Higuchi (linear vs. t1/2) |
Fickian diffusion |
[25] |
| PEVA (VA content, 40%) |
Membrane | Quinupramine | w/ | Higuchi (linear vs. t1/2) |
Fickian diffusion |
[26] |
| PEVA | Thin film | Acyclovir Chlorhexidine diacetate |
w/o | Near zero-order (~ 8 d) |
Non-Fickian diffusion |
[27] |
| PEVA | Drug-eluting stent coating |
5-Fluorouracil | w/ | Biphasic pattern (~20 d) |
Fickian diffusion |
[28] |
| PEVA (VA content, 40%) |
Disk-shape Film | Chlorhexidine diacetate |
w/ | Near-zero order (~ 7 d) |
Non-Fickian diffusion |
[29] |
| PEVA (VA content, 40%) |
Membrane | Furosemide | w/ | Higuchi (linear vs. t1/2) |
Fickian diffusion |
[30] |
| Dextran sulfate | Microcapsule | Insulin | w/ | Biphasic pattern (~12 h) |
Fickian diffusion |
[31] |
| Methacrylated dextran |
Hydrogel | Vitamin E | ~3 h | Biphasic | Swelling | [32] |
| HPMC with β- CD |
Tablet | Difunisal | w/o | Zero-order for nonsoluble β- CD First-order for soluble β-CD |
Non-Fickian diffusion |
[33] |
w/, with; w/o, without.
2.2 Polydimethylsiloxane
Polydimethylsiloxane (PDMS) is different from most other biomedical polymers in that the backbone consists of inorganic Si-O-Si units instead of hydrocarbon chains (Figure 3). Polysiloxanes are very flexible due to large bond angles and bond lengths when compared to those found in more basic polymers such as polyethylene [37]. In the development of three-dimensional structures, vinyl-terminated polydimethylsiloxanes are crosslinked by branched polydimethylsiloxanes with reactive SiH- groups under the catalysis of platinum [38]. Due to the hydrophobic nature of crosslinked PDMS (Figure 3), hydrophobic drugs are commonly loaded in PDMS-based delivery devices to achieve prolonged release profiles. As shown in Table 1, drug release from PDMS-based delivery devices can be sustained to over a month. Similar to polyurethanes, PDMS can also be fabricated into reservoir- and matrix-type devices (Figure 2). For matrix-type devices, drug release is mainly controlled by diffusion as detailed in Table 1, and the cumulative release is linear with respect to the square root of time (t1/2). As for crosslinked PDMS network, the network density is described by the average molecular weight Mn (number average) of the crosslinked units [38]. In addition to crosslink density, water uptake is another important impact factor which may affect the degree of swelling and solute transport within the PDMS network. Riggs et al studied the water uptake kinetics of silicone elastomers using 3He ion-beam analysis and their study demonstrated that water uptake was initially linear with time and then linear with t1/2 which indicated a Fickian profile [39]. Malcolm et al investigated the metronidazole release kinetics from crosslinked silicone elastomers and all of the silicone systems evaluated were shown to obey simple matrix-type t1/2 kinetics due to the fact that most of the drug within the systems existed in the solid state [25]. Thus, there seems to be a correlation between water uptake and release kinetics for the matrix-type PDMS devices.
In addition, zero-order release pattern can be achieved by fabricating PDMS into reservoir-type devices. For instance, Maeda et al designed a covered-rod formulation with a silicone inner matrix containing active ingredient and a silicone outer layer functioning as the rate-controlling membrane. In contrast to the typical first-order release profile with matrix-type devices, near zero-order release of ivermectin (IVM) from a PDMS reservoir-type device was observed. With the addition of poly(ethylene glycol) (PEG4000) in the matrix, a four-fold increase in IVM release velocity was observed while the zero-order profile has been maintained [22], which was mainly due to the effect of PEG as a solubility enhancing agent. Studies on PDMS based intravaginal rings (reservoir-type, IVR) for the delivery of a hydrophobic drug TMC120 also displayed a near zero-order release profile with a short initial burst phase [23,24]. The initial burst was attributed to the enhanced dissolution of the active drugs within the core of the ring, and the incorporation of hydrophilic lactose greatly decreased the burst effect while increasing the release rate in a concentration-dependent manner [23].
2.3 Poly(ethylene vinyl acetate) (PEVA)
PEVA is the copolymer of ethylene and vinyl acetate (VA) (Figure 1). In biomedical engineering, PEVA has been used in the development of medical and controlled drug delivery devices by employing casting and freeze drying methods. PEVA based devices are designed to slowly release drug compounds over a relatively long period of time [40]. Subcutaneous implantation of ethylene-vinyl acetate copolymer films in Sprague-Dawley rats confirmed that the base polymer provoked no inflammatory responses and the polymer had good tissue compatibility [41]. Moreover, PEVA is readily available with a variety of VA contents, ranging from 0% to 40%. The permeability of these copolymer films changes substantially with varying VA content and thus it is possible to tailor the release rate to a desired value by slightly changing the membrane compositions [42]. An increase in crystallinity would also reduce the diffusivity of polymer [43]. Similarly, PEVA is also a diffusion-controlled polymer, and it has been formulated into either microporous films to achieve zero-order release or matrix-type devices to sustain drug release over time (Table 1).
3. Biodegradable polymeric matrices
3.1 Overview
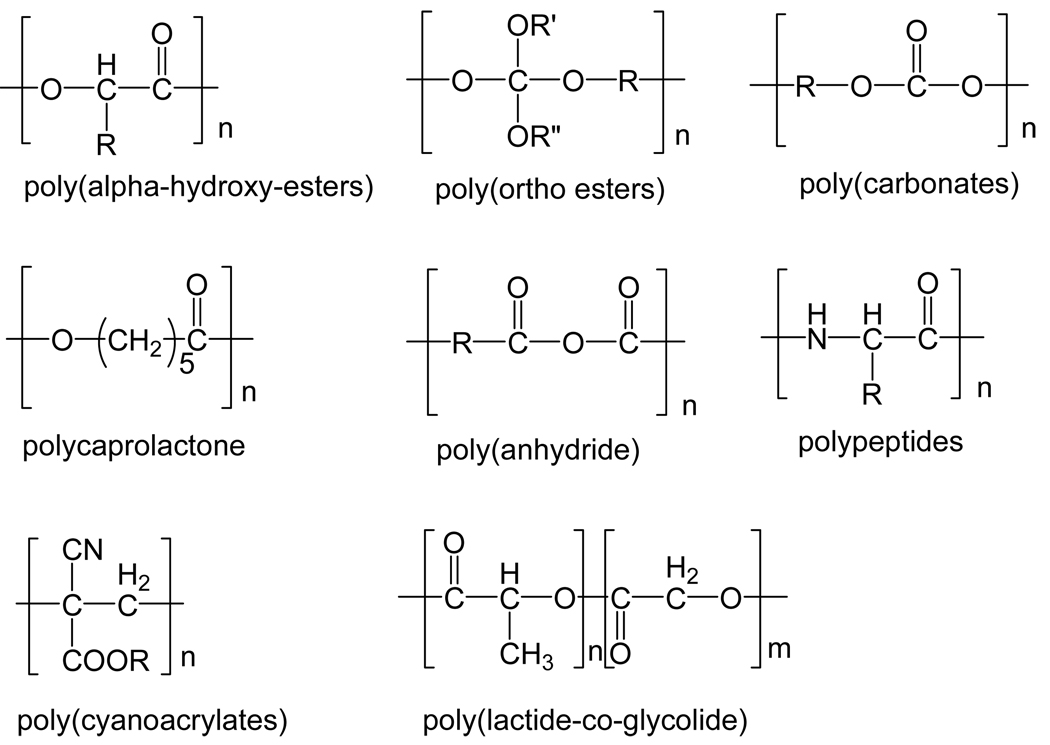
Biodegradable polymers are widely used in the development of controlled delivery systems that can dramatically improve patient compliance and reduce side effects through extended dosing and targeting [44]. Several pharmaceutical products based on biodegradable delivery systems have been approved by the FDA, including hormones, antitumour drugs and antibiotics [45]. In general, biodegradable polymers contain labile bonds such as ester-, amide-, and anhydride-bonds that are prone to hydrolysis or enzymatic degradation (Figure 4). Surface degradation and bulk degradations are two typical modes of degradation. In a surface-degrading polymer, degradation is confined to the outer surface of the device [46,47]. In a bulk-degrading polymer, however, degradation occurs homogeneously throughout the material [48]. Water is an important factor during hydrolysis and thus water intrusion into the device is of significant importance for the study of degradation kinetics as well as release kinetics. The degradation of semicrystalline polymers occurs in two stages: i.) The first stage consists of water infusion into the amorphous regions with random hydrolytic scission of labile bonds, such as ester bonds; ii.) The second stage starts when most of the amorphous regions are degraded [49]. As degradation results in the scission of polymer chain, the change in the average molecular weight of the polymer could be used to quantify the degradation process over time. Using gel permeation chromatography (GPC), the degradation process is usually characterized by plotting the average molecular weight of the degraded material versus time. The following two equations are widely used to describe the degradation kinetics:
| (1) |
| (2) |
where Mw(t) and Mw0 are the average polymer molecular weight at time t and zero. kdegr denotes the apparent degradation rate constant of the polymer. Eq. 2 was successfully applied to the degradation data of PLGA microparticles [50,51].
Figure 4.
Representative functional groups of biodegradable polymers Adapted from [52].
Polymer degradation has been defined by Siepmann and Gopferich as the chain scission process by which polymer chains are cleaved into oligmers and monomers, while bioerosion refers to the loss of material from bulk or surface in contact with a biological system [52]. By virtue of these definitions, the two concepts are not mutually exclusive but are interrelated. In this section, representative polymers that undergo either chain scission process and/or mass loss will be discussed.
3.2 Polyesters
Polyester is a class of polymers characterized by ester linkages in the backbone, such as poly(lactic acid) (PLA), poly(glycolic acid) (PGA), poly(lactide-co-glycolide) (PLGA), etc. PLGA is one of the most commonly used biodegradable polymers in developing particulate drug delivery systems [53]. PLGA is synthesized by ring-opening copolymerization of two different monomer, the cyclic dimmers (1,4-dioxane-2,5-diones) of glycolic acid and lactic acid [54]. PLGA degrades via hydrolysis of its ester linkages in the presence of water. Due to the hydrophobic nature of PLGA, PLGA nano-/microparticles with core-shell structures are prepared through various emulsification processes and hydrophilic drugs could be encapsulated in the hydrophilic core of the particles [55], while hydrophobic drugs tend to distribute in the hydrophobic shell [56]. The typical release profile for PLGA particulate delivery systems is the initial burst phase followed by a near-zero order phase [57]. Various intramuscular or subcutaneous controlled delivery systems in the form of implants or microparticles have been developed using biodegradable polyesters such as PLA and PLGA [58]. In vitro release study of diltiazem hydrochloride and buserelin acetate from in situ forming delivery systems (ISM, PLA or PLGA solution dispersed in an external oil phase) displayed a triphasic release pattern (Table 2) [59]. The initial burst was most likely due to the rapid release of surface associated drug molecules, the second phase was probably due to material degradation via chain scission, and the third phase was mainly the result of polymer erosion which led to the loss of bulk materials [60]. Though PLA and PLGA are bulk-erosion type biodegradable materials, studies showed that release kinetics of selected solutes from such biodegradable polymeric matrices are not simply driven by degradation [61,62]. In the early stage, the concentration gradient and the shape of the device seem to have a more profound impact on the release rate. While in the later stage, degradation becomes the dominant driving force and thus the release profile corresponded to the degradation kinetics of the material [62]. In addition to the property and the structure of the material, the physicochemical properties of the drug compounds also influence the release behavior. For example, the in vitro release of a hydrophobic drug, estradiol, from PLGA nanoparticles displayed zero-order release for 31 – 54 days, and the linear release pattern was observed with all formulation groups, which has been found to occur through diffusion-cum-degradation mediated process (Table 2) [56]. In comparison, the release of a hydrophilic drug, insulin, from PLGA microcapsules displayed a triphasic pattern with approximately 20% of the insulin released within 24 h, 40% released after 10 days and approximately 50% after 30 days (Table 2) [63].
Table 2.
Summary of release kinetics and transport mechanisms of degradable polymer based delivery devices
| Type of material | Type of device |
Loaded drug | Burst release |
Release kinetics | Transport mechanism |
Ref. |
|---|---|---|---|---|---|---|
| PLGA/PLA | Microparticle | Diltiazem hydrochloride |
2h | Triphasic pattern | Diffusion and erosion |
[59] |
| PLGA | Nanoparticle | Estradiol | w/o | Zero order up to 31 ~54 d |
Diffusion-cum- degradation |
[56] |
| PLGA | Microcapsule | Insulin | 20%, 24h |
Triphasic pattern | Diffusion and erosion |
[63] |
| p(FAD-SA) 50:50 | Implantable disk |
Cefazolin sodium |
w/o | 100%, 14 d | Diffusion | |
| Bupivacaine free base |
w/o | 90%, 35 d | Diffusion and degradation |
[64] | ||
| Taxol | w/o | 15%, 77d | Degradation | |||
| PEG hydrogel with degradable crosslinks |
Disk | Bovine serum albumin |
w/o | Zero order in the presence of human neutrophil elastase |
Triggered degradation |
[67] |
| Poly(ortho ester amide) copolymer |
NA | FITC-dextran | w/o | Near zero order | Erosion | [68] |
| HPMC | Tablet | Adinazolam mesylate |
w/ | Near zero order, 10h | Swelling and dissolution |
[72] |
w/, with; w/o, without;
NA, not available
3.3 Polyanhydrides
Polyanhydrides are a group of surface-erosion dominated biodegradable materials. Release study on a polyanhydride (poly(fatty acid dimer-sebacic acid), p(FAD-SA), 50:50 w/w) based implant for local drug delivery revealed that the release kinetics was related to the drug solubility and the intrinsic dissolution rate [64]. Three model drugs of different aqueous solubilities, which included cefazolin sodium (350 mg/ml), bupivacaine free base (0.56 - 0.7 mg/ml), and taxol (0.042 mg/ml), have been investigated. Cefazolin sodium achieved 100% release in 14 days while 90% bupivacaine free base was released in 35 days. However, only 15% taxol was released in 77 days (Table 2) [64]. Therefore, the hydrophilic and hydrophobic nature of the drugs may potentially affect release rate and cumulative release percentage from the surface-erosion type devices. In the case of taxol, the degradation of polyanhydride might be the main driving force for taxol release, while for cefazolin sodium, the concentration gradient between the devices and the release medium would be dominant for solute transport [64]. Manoharan et al investigated poly 1,3-bis-(p-carboxyphenoxy) propane-co-sebacic acid (p(CPP:SA)) microspheres for controlled delivery of basal insulin. Insulin was released within 3 days from SA-only microspheres, while a significant amount of insulin was not released from CPP-only microspheres over a month due to the slow degradation in CPP polymers. By tailoring the CPP:SA ratios of the copolymer, initial burst could be reduced and insulin release was prolonged over a month with 67% cumulative release at day 35 [65].
3.4 Stimuli-triggered biodegradable polymer
Environmentally sensitive polymeric delivery systems are designed to achieve targeted delivery and controlled release in vivo upon specific stimuli, such as pH, ionic strength, enzyme-substrate, magnetic, thermal, electrical, ultrasound, etc [66]. Drug release from pH- and enzyme-sensitive polymeric delivery systems is mainly attributed to stimuli-triggered degradation. Aimetti and coworkers developed a poly(ethylene glycol) hydrogel platform with human neutrophil elastase sensitive peptide crosslinks. The crosslinked hydrogel was formed using thiol-ene photopolymerization, rendering the gel degradable at sites of inflammation. A zero-order release of bovine serum albumin in the presence of human neutrophil elastase has been observed, and the release was arrested in the absence of human neutrophil elastase, indicating enzyme-triggered degradation was the driving force for BSA release from this gel matrix (Table 2) [67]. Another example is poly(ortho ester amides) copolymer, the degradation of which is triggered by acids. Both the mass loss kinetics of poly(ortho ester amides) in physiological aqueous buffers and the release of fluorescently labeled dextran followed the near zero-order pattern, suggesting the release was predominantly driven by surface restricted polymer erosion (Table 2). Moreover, the rates of polymer erosion and drug release were much faster at pH 5.0 than at pH 7.4 [68].
3.5 Polymer for dissolution controlled drug delivery
Dissolution of polymers in solvents, an important phenomenon in polymer science, has been extensively applied in areas such as microlithography, controlled drug release, membrane science, etc [69]. In general, polymer dissolution involves two transport processes, i.e. solvent diffusion and chain disentanglement [70]. Though polymer dissolution does not result in the scission of polymer chains, it does lead to the loss of bulk material. One example is polysaccharides, a class of hydrophilic macromolecules that are widely used in pharmaceutical industry owing to low toxicity, biocompatibility, availability and abundance. Polysaccharides such as hydroxypropyl methylcellulose (HPMC), cyclodextrin, dextran, gellan gum, remain stable under physiological pH and temperature, but will undergo hydrolysis at extreme pH and temperatures. More importantly, polysaccharides undergo dissolution in the aqueous medium due to solvent penetration effect, swelling, and polymer chain disentanglement and relaxation [71]. Thus, solute transport from polysaccharides-based material systems could be driven by diffusion and/or dissolution. For example, the fractional release of adinazolam mesylate from tablets consisting of HPMC matrices corresponded well with the fractional release of HPMC, indicating drug release is primarily driven by dissolution (Table 2) [72].
4. Mathematical models for drug release kinetics from polymeric systems
Mathematical modeling of drug release kinetics provides a basis for the study of mass transport mechanisms that are involved in the control of drug release [73]. There have been several nicely written reviews on mathematical modeling for bioerodible polymeric delivery systems [52], dissolution controlled drug delivery systems [69], microsphere delivery systems [2] and hydrogel networks [74]. In general, diffusion, erosion, and degradation are the most important mechanisms for solute transport from polymeric matrices. Mathematical models based on each aforementioned mechanism are summarized here. In addition, models for materials with more complex compositions and structures are also discussed.
4.1 Empirical models
Several commonly used power law equations for modeling release kinetics are summarized (Table 3). These models are easy to use and the established empirical rules may help explain transport mechanism(s). However, these models do not provide additional insights into a more complex transport mechanism. Furthermore, these models might fail whenever there is a need for taking into account specific physicochemical processes [52]. For instance, Ritger-Peppas (Eq 4) and Peppas-Sahlin (Eq 5) equations have been applied to describe the release of sodium salicylate from HPMC tablets, indicating a non-Fickian drug release mechanism. The study also revealed that polymer erosion, swelling and dissolution were all involved in the release process and the authors suggested that the conclusion of a non-Fickian drug release mechanism, simply based on the diffusional exponent, n, of the Peppas models (Eq 4), can be misleading [80].
Table 3.
Empirical mathematical models for drug release kinetics
| Model | Expression | Eq. | Application | Ref. | |
|---|---|---|---|---|---|
| Higuchi | (3) | Fickian diffusion | [75] | ||
| Ritger- Peppas |
(4) | n=1, Case II transport; n=0.5, Fickian diffusion; 0.5<n<1, non-Fickian diffusion |
[76] | ||
| Peppas- Sahlin |
(5) | Non-Fickian diffusion | [77] | ||
| Alfrey |
|
(6) | Non-Fickian diffusion (sigmoid) |
[78] | |
| Zero- order |
(7) | Case II transport | [79] |
4.2 Diffusion controlled models
Derived from Fick’s second law of diffusion, drug release in the case of slab-like devices is described by the following equation [80]:
| (8) |
where Mt is the amount of drug released at time t, M0 is the total mass of drug loaded into the device, D is the diffusion coefficient of the drug within the polymer matrix, π is 3.14, and h is the thickness of the device. This is an early-time approximation which holds for the release of the first 60% of cumulative release, i.e. 0 ≤ Mt/M0 ≤ 0.6.
The late-time approximation, which holds for the final portion of the drug release, i.e. 0.4 ≤ Mt/M0 ≤ 1.0, is described by the following equation [82]:
| (9) |
The assumption for the application of the above equations is the dimension and physical properties of the material matrices do not change during the release process, i.e. there is no degradation or mass loss of the bulk materials. To predict the release profile, the diffusion coefficient of the solute within the polymer matrix (D) should be available, which could be measured by nuclear magnetic resonance and fluorescence correlation spectroscopy [83]. Furthermore, Eq. 8 and 9 have also been used to predict the diffusional coefficients of functional proteins within the self-assembling peptide nanofiber hydrogel scaffold [84] and the diffusional coefficients of theophylline in the poly(acrylic acid-g-ethylene glycol) hydrogels [79]. The models achieved good correlations with experimental data in both studies, indicating the transport mechanism was primarily Fickian diffusion.
4.3 Degradation based models
4.3.1 Polymer dissolution based model
Polymer dissolution refers to the process that polymer begins to release its contents to the surrounding fluid when in the presence of a thermodynamically compatible solvent [69]. Drug release from such polymeric matrices can be controlled either by solute diffusion and/or polymer dissolution [85]. Narasimhan and Peppas developed a model for polymer dissolution based on the molecular mechanism. The model describes solute transport in one-dimensional system, such as a film, slab, disk or tablet. In Eq 10, (S-R) is defined as the gel layer thickness and the variation of the gel-layer thickness (S-R) with time was established [84].
| (10) |
In Eq. 10, parameters A and B are defined as:
| (11) |
| (12) |
An expression for the cumulative release was derived as:
| (13) |
l is the half-thickness of the polymer, D is the diffusion coefficient of the solvent and Dd is the diffusion coefficient of the drug. v1* and vd* are characteristic concentrations of solvent and drug, respectively. v1,eq and vd,eq are equilibrium concentrations of solvent and drug. kd is the disentanglement rate of the polymer chains, which could be calculated using reptation theory [86]. To investigate the effect of various parameters on the drug release behavior, the normalized drug released as a function of time was simulated using drugs of different molecular sizes. An increase of drug release was observed with a higher drug diffusion coefficient. Also, case II behavior was observed as α (α = A/B) approaching zero [85]. The model successfully captures Fickian and Case II type behavior and the transition state in between. Both release patterns have been well characterized using this model, e.g. cimetidine hydrochloride release from PVA tablet, a Fickian diffusion driven process and sodium diclofenac release from a PVA tablet, a zero-order release pattern [87]. The model was demonstrated to be valid due to the good agreement between experimental data and the equation.
4.3.2 Erosion based model
Hopfenberg’s model can be applied to surface eroding polymer matrices where a zero-order surface detachment of the drug is the rate limiting release step. The equation is valid for spheres, cylinders and slabs:
| (14) |
Mt and M∞ are the cumulative amounts of drug released at time t and at infinite time; k0 refers to the erosion rate constant; c0 denotes the initial drug concentration within the matrix; a is the radius of a cylinder or sphere or the half-thickness of a slab; n is a ‘shape factor’ representing spherical (n=3), cylindrical (n=2) or slab geometry (n=1) [88]. Karasulu and coworkers’ study showed the predicted values of cylindrical tablet were not in good accordance with the observed values when using Eq 14 [88].
Following the analysis, Katzhendler et al developed a general mathematical model for drug release from an erodible matrix. The model takes into account radial and axial erosion
| (15) |
Where ka is the radial erosion rate constant, kb is the axial erosion rate constant and a0 and b0 are the tablets’ initial radius and thickness, respectively. When ka ≈ kb, the release profiles of theophylline from cylindrical tablet could be well described by Eq 15 [89].
Rothstein et al developed a unified model for both surface- and bulk-eroding materials. This model combines diffusion-reaction equations, taking into account the system’s hydration kinetics, dissolution and pore formation to compute drug release. Eq. 16 below describes the presence of water within the polymer matrix.
| (16) |
where Cw is the time-dependent concentration of water, Dw is the diffusivity of water in the polymer matrix, k is the degradation rate constant, and Mw is the polymer molecular weight.
The kinetics of hydrolysis can be described by following equation.
| (17) |
The dissolution of the drug can be calculated with a second order rate expression.
| (18) |
where kdis is the intrinsic dissolution rate constant Csn is the normalized concentration of solid drug in the polymer matrix, CAn is the difference between the aqueous agent concentration and its maximum solubility (CAmx), and CWn is the normalized concentration of water. The position- r and time- t dependant in a polymer matrix can be calculated from Fick’s second law and the dissolution rate expression.
| (19) |
where Deff is an effective diffusivity term. Integrating the total normalized concentration of agent in the matrix over all space yields the cumulative fraction of agent remaining in the matrix at each point in time (Eq. 20)
| (20) |
The cumulative fraction of drug release R(t), is simply (Eq. 21)
| (21) |
The Deff term depends on the matrix porosity (ε) and the diffusivity of the agent through the porous matrix (DA); (Deff = DA·ε). The time- and space- dependant matrix porosity follows a cumulative normal distribution function based on a molecular weight or degradation rate distribution of the given polymer (Eq 22).
| (22) |
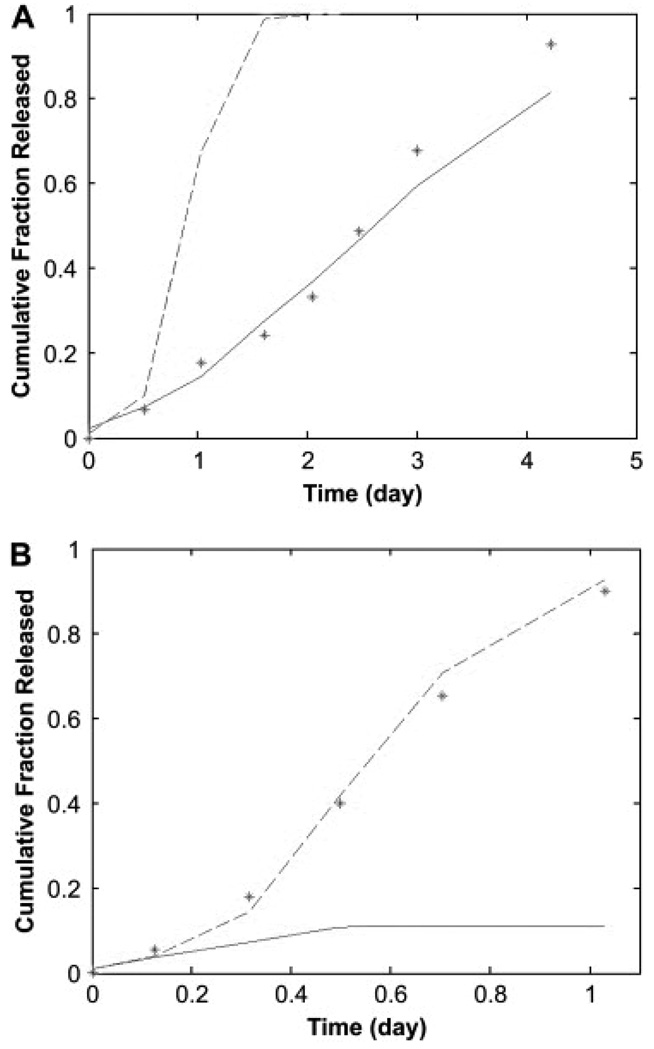
The variance (σ2) is based on the crystallinity of the polymer matrix and corresponding distribution of degradation rates. The molecular weight of the polymer matrix during release (Mw,r) has been previously correlated to the molecular weight of the agent for common biodegradable systems [90]. The model has been successfully applied to dye release data from POE disks (Figure 5).
Figure 5.
Predictions of release from (A) bulk eroding and (B) surface eroding poly(orthoester) matrices. Predictions have been made for the experimental data for dye release asterisks, while accounting for the hydrolysis of the anhydride excipient, with the complete model (solid line, (A) SSE = 0.0237 and (B) SSE = 1.1539) and the simplified version which assumes bulk erosion (dashed line, (A) SSE = 1.0077 and (B) SSE = 0.0061). For calculations in both A and B, the following parameters were used: Mw,0 = 28.2 kDa, Mw,r = 10.2 kDa, Rp = 5 mm, and L = 1.4 mm. Based on the different anhydride contents, DA = 1.44 × 10−12 m2/s in A and DA = 9.75 × 10−12 m2/s in B [90].
Reprinted from Biomaterials, 30, Rothstein SN, Federspiel WJ, Little SR, A unified mathematical model for the prediction of controlled release from surface and bulk eroding polymer matrice, 1657–64. Copyright (2009), with permission from Elsevier.
4.4 Mathematical models for multi-component system
Lao and coworkers developed a combined mathematical model for PCL and PLGA polymer blends. The model development has been conducted through the modeling of release kinetics of each material component respectively. PCL is the type of slowly degrading polymer which takes over two years to be completely degraded under physiological conditions. Eq. 23 was developed for neat PCL film, in which the first term represents the burst phase and the second term describes the diffusion-controlled release. It is also important to note that no degradation term in Eq. 17 for pure PCL films. The model developed for PLGA took into consideration all three steps i.e. burst release, diffusion, and degradation (Eq. 24) [91]
| (23) |
| (24) |
| (25) |
Here, fPCL and fPLGA represent the fractions of drug that partition into and are released from PCL and PLGA phases, respectively, the sum of which is equal to 1.
Though not discussed in detail, drug release profile is related to the forms of delivery devices, for example sphere, disk, film, cylinder, etc. The aforementioned mathematical models are applicable to a certain type of devices. Table 4 summarizes the applicability and common assumptions for the previously discussed mathematical models. To sum up, no universally applicable mathematical models are available for release kinetics from non-degradable or degradable polymer systems due to the multiple factors involved during the process of solute transport. The established models seem to be material specific, drug specific, and formulation specific. Therefore, the applicability of a specific model should be carefully reviewed before it is applied to experimental data, such as the structural characteristics of materials, physicochemical properties of model drugs, dimension and geometry of the delivery devices, and any assumptions or limiting cases related to the model.
Table 4.
Summary of the mathematical models
| Mechanism of Transport |
Eq. | Form of Devices | Assumptions |
|---|---|---|---|
| Diffusion | (8), (9) | slab, disk | i) Diffusion takes place only in one dimension ii) Constant drug diffusion coefficient iii) No matrix swelling or degradation |
| Dissolution | (10), (11), (12), (13) |
slab, disk, film | i) Two moving boundaries: R, the glassy-rubbery interface; S, the rubbery-solvent interface ii) Constant drug and solvent diffusion coefficient |
| Erosion | (14) | sphere, cylinder, slab | i) Zero-order surface detachment of drug ii) Constant material erosion rate |
| (15) | slab, cylinder | i) Zero-order surface detachment of drug ii) Constant material erosion rate iii) Two dimensional erosion, i.e. axial and radial erosion |
|
| (16), (17), (18), (19), (20), (21), (22) |
slab, disk | i) Deff is related to matrix porosity (ε) ii) Second order polymer degradation kinetics iii) Applicable to both surface- and bulk- eroding materials |
5. Expert opinion
In the design and development of a therapeutic agent, in vitro release study has been considered as one of the key standards to evaluate and optimize the formulation. The in vitro release results reveal the structure-function relationship of the material matrices, contribute to the tailoring of material for optimal controlled release and also provide insights into the performance of the formulation in vivo. However, a major concern with in vitro release study is the lack of direct correlation between in vitro and in vivo release profiles. Currently, attentions have been focused on the in vivo release studies and the correlation between in vitro and in vivo release data [92,93]. The physiological conditions are much more complex than buffer solutions that are commonly employed for in vitro evaluations. The release profile of a drug may be affected by various proteins, cells, and enzymes in vivo. For example, simulated release medium including intestinal fluid, gastric fluid, saliva, lachrymal fluid, and blood serum can be employed to enhance the accuracy of evaluation. Alternatively, in vivo release models can be developed but they are often time laborious and costly. Additionally, the complex compositions of tissue fluids also present great challenges on the sensitivity and reliability of a single conventional analytical method. Nevertheless, the rapid development in advanced analytical techniques, such as liquid chromatography coupled with mass spectrometry, fluorescent probes, and mass imaging techniques provide potential means to conquer these difficulties.
In case studies of release kinetics, burst release is a phenomenon commonly observed in delivery devices of different forms and compositions. The burst effect may be favorable for certain indications or applications such as wound treatment, encapsulated flavors, targeted delivery and pulsatile release. However, it is also likely to cause negative effects such as local/systemic toxicity, short in vivo half-life, shortened release profile that requires more frequent dosing [94]. Burst release is often associated with device geometry, surface characteristics of host material, heterogeneous distribution of drugs within the polymer matrix, intrinsic dissolution rate of drug, heterogeneity of matrices (pore density), etc. However, few studies have been conducted to develop mechanism based mathematical models for burst release. To better predict the burst release, it would be worthwhile developing models to elucidate the mechanisms of burst release.
In addition, it would be of great significance to develop models that take into account physiological conditions, including such variables as pH, osmotic pressure, cellular tissue reactions, enzyme concentration, and etc [52]. This would benefit the mathematical prediction for the stimuli-triggered delivery systems as well as material systems employed under (patho)physically relevant conditions. Some preliminary studies have been well documented in the review paper by Lin and Metters [74]. However, mathematical models that can represent the real physiological conditions have yet to be developed. Furthermore, the goal for mathematical modeling of release kinetics is to elucidate the potential transport mechanisms, especially the structure-function relationship of the material system. In return, understanding of the fundamentals will provide guidance for future material design and device development.
A current trend in the controlled drug delivery field is the development of multi-component material systems, i.e. integrating multiple materials with diverse physicochemical properties. For instance, semi-interpenetrating networks composed of crosslinked, stable PEG matrices and biodegradable labile gelatin macromolecules have shown to be effective drug delivery matrices and tissue scaffold for wound healing [95,96]. As a result, the release kinetics is driven by multiple factors and cannot be described by a single mathematical model mentioned previously [97]. To better elucidate drug transport mechanism and predict transport behavior, it is crucial to “build up” the connection between measurements at the molecular level (e.g. solute diffusion coefficients, drug/polymer interaction parameter, drug/polymer crystallization behavior, etc.) and drug release kinetics.
Acknowledgements
This manuscript was funded by a NIH grant (R01-EB006613)
Footnotes
Declaration of interest
The authors state no conflict of interest and have received no payment in preparation of this manuscript.
Bibliography
Papers of special note have been highlighted as either of interest (•) or of considerable interest (••) to readers.
- 1.Langer R. New methods of drug delivery. Science. 1990;249:1527–1533. doi: 10.1126/science.2218494. [DOI] [PubMed] [Google Scholar]
- 2. Artifin DY, Lee LY, Wang CH. Mathematical modeling and simulation of drug release from microspheres: implication to drug delivery systems. Adv Drug Deliv Rev. 2006;58:1274–1325. doi: 10.1016/j.addr.2006.09.007. •• This article provided a comprehensive review of existing mathematical models and simulations of drug release from polymeric microspheres.
- 3.Grassi M, Grassi G. Mathematical modeling and controlled drug delivery: matrix systems. Curr Drug Deliv. 2005;2:97–116. doi: 10.2174/1567201052772906. [DOI] [PubMed] [Google Scholar]
- 4.Pillai O, Panchagnula R. Polymers in drug delivery. Curr Opin Chem Biol. 2001;5:447–451. doi: 10.1016/s1367-5931(00)00227-1. [DOI] [PubMed] [Google Scholar]
- 5.Katz JL, Ambrose CG, Mcmillin C, Spencer P. Encyclopedia of biomaterials and biomedical engineering. New York: Marcel Dekker; 2004. Orthopedic biomaterials. [Google Scholar]
- 6.Fung LK, Saltzman WM. Polymeric implants for cancer chemotherapy. Adv Drug Deliv Rev. 1997;26:209–230. doi: 10.1016/s0169-409x(97)00036-7. [DOI] [PubMed] [Google Scholar]
- 7.Siepmann J, Siepmann F. Mathematical modeling of drug delivery. Int J Pharm. 2008;364:328–343. doi: 10.1016/j.ijpharm.2008.09.004. [DOI] [PubMed] [Google Scholar]
- 8.Lin SB, Hwang KS, Tsay SY, Cooper SL. Segmental orientation studies of polyether polyurethane block copolymers with different hard segment lengths and distributions. Colloid Polym Sci. 1985;263:128–140. [Google Scholar]
- 9.Ebewele RO. Polymer science and technology. CRC Press LLC; 2000. [Google Scholar]
- 10.Yilgör E, Yurtsever E, Yilgör I. Hydrogen bonding and polyurethane morphology. II. Spectroscopic, thermal and crystallization behavior of polyether blends with 1,3-dimethylurea and a model urethane compound. Polymer. 2002;43:6561–6568. [Google Scholar]
- 11.Shah PN, Manthe RL, Lopina ST, Yun YH. Electrospinning of L-tyrosine polyurethanes for potential biomedical applications. Polymer. 2009;50:2281–2289. [Google Scholar]
- 12.Grzybowski J, Janiak MK, Oidak E, et al. New cytokine dressings. II. Stimulation of oxidative burst in leucocytes in vitro and reduction of viable bacteria within an infected wound. Int J Pharm. 1999;184:179–187. doi: 10.1016/s0378-5173(99)00064-2. [DOI] [PubMed] [Google Scholar]
- 13.Donelli G, Francolini I, Ruggeri V, et al. Pore formers promoted release of an antifungal drug from functionalized polyurethanes to inhibit Candida colonization. J Applied Microbiol. 2006;100:615–622. doi: 10.1111/j.1365-2672.2005.02801.x. [DOI] [PubMed] [Google Scholar]
- 14.Simmons A, Padsalgikar AD, Ferris LM, Poole-Warren LA. Biostability and biological performance of a PDMS-based polyurethane for controlled drug release. Biomaterials. 2008;29:2987–2995. doi: 10.1016/j.biomaterials.2008.04.007. [DOI] [PubMed] [Google Scholar]
- 15.Aparicio Gallego E, Castilla Peris C, Díez García MT, et al. Therapeutic behavior of a hydrocolloid dressing. Its evolution in the treatment of acute and chronic dermal ulcers. Rev Enferm. 2005;28:49–55. [PubMed] [Google Scholar]
- 16.Li B, Davidson JM, Guelcher SA. The effect of the local delivery of platelet-derived growth factor from reactive two-component polyurethane scaffolds on the healing in rat skin excisional wounds. Biomaterial. 2009;30:3486–3494. doi: 10.1016/j.biomaterials.2009.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kang E, Vedantham K, Long X, et al. Drug-eluting stent for delivery of signal pathway-specific 1,3-Dipropyl-8-cyclopentyl xanthine. Mol Pharm. 2009;6:1110–1117. doi: 10.1021/mp8002623. [DOI] [PubMed] [Google Scholar]
- 18.Simmons A, Padsalgikar AD, Ferris LM, Poole-Warren LA. Biostability and biological performance of a PDMS-based polyurethane for controlled drug release. Biomaterials. 2008;29:2987–2995. doi: 10.1016/j.biomaterials.2008.04.007. [DOI] [PubMed] [Google Scholar]
- 19.Schierholz JM, Steinhauser H, Rump AFE, et al. Controlled release of antibiotics from biomedical polyurethanes: morphological and structural features. Biomaterials. 1997;18:839–844. doi: 10.1016/s0142-9612(96)00199-8. [DOI] [PubMed] [Google Scholar]
- 20.Chang CP, Chang JC, Ichikawa K, Dobashi T. Permeability of dye through poly(urea-urethane) microcapsule membrane prepared from mixtures of di- and tri-isocyanate. Colloids Surf B Biointerfaces. 2005;44:187–190. doi: 10.1016/j.colsurfb.2005.06.013. [DOI] [PubMed] [Google Scholar]
- 21.Chen X, Liu W, Zhao Y, et al. Preparation and characterization of PEG-modified polyurethane pressure-sensitive adhesives for transdermal drug delivery. Drug Dev Ind Pharm. 2009;35:704–711. doi: 10.1080/03639040802512235. [DOI] [PubMed] [Google Scholar]
- 22.Maeda H, Brandon M, Sano A. Design of controlled-release formulation for ivermectin using silicone. Int J Pharm. 2003;261:9–19. doi: 10.1016/s0378-5173(03)00293-x. [DOI] [PubMed] [Google Scholar]
- 23.Woolfson AD, Malcolm RK, Morow RJ, et al. Intravaginal ring delivery of the reverse transcriptase inhibitor TMC 120 as an HIV microbicide. Int J Pharm. 2006;325:82–89. doi: 10.1016/j.ijpharm.2006.06.026. [DOI] [PubMed] [Google Scholar]
- 24.Malcolm RK, Woolfson AD, Toner CF, et al. Long-term, controlled release of the HIV microbicide TMC120 from silicone elastomer vaginal rings. J Antimicrob Chemother. 2005;56:954–956. doi: 10.1093/jac/dki326. [DOI] [PubMed] [Google Scholar]
- 25.Malcolm RK, McCullagh SD, Woolfson AD, et al. Controlled release of a model antibacterial drug from a novel self-lubricating silicone biomaterial. J Control Rel. 2004;97:313–320. doi: 10.1016/j.jconrel.2004.03.029. [DOI] [PubMed] [Google Scholar]
- 26.Kim J, Kim WJ, Kim SJ, et al. Release characteristics of quinupramine from the ethylene-vinyl acetate matrix. Int J Pharm. 2006;315:134–139. doi: 10.1016/j.ijpharm.2006.03.019. [DOI] [PubMed] [Google Scholar]
- 27.Tallury P, Alimohammadi N, Kalachandra S. Poly(ethylene-co-vinyl acetate) copolymer matrix for delivery of chlorhexidine and acyclovir drugs for use in the oral environment: effect of drug combination, copolymer composition and coating on the drug release rate. Dent Mater. 2007;23:404–409. doi: 10.1016/j.dental.2006.02.011. [DOI] [PubMed] [Google Scholar]
- 28.de Queiroz AA, Abraham GA, Higa OZ. Controlled release of 5-fluorouridine from radiation-crosslinked poly(ethylene-co-vinyl acetate) films. Acta Biomater. 2006;2:641–650. doi: 10.1016/j.actbio.2006.05.010. [DOI] [PubMed] [Google Scholar]
- 29.Arnold RR, Wei HH, Simmons E, et al. Antimicrobial activity and local release characteristics of chlorhexidine diacetate loaded within the dental copolymer matrix, ethylene vinyl acetate. J Biomed Mat Res Part B. 2008;86B:506–513. doi: 10.1002/jbm.b.31049. [DOI] [PubMed] [Google Scholar]
- 30.Cho CW, Choi JS, Shin SC. Controlled release of furosemide from the ethylene-vinyl acetate matrix. Int J Pharm. 2005;299:127–133. doi: 10.1016/j.ijpharm.2005.05.001. [DOI] [PubMed] [Google Scholar]
- 31.Zheng J, Yue X, Dai Z, et al. Novel iron-polysaccharide multilayered microcapsules for controlled insulin release. Acta Biomater. 2009;5:1499–1507. doi: 10.1016/j.actbio.2009.01.017. [DOI] [PubMed] [Google Scholar]
- 32.Cassano R, Trombino S, Muzzalupo R, et al. A novel dextran hydrogel linking trans-ferulic acid for the stabilization and transdermal delivery of vitamin E. Eur J Pharm Biopharm. 2009;72:232–238. doi: 10.1016/j.ejpb.2008.10.003. [DOI] [PubMed] [Google Scholar]
- 33.Zugasti ME, Zornoza A, Goñi Mdel M, et al. Influence of soluble and insoluble cyclodextrin polymers on drug release from hydroxypropyl methylcellulose tablets. Drug Dev Ind Pharm. 2009;35:1264–1270. doi: 10.1080/03639040902882306. [DOI] [PubMed] [Google Scholar]
- 34.Caracciolo PC, Buffa F, Abraham GA. Effect of the hard segment chemistry and structure on the thermal and mechanical properties of novel biomedical segmented poly(esterurethanes) J Mater Sci Mater Med. 2009;20:145–155. doi: 10.1007/s10856-008-3561-8. [DOI] [PubMed] [Google Scholar]
- 35.Li B, Yoshii T, Hafeman AE, et al. The effects of rhBMP-2 released from biodegradable polyurethane/microsphere composite scaffolds on new bone formation in rat femora. Biomaterials. 2009;30 doi: 10.1016/j.biomaterials.2009.08.038. 6789-79. [DOI] [PubMed] [Google Scholar]
- 36.Li Z, Yang X, Wu L, et al. Synthesis, characterization and biocompatibility of biodegradable elastomeric poly(ether-ester urethane)s based on poly(3-hydroxybutyrate-co-3-hydroxyhexanoate) and poly(ethylene glycol) via melting polymerization. J Biomater Sci Polym Ed. 2009;20:1179–1202. doi: 10.1163/156856209X452944. [DOI] [PubMed] [Google Scholar]
- 37.Patil RD, Mark JE. Evaluations of forcefields for aromatic polysiloxanes, and some applications to poly(diphenylsiloxane) Comput Theor Polym Sci. 2000;10:189–195. [Google Scholar]
- 38.Zimmermann I. Development of a long-acting therapeutic system: Part I: A method to produce silicon rubbers with well-defined microstructures. Eur J Pharm Biopharm. 2005;59:217–228. doi: 10.1016/j.ejpb.2004.07.006. [DOI] [PubMed] [Google Scholar]
- 39.Riggs PD, Clough AS, Jenneson PM, et al. 3He ion-bean analysis of water uptake and drug delivery. J Control Release. 1999;61:165–174. doi: 10.1016/s0168-3659(99)00116-9. [DOI] [PubMed] [Google Scholar]
- 40.Biondi M, Ungaro F, Quaglia F, Netti PA. Controlled drug delivery in tissue engineering. Adv Drug Deliv Rev. 2008;60:229–242. doi: 10.1016/j.addr.2007.08.038. [DOI] [PubMed] [Google Scholar]
- 41.Kamalesh S, Tan P, Wang J, et al. Biocompatibility of electroactive polymers in tissues. J Biomed Mater Res. 2000;52:467–478. doi: 10.1002/1097-4636(20001205)52:3<467::aid-jbm4>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 42.Tallury P, Alimohammadi N, Kalachandra S. Poly(ethylene-co-vinyl acetate) copolymer matrix for delivery of chlorhexidine and acyclovir drugs for use in the oral environment: effect of drug combination, copolymer composition and coating on the drug release rate. Dent Mater. 2007;23:404–409. doi: 10.1016/j.dental.2006.02.011. [DOI] [PubMed] [Google Scholar]
- 43.Fu JC, Moyer DL, Hagemeier C. Effect of comonomer ratio on hydrocortisone diffusion from sustained-release composite capsules. J Biomed Mater Res. 1978;12:249–254. doi: 10.1002/jbm.820120302. [DOI] [PubMed] [Google Scholar]
- 44.Lewis DD. Biodegradable polymers as drug delivery systems. New York: Marcel Dekker; 1990. Controlled release of bioactive agents from lactide/glycolide polymers. [Google Scholar]
- 45.Dorati R, Genta I, Colonna C, et al. Investigation of the degradation behavior of poly(ethylene glycol-co-D,L-lactide) copolymer. Polymer Degradation and Stability. 2007;92:1660–1668. [Google Scholar]
- 46.Heller J. Controlled release of biologically active compounds from bioerodible polymers. Biomaterials. 1980;1:51–57. doi: 10.1016/0142-9612(80)90060-5. [DOI] [PubMed] [Google Scholar]
- 47.Heller J, Baker RW, Gale RM, et al. Controlled drug release by polymer dissolution. I. Partial esters of maleic anhydride copolymers-properties and theory. J Appl Polym Sci. 1978;22:1191–2009. [Google Scholar]
- 48.Park K, Shalaby WSW, Park H. Biodegradable hydrogels for drug delivery. Lancaster: Technomic publishing company; 1993. p. 189. [Google Scholar]
- 49.Karlsson S, Albertsson AC. Degradable polymers: principles and applications. London: Chapman & Hall; 1995. Techniques and mechanisms of polymer degradation. [Google Scholar]
- 50.Charlier A, Leclerc B, Couarraze G. Release of mifepristone from biodegradable matrices: experimental and theoretical evaluations. Int J Pharm. 2000;200:115–120. doi: 10.1016/s0378-5173(00)00356-2. [DOI] [PubMed] [Google Scholar]
- 51.Klose D, Siepmann F, Elkharraz K, Siepmann J. PLGA-based drug delivery systems: Importance of the type of drug and device geometry. Int J Pharm. 2008;354:95–103. doi: 10.1016/j.ijpharm.2007.10.030. [DOI] [PubMed] [Google Scholar]
- 52.Siepmann J, Göpferich A. Mathematical modeling of bioerodible, polymeric drug delivery systems. Adv Drug Deliv Rev. 2001;48:229–247. doi: 10.1016/s0169-409x(01)00116-8. [DOI] [PubMed] [Google Scholar]
- 53.Singh L, Kumar V, Ratner BD. Generation of porous microcellular 85/15 poly (DL-lactide-co-glycolide) foams for biomedical applications. Biomaterials. 2004;25:2611–2617. doi: 10.1016/j.biomaterials.2003.09.040. [DOI] [PubMed] [Google Scholar]
- 54.Astete CE, Sabliov CM. Synthesis and characterization of PLGA nanoparticles. J Biomater Sci Polym Ed. 2006;17:247–289. doi: 10.1163/156856206775997322. [DOI] [PubMed] [Google Scholar]
- 55.Kakizawa Y, Nishio R, Hirano T, et al. Controlled release of protein drugs from newly developed amphiphilic polymer-based microparticles composed of nanoparticles. J Control Release. 2009 doi: 10.1016/j.jconrel.2009.09.024. published online 3 Oct 2009, doi:10.1016/j.jconrel.2009.09.024. [DOI] [PubMed] [Google Scholar]
- 56.Sahana DK, Mittal G, Bhardwaj V, Ravi Kumar MNV. PLGA nanoparticles for oral delivery of hydrophobic drugs: influence of organic solvent on nanoparticle formation and release behavior in vitro and in vivo using estradiol as a model drug. J Pharm Sci. 2008;97:1530–1542. doi: 10.1002/jps.21158. [DOI] [PubMed] [Google Scholar]
- 57.Li Y, Pei Y, Zhang X, et al. PEGylated PLGA nanoparticles as protein carriers: synthesis, preparation and biodistribution in rats. J Control Release. 2001;71:203–211. doi: 10.1016/s0168-3659(01)00218-8. [DOI] [PubMed] [Google Scholar]
- 58.Brannon-Peppas L. Recent advances on the use of biodegradable microparticles and nanoparticles in controlled drug delivery. Int J Pharm. 1995;116:1–9. [Google Scholar]
- 59.Kranz H, Bodmeier R. A novel in situ forming drug delivery system for controlled parenteral drug delivery. Int J Pharm. 2007;332:107–114. doi: 10.1016/j.ijpharm.2006.09.033. [DOI] [PubMed] [Google Scholar]
- 60.Grizzi I, Garreau H, Li S, Vert M. Hydrolytic degradation of devices based on poly(dl-lactic acid) size-dependence. Biomaterials. 1995;16:305–311. doi: 10.1016/0142-9612(95)93258-f. [DOI] [PubMed] [Google Scholar]
- 61.Biondi M, Ungaro F, Quaglia F, Netti PA. Controlled drug delivery in tissue engineering. Adv Drug Deliv Rev. 2008;60:229–242. doi: 10.1016/j.addr.2007.08.038. [DOI] [PubMed] [Google Scholar]
- 62.Wang XT, Venkatraman SS, Boey FYC, et al. Controlled release of sirolimus from a multilayered PLGA stent matrix. Biomaterials. 2006;27:5588–5595. doi: 10.1016/j.biomaterials.2006.07.016. [DOI] [PubMed] [Google Scholar]
- 63.Kim BS, Oh JM, Hyun H, et al. Insulin-loaded microcapsules for in vivo delivery. Mol Pharm. 2009;6:353–365. doi: 10.1021/mp800087t. [DOI] [PubMed] [Google Scholar]
- 64.Park ES, Maniar M, Shah JC. Biodegradable polyanhydride devices of cefazolin sodium, bupivacaine, and taxol for local drug delivery: preparation, and kinetics and mechanism of in vitro release. J Control Release. 1998;52:179–189. doi: 10.1016/s0168-3659(97)00223-x. [DOI] [PubMed] [Google Scholar]
- 65.Manoharan C, Singh J. Evaluation of polyanhydride microspheres for basal insulin delivery: Effect of copolymer composition and zinc salt on encapsulation, in vitro release, stability, in vivo absorption and bioactivity in diabetic rats. J Pharm Sci. 2009;98:4237–4250. doi: 10.1002/jps.21741. [DOI] [PubMed] [Google Scholar]
- 66.Kim SW, Kim JH, Jeon O, et al. Engineered polymers for advanced drug delivery. Eur J Pharm Biopharm. 2009;71:420–430. doi: 10.1016/j.ejpb.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Aimetti AA, Machen AJ, Anseth KS. Poly(ethylene glycol) hydrogels formed by thiol-ene photopolymerization for enzyme-responsive protein delivery. Biomaterials. 2009;30:6048–6054. doi: 10.1016/j.biomaterials.2009.07.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Tang R, Palumbo RN, Ji W, Wang C. Poly(ortho ester amides): acid-labile temperature-responsive copolymers for potential biomedical applications. Biomacromolecules. 2009;10:722–727. doi: 10.1021/bm9000475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Narasimhan B. Mathematical models describing polymer dissolution: consequences for drug delivery. Adv Drug Deliv Rev. 2001;48:195–210. doi: 10.1016/s0169-409x(01)00117-x. • This paper is of considerable interests for polymer dissolution controlled delivery systems
- 70.Miller-Chou BA, Koening JL. A review of polymer dissolution. Prog Polym Sci. 2003;28:1223–1270. [Google Scholar]
- 71.Bonacucina G, Cespi M, Palmieri GF. Evaluation of dissolution kinetics of hydrophilic polymers by use of acoustic spectroscopy. Int J Pharm. 2009;377:153–158. doi: 10.1016/j.ijpharm.2009.04.043. [DOI] [PubMed] [Google Scholar]
- 72.Ju RTC, Nixon PR, Patel MV. Drug release from hydrophilic matrices. 2. A mathematical model based on the polymer disentanglement concentration and the diffusion layer. J Pharm Sci. 1995;84:1464–1477. doi: 10.1002/jps.2600841214. [DOI] [PubMed] [Google Scholar]
- 73.Siepmann J, Peppas NA. Preface: Mathematical modeling of controlled drug delivery. Adv Drug Deliv Rev. 2001;48:137–138. doi: 10.1016/s0169-409x(01)00111-9. [DOI] [PubMed] [Google Scholar]
- 74. Lin CC, Metters AT. Hydrogels in controlled release formulations: network design and mathematical modeling. Adv Drug Deliv Rev. 2006;58:1379–1408. doi: 10.1016/j.addr.2006.09.004. •• An excellent review on mathematical modeling of hydrogel delivery systems
- 75.Higuchi T. Mechanism of sustained-action medication. Theoretical analysis of rate of release of solid drugs dispersed in solid matrices. J Pharm Sci. 1963;52:1145–1149. doi: 10.1002/jps.2600521210. [DOI] [PubMed] [Google Scholar]
- 76.Ritger PL, Peppas NA. A simple equation for description of solute release I. Fickian and non-fickian release from non-swellable devices in the form of slabs, spheres, cylinders or discs. J Control Release. 1987;5:23–36. [PubMed] [Google Scholar]
- 77.Peppas NA, Sahlin JJ. A simple equation for the description of solute release. III. Coupling of diffusion and relaxation. Int J Pharm. 1989;57:169–172. [Google Scholar]
- 78.Alfrey T, Gurnee EF, Lloyd WG. Diffusion in glassy polymers. J Polymer Sci C: Polymer Symposia. 1966;12:249–261. [Google Scholar]
- 79.Serra L, Domenech J, Peppas NA. Drug transport mechanisms and release kinetics from molecularly designed poly(acrylic acid-g-ethylene glycol) hydrogels. Biomaterials. 2006;27:5440–5451. doi: 10.1016/j.biomaterials.2006.06.011. [DOI] [PubMed] [Google Scholar]
- 80.Ferrero C, Massuelle D, Doelker E. Towards elucidation of the drug release mechanism from compressed hydrophilic matrices made of cellulose ethers. II. Evaluation of a possible swelling-controlled drug release mechanism using dimensionless analysis. J Control Release. 2009 doi: 10.1016/j.jconrel.2009.09.011. published online 18 September 2009, doi:10.1016/j.jconrel.2009.09.011. [DOI] [PubMed] [Google Scholar]
- 81.Brazel CS, Peppas NA. Mechanisms of solute and drug transport in relaxing, swellable, hydrophilic glassy polymers. Polymers. 1999;40:3383–3398. [Google Scholar]
- 82.Park K, Shalaby WSW, Park H. Biodegradable hydrogels for drug delivery. PA: Technomic publishing company; 1993. p. 191. [Google Scholar]
- 83.Modesti G, Zimmermann B, Börsch M, et al. Diffusion in model networks as studied by NMR and fluorescence correlation spectroscopy. Macromolecules. 2009;42:4681–4689. doi: 10.1021/ma900614j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Koutsopoulos S, Unsworth LD, Nagai Y, Zhang S. Controlled release of functional proteins through designer self-assembling peptide nanofiber hydrogel scaffold. Proc Natl Acad Sci USA. 2009;106:4623–4628. doi: 10.1073/pnas.0807506106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Narasimhan B, Peppas NA. Molecular analysis of drug delivery systems controlled by dissolution of the polymer carrier. J Pharm Sci. 1997;86:297–304. doi: 10.1021/js960372z. [DOI] [PubMed] [Google Scholar]
- 86.Meister BJ. Uniting molecular network theory and reptation theory to predict the rheological behavior of entangled linear polymers. Macromolecules. 1989;22:3611–3619. [Google Scholar]
- 87.Narasimhan B, Peppas NA. Molecular analysis of drug delivery systems controlled by dissolution of the polymer carrier. J Pharm Sci. 1997;86:297–304. doi: 10.1021/js960372z. [DOI] [PubMed] [Google Scholar]
- 88.Hopfenberg HB. Controlled release from erodible slabs, cylinders, and spheres. In: Paul DR, Harris FW, editors. ACS Symp. Ser. No.33. American Chemical Society. Washington: Controlled release polymeric formulations; 1976. pp. 26–32. [Google Scholar]
- 89.Karasulu HY, Ertan G, Kose T. Modeling of theophylline release from different geometrical erodible tablets. Eur J Pharm Biopharm. 2000;49:177–182. doi: 10.1016/s0939-6411(99)00082-x. [DOI] [PubMed] [Google Scholar]
- 90. Rothstein SN, Federspiel WJ, Little SR. A unified mathematical model for the prediction of controlled release from surface and bulk eroding polymer matrices. Biomaterial. 2009;30:1657–1664. doi: 10.1016/j.biomaterials.2008.12.002. •• The first unified model to predict release behaviors from both surface eroding and bulk eroding matrices
- 91.Lao LL, Venkatraman SS, Peppas NA. Modeling of drug release from biodegradable polymer blends. Eur J Pharm Biopharm. 2008;70:796–803. doi: 10.1016/j.ejpb.2008.05.024. [DOI] [PubMed] [Google Scholar]
- 92.Liu WH, Song JL, Liu K, et al. Preparation and in vitro and in vivo release studies of Huperzine A loaded microspheres for the treatment of Alzheimer’s disease. J Control Release. 2005;107:417–427. doi: 10.1016/j.jconrel.2005.03.025. [DOI] [PubMed] [Google Scholar]
- 93.Kelm J, Regitz T, Schmitt E, et al. In vivo and in vitro studies of antibiotic release from and bacterial growth inhibition by antibiotic-impregnated polymethlmethacrylate hip spacers. Antimicrob Agents Chemother. 2007;50:332–335. doi: 10.1128/AAC.50.1.332-335.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Huang X, Brazel CS. On the importance and mechanisms of burst release in matrix-controlled drug delivery system. J Control Release. 2001;15:121–136. doi: 10.1016/s0168-3659(01)00248-6. • An excellent review on the mechanisms and mathematical models of burst release effect\
- 95.Burmania JA, Kao WJ. Cell interaction with protein-loaded interpenetrating networks containing modified gelatin and poly(ethylene glycol) diacrylate. Biomaterials. 2003;24:3921–3930. doi: 10.1016/s0142-9612(03)00270-9. [DOI] [PubMed] [Google Scholar]
- 96.Kleinbeck KR, Faucher L, Kao WJ. Multifunctional in situ photopolymerized semi-interpenetrating network system is an effective donor site dressing: a cross comparison study in a swine model. J Burn Care Res. 2008;3:37–45. doi: 10.1097/BCR.0b013e3181921f98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Fu Y, Kao WJ. Drug release kinetics and transport mechanisms from semi-interpenetrating networks of gelatin and poly(ethylene glycol) diacrylate. Pharm Res. 2009;26:2115–2124. doi: 10.1007/s11095-009-9923-1. [DOI] [PMC free article] [PubMed] [Google Scholar]