Abstract
This paper presents new approaches for the assessment of the arterial and reference diameters in (cardio-)vascular X-ray images, designed to overcome the problems experienced in conventional quantitative coronary and vascular angiography approaches. In single or “straight” vessel segments, the arterial and reference diameter directions were made independent of each other in order to be able to measure the minimal lumen diameter (MLD) more accurately, especially in curved vessel segments. For ostial segments, an extension of this approach was used, to allow measurement of ostial lesions in sidebranches more proximal than using conventional methods. Furthermore, two new bifurcation approaches were developed. The validation study shows that the straight segment approach results in significant smaller MLDs (on average 0.032 mm) and the ostial approach achieves on average an increase in %DS of 3.8% and an increase in lesion length of 0.59 mm due to loosening the directional constraint. The validation of our new bifurcation approaches in phantom data as well as clinical data shows only small differences between pre- and post-intervention measurements of the reference diameters outside the bifurcation core (errors smaller than 0.06 mm) and the bifurcation core area (errors smaller than 1.4% for phantom data). In summary, these new approaches have led to further improvements in the quantitative analyses of (cardio-)vascular X-ray angiographies.
Keywords: QCA, Quantitative coronary angiography, QVA, Diameter function, Ostial analysis, Bifurcation analysis
Introduction
Over the last several decades, quantitative coronary angiography (QCA) has become the standard in the assessment of coronary artery stenosis. Its methods are widely used in hospitals and core laboratories all over the world to measure accurately the severity of coronary artery lesions and other clinically relevant parameters. Although the accuracy and precision of the system have been presented in many validation studies [1–8], there is still room for further improvements especially for cases with extreme vessel morphologies such as highly curved vessels and complex-shaped lesions.
In addition, the treatment of the more complex vessel structures, such as bifurcations and sidebranches [9–11], has received a great deal of attention over the last few years. Since more and more interventions are performed in this field, there is an increasing demand for a system that can accurately measure all clinically relevant parameters in those particular cases. With that in mind, we developed a new pathline detection algorithm that is more robust and suitable for ostial and bifurcation vessel segments [12, 13]. Furthermore, we carried out research on a novel contour detection approach, the WaveContour, designed to accurately detect the contours in a wide range of vessel sizes and different vessel morphologies [14].
In this publication, the focus is on the accurate and robust assessment of the vessel sizes in a wide range of morphologies and the proper estimation of the size and course of the original healthy vessels, which are denoted reference diameter functions and reference contours, respectively.
The organization of this manuscript is as follows: first, the new approach for the assessment of the arterial and reference diameters of a single segment is presented. Next, the approach is extended towards the analysis of (the ostium of) a sidebranch with its benefit clearly demonstrated. Thereafter, the latest bifurcation analysis approaches will be discussed. For all the mentioned approaches, validation studies have been carried out, of which the most important results will be presented. The manuscript is concluded by a discussion and conclusions.
Methods and materials
The new diameter function
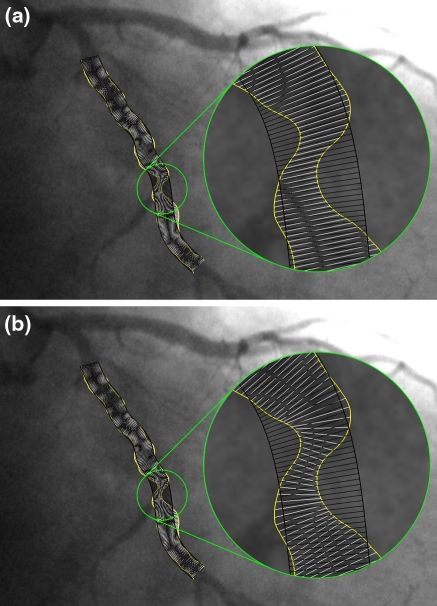
To quantify the degree of severity of a lesion accurately, the arterial diameters must be calculated reliably and a good estimation of the original healthy vessel size, hereinafter referred to as the “reference diameter function”, must be available. This reference diameter function is an interpolated reference line based on the model of a constantly tapering vessel. Traditionally, the arterial and reference diameter values are measured at the same positions and in the same directions. This was required, since there had to be a one-to-one correspondence between the arterial and reference diameters. In most of the cases, the assumption that the actual vessel and the reconstructed vessel lie in approximately the same direction, holds. However, in cases where there is a lesion with a complex morphology or when the vessel is highly curved, this approximation may not be true, see Fig. 1a.
Fig. 1.
An example where directions of arterial and reference diameters should be very different. The white lines represent the arterial diameters, while the black lines represent the reference diameters. a Traditional measurement: direction of arterial diameters is not correct, b the diameters with our new diameter method
To ensure the correct directions of the arterial diameters, the central lumen line through the vessel is used to calculate the arterial diameters. Since the direction of this centerline is always locally perpendicular to the narrowest opening of a vessel, the arterial diameters, which are perpendicular to the centerline, should represent the shortest distance between the vessel walls. To assess the reference diameters, however, the global direction of the healthy vessel needs to be defined, which will result in a much smoother centerline. Therefore, the directions of the arterial diameters and the reference diameters must be relatively independent of each other. By doing that, a different correspondence needs to be defined between the arterial and reference diameters in order to be able to calculate the clinically relevant stenosis parameters.
The first step of our diameter calculation approach is the calculation of the arterial centerline using the two detected arterial contours as input. To this end, a medial axis is calculated between the two arterial contours using the wavefront propagation [15] and this medial axis is smoothed subsequently. The result is used as a centerline, with the diameters measured perpendicular to this centerline at positions sampled equidistantly along the centerline.
These diameter measurements are presented in a graph, denoted as the “arterial diameter function”. From this arterial diameter function an interpolated reference diameter function is calculated using linear regression (see Reiber et al. [1]). Next, the global direction of the vessel as it would have been in the healthy state is calculated, and this global direction results in the reference centerline. This reference centerline, along with the reference diameter function, is then used for the placement and orientation of the reference diameters. This is done in exactly the same way as the arterial diameters are positioned based on the arterial centerline: The reference diameters are calculated perpendicular to the reference centerline at positions equidistantly spaced along the reference centerline. Finally, the arterial diameters are linked with the reference diameters for a good correspondence.
The new ostial analysis
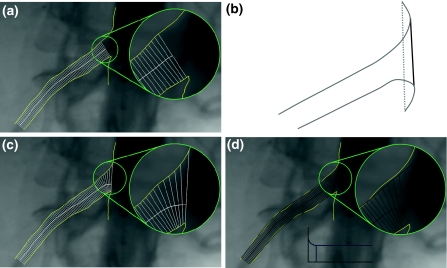
When analyzing an ostial segment, we face a different problem: How to measure the diameters at the beginning of the ostium. When the sidebranch is not at a 90 degree angle to the main vessel, a single or straight segment analysis (as discussed above) is not able to cover the ostium, as can be seen in Fig. 2a.
Fig. 2.
Results of a the straight analysis, b the ostium calculation, c the new ostial arterial and d the new ostial reference diameter calculations
In the most proximal part, the diameters could not be measured, because they intersected only with one of the two arterial contours. To solve this problem the direction of the diameters needs to be changed in such a way that the diameters turn towards the ostium of the vessel. In order to achieve this, the very first diameter of the sidebranch, the one that is touching (and in line with) the main vessel, needs to be found. This is not always simply the line that connects the two start points of the contours (see Fig. 2b dotted grey line). If the contours extend into the main vessel, as shown in Fig. 2b, the common tangent of both contours is calculated and used as the first diameter (black line).
The rest of the diameters (between the first one in the ostium and the previously calculated straight part) are fitted perpendicularly to a prolongation of the “straight” centerline. This centerline prolongation is achieved by means of a spline that starts perpendicularly to the first diameter and smoothly connects to the centerline that was previously calculated. Note that the spline part of the final centerline does not necessarily lie in the middle of the respective arterial diameters.
Similar to the straight segment arterial diameter calculation, the measured arterial diameters are put into an arterial diameter function graph and used to calculate the interpolated reference diameter function. However, the assumption of a constantly tapering vessel does not hold for the ostium of the segment. The morphology of the ostium makes the corresponding reference diameters increase, depending on the angle at which the sidebranch is connected to the main vessel (Fig. 2d).
For the straight part of the segment, the reference diameter function and reference centerline are calculated in the normal way. However, for the ostium, we must estimate the reference diameters differently. The first reference diameter will be in the direction of the first arterial diameter. The following reference diameters will gradually fan towards the straight part, similar to the interpolation of the arterial diameters. The results of this method can be seen in Fig. 2c and d.
The new bifurcation analysis
The bifurcations represent a different category in a vessel’s anatomy. Their various morphologies make them challenging to analyze. For example, when analyzing bifurcation lesions by means of two straight segment analyses over the bifurcation, the interpolated reference diameter functions do not accurately predict the course of the healthy vessel segments, as shown by Lansky et al. [16] and Goktekin et al. [17]. When on the other hand measuring the proximal and the two distal vessel segments independently from each other by performing three straight segment analyses, lesions inside the bifurcation core cannot be measured and the procedure is very time consuming. To circumvent all these problems, we have developed new approaches for the special case of bifurcations.
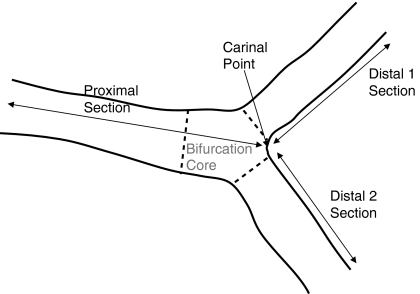
Bifurcations can be divided into four building blocks, which are called segments, as shown in Figs. 3 and 5 by the different areas: the bifurcation core (the central part of the bifurcation which begins where the common vessel starts to split into two branches and ends at the carinal point), the proximal segment (the common part of the vessel before the bifurcation core), and the two distal segments, representing the branches.
Fig. 3.
Partitioning of the bifurcation into three sections
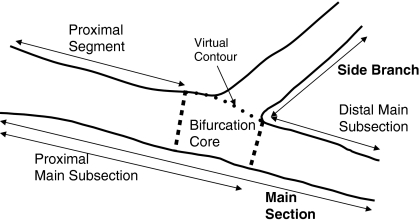
Fig. 5.
Partitioning of the bifurcation into two sections, the main section and the side branch section
In order to analyze the various morphologies of the bifurcations properly, new methods were developed, that aim at covering the entire bifurcation and producing reliable reference estimations, without the drawback of several parts being analyzed twice. Two new types of bifurcation models were designed that cover the vast majority of bifurcation morphologies: a Y-shape and a T-shape model. Both models are combinations of the four previously defined segments.
The Y-shape model
This model is used in case of a Y-shape bifurcation, where the distal branches have roughly the same size, roughly the same angle with the proximal vessel and a narrow angle between the two distal branches. In this model, the segment of analysis is divided into three sections: a proximal section and two distal sections. The proximal section of this model consists of the proximal segment extended with the bifurcation core, whereas the two distal sections consist of one distal segment each, as can be seen in Fig. 3.
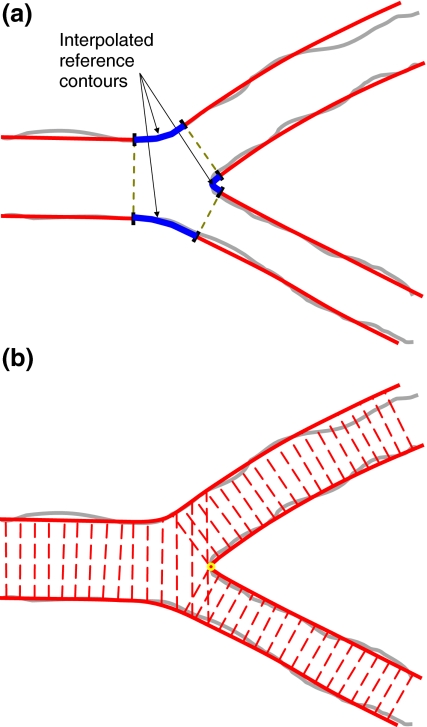
As opposed to the straight and ostial approaches, the final reference diameters can only be calculated after the bifurcation’s reference contours have been created. These contours are built upon the three pairs of reference contours coming from the three “straight” segments: proximal, distal 1 and distal 2, respectively. These six contours are subsequently connected two by two by means of splines, in order to create the three reference contours of the bifurcation, as shown in Fig. 4a.
Fig. 4.
a Interpolation of the reference contours in the bifurcation core; and b the reference diameters in the Y-shape analysis
As already mentioned, for the two distal sections, classical straight analyses are carried out to calculate the arterial and reference diameters. In the proximal section, however, the bifurcation core violates the linear tapering assumption. Therefore, the reference diameters for the bifurcation core part are “passively” calculated based on the already calculated left and right reference contours of the bifurcation, see Fig. 4b.
This model covers all vessel regions completely. There may be a small region of overlap between the proximal and distal sections, depending on the angle between them. This is required in order to always ensure a complete coverage of the bifurcation.
The T-shape model
In this model, the segment of analysis consists of two sections: a main section and a side branch section that splits off, as shown in Fig. 5. This model is thereby used for bifurcations that are uneven, having one distal vessel much larger than the other one. It also covers the case where there is a wide angle between the distal branches and the case where one of the branches continues in the direction of the main vessel while the other one branches away at a steep angle with respect to the first one (a T-shape bifurcation).
The main section consists of two parts: the proximal main subsection and the distal main subsection, where the proximal main subsection itself consists of the proximal segment and the bifurcation core. This division into two sections requires a virtual contour to define the boundary between them (explained later).
Analogous to the previously described Y-shape model, the reference contours are estimated before the reference diameters, by means of splines that connect the three pairs of “straight” reference contours computed outside the bifurcation core.
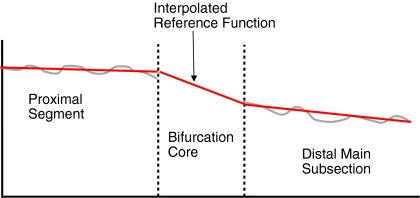
Analyzing the main section cannot be done by one single straight analysis since the proximal diameters are larger than the distal ones, the “step down phenomenon” [16], and therefore cannot be approximated by a linear interpolation. Therefore, the arterial and reference diameters are calculated for the proximal and distal segments separately by means of classical straight analyses. In the bifurcation core, the reference diameter function is linearly interpolated. This can be seen as a transition area in the middle of the diameter function plot (Fig. 6).
Fig. 6.
Reference diameter function of the main section
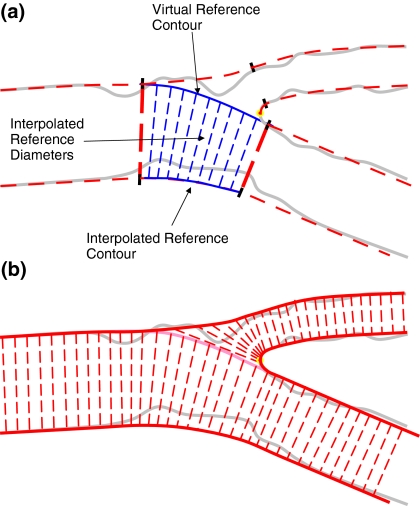
By using the spline-based reference contours (Fig. 4a) and the linearly interpolated reference diameters lengths (Fig. 6), a virtual reference contour is created, which connects the proximal and distal main vessel contour inside the bifurcation core, and hereby separating the side branch from the main vessel (Fig. 7). Inside the bifurcation core, the reference diameters ensure a smooth connection between the proximal and the distal main subsection. The virtual reference contour is also used to delimit the arterial diameters in the bifurcation core. By keeping this contour equal for the arterial and reference diameters it is ensured that virtually any obstruction inside the bifurcation core is found opposite to the side branch. The obstructions lying on the other side will be covered by the side section.
Fig. 7.
a The virtual reference contour that bridges the side branch and b the reference diameters in the T-shape analysis
The side section is automatically analyzed by means of an ostial model, starting from the interpolated contour that delineates the bifurcation core, and covering the rest of the side branch (Fig. 7). In this way, all vessel regions are completely covered and virtually no section overlap is generated.
Validation materials
Straight analysis
To asses the performance of our new diameter function method for straight segments, a validation study was carried out and the earlier mentioned criterion was used: the algorithm must be able to measure the correct arterial diameters in cases with strange lesion morphologies or highly curved vessels. To that end, a routinely acquired data set of digital angiograms was composed, consisting of a wide variety of vessels, with lesions of various severities, curved and relatively straight vessels, coronary and vascular cases. This data set was used to carry out a comparison between the new and conventional diameter function approach by measuring the minimal lumen diameters (MLDs).
To show the additional value of our new method more clearly, the data set was divided into two different groups: one group with approximately straight vessels and another group with more curved vessels. This division was made by estimating the difference in direction of the arterial and reference vessel at the lesion position and taking a 10 degree threshold value into account. This was done for 46 coronary cases (29 straight and 17 curved) and 24 vascular cases (18 straight and 6 curved), resulting in four data sets.
All analyses were performed by an experienced analyst using standard operating procedures (SOPs) for frame selection, segment selection and contour correction.
Ostial analysis
To validate the new approach for diameter calculation in ostial segments, a similar study was carried out. The diameters distally in the vessel are calculated as a straight vessel, which means that the previously mentioned validation results of the straight vessel analysis also apply to ostial vessel segments with lesions outside the ostium. The new aspect of the ostial analysis approach is the measurement inside the ostium and therefore only vessel segments with proximal lesions are included.
For the validation, a set of 22 clinical cases was collected (9 coronary and 13 vascular) and the severity of the ostial lesions was calculated using the new and the conventional approach. The percentage diameter stenosis was used as a parameter to asses the performance of the ostial extension. It takes into account both arterial and reference diameters, which is important, since the new ostial analysis has an effect on both. Besides that, the length of the lesions was measured and compared as well.
All analyses were once again performed by an experienced analyst using SOPs for frame selection, segment selection and contour correction.
Bifurcation analysis
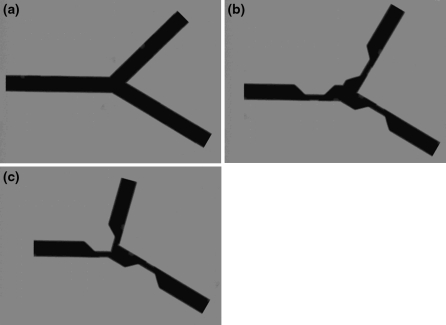
The performance of our new bifurcation approach was assessed using a set of artificial images and two sets of clinical data. The artificial images consisted of a set of twelve different bifurcation morphologies, showing four different angles between the two distal branches (60, 75, 90 and 105 degrees, with one branch fixed), each having a version without lesions, with separate lesions and with a combined lesion, as can be seen in Fig. 8. These artificial images were analyzed by an experienced analyst using the Y-shape analysis and the T-shape analysis models.
Fig. 8.
Examples of the artificial images: a 75 degrees without lesions, b 90 degrees with separate lesions, and c 105 degrees with a combined lesion
The clinical data that has been used consisted of two different coronary artery datasets. The first set contained ten cases, pre- and post-intervention, randomly selected from the Diverge trial, which uses the DEVAX stent, a self expanding carinal skirt stent [18]. These images were analyzed at the cardiovascular research foundation (CRF) using the Y-shape model. The second set contained nine cases, pre- and post-intervention, randomly selected from the TriReme medical TOP study, which uses stenting in the main branch with side branch conservation. These images were again analyzed at the CRF, this time using the T-shape analysis.
In the DEVAX study, as well as the TriReme study, a number of post-intervention analyses showed clearly the effects of an overdilated stent. Since this validation has the purpose to compare the reference and arterial results to a normal healthy vessel, the measured segments that showed an overdilation were excluded from the validation.
For the artificial images as well as the clinical data, the reference diameters just outside the bifurcation core were compared in the pre- and post-intervention analyses to prove the robustness of our reference diameter calculation in the straight segments that are influenced by the bifurcation. These diameters were measured in segments of 15 mm for the phantom data and 5 mm for the clinical data, located just distal of the bifurcation core. Furthermore, the arterial and reference diameters of the post- analysis were compared, at the same locations to assess the correctness of the reference estimation when there are no lesions.
Besides the measurements just outside the bifurcation core, the area of the bifurcation core itself was measured as well. The definition of the bifurcation core area is different for Y-shape and T-shape since in T-shape it is delimited by the virtual contour, as can be seen in Figs. 3 and 5. The value of the bifurcation core area can be calculated using the arterial contours and diameters, resulting in an arterial bifurcation core area, and using reference contours and diameters, resulting in a reference bifurcation core area.
For the artificial images as well as the clinical data, the reference bifurcation core areas were compared in the pre- and post-intervention analyses to asses the robustness of the reference estimation inside the bifurcation. Finally, in the post-intervention analysis, the arterial and reference areas were compared to validate the correctness of the reference estimation.
Statistical analysis
The measurements that have been done in the validation studies are comparisons between the new and the conventional methods or between pre- and post-analyses. In order to evaluate the comparisons, the differences are measured and the mean difference and the standard deviation of the differences are calculated, representing consecutively the systematic and random differences. Furthermore a paired T-Test is performed on the measurements, to calculate the P values and determine the significance of the differences. A P value smaller than 0.05 is considered a significant difference and printed bold in the result tables.
Results
Straight analysis
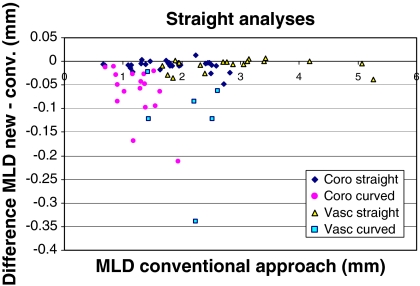
The results of the MLD measurements for our novel diameter calculation method are shown in Fig. 9.
Fig. 9.
The differences in MLD between the new and the conventional approach, for curved (more than 10 degrees difference between arterial and reference diameter at the obstruction) and straight (<10 degrees difference) vessels, coronary and vascular
As can be seen from Fig. 9 and Table 1, there is only very little difference (on average 0.009 mm), between the new and the conventional approach when measuring coronary or peripheral vessels that are approximately straight. Note that these small differences are significant. In curved vessels, however, the new approach performs better, which is demonstrated by the smaller MLDs measured by the new approach. For coronary arteries this difference is on average 0.066 mm and for peripheral arteries 0.125 mm, both highly statistically significant.
Table 1.
The differences in MLD between the new and the conventional approach
| Differences in MLD new–conv. (mm) | |||
|---|---|---|---|
| Systematic | Random | P value | |
| Coronary straight (N = 29) | −0.009 | 0.011 | 0.0002 |
| Coronary curved (N = 17) | −0.066 | 0.054 | 0.0001 |
| Vascular straight (N = 18) | −0.009 | 0.014 | 0.018 |
| Vascular curved (N = 6) | −0.125 | 0.111 | 0.040 |
| Total | −0.032 | 0.056 | 0.00001 |
Ostial analysis
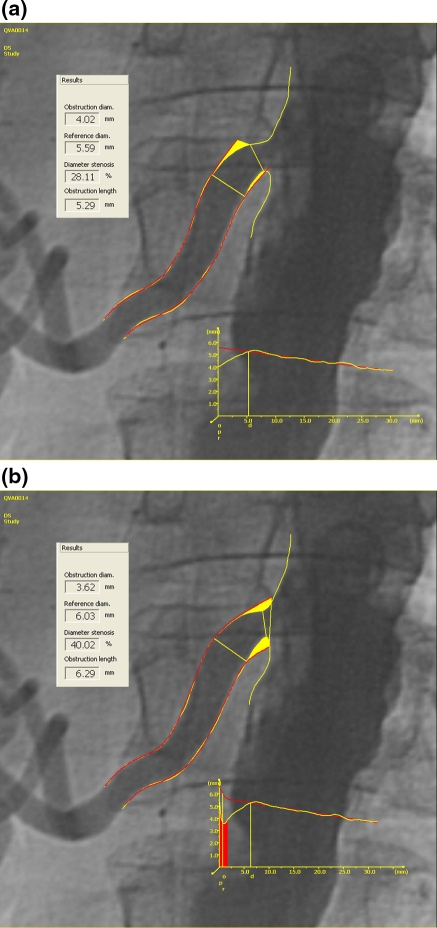
The validation results for our novel diameter measurement approach in ostial segments are best shown by an example (Fig. 10). As can be seen here, the measurement can be performed more proximal in the new analysis resulting in a larger percentage diameter stenosis and a longer lesion length. The overall results are shown in Table 2.
Fig. 10.
An example of the a straight segment measurements and b the enhanced ostial measurements
Table 2.
The differences in percentage diameter stenosis and lesion length between the new and the conventional approach
| Difference in %DS: new–conv. | Difference in lesion length: new–conv. (mm) | |||||
|---|---|---|---|---|---|---|
| Systematic | Random | P value | Systematic | Random | P value | |
| Coronary (N = 9) | 2.3 | 4.2 | 0.13 | 0.65 | 0.66 | 0.04 |
| Vascular (N = 13) | 4.9 | 7.9 | 0.05 | 0.56 | 1.71 | 0.30 |
| Total | 3.8 | 6.6 | 0.01 | 0.59 | 1.37 | 0.08 |
Overall, our new approach for measuring ostial lesions generally results in a higher percentage diameter stenosis (3.8%), and a slightly longer lesion length (0.59 mm) compared to the conventional straight analysis.
Bifurcation analysis
The validation results of the arterial and reference diameters of our new bifurcation approach just outside the bifurcation core can be seen in Table 3.
Table 3.
The differences in reference values between the pre- and post-intervention analyses and the differences between the arterial and reference values in the post-intervention analyses, measured just outside the bifurcation core
| Model | Difference in reference: post–pre (mm) | Difference in post: reference–arterial (mm) | |||||
|---|---|---|---|---|---|---|---|
| Systematic | Random | P value | Systematic | Random | P value | ||
| Phantom (N = 16) | Y-shape | 0.016 | 0.031 | 0.02 | 0.002 | 0.008 | 0.48 |
| T-shape | 0.003 | 0.035 | 0.65 | −0.019 | 0.104 | 0.61 | |
| Clinical (N = 12) | Y-shape | 0.057 | 0.368 | 0.54 | 0.018 | 0.089 | 0.48 |
| T-shape | 0.041 | 0.246 | 0.49 | −0.007 | 0.177 | 0.91 | |
The differences in the reference measurements just distal of the bifurcation core are very small for both the artificial and the clinical images, although the difference is statistically significant for the Y-shape model in the artificial images. In the post-intervention analyses, the difference in arterial and reference measurements in the artificial images as well as the clinical data are very small.
Furthermore, the measurements of the arterial and reference bifurcation core areas are shown in Table 4.
Table 4.
The differences in reference bifurcation core areas between the pre- and post-intervention analyses and the differences between the arterial and reference bifurcation core areas in the post-intervention analyses
| Model | Difference in reference area: post–pre | Difference in area post: reference–arterial | |||||
|---|---|---|---|---|---|---|---|
| Difference (mm2) | Difference (%) | P value | Difference (mm2) | Difference (%) | P value | ||
| Phantom (N = 8) | Y-shape | −0.45 | −1.35 | 0.50 | 1.09 | 3.10 | 0.08 |
| T-shape | 0.18 | 0.53 | 0.50 | 1.36 | 4.60 | 0.0003 | |
| Clinical (N = 6) | Y-shape | 2.49 | 13.89 | 0.04 | −0.80 | −5.73 | 0.28 |
| T-shape | 0.36 | 3.72 | 0.34 | −0.90 | −10.84 | 0.24 | |
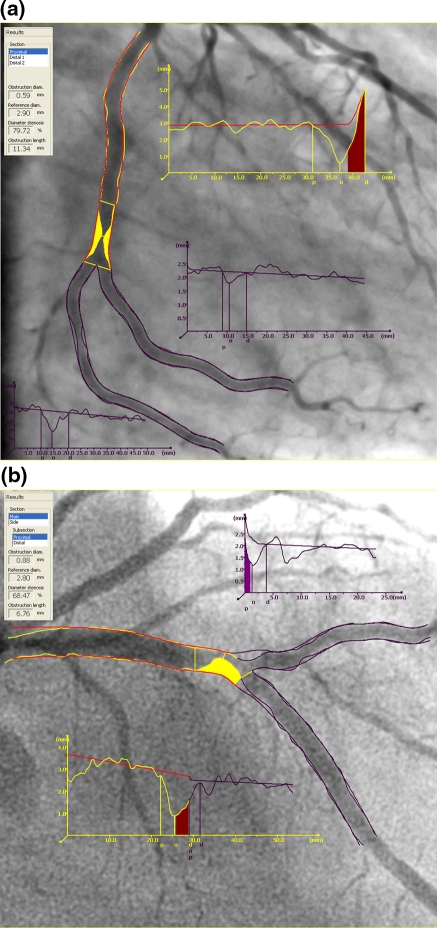
It shows that the differences between the reference bifurcation core areas in the pre- and post-intervention analyses are very small and not significant for the phantom and for the clinical data, except the clinical Y-shape data (13.89%). The post-intervention analyses show reference bifurcation core areas that are slightly larger than the arterial areas for the phantom data (Y-shape 4.6% was significant) whereas the clinical data show reference areas that are smaller than the arterial areas (−5.73 and −10.84%). Note that the absolute differences in the phantoms are larger than in the clinical data, whereas the relative differences are smaller. This is due to the fact that the phantom is larger than the average vessel in the clinical images (5 and 2–3 mm, respectively). An example of the final results of a Y-shape analysis can be seen in Fig. 11a, and a T-shape analysis in Fig. 11b.
Fig. 11.
An example of a the Y-shape and b the T-shape analysis results
Discussion
In this paper, our new approach for the measurement of arterial and reference diameters is presented. In case of straight vessel segments, the goal was to develop a robust method for measuring the obstruction diameter when the vessel is highly curved or has a complex shape. As can be seen in the validation data, the new approach achieves this goal and measures on average a smaller obstruction diameter than the conventional method. When only the “normal” vessel segments are taken into account, the measurements of the new and conventional approaches are very much comparable. For the more extreme cases, however, a significant difference of 0.08 mm is observed with the new approach which is more in line with one’s expectation.
The method relies on removing the connection between the directions of the arterial and reference diameters, which makes sense especially when the local direction of the diseased vessel and the reference vessel differ much due to a high curvature or a complexly shaped lesion. Removing the connection means that it is possible to measure both arterial and reference diameters in the correct directions; on the other hand, it introduces a problem of correspondence between the two. This is solved by resampling the arterial diameters at positions where the arterial centerline crosses the reference diameters.
As discussed earlier in “The new ostial analysis”, the old ostial diameter measurement approach suffers from the fact that the diameters do not cover the entire proximal part (ostium) of the sidebranch. As can be derived from Fig. 2, this problem mainly holds for sidebranches that have a small angle with respect to the main vessel. The validation data shows that the new method allows better measurements of the minimal diameter and length of lesions proximal in sidebranches, which could not be achieved using the conventional method.
As can be seen in the validation data of the new bifurcation approaches, the reference diameters outside the bifurcation core show a very good correspondence between pre- and post-intervention (smaller than 0.06 mm). This means that the reference contours and diameters are very robust and that the references that were measured pre-intervention are a reliable estimation for the undiseased vessels. This holds for the artificial images as well as the clinical data. Furthermore, the results of the post-intervention analyses show only very small differences between the arterial and reference values for both artificial and clinical data. For the T-shape analyses, this data was only available for the main distal subsection, reducing the size of the dataset by a factor of two. To increase the number of measurements, also the images of the DEVAX-study were analyzed with the T-shape model and included in the dataset. For the sidebranch, an average value could not be measured in a similar way, but instead, the diameter was measured at one single location, the end of the ostium (5 mm after the bifurcation core), which showed similar results: a difference of 0.028 mm with a P value of 0.67.
Also the reference bifurcation core areas show a very good correspondence between pre- and post-intervention in both the phantom images and the clinical T-shape data. Only the results of the Y-shape study in clinical data show a larger difference (13.89%) in reference bifurcation core area. This is due to the fact that although the cases with an overdilated stent had been excluded, two borderline cases were still present in the dataset. Since the analyzed sections were short, there was not enough normal vessel present, which caused the reference contours to follow the arterial contours and go too wide. Without the data of these two cases, this difference goes down to 8.9%, with a P value of 0.23.
In the post-intervention analyses of the phantom images, the reference bifurcation core areas are slightly larger than the arterial areas. This can be explained by the fact that our method interpolates the reference contours from the different sections in a smooth way, which is more likely in real clinical data. Since our artificial images show sharp angles between the segments, the reference bifurcation core area is slightly larger, which turns out to be a significant difference in T-shape (1.36 mm2 or 4.60%) due to the small random errors in the measurements (0.15 mm2). In the clinical cases, the bifurcation core areas show a slightly smaller reference area compared to the arterial area (not significant).
The new parameter that is introduced here, the bifurcation core area and more specifically the percentage bifurcation core area reduction, is an interesting parameter that quantifies the severity of lesions inside the bifurcation core, similar to the percentage diameter reduction that is used in the straight segments. It can be used to monitor the vessel over time or during an intervention, or to assess the results of the intervention procedure afterwards.
Conclusions
The new approach for measuring the arterial and reference diameters, presented in this paper, has proven to outperform the conventional QCA approaches. For the straight vessel segments, it was demonstrated that releasing the connection between the direction of the arterial and reference diameters results in a significantly better measurement of the obstruction diameter in highly curved parts of the vessel. For “normal” straight segments, only very small differences were found between the new and the conventional approach.
Our newly developed method for the analysis of ostial vessel segments has proven to achieve accurate measurements of diameters and lengths of proximal lesions in sidebranches, which could not be achieved using the conventional method.
Furthermore, it was demonstrated that our two new bifurcation approaches achieve accurate results in the segments just outside the bifurcation core and produce reliable measurements of the arterial and reference bifurcation core areas.
In summary, a major step forward has been set in the quantitative analyses of coronary and vascular lesions from X-ray angiographies. These methodological improvements will provide accurate and robust solutions for all the clinical research angiographic QCA applications.
Acknowledgments
We would like to thank the Cardiovascular Research Foundation (CRF) in New York and in particular Alexandra Lansky M. D. and Maria Corral for analyzing the clinical data and therefore helping us validating our new bifurcation approaches.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- 1.Reiber JHC, Tuinenburg JC, Koning G, Janssen JP, Rareş A, Lansky AJ, Goedhart B (2009) Chapter 2.2: quantitative coronary arteriography. In: Oudkerk M, Reiser MF (eds) Coronary radiology, 2nd revised edn. Baert AL, Knauth M, Sartor K (eds) Series: medical radiology, Sub-series: diagnostic imaging. Springer, Berlin, pp 41–65
- 2.Reiber JHC, Schiemanck LR, van der Zwet PMJ, Goedhart B, Koning G, Lammertsma M, Danse M, Gerbrands JJ, Schalij MJ, Bruschke AVG. State of the art in quantitative coronary arteriography as of 1996. In: Reiber JHC, Serruys PW, editors. Cardiovascular imaging. Dordrecht: Kluwer; 1996. pp. 39–56. [Google Scholar]
- 3.Tuinenburg JC, Koning G, Seppenwoolde Y, Reiber JHC. Is there an effect of flat-panel-based imaging systems on quantitative coronary and vascular angiography? Cathet Cardiovasc Interv. 2006;68:561–566. doi: 10.1002/ccd.20797. [DOI] [PubMed] [Google Scholar]
- 4.Reiber JHC, Koning G, von Land CD, van der Zwet PM. Why and how should QCA systems be validated? In: Reiber JHC, Serruys PW, editors. Progress in quantitative coronary arteriography. Dordrecht: Kluwer; 1994. pp. 33–48. [Google Scholar]
- 5.Reiber JHC, Serruys PW. Quantitative coronary arteriography. In: Marcus ML, Skorton DJ, Schelbert HR, Wolf GL, editors. Cardiac imaging. Philadelphia: Saunders; 1991. pp. 211–281. [Google Scholar]
- 6.Reiber JHC, van der Zwet PMJ, von Land CD. Quantitative coronary arteriography: equipment and technical requirements. In: Reiber JHC, Serruys PW, editors. Advances in quantitative coronary arteriography. Dordrecht: Kluwer; 1992. pp. 75–111. [Google Scholar]
- 7.Reiber JHC, Serruys PW, Kooijman CJ, Wijns W, Slager CJ, Gerbrands JJ, Schuurbiers JCH, den Boer A, Hugenholtz PG. Assessment of short-, medium-, and long-term variations in arterial dimensions from computer-assisted quantitation of coronary cineangiograms. Circulation. 1985;71:280–288. doi: 10.1161/01.cir.71.2.280. [DOI] [PubMed] [Google Scholar]
- 8.van der Zwet PMJ, von Land CD, Loois G, Gerbrands JJ, Reiber JHC (1990) An on-line system for the quantitative analysis of coronary arterial segments. Comput Cardiol 17:157–160
- 9.van Assen HC, Vasbinder B, Stoel BC, Putter H, van Engelshoven JMA, Reiber JHC. Quantitative assessment of the morphology of renal arteries from x-ray images; quantitative vascular analysis (QVA) Invest Radiol. 2004;39:365–373. doi: 10.1097/01.rli.0000126178.51618.13. [DOI] [PubMed] [Google Scholar]
- 10.Lefevre T, Louvard Y, Morice MC, Dumas P, Loubeyre C, Benslimane A, Premchand RK, Guillard N, Piechaud JF. Stenting of bifurcation lesions: classification, treatments, and results. Cathet Cardiovasc Interv. 2000;49(3):274–283. doi: 10.1002/(SICI)1522-726X(200003)49:3<274::AID-CCD11>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- 11.Louvard Y, Lefevre T, Morice MC. Percutaneous coronary intervention for bifurcation coronary disease. Heart. 2004;90:713–722. doi: 10.1136/hrt.2002.007682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Janssen JP, Koning G, de Koning PJH, Tuinenburg JC, Reiber JHC. A novel approach for the detection of pathlines in x-ray angiograms: the wavefront propagation algorithm. Int J Cardiovasc Imaging. 2002;18(5):317–324. doi: 10.1023/A:1016004005730. [DOI] [PubMed] [Google Scholar]
- 13.Janssen JP, Koning G, de Koning PJH, Tuinenburg JC, Reiber JHC. Validation of a new method for the detection of pathlines in vascular X-ray images. Invest Radiol. 2004;39(9):524–530. doi: 10.1097/01.rli.0000131478.50630.9f. [DOI] [PubMed] [Google Scholar]
- 14.Janssen JP, Koning G, de Koning PJH, Bosch JG, Tuinenburg JC, Reiber JHC. A new approach to contour detection in X-ray arteriograms: the Wavecontour. Invest Radiol. 2005;40(8):514–520. doi: 10.1097/01.rli.0000170811.71023.6e. [DOI] [PubMed] [Google Scholar]
- 15.Adalsteinsson D, Sethian JA. A fast level set method for propagating interfaces. J Comp Phys. 1995;118:269–277. doi: 10.1006/jcph.1995.1098. [DOI] [Google Scholar]
- 16.Lansky T, Costa M, et al. Quantitative angiographic methods for bifurcation lesions: a consensus statement of the EBC. C&CI. 2009;73:258–266. doi: 10.1002/ccd.21814. [DOI] [PubMed] [Google Scholar]
- 17.Goktekin O, Kaplan S, Dimopoulos K, Barlis P, Tanigawa J, Vatankulu MA, Koning G, Tuinenburg JC, Mario CD. A new quantitative analysis system for the evaluation of coronary bifurcation lesions: comparison with current conventional methods. Cathet Cardiovasc Interv. 2007;69(2):172–180. doi: 10.1002/ccd.20946. [DOI] [PubMed] [Google Scholar]
- 18.Verheye S, Agostoni P, Dubois CL, et al. 9-Month clinical, angiographic, and intravascular ultrasound results of a prospective evaluation of the Axxess self-expanding biolimus A9-eluting stent in coronary bifurcation lesions: the DIVERGE (drug-eluting stent intervention for treating side branches effectively) study. J Am Coll Cardiol. 2009;53(12):1031–1039. doi: 10.1016/j.jacc.2008.12.012. [DOI] [PubMed] [Google Scholar]