The Effect of Alcohol Consumption on Mortality: Regression Discontinuity Evidence from the Minimum Drinking Age

Abstract

We estimate the effect of alcohol consumption on mortality using the minimum drinking age in a regression discontinuity design. We find large and immediate increases in drinking at age 21, including a 21 percent increase in recent drinking days. We also find a discrete 9 percent increase in the mortality rate at age 21, primarily due to motor vehicle accidents, alcohol-related deaths, and suicides. We estimate a 10 percent increase in the number of drinking days for young adults results in a 4.3 percent increase in mortality. Our results suggest policies that reduce drinking among young adults can have substantial public health benefits. (JEL I12, I18)

Does alcohol consumption by young adults increase mortality? A role for alcohol-related impairment in motor vehicle fatalities among youths is widely acknowledged in the popular press and in academic literature in public health and economics. Research in biology, psychology, and medicine has identified several possible mechanisms. For example, in laboratory settings alcohol consumption has been shown to result in reduced inhibition, increased aggression, compromised motor skills, and blurred vision. Given these physical and behavioral consequences of alcohol consumption, it is not surprising that alcohol has been strongly associated not only with motor vehicle fatalities but also other types of mortality such as suicide, homicide, and deaths from falls, burns, and drowning.¹

Understanding whether there is a causal link between youth alcohol consumption and mortality is especially relevant for public policy given that over half of young adults drink and about one-third drink heavily (i.e., five or more drinks at one time). But providing precise estimates of the strength of the causal relationship between alcohol consumption and mortality is complicated by the usual problem of unobserved heterogeneity among individuals that is likely related to alcohol consumption and to the determinants of mortality. Some of the strongest research to date has made use of changes in minimum legal drinking ages (MLDA) that occurred in the 1970s and 1980s. Specifically, the majority of US states experimented with drinking ages of 18, 19, and 20 before federal legislation in 1984 required that all states adopt an MLDA of 21 years old. Several studies that use these state policy changes as “natural experiments” find that a higher drinking age reduces alcohol consumption by young adults and fatalities from motor vehicle accidents (see Alexander C. Wagenaar and Traci L. Toomey 2002 for a detailed review).

There are, however, some important limitations of the existing research on state drinking age changes, youth alcohol consumption, and mortality. First, although the literature using state changes in the drinking age finds consistent evidence that the policies affected motor vehicle fatalities, there is far less research on the effects of the minimum legal drinking age on the other leading causes of death among young adults such as suicide, drug overdose, alcohol overdose, and homicide. And what research does exist reaches contradictory conclusions.² Second, there is not universal consensus regarding whether and how much the national movement toward an MLDA of 21 years old affected youth alcohol consumption.³ Finally, and perhaps most importantly, one may be concerned that bias due to policy preferences is not eliminated even when using state changes in the MLDA that were “induced” by threatened loss of federal highway funding in the 1984 Minimum Drinking Age Law. For example, the states that initially reduced their MLDA down from 21 years old—the only states for whom federal compulsion creates meaningful variation—are arguably different from those states that never changed their MLDA in unobserved ways that may be related to the determinants of youth drinking and mortality (e.g., anti-drinking sentiment). Similarly, the speed with which states chose to comply with the federal mandate is also plausibly nonrandom.

In this paper, we estimate the causal effect of alcohol consumption on mortality using a regression discontinuity (RD) design. This RD design uses the fact that the MLDA produces sharp differences in alcohol access for young adults on either side of age 21. Since the observed and unobserved determinants of alcohol consumption and mortality are likely to trend smoothly across the age-21 threshold, we can use the estimates of discontinuous jumps in alcohol consumption and mortality at age 21 to identify the causal effect of alcohol consumption on mortality among young adults. The RD design also addresses concerns about policy endogeneity that have been raised as criticisms of the research designs used in much of the prior literature. By implementing an RD design using the MLDA, which has been set at 21 years old for two decades, we can be confident that our results are not biased by unobserved factors that determine policy.

We use detailed survey data on alcohol consumption and a census of deaths in the United States to provide compelling graphical and regression-based evidence that the MLDA laws result in sharp differences in alcohol consumption and mortality for youths on either side of the age-21 threshold.⁴ To implement the RD design, we estimate the reduced-form impact of the MLDA on alcohol consumption and mortality using both parametric and nonparametric regression discontinuity models. We show that the MLDA laws reduce drinking by 11–21 percent depending on the consumption measure being examined. These estimates are new and interesting in their own right and are substantially larger than most of the existing estimates from the literature on drinking ages. We then show that the increase in alcohol consumption that occurs at age 21 results in an immediate 9 percent increase in mortality, with the largest effects due to motor vehicle accidents, suicides, and deaths with an explicit mention of alcohol. We then combine these estimates to obtain the implied instrumental variables estimate of the impact of alcohol consumption on mortality. Specifically, we estimate that a 1 percent increase in the number of days on which 21-year-olds drink or drink heavily is associated with a 0.4 percent increase in mortality. This is the first direct estimate of this elasticity in the large literature on drinking ages, alcohol consumption, and mortality that we are aware of, and it is of significant value to policymakers designing interventions intended to reduce alcohol consumption and its adverse effects, particularly among young adults.

The remainder of the paper proceeds as follows. Section I describes the National Health Interview Survey alcohol consumption data and the National Center for Health Statistics mortality detail data that we use for this study. Section II provides a detailed description of the empirical methods. Section III presents the main results, and Section IV offers a discussion and concludes.

I. Data

This project uses two main data sources. For the consumption analyses, we use survey data on alcohol consumption from the National Health Interview Survey (NHIS) for the period of 1997–2005. To evaluate the impact of alcohol consumption on mortality, we use the National Center for Health Statistics’ mortality detail files for the 1997 to 2004 period, and we use population estimates from the census to convert mortality counts into rates. For both parts of the analysis, we focus on young adults age 19–22, inclusive.

The NHIS is a survey of a stratified random sample of the US population that asks respondents about a variety of health outcomes and behaviors including alcohol consumption. The questions about alcohol consumption were included as part of the sample adult survey from 1997 to 2005. We have obtained access to a confidential version of these data with information on the respondents’ exact date of birth and exact interview date, which we use to compute the exact age at which an individual was surveyed. Each NHIS survey asked a variety of questions about alcohol consumption.⁵ We consider five main outcomes using responses to these questions. The first three outcomes are measures of drinking participation: whether the respondent reported having consumed 12 or more drinks in her lifetime, whether the respondent reported having consumed 12 or more drinks in any one year, and whether the respondent reported engaging in any “heavy” drinking in the previous year.⁶ We also examine two measures of drinking frequency and intensity: the percentage of days on which an individual drinks and the percentage of days on which an individual engages in “heavy” drinking.

There are two potential problems with using the NHIS to estimate the change in alcohol consumption behavior that occurs at age 21. The first is that the questions on alcohol consumption typically refer to the prior 12 months. This feature implies that in the first months after turning 21, the reference period is largely composed of the person’s twentieth year. However, despite being asked about their behavior over the past year, respondents can choose to report on their alcohol consumption over the past year, the past month, or the past week. Fortunately, when asked how many days they drank in the past year, 71 percent of the respondents interviewed in the month after they turned 21 answered using a reference period of either the past week or the past month.⁷ The other potential problem with our alcohol consumption analysis is the possibility that drinking is underreported due to desirability bias. This is a particular problem for this research design because there may be a discontinuous change in the desirability bias at age 21 since the behavior in question is illegal for people under 21 years old. This could generate a discrete increase in the reported level of alcohol consumption at age 21 even if there is no true change in behavior. Fortunately, there are three compelling pieces of evidence that the increase in alcohol consumption we document in this paper is not due to desirability bias. First, as we show below, there is a large discrete increase in alcohol-related deaths (e.g., alcohol overdoses) at age 21. This is indirect but compelling evidence of a change in alcohol consumption. Second, we show below that a majority of young adults under age 21 reports that they have consumed at least 12 drinks in their lifetime and that there is essentially no change in reported lifetime drinking participation rates at age 21. Both of these facts are inconsistent with desirability bias driving our consumption results. Finally, as documented above, individuals interviewed in the month just after their twenty-first birthday reported alcohol consumption behavior that is much more similar to that of 20-year-olds than of 21-year-olds. If the increase in reported alcohol consumption we document were due to desirability bias, the reported consumption would change immediately at age 21. Though there may be some desirability bias, the pattern we observe is most consistent with honest responses to a retrospective question.

The mortality data come from the NCHS confidential national mortality detail files and include the decedent’s date of birth and date of death. These data are derived from death certificates and include the universe of all deaths in the United States during the period of 1997–2004.⁸ We use information on the cause of death as reported on the death certificate to create two categories: deaths due to internal causes and deaths due to external causes.⁹ We then split the deaths due to external causes into the following mutually exclusive subcategories: homicides, suicides, motor vehicle accidents, deaths with a mention of alcohol, deaths with a mention of drug use, and deaths due to other external causes.¹⁰ To account for a pronounced twenty-first-birthday mortality effect (see the day-specific death rates in Web Appendix A), for all outcomes we report estimates from regression models that include dummy variables for the twenty-first birthday and the day after.¹¹ In nearly all cases the inclusion of these birthday dummies does not change the main results.

II. Methods

Consider a simple reduced-form model:

$$y_{ai}=X_{ai}{\beta }^y+g^y(a)+D_{ai}{\pi }^y+v_{ai}^y,$$ (1)

where y_ai is an outcome measure for individual i at age a; X_ai represents a set of measured characteristics of individual i at age a; g^y(a) is a smooth function representing the age profile of the outcome y (e.g., a low-order polynomial); D_ai is an indicator for being 21 years old or older; and $v_{ai}^y$ is an unobserved error component. The parameter π^y measures any discrete change in the expectation of y_ai that occurs precisely at age 21. Since the age profile and the dummy D_ai are the same for all individuals with the same age, identification of π^y arises from variation across age cells. Let y denote the population mean of the outcome variable y in age cell a. Ignoring within-age cell variation in the X’s or assuming the data have been adjusted for such variation, equation (1) implies

$$y_a=E[y_{ai}|{\text{age}}_i=a]=X_a{\beta }^y+g^y(a)+D_a{\pi }^y+v_a^y.$$ (2)

We estimate the model above by modeling g^y(a) as a low-order polynomial.

In addition to estimating the discontinuity parametrically as described above, we also estimate it nonparametrically using local linear regression as detailed in Jinyong Hahn, Petra Todd, and Wilbert van der Klaauw (2001). To estimate the discontinuity nonparametrically we implement a local linear regression procedure using the bandwidth selection procedure suggested in Jianqing Fan and Irene Gijbels (1996). We then use this bandwidth and a triangular kernel to fit local linear regressions on each side of age 21, and we estimate the limit of the expectation function from the left and the right of age 21. We compare the nonparametric estimates with the polynomial estimates to ensure that the results are robust to specification.

The reduced-form approach of equation (2) will let us estimate the impact of the MLDA laws on alcohol consumption and mortality. For other purposes it is helpful to interpret the discontinuity in y in the context of an underlying causal structure. We can obtain the implied instrumental variables estimate of the causal effect of alcohol consumption on mortality by forming the ratio of the estimated discontinuity in mortality at age 21 to the estimated discontinuity in alcohol consumption.

III. Results

This section is divided into two subsections. In the first subsection, we document the substantial increase in alcohol consumption that occurs when people turn 21. In the second subsection, we estimate how much the age-specific mortality rate increases after age 21 and determine what particular causes of death are driving the increase. We also examine how the increase in mortality is distributed across gender, race, and educational attainment.

A. Alcohol Consumption

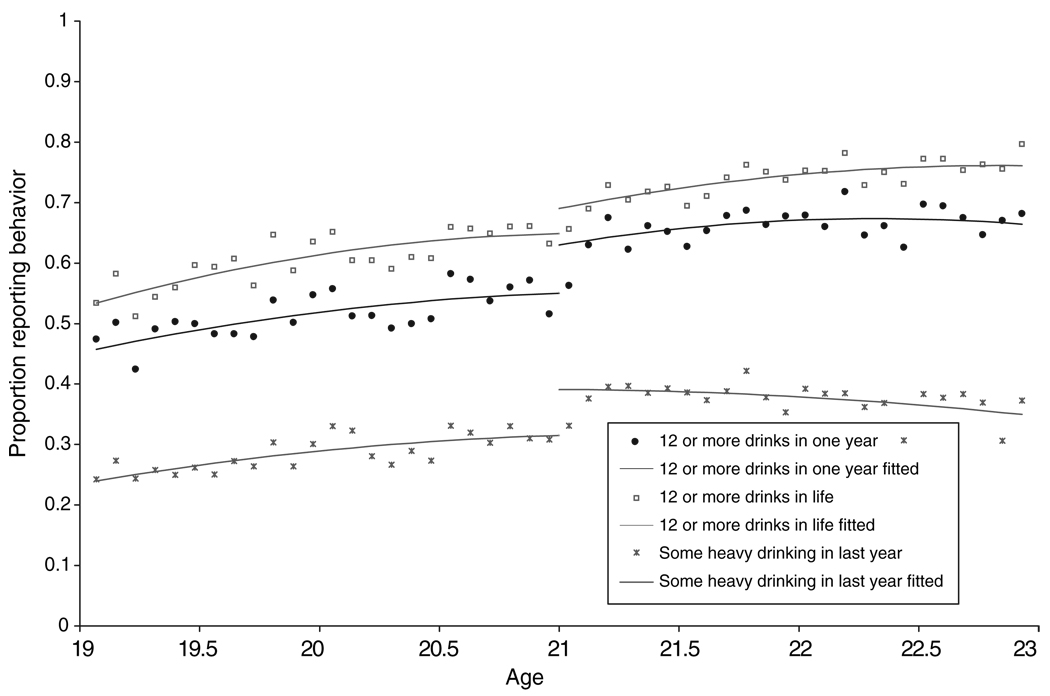
In this subsection, we document how the frequency and intensity of alcohol consumption changes when people turn 21 years old.¹² In Figure 1 we present the age profiles for the proportion of respondents who reported consuming 12 or more alcoholic drinks in any one year, those who reported consuming 12 or more drinks during their entire lifetime, and those who reported any heavy drinking in the past year. To make the age profile less noisy, the proportions have been calculated for 30-day blocks of age rather than individual days. We have superimposed the fitted lines from regressions on the underlying micro data over these proportions.¹³ The figure shows that about 65 percent of 20-year-olds in the NHIS reported having consumed 12 or more drinks in their lifetime, and there is not much increase in drinking at age 21.¹⁴

Figure 1. Age Profile of Drinking Participation.

Notes: NHIS Sample Adult 1997–2005. Cells are the proportion of people in a 30-day block that report the behavior. The regression line is a second-order polynomial fitted on unweighted individual observations on either side of the age 21 cutoff.

In the top panel of Table 1, we present the regression estimates of the increase in the proportion of people who reported they had consumed 12 or more drinks in their lifetime. The regression in the first column of the panel is the one that generated the fitted line in Figure 1. This regression confirms that the increase in the figure is about 4 percentage points and is statistically insignificant.¹⁵ In the second column of the top panel, we present the same regression using the NHIS sample weights to obtain the predicted jump at age 21 for the entire US population. Adjusting for the sampling weights modestly decreases the point estimate of the age-21 discontinuity and increases the standard errors because some individuals have very large weights. In the third specification, we include dummy variables for people interviewed on their twenty-first birthday or the day immediately after. We also add dummy variables for the four census regions, male, black, Hispanic, no high school diploma, employment status, and health insurance coverage. Though these covariates are correlated with alcohol consumption, their inclusion has little impact on the estimated size of the discontinuous jump at age 21. In the fourth specification, we add a cubic term to the polynomial model, which substantially reduces the size of the estimated jump. The p-values from the Wald statistic (bottom row) suggest that the third specification is the preferred model of the four parametric models, a pattern that holds for all the measures of alcohol consumption we examine. Finally, in column 5, we present the results from a local linear regression with the rule-of-thumb bandwidth for each side of the age-21 cutoff (Fan and Gijbels 1996). This estimate also indicates a small and statistically insignificant discontinuity at age 21 in the likelihood of ever having consumed 12 alcoholic drinks. We focus on the results from the parametric models because they are less sensitive to the retrospective nature of the questions than the nonparametric models. That the discontinuity in lifetime drinking participation at age 21 is very small and statistically insignificant is important because it suggests that the abrupt increase in mortality at age 21 that we document below is not due to people having their first experience with alcohol.

Table 1.

Alcohol Consumption: Participation

	(1)	(2)	(3)	(4)	(5)
12 or more drinks in lifetime
Over 21	0.0418 (0.0242)	0.0316 (0.0301)	0.0268 (0.0292)	0.0198 (0.0423)	0.0199 (0.0179)
Observations	16,107	16,107	16,107	16,107
R2	0.02	0.03	0.10	0.10
Prob > Chi-Squared			0.00	0.61
12 or more drinks in one year
Over 21	0.0796 (0.0254)	0.0657 (0.0313)	0.0611 (0.0301)	0.0603 (0.0438)	0.0461 (0.0218)
Observations	16,107	16,107	16,107	16,107
R2	0.02	0.03	0.11	0.11
Prob > Chi-Squared			0.00	0.56
Any heavy drinking in last year
Over 21	0.0761 (0.0248)	0.0527 (0.0304)	0.0492 (0.0291)	0.0262 (0.0430)	0.0398 (0.0201)
Observations	16,107	16,107	16,107	16,107
R2	0.01	0.01	0.10	0.10
Prob > Chi-Squared			0.00	0.67
Covariates	N	N	Y	Y	N
Weights	N	Y	Y	Y	N
Quadratic terms	Y	Y	Y	Y	N
Cubic terms	N	N	N	Y	N
LLR	N	N	N	N	Y

Notes: The first column of each panel contains the regression from the corresponding figure. Robust standard errors are in parentheses. Covariates include dummies for census region, race, gender, health insurance, employment status, twenty-first birthday, twenty-first birthday + 1 day, and looking for work. Weights are the NHIS adult sample weights and reduce the precision of the regressions significantly as the weights vary substantially across observations. People reporting five or more drinks on one day (Nt necessarily in one sitting) are coded as heavy drinkers. The first four columns give the estimates from polyNmial regressions on age interacted with a dummy for being over 21. The age variable is centered on 21, so the Over 21 variable gives us an estimate of the discontinuous increase at age 21. In the fifth column, we present the results of a local linear regression procedure with a rule-of-thumb bandwidth. For this procedure, we follow Fan and Gijbels (1996) and fit a fourth order polyNomial separately on each side of the age-21 cutoff. We use the fit of this regression to estimate the average second derivative of the expectation function (D) and the mean squared error of this function (σ²). The rule-of-thumb bandwidth is h = c(σ² R/D), where c is a constant that depends on the kernel (c = 3.44 for a triangular kernel), and R is the range of the running variable (i.e., the range of ages used to estimate the polyNmial on each side). We then use this bandwidth, and a triangular kernel, to fit local linear regressions on each side of age 21, and estimate the limit of the expectation function from the left and the right of age 21. The local linear regressions have two fewer observations because the twenty-first birthday and the day after the twenty-first birthday have been dropped.

Figure 1 also plots the age profile of the proportion of people who reported consuming 12 or more drinks in one year (represented by the dark circles) and 5 or more drinks on a single day at least once in the previous year (represented by the crosses). The regression line superimposed on the dark circles in Figure 1 and the corresponding regression results in the second panel of Table 1 indicate that the increase in the probability of drinking 12 or more drinks in one year is about 6 percentage points and is statistically significant in the preferred quadratic specification with covariates and the twenty-first birthday dummies (column 3). Relative to the one-year drinking participation rate of young adults just under age 21 of about 55 percent, our preferred estimate suggests an increase of about 11 percent. Our preferred estimate in the bottom panel of Table 1 also indicates a sharp and statistically significant increase in the probability of any heavy drinking in the past year of about 5 percentage points at age 21. This represents an increase of approximately 16 percent relative to the heavy drinking participation rate of people just under 21, though these estimates are somewhat sensitive to the inclusion of the cubic term in age. For all outcomes in Figure 1, it is likely that the specification with the cubic term in age produces smaller estimated discontinuities because it is more sensitive to the retrospective nature of the question.

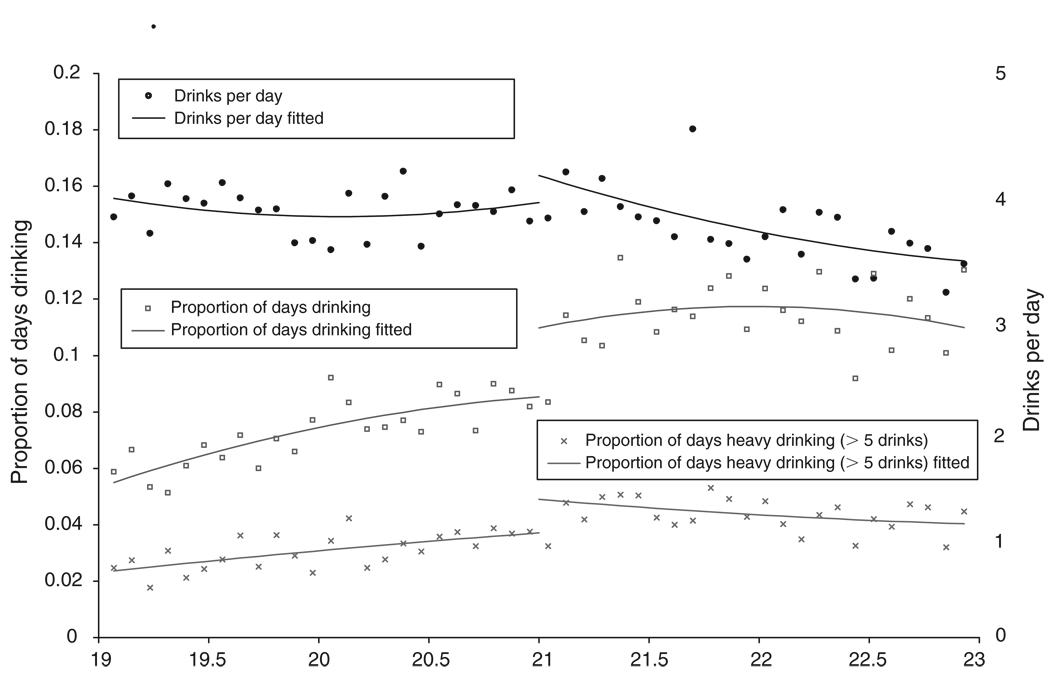
In Figure 2, we present the age profiles of various measures of drinking intensity. The figure reveals a discrete jump of about 2 percentage points in the proportion of days drinking any alcohol (represented by the hollow squares). In the top panel of Table 2, we present the corresponding regression estimates for proportion of days drinking, which confirm that the increase we observe in the figure is about 2–2.5 percentage points across all specifications with a quadratic in age. This is substantial given that the average 20-year-old reported drinking on about 8.5 percent of days (i.e., a 21 percent increase in drinking days relative to people just under 21 shown in column 3). As with the drinking participation outcomes in Table 1, we find that the addition of a cubic term substantially reduces the estimate of the jump at age 21, though Figure 2 shows that this likely is due to the low level of reported drinking among people interviewed just after their twenty-first birthday. Importantly, the model with the cubic in age is not supported by the data. Figure 2 also shows evidence of an increase in the proportion of days of heavy drinking (represented by crosses). Though the corresponding regressions presented in the middle panel of Table 2 reveal that the 20 percent increase in heavy drinking days at age 21 in the preferred specification is not statistically significant, the estimated proportional increase is remarkably similar to the increase in regular drinking days. Together with the evidence that the probability of any heavy drinking days increases significantly at age 21, these results suggest that the amount of heavy drinking increases in response to the easier alcohol availability that results from turning 21.¹⁶

Figure 2. Age Profile of Drinking Intensity.

Notes: People can report their drinking for the last week, month, or year; 71 percent of respondents used a reference period of one week or one month. Average number of drinks per day is for people who reported some drinking.

Table 2.

Alcohol Consumption: Intensity

	(1)	(2)	(3)	(4)	(5)
Proportion of days drinking
Over 21	0.0245 (0.0086)	0.0180 (0.0097)	0.0182 (0.0095)	0.0119 (0.0135)	0.0107 (0.0072)
Observations	16,107	16,107	16,107	16,107
R2	0.02	0.02	0.07	0.07
Prob > Chi-Squared			0.00	0.56
Proportion of days heavy drinking
Over 21	0.0120 (0.0061)	0.0075 (0.0063)	0.0075 (0.0062)	0.0021 (0.0091)	0.0026 (0.0048)
Observations	15,825	15,825	15,825	15,825
R2	0.00	0.01	0.05	0.05
Prob > Chi-Squared			0.00	0.72
Drinks per day on days drinking
Over 21	0.2387 (0.2810)	0.2068 (0.3403)	0.2465 (0.3291)	0.2806 (0.4782)	0.1886 (0.2024)
Observations	9,906	9,906	9,906	9,906
R2	0.00	0.00	0.07	0.07
Prob > Chi-Squared			0.00	0.92
Covariates	N	N	Y	Y	N
Weights	N	Y	Y	Y	N
Quadratic terms	Y	Y	Y	Y	N
Cubic terms	N	N	N	Y	N
LLR	N	N	N	N	Y

Notes: See Notes from Table 1. People can report their drinking for the last week, month, or year. For people who reported any drinking, 71 percent of those interviewed in the month after they turned 21 reported about their drinking in the last week or month rather than the last year. The dependent variable “Drinks per Day” is the number of drinks the respondent reported drinking on a typical day in which they consumed some alcohol.

Finally, before examining the increase in mortality rates that results from the increase in alcohol consumption documented above, we examine the possibility that there are other changes occurring at age 21 that could confound our analysis. That the regression estimates are robust to the inclusion of covariates (i.e., moving from specification 2 to 3 in Table 1 and Table 2) suggests that the observable characteristics are smoothly distributed across the discontinuity. In Table 3, we provide a more direct test that demographic characteristics, employment status, insurance status, and educational attainment all evolve smoothly through the age 21 threshold. We find no evidence of a discrete change at age 21 in any of these characteristics, and this is confirmed visually in Web Appendix G.¹⁷ That these observable characteristics are smoothly distributed across the discontinuity suggests that the unobservable characteristics are also distributed smoothly across the discontinuity and reduces our concerns about omitted variables bias.

Table 3.

Age Profile of Demographic Characteristics from the NHIS

	Male	White	Black	Hispanic	No HS Diploma	HS Diploma	Employed	Looking for work	No health insurance
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
Over 21	0.0156	0.0172	−0.0250	0.0095	−0.0108	0.0040	0.0019	−0.0061	0.0043
	(0.0260)	(0.0293)	(0.0211)	(0.0203)	(0.0230)	(0.0291)	(0.0302)	(0.0171)	(0.0293)
Constant	0.4405	0.6440	0.1415	0.1638	0.1810	0.2941	0.6453	0.0849	0.2970
	(0.0168)	(0.0195)	(0.0137)	(0.0129)	(0.0154)	(0.0194)	(0.0203)	(0.0114)	(0.0191)
Observations	16,107	16,107	16,107	16,107	16,107	16,107	16,107	16,107	16,107
R2	0.00	0.00	0.00	0.00	0.01	0.00	0.01	0.00	0.00

Notes: Sample from NHIS Sample Adult File (1997–2005). Standard errors in parentheses. The regressions do not include covariates other than a second order polynomial in age interacted with the over 21 dummy. Since Age 5 persons age 2 – 21, the constant is the predicted value for people about to turn 21.

B. Mortality

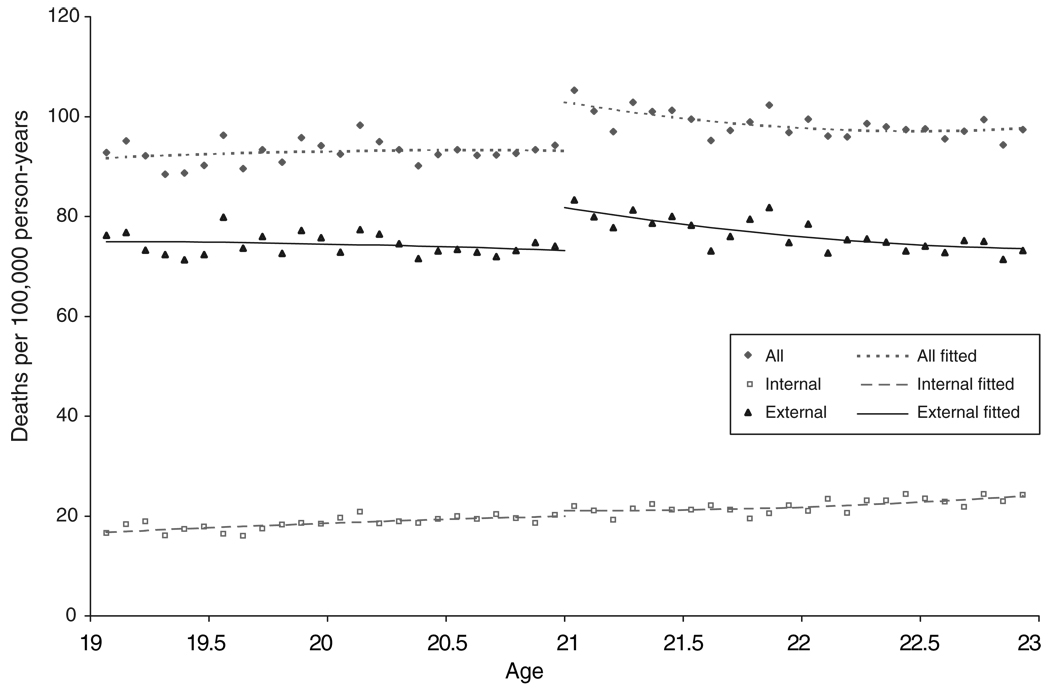
In this section, we evaluate whether the increase in alcohol consumption documented above results in an increase in mortality rates. In Figure 3, we present the overall age profile of deaths per 100,000 person years, and we also show the age pro- files separately for deaths due to internal and external causes. We computed deaths per 100,000 person years by dividing the total number of deaths at a particular age by the total number of years lived at that age by everyone in the cohort. External causes of death include motor vehicle accidents, suicide, homicide, deaths with a mention of alcohol use, deaths with a mention of drug use, and other deaths due to external injuries. Figure 3 shows a sharp increase in overall mortality at age 21 of about 10 deaths per 100,000 person years. Grouping the deaths by cause reveals that for this age group the majority of deaths are due to external causes and the increase in deaths at age 21 is attributable largely to deaths due to external causes.

Figure 3. Age Profile for Death Rates.

Notes: Deaths from the National Vital Statistics Records. Includes all deaths that occurred in the United States between 1997–2003. The population denominators are derived from the census. See online Appendix C for a list of causes of death.

Table 4 presents the regression estimates corresponding to Figure 3. The dependent variable in the regression is the log of the total number of people who died at an exact age (in years and days) during the 1997–2004 period. We estimate the model over the 1,460 days between ages 19 and 22, inclusive.¹⁸ The coefficient of interest on the over 21 indicator can, for small changes, be interpreted as the percentage change in deaths at age 21. In the first column of each panel, we present the estimates from fitting a quadratic polynomial to the age profile of deaths. In the second column, we add a dummy for the twenty-first birthday and a dummy for the day immediately after. In the third specification of each panel, we add a cubic term to the polynomial. In the fourth column, we present the estimate from a local linear regression with a rule-of-thumb bandwidth for each side of the age-21 cutoff (Fan and Gijbels 1996).¹⁹ The p-values from the Wald statistic (bottom row) suggest that the second specification is the preferred model of the three parametric models. However, all four specifications give us very similar estimates and confirm what we observed in Figure 3, that there is a statistically significant 9 percent increase in overall mortality when people turn 21 that is mostly due to a 10 percent increase in deaths due to external causes.²⁰

Table 4.

Discontinuity in Log Deaths at Age 21

	(1)	(2)	(3)	(4)
deaths due to all causes
Over 21	0.096	0.087	0.091	0.074
	(0.018)	(0.017)	(0.023)	(0.016)
Observations	1,460	1,460	1,460	1,458
R2	0.04	0.05	0.05
Prob > Chi-Squared		0.000	0.735
Deaths due to external causes
Over 21	0.110	0.100	0.096	0.082
	(0.022)	(0.021)	(0.028)	(0.021)
Observations	1,460	1,460	1,460	1,458
R2	0.06	0.08	0.08
Prob > Chi-Squared		0.000	0.788
Deaths due to internal causes
Over 21	0.063	0.054	0.094	0.066
	(0.040)	(0.040)	(0.053)	(0.031)
Observations	1,460	1,460	1,460	1,458
R2	0.10	0.10	0.10
Prob > Chi-Squared		0.000	0.525
Covariates	N	Y	Y	N
Quadratic terms	Y	Y	Y	N
Cubic terms	N	N	Y	N
LLR	N	N	N	Y

Notes: See Notes from Table 1. The dependent variable is the log of the number of deaths that occurred x days from the person’s twenty-first birthday. External deaths include all deaths with mention of an injury, alcohol use, or drug use. The Internal Death category includes all deaths Nt coded as external. Please see Web Appendix C for the ICD codes for each of the categories above. The first three columns give the estimates from polyNmial regressions on age interacted with a dummy for being over 21.

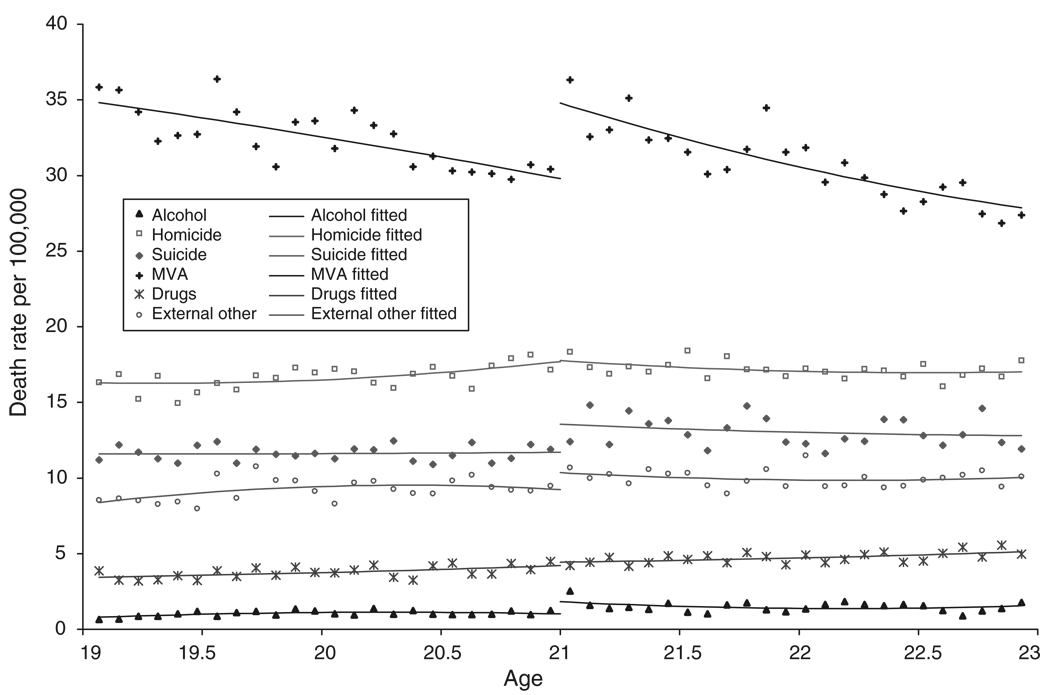
Figure 4 plots the age profile of external deaths separately by cause. The figure shows a large and noticeable increase in motor vehicle accidents at age 21, with smaller but noticeable discontinuities in alcohol-related deaths (e.g., alcohol overdoses) and suicides. We find no visual evidence of increases in deaths attributable to drugs or homicide at age 21. Table 5 presents the corresponding regression results and confirms what we saw in Figure 4, that deaths with an explicit mention of alcohol increase by about 35 percent at age 21, homicides exhibit essentially no change, and the suicide rate increases by over 16 percent. Table 5 also shows that deaths due to motor vehicle accidents increase by about 15 percent at age 21.²¹ Estimates of external deaths attributable to drugs are not estimated precisely, while deaths due to “other external causes” (i.e., all deaths due to external causes not included elsewhere in Table 5) show evidence of a discrete increase of about 10 percent, an estimate that nears statistical significance in some of the models.²² This result for “other external deaths” provides evidence of a causal relationship between alcohol consumption and deaths due to fires, falls, and drownings.

Figure 4. Age Profiles for Death Rates by External Cause.

Notes: See notes to Figure 3. The categories are mutally exclusive. The order of precedence is homicide, suicide, MVA, deaths with a mention of alcohol, and deaths with a mention of drugs. The ICD-9 and ICD-10 Codes are in Appendix C.

Table 5.

Discontinuity in Log Deaths at Age 21 Due to External Causes

	(1)	(2)	(3)	(4)	(1)	(2)	(3)	(4)
	Alcohol				Homicide
Over 21	0.388	0.346	0.406	0.441	0.009	0.002	−0.003	−0.014
	(0.119)	(0.116)	(0.156)	(0.117)	(0.045)	(0.045)	(0.061)	(0.041)
Observations	1,460	1,460	1,460	1,458	1,460	1,460	1,460	1,458
R2	0.03	0.04	0.04			0.01	0.01	0.01
Prob > Chi-Squared		0.000	0.228			0.000	0.495
	Suicide				Motor vehicle accidents
Over 21	0.160	0.154	0.135	0.105	0.158	0.143	0.145	0.139
	(0.059)	(0.059)	(0.086)	(0.045)	(0.033)	(0.032)	(0.044)	(0.032)
Observations	1,460	1,460	1,460	1,458	1,460	1,460	1,460	1,458
R2	0.02	0.02	0.02	0.15	0.16	0.16
Prob > Chi-Squared		0.000	0.892	0.000	0.666
	Drugs				Other external causes
Over 21	0.070	0.067	0.004	−0.016	0.087	0.098	0.098	0.074
	(0.081)	(0.082)	(0.107)	(0.078)	(0.060)	(0.059)	(0.075)	(0.043)
Observations	1,460	1,460	1,460	1,458	1,460	1,460	1,460	1,458
R2	0.04	0.04	0.04	0.01	0.01	0.01
Prob > Chi-Squared		0.000	0.643			0.000	0.877
Covariates	N	Y	Y	N	N	Y	Y	N
Quadratic terms	Y	Y	Y	N	Y	Y	Y	N
Cubic terms	N	N	Y	N	N	N	Y	N
LLR	N	N	N	Y	N	N	N	Y

Notes: See Notes from Table 4. There are 276 observations where there are N deaths coded as due to alcohol; for this variable 0.5 was added to the dependent variable before taking the log. There are 15 observations where there are N deaths coded as due to drug use; for this variable 0.5 was added to the count before taking the log.

In Web Appendix O, we present the estimates of how the increase in total mortality varies by gender, race, and education. The regressions stratified by gender reveal that men experience a 10 percent increase in mortality and account for the majority of the overall increase in mortality. The regressions stratified by race reveal that the increase in deaths is largely driven by the 15 percent increase in deaths among whites, despite the fact that they have considerably lower death rates than either blacks or Hispanics. In the final panel, we present the result by educational attainment. These regressions reveal that the overall increase in deaths is driven largely by a 9 percent increase in deaths among high school graduates and a 17 percent increase in deaths among people attending college. In summary, the overall increase in mortality rates we observe at age 21 is due to large increases in mortality among white males who are high school graduates or are attending college.²³

Discussion and Conclusion

In this paper, we document that age-based restrictions on access to alcohol have a substantial effect on both alcohol consumption and mortality. Individuals just over age 21 report drinking on 21 percent more days than individuals just under 21 years old, and we estimate a similar proportional increase for heavy drinking days. We find no evidence of an increase in the average number of drinks people consumed on days of drinking, nor do we find a shift in the distribution of drinking intensity. We find that this increase in alcohol consumption results in a 9 percent increase in mortality at age 21. When we disaggregate by cause of death, we find particularly large increases for alcohol-related deaths, motor vehicle fatalities, and suicides.

Our results provide new evidence on some commonly held beliefs about how the increase in drinking causes an increase in mortality. First, the mortality effects we observe are not due entirely to “new” drinkers, those without previous exposure to alcohol. This is borne out by the very small increases (in both absolute and proportional terms) in first-time use of alcohol at age 21. Second, the mortality effects are also unlikely to be driven by people’s first experiences with heavy drinking. Figure 1 shows that people do experiment with heavy drinking immediately after they turn 21. But if the increase in mortality were caused by experimentation with heavy drinking, then mortality rates should rise discretely at age 21 and return rapidly to the pre-21 level. Figure 3 and Figure 4 show that this is not the case. As noted above, we do not find any evidence of a disproportionate increase in drinking intensity, which suggests that the increase in mortality rates is due to an increase in the number of days on which people drink or drink heavily.²⁴ If the increase in mortality is due to the increase in the number of days on which people drink or drink heavily, then the implied elasticity is 0.43 for individuals who change their drinking behavior because of the law (i.e., 0.091/0.21). This elasticity suggests that a substantial proportion of deaths among 21-year-olds are due directly to alcohol consumption. It also suggests that the cost of an increase in alcohol consumption is potentially quite high.²⁵ Our estimates suggest that reducing the drinking age nationally to age 20 would result in approximately 408 additional deaths among 20-year-olds.²⁶ Given a value of a statistical life of $8.4 million (in 2007 US dollars) this gives a total cost of about $3.4 billion per year.²⁷

Finally, our finding that policies that reduce alcohol consumption among young adults substantially reduce mortality is extremely relevant for current and ongoing public policy debates about stricter alcohol control targeted at youths. Given that over half of 18-to-20-year-olds report recent alcohol consumption, and about onethird report heavy episodic or “binge” drinking, there is wide latitude to affect alcohol consumption in this age group. Moreover the majority of acute alcohol-related deaths occur among 18- to 24-year-olds. Our results therefore suggest that stricter alcohol control targeted toward young adults could result in meaningful reductions in mortality, substantially reducing the number of life years lost to alcohol.