Protrusion of a Virtual Model Lamellipodium by Actin Polymerization: A Coarse-grained Langevin Dynamics Model

Abstract

We report the development of a coarse-grained Langevin dynamics model of a lamellipodium featuring growing F-actin filaments in order to study the effect of stiffness of the F-actin filament, the G-actin monomer concentration, and the number of polymerization sites on lamellipodium protrusion. The virtual lamellipodium is modeled as a low-aspect-ratio doubly capped cylinder formed by triangulated particles on its surface. It is assumed that F-actin filaments are firmly attached to a lamellipodium surface where polymerization sites are located, and actin polymerization takes place by connecting a G-actin particle to a polymerization site and to the first particle of a growing F-actin filament. It is found that there is an optimal number of polymerization sites for rapid lamellipodium protrusion. The maximum speed of lamellipodium protrusion is related to competition between the number of polymerization sites and the number of available G-actin particles, and the degree of pulling and holding of the lamellipodium surface by non-polymerizing actin filaments. The lamellipodium protrusion by actin polymerization displays saltatory motion exhibiting pseudo-thermal equilibrium: the lamellipodium speed distribution is Maxwellian in two dimensions but the lamellipodium motion is biased so that the lamellipodium speed in the direction of the lamellipodium motion is much larger than that normal to the lamellipodium motion.

1. Introduction

Cell migration is an important part of many cellular activities such as wound healing, tumor cell metastasis, and morphogenesis [9] and is a complex biological process accompanied with activities of the actin cytoskeleton, plasma membrane, integrin adhesion receptors and signaling systems activating numerous proteins. Protrusion occurring at the cell leading edge is the very first step in the cell migration cycle, followed by adhesion of the protrusion to the substrate, translocation by contraction and retraction, and de-adhesion of the cell posterior. Protrusion of the cell's leading edge relies on the treadmilling of actin filaments, such that new actin filaments are polymerized at the forward or leading edge of the cell (barbed end) whereas old actin filaments dissemble toward the rear (pointed end) of the lamellipodium which is a broad, flat sheet-like structure with ranging from 1 to 10 micrometers in width [1, 12] and approximately 0.2 μm in thickness [1].

Although it is well known that the actin polymerization is involved in cell migration from the biological point of view, the exact mechanism of force generation is still not clear. One possible mechanism of force generation at the cell leading edge, lamellipodium, would be a polymerization “Brownian Ratchet” model proposed by Peskin et al. [37]. They proposed that when the end of an actin filament is in contact with cell membrane, growth of the actin filament could act as a ratchet to push the cell membrane forward. In this model, movement of the cell membrane caused by thermal energy produces space between the cell membrane and a growing F-actin filament. When there is enough space for G-actin monomer to locate between the growing F-actin filament and the cell membrane, the insertion of G-actin monomer (polymerization) takes place. The inserted G-actin monomer prevents the cell membrane from backsliding to its original position and ratchets the cell membrane forward generating a protrusive force. Mogilner and Oster [33] modified the original Brownian ratchet model by combining it with the elastic properties of an actin filament and proposed an “Elastic Brownian Ratchet” model where F-actin filaments readily bend so that cell membrane does not need to fluctuate to allow actin insertion. In this case, most of Brownian motion occurs in the bending of actin filaments and when the actin filament bends sufficiently far from the cell membrane, actin monomers can be inserted and polymerized. Both models require an uncoupling of the cell membrane from actin filaments to allow actin polymerization to occur.

Much attention has been given to the bacterial pathogen Listeria monocytogens as a simplified model system because its motion shares many of the essential features of actin-based cell motility. Listeria monocytogens propels itself through the host cell cytoplasm by polymerizing a network of host cell actin filaments [6, 21, 22, 28-31, 33, 44, 45]. Actin monomers are polymerized by proteins at the posterior end of the bacteria at the same rate as that of the bacterial cell propulsion, indicating that the growth of actin filaments causes the bacteria to move forward [45].

Using a high-resolution laser-tracking technique, Kuo and McGrath [28] found that fluctuations of Listeria body are much smaller than the size of G-actin monomer, and Listeria has episodes of motility with pauses spaced at about 5 nm corresponding to the periodicity of the actin filament. Gerbal et al. [22] used optical tweezers to attempt to detach the actin tail from Listeria body by applying a force of 10 pN between the bacterium and its tail for several minutes and failed to pull the tail from the bacterium. These findings suggest that as actin filaments elongate, they remain firmly attached to motile bacterial surface. In this case, growing filaments push the bacterium surface forward at the same time that other non-polymerizing actin filaments pull and hold the bacterium [22]. Based on these observations, several models such as a “Stacked Rubber Band” model of Gerbal et al. [21], a “Lock, Load & Fire” model of Dickinson and Purich [15], and a “Tethered Ratchet” model of Mogilner and Oster [33] have been developed. Particularly, in the “Stacked Rubber Band” model, Gerbal et al. developed a continuum (macroscopic) model of Listeria propulsion and proposed that the addition of new actin filaments induces elastic deformations in the gel: the previously formed layers are compressed by a new polymerized layer at the bacterium surface. Thus, the protrusive force is generated by using the free energy produced by actin polymerization which is first stored as elastic energy. However, this model does not provide a detailed molecular mechanism at the microscopic scale.

Many attempts have been made to measure protrusive force generated by actin filament polymerization by using glass microneedles [30], atomic force microscope [36, 39], and optical traps [19], giving values for the protrusive force in the range of several nN/μm² [19]. In particular, Prass et al. [39] have directly measured the lamellipodial protrusive force using an atomic force microscopy of which a cantilever is placed in the path of a migrating keratocyte in order to obtain the maximum force that the lamellipod could produce and the characteristic force-velocity relation for the lamellipod. Although it has not been measured in lamellipodia, protrusive force in other actin based structures is strongly associated with the mechanical properties of actin filament bundles crosslinked by actin-binding proteins such as α-actinin in cytoskeletal bundles, fascin in filopodia, and plastin in microvilli and stereocilia, mediating actin bundle stiffness [13]. We expect that the protrusive force in lamellipodium and its extension is also affected by the mechanical property of crosslinked actin filament bundles, which is associated with elastic energy stored during actin polymerization.

Computer simulations and theoretical studies [3, 16, 17, 24, 25, 40-42, 46] have improved our understanding of the behavior of lamellipodium protrusion, cell migration and Listeria propulsion. They are useful not only because their results can be both quantitatively and qualitatively compared with experimental results but also because they can describe the behavior of the systems using multiple variables and identify key parameters that play crucial roles in the overall behavior of the systems.

Recently, Schaus et al. [42] have developed a 2D stochastic computer model of lamellipodial protrusion based on the dendritic-nucleation/array-treadmilling mechanism with incorporating diffusion, stochastic kinetics, and elastic filament and plasma membrane mechanics. In this work, they could establish the self-organization of lamellipodiual actin filaments into orientation at ±35 degrees with respect to the direction of protrusion. This pattern was robust with respect to plasma membrane surface and bending energies and to actin concentration, under the condition of protection from capping at the leading edge. However, it is not clear whether the similar pattern would be established when their model is adopted in 3D.

Satyanarayana and Baumgaertner have used Monte Carlo methods to simulate actin-based cell migration in two dimensions [41]. In this study, a cell was modeled as a ring polymer on the square lattice and polymerization kinetics for the actin network were controlled by appropriate reaction probability. Various scaling laws were established that relate the size of the model cell to the concentration of polymerized and unpolymerized actin molecules and the length of the enclosing membrane. However, the primary drawbacks of these particle-based (actin-based) Monte Carlo simulations of cell migration in two dimensions are the unrealistically small size of the model cell or membrane, and a time scale which is too short to study cell migration behavior induced by actin polymerization. Therefore, it is desirable to develop more elaborate cell or membrane models, for example, in three dimensions and using appropriate length and time scales to relate the simulations to realistic situations. Such a model would permit molecular-level insights into cell protrusion and the role of actin polymerization for generating protrusive force acting on the cell membrane.

Accordingly, in this paper we present a virtual model lamellipodium utilizing actin polymerization for its directional motion (protrusion) as the first step of the cell migration cycle. It is noted that the model lamellipodium we have developed is not of a whole cell but of a part of a cell. The model uses a coarse-grained Langevin dynamics method that allows us to simulate a lamellipodium of size comparable to a real one and on a time scale long enough to study lamellipodium protrusion. We adopt a coarse-grained model (defined in Section 2 below) because, short of using prodigious levels of computing power, it is unlikely that one can model in a molecularly detailed way the full process of cell migration cycle using molecular simulation methods such as Monte Carlo and molecular dynamics simulations due to the biological complexity and resulting computational requirements. At the cost of details of essential components of actin polymerization with simplification of their roles, our aim in this paper is to develop a particle-based virtual model lamellipodium, in three dimensions, which could play the role of a bridge between microscopic and macroscopic models of protrusive force generation by actin polymerization.

The model we develop allows us to study the effect of stiffness of the F-actin filament, G-actin monomer concentration, and number of polymerization sites on lamellipodium protrusion. In our simulation-based model, F-actin filaments are firmly attached on the lamellipodium surface as observed from experiments [22, 28] and the force opposing a compression force is generated by imposing a bond angle (bending) potential at the interface between lamellipodium surface and F-actin filaments. This combined protrusive force from actin polymerization results in lamellipodium extension at a certain mean speed. Our approach reveals how the mean speed of a lamellipodium depends on the number of polymerization sites at the lamellipodium surface and the number of available G-actin particles, providing a microscopic mechanism for protrusive force generation by actin polymerization.

The remainder of this paper is organized as follows. Section 2 contains a description of our model and the simulation methodology. In Section 3, the results of our model lamellipodium are shown with analysis of motion of the model lamellipodium in terms of mean-square displacement of the center of mass of the lamellipodium and its mean speed. Finally, in Section 4, we summarize our results.

2. Model and Simulation

2.1. Coarse-grained Langevin-dynamics-based model of lamellipoi dum protrusion

We developed a coarse-grained (bead-spring) Langevin-dynamics-based model of lamellipodium protrusion induced by actin polymerization. A coarse-grained system was used to reduce the overall number of particles involved in the system and subsequently to reduce the computational time per simulation time step. In doing so, we ignore several of the details of the chemical structure of components such as G-actin monomers, polymerization sites and cell membrane molecules.

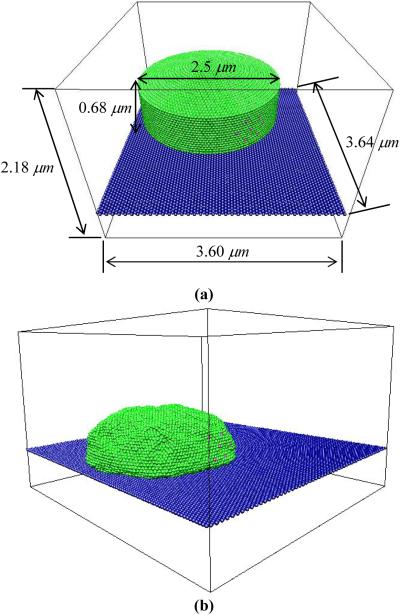
Our system consists of particles comprising the virtual lamellipodium, G-actin particles, F-actin filament (polymerized G-actin), polymerization sites, and extracellular matrix (ECM) surface. The virtual lamellipodium enclosing the G-actin particles is on top of the ECM surface that is modeled as a hexagonally packed sheet. The polymerization sites where actin polymerization takes place forming F-actin filaments are locally positioned on the lamellipodium surface. We model a virtual lamellipodium as a low-aspect-ratio doubly capped cylinder (see Fig. 1). The cylinder was formed by wrapping a hexagonally packed sheet consisting of C × L particles around the cylinder axis. Here, C is the number of particles forming the circumference of the cylinder and L is the number of particles along the cylinder axis. Both ends of the cylinder are closed by a flat circular cap with C particles in its circumference. All particles belonging to the virtual lamellipodium are connected with the six nearest-neighbors, as is typical of the head groups in a two-dimensional lipid bilayer. As seen in Fig. 1, the conformation of the virtual lamellipodium was relaxed before the simulation run and during this relaxation it assumed a bell shape.

Fig. 1.

(Color online) Snapshots of a virtual lamellipodium on ECM surface. Green particles represent the virtual lamellipodium, pink ones polymerization sites, and blue ones ECM surface. A virtual lamellipodium is modeled as a low-aspect-ratio doubly capped cylinder formed by wrapping a hexagonally packed sheet. F-actin filaments are firmly attached to a lamellipodium surface where polymerization sites are located, and actin polymerization takes place by connecting a G-actin particle to a polymerization site and to the first particle of a growing F-actin filament whose stiffness is given by bond angle potential. The thermal motion and stiff bond angle potential pushes the lamellipodium wall away from the F-actin filament to accommodate the added particles. The conformation of the virtual lamellipodium was relaxed (a) before the simulation run and (b) during this relaxation it assumed a bell shape.

With the geometry of our simulation system established, we next define various interactions which control the static and dynamic properties of a system. Each particle forming the virtual lamellipodium, is connected to its six nearest neighbors via a harmonic bond potential,

$$U_{\mathit{bond}}=\frac{1}{2}{k}_{\mathit{spring}}{(b-b_0)}^2,$$ (1)

where k_spring is the spring constant set to be k_spring = 100k_BT / σ², k_B is the Boltzmann constant, T the absolute temperature, and σ the particle diameter. b is the distance between neighboring particles, and the equilibrium bond length b₀ is set to be b₀ = 1.0σ. Potentials of the form Eq. 1 are frequently used to describe effective interactions between segments of a polymer. Because of the similarity of the energy function to that of a spring, bead spring models for macromolecular systems, consisting of centers of force (beads) connected by forces of the form Eq. 1 are typical coarse-grained models for polymers in which each bead represents a significant segment of the polymer chain (in fact, they typically represent portions of the chain that can be considered inflexible over the domain of the portion) [8].

In addition to the harmonic bond potential, all particles in the system (particles for virtual lamellipodium, G-actin particles, F-actin filaments and ECM surface) interact via the truncated-shifted Lennard-Jones (LJ) potential,

$$U_{LJ}\left(r_{ij}\right)=\{\begin{array}{cc}\hfill 4{\epsilon }_{LJ}\left[{\left(\frac{\sigma }{r_{ij}}\right)}^{12}-{\left(\frac{\sigma }{r_{ij}}\right)}^6-{\left(\frac{\sigma }{r_{\mathit{cut}}}\right)}^{12}+{\left(\frac{\sigma }{r_{\mathit{cut}}}\right)}^6\right],\hfill & \hfill r\le r_{\mathit{cut}},\hfill \\ \hfill 0,\hfill & \hfill r>r_{\mathit{cut}}\hfill \end{array}\phantom{\}}$$ (2)

where r_ij is the distance between two interacting i^th and j^th particles and r_cut is a cutoff distance beyond which the interactions are ignored. The value of LJ interaction parameter ε_LJ is set to be ε_LJ = k_BT. The truncated-shifted LJ (TSLJ) potential is frequently used to model the interaction between the particles (beads in a bead-spring model of polymers) in coarse-grained representations of macromolecular systems. The usual LJ potential does not include the last two terms (i.e., corresponds to r_cut → ∞) and includes short-ranged repulsion (modeled by the r^-12 term) and long-ranged attraction (modeled by the r^-6 term) due to dispersion interactions. In Langevin dynamics simulations, it is typical to ignore the interaction beyond a cutoff distance r_cut, beyond which it has little effect on the dynamics; by subtracting the value of the LJ potential at the r_cut, the TSLJ potential goes smoothly to zero at r_cut, and hence has no discontinuity.

F-actin filaments are assembled by G-actin particles forming long polymers, thus interactions between particles in the F-actin filaments are given by bond interactions and non-bonded interactions, TSLJ, (Eqs. 1 and 2, respectively). In addition, a bond angle (bending) potential is used to model the stiffness of actin filaments between the two bonds connecting any three consecutive particles of an F-actin filament as follows:

$$U_{\mathit{angle}}=\left({\theta }_i\right)=\frac{1}{2}{k}_{\mathit{angle}}{({\theta }_i-{\theta }^{°})}^2.$$ (3)

This potential is harmonic in the bond angle θ_i, defined as the angle between the α - β and β - γ bonds connecting three consecutive particles α - β - γ, tending to constrain the angle to its equilibrium value θ°. In our model, θ° = π, corresponding to the three particles being collinear. The quantity k_angle is the angle harmonic constant; larger values of k_angle make the actin filament stiffer.

The simulations of the model lamellipodium were performed in a statistical mechanical ensemble in which the number of particles (N), volume (V), and temperature (T) are held constant (the NVT ensemble). Periodic boundary conditions [4] are used to eliminate boundary effects. However, because of the short range of the bead-bead potentials, there is no interaction between the model lamellipodium and its periodic images. Hence, in essence, the model lamellipodium is isolated in an infinite ECM sheet. The constant temperature is achieved by coupling the system to a thermal bath represented by a Langevin thermostat.[2] This simulates the particles being surrounded by an implicit solvent (i.e., a solvent which is not explicitly represented in the simulation) with which they are in thermal equilibrium. In this case, the equation of motion for the i^th particle is

$$m\frac{d{\overrightarrow{v}}_i}{dt}={\overrightarrow{F}}_i^D+{\overrightarrow{F}}_i^F+{\overrightarrow{F}}_i^R,$$ (4)

where m is the particle's mass. ${\overrightarrow{F}}_i^D$ is the net deterministic force acting on the i^th particle obtained from the forces generated by harmonic bond (Eq. 1), TSLJ (Eq. 2) and bond angle bending (Eq. 3) interactions with the relevant neighboring particles. The hydrodynamic drag of the solvent on the particles is included through the frictional force ${\overrightarrow{F}}_i^F=-{\overrightarrow{v}}_i\xi$, where $\overrightarrow{v}$ is the i^th particle's velocity and ξ is the friction coefficient coupling the system to the thermal bath and is equal to ξ = m / τ_LJ, where τ_LJ is the standard LJ-time. In a more precise form of Langevin dynamics, the parameter ξ would be related to the viscosity of the solvent and the size of the particle; in the model presented here, we choose ξ to be a typical value, namely that for a polymer dissolved in an implicit solvent consisting of its particles. The quantity ${\overrightarrow{F}}_i^R$ is the stochastic force modeling random collisions between a particle and the solvent, and can be calculated using the fluctuation-dissipation theorem [18]. It has the properties of zero average value, $\langle {\overrightarrow{F}}_i^R\left(t\right)\rangle =0$, and δ-functional correlations, $\langle {\overrightarrow{F}}_i^R\left(t\right){\overrightarrow{F}}_i^R\left(t^{\prime }\right)\rangle =6\xi k_{B}T\delta (t-t^{\prime })$. The velocity-Verlet algorithm [20] with a time step Δt = 0.002τ_LJ was used to integrate the equations of motion (4).

2.2. Details of simulation

Simulations were carried out by the following procedure. An ECM surface over which our model lamellipodium moves was built with a hexagonally packed sheet consisting of 70×80 particles of diameter, σ. At the beginning of a simulation, the virtual lamellipodium of the low-aspect-ratio doubly capped cylinder of size C×L (150×15) (The total number of particles comprising of the virtual lamellipodium is 5852 when both particles of the cylinder and two end caps are counted.) was put 1.5σ above the ECM surface whose position was fixed during the simulation. Bonds were connecting particles of the lamellipodium to their six nearest-neighboring particles on the lamellipodium surface making the virtual lamellipodium stable in shape as well as preventing G-actin particles from escaping. In this case, the lamellipodium was rigid and was not allowed much deformation. In addition, collisions between G-actin particles and lamellipodium membrane particles further helped stabilize the lamellipodium shape.

The cutoff distance r_cut was 2.5σ between ECM particles and bottom particles of the low-aspect-ratio doubly capped cylinder (combination of attractive and repulsive interactions in TSLJ), and it was $\sqrt[6]{2\sigma }$ between all other pairs (purely repulsive interaction in TSLJ). Because the initial distance between the ECM and the bottom of the model lamellipodium was 1.5σ, which was smaller than the cutoff distance r_cut = 2.5σ, the attractive interaction of TSLJ led the model lamellipodium to be always near the ECM.

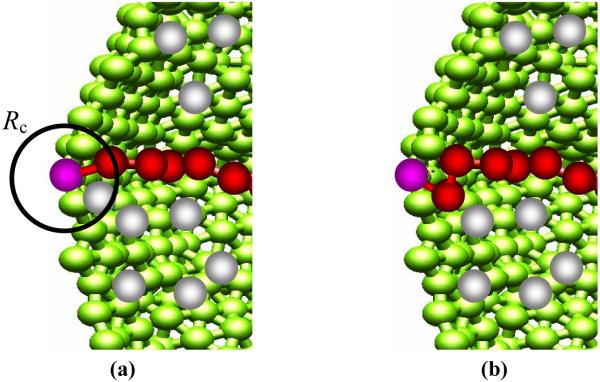
In our model, the attachment of lamellipodium associated with ECM through ligand-receptor bindings was not explicitly taken into account. Instead, it was assumed that average of this interaction was continuously acting on the ECM surface in the form of the above-described TSLJ potential. On the lamellipodium surface, we located multiple polymerization sites, M_p, (i.e., Mp =1, 3, 5, 7, 9, 11, 15, 21, 27, and 33) whose distance between nearest polymerization sites was carefully chosen to be larger than a capture radius R_c = 2.0σ, which will be described below. This allowed us to simulate actin polymerization processes that would not compete with nearest neighboring polymerization sites. The first polymerization site was taken from lamellipodium membrane particles of half-height from the bottom of the cylindrical-shaped model lamellipodium. Next polymerization sites were regularly distributed in a rectangular area of lamellipodium surface with an equal distance in between them and with the first polymerization site being in the middle of the rectangular area. The overall location of the polymerization sites are biased to one side of the lamellipodium. (see Fig. 1) G-actin particles, as the last component of the model system, were randomly distributed inside the low-aspect-ratio doubly capped cylinder with density from c = 0.0188σ^-3 to c = 0.1505σ^-3.

Now that we have all the ingredient for running a simulation, the actin polymerization process, the most crucial step, is described as follows: the actin polymerization process is modeled as successive bond formation. A first bond is formed by connecting a G-actin particle and a polymerization site with an equilibrium bond length 2σ if the G-actin particle was within the capture radius R_c = 2.0σ from the polymerization site. Next, other G-actin particles within R_c from the polymerization site, but the closest one to the polymerization site, form a next bond. In this case, two new bonds are formed and one old bond is removed: A G-actin particle is connected to a polymerization site and to the first actin particle of a growing F-actin filament while the bond between the polymerization site and the first actin particle is removed. Further polymerization events are performed by repeating the last polymerization process, and independently occurs at different polymerization site (see Fig. 2). In this way, we are modeling firmly attached actin filament.

Fig. 2.

(Color online) Schematic representation of the chain polymerization process: (1) particle selection and (b) bond connection. The color code is as follows: cell - green; G-actin particles - gray; F-actin filaments - red; polymerization sites - pink. Used system parameters in this figure are as follows: angle harmonic constant is k_angle = 0k_BT/rad² (flexible actin filament) and the number of polymerization sites, M_p = 1.

It is noted that transient tethering might occur in biology as the model of Mogilner and Oster suggests [33]. However, modeling of polymerization process in our simulation is based on the experimental observations showing that listeria tail firmly attaches to listeria body from optical tweezer experiments [22]. Of course, it does not say all actin filaments are attached to the listeria body. It is not clear whether the same filament-attachment mechanism causes the generation of protrusive force in lamellipodium protrusion. It is our assumption that the same mechanism would be the cause for the force generation in lamellipodium protrusion because listerial motion shares many of the essential features of actin-based cell motility. However, some actin filaments may be attached and others not, or they are only transiently attached during the actin polymerization process. Considering a distribution of transiently attached actin filaments, or a distribution of attached and unattached actin filaments could be another system that we can look at in the future.

After an F-actin filament achieves a degree of polymerization N_p = 10, its length N_p is kept constant for the rest of the simulation run by removing a bond connecting a particle at the terminal end as a new G-actin particle is added to the filament. In doing so, we are assuming that polymerization phase is in a steady state with no net change in the total mass of filaments and that the energy required for polymerization is supplied by the energy released from the depolymerization process. However, this energy transfer is not taken into account explicitly in our simulation; rather, this assumption is a justification why the polymerization and depolymerization can take place without any obvious energy sources. Depolymerized G-actin particles are available for further polymerization when they move to proximity of the polymerization sites. Note, however, that this is diffusion-limited - a depolymerized particle has to diffuse to the near vicinity of the polymerization site in order to be used again. Thus, filament length will affect the polymerization rate. We have not studied this effect; however, it would be good topic for future work.

To model the stiffness of filaments, an angle harmonic potential is imposed to the first two bonds connecting three consecutive particles with angle harmonic constant, k_angle, (i.e., k_angle = 0, 5, 10, 20, 40, 60, 80, and 100 k_BT/rad²). The F-actin filament beyond two consecutive bonds from the polymerization sites was fixed in space. That is to say that fixed F-actin filaments have velocity and force values of 0. In real cells, the polymerized actin filaments adhere to the extracellular matrix individually by means of transmembrane integrin receptors [25, 47] and other integrin-associated proteins, which is modeled here by keeping the F-actin filament fixed in space. The thermal motion and stiff bond angle potential pushes the lamellipodium wall away from the F-actin filament to accommodate the added particles. It should be noted that the kinetics of the polymerization process is not explicitly taken into account in our simulations; however, we would expect that including the polymerization kinetics would decrease the net polymerization rate normalized for G-actin concentration, k_p, which is determined by the G-actin monomer concentration, c, and the size of the capture radius, R_c, in our simulation.

We use periodic boundary conditions in the x and y directions with simulation box size L_x = 70σ, L_y = 69.3σ, and L_z = 42σ. The ECM is located at z = 15σ. Each simulation run lasted 1×10⁷ integration steps and the final 8×10⁶ integration steps have been used for calculating various physical quantities such as mean-square displacement of the center of mass of the virtual lamellipodium and its mean speed.

2.3. Conversion of units

To understand the results of our coarse-grained Langevin dynamics simulation and to make comparisons with experimental observations, we convert the two basic reduced units, length σ and time scale τ_LJ, to real units. First, it is assumed that our lamellipodium size is about 2.5 μm as a usual lamellipodium has size of 1 - 10 μm [1, 12]. This allows us to determine particle size in real units. In our simulation, there are 150 particles along the circumference of the virtual lamellipodium having diameter, 150σ/π which is assumed to be 2.5 μm, resulting in the particle size being σ = 0.052μm. The height of the model lamellipodium, 0.68 μm, is estimated from this particle size. The size of G-actin monomers is well-known and approximately 5 nm. Therefore, our G-actin particle corresponds not to a single G-actin monomer but a few hundreds of G-actin monomers. In such a representation, polymerization and depolymerization events are assumed to be averaged over long time and large length scales.

The number of G-actin monomers inside a G-actin particle can be estimated, when it is considered that F-actin filaments are highly cross-linked and compacted as in a polymer melt state and it is assumed that size dependence of F-actin filaments is given by R = N^1/2l following that of a Gaussian polymer chain, where R is the size of small section of F-actin filaments or σ in our simulation, N the number of G-actin monomers inside the section, and l the size of G-actin monomer. Thus, in our calculation, N = (R/l)² = 110 or 100 - 150. It is important to note that since a G-actin particle is corresponding to 100 - 150 G-actin monomers, this scaling also applies to other particles. For example, the effective number of polymerization sites in our simulation is not of the order of tens but of thousands.

The effective number of polymerization sites or actin filaments per unit length is estimated as NΔV_p /(2V_pσ) where V_p is volume of a particle and ΔV_p volume of outer shell of the particle with the w3idth of G-actin monomer size. The numerical factor of 2 in the denominator stems from the consideration that polymerization-related proteins are located in the inward hemispheric shell of the particle. Using these values, the effective number of F-actin filaments per micrometer is calculated to be 600μm^-1 which is similar to the observed value of 240μm^-1 reported by Abraham et al. [1]. With the length scale σ = 0.052μm and effective number of G-actin monomers per particle N = 110, the G-actin monomer concentration in our simulation corresponds to the range from 24 μM to 192 μM. In real cells, G-actin monomer concentration has a range from several to hundreds of μM and the concentration of polymerized actin is known to be about 1000 μM [38].

To determine the simulation time-scale, we need to know dynamic quantities such as the diffusion coefficient of G-actin particle D_p which can be related to the mean square displacement 〈r(t)²〉=〈(r(t₀ + t)-r(t₀))²〉 of the particles by 〈r(t)²〉 = 6D_pt where t is the time. We cannot directly determine D_p in our simulation; however, we can deduce it from an experimental observation that the diffusion coefficient, D_G, of G-actin monomer is 30 μm²/sec at low G-actin monomer concentration [1]. If there is no possibility for G-actin particle to interact with other G-actin particles due to a low monomer concentration, the time required to move a distance equal to the G-actin particle size (σ) is equal to t =τ_LJ=σ²/D_p, which is the simulation time scale that we need to know. Dynamics of particles, such as our system controlled by the random force or thermal fluctuation, corresponds to Rouse dynamics[10, 18]. In this case, the diffusion coefficient of a polymer chain of length N is inversely proportional to N, resulting in D_p = D_G/N and subsequently leading toτ_LJ =σ² N/D_G = 0.052² ×110/30 = 0.01sec. Detailed system information and conversion of units is summarized in Table 1.

Table 1.

List of Notations and System Parameters

Meaning	Value
size of G-actin particle, σ	0.052 μm
simulation time, τLJ	0.01 seconds
integration time, 0.002 τLJ	0.00002 seconds
overall simulation time	200 seconds
size of simulation box (x × y × z)	3.64 μm × 3.60 μm × 2.18 μm
size of a virtual model lamellipodium	diameter: 2.5 μm; height: 0.68 μm (5852 particles)
size of ECM surface	length: 3.64 μm; width: 3.60 μm (5600 monomers)
G-actin monomer concentration, c	24, 48, 96, and 192 μM
number of polymerization sites, Mp	1, 3, 5, 7, 9, 11, 15, 21, 27, and 33
LJ interaction parameter, εLJ	1.0 kBT
angle harmonic constant, kangle	0, 5, 10, 20, 40, 60, 80, and 100 kBT/rad2

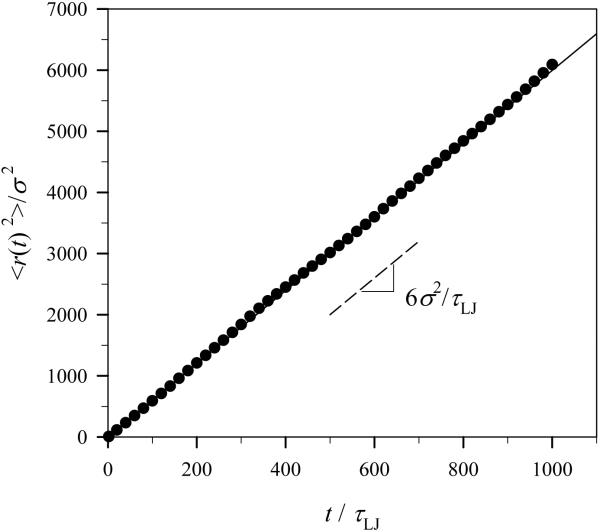
In order for us to make sure that we get the relation τ_LJ =σ ²/D_p from our model, the mean square displacement of particles at low G-actin particle concentration c = 0.001σ^-3, or 0.13 μM, was plotted in Fig. 3. The dashed line in the plot shows the slope of the best-fit to the obtained data and has a value of 6σ ² /τ_LJ, in our simulation units, which should be equal to 6 D_p indicating the random motion of particles. From this relation, we verify that τ_LJ =σ²/D_p. In addition, when the motion of an isolated particle is governed by Eq. 4, its mean square displacement, 〈r(t)²〉, can be analytically solved as follows [10]:

$$\langle r{\left(t\right)}^2\rangle =\frac{v_0^2}{{\xi }^2}{(1-\exp (-\xi t))}^2+\frac{3k_{B}T}{m{\xi }^2}(2\xi t-3+4\exp (-\xi t)-\exp (-2\xi t)),$$ (5)

where ν₀ is the initial velocity of the monomer. The solid line in Fig. 3 is this analytical solution which matches exactly with simulation data.

Fig. 3.

Mean-square displacement of particles during simulation runs at monomer concentration c = 0.001σ^-3, or 0.13 μM. The dashed and solid lines in the plot are the best-fit to the data points and the analytical solution of Eq. 5 for a single particle, respectively.

3. Results and Discussion

3.1. Movement of the virtual lamellipodium

The G-actin particles move in a random walk (including non-overlapping) fashion inside the virtual lamellipodium. When a G-actin particle approaches one of polymerization sites on the lamellipodium surface within the capture radius 2σ = 0.104μm, a polymerization event takes place. A G-actin particle is polymerized by connecting it to the first particle of the growing F-actin filament and then to the polymerization site, thereby forming two new bonds. To maintain the steady state of a polymerization phase, we eliminate two old bonds once the polymerization length is equal to N_p=10; one bond connecting the first F-actin particle and the polymerization site, and the last bond of the F-actin filament that is attached to the last G-actin particle of the chain. Since the newly formed bonds have a tendency to become straight by the imposed bond angle (bending) potential with the angle harmonic constant k_angle and the rest of bonds stay fixed at their positions, there exists a protrusive force to push the virtual lamellipodium outward. In this case, the virtual lamellipodium exhibits ballistic motion (〈r(t)²〉 ∝ t ²).

It should be noted that in our simulation we are not simulating individual G-actin polymerization and depolymerization processes in which many proteins such as nucleating and branching complex, Arp2/3, capping proteins, and severing and depolymerizing factor, ADF/cofilin are involved, but rather we are simulating averaged polymerization and depolymerization events over longer time and larger length scales that are much larger and longer than real length and time. Also, Y-shaped actin network formation with 70° between junctioned F-actin filaments [38] and periodic lamellipodium contractions or the formation of actin waves depending on ECM rigidity [23] cannot be addressed by our model due to the representation of the G-actin particle as a section of G-actin monomers and the long time scales simulated.

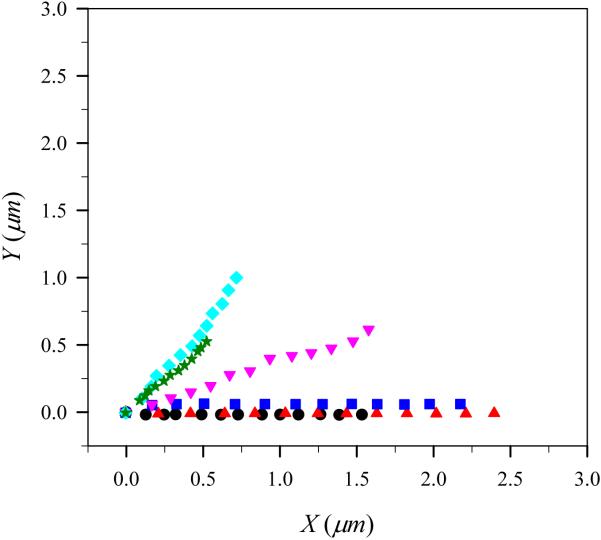
To show the characteristics of the motion of the virtual lamellipodium, we plotted trajectories of the center of mass of the virtual lamellipodium with a G-actin monomer concentration c = 48μM with various number of polymerization sites M_p in Fig. 4. In this figure, the angle harmonic constant is k_angle=100k_BT/rad². One can immediately notice from Fig. 4 that the virtual lamellipodium exhibits directional motion. It is interesting to point out that if polymerization sites were uniformly distributed along the circumference of virtual lamellipodium of a low-aspect-ratio doubly capped cylindrical shape, the motion of lamellipodium would not exhibit this directional motion. (i.e., it would on average be isotropic.) A virtual lamellipodium with too few (M_p = 3) or too many (M_p = 33) polymerization sites travels a shorter distance from the origin when compared with those with moderate number of polymerization sites. With no polymerization event, the virtual lamellipodium showed a movement in a random-walk fashion because the most dominant force acting on the virtual lamellipodium is the random force as in Eq. 4. The direction of the lamellipodium movement is mainly governed by the location of the polymerization sites. As M_p increases, the area where polymerization events take place also increases. This leads high fluctuation in the direction of the lamellipodium motion. Thus, in Fig. 4, we see the direction of the lamellipodium motion changes as M_p increases.

Fig. 4.

(Color online) Trajectories of the center of mass of the model lamellipodium during simulation runs for different number of polymerization sites with angle harmonic constant k_angle=100 k_BT/rad² at G-actin monomer concentration c=48 μM. Filled circles, triangles, squares, reverse triangles, diamond, and stars correspond to the number of polymerization sites, M_p=3, 9, 15, 21, 27, and 33, respectively. At the beginning of simulations, the model lamellipodium is located at the origin.

It is also important to note that even if polymerizations took place at the polymerization sites, the virtual lamellipodium did not show perfect directional motion unless the bond angle potential was imposed, indicating that stiffness of F-actin filament of Young's modulus of 10³-10⁴ Pa [21] plays an important role in generating protrusive force. On the other hand, polymerization of soft materials such as a polysaccharide gel with lower elastic modulus of 10^-1-10¹ Pa [35] may generate a protrusive force if rapid polymerization would occur in a chamber such as a nozzle, with one end capped and the other open, which results in the improvement of the elastic properties of the polysaccharide gel by the compression of the gel, as is observed in cyanobacteria, myxobacteria and flexibacteria [27].

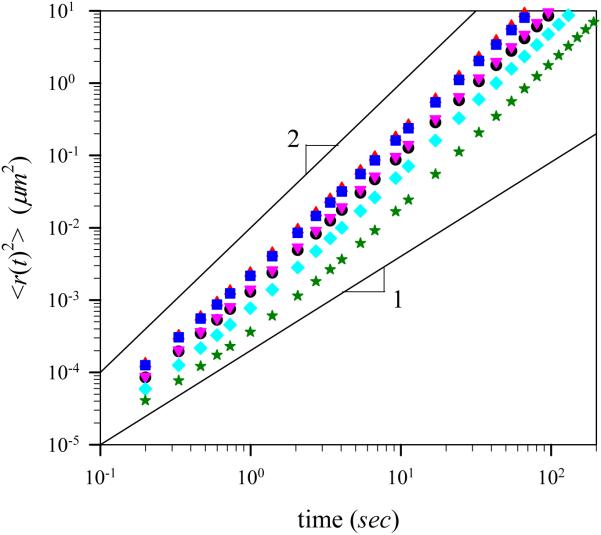
Figure 5 shows the mean-square displacement 〈r(t)²〉 of the center of mass of the virtual lamellipodium averaged during the simulation run as a function of time for different number of polymerization sites, M_p, at G-actin monomer concentration 48 μM with k_angle=100k_BT/rad². There exist two distinct regimes. For shorter time intervals t < t*, the motion of the virtual lamellipodium is diffusive, which is implicated by the linear dependence of the mean-square displacement on the time interval t. For longer time intervals t > t*, the virtual lamellipodium exhibits ballistic movement. Therefore, the mean square displacement of the center of mass of the virtual lamellipodium has two contributions: one due to ballistic motion with average velocity ν_L and the second due to random motion caused by velocity fluctuation. In these cases, the mean-square displacement can be expressed as follows [27]:

$$\langle r{\left(t\right)}^2\rangle =v_L^2{t}^2+6D_{L}t,$$ (6)

where D_L is the diffusion coefficient of the virtual lamellipodium. Crossover between the diffusive and ballistic regimes takes place when both terms become of the same order of magnitude. It is important to note that we have a movement transition of the model lamellipodium from diffusive to ballistic regime, whereas for a molecular motion in a thermal equilibrium, the transition is reversed. The appearance of the ballistic regime indicates the existence of the constant protrusive force acting on the virtual lamellipodium. The magnitude of this force depends on the number of polymerization sites and degree of stiffness of the F-actin filaments, as discussed in the following sections.

Fig. 5.

(Color online) Mean-square displacement of the center of mass of the model lamellipodium during simulation runs for different number of polymerization sites with angle harmonic constant k_angle=100 k_BT/rad² at G-actin monomer concentration c=48 μM. The solid lines with slopes 1 and 2 are shown to demonstrate two different asymptotic regimes with diffusive and ballistic motion, respectively. Notations are the same as in Fig. 4.

3.2. Velocity of the virtual model lamellipodium

The velocity of the virtual lamellipodium can be obtained by calculating the square root of a slope in the ballistic regime in a plot of a mean-square displacement divided by time versus time. Alternatively, in order to obtain a better statistical value, we defined the speed of the virtual lamellipodium as the displacement of the center of mass of the virtual lamellipodium during 10⁴ integration time step and averaged over the simulation runs to obtain the mean speed and used this mean speed for dynamical analysis of the lamellipodium motion. The velocity value of the virtual lamellipodium obtained from the slope in the ballistic regime was always within one tenth of the standard deviation of mean speed.

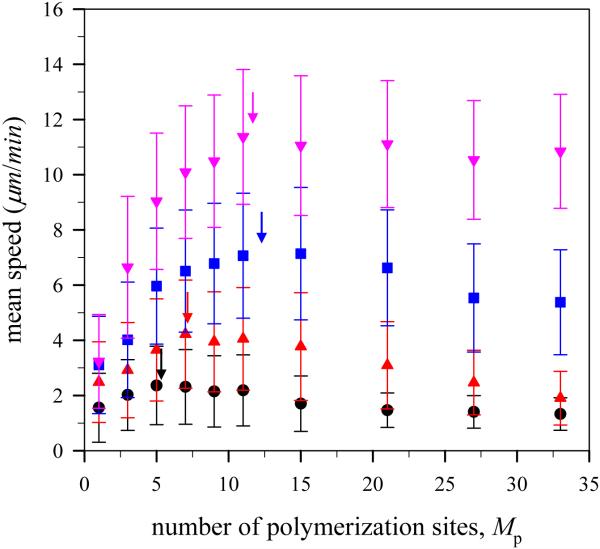
Figure 6 depicts the mean speed of the virtual lamellipodium during simulation runs for different number of polymerization sites with angle harmonic constant k_angle=100k_BT/rad² at various G-actin monomer concentrations. The magnitude of mean speed is in a range of 2 to 12 μm/min which is similar to observed experimental values ~ 0.3 μm/sec or 18 μm/min [1, 38] and ~ 6μm/min [11], and theoretical values < 0.3 μm/sec [5]. In the case of the virtual lamellipodium with no polymerization events at G-actin monomer concentration c=192μM, the mean speed was 1.5 μm/min, and the direction of motion changed continuously in a random-walk fashion. It is noted that this random motion with stochastic force results from thermal fluctuation, however, a polymerizing model lamellipodium with randomly distributed polymerization sites along the circumference of the model would also exhibit a random motion. In this case, the origin of stochastic force for the lamellipodium motion is the random directional change of protrusive force. Thus, the non-uniform distribution of polymerization sites as in our simulation provides the source of directed motion and significant lamellipodium speed.

Fig. 6.

(Color online) Mean speed of the model lamellipodium during simulation runs for different number of polymerization sites with harmonic angle constant k_angle=100k_BT/rad² at different G-actin monomer concentration c=24 μM (●), 48 μM (▲), 96 μM (■), and 192 μM (▾).

Figure 6 clearly shows that there are an optimal number of polymerization sites for rapid lamellipodium protrusion. Interestingly, this result agrees with other models in the literature [25, 32] where polymerized actin filaments are not attached to the lamellipodium surface. The optimal number of polymerization sites showing the fastest motion of the virtual lamellipodium at different G-actin monomer concentrations is indicated by arrows in Fig. 6. The optimal number of polymerization sites at low G-actin monomer concentration c=24μM is 5 and increases with increasing G-actin monomer concentration and reaches a plateau. Keeping the number of polymerization sites the same, the virtual lamellipodium moves faster at higher G-actin monomer concentration.

In general, the virtual lamellipodium with more polymerization sites and more available G-actin particles has more frequent polymerization events and subsequently generates stronger protrusive force resulting in faster lamellipodium motion because the protrusive force is additive. That is, although the average polymerization rate at each polymerization site is constant for a given simulation, the net protrusive force is obtained from the sum of individual protrusive forces at the polymerization sites. However, if there were too many polymerization sites, such that a large number of G-actin particles were consumed in a short period of time, then the number of available G-actin particles to be polymerized would decrease as would the net polymerization rate normalized for G-actin concentration, defined as the number of polymerization events per time and G-actin monomer concentration, resulting in weak protrusive force in the long term. For this reason, there are an optimal number of polymerization sites for achieving rapid lamellipodium protrusion. The number of available G-actin particles to be polymerized increases with increasing G-actin monomer concentration. The optimal number of polymerization sites or the peak position of maximum speed, therefore, increases with increasing G-actin monomer concentration.

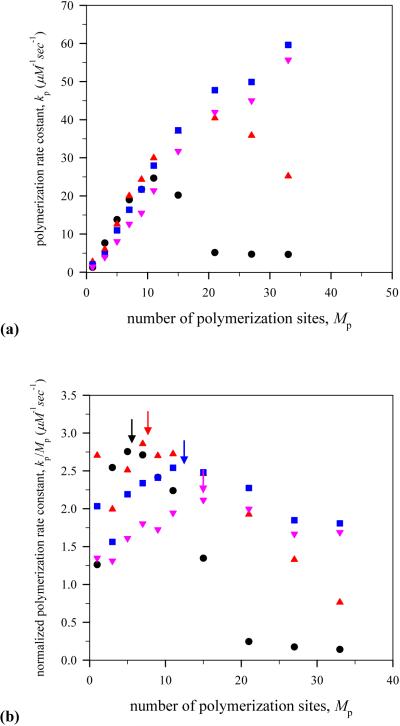
In order for us to see how the mean speed of the virtual lamellipodium is associated with a polymerization rate, the net polymerization rate normalized for G-actin concentration, k_p, as a function of the number of polymerization sites is plotted at different G-actin monomer concentrations in Fig. 7. As seen in Fig. 7 (a), at low G-actin monomer concentrations such as c=24 and 48 μM, the net polymerization rate normalized for G-actin concentration first increases as the number of polymerization sites increases and then decrease at the number of polymerization sites M_p=11 and M_p=21, respectively. On the other hand, at high G-actin monomer concentrations such as c=96 and 192 μM, the net polymerization rate normalized for G-actin concentration continuously increases as the number of polymerization sites increases.

Fig. 7.

(Color online) Dependence of polymerization rate on the number of polymerization sites. (a) net polymerization rate normalized for G-actin concentration, k_p, and (b) polymerization rate constant, $k_p^0$. Notations are the same as in Fig. 6.

The dependence of the net polymerization rate normalized for G-actin concentration on the number of polymerization sites at low G-actin monomer concentrations explains the existence of the optimal number of polymerization sites for rapid lamellipodium protrusion as shown in Fig. 6. However, it is not completely satisfactory because the peak positions showing the maximum net polymerization rate normalized for G-actin concentration are off from those showing the fastest lamellipodium motion in Fig. 6. This is more dramatic in the case of high G-actin monomer concentrations where the continuous increase in the polymerization rate takes place. This discrepancy between the dependence of the mean speed and that of the net polymerization rate normalized for G-actin concentration on the number of polymerization sites can be explained by means of the polymerization rate constant, $k_p^0$, which is obtained by dividing k_p by the number of polymerization sites, M_p, as shown in Fig. 7 (b). Now, the maximum peaks in $k_p^0$ at different G-actin monomer concentrations match well with those of maximum mean speed.

The mean speed of the virtual lamellipodium has two contributions. One is due to a competition between the number of polymerization sites and the number of available G-actin monomers as mentioned earlier and in other literature [32], and the second is as follows: F-actin filaments under polymerization events push the lamellipodium surface outward while other non-polymerizing filaments (fixed in space) pull and hold the lamellipodium surface stalling on lamellipodium protrusion. As a polymerization event rarely occurs at multiple polymerization sites at the same time, the mean speed of the virtual lamellipodium is inversely proportional to the number of polymerization sites. Therefore, the mean speed of the virtual lamellipodium can be expressed as $v_L~k_p^0=k_p∕M_p$. The actin monomer assembly rate constant at the barbed end of lamellipodium or polymerization rate constant, is reported ~ 12 μM^-1sec^-1 [38] which is within our simulation results, 5 ~ 60 μM^-1sec^-1.

In our simulations, protrusive force is generated by the compression of F-actin filaments occurring near the lamellipodium surface. This compression force is opposed by the stiffness of the F-actin filament which is imposed by the bond angle (bending) potential. This process of protrusive force generation is somewhat similar to that of the “Stacked Rubber Band” model [21] where the previously formed layers are compressed by a new polymerized layer at the bacterium surface. However, our model differs from the “Stacked Rubber Band” model which is developed in a continuum (macroscopic) scale in that ours is dealing with protrusive force generation on a microscopic scale.

The protrusive pressure acting on the lamellipodium surface is calculated during simulation runs for the system with parameters c=24μM, M_p=5, and k_angle=100k_BT/rad² and it is 69 k_BT/σ³ or 2 nN/μm² at 298K which is in a good agreement with the experimentally observed values, 2 nN/μm² for keratocytes [39] and ~ 10 nN/μm² for fibroblasts [1].

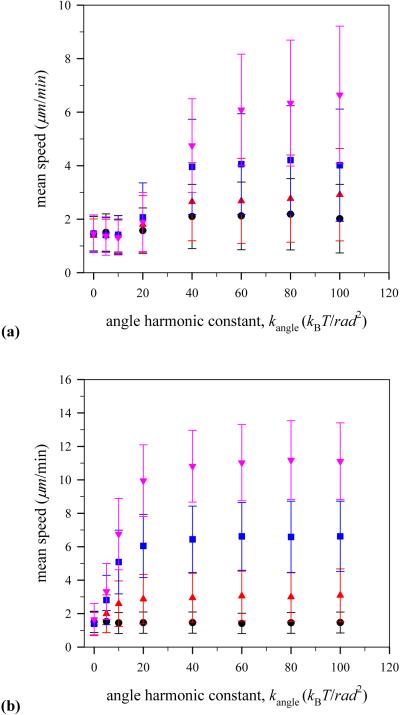
Figure 8 shows how mean speed of the virtual lamellipodium relies on the stiffness of F-actin filament which is described by the angle harmonic constant k_angle in the bond bending energy as seen in Eq. 3. In this case, the intrinsic persistence length is directly proportional to k_angle. The persistence length, L_p, is defined as the length of n filament particles which forms an arc of 1 radian with a bond bending energy of k_BT. From the definition, we define that the intrinsic persistence length is L_p = k_angleσ/k_BT [43]. Thus, in our simulation, L_p varies from 0 to 100σ or 0 - 5.2μm. We note that the maximum persistence length in our simulations is smaller than range of experiment values, 10 - 20μm [26]. However, the fundamental mechanism to generate a protrusive force from stored bending energy does not change.

Fig. 8.

(Color online) Mean speed of the model lamellipodium during simulation runs for different angle harmonic constant k_angle with the number of polymerization sites (a) M_p=3 and (b) M_p=21. Notations are the same as in Fig. 6.

When there are only a few polymerization sites (M_p = 3) on the lamellipodium surface (see Fig. 8 (a)), a F-actin filament with low stiffness k_anlge < 20k_BT/rad² is unable to generate strong enough protrusive force to push the lamellipodium surface outward as can be seen by comparing the mean speed of the virtual lamellipodium in this regime, 1.4 μm/min, with that of the lamellipodium with no polymerization events, 1.5 μm/min. As the F-actin filament becomes stiffer, the model lamellipodium exhibits faster motion and its mean speed reaches a plateau. Interestingly, the mean lamellipodium speed scales with higher G-actin monomer concentrations, and the plateau in the lamellipodium speed plot is also higher. On the other hand, with a large number of polymerization sites (M_p = 21) on the plasma membrane (see Fig. 8 (b)), even an F-actin filament with low stiffness k_anlge < 20k_BT/rad² enables the model lamellipodium to move forward by generating strong enough protrusive force, providing that there are enough available G-actin particles to polymerize with. However, lamellipodium motion at low G-actin monomer concentration such as c = 24μM becomes sluggish at the highest value of angle harmonic constant k_angle = 100k_BT/rad ² in our simulation due to the reduction of polymerization rate per polymerization site as discussed before.

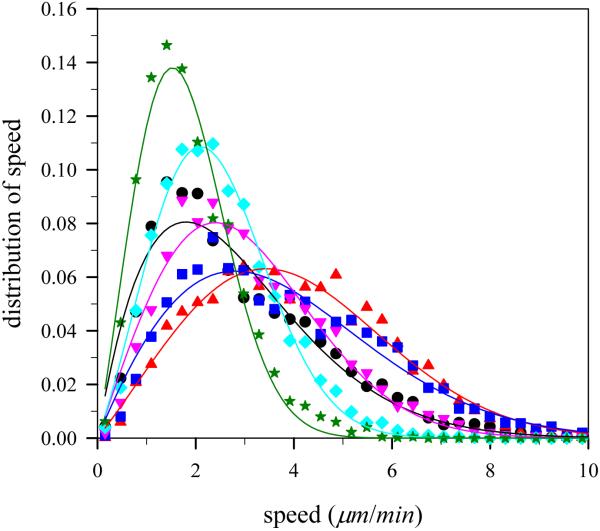
3.4. Distribution of mean speed of virtual lamellipodium

The distribution of lamellipodium speed provides information about distribution of lamellipodium displacement during short period of time. The lamellipodium protrusion by actin polymerization displays saltatory lamellipodium motion, which is defined as irregularly alternating active and passive periods of motion, because the model lamellipodium moves forward when actin polymerization takes place, while it does not move much in a non-polymerizing state. In our simulation, although polymerization takes place within a very short time, one integration time step, it takes some integration time steps for an actin filament to stretch itself out and to push the lamellipodium surface forward in response to the nature of stiff filament. Thus, while a filament pushes the lamellipodium surface forward, the lamellipodium motion is in a non-steady state. For the case of salutatory lamellipodium movement, distribution of lamellipodium displacement or that of lamellipodium speed will exhibit a Poisson distribution if analyzed on time scales short enough to exclude non-steady states of the lamellipodium motion. Although velocity has not been measured for lamellipodia protrusion, distribution of cell velocity was found to follow the Poisson distribution in several cell types using computer controlled video icroscopy [14].

On the other hand, if the fluctuation of lamellipodium displacement was analyzed on a long time scale, then the relative fluctuation in stationary lamellipodium motion would become small and the distribution of lamellipodium speed would follow a Gaussian or Maxwell distribution. In deed, according to the report of Betz et al. [7] on a bistable stochastic process of neuronal growth, distributions of lamellipodium retraction and protrusion are Gaussian. Interestingly, cells in aggregates of neural retinal cells obtained from chicken embryos also showed a Maxwell distribution for the cell velocity [34]. In our simulations, since averaged actin polymerization occurs within a very short time, one integration time step, and trajectories of the center of mass of the virtual lamellipodium were analyzed on a long time scale, ~10⁴ integration time steps, the distribution of lamellipodium speed will be Maxwellian.

Figure 9 shows the distributions of lamellipodium speed with angle harmonic constant k_angle = 100k_BT/rad ² at various number of polymerization sites. In agreement with expectations, the speed distributions obtained from our simulations fit with Maxwell distributions, P(s) = as exp(- bs²) where a and b are fitting parameters and s is the lamellipodium speed. We can determine the most probable speed s_max by differentiating the Maxwell speed distribution and finding its maximum, and find that $s_{\max }={(1∕2b)}^{1∕2}$. In addition, the mean speed 〈s〉 from the Maxwell distribution can be found by integrating sP(s) and is equal to $\langle s\rangle ={(\pi ∕4b)}^{1∕2}$. The root mean square of the speed, $s_{\mathit{rms}}=\sqrt{{\int }_0^{\infty }{s}^{2}P\left(s\right)ds}={(1∕b)}^{1∕2}$, last but not least, is defined as the square root of the average squared speed and can be related to the thermal energy: $s_{\mathit{rms}}^2=2k_{B}T∕m$ by using the energy equipartition theorem in two dimensions. By combining the above two equations, we obtain $b=m∕2k_{B}T$. If $1∕s_{\mathit{rms}}^2$ obtained from the simulation is close to the Maxwell distribution parameter b, then it indicates that the motion of the lamellipodium is in the thermal equilibrium. For the case of M_p = 3 and k_angle = 100k_BT/rad ², the parameter b obtained from fitting the curve is 0.0865min²/μm² and the root mean square of the speed, s_rms, is 3.605 μm/min. Thus $1∕s_{\mathit{rms}}^2=m∕2k_{B}T=0.0769{\min }^2∕\mu m^2$ and this value is close to b = 0.0865min²/μm² confirming that the motion of the model lamellipodium is originating from the collective thermal motion of the individual particles of the lamellipodium exhibiting pseudo-thermal equilibrium. That is, true thermal equilibrium would result in equipartition of the thermal energy, such that $s_{\Vert }^2~s_{\perp }^2$ where ∥ is the direction of the lamellipodium motion and ⊥ is the normal direction to the lamellipodium motion. However, in our case, the lamellipodium motion is biased so that $s_{\Vert }^2\gg s_{\perp }^2$. Note that there are interrelations among three speeds described above. For instance, the ratio of the mean speed to the most probable speed is $\langle s\rangle ∕s_{\max }=\sqrt{\pi ∕2}$ in two dimensions and the obtained ratio 〈s〉/s_max from Fig. 9 is equal to 1.15 which is close to $\sqrt{\pi ∕2}\approx 1.25$ and the typical speeds are related as follows: s_max < 〈s〉 < s_rms.

Fig. 9.

(Color online) Distribution of the model lamellipodium speed at G-actin monomer co ncentration c=48 μM with angle harmonic constant k_angle=100k_BT/rad² at various number of polymerization sites, M_p. Notations are the same as in Fig. 4.

4. Conclusions

We developed a particle-based virtual model lamellipodium where actin polymerization takes place at the interface between plasma membrane and actin filaments. A coarse-grained Langevin dynamics method was applied to this model and successfully showed that this particle-based method could be used to connect between microscopic and macroscopic models of protrusive force generation at the cell leading edge induced by actin polymerization.

We have studied the effect of stiffness of F-actin filament, G-actin monomer concentration, and number of polymerization sites on the protrusion of a virtual model lamellipodium utilizing actin polymerization for its directional motion. When F-actin filaments are firmly attached on the lamellipodium surface, the protrusive force acting on the lamellipodium surface is generated by the growth of F-actin filaments with an imposed bond angle (bending) potential at the interface between the lamellipodium surface and the F-actin filaments. It is found that stiff F-actin filaments, which can store large enough elastic energy during actin polymerization, are necessary to generate protrusive force when G-actin monomer concentration is low, on the other hand, less stiff F-actin filaments can also generate protrusive force if enough G-actin monomers are supplied for actin polymerization.

At the given stiffness of F-actin filaments, the mean speed of the virtual lamellipodium has two contributions: One is due to a competition between the number of polymerization sites and the number of available G-actin monomers and the second is due to a competition between the number of polymerization events pushing the lamellipodium surface forward and the number of non-polymerizing sites holding and preventing the lamellipodium surface from moving forward. Due to those competitions, there exist an optimal number of polymerization sites for rapid lamellipodium protrusion. The lamellipodium protrusion by actin polymerization displays saltatory motion exhibiting pseudo-thermal equilibrium: the lamellipodium speed distribution is Maxwellian in two dimensions but the lamellipodium motion is biased so that the lamellipodium speed in the direction of the lamellipodium motion is much larger than that normal to the lamellipodium motion.

In this paper, we have focused on how a virtual model lamellipodium protrudes by actin polymerization occurring at the cell leading edge. We found that various quantities such as lamellipodium speed, polymerization rate constant, and protrusive pressure are in agreement with observed experimental values although the process of actin polymerization was simplified and modeled by using only two components, G-actin particles and polymerization sites, due to computational complexities. However, it should be noted that other essential proteins for the actin polymerization process such as nucleating and branching complex (Arp2/3), capping proteins, and severing and depolymerizing factor (ADF/cofilin) should be explicitly included in particle-based simulations such as molecular dynamics and Monte Carlo methods in order to get closer to a realistic situation where protrusive force is generated by the formation of branches and crosslinks of actin filaments found in real cells. Nonetheless, the results presented above show how a simple actin polymerization process could generate a protrusive force used for the directional motion of a virtual lamellipodium.