Proton-Coupled Electron Transfer in Photosystem II: Proton Inventory of a Redox Active Tyrosine

Abstract

Photosystem II (PSII) catalyzes the light driven oxidation of water and the reduction of plastoquinone. PSII is a multisubunit membrane protein; the D1 and D2 polypeptides form the heterodimeric core of the PSII complex. Water oxidation occurs at a manganese-containing oxygen evolving complex (OEC). PSII contains two redox active tyrosines, Y_Z and Y_D, which form the neutral tyrosyl radicals, Y_z ^• and Y_D ^•. Y_D has been assigned as tyrosine 160 in the D2 polypeptide through isotopic labeling and site-directed mutagenesis. While Y_D is not directly involved in the oxidation of water, it has been implicated in the formation and stabilization of the OEC. PSII structures have shown Y_D to be within hydrogen bonding distance of histidine 189 in the D2 polypeptide. Spectroscopic studies have suggested that a proton is transferred between Y_D and histidine 189 when Y_D is oxidized and reduced. In our previous work, we used ²H²O solvent exchange to demonstrate that the mechanism of Y_D proton-coupled electron transfer (PCET) differs at high and low pH (Jenson, D. L.; Evans, A.; Barry, B. A. J. Phys. Chem. B 2007, 111, 12599–12604). In this paper, we utilize the proton inventory technique to obtain more information concerning the PCET mechanism at high pH. The hypercurvature of the proton inventory data provides evidence for the existence of multiple, proton donation pathways to Y_D ^•. In addition, at least one of these pathways must involve the transfer of more than one proton.

Photosystem II (PSII) is a thylakoid membrane bound protein that catalyzes the oxidation of water and the reduction of plastoquinone in a four photon mechanism. Electron transfer is initiated through the photooxidation of a chlorophyll molecule. The electron is transferred to a quinone, Q_A, which acts as a one electron acceptor. Q_A ⁻ reduces Q_B, which can accept two electrons and two protons. Two Q_B molecules are reduced during each catalytic cycle of PSII. This process ultimately results in the production of molecular oxygen from water at a manganese-containing oxygen-evolving complex (OEC). PSII is a multisubunit membrane associated complex. The D1 and D2 polypeptides compose the heterodimeric core of PSII (reviewed in ¹).

Two redox active tyrosines are present in PSII.² Y_z is the oxidant for the OEC and is tyrosine 161 of the D1 polypeptide.³ Y_D is tyrosine 160 of the D2 polypeptide.⁴ Despite their symmetrical arrangement in PSII,^5–8 the function and decay kinetics of Y_Z ^• and Y_D ^• are different.⁹ Y_Z ^• decays on the microsecond to millisecond timescale,^10,11 whereas Y_D ^• decays on the minutes to hours time scale.^2,4 Of the two tyrosines, only Y_Z is directly involved in water oxidation.^3,12,13 However, Y_D may be important in the in the assembly¹⁴ and stability¹⁵ of the OEC. There is a large change in the tyrosine pK_a upon radical formation.¹⁶ Singlet tyrosine has a pK_a of ~10 and the phenolic side chain is expected to be protonated at physiological pH. The tyrosyl radical has a pK_a of < 0 and the phenolic side chain is expected to be deprotonated at physiological pH.¹⁶ This change in phenolic pK_a means that redox-active tyrosines participate in proton-coupled electron transfer (PCET) reactions in enzymes.

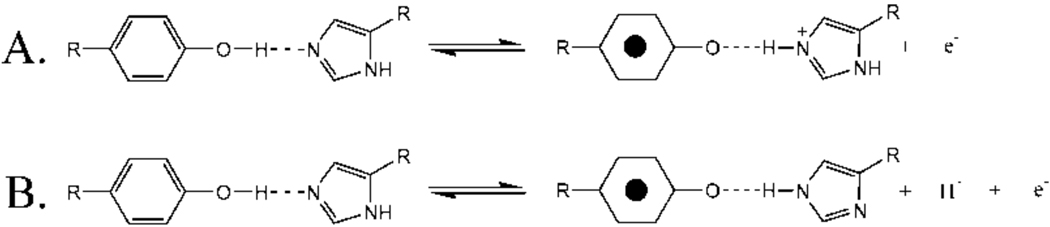
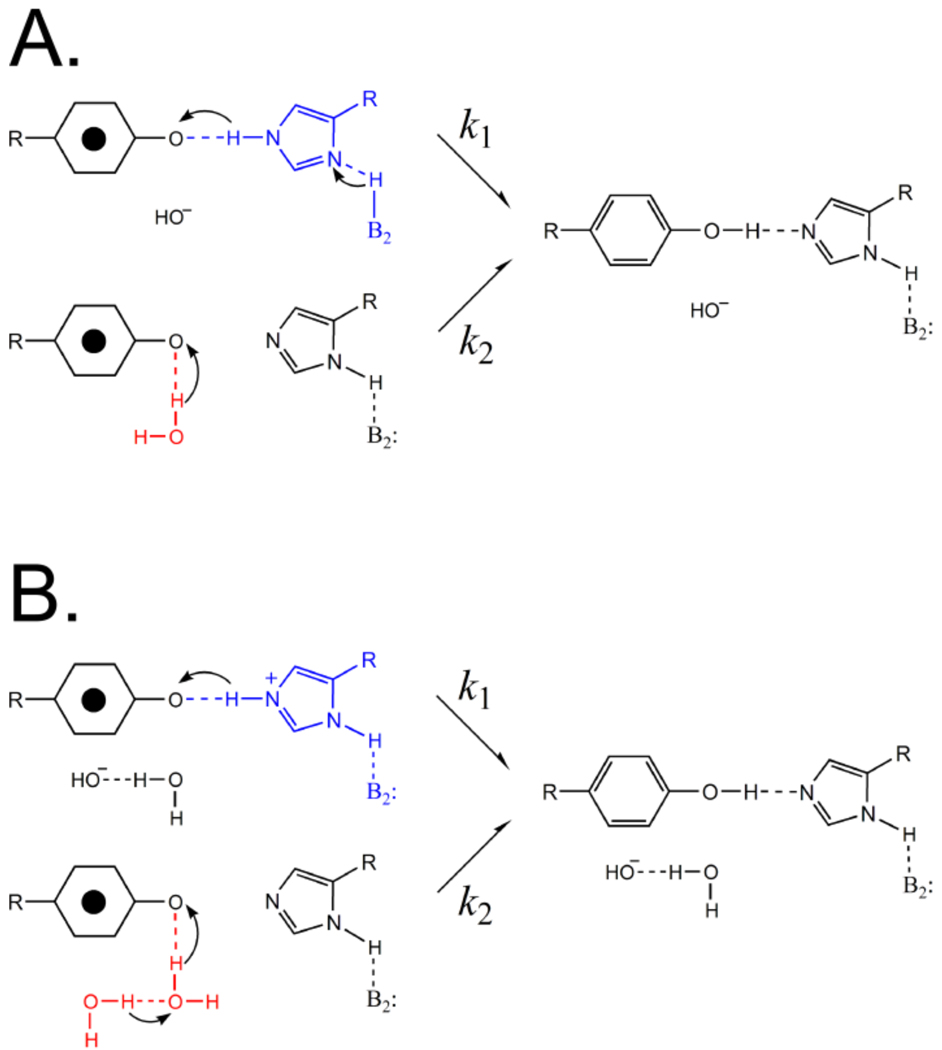
Crystal structures, available from 2.9–3.8 Å, indicate that His189 is within hydrogen bonding distance of Y_D.^5–8 Furthermore, EPR and FT-IR spectroscopy have shown that His189D2 and YD^• are hydrogen bonded and that a proton is transferred between Y_D and His189.^17,18 A one proton rocking mechanism was proposed for this proton-coupled electron transfer reaction.¹⁹ This rocking mechanism is illustrated in Scheme 1. When Y_D is oxidized and the proton is transferred to His189, His189 may retain the proton, become cationic, and then redonate the proton back to the tyrosyl radical when the radical is re-reduced (Scheme 1A). Alternatively (Scheme 1B), histidine may lose the proton to another proton acceptor and become neutral after accepting a proton. Scheme 1B requires that a series of proton accepting molecules participate in the PCET reaction. Because protons are transferred along with the electron, kinetic isotope effects may be observable in either the rocking mechanism (Scheme 1A) or the multiproton pathway (Scheme 1B).

Scheme 1.

Our previous work, utilizing ²H₂O solvent exchange, has established that a solvent isotope effect is observed on the Y_D ^• PCET reactions at some pL values, where L is the lyonium ion. This work showed that the mechanism of Y_D ^• PCET differs at high and low pL.²⁰ In this paper, we examine the effect of varying ¹H₂O:²H₂O ratio on the rate of Y_D ^• reduction at pL 8.0, at which a significant solvent isotope effect was observed. This measurement records a proton inventory, which provides insight into the mechanism of proton transfer reactions and into the number of protons transferred in the rate limiting step of a reaction.^21,22

Materials and Methods

PSII was isolated from market spinach,²³ with the modifications described.²⁴ Oxygen evolution rates were ≥ 600 µmol O₂ (mg chl h)⁻¹.²⁵ The OEC, as well as the 18, 24 and 33 kDa polypeptides, were removed from PSII by treatment with tris(hydroxymethyl)aminomethane (Tris) buffer (final concentration 0.8 M Tris-HCl and 2.0 mM tetrasodium ethylenediaminetetraacetic acid (EDTA) at pH 8.0.²⁶ The pL of the ²H₂O containing buffers is reported as the uncorrected meter reading, because the small, characteristic solvent isotope effect on the pK_a is approximately offset by the ²H₂O-induced change in the response of the glass pH electrode.^{21 2}H₂O exchange was conducted by a method similar to the one previously described.²⁰ The Tris-treated PSII samples were pooled and dialyzed against SHN buffer (50 mM HEPES, 15 mM NaCl, 400 mM sucrose, pL 8.0) containing varying mole fractions of ¹H₂O: ²H₂O. The mole fractions (as ¹H₂O:²H₂O) employed were 100:0, 80:20, 70:30, 60:40, 50:50, 40:60, 30:70 and 0:100 percent. The pL was adjusted using NaO²H dissolved in L₂O with the appropriate ¹H:²H mole fraction. ²H₂O was purchased from Cambridge Isotope Laboratories 99% ²H₂O enrichment, Andover, CA). The two rounds of dialysis (9 h, followed by 16 h) occurred at 4° C in the dark and utilized dialysis membranes (Spectrum, Laguna Hills, CA) with 6–8 kDa cutoff. The volume for each round of dialysis was 500 mL (1:50 dilution). The dialyzed samples were stored at −70° C in 500 µL aliquots until use.

A Bruker EMX X-band electron paramagnetic resonance (EPR) spectrometer equipped with a Bruker ER4119HS cavity was used for EPR analysis.^18,20,27 The cavity was purged with dry nitrogen. The temperature was maintained at 298.1 K using a Bruker ER4131VT variable temperature controller. A Wilmad-Lab Glass (Buena, NJ) WG-808-S-Q small volume flat cell was utilized in all experiments. Chlorophyll concentrations, indicative of Y_D ^• radical concentration,²⁸ were determined before the analysis of each sample. The mean chlorophyll concentration of the PSII samples used in the EPR experiments was 1.86 ± 0.15 mg/mL Because the reduction of the terminal electron acceptor, Q_B, in PSII is associated with proton uptake, all samples contained 10 µM of 3-(3,4-dichlorophenyl)-1,1-dimethylurea (DCMU) to inhibit the formation of Q_B ⁻. The DCMU was delivered from a stock solution dissolved in ethanol, and the total concentration of ethanol in the samples was < 0.5%. The DCMU-induced inhibition of Q_B reduction results in Q_A becoming the terminal PSII electron acceptor. Because the oxidation of Q_A ⁻ is not proton dependent, solvent isotope effects are not expected as a result of Q_A redox chemistry. The microwave power used in these experiments was shown to be non-saturating when compared to a microwave saturation curve²⁹ obtained under the conditions reported here.

The EPR conditions for kinetic traces were as follows: frequency = 9.46 GHz; static field = 3361 ± 1 G; resolution = 8192 points; microwave power = 1.01 mW; receiver gain = 3.56 × 10⁶; modulation frequency = 100 kHz; modulation amplitude = 5.0 G; conversion time = 164 ms; time constant = 5.24 s; analysis time = 1342 s. The PSII samples were excited by 120 flashes at 1 Hz from a Continuum Surelite III (Santa Clara, CA) Nd:YAG laser at the 532 nm second harmonic. The laser intensity was 50 ± 1 mJ/cm². The best fits were to biphasic decay, with one exponential phase giving 89–95% of the amplitude, as determined by the χ² values. The laser beam was expanded by using a cylindrical lens in order to give greater coverage over the sample. Kinetic traces were fit using IGOR Pro software (Lake Oswego, OR). Data analysis began 56 s after the cessation of laser excitation in order to eliminate contributions from Y_Z ^• (τ = 200 ms) and other rapidly decaying radical species.³⁰ Four sets of kinetics were determined on each individual sample, and the kinetics were found to be comparable within each set. Either six or eight samples were analyzed at each ¹H₂O:²H₂O mole fraction, for a total of 24 or 32 individual kinetic traces for each point.

A background signal was subtracted from each kinetic transient. Because the decay of Y_D ^• was not complete between the kinetic traces, due to long half-life of Y_D ^•, an off-resonance scan was taken at a static field, which was −88 G from the field position used to acquire the kinetic transients. This off-resonance scan was taken before each kinetic transient. The off-resonance scan was observed for 336 s, and the mean was subtracted from each point of the following kinetic trace. The EPR conditions for the off-resonance scan were the same as for the kinetic traces, except that the static field was 3273 ± 1 G. At this magnetic field, no free radical resonances were observed.

The EPR conditions for the field swept spectra were as follows: frequency = 9.46 GHz; center field = 3373 G; sweep width = 60 G; resolution = 1024 points; microwave power = 1.01 mW; receiver gain = 3.56 × 10⁶; modulation frequency = 100 kHz; modulation amplitude = 5.0 G; conversion time = 164 ms; time constant = 5.24 s; sweep time = 168 s; sweeps = 6; total time = 1008 s.

Results

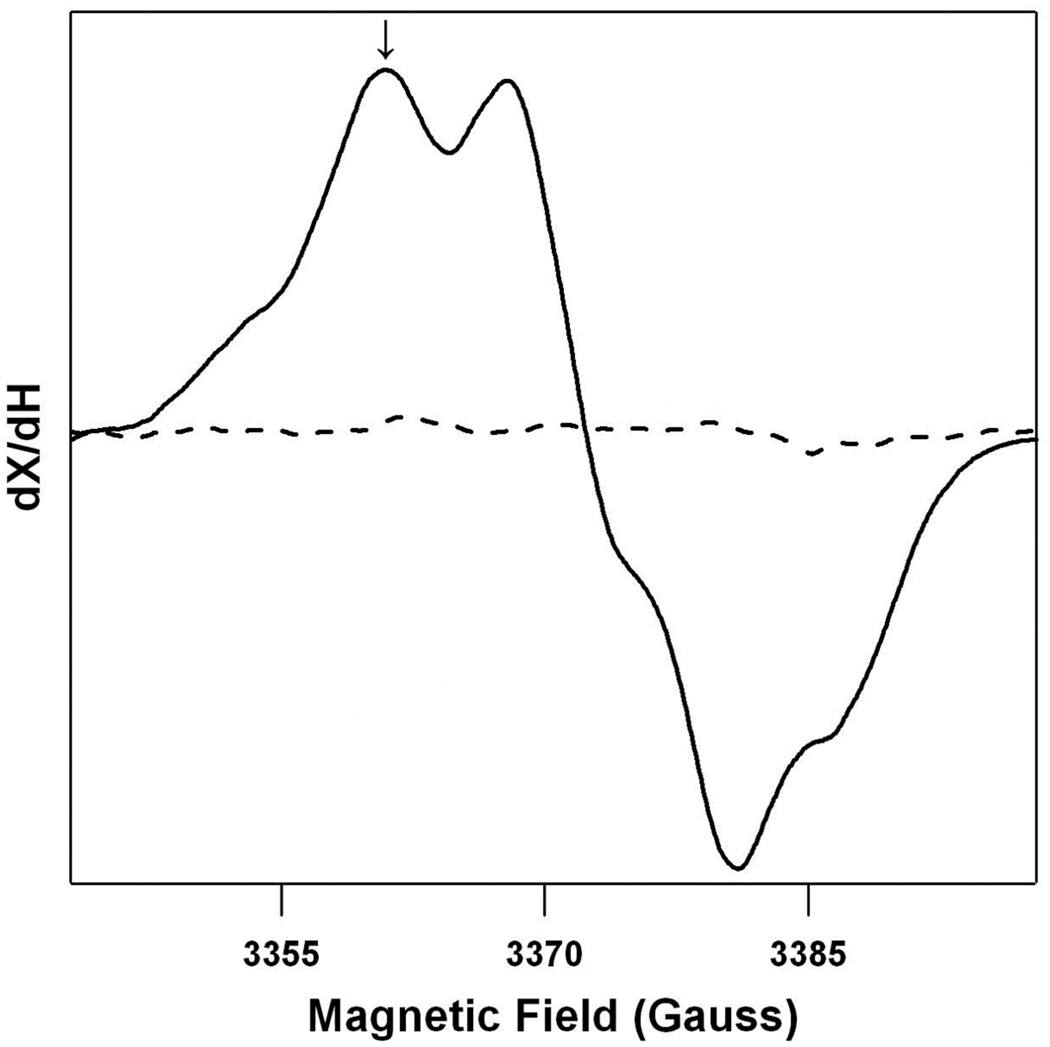
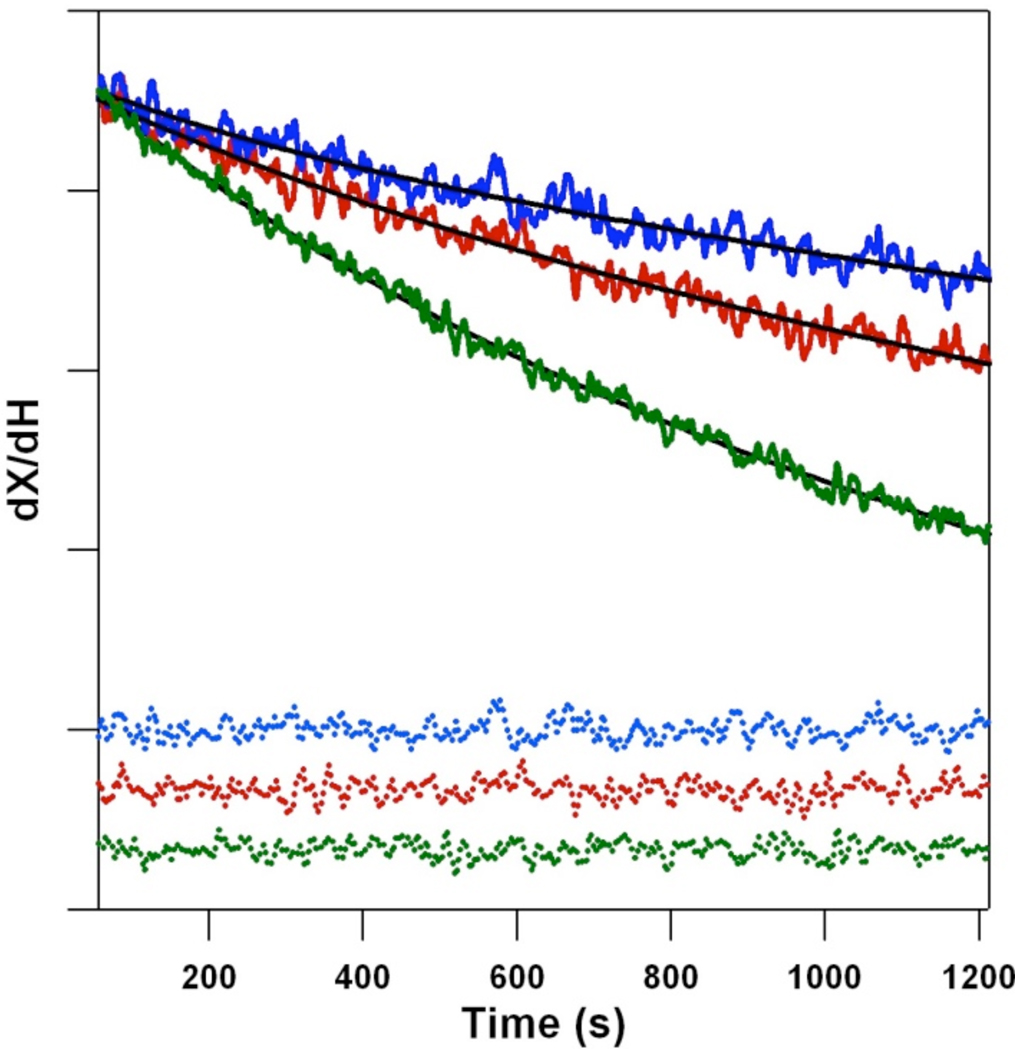
Figure 1 shows a typical field swept EPR spectrum of the dark stable radical, Y_D ^•, in a PSII sample. This spectrum was observed one minute following illumination (solid line) and was not detected in a buffer blank (dotted line). The decay rate of Y_D ^• was monitored after illumination at the indicated field position (Figure 1, arrow and Figure 2). Contributions from Y_Z ^• and fast decaying radicals were avoided by the fitting procedure (see Materials and Methods). Control experiments showed that the derived kinetics of Y_D ^• decay were similar when monitored at other field positions (data not shown). Figure 2 shows representative kinetic traces from a single sample, recorded in 100% ¹H₂O (green), a 50:50% ¹H₂O:²H₂O mixture (red), and 100% ²H₂O (blue). Fits to the data are shown as superimposed solid lines; the residuals are color-coded in dotted lines at the bottom of the figure. As expected from our previous work, the rate of Y_D ^• decay decreases as the ²H₂O concentration increases.

Figure 1.

The field swept EPR spectrum of Y_D ^• in SHN, pH 8.0 buffer (solid line) and a SHN, pH 8.0 buffer blank, which lacks the protein sample (dotted line). The arrow indicates the field position at which the kinetic transients were acquired.

Figure 2.

EPR data showing representative kinetic transients (solid lines) and residuals (dotted lines), associated with the decay of Y_D ^•. The data were acquired in 100% ¹H₂O (green), a 50% ¹H₂O:²H₂O mixture (red), and 100% ²H₂O (blue). The magnetic field was 3361 ± 1 G. Fits to the data at each ²H₂O concentration are shown as black lines. Each kinetic trace is the average of four traces recorded on one sample. To give the final set of kinetic parameters analyzed in Figure 3, Figure 4 and Table 1, data from 6–8 samples were averaged. For presentation purposes only, the transients shown in this figure were normalized to the data at 100% ¹H₂O. The data for the first 56 s, which were excluded from the fits, are not shown. The tick marks correspond to 10,000 ARB.U. See Materials and Methods for experimental conditions.

Table 1 summarizes the derived rate constants and amplitudes for Y_D ^• decay at pL 8.0, as a function of ²H₂O mole fraction. As observed previously, the kinetic fits gave a single majority phase, corresponding to ≥89% of the decay amplitude.²⁰ Additionally, the initial signal amplitude, normalized to chlorophyll concentration, showed no significant variation (Table 1). As expected, the rate of Y_D ^• decay was slow, occurring over the minutes time scale (Figure 2). The derived rate constants were comparable, within a factor of two, to those derived in our earlier work.²⁰ However, compared to our previous work at room temperature, the observed, maximum kinetic isotope effect (KIE) in Table 1 was somewhat larger (3.5 ± 0.5 at 25° C versus 2.4 ± 0.5 at 20° C). This is attributed to a temperature effect on the reaction.³¹

Table 1.

Kinetics of Y_D ^• reduction in ²H₂O, as assessed by EPR spectroscopy.^a

Mole Fraction 2H2O	Rate Constant (10−4 s−1)	Relative Amplitude (%)	EPR Signal Intensityb [ARB.U./(mg chl/mL)]	Rate Relative to 100% 2H2O
0	5.90 ± 0.43	92 ± 4	22600 ± 1600	3.47 ± 0.55 (KIE)
20	4.10 ± 0.73	91 ± 6	21400 ± 970	2.41 ± 0.55
30	3.35 ± 0.39	89 ± 5	23700 ± 2200	1.97 ± 0.36
40	3.13 ± 0.22	94 ± 1	21600 ± 1700	1.84 ± 0.29
50	2.84 ± 0.56	92 ± 2	21500 ± 2200	1.67 ± 0.40
60	2.23 ± 0.60	91 ± 3	21100 ± 1200	1.31 ± 0.40
70	2.57 ± 0.15	94 ± 2	20400 ± 3100	1.51 ± 0.23
100	1.70 ± 0.24	95 ± 3	20300 ± 1600	1.00 ± 0.34

^aThe means are the average of 6–8 samples. The error is reported as ± one standard deviation. All samples contained 10 µM DCMU to inhibit Q_B ⁻ formation. The transients were fit to a biexponential decay using IGOR Pro software (Wavemetrics, Lake Oswego, OR). The quality of the least squares fit was determined by the χ² value.

^bSignal intensity at 56 s, in arbitrary units.

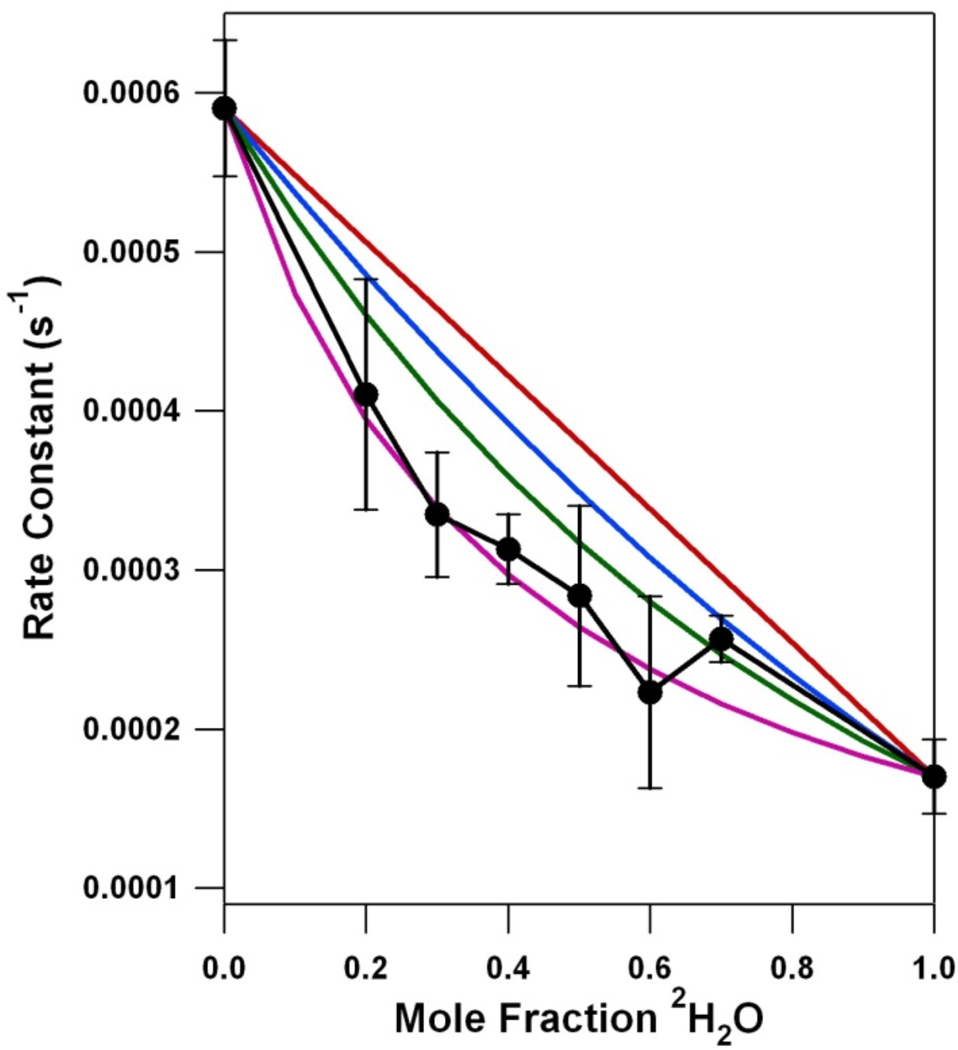
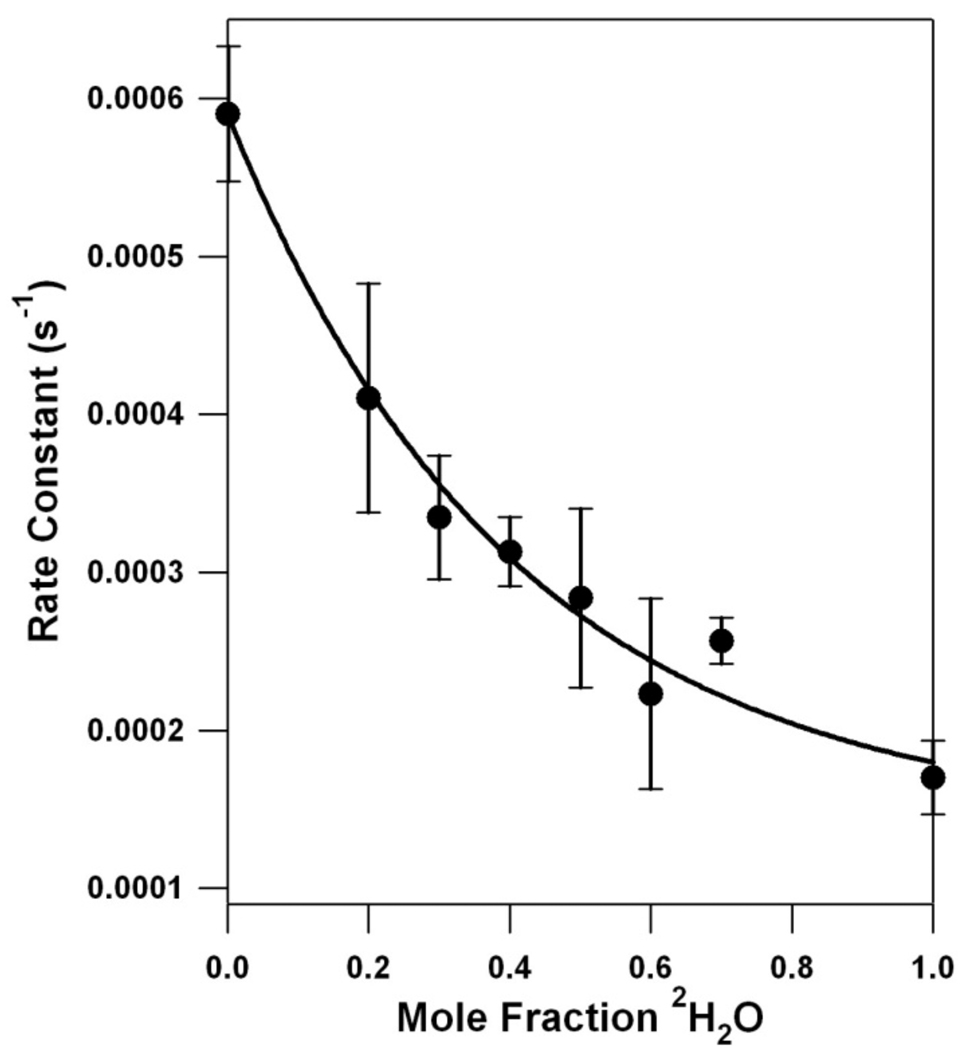
Figure 3 presents the derived rate constant for Y_D ^• decay as a function of increasing ²H₂O mole fraction. The data show a nonlinear dependence. This effect is not caused by a limitation of ²H exchange. Previous studies have shown that the exchange of the Y_D phenoxyl proton occurs with a half-life of approximately 9 h at pL 7.0.³² Given that the conditions employed here utilize higher pL (8.0), our total dialysis time of 25 h is sufficient for complete ²H exchange in the Y_D pocket.

Figure 3.

Proton inventory for the Y_D ^• PCET reaction at pL 8.0. The black line is the experimental data, showing the dependence of rate constant on mole fraction ²H₂O, as assessed by transient EPR spectroscopy. The kinetic parameters are shown in Table 1. The error bars represent one standard deviation. The red line simulates a one proton, transition state proton inventory. The blue line simulates a two proton, transition state proton inventory. The green line simulates a “many proton” inventory. The purple line, an example of hypercurvature, simulates a one proton, reactant state proton inventory. See Table 2 for the parameters and equations employed to simulate the proton inventory data.

For comparison with the data, Figure 3 shows simulations, illustrating the expected plots for a one (red), two (blue), and “many proton” (green) transfer in the transition state.^21,22 The relation between rates, fractionation factors and the mole fraction deuterium in the solvent is given by the Gross-Butler equation,

$${\mathrm{v}}_{\mathrm{n}}={\mathrm{v}}_0*\frac{{\displaystyle \prod _i(1-\mathrm{n}+\mathrm{n}{\varphi }_{\mathrm{T}i})}}{{\displaystyle \prod _j(1-\mathrm{n}+\mathrm{n}{\varphi }_{\mathrm{R}j})}}$$

where n is the mole fraction of ²H₂O; v_n is the rate constant at mole fraction n; v₀ is the rate constant in pure ¹H₂O; the products, i and j, are over the number of protons transferred in the transition and reactant state, respectively; ϕ_T is the transition state fractionation factor; and ϕ_R is the reaction state fractionation factor. Fractionation factors measure the preference of a particular site for deuterium relative to a bulk water molecule.^21,22 The kinetic isotope effect (KIE) is defined as KIE = k_H/k_D = ϕ_R/ϕ_T, where k_D is the rate constant in ²H₂O and k_H is the rate constant in ¹H₂O. If it is assumed that the reactant state fractionation factor is equal to one, the denominator in the Gross-Butler equation reduces to unity and only the numerator remains.^21,22 This assumption is usually valid in proteins, as most protonic sites in proteins (including carboxylic acid, imidazole, amine and hydroxyl functional groups) have reactant state fractionation factors that are near unity.³³ The sulfhydyl group is known to have a reactant state fractionation factor that is not unity (ϕ_R = 0.55), but we do not expect proton donation from cysteine in our proton inventory experiments.^5–8

If one proton is transferred in the transition state, a linear plot results when the rate is plotted against mole fraction ²H₂O (Table 2). A two proton transfer in the transition state, assuming equal fractionation factors for the two events, results in a quadratic plot. Curves of cubic and higher order have been previously derived for an exponential “many proton” model.^21,22 The proton inventory experiment lacks the resolution to differentiate between models in which three or more protons are being transferred. It is not usually possible to know the individual fractionation factors when two or more protons are transferred, so an average fractionation factor value is usually assigned.

Table 2.

Simulation parameters for models presented in Figure 3 and Figure 4.

Plot Type	v0	v100	ϕT1	ϕT2	ϕR	Equation*
One Protona	0.000590	0.000170	0.288	NA	1.00	vn = v0 * (1−n + 0.288n)
Two Protona	0.000590	0.000170	0.288	NA	1.00	${\mathrm{v}}_{\mathrm{n}}={\mathrm{v}}_0*{(1-\mathrm{n}+\mathrm{n}\sqrt{0.288})}^2$
Many Protona	0.000590	0.000170	0.288	NA	1.00	vn = v0*(0.288)n
Reactant Statea (Hypercurvature)	0.000590	0.000170	1.00	NA	3.47	vn = v0*(1−n + 3.47n)−1
Multipathwayb (Hypercurvature )	0.000590	0.000170	0.083	0.97	1.00	vn = v0*[0.75*(0.083)n + 0.25*(1−n + 0.97n)]

^*

The relation between rates, fractionation factors and the mole fraction deuterium in the solvent is given by the Gross-Butler equation,

$${\mathrm{v}}_{\mathrm{n}}={\mathrm{v}}_0*\frac{{\displaystyle \prod _i(1-\mathrm{n}+\mathrm{n}{\varphi }_{\mathrm{T}i})}}{{\displaystyle \prod _j(1-\mathrm{n}+\mathrm{n}{\varphi }_{\mathrm{R}j})}}$$

where n is the mole fraction of ²H₂O; v_n is the rate constant at mole fraction n; v₀ is the rate constant in pure ¹H₂O; the products, i and j, are over the number of protons transferred in the transition and reactant state, respectively; ϕ_T is the transition state fractionation factor; and ϕ_R is the reaction state fractionation factor. The kinetic isotope effect (KIE) is defined as KIE=k_H/k_D=ϕ_R/ϕ_T, where k_D is the rate constant in ²H₂O and k_H is the rate constant in ¹H₂O. In the multipathway model, 0.75 represents the fractional contribution to the rate from ϕ_T1 and 0.25 represents the fractional contribution to the rate from ϕ_T2.

^aModels presented in Figure 3.

^bModel presented in Figure 4.

Figure 3 shows that a plot of Y_D ^• decay rate versus ²H₂O mole fraction exhibits hypercurvature, that is, the data points fell below the rate constants predicted for the “many proton” (Figure 3, green line), two proton (Figure 3, blue line), and one proton (Figure 3, red line) reactions. The hypercurvature in the proton inventory data could be fit well with two different models (Table 2). In the first “reactant state model,” the KIE is solely attributable to one proton being transferred in the reactant state, when the transition state fractionation factor is equal to unity (Figure 3, purple line). In the second “multipathway model,” there is more than one proton donor to Y_D ^• (Figure 4). The parameters used to fit these models to the data are presented in Table 2.

Figure 4.

Simulation of the proton inventory for Y_D ^• using a multipathway model (black line). The experimental data are shown as black dots and are repeated from Figure 3. The error bars represent one standard deviation. See Table 2 for the parameters and equations employed.

Scatter plots of the theoretical rate constant versus the experimental rate constant for each model were constructed (data not shown). The one proton, reactant state model gave a correlation coefficient of 0.991, a slope of 1.01 and a y-intercept of 0.000. The multipathway model gave a correlation coefficient of 0.990, a slope of 0.999 and a y-intercept of 0.000. Therefore, both models are highly correlated with the experimental data. The implications are discussed below.

Discussion

The proton inventory technique

The proton inventory technique monitors the number of protons transferred in the rate limiting step of an enzymatic reaction.²² When the reactant state fractionation factor, ϕ_R, is one and the denominator of the Gross-Butler equation is unity, the equation predicts a linear proton inventory if one proton is transferred (Figure 3, red line; and Table 2). For example, many serine proteases exhibit one proton, transition state proton inventories,^22,34 due to the abstraction of a single serine proton by imidazole during the rate-limiting step.²² A linear proton inventory would be expected in the rocking model for Y_D/His189D2 PCET (Scheme 1A). In this case, the KIE would be expected to be generated through a single proton transfer in the transition state.²²

On the other hand, a quadratic dependence in a proton inventory experiment indicates that two protons are being transferred in the rate limiting step (Figure 3, blue line; and Table 2). Generally, the individual values of ϕ_T are not known and (1/KIE)^1/2 is assigned as an average value.^21,22 For example, ribonuclease A gives a two proton, transition state proton inventory.³⁵ The rate limiting, concerted transfer occurs when the phosphodiester bond is cleaved by the donation of a proton from histidine and the abstraction of the second proton from water.³⁵

A proton inventory experiment normally lacks the resolution to differentiate between mechanisms transferring more than two protons in the rate limiting step.²² Curves of cubic and higher order are usually separated by an amount less than the error in measurement.²² As a consequence, when more than two protons are transferred in the rate limiting step, the mechanism is described as “many proton” and is modeled with an exponential dependence (Figure 3, green line).^21,22 Again, the individual values of ϕ_T are not usually known and 1/KIE is taken as the average fractionation factor.^21,22 An example of this type of proton inventory occurs in carbonic anhydrase,³⁶ in which a coordinated zinc ion transfers a proton to a histidine via a water transport chain.³⁶

As the number of protons transferred grows large, transition state fractionation factors approach unity.^22,36 This “infinite site” model can result from conformational or charge distribution changes in solvating water molecules.^22,36

Hypercurvature in the proton inventory experiment

The interpretations described above apply if the reactant state fractionation factors are equal to unity (i.e., the kinetic isotope effect is generated in the transition state) and if one step in the reaction is rate-limiting.³⁷ If these conditions are not met, more complex proton inventory plots are obtained. Figure 3 shows that the Y_D ^• proton inventory data exhibit hypercurvature and bow below the predicted many proton, exponential plot (Figure 3, green line).²² A proton inventory experiment exhibits hypercurvature either when proton transfer occurs in the reactant state (reactant state model), not in the transition state (reactant state model), or when there are multiple pathways for proton transfer (multipathway model). The hypercurvature, observed in the Y_D ^• proton inventory data (Figure 3), indicates that Y_D ^• PCET is more complex than a one proton, rocking mechanism (Scheme 1A).

Reactant state model

The first explanation for hypercurvature occurs when the KIE results from a reactant state proton transfer reaction.²² Figure 3 (Figure 3, purple line and Table 2) shows that a model with a significant reaction state fractionation factor (3.47) and a transition state fractionation factor of one fits the Y_D ^• proton inventory data. However, the magnitude of the required reactant state fractionation factors must be reasonable. To explain our data, ϕ_R must be at least 3.47 (Table 1 and Table 2), if a single reactant state proton is transferred in the rate limiting step. ϕ_R must be at least (3.47)^1/2 = 1.86, if two reactant state protons are transferred in the rate limiting step. These ϕ_R values are too large to be realistic, because reactant state fractionation factors are in the range of 0.4–1.3 and are usually assumed to be unity.³⁸ There are only a few cases in enzymes where the reaction state fractionation factors differ significantly from unity and rarely is the value greater than one.³⁸ Significant reactant state fractionation factors in enzymes usually occur through interactions with cysteine (ϕ_R = 0.55), metal-bound waters (ϕ_R = 0.4–0.8), and hydronium (ϕ_R = 0.69).³⁸ Given the magnitude of the reaction state fractionation factor required to model our data (Table 2), we conclude that the hypercurvature is unlikely to result from reactant state proton transfer.

Multipathway model

The second possible explanation for hypercurvature is the existence of multiple proton donation pathways.²² For example, in a system in which there are two parallel pathways for proton transfer (Figure 5), k_obs is the sum of the two rate constants, k₁ + k₂. Substituting in the Gross-Butler equation, assuming that the reactant state fractionation factors are unity, and accounting for the relative contribution of k₁ and k₂ in k_obs the following can be derived:

$${\mathrm{v}}_{\mathrm{n}}={\mathrm{v}}_0*[{{\mathrm{f}}_1}^{*}{\displaystyle \prod _i(1-\mathrm{n}+\mathrm{n}{\varphi }_{\mathrm{T}i})+(1-{\mathrm{f}}_1{)}^{*}{\displaystyle \prod _j(1-\mathrm{n}+\mathrm{n}{\varphi }_{\mathrm{T}j})]}}$$

where f₁ equals the fractional contribution to k_obs from k₁ and (1-f₁) equals the fractional contribution to k_obs from k₂. It is important to note that if both parallel pathways involve only one proton, then only a linear proton inventory will result, because the sum of two lines gives a linear slope. Therefore, to explain proton inventory hypercurvature, at least one of the pathways must involve the transfer of multiple protons in the transition state.

Figure 5.

Schematic of two possible proton donation pathways for Y_D ^•. The straight arrows indicate electron transfer. The curved arrows indicate proton, not electron, movement. In (A), His189D2 (reaction k₁, blue) is involved in a multiple proton pathway, which must involve three or more protons, of which two are shown. An internal water molecule (reaction k₂, red) acts as a single proton donor. Alternatively, in (B), His189D2 (reaction k₁, blue) acts as a single proton donor, and a chain of internal water molecules (reaction k₂, red), of which two are shown, is involved in a multiple proton pathway.

Evidence for multiple proton donation pathways to Y_D ^• in PSII

The literature provides evidence for a proton acceptor for Y_D other than His189D2. In a His189Leu site-directed mutant, an EPR signal attributable to Y_D ^• was detected, and the decay of this signal showed the unusually slow reduction kinetics of Y_D ^•.¹⁸ Upon rescue with imidazole, the yield of Y_D ^• was increased, and its decay rate was accelerated to a value similar to that seen in the wild-type.¹⁸ It has also been demonstrated that Y_D ^• is able to form in His189Gln mutants.³⁹ In that work, the observed Y_D ^• g_x tensor component of 2.00832 indicated that Y_D ^• was a neutral radical,³⁹ as opposed to the low g_x value (< 2.0045) that would be expected for a phenoxyl radical cation.^40,41 The observation of a neutral tyrosyl radical in the His189Gln mutant indicates that there is a proton acceptor other than His189D2 for Y_D.

Parameters for a Y_D ^• multipathway proton transfer model

As shown in Figure 4, a multiproton, parallel transfer pathway can explain hypercurvature in our proton inventory experiment. To fit the data in Figure 4, the first proton donation pathway is modeled as a “many proton” pathway in 75% abundance with a transition state fractionation factor of 0.083 (Table 2). The exact number of protons transferred cannot be determined in a “many proton” model. We can only determine that the number of protons being transferred is greater than or equal to three. A three proton model would predict a fractionation factor of (0.083)^1/3 (KIE =2.3), and a four proton model would produce four equivalent fractionation factors of (0.083)^1/4 (KIE = 1.8). These are reasonable KIE values for biological systems. Alternatively, a solvent effect, with fractionation factors near unity, may occur. However, there is sufficient evidence to support a multiproton pathway consisting either of His189D2 or a chain of water molecules.

To fit the hypercurvature in Figure 4, a second proton donation pathway must also be included. We have modeled this second pathway as a one proton, transition state pathway in 25% abundance (Table 2) with a small transition state fractionation factor of 0.97. It should be noted that, while the set of parameters shown in Table 2 adequately represent the data, our fitting procedure does not establish that this combination of parameters is a unique fit to the data.

Possible identities of PSII proton donors on the multipathway model

The model above proposes that there are two pathways of proton donation to Y_D ^•, one involving multiple protons and one involving a single proton. Possible assignment of proton donors on the two pathways are illustrated in Figure 5A and B. In Figure 5A, the multiple proton pathway is proposed to involve His189D2 (Figure 5A) and other amino acid residues, and in Figure 5B, the multiple proton pathway is proposed to involve a chain of water molecules (Figure 5B).

When Y_D ^• is reduced, the histidine may donate a proton to the tyrosyl radical and then accept a proton from other nearby bases (Figure 5A). Although histidine pK_a values are usually ~6 in proteins, the local protein environment can dramatically shift pK_a values. Alternatively, there may be no subsequent protonation of the histidine, and then His189D2 would be involved as a one proton relay (Figure 5B).

The PSII literature provides support for the idea of a multiple proton pathway involving His189D2 (Figure 5A).^40–44 For example, it was reported that the value of the Y_D ^• g_x tensor component was 2.00643 when Y_D ^• was generated cryogenically at alkaline pH. When the radical is generated at physiological temperature, the g_x tensor component is 2.00756.⁴² The lower g_x component may be consistent with an electropositive environment near Y_D ^•, such as an imidazolium cation.^40–42,45 One explanation for the thermal g_x shift is a relaxation of the protein and the subsequent deprotonation of His189D2.⁴²

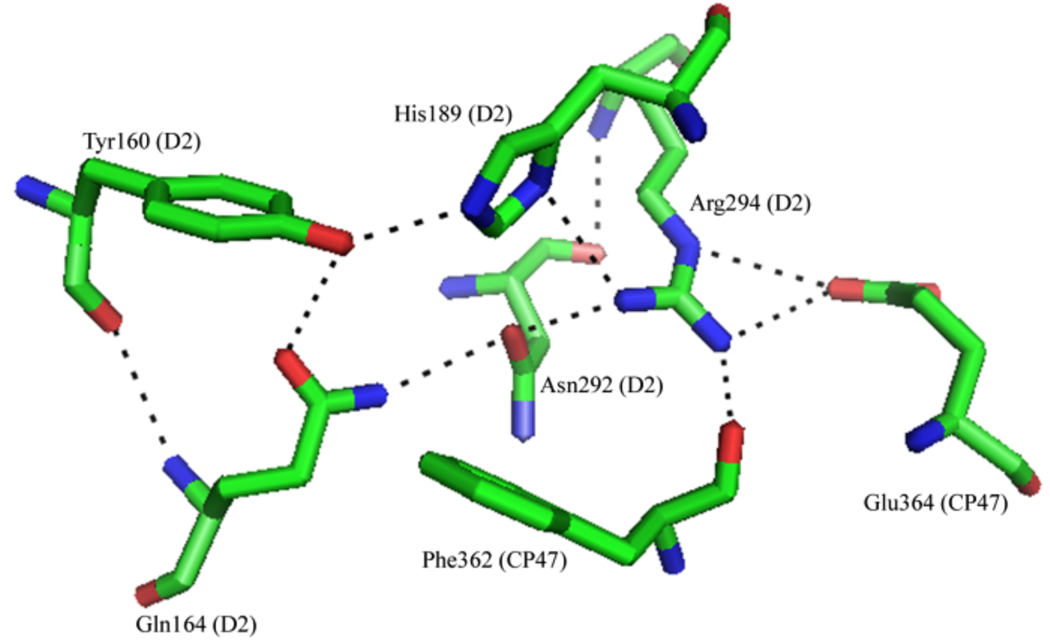
If the His189D2 proton transfer pathway is multiproton (Figure 5A), the identity of the second proton donor to His189D2 is of interest. PSII crystal structures (Figure 6) indicate that Arg294D2 is 2.8 ± 0.4 Å from the π-nitrogen of His189D2 and may be able to act as a proton donor to His189D2.^5–8 However, such a reaction would require a pK_a shift of 4–5 orders of magnitude for the arginine and histidine residues. This change in pK_a may be unlikely, but could possibly be achieved as a result of the relatively hydrophobic nature of the Y_D pocket^5–8 or as a result of electrostatic interactions near Arg294. Further reinforcing the importance of Arg294D2, a Arg294Trp mutant was shown to be unable to grow photoautotrophically and was quickly deactivated by light.⁴⁶ However, the reason for the mutant’s inability to grow photoautotrophically may be structural,⁴⁶ because Arg294D2 sits at the interface of the D2 and CP47 subunits and is presumed to be within hydrogen bonding distance of Glu364CP47.^5–8

Figure 6.

X-ray structure of PSII at 3.0 Å, showing the local environment of Y_D (pdb entry 2AXT⁵).

If the His189D2 pathway involves only a single proton, then the competing pathway must involve multiple protons to fit our data (Figure 5B). The proton donating groups on the second parallel pathway may be bound water molecules (Figure 5B, reaction 2), because the Y_D pocket has been shown to be accessible to the surrounding media. For example, it was reported that at least two water molecules are structurally coupled to Y_D, either through a direct hydrogen bond or within the hydrogen bond network around Y_D (Figure 6).⁴⁷ However, it should be noted that the environment of Y_D ^• can be altered by ionic interactions.⁴⁸ Second, an exchangeable proton that is hydrogen bonded to the phenolic oxygen of Y_D ^• has been detected.^32,49 Finally, it is has been demonstrated that imidazole can be exchanged into the region surrounding Y_D in a site-directed mutant.¹⁸

Proton transfer mechanism at low pH

In our earlier work, we determined that Y_D ^• reduction occurs through two different mechanisms at high and low pL.²⁰ In the acidic pL region, the mechanism was proposed to be a pre-equilibrium proton transfer reaction, followed by an electron transfer reaction (PTET mechanism).²⁰ The smaller KIE observed at low pL was attributed to a small ΔpK_a shift (~0.5 units), which occurs in weak acids due to ²H₂O substitution. The determination of the number of protons transferred at acidic pL is inaccessible to the proton inventory technique, due to the small KIE observed in that region.^20–22 At alkaline pL, the larger KIE led to a proposal of a coupled proton-electron transfer (CPET) mechanism.²⁰

Summary

We present data showing that Y_D ^• PCET is more complex than previously suggested, at least at high pH values. To explain our data, multiple PCET pathways must exist at pL 8.0. Also, at least one of these pathways must involve multiple proton transfer reactions. We propose that one PCET pathway involves His189D2, wand that the second PCET pathway involves water as the proton donor.

Abbreviations

ARB. U

Arbitrary units

DCMU

3-(3,4-dichlorophenyl)-1,1-dimethylurea

EPR

electron paramagnetic resonance

FT-IR

Fourier transform infrared

OEC

oxygen-evolving complex

KIE

kinetic isotope effect

PSII

Photosystem II

PCET

proton-coupled electron transfer

SHN

pL 8.0 buffer (400 mM sucrose, 50 mM HEPES, 15 mM NaCl)

Tris

Tris(hydroxymethyl)aminomethane

HEPES

4-(2-Hydroxyethyl)piperazine-1-ethanesulfonic acid