A Design-Adaptive Local Polynomial Estimator for the Errors-in-Variables Problem

Abstract

Local polynomial estimators are popular techniques for nonparametric regression estimation and have received great attention in the literature. Their simplest version, the local constant estimator, can be easily extended to the errors-in-variables context by exploiting its similarity with the deconvolution kernel density estimator. The generalization of the higher order versions of the estimator, however, is not straightforward and has remained an open problem for the last 15 years. We propose an innovative local polynomial estimator of any order in the errors-in-variables context, derive its design-adaptive asymptotic properties and study its finite sample performance on simulated examples. We provide not only a solution to a long-standing open problem, but also provide methodological contributions to error-invariable regression, including local polynomial estimation of derivative functions.

1. INTRODUCTION

Local polynomial estimators are popular techniques for nonparametric regression estimation. Their simplest version, the local constant estimator, can be easily extended to the errors-in-variables context by exploiting its similarity with the deconvolution kernel density estimator. The generalization of the higher order versions of the estimator, however, is not straightforward and has remained an open problem for the last 15 years, since the publication of Fan and Truong (1993). The purpose of this article is to describe a solution to this longstanding open problem: we also make methodological contributions to errors-in-variable regression, including local polynomial estimation of derivative functions.

Suppose we have an iid sample (X₁, Y₁), …, (X_n, Y_n) distributed like (X, Y), and we want to estimate the regression curve m(x) = E(Y|X = x) or its νth derivative m^(ν)(x). Let K be a kernel function and h > 0 a smoothing parameter called the bandwidth. When X is observable, at each point x, the local polynomial estimator of order p approximates the function m by a pth order polynomial $m_p(z)\equiv {\sum }_{k=0}^p{\beta }_{x,k}{(z-x)}^k$, where the local parameters β_x = (β_x,0, …, β_x,p) are fitted locally by a weighted least squares regression problem, via minimization of

$$\sum _{j=1}^n{[Y_j-m_p(X_j)]}^2{K}_h(X_j-x),$$ (1)

where K_h(x) = h⁻¹K(x/h). Then m(x) is estimated by m̂(x) = β̂_{x, 0} and m^(ν)(x) is estimated by ${\widehat{m}}_p^{(v)}(x)=v!{\widehat{\beta }}_{x,v}$ (see Fan and Gijbels 1996). Local polynomial estimators of order p > 0 have many advantages over other nonparametric estimators, such as the Nadaraya-Watson estimator (p = 0). One of their attractive features is their capacity to adapt automatically to the boundary of the design points, thereby offering the potential of bias reduction with no or little variance increase.

In this article, we consider the more difficult errors-in-variables problem, where the goal is still to estimate the curve m(x) or its derivative m^(ν)(x), but the only observations available are an iid sample (W₁, Y₁), …, (W_n, Y_n) distributed like (W, Y), where W = X + U with U independent of X and Y. Here, X is not observable and instead we observe W, which is a version of X contaminated by a measurement error U with density f_U. In this context, when p = 0, m_p(X_j) = β_x,0, and a consistent estimator of m can simply be obtained after replacing the weights K_h(X_j − x) in (1) by appropriate weights depending on W_j (see Fan and Truong 1993). For p > 0, however,

$$m_p(X_j)=\sum _{k=0}^p{\beta }_{x,k}{(X_j-x)}^k$$

depends on the unobserved X_j. As a result, despite the popularity of the measurement error problem, no one has yet been able to extend the minimization problem (1) and the corresponding local pth order polynomial estimators for p > 0 to the case of contaminated data. An exception is the recent article by Zwanzig (2007), who constructed a local linear estimator of m in the context where the U_i’s are normally distributed, the density of the X_i’s is known to be uniform U[0, 1], and the curve m is supported on [0, 1].

We propose a solution to the general problem and thus generalize local polynomial estimators to the errors-in-variable case. The methodology consists of constructing simple unbiased estimators of the terms depending on X_j, which are involved in the calculation of the usual local polynomial estimators. Our approach also provides an elegant estimator of the derivative functions in the errors-in-variables setting.

The errors-in-variables regression problem has been considered by many authors in both the parametric and the non-parametric context. See, for example, Fan and Masry (1992), Cook and Stefanski (1994), Stefanski and Cook (1995), Ioannides and Alevizos (1997), Koo and Lee (1998), Carroll, Maca, and Ruppert (1999), Stefanski (2000), Taupin (2001), Berry, Carroll, and Ruppert (2002), Carroll and Hall (2004), Staudenmayer and Ruppert (2004), Liang and Wang (2005), Comte and Taupin (2007), Delaigle and Meister (2007), Hall and Meister (2007), and Delaigle, Hall, and Meister (2008); see also Carroll, Ruppert, Stefanski, and Crainiceanu (2006) for an exhaustive review of this problem.

2. METHODOLOGY

In this section, we will first review local polynomial estimators in the error-free case to show exactly what has to be solved in the measurement error problem. After that, we give our solution.

2.1 Local Polynomial Estimator in the Error-free Case

In the usual error-free case (i.e., when the X_i’s are observable), the local polynomial estimator of m^(ν)(x) of order p can be written in matrix notation as

$${\widehat{m}}_p^{(\nu )}(x)=\nu !{\mathit{e}}_{\nu +1}^{\top }{({\mathit{X}}^{\top }\mathit{KX})}^{-1}{\mathit{X}}^{\top }\mathit{Ky},$$

where ${\mathit{e}}_{\nu +1}^{\top }=(0,\dots ,0,1,0,\dots ,0)$ with 1 on the (ν + 1)th position, y^⊤ = (Y₁, …, Y_n), X = {(X_i − x)^j}_{1≤i≤n,0≤j≤p} and K = diag{K_h(X_j − x)} (e.g., see Fan and Gijbels (1996, p. 59).

Using standard calculations, this estimator can be written in various equivalent ways. An expression that will be particularly useful in the context of contaminated errors, where we observe neither X nor K, is the one used in Fan and Masry (1997), which follows from equivalent kernel calculations of Fan and Gijbels (1996, p. 63). Let

$${\mathit{S}}_n=\left(\begin{array}{ccc}{S}_{n,0}(x)& \dots & S_{n,p}(x)\\ ⋮& \ddots & ⋮\\ S_{n,p}(x)& \dots & S_{n,2p}(x)\end{array}\right),{\mathit{T}}_n=\left(\begin{array}{c}{T}_{n,0}(x)\\ ⋮\\ T_{n,p}(x)\end{array}\right),$$

where

$$\begin{array}{l}{S}_{n,k}(x)=\frac{1}{n}\sum _{j=1}^n{\left(\frac{X_j-x}{h}\right)}^k{K}_h(X_j-x),\\ T_{n,k}(x)=\frac{1}{n}\sum _{j=1}^n{Y}_j{\left(\frac{X_j-x}{h}\right)}^k{K}_h(X_j-x).\end{array}$$

Then the local polynomial estimator of m⁽ⁿ⁾(x) of order p can be written as

$${\widehat{m}}_p^{(\nu )}(x)=\nu !h^{-\nu }{\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}_n^{-1}{\mathit{T}}_n.$$

2.2 Extension to the Error-case

Our goal is to extend ${\widehat{m}}_p^{(\nu )}(x)$ to the errors-in-variables setting, where the data are a sample (W₁, Y₁), …, (W_n, Y_n) of contaminated iid observations coming from the model

$$\begin{array}{l}{Y}_j=m(X_j)+{\eta }_j,W_j=X_j+U_j,E({\eta }_j\mid X_j)=0,\\ \text{with}{X}_j\sim f_X\text{and}{U}_j\sim f_U,\end{array}$$ (2)

where U_j are the measurement errors, independent of (X_j, Y_j, η_j), and f_U is known.

For p = 0, a rate-optimal estimator has been developed by Fan and Truong (1993). Their technique is similar to the one employed in density deconvolution problems studied in Stefanski and Carroll (1990) (see also Carroll and Hall 1988). It consists of replacing the unobserved K_h(X_j − x) by an observable quantity L_h(W_j − x) satisfying

$$E[L_h(W_j-x)\mid X_j]=K_h(X_j-x).$$

In the usual nomenclature of measurement error models, this means that L_h(W_j − x) is an unbiased score for the kernel function K_h(X_j − x).

Following this idea, we would like to replace (X_j − x)^kK_h(X_j − x) in S_n,k and T_n,k by (W_j − x)^kL_k,h(W_j − x), where L_k,h(x) = h⁻¹L_k(x/h), and each L_k potentially depends on h and satisfies

$$E\left\{{(W_j-x)}^k{L}_{k,h}(W_j-x)\mid X_j\right\}={(X_j-x)}^k{K}_h(X_j-x).$$ (3)

That is, we propose to find unbiased scores for all components of the kernel functions. Thus, using the substitution principle, we propose to estimate m^(ν)(x) by

$${\widehat{m}}_p^{(\nu )}(x)=\nu !h^{-\nu }{\mathit{e}}_{\nu +1}^{\top }{\widehat{\mathit{S}}}_n^{-1}{\widehat{\mathit{T}}}_n,$$ (4)

where Ŝ_n = {Ŝ_n,j+l(x)}_0≤j,l≤p and T̂_n = {T̂_n,0(x), …, T̂_n,p(x)}⊤ with

$$\begin{array}{l}{\widehat{S}}_{n,k}(x)=n^{-1}\sum _{j=1}^n{\left(\frac{W_j-x}{h}\right)}^k{L}_{k,h}(W_j-x),\\ {\widehat{T}}_{n,k}(x)=n^{-1}\sum _{j=1}^n{Y}_j{\left(\frac{W_j-x}{h}\right)}^k{L}_{k,h}(W_j-x).\end{array}$$

The method explained earlier seems relatively straightforward but its actual implementation is difficult, and this is the reason that the problem has remained unsolved. The main difficulty has been that it is very hard to find an explicit solution L_k,h(·) to the integral Equation (3). In addition, a priori it is not clear that the solution will be independent of other quantities such as X_j, x, and other population parameters. Therefore, this problem has remained unsolved for more than 15 years.

The key to finding the solution is the Fourier transform. Instead of solving (3) directly, we solve its Fourier version

$$\text{E}\left[{\phi }_{\{{(W_j-x)}^k{L}_{k,h}(W_j-x)\}}(t)\mid X_j\right]={\phi }_{\{{(X_j-x)}^k{K}_h(X_j-x)\}}(t),$$ (5)

where, for a function g, we let φ_g denote its Fourier transform, whereas for a random variable T, we let φ_T denote the characteristic function of its distribution.

We make the following basic assumptions:

Condition A:∫|φ_X|< ∞; φ_U(t) ≠ 0 for all t; ${\phi }_K^{(\ell )}$ is not identically zero and $\int \mid {\phi }_K^{(\ell )}(t)/{\phi }_U(t/h)\mid dt<\infty$ for all h > 0 and 0 ≤ l ≤ 2p.

Condition A generalizes standard conditions of the deconvolution literature, where it is assumed to hold for p = 0. It is easy to find kernels that satisfy this condition. For example, kernels defined by φ_K(t) = (1 − t²)^q·1_[−1,1](t), with q ≥ 2p, satisfy this condition.

Under these conditions, we show in the Appendix that the solution to (5) is found by taking L_k (in the definition of L_k,h) equal to

$$L_k(u)=u^{-k}{K}_{U,k}(u),$$

with

$$K_{U,k}(x)=i^{-k}\frac{1}{2\pi }\int e^{-\mathit{itx}}\frac{{\phi }_K^{(k)}(t)}{{\phi }_U(-t/h)}dt.$$

In other words, our estimator is defined by (4), where

$$\begin{array}{l}{\widehat{S}}_{n,k}(x)=n^{-1}\sum _{j=1}^n{K}_{U,k,h}(W_j-x)\text{and}\\ {\widehat{T}}_{n,k}(x)=n^{-1}\sum _{j=1}^n{Y}_j{K}_{U,k,h}(W_j-x),\end{array}$$ (6)

with K_U,k,h(x) = h⁻¹K_U,k(x/h). Note that the functions K_U,k depend on h, even though, to simplify the presentation, we did not indicate this dependence explicitly in the notations.

In what follows, for simplicity, we drop the p index from ${\widehat{m}}_p^{(\nu )}(x)$. It is also convenient to rewrite (4) as

$${\widehat{m}}^{(\nu )}(x)=h^{-\nu }\nu !\sum _{k=0}^p{\widehat{S}}^{\nu ,k}(x){\widehat{T}}_{n,k}(x),$$

where Ŝ^ν,k(x) denotes the (ν + 1, k + 1)th element of the inverse of the matrix Ŝ_n.

3. ASYMPTOTIC NORMALITY

3.1 Conditions

To establish asymptotic normality of our estimator, we need to impose some regularity conditions. Note that these conditions are stronger than those needed to define the estimator, and to simplify the presentation, we allow overlap of some of the conditions [e.g., compare condition A and condition (B1) which follows].

As expected because of the unbiasedness of the score, and as we will show precisely, the asymptotic bias of the estimator, defined as the expectation of the limiting distribution of m̂^(ν)(x) − m^(ν)(x), is exactly the same as in the error-free case. Therefore, exactly the same as in the error-free case, the bias depends on the smoothness of m and f_X, and on the number of finite moments of Y and K. Define τ² (u) = E[{Y − m(x)}²|X = u]. Note that, to simplify the notation, we do not put an index x into the function τ, but it should be obvious that the function depends on the point x where we wish to estimate the curve m. We make the following assumptions:

Condition B:

(B1) K is a real and symmetric kernel such that ∫K(x) dx = 1 and has finite moments of order 2p + 3;

(B2) h → 0 and nh → ∞as n → ∞

(B3) f_X(x) > 0 and f_X is twice differentiable such that $\mid \mid f_X^{(j)}\mid {\mid }_{\infty }<\infty$ for j = 0, 1, 2;

(B4) m is p + 3 times differentiable, τ²(·) is bounded, ||m^(j)||_∞<∞ for j = 0, …, p + 3, and for some η > 0, E{|Y_i − m(x)|^2+η|X= u} is bounded for all u.

These conditions are rather mild and, apart from the assumptions on the conditional moments of Y, they are fairly standard in the error-free context. Boundedness of moments of Y are standard in the measurement error context (see Fan and Masry 1992; Fan and Truong 1993).

The asymptotic variance of the estimator, defined as the variance of the limiting distribution of m β^(ν)(x) − m^(ν)(x) differs from the error-free case because, as usual in deconvolution problems, it depends strongly on the type of measurement errors that contaminate the X-data. Following Fan (1991a,b,c), we consider two categories of errors. An ordinary smooth error of order β is such that

$$\underset{t\to +\infty }{lim}{t}^{\beta }{\phi }_U(t)=c\text{and}\underset{t\to +\infty }{lim}{t}^{\beta +1}{\phi }_U^{\prime }(t)=-c\beta$$ (7)

for some constants c > 0 and β > 1. A supersmooth error of order β > 0 is such that

$$\begin{array}{l}{d}_0\mid t{\mid }^{{\beta }_0}exp(-\mid t{\mid }^{\beta }/\gamma )\le \mid {\phi }_U(t)\mid \le d_1\mid t{\mid }^{{\beta }_1}exp(-\mid t{\mid }^{\beta }/\gamma )\\ \text{as}\mid t\mid \to \infty ,\end{array}$$ (8)

with d₀, d₁, γ, β₀, and β₁ some positive constants. For example, Laplace errors, Gamma errors, and their convolutions are ordinary smooth, whereas Cauchy errors, Gaussian errors, and their convolutions are supersmooth. Depending on the type of the measurement error, we need different conditions on K and U to establish the asymptotic behavior of the variance of the estimator. These conditions mostly concern the kernel function, which we can choose; they are fairly standard in deconvolution problems and are easy to satisfy. For example, see Fan (1991a,b,c) and Fan and Masry (1992). We assume:

Condition O (ordinary smooth case):

||φ′_U||_∞ < ∞ and for k = 0, …,2p + 1, $\mid \mid {\phi }_K^{(k)}\mid {\mid }_{\infty }<\infty$ and $\int \left[\mid t{\mid }^{\beta }+\mid t{\mid }^{\beta -1}\right]\mid {\phi }_K^{(k)}(t)\mid dt<\infty$ and, for 0 ≤k, k′ ≤ 2p, $\int \mid t{\mid }^{2\beta }\mid {\phi }_K^{(k)}(t)\mid ·\mid {\phi }_K^{(k^{\prime })}(t)\mid dt<\infty$.

Condition S (supersmooth case):

φ_K is supported on [−1, 1] and, for k = 0, …, 2p, $\mid \mid {\phi }_K^{(k)}\mid {\mid }_{\infty }<\infty$;

In the sequel we let Ŝ = Ŝ_n, μ_j = ∫u^jK(u)du, S = (μ_K+ℓ)_{0≤k, l≤p,},S̃ = (μ_K±ℓ+1)_{0≤k, l≤p}, μ = (μ_p+1, …_, μ_2p+1)^⊤ μ̃ = (μ_p+2, …_, μ_2p+2) and, for any square integrable function g, we define R(g)= ∫ g^2. Finally, we let S ^i,j denote the (i+1,+ j + 1)th element of the matrix ${\mathit{S}}^{-1}{f}_X^{-1}(x)$ and, for c as in (7),

$${\mathit{S}}^{\ast }={\left({(-1)}^{k^{\prime }}{i}^{k^{\prime }-k}\frac{1}{2\pi c^2}\int \mid t{\mid }^{2\beta }{\phi }_K^{(k)}(t){\phi }_K^{(k^{\prime })}(t)dt\right)}_{0\le k,k^{\prime }\le p}.$$

Note that this matrix is always real because its (k, k′)th element is zero when k + k′is odd, and i^k′−_k = (−1)^(k′−_k^)/2 otherwise.

3.2 Asymptotic Results

Asymptotic properties of the estimator depend on the type of error that contaminates the data. The following theorem establishes asymptotic normality in the ordinary smooth error case.

Theorem 1

Assume (7). Under Conditions A, B, and O, if nh^{2β+ 2ν+ 1}→ ∞ and nh^2β+4→ ∞ we have

$$\frac{{\widehat{m}}^{(\nu )}(x)-m^{(\nu )}(x)-\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}}{\sqrt{var\{{\widehat{m}}^{(\nu )}(x)\}}}\stackrel{ℒ}{\to }N(0,1)$$

where $var\{{\widehat{m}}^{(\nu )}(x)\}=e_{\nu +1}^{\top }{\mathit{S}}^{-1}{\mathit{S}}^{\ast }{\mathit{S}}^{-1}{\mathit{e}}_{\nu +1}\frac{{(\nu !)}^2({\tau }^2{f}_X)\ast f_U(x)}{f_X^2(x)n{h}^{2\beta +2\nu +1}}+o(\frac{1}{n{h}^{2\beta +2\nu +1}})$, and

1. if p − ν is odd

   $$\begin{array}{l}\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}^{-1}\mathit{\mu }\frac{\nu !}{(p+1)!}{m}^{(p+1)}(x)h^{p+1-\nu }\\ +o(h^{p+1-\nu });\end{array}$$

2. if p − ν is even

   $$\begin{array}{l}\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}^{-1}\stackrel{\sim }{\mathit{\mu }}\frac{\nu !}{(p+2)!}\\ \left[m^{(p+2)}(x)+(p+2)m^{(p+1)}(x)\frac{{f^{\prime }}_X(x)}{f_X(x)}\right]h^{p+2-\nu }-{\mathit{e}}_{\nu +1}^{\top }\\ {\mathit{S}}^{-1}\stackrel{\sim }{\mathit{S}}{\mathit{S}}^{-1}\mathit{\mu }\frac{\nu !}{(p+1)!}{m}^{(p+1)}(x)\frac{{f^{\prime }}_X(x)}{f_X(x)}{h}^{p+2-\nu }+o(h^{p+2-\nu }).\end{array}$$

From this theorem we see that, as usual in nonparametric kernel deconvolution estimators, the bias of our estimator is exactly the same as the bias of the local polynomial estimator in the error-free case, and the errors-in-variables only affect the variance of the estimator. Compare the previous bias formulas with Theorem 3.1 of Fan and Gijbels (1996), for example. In particular, our estimator has the design-adaptive property discussed in Section 3.2.4 of that book.

The optimal bandwidth is found by the usual trade-off between the squared bias and the variance, which gives h ~ n^{−1/(2β + 2p+3)} if p − ν is odd and h ~ n^{−1/(2β + 2p+5)} if p − ν is even. The resulting convergence rates of the estimator are, respectively, n^{− (p+1−ν)/(2β + 2p+3)} if p − ν is odd and n^{− (p+2−ν)/(2β + 2p+5)} if p − ν is even. For p = ν = 0, our estimator of m is exactly the estimator of Fan and Truong (1993) and has the same rate, that is n^{−2/(2β +5)} (remember that we only assume that f_X is twice differentiable). For p = 1 and ν = 0, our estimator is different from Fan and Truong (1993), but it converges at the same rate. For p > 1 and ν = 0, our estimator converges at faster rates.

Remark 1: Which p should one use?

This problem is essentially the same as in the error-free case (see Fan and Gijbels, 1996, Sec. 3.3). In particular, although, in theory using higher values of p reduces the asymptotic bias of the estimator without increasing the order of its variance, the theoretical improvement for p − ν > 1 is not generally noticeable in finite samples. In particular, the constant term of the dominating part of the variance can increase rapidly with p. However, the improvement from p − ν = 0 to p − ν = 1 can be quite significant, especially in cases where f_X or m are discontinuous at the boundary of their domain, in which case the bias for p − ν = 1 is of smaller order than the bias for p − ν = 0. In other cases, the biases of the estimators of orders p and p + 1, where p − ν is even, are of the same order. See Sections 3.3 and 5.

Remark 2: Higher order deconvolution kernel estimators

As usual, it is possible to reduce the order of the bias by using higher order kernels, i.e., kernels that have all their moments up to order k, say, vanishing, and imposing the existence of higher derivatives of f_X and m, as was done in Fan and Truong (1993). However, such kernels are not very popular, because it is well known that, in practice, they increase the variability of estimators and can make them quite unattractive (e.g., see Marron and Wand 1992). Similarly, one can also use the infinite order sinc kernel, which has the appealing theoretical property that it adapts automatically to the smoothness of the curves (see Diggle and Hall 1993; Comte and Taupin 2007). However, the trick of the sinc kernel does not apply to the boundary setting. In addition, this kernel can only be used when p = ν = 0, because ${\phi }_K^{(\ell )}\equiv 0\forall \ell >0$, where it can sometimes work poorly in practice, especially in cases where f_X or m have boundary points (see Section 5 for illustration).

The next theorem establishes asymptotic normality in the supersmooth error case. In this case, the variance term is quite complicated and asymptotic normality can only be established under a technical condition, which generalizes Condition 3.1 (and Lemma 3.2) of Fan and Masry (1992). This condition is nothing but a refined version of the Lyapounov condition, and it essentially says that the bandwidth cannot converge to zero too fast. It should be possible to derive more specific lower bounds on the bandwidth, but this would require considerable technical detail and therefore will be omitted here. In the next theorem we first give an expression for the asymptotic bias and variance of m̂^(ν)(x) defined as, respectively, the expectation and the variance of h^−νν!Z_n, the asymptotically dominating part of the estimator, and where Z_n is defined in (A.3). Then, under the additional assumption, we derive asymptotic normality.

Theorem 2

Assume (8). Under conditions A, B, and S, if h = d(2/γ)^1/β(ln n) ^−1/β with d > 1, then

1. Bias{m̂^(ν)(x)} is as in Theorem 1 and var{m̂^(ν)(x)} = o (Bias²{m̂^(ν)(x)})

2. If, in addition, for U_n,1 defined in the Appendix at Equation (A.5), there exists r > 0 such that for b_n = h^β/(2r+10), $E[U_{n,1}^2]\ge C_1^2{f}_X^{-2}(x)h^{2{\beta }_0·1\{{\beta }_0<1/2\}-1}exp\{2-4\beta b_n\}/h^{\beta }\gamma$, with 0 < C₁ < ∞ independent of n, then we also have

   $$\frac{{\widehat{m}}^{(\nu )}(x)-m^{(\nu )}(x)-\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}}{\sqrt{var\{{\widehat{m}}^{(\nu )}(x)\}}}\stackrel{ℒ}{\to }N(0,1).$$

When h = d(2/γ)^1/β(ln n) ^−1/β with d > 1, as in the theorem, it is not hard to see that, as usual in the supersmooth error case, the variance is negligible compared with the squared bias and the estimator converges at the logarithmic rate {log(n)} ^{− (p+1−ν)/β} if p − ν is odd, and {log(n)} ^{− (p+2−ν)/β} if p − ν is even. Again, for p = ν = 0, our estimator is equal to the estimator of Fan and Truong (1993) and thus has the same rate.

3.3 Behavior Near the Boundary

Because the bias of our estimator is the same as in the error-free case, it suffers from the same boundary effects when the design density f_X is compactly supported. Without loss of generality, suppose that f_X is supported on [0, 1] and, for any integer k ≥ 0 and any function g defined in [0, 1] that is k times differentiable on ]0, 1[, let g̃^(k) (x) = g^(k)(0⁺) · 1_{x=0} + g^(k)(1⁻) · 1_{x=1} + g^(k)(x) · 1_{0<x<1} We derive asymptotic normality of the estimator under the following conditions, which are the same as those usually imposed in the error-free case:

Condition C:

(C1)–(C2) Same as (B1)–(B2);

(C3) f_X(x) > 0 for x ε]0, 1[ and f_X is twice differentiable such that $\mid \mid f_X^{(j)}\mid {\mid }_{\infty }<\infty$ for j=0,1,2;

(C4) m is p + 3 times differentiable on ]0, 1[, τ² is bounded on [0, 1] and continuous on ]0, 1[, ||m^(j)||_∞< ∞ on [0, 1] for j =0,…, p + 3 and there exists η > 0 such that E{|Y_i −m(x)|^2)+η|X = u} is bounded for all u ε[0, 1].

We also define ${\mu }_k(x)={\int }_{-x/h}^{(1-x)/h}{x}^{k}K(x)dx$, S_B(x) = (μ_k+k′(x))_{0≤ k,k′≤p}, μ (x) = {μ_p+1(x), …,μ_2p+1(x)}^⊤ and

$$\begin{array}{l}{\mathit{S}}_B^{\ast }(x)=\{\int {\stackrel{\sim }{\tau }}^2(x-u+hz){\stackrel{\sim }{f}}_X(x-u+hz)K_{U,k}(z)K_{U,k^{\prime }}(z)\\ {f_U(u)dudz\}}_{0\le k,k^{\prime }\le p}.\end{array}$$

For brevity, we only show asymptotic normality in the ordinary smooth error case. Our results can be extended to the supersmooth error case: all our calculations for the bias are valid for supersmooth errors, and the only difference is the variance, which is negligible in that case.

The proof of the next theorem is similar to the proof of Theorem 1 and hence is omitted. It can be obtained from the sequence of Lemmas B10 to B13 of Delaigle, Fan, and Carroll (2008). As for Theorem 2, a technical condition, which is nothing but a refined version of the Lyapounov condition, is required to deal with the variance of the estimator.

Theorem 3

Assume (7). Under Conditions A, C, and O, if nh^2β+2ν+1 → ∞ and nh^2β+4 → ∞ as n → ∞ and ${\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}_B^{-1}(x){\mathit{S}}_B^{\ast }(x){\mathit{S}}_B^{-1}(x){\mathit{e}}_{\nu +1}\ge C_1{h}^{-2\beta }$ for some finite constant C₁ > 0, we have

$$\frac{{\widehat{m}}^{(\nu )}(x)-m^{(\nu )}(x)-\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}}{\sqrt{var\{{\widehat{m}}^{(\nu )}(x)\}}}\stackrel{ℒ}{\to }N(0,1)$$

where $\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}_B^{-1}(x)\mathit{\mu }(x)\frac{\nu !}{(p+1)!}{\stackrel{\sim }{m}}^{(p+1)}(x)h^{p+1-\nu }+o(h^{p+1-\nu })$ and $var\{{\widehat{m}}^{(\nu )}(x)\}={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}_B^{-1}(x){\mathit{S}}_B^{\ast }(x){\mathit{S}}_B^{-1}(x){\mathit{e}}_{\nu +1}\frac{{(\nu !)}^2}{\stackrel{\sim }{f_X^2}(x)n{h}^{2\nu +1}}+o\left(\frac{1}{n{h}^{2\beta +2\nu +1}}\right)$.

As before, the bias is the same as in the error-free case, and thus all well-known results of the boundary problem extend to our context. In particular, the bias of the estimator for p − ν even is of order h^{p+1 − ν}, instead of h^{p+ 2 − ν} in the case without a boundary, whereas the bias of the estimator for p − ν odd remains of order h^{p+1 − ν}, as in the no-boundary case. In particular, the bias of the estimator for p − ν = 0 is of order h, whereas it is of order h² when p − ν = 1. For this reason, local polynomial estimators with p − ν odd, and in particular with p − ν = 1, are often considered to be more natural.

Note that in deconvolution problems, kernels are usually supported on the whole real line (see Delaigle and Hall, 2006), the presence of the boundary can affect every point of the type x = ch or x = 1 − ch, with c a finite constant satisfying 0 ≤ c ≤ 1/h. For x = ch, it can be shown that

$$\begin{array}{l}\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}_B^{-1}(x)\mathit{\mu }(x)\frac{\nu !}{(p+1)!}{m}^{(p+1)}(0^{+})h^{p+1-\nu }\\ +o(h^{p+1-\nu }),\end{array}$$

whereas if x = 1 − ch, we have

$$\begin{array}{l}\text{Bias}\{{\widehat{m}}^{(\nu )}(x)\}={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}_B^{-1}(x)\mathit{\mu }(x)\frac{\nu !}{(p+1)!}{m}^{(p+1)}(1^{-})h^{p+1-\nu }\\ +o(h^{p+1-\nu }).\end{array}$$

4. GENERALIZATIONS

In this section, we show how our methodology can be extended to provide estimators in two important cases: (1) when the measurement error distribution is unknown; and (2) when the measurement errors are heteroscedastic. In the interest of space we focus on methodology and do not give detailed asymptotic theory.

4.1 Unknown Measurement Error Distribution

In empirical applications, it can be unrealistic to assume that the error density is known. However, it is only possible to construct a consistent estimator of m if we are able to consistently estimate the error density itself. Several approaches for estimating this density f_U have been considered in the nonparametric literature. Diggle and Hall (1993) and Neumann (1997) assumed that a sample of observations from the error density is available and estimated f_U nonparametrically from those data. A second approach, applicable when the contaminated observations are replicated, consists in estimating f_U from the replicates. Finally, in some cases, if we have a parametric model for the error density f_U and additional constraints on the density f_X, it is possible to estimate an unknown parameter of f_U without any additional observation (see Butucea and Matias 2005; Meister 2006).

We give details for the replicated data approach, which is by far the most commonly used. In the simplest version of this model, the observations are a sample of iid data (W_j1, W_j2, Y_j), j = 1, …, n, generated by the model

$$\begin{array}{l}{Y}_j=m(X_j)+{\eta }_j,W_{jk}=X_j+U_{jk},k=1,2,\text{E}({\eta }_j\mid X_j)=0,\\ \text{with}{X}_j\sim f_X\text{and}{U}_{jk}\sim f_U,\end{array}$$ (9)

where the U_jk’s are independent, and independent of the (X_j, Y_j, η_j)’ s.

In the measurement error literature, it is often assumed that the error density, f_U(;θ) is known up to a parameter θ, which has to be estimated from the data. For example, if θ = var(U), the unknown variance of U, a $\sqrt{n}$ consistent estimator is given by

$$\widehat{\theta }={\{2(n-1)\}}^{-1}\sum {(W_{j1}-W_{j2}-{\overline{W}}_1+{\overline{W}}_2)}^2,$$ (10)

where ${\overline{W}}_k=n^{-1}{\sum }_{j=1}^n{W}_{jk}$ (see, for example, Carroll et al. 2006, Equation 4.3). Taking φ_U(;θ̂) to be the characteristic function corresponding to f_U(;θ̂) we can extend our estimator of m^(ν) to the unknown error case by replacing φ_U by φ_U (;θ̂) everywhere.

In the case where no parametric model for f_U is available, some authors suggest using a nonparametric estimator of f_U. For general settings (see Li and Vuong 1998; Schennach 2004a,b; Hu and Schennach 2008). In the common case where the error density f_U is symmetric, Delaigle et al. (2008) proposed to estimate φ_U(t) by ${\widehat{\phi }}_U(t)=\mid n^{-1}{\sum }_{j=1}^{n}cos\{it(W_{j1}-W_{j2})\}{\mid }^{1/2}$. Following the approach they use for the case p = ν = 0, we can extend our estimator of m^(ν) to the unknown error case by replacing φ_U by φ̂_U everywhere, adding a small positive number to φ̂_U when it gets too small. Detailed convergence rates of this approach have been studied by Delaigle et al. (2008) in the local constant case (p = 0), where they show that the convergence rates of this version of the estimator is the same as that of the estimator with known f_U, as long as f_X is sufficiently smooth relative to f_U. Their conclusion can be extended to our setting.

4.2 Heteroscedastic Measurement Errors

Our local polynomial methodology can be generalized to the more complicated setting where the errors U_i are not identically distributed. In practice, this could happen when observations have been obtained in different conditions, for example if they were collected from different laboratories. Recent references on this problem include Delaigle and Meister (2007 Delaigle and Meister (2008) and Staudenmayer, Ruppert, and Buonaccorsi (2008). In this context, the observations are a sample (W₁, Y₁), …, (W_n, Y_n) of iid observations coming from the model

$$\begin{array}{l}{Y}_j=m(X_j)+{\eta }_j,W_j=X_j+U_j,\text{E}({\eta }_j\mid X_j)=0,\\ \text{with}{X}_j\sim f_X\text{and}{U}_j\sim f_{U_j},\end{array}$$ (11)

where the U_j’s are independent of the (X_j, Y_j)’s. Our estimator cannot be applied directly to such data because there is no common error density f_U, and therefore K_U,k is not defined. Rather, we need to construct appropriate individual functions K_Uj,k and then replace Ŝ_n,k(x) and T̂_n,k(x) in the definition of the estimator, by

$$\begin{array}{l}{\widehat{S}}_{n,k}^H(x)=n^{-1}\sum _{j=1}^n{K}_{U_j,k,h}(W_j-x)\text{and}\\ {\widehat{T}}_{n,k}^H(x)=n^{-1}\sum _{j=1}^n{Y}_j{K}_{U_j,k,h}(W_j-x),\end{array}$$ (12)

where we use the superscript H to indicate that we are treating the heteroscedastic case. As before, we require that $E\{{\widehat{S}}_{n,k}^H(x)\mid X_1,\dots ,X_n\}=S_{n,k}(x)$ and $E\{{\widehat{T}}_{n,k}^H(x)\mid X_1,\dots ,X_n\}=T_{n,k}(x)$.

A straightforward solution would be to define K_Uj,k by

$$K_{U_j,k}(x)=i^{-k}\frac{1}{2\pi }\int e^{-\mathit{itx}}{\phi }_K^{(k)}(t)/{\phi }_{U_j}(-t/h)dt,$$

where φ_Uj is the characteristic function of the distribution of U_j. However, theoretical properties of the corresponding estimator are generally not good, because the order of its variance is dictated by the least favorable error densities (see Delaigle and Meister 2007 see Delaigle and Meister 2008). This problem can be avoided by extending the approach of those authors to our context by taking

$$K_{U_j,k}(x)=i^{-k}\frac{1}{2\pi }\int e^{-\mathit{itx}}\frac{{\phi }_{U_j}(-t){\phi }_K^{(k)}(t)}{n^{-1}{\sum }_{j=1}^n\mid {\phi }_{U_j}(t/h){\mid }^2}dt.$$

Alternatively, in the case where the error densities are unknown but replicates are available as at (9) we can use instead

$$\begin{array}{l}{\widehat{S}}_{n,k}^H(x)=n^{-1}\sum _{j=1}^n{K}_{U_j,k,h}({\overline{W}}_j-x)\text{and}\\ {\widehat{T}}_{n,k}^H(x)=n^{-1}\sum _{j=1}^n{Y}_j{K}_{U_j,k,h}({\overline{W}}_j-x),\end{array}$$ (13)

where W̄_j = (W_j1 + W_j2)/2 and

$${\stackrel{\sim }{K}}_{U_j,k}(x)=i^{-k}\frac{1}{2\pi }\int e^{-\mathit{itx}}\frac{{\phi }_K^{(k)}(t)}{n^{-1}{\sum }_{j=1}^n{e}^{it(W_{j1}-W_{j2})/2}}dt,$$

adding a small positive number to the denominator when it gets too small. This is a generalization of the estimator of Delaigle and Meister (2008).

5. FINITE SAMPLE PROPERTIES

5.1 Simulation Settings

Comparisons between kernel estimators and other methods have been carried out by many authors in various contexts, with or without measurement errors. One of their major advantages is that they are simple and can be easily applied to problems such as heteroscedasticity (see Section 4.2), nonparametric variance, or mode estimation and detection of boundaries. See also the discussion in Delaigle and Hall (2008). As for any method, in some cases kernel methods outperform, and in other cases are outperformed by other methods. Our goal is not to rederive these well-known facts, but rather to illustrate the new results of our article.

We applied our technique for estimating m and m⁽¹⁾ to several examples to include curves with several local extrema and/or an inflection point, as well as monotonic, convex and/or unbounded functions. To summarize the work we are about to present, our simulations illustrate in finite samples:

• the gain that can be obtained by using a local linear estimator (LLE) in the presence of boundaries, in comparison with a local constant estimator (LCE);

• properties of our estimator of m⁽¹⁾ for p = 1 (LPE1) and p = 2 (LPE2);

• properties of our estimator when the error variance is estimated from replicates;

• the robustness of our estimator against misspecification of the error density;

• the gain obtained by using our estimators compared with their naive versions (denoted, respectively, by NLCE, NLLE, NLPE1, or NLPE2), which pretend there is no error in the data;

• the properties of the LCE using the sinc kernel (LCES) in the presence of boundary points.

We considered the following examples: (1) m(x) = x³ exp(x⁴/1,000) cos(x) and η ~ N(0, 0.6²); (2) m(x) = 2x exp(−10x⁴/81), η ~ N(0, 0.2²); (3) m(x) = x³, η ~ N(0, 1.2²); (4) m(x) = x⁴, η ~ N(0, 4²). In cases (1) and (2) we took X ~ 0.8X₁ + 0.2X₂, where X₁ ~f_X1(x) = 0.1875x²1_[−2,2](x) and X₂ ~ U[−1, 1]. In cases (3) and (4) we took X ~ N(0, 1).

In each case considered, we generated 500 samples of various sizes from the distribution of (W, Y), where W = X + U with U ~ Laplace or normal of zero mean, for several values of the noise-signal-ratio var(U)/var(X). Except otherwise stated, we used the kernel whose Fourier transform is given by

$${\phi }_K(t)={(1-t^2)}^8·1_{[-1,1]}(t).$$ (13)

To illustrate the potential gain of using local polynomial estimators without confounding the effect of an estimator with that of the smoothing parameter selection, we used, for each method, the theoretical optimal value of h; that is, for each sample, we selected the value h minimizing the Integrated Squared Error ISE = ∫ {m^(ν)(x) − m̂^(ν)(x)}² dx, where m̂^(ν) is the estimator considered.

In the case where ν = 0, a data-driven bandwidth procedure has been developed by Delaigle and Hall (2008). For example, for the LLE of m, N_W, and D_W, in Section 3.1 of that article, are equal to N_W = T̂_n,2Ŝ_n,0 − T̂_n,1Ŝ_n,1 and $D_W={\widehat{S}}_{n,2}{\widehat{S}}_{n,0}-{\widehat{S}}_{n,1}^2$, respectively (see also Figure 2 in that article). Note that the fully automatic procedure of Delaigle and Hall (2008) also includes the possibility of using a ridge parameter in cases where the denominator D_W(x) gets too small. It would be possible to extend their method to cases where ν > 0, by combining their SIMulation EXtrapolation (SIMEX) idea with data-driven bandwidths used in the error-free case, in much the same way as they combined their SIMEX idea with cross-validation for the case ν = 0. Although not straightforward, this is an interesting topic for future research.

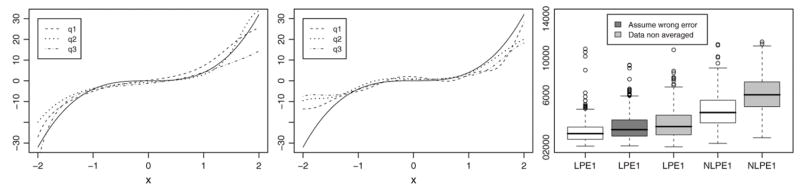
Figure 2.

Estimates of the density function m⁽¹⁾ for curve (4) when U is Laplace, var(U) = 0.4var(X) and n = 250, using our local linear method (LPE1, left) and the naive local linear method that ignores measurement error (NLPE1, center), when data are averaged and var(U) is estimated by (10). Right: boxplots of ISEs, var(U) estimated by (10). Data averaged except for boxes 3 and 5. Box 2 wrongly assumes Laplace error.

5.2 Simulation Results

In the following figures, we show boxplots of the 500 calculated ISEs corresponding to the 500 generated samples. We also show graphs with the target curve (solid line) and three estimated curves (q₁, q₂, and q₃) corresponding to, respectively, the first, second, and third quartiles of these 500 calculated ISEs for a given method.

Figure 1 shows the quantile estimated curves of m at (2) and boxplots of the ISEs, for samples of size n = 500, when U is Laplace and var(U) = 0.2var(X). As expected by the theory, the LCE is more biased than the LLE near the boundary. Similarly, the LCES is more biased and variable than the LLE. As usual in measurement error problems, the naive estimators that ignore the error are oversmoothed, especially near the modes and the boundary. The boxplots show that the LLE tends to work better than the LCE, but also tends to be more variable. Except in a few cases, both outperform the LCES and the naive estimators.

Figure 1.

Estimated curves for case (2) when U is Laplace, var(U) = 0.2 var (X) and n = 500. Estimators: local linear estimator (LLE, top left), local constant estimator (LCE, top center), the naive local linear estimator that ignores measurement error (NLLE, top right), the local constant estimators using the sinc kernel (LCES, bottom left), and boxplots of the ISEs (bottom center). Bottom right: boxplots of the ISEs for case (1) when U is normal, var(U) = 0.2 var (X) and n = 250. Data are averaged replicates and var(U) is estimated by (10).

Figure 1 also shows boxplots of ISEs for curve (1) in the case where U is normal, var(U) = 0.2var(X) and n = 250. Here we pretended var(U) was unknown, but generated replicated data as at (9) and estimated var(U) via (10). Because the error variance of the averaged data W̄_i = (W_i1 + W_i2)/2 is half the original one, we applied each estimator with these averaged data, either assuming U was normal, or wrongly assuming it was Laplace, with unknown variance estimated. We found that the estimator was quite robust against error misspecification, as already noted by Delaigle (2008) in closely connected deconvolution problems. Like there, assuming Laplace distribution often worked reasonably well (see also Meister 2004). Except in a few cases, the LLE worked better than the LCE, and both outperformed the LCES and the NLLE (which itself outperformed the NLCE not shown here).

At Figure 2 we show results for estimating the derivative of curve (4) in the case where U is Laplace, var(U) = 0.4var(X), and n = 250. We assumed the error variance was unknown, and we generated replicated data and estimated var(U) by (10). We applied the LPE1 on both the averaged data and the original sample of non-averaged replicated data. For the averaged data, the errors distribution is that of a Laplace convolved with itself, and we took either that distribution or wrongly assumed that the errors were Laplace. We compared our results with the naive NPLE1. Again, taking the error into account worked better than ignoring the error, even when a wrong error distribution was used, and whether we used the original data or the averaged data.

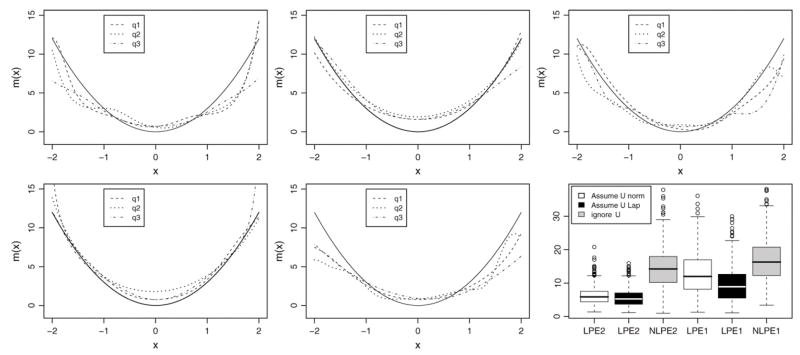
Finally, Figure 3 concerns estimation of the derivative function m⁽¹⁾ in case (3) when U is normal with var(U) = 0.4var(X) and n = 500. We generated replicates and calculated the LPE1 and LPE2 estimators assuming normal errors or wrongly assuming Laplace errors, and pretended the error variance was unknown and estimated it via (10). In this case as well, taking the measurement error into account gave better results than ignoring the errors, even when the wrong error distribution was assumed. The LPE2 worked better at the boundary than the LPE1, but at the interior it is the LPE1 that worked better.

Figure 3.

Estimates of the derivative function m⁽¹⁾ for case (3) when U is normal with var(U) = 0.4var(X) and n = 500, using our local linear method (LPE1, top left) and local quadratic method (LPE2, top center) assuming that U is normal, using the LPE1 (top right) and LPE2 (bottom left) wrongly assuming that the error distribution is Laplace, or using the NLPE2 (bottom center). Boxplots of the ISEs (bottom right). Data are averaged replicates and var(U) is estimated by (10).

6. CONCLUDING REMARKS

In the 20 years since the invention of the deconvoluting kernel density estimator and the 15 years of its use for local constant, Nadaraya-Watson kernel regression, the discovery of a kernel regression estimator for a function and its derivatives that has the same bias properties as in the no-measurement-error case has remained unsolved. By working with estimating equations and using the Fourier domain, we have shown how to solve this problem. The resulting kernel estimators are readily computed, and with the right degrees of the local polynomials, have the design adaptation properties that are so valued in the no-error case.

APPENDIX: TECHNICAL ARGUMENTS

A.1 Derivation of the Estimator

We have that

$$\begin{array}{l}{\phi }_{\{{(X_j-x)}^k{K}_h(X_j-x)\}}(t)=\int e^{\mathit{itx}}{(X_j-x)}^k{K}_h(X_j-x)dx\\ =h^k{e}^{{\mathit{itX}}_j}\int e^{-\mathit{ithu}}{u}^{k}K(u)du\\ =i^{-k}{h}^k{e}^{{\mathit{itX}}_j}{\phi }_K^{(k)}(-ht),\end{array}$$

where we used the fact that ${\phi }_K^{(k)}(t)=i^k\int e^{\mathit{itu}}{u}^{k}K(u)du$. Similarly, we find that

$${\phi }_{\{{(W_j-x)}^k{L}_{k,h}(W_j-x)\}}(t)=i^{-k}{h}^k{e}^{it{W}_j}{\phi }_{L_k}^{(k)}(-ht).$$

Therefore, from (5) and using E[e^itW_j|X_j] = e^itX_jφ_U(t), L_k satisfies

$${\phi }_{L_k}^{(k)}(-ht)={\phi }_K^{(k)}(-ht)/{\phi }_U(t).$$

From ${\phi }_{L_k}^{(k)}(t)=i^k\int e^{\mathit{itu}}{u}^k{L}_k(u)du$ and the Fourier inversion theorem, we deduce that

$$i^k{u}^k{L}_k(u)=\frac{1}{2\pi }\int e^{-\mathit{itu}}{\phi }_{L_k}^{(k)}(t)dt=\frac{1}{2\pi }\int e^{-\mathit{itu}}{\phi }_K^{(k)}(t)/{\phi }_U(-t/h)dt.$$

A.2 Proofs of the Results of Section 3

We show only the main results and refer to a longer version of this article, Delaigle et al. (2008), for technical results that are straightforward extensions of results of Fan (1991a), Fan and Masry (1992) and Fan and Truong (1993).

In what follows, we will first give the proofs, referring to detailed Lemmas and Propositions that follow. A longer version with many more details is given by Delaigle et al. (2008).

Before we provide detailed proofs of the theorems, note that because Ŝ^ν,k, k = 0, … p represents the (ν + 1)th row of ${\widehat{\mathit{S}}}_n^{-1}$, we have

$$\sum _{k=0}^p{\widehat{S}}^{\nu ,k}{\widehat{S}}_{n,k+j}=0,\text{if}j\ne \nu \text{and}1\text{if}j=\nu .$$

Consequently, it is not hard to show that

$$h^{\nu }{(\nu !)}^{-1}[{\widehat{m}}^{(\nu )}(x)-m^{(\nu )}(x)]=\sum _{k=0}^p{\widehat{S}}^{\nu ,k}(x){\widehat{T}}_{n,k}^{\ast }(x),$$ (A.1)

where

$${\widehat{T}}_{n,k}^{\ast }(x)={\widehat{T}}_{n,k}(x)-\sum _{j=0}^p{h}^j\frac{m^{(j)}(x)}{j!}{\widehat{S}}_{n,k+j}(x).$$ (A.2)

Proof of Theorem 1

We give the proof in the case where p − ν odd. The case p − ν even is treated similarly by replacing everywhere S^ν,k(x) by S^ν,k(x) − hS̆ ^ν,k.

From (A.1) and Lemma A.1, we have

$$h^{\nu }{(\nu !)}^{-1}\{{\widehat{m}}^{(\nu )}(x)-m^{(\nu )}(x)\}=Z_n(x)+O_P(h^{p+3}),$$ (A.3)

where

$$Z_n(x)=\sum _{k=0}^p{S}^{\nu ,k}(x){\widehat{T}}_{n,k}^{\ast }(x).$$ (A.4)

We deduce from Propositions A.1 and A.2 that the O_P(h^p+3) term in (A.3) is negligible. Hence, h^ν(ν!)⁻¹[m̂^(ν)(x) − m^(ν)(x)] is dominated by Z_n, and to prove asymptotic normality of m̂^(ν)(x), it suffices to show asymptotic normality of Z_n. To do this, write $Z_n=n^{-1}{\sum }_{i=1}^n{U}_{n,i}$, where

$$\begin{array}{l}{U}_{n,i}\equiv P_{n,i}+Q_{n,i},\\ P_{n,i}=\sum _{k=0}^p{S}^{\nu ,k}(x)\{Y_i-m(x)\}{K}_{U,k,h}(W_i-x),\\ Q_{n,i}=-\sum _{k=0}^p\sum _{j=1}^p{S}^{\nu ,k}(x)h^j\frac{m^{(j)}(x)}{j!}{K}_{U,k+j,h}(W_i-x).\end{array}$$ (A.5)

As in Fan (1991a), to prove that

$$\frac{{\sum }_{j=1}^n{U}_{n,j}-nE{U}_{n,j}}{\sqrt{nvar{U}_{n,j}}}\stackrel{ℒ}{\to }N(0,1),$$ (A.6)

it suffices to show that for some η > 0,

$$\underset{n\to \infty }{lim}\frac{\text{E}\mid U_{n,1}{\mid }^{2+\eta }}{n^{\eta /2}{[\text{E}{U}_{n,1}^2]}^{(2+\eta )/2}}=0.$$ (A.7)

Take η as in (B4) and let κ(u) = E{|Y − m(x)|^2+η|X = u}. We have

$$\begin{array}{l}E\mid P_{n,j}{\mid }^{2+\eta }=\iint \kappa (\upsilon ){\mid \sum _{k=0}^p{h}^{-1}{S}^{\nu ,k}(x)K_{U,k}\left(\frac{x-u-\upsilon }{h}\right)\mid }^{2+\eta }\\ f_X(\upsilon )f_U(u)dud\upsilon \le C{h}^{-1-\eta }\underset{0\le k\le p}{max}\\ \mid \mid K_{U,k}\mid {\mid }_{\infty }^{\eta }·\int \mid K_{U,k}(u){\mid }^{2}du\le C{h}^{-\beta (2+\eta )-1-\eta },\end{array}$$

from Lemma B.5 of Delaigle et al. (2008), and where, here and below, C denotes a generic positive and finite constant. Similarly, we have

$$\begin{array}{l}E\mid Q_{n,j}{\mid }^{2+\eta }=E{\mid \sum _{k=0}^p\sum _{j=1}^p{S}^{\nu ,k}(x)h^j\frac{m^{(j)}(x)}{j!}{K}_{U,k+j,h}(W_i-x)\mid }^{2+\eta }\\ =O(h^{1-\beta (2+\eta )}),\end{array}$$

and thus E|U_{n, j}|^2+η ≤ Ch^{−β(2+η)−1−η}.

For the denominator, it follows from Proposition A.2 and Lemma B.7 of Delaigle et al. (2008) that

$$\begin{array}{l}E[U_{n,j}^2]=h^{-2\beta -1}{f}_X^{-2}(x)({\tau }^2{f}_X)\ast f_U(x){\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}^{-1}{\mathit{S}}^{\ast }{\mathit{S}}^{-1}{\mathit{e}}_{\nu +1}\\ =C{h}^{-2\beta -1}\{1+o(1)\}.\end{array}$$

We deduce that (A.7) holds and the proof follows from the expressions of E(U_{n, j}) and var(U_{n, j}) given in Propositions A.1 and A.2.

Proof of Theorem 2

Using similar techniques as in the ordinary smooth error case and Lemmas B.8 and B.9 of the more detailed version of this article (Delaigle et al. 2008), it can be proven that (A.3) holds in the supersmooth case as well, and under the conditions of the theorem, the O_P(h^p+3) is negligible. Thus, as in the ordinary smooth error case, it suffices to show that, for some η > 0, (A.7) holds.

With P_n,i and Q_n,i as in the ordinary smooth error case, we have

$$\begin{array}{l}E\mid P_{n,i}{\mid }^{2+\eta }\le C{h}^{-1-\eta }\underset{0\le k\le p}{max}\mid \mid K_{U,k}\mid {\mid }_{\infty }^{\eta }·\int \mid K_{U,k}(u){\mid }^{2}du\\ \le C{h}^{{\beta }_2(2+\eta )-1-\eta }exp\{(2+\eta )h^{-\beta }/\gamma \},\\ E\mid Q_{n,j}{\mid }^{2+\eta }\le Ch\underset{1\le k\le 2p}{max}\int \mid K_{U,k}(y){\mid }^{2+\eta }dy\\ \le C{h}^{{\beta }_2(2+\eta )+1}exp\{(2+\eta )h^{-\beta }/\gamma \},\end{array}$$

with β₂ = β₀·1{β₀ < 1/2}, where, here and later, C denotes a generic finite constant, and where we used Lemma B.9 of Delaigle et al. (2008). It follows that $E[U_{n,i}^{2+\eta }]\le C{h}^{{\beta }_2(2+\eta )-1-\eta }exp\{(2+\eta )h^{-\beta }/\gamma \}$. Under the conditions of the theorem, we conclude that (A.7) holds for any η > 0 and (A.6) follows.

Lemma A.1

Under the conditions of Theorem 1, suppose that, for all 0 ≤ k ≤ 2p, we have, when p − ν is odd, (nh)^−1/2 {R(K_U,k)}^1/2 = O(h^p+1) and when p − ν is even, (nh)^−1/2 {R(K_U,k)}1/2 = O(h^p+2). Then,

$$\sum _{k=0}^p{\widehat{S}}^{\nu ,k}(x){\widehat{T}}_{n,k}^{\ast }(x)=\sum _{k=0}^p{R}^{\nu ,k}(x){\widehat{T}}_{n,k}^{\ast }(x)+O_P(h^{p+3}),$$ (A.8)

Where R^ν,k(x) = S^ν,k(x) if p − ν is odd and R^{ν, k}(x) = S^ν,k(x) − hS̆^ν,k(x) if p − ν is even, and where S̆^i,j denotes ${f^{\prime }}_X(x)f_X^{-2}(x){\left({\mathit{S}}^{-1}\stackrel{\sim }{\mathit{S}}{\mathit{S}}^{-1}\right)}_{i,j.}$

Proof

The arguments are an extension of the calculations of Fan and Gijbels (1996, pp. 62 and 101–103). We have

$${\widehat{T}}_{n,k}^{\ast }(x)=E\{{\widehat{T}}_{n,k}^{\ast }(x)\}+O_P\left[\sqrt{var\{{\widehat{T}}_{n,k}^{\ast }(x)\}}\right].$$

By construction of the estimator, $E[{\widehat{T}}_{n,k}^{\ast }(x)]$ is equal to the expected value of its error-free counterpart $T_{n,k}^{\ast }(x)=T_{n,k}(x)-{\sum }_{j=0}^p{h}^j{(j!)}^{-1}{m}^{(j)}(x)S_{n,k+j}(x)$, which, by Taylor expansion, is easily found to be

$$\begin{array}{l}E[T_{n,k}^{\ast }(x)]=\frac{m^{(p+1)}(x)}{(p+1)!}{f}_X(x){\mu }_{k+p+1}{h}^{p+1}\\ +\left[\frac{m^{(p+1)}(x)}{(p+1)!}{f^{\prime }}_X(x)+\frac{m^{(p+2)}(x)}{(p+2)!}{f}_X(x)\right]\\ \times {\mu }_{k+p+2}{h}^{p+2}+o(h^{p+2}).\end{array}$$ (A.9)

Because K is symmetric, it has zero odd moments, and thus $E[T_{n,k}^{\ast }(x)]\asymp h^{p+1}$ if k + p is odd and $E[T_{n,k}^{\ast }(x)]\asymp h^{p+2}$ if k + p is even. Moreover,

$$\begin{array}{l}var\{{\widehat{T}}_{n,k}^{\ast }(x)\}=var\{{\widehat{T}}_{n,k}(x)-m(x){\widehat{S}}_n,k(x)-\sum _{j=1}^p{h}^j{(j!)}^{-1}\\ m^{(j)}(x){\widehat{S}}_{n,k+j}(x)\}\\ =O\left[var\{{\widehat{T}}_{n,k}(x)-m(x){\widehat{S}}_{n,k}(x)\}\right]+O\left[\sum _{j=1}^{p}var\{{\widehat{S}}_{n,k+j}(x)\}\right]\\ =O\left\{R(K_{U,k})/(nh)\right\}+O\left\{\sum _{j=1}^{p}R(K_{U,j+k})/(nh)\right\},\end{array}$$

where we used

$$\begin{array}{l}var[{\widehat{T}}_{n,k}(x)-m(x){\widehat{S}}_{n,k}(x)]\le {(n{h}^2)}^{-1}E\left[{\{Y-m(x)\}}^2{k}_{U,k}^2\{(W-x)/h\}\right]\\ ={(n{h}^2)}^{-1}E\left(E\left[{\{Y-m(x)\}}^2{K}_{U,k}^2\{(W-x)/h\}\mid X\right]\right)\\ ={(n{h}^2)}^{-1}E\left({\tau }^2(X)K_{U,k}^2\{(W-x)/h\}\mid X\right)\\ ={(n{h}^2)}^{-1}\iint {\tau }^2(y)K_{U,k}^2\{(y+u-x)/h\}{f}_X(y)\\ f_U(u)dydu\le {(nh)}^{-1}\mid \mid {\tau }^2{f}_X\mid {\mid }_{\infty }R(K_{U,k})\end{array}$$

and results derived in the proof of Lemma B.1 of Delaigle et al. (2008).

Using our previous calculations, we see that when k + p is odd,

$${\widehat{T}}_{n,k}^{\ast }(x)=c_1{h}^{p+1}+o_P(h^{p+1})$$

whereas, for k + p even,

$${\widehat{T}}_{n,k}^{\ast }(x)=c_2{h}^{p+2}+o_P(h^{p+2}),$$

where c₁ and c₂ denote some finite nonzero constants (depending on x but not on n). Now, it follows from Lemmas B.1 and B.5 of Delaigle et al. (2008) that, under the conditions of the lemma, Ŝ = f_X(x)S + hf′_X(x)S̃) O_P(h²). Let I denote the identity matrix. By Taylor expansion, we deduce that

$$\begin{array}{l}{\widehat{\mathit{S}}}^{-1}={\left\{f_X(x)\mathit{S}+h{f^{\prime }}_X(x)\stackrel{\sim }{\mathit{S}}\right\}}^{-1}+O_P(h^2)\\ ={(\mathit{I}+h{f^{\prime }}_X(x)f_X^{-1}(x){\mathit{S}}^{-1}\stackrel{\sim }{\mathit{S}})}^{-1}{\mathit{S}}^{-1}{f}_X^{-1}(x)+O_P(h^2)\\ ={\mathit{S}}^{-1}{f}_X^{-1}(x)-h{\mathit{S}}^{-1}\stackrel{\sim }{\mathit{S}}{\mathit{S}}^{-1}{f^{\prime }}_X(x)f_X^{-2}(x)+O_P(h^2).\end{array}$$

Thus, we have Ŝ^i,j = S^i,j − hS̆^i,j + O_P(h²), where, due to the symmetry properties of the kernel, S^i,j = 0 when i + j is odd, whereas S̆^ν,j = 0 when i + j is even. This concludes the proof.

Proposition A.1

Under Conditions A, B, and O, we have for p − ν odd

$$E[\nu !h^{-\nu }{Z}_n]={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}^{-1}\mathit{\mu }\frac{\nu !}{(p+1)!}{m}^{(p+1)}(x)h^{p+1-\nu }+o(h^{p+2-\nu })$$

and, for p − ν even,

$$\begin{array}{l}E[\nu !h^{-\nu }{Z}_n]={\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}^{-1}\stackrel{\sim }{\mu }\frac{\nu !}{(p+2)!}\\ \times \left[(p+2)m^{(p+1)}(x)\frac{{f^{\prime }}_X(x)}{f_X(x)}+m^{(p+2)}(x)\right]h^{p+2-\nu }\\ -{\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}^{-1}\stackrel{\sim }{\mathit{S}}{\mathit{S}}^{-1}\mathit{\mu }\frac{\nu !}{(p+1)!}\\ m^{(p+1)}(x)\frac{{f^{\prime }}_X(x)}{f_X(x)}{h}^{p+2-\nu }+o(h^{p+2-\nu }).\end{array}$$

Proof

From (A.4), we have $E[Z_n]={\sum }_{k=0}^p{R}^{\nu ,k}(x)E[T_{n,k}^{\ast }(x)]$ where $E[T_{n,k}^{\ast }(x)]$ is given at (A.9). It follows that

$$\begin{array}{l}E[Z_n]=\sum _{k=0}^p{S}^{\nu ,k}(x)\frac{m^{(p+1)}(x)}{(p+1)!}{f}_X(x){\mu }_{k+p+1}{h}^{p+1}\\ +\sum _{k=0}^p{S}^{\nu ,k}(x)[\frac{m^{(p+1)}(x)}{(p+1)!}{f^{\prime }}_X(x)\\ +\frac{m^{(p+2)}(x)}{(p+2)!}{f}_X(x)]{\mu }_{k+p+2}{h}^{p+2}\\ -\sum _{k=0}^p{\stackrel{⌣}{S}}^{\nu ,k}(x)\frac{m^{(p+1)}(x)}{(p+1)!}{f^{\prime }}_X(x){\mu }_{k+p+1}{h}^{p+2}+o(h^{p+2}).\end{array}$$

Recall that S^ν_,^k(x) = 0 unless k + ν is even and S̆^ν_,^k (x) = 0 unless k + ν is odd, and write k + p = (k + ν) + (p − ν). If k + ν is even and p − ν is odd or k + ν is odd and p − ν is even, then k + p is odd and thus μ_k+p+2 = 0. If k + ν is odd and p − ν is odd or if k + ν is even and p − ν is even, then using similar arguments we find μ_k+p+1 = 0.

Proposition A.2

Under Conditions A, B, and O, we have

$$\begin{array}{l}var(\nu !h^{-\nu }{Z}_n)={\mathit{e}}_{v+1}^{\top }{\mathit{S}}^{-1}{\mathit{S}}^{\ast }{\mathit{S}}^{-1}{\mathit{e}}_{v+1}\frac{{(\nu !)}^2({\tau }^2{f}_X)\ast f_U(x)}{f_X^2(x)n{h}^{2\beta +2\nu +1}}\\ +o\left(\frac{1}{n{h}^{2\beta +2\nu +1}}\right).\end{array}$$

Proof

Let U_n as in the proof of Theorem 1. We have

$$var(U_{n,i})=var(P_{n,i})+var(Q_{n,i})+2cov(P_{n,i},Q_{n,i}).$$

We split the proof into three parts.

1. To calculate var(P_n,i), note that

   $$\begin{array}{l}E[\{Y_i-m(x)\}{K}_{U,k,h}(W_i-x)]\\ =\int \{m(x+h\upsilon )-m(x)\}{\upsilon }^{k}K(\upsilon )f_X(x+h\upsilon )d\upsilon =O(h),\end{array}$$

   and, noting that each K_U,k is real, we have,

   $$\begin{array}{l}E\left[{\{Y_i-m(x)\}}^2{K}_{U,k,h}(W_i-x)K_{U,k^{\prime },h}(W_i-x)\right]\\ =\int E\left[{\{Y_i-m(x)\}}^2\mid X=\upsilon \right]E[K_{U,k,h}(W_i-x)\\ \times K_{U,k^{\prime },h}(W_i-x)\mid X=\upsilon ]f_X(\upsilon )d\upsilon \\ =\int \int {\tau }^2(\upsilon )K_{U,k,h}(\upsilon +u-x)K_{U,k^{\prime },h}(\upsilon +u-x)f_U(u)f_X(\upsilon )dud\upsilon \\ =h^{-1}\int \int {\tau }^2(x+hz-u)K_{U,k}(z)K_{U,k^{\prime }}(z)f_U(u)f_X(x+hz-u)dudz\\ =h^{-2\beta -1}({\tau }^2{f}_X)\ast f_U(x){(-1)}^{k^{\prime }}{i}^{-k-k^{\prime }}\frac{1}{2\pi c^2}\int \mid t{\mid }^{2\beta }\\ {\phi }_K^{(k)}(t){\phi }_K^{(k^{\prime })}(t)dt+o(h^{-2\beta -1}),\end{array}$$

   where we used (B.1) of Delaigle et al. (2008), which states that

   $$\begin{array}{l}\underset{n\to \infty }{lim}{h}^{2\beta }\int K_{U,k}(\upsilon )K_{U,k^{\prime }}(\upsilon )g(x-h\upsilon )d\upsilon \\ =i^{-k-k^{\prime }}{(-1)}^{-k^{\prime }}\frac{g(x)}{c^2}\frac{1}{2\pi }\int \mid t{\mid }^{2\beta }{\phi }_K^{(k)}(t){\phi }_K^{(k^{\prime })}(t)dt\end{array}$$

   with c as in (7). Finally

   $$\begin{array}{l}cov\left[\{Y_i-m(x)\}{K}_{U,k,h}(W_i-x),\{Y_i-m(x)\}{K}_{U,k^{\prime },h}(W_i-x)\right]\\ =h^{-2\beta -1}({\tau }^2{f}_X)\ast f_U(x){(-1)}^{k^{\prime }}{i}^{-k-k^{\prime }}\frac{1}{2\pi c^2}\int \mid t{\mid }^{2\beta }{\phi }_K^{(k)}(t){\phi }_K^{(k^{\prime })}(t)dt+o(h^{-2\beta -1}),\end{array}$$

   and thus

   $$var(P_{n,i})=h^{-2\beta -1}({\tau }^2{f}_X)\ast f_U(x)\sum _{k,k^{\prime }=0}^p{S}^{\nu ,k}(x)S^{\nu ,k^{\prime }}(x)S_{k,k^{\prime }}^{\ast }+o(h^{-2\beta -1}).$$

   Now $(S^{\nu ,0},\dots ,S^{\nu ,p})={\mathit{e}}_{v+1}^{\top }{\mathit{S}}^{-1}{f}_X^{-1}(x)$, which implies that

   $$var(P_{n,i})=h^{-2\beta -1}{f}_X^{-2}(x)({\tau }^2{f}_X)\ast f_U(x){\mathit{e}}_{\nu +1}^{\top }{\mathit{S}}^{-1}{\mathit{S}}^{\ast }{\mathit{S}}^{-1}{\mathit{e}}_{\nu +1}+o(h^{-2\beta -1}).$$

2. To calculate var(Q_n,i), note that E{K_U,k+j,h(W_i − x)} = ∫ v^k+jK(v)f_X(x + hv) dv = O(1) and |E{K_U,k+j,h(W_i − x)K_{U,k′+j′,h}(W_i − x)}| = O(h^−2β−1), by Lemma B.6 of Delaigle et al. (2008), which implies that

   $$cov\{K_{U,k+j,h}(W_i-x),K_{U,k^{\prime }+j^{\prime },h}(W_i-x)\}=O(h^{-2\beta -1})$$

   and var(Q_n,i) = O(h^−2β+1), which is negligible compared with var(P_n,i).

3. We conclude from (1) and (2) that var(U_n,i) = var(P_n,i){1 + o(1)}, which proves the result.