Just a Proton: Distinguishing the Two Electronic States of Five-Coordinate High-Spin Iron(II) Porphyrinates with Imidazole/ate Coordination

Abstract

We report detailed studies on two S = 2 electronic states of high-spin iron(II) porphyrinates. These two states are exemplified by the five-coordinate derivatives with either neutral imidazole or anionic imidazolate as the axial ligand. The application of several physical methods all demonstrate distinctive differences between the two states. These include characteristic molecular structure differences, Mössbauer spectra, magnetic circular dichroism spectroscopy, and integer-spin EPR spectral distinctions. These distinctions are supported by DFT calculations. The two states are characterized by very different spatial properties of the doubly occupied orbital of the high-spin species that are consonant with the physical properties.

Introduction

The wide range of physiological functions carried out by the heme proteins with the same prosthetic group, the iron derivative of protoporphyrin IX, has continued to fascinate and perplex. Some aspects of heme protein function appear to be controlled by obvious changes in the proximal axial ligand to iron. For example, the cytochrome P-450's and NO reductase are coordinated by an anionic cysteine ligand and the catalases are coordinated by an anionic tyrosinate. However, the most common proximal ligand in the heme proteins is the histidyl residue that is equivalent to imidazole, a nominally neutral ligand. Proteins with histidine ligation still maintain a wide variety of functions that include oxygen transport and storage in the globins, oxygen respiration in cytochrome c oxidase and oxygen utilization and oxidation in the peroxidases, oxidases, cyclooxygenase, NO reduction in bacterial NO reductase (NorBC), NO signalling in soluble guanylate cyclase (sGC), and NO transport in nitrophorins.

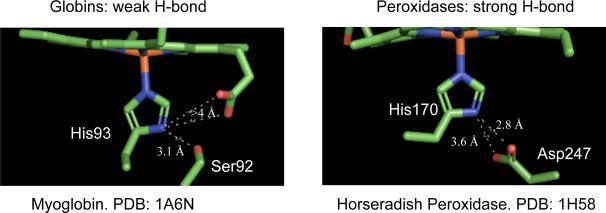
A common feature in many of these systems is the appearance of a hydrogen bond to the proximal histidine ligand as shown in Figure 1 for deoxymyoglobin¹ and horseradish peroxidase.² The strength of these hydrogen bonds is thought to vary from very weak proton donation to complete donation to form the imidazolate ligand.^3–9 The notion that a strong hydrogen bond has a strong influence on heme protein behavior is longstanding but has been difficult to investigate in a systematic manner. Clearly there are significant differences in the nature of the hydrogen bonds formed to the proximal histidine of the heme proteins. Three distinctly different types of hydrogen bonds are formed: the globins and a number of other proteins form a weak hydrogen bond between histidine and a nearby carbonyl or alcohol group, the peroxidases that are hydrogen-bonded to a conserved aspartate and the oxidases that are hydrogen-bonded to a conserved glutamate. The idea continues to appeal that in the peroxidases, which have a conserved aspartate that is hydrogen-bonded to the histidine, the histidine shows imidazolate-like character. This strong hydrogen bond is thought to stabilize higher oxidation states of iron and to distinctly alter the chemical behavior of the peroxidases relative to the globins. Nevertheless, the role of this hydrogen bond is still one of the unresolved issues concerning the peroxidases.

Figure 1.

Comparison of the coordination group geometries of the high-spin iron(II) porphyrinates with 2-methylimidazole (left) and imidazolate (right) as the axial ligand.

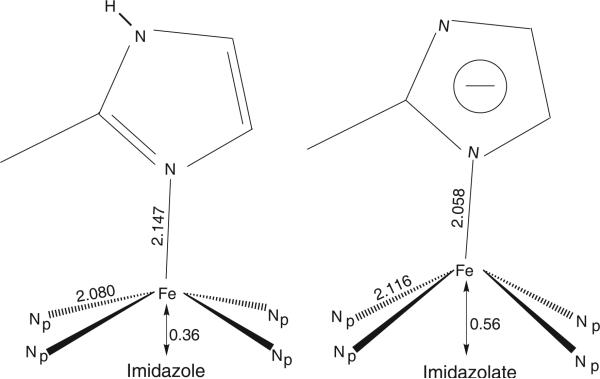
As part of a systematic study of five-coordinate iron(II), we have synthesized and characterized a number of five-coordinate imidazole- and imidazolate-ligated iron(II) porphyrinate derivatives.^10–15 This work reports the effects observed on the molecular and electronic structure when an imidazole ligand in five-coordinate iron(II) porphyrinate derivatives of the type [Fe(Por)(2-MeHIm)]¹⁶ is deprotonated.¹² Both imidazole- and imidazolate-ligated iron(II) porphyrinates exhibit an S = 2 (quintet) ground state, but the structural parameters of the coordination group are distinct with both axial and equatorial bond distance differences and large differences in the displacement of iron from the porphyrin plane. These differences are schematically depicted in Figure 2 for the iron(II) derivatives with imidazole and imidazolate as the axial ligand and where averaged values for several examples of each have been given.

Figure 2.

Comparison of the coordination group geometries (averaged values) of the high-spin iron(II) porphyrinates with 2-methylimidazole (left) and 2-methylimidazolate (right) as the axial ligand.

In addition to the structural differences, characterization by Mössbauer spectroscopy showed that the imidazole derivatives were electronically quite distinct from the imidazolate complexes. Measurements in applied magnetic field allowed the determination of the sign of the quadrupole splitting that was found to be negative for all imidazole derivatives (V_zz < 0) and positive (V_zz > 0) for the imidazolate species. Moreover, the asymmetry parameter for the imidazole species was found to be very large, whereas that for the imidazolate derivatives was small. The differences in the Mössbauer spectra obtained in applied magnetic fields indicate that the doubly occupied d orbital is different in the two classes. This change in the d-electron configuration is clearly consistent with all observed differing features of the two classes. These results are strikingly similar to those observed for protein examples. Reduced HRP was studied by Mössbauer spectroscopy and compared with deoxymyoglobin.^{17, 18} These Mössbauer studies, in a strong magnetic field, showed remarkable differences between reduced HRP and deoxymyoglobin even though both are five-coordinate hemes with histidine as the axial ligand. Reduced HRP has a positive quadrupole splitting constant and a rather small asymmetry value,¹⁸ whereas deoxyMb has a negative value of the quadrupole splitting constant and a large asymmetry constant.¹⁹ To our knowledge, these Mössbauer measurements in applied magnetic field are the only ones available for iron(II) heme proteins with a proximal histidine, although deoxymyoglobin and deoxyhemoglobin have been often measured.

These results led us to conclude that there are at least two S = 2 states of high-spin iron(II) porphyrinates with distinctly different d-electron configurations that arise from proximal ligand effects. The one class of high-spin iron(II) derivatives, which we will call Class N, is represented by the coordination of neutral nitrogen donors in small molecule systems and in the proteins by deoxymyoglobin and deoxyhemoglobin. The second class, which we will call Class A, is represented by the coordination of anionic imidazolate and other anions in small molecule systems and reduced HRP in the proteins. The important class of cysteine-ligated hemes and heme proteins also probably belong to this class although this has been established only for heme derivatives.²⁰ In this paper, we explore a number of characterization processes that could provide ways to distinguish between the two classes. These include integer-spin EPR measurements, magnetic circular dichroism spectroscopy, structure, and a reexamination of the Mössbauer fitting analysis of spectra in applied magnetic field. We have also explored DFT calculations and how different functionals replicate (or fail to) the experimental results. We conclude that the distinction of Class N and Class A electronic structures represents a real and useful dichotomy for high-spin iron(II) porphyrinates. We further conclude that all methods tested allow for the detection of electronic state distinctions (or differences) and that they are applicable to a variety of systems.

Experimental Section

General Information

All reactions and manipulations for the iron(II) porphyrinate derivatives were carried out under argon using a double-manifold vacuum line, Schlenkware and cannula techniques. Benzene and hexanes were distilled over sodium benzophenone ketyl. Chlorobenzene was washed with concentrated sulfuric acid, then with water until the aqueous layer was neutral, dried with MgSO₄, and distilled twice over P₂O₅ under argon. Hexanes were distilled over sodium benzophenone. All solvents were degassed prior to use by three freeze/pump/thaw cycles. Ethanethiol (Aldrich) was used as received. 2-Methylimidazole (Aldrich) was recrystallized from toluene/methanol and dried under vacuum. All other chemicals were used as received from Aldrich or Fisher. meso-Tetraphenylporphyrin (H₂TPP) was prepared according to Adler et al.²² and octaethylporphyrin (H₂OEP) was purchased from Mid-century. [Fe(Por)Cl] derivatives were prepared according to a modified Adler preparation,²³ and used to prepare the analogous [Fe(Por)]₂O species.²⁴

Synthesis of [K(2-MeIm⁻)]

In the drybox, 2-methylimidazole (1.52 g, 19 mmol) was dissolved in 20 mL of THF, then KH (0.72 g, 18 mmol) was added slowly. The mixture was stirred for 3 h, then filtered by cannula, the resulting solid was dried under vacuum at 60 °C for 6 h, collected, and stored under argon.

Synthesis of [Fe(Por)] Derivatives

[Fe(Por)]₂O (0.03 mmol) was dissolved in 10 mL of benzene, and 1 mL of ethanethiol was added by syringe. The mixture was stirred at room temperature for 3 days, then was layered with hexanes for crystallization. Crystalline [Fe(Por)] was collected after several days, stored under argon and used for preparing solutions for the MCD measurements.

Synthesis of [K(222)][Fe(OEP)(2-MeIm⁻)]

[Fe(OEP)]₂O (38 mg, 0.03 mmol) was dissolved in 10 mL of benzene, 1 mL of ethanethiol was added by syringe, and stirred at room temperature for 3 days. The solvent was removed under vacuum and the solid was dried for another hour. A suspension of excess K(2-MeIm⁻) (28 mg, 0.23 mmol) and Kryptofix 222¹⁶ (70 mg, 0.19 mmol) in 15 mL of chlorobenzene was added to the [Fe(II)(OEP)] solid by cannula, then stirred for 1/2 h and cannula filtered to another Schlenk flask. X-Ray quality crystals were obtained after three weeks by liquid diffusion using hexanes as nonsolvent in 8 mm × 250 mm sealed glass tubes.

Synthesis of [K(222)][Fe(TPP)(2-MeIm⁻)]

[Fe(TPP)]₂O (40 mg, 0.03 mmol) was dissolved in 10 mL of benzene, 1 mL of ethanethiol was added by syringe, and stirred at room temperature for 3 days. The solvent was removed under vacuum, the solid was dried for another hour, and then dissolved in 10 mL of toluene. A suspension of excess K(2-MeIm⁻) (24 mg, 0.20 mmol) and Kryptofix 222 (49 mg, 0.13 mmol) in 10 mL of toluene was added to the above solution, the resulting precipitate was cannula filtered, dried under vacuum for 1/2 h, then dissolved in 10 mL of chlorobenzene. The resulting solution was cannula filtered to another Schlenk flask. X-Ray quality crystals were obtained after three weeks by liquid diffusion using hexanes as nonsolvent in 8 mm × 250 mm sealed glass tubes.

Synthesis of [Na(222)][Fe(TPP)Cl]

Crystals of Na(222)[Fe(TPP)Cl] were initially prepared accidentally during the reaction of [Fe(TPP)] with NaN₃ in CH₂Cl₂. [Fe(TPP)]₂O (40 mg, 0.03 mmol) was dissolved in 10 mL of chlorobenzene, and 1 mL of ethanethiol was added by syringe. The mixture was stirred at room temperature for 3 days, then the solution was transferred into a Schlenk flask containing sodium azide (5 mg) and Kryptofix 222 (27 mg, 0.07 mmol). The mixture was stirred for 1 h, the resulting precipitate was filtered and dried under vacuum for 0.5 h. Then it was redissolved in CH₂Cl₂ (6 mL), filtered, X-ray quality crystals were obtained in 8 mm × 250 mm sealed glass tubes by liquid diffusion using hexanes as nonsolvent. There were several different crystals formed, one of which was Na(222)[Fe(TPP)Cl], whose structure is described herein.

Instrumental Techniques

Mössbauer measurements were performed on a constant acceleration spectrometer from 4.2 K to 298 K in small field and at 4.2 K in several fields between 0.75 and 9 T using a superconducting magnet system (Knox College). Microcrystalline solids for Mössbauer measurements were obtained by liquid diffusion in Schlenk tubes using hexanes as the nonsolvent. The solids were isolated in an inert-atmosphere box and immobilized in Apiezon M grease.

MCD spectra were obtained on frozen glasses in the mixed solvent of toluene and methylene chloride (1:1) at liquid He temperatures (1.8-25 K). A CD spectropolarimeter (Jasco 810) with S1 and S20 photomultiplier tubes as detectors were used where the sample compartment was modified to accommodate an Oxford instruments SM4-7T magnetocryostat. Spectral sample solutions were prepared from Fe(TPP) in the presence of excess ligand (and 222 for the anionic derivatives) and concentrations were determined by UV-vis spectroscopy at the same time as the MCD measurements. The samples were frozen in metallic sample compartments between two Infrasil quartz disks separated by 3 mm neoprene spacers. Typical sample concentrations were in the range of 0.2-1.0 mM. (University of Michigan)

X-band EPR spectra of powder and solution samples were recorded on a Bruker 300 spectrometer equipped with an Oxford ESR-910 liquid helium cryostat and a Bruker bimodal cavity for generation of the microwave fields parallel and perpendicular to the static field. The microwave frequency was calibrated with a frequency counter, and the magnetic field was calibrated with a NMR gaussmeter. The sample temperature was calibrated with a carbon-glass resistor (Lake Shore CGR-1-1000) placed in an EPR tube to mimic a sample. The powder samples were prepared in EPR tubes fitted with graded quartz to Pyrex tops and flame sealed. The solution samples were 5-6 mM in chlorobenzene and frozen in standard quartz tubes. All experimental data were collected under nonsaturating microwave conditions with a modulation frequency of 100 kHz. The EPR spectra and temperature dependence were analyzed by diagonalization of the spin Hamiltonian H = S·D·S+βS·g·B. The simulations were generated with consideration of all intensity factors relative to a CuEDTA spin standard which allowed computation of simulated spectra for a specific sample amount. The simulations therefore allow a quantitative determination of signal intensities. The Windows software package (SpinCount) is available for general application (www.chem.cmu.edu/groups/hendrich/facilities/index.html). (Carnegie Mellon University)

DFT Calculations

The structures of the complexes [Fe(TPP)(2-MeHIm)], [Fe(TPP)(2-MeIm⁻)]⁻, and [Fe(TPP)Cl]⁻ were fully optimized without simplifications applying the BP86 functional²⁵ together with Ahlrichs’ TZVP basis set²⁶ using Gaussian 03.²⁷ Zero-field splitting and Mössbauer parameters were calculated for both the DFT-optimized and crystal structures (with hydrogen atoms added in idealized positions) using the program ORCA.²⁸ These calculations were performed with BP86/TZVP, BP86/TZVP with the larger CP(PPP) basis set²⁹ on iron, and B3LYP/TZVP again using CP(PPP) for iron. Here, B3LYP is Becke's three-parameter hybrid functional.³⁰ The Mössbauer isomer shifts were obtained from the calculated total electron densities at the iron nucleus using empirical correlations established by Neese and coworkers.³¹ Orbitals were plotted using GaussView. (University of Michigan)

Results and Analysis

X-Ray Structure

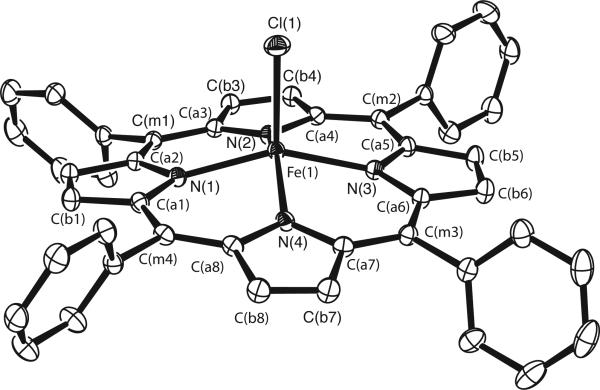
The structure of the [Fe(TPP)Cl]⁻ anion is illustrated in the ORTEP diagram of Figure 3. The anion has many common features with other anionic high-spin five-coordinate iron(II) porphyrinates including the large values of Fe–N_p and the large iron out-of-plane displacements. Selected values are compared in Table 1.^32–36 The strong similarity of [Fe(TPP)Cl]⁻ and [Fe(TpivPP)Cl]⁻ is to be noted. Also to be noted are the common features with the imidazolate structures that were schematically depicted in Figure 2. These include the larger Fe–N_p and Fe out-of-plane displacements –all distinctly different from those of the imidazole complexes. Complete experimental details and experimental results are given in the Supporting Information.

Figure 3.

ORTEP diagram (50% probability ellipsoid) of the [Fe(TPP)Cl]⁻ anion illustrating the atom labeling scheme. Hydrogen atoms have been omitted for clarity.

Table 1.

Selected Distances (Å) for Iron(II) Porphyrinates with Anionic Ligands.

Complex	<Fe–Np >a,b	Fe–Lb	ΔN4b	ref.
[Fe(TPP)Cl]–	2.1161(11)	2.3400(5)	0.56	tw
[Fe(TpivPP)Cl]–	2.108(15)	2.301(2)	0.53	32
[Fe(TPP)(2-MeIm–)]–	2.118(13)	2.056(81)c	0.56	12
[Fe(OEP)(2-MeIm–)]–	2.113(4)	2.060(2)	0.56	12
[Fe(TpivPP)(2-MeIm–)]–	2.11(2)	2.002(15)	0.52	33
[Fe(TpivPP)(NO3)]–	2.070(16)	2.069(4)	0.42	34
[Fe(TPP)(SC2H5)]–	2.096(4)	2.360(2)	0.52	35
[Fe(TpivPP)(SC2H5)]–	2.074(10)	2.324(2)	0.44	21
[Fe(TpivPP)(OC6H5)]–	2.114(2)	1.937(4)	0.56	36
[Fe(TpivPP) (O2CCH3)]–	2.107(2)	2.034(3)	0.55	36

^aAverage Fe–N_p distance.

^bValue in Å.

^cLarge error owing to a disordered ligand.

EPR Spectra

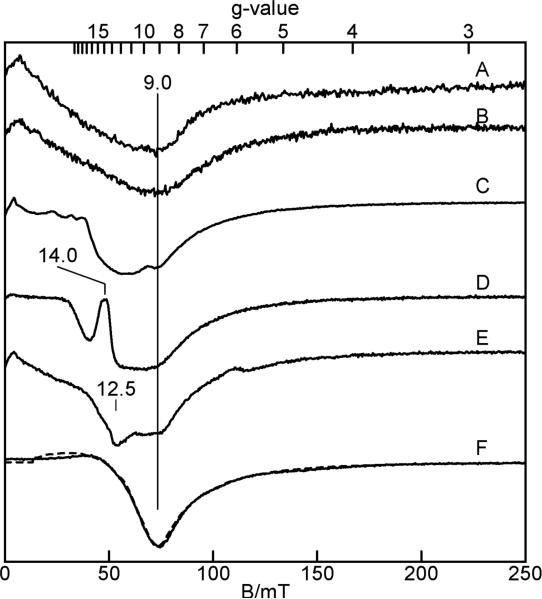
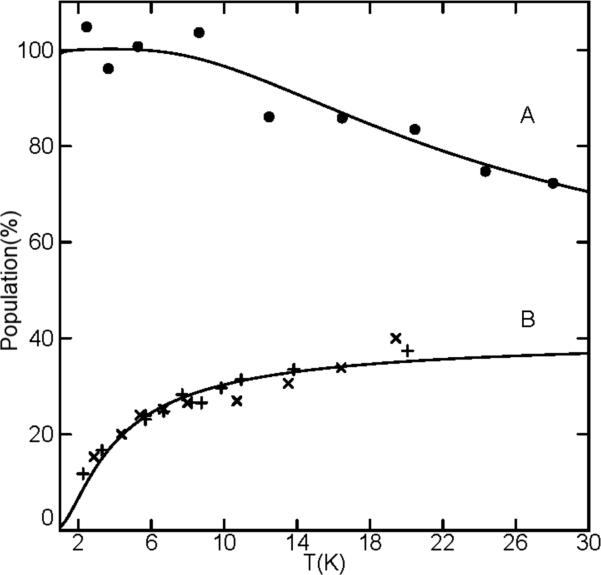
Figure 4 shows parallel-mode X-band EPR spectra of imidazole- and imidazolate-ligated iron(II) porphyrinates. All species display signals near g = 9 indicative of an S = 2 state. Solution samples of [Fe(TPP)(2-MeHIm)] and [Fe(TPP)(2-MeHIm)]₂·2-MeHIm did not show parallel-mode EPR signals. The absence of a solution spectrum is probably the result of modest intermolecular interactions in solution. The spectrum of [Fe(TPP)(2-MeHIm)] (Figure 4A) is nearly identical to that of the sample of [Fe(TPP)(2-MeHIm)]₂·2-MeHIm (Figure 4B) containing the two independent molecules: [Fe(TPP)(2-MeHIm)] and hydrogen-bonded [Fe(TPP)(2-MeHIm)]. This result indicates that the hydrogen-bonded [Fe(TPP)(2-MeHIm)] molecule does not produce an EPR signal, presumably due to a large D and E/D values of this molecule. For large D and E/D, the energy spacing between all spin levels may be too large to observe transitions at the X-band frequency. The temperature dependence of the EPR signal of both samples is shown in Fig. 5B, plotted as signal amplitude (base-to-trough) times temperature. For T > 20 K, signal broadening makes determination of the amplitude unreliable. Both samples show the same trend in signal amplitude with temperature: the signal originate from an excited state doublet. The theoretical curve is the percent population of the uppermost doublet of an S = 2 system with D = +0.9 cm⁻¹ and E/D = 0.1. However, it is not possible to quantitatively simulate this signal with these zero-field parameters. The simulation of the signal from the ground doublet with these parameters matches the spectrum and agrees with the sample amount, but this doublet does not reproduce the temperature dependence shown in Fig. 5B. Thus, we conclude that the magnetic properties of this spin system are not adequately described by a spin Hamiltonian formalism. A similar problem is known for the description of the EPR data of deoxymyoglobin. Deoxymyoglobin shows an EPR spectrum similar that of these Fe(TPP)(2-MeHIm) complexes, and its characteristics are also not adequately described with a spin Hamiltonian.³⁷

Figure 4.

Parallel-mode X-band EPR spectra of (A) Fe(TPP)(2-MeHIm)], powder; (B) [Fe(TPP)(2-MeHIm)]₂·2-MeHIm, powder; K(222)[Fe(TPP)(2-MeIm⁻)], 6 mM in chlorobenzene (C) and powder (D); K(222)[Fe(OEP)(2-MeIm⁻)], 6 mM in chlorobenzene (E) and powder (F). Experimental conditions: temperature 2 K; microwave power, 0.02 mW at 9.3(1) GHz. Simulation parameters (F, dashed line): S = 2, D = −8cm⁻¹, E/D = 0.10, σ(E/D) = 0.02, g_z = 2.26.

Figure 5.

The temperature dependence of the EPR signals of (A) K(222)[Fe(OEP)(2-MeIm⁻)], (B) [Fe(TPP)(2-MeHIm)] (x), and (B) [Fe(TPP)(2-MeHIm)]₂·2-MeHIm (+) plotted as signal amplitude times temperature. The theoretical curves are the percent populations of an S = 2 (E/D = 0.1) system for (A) the lowermost doublet with D = −8cm⁻¹, and (B) the uppermost doublet with D = +0.9 cm⁻¹. Estimate of D-value of [Fe(TPP)(2-MeHIm) complex from the temperature dependence of the EPR signal.

The EPR spectra from the imidazolate-ligated complex K(222)[Fe(TPP)(2-MeIm⁻)] are more complicated (Fig. 4C, D). It appears that both solution and powder samples have multiple species present with features near g = 14 and 9. The temperature dependence of these signals is complicated by the presence of multiple species, but overall suggests D < 0 with signals originating from the ground doublet. In contrast, the EPR spectrum of imidazolate-ligated K(222)[Fe(OEP)(2-MeIm⁻)] shows a single species in the solid state (Fig. 4F). A plot of the signal times temperature is shown in Fig. 5A. The theoretical curve is percent population for the lowermost doublet of an S = 2 system with D = −8cm⁻¹ and E/D = 0.1. A simulation using these parameters for the ground doublet is overlaid on the spectrum (dashed line). This simulation is in quantitative agreement with the spectrum and the sample amount. The solution sample of this complex (Fig. 4E) also shows multiple species.

We can draw two conclusions from the results described here. First, the imidazole- and imidazolate-ligated iron(II) porphyrin complexes exhibit very different electronic properties. Based on the determination of the sign and magnitude of the D-value, we can conclude that the electronic structures of these complexes must be different. Second, these complexes show a parallel-mode EPR signal indicative of electronic properties with significant distortion from axial symmetry. This finding correlates well with crystallographic data which shows that the Fe–N_Im bond is not along the heme normal.

Mössbauer Spectra

Mössbauer spectra for both imidazole and imidazolate-ligated derivatives have been measured in strong applied magnetic fields and previously reported.^11–15 The two classes were found, without question, to have opposite values for the sign of the quadrupole splitting. Quadrupole splitting values for the imidazole-ligated derivatives were in the range of 1.96 to 2.40 mm/s at 4.2 K with negative sign for the value, whereas those for imidazolate were in the range of 3.60 to 3.71 mms/s and with positive signs. However in the initial fits, the sign of the D-value was not found to be distinctly different in the two classes. The apparent difficulty of assigning the sign of D was commented on in our earliest work on imidazole derivatives.¹¹ Even so, in view of the integer-spin EPR results, the fitting of the previously obtained Mössbauer spectra have been reexamined to determine if the Mössbauer spectra will show sensitivity to the sign of D for the two classes. Our conclusion remains that the sign of D is ambiguous in the fits. Notwithstanding the ambiguity in the sign determination, good simulations of the Mössbauer data can be obtained with the use of the E/D and D parameters given above from the EPR measurements. When there are large values of D, in systems that will be EPR silent, the high-field Mössbauer data can unambiguously determine the sign of D. However, for the smaller D values seen in the imidazolate compounds, integer-spin EPR is crucial for the determination of this sign.

Magnetic Circular Dichroism Spectra

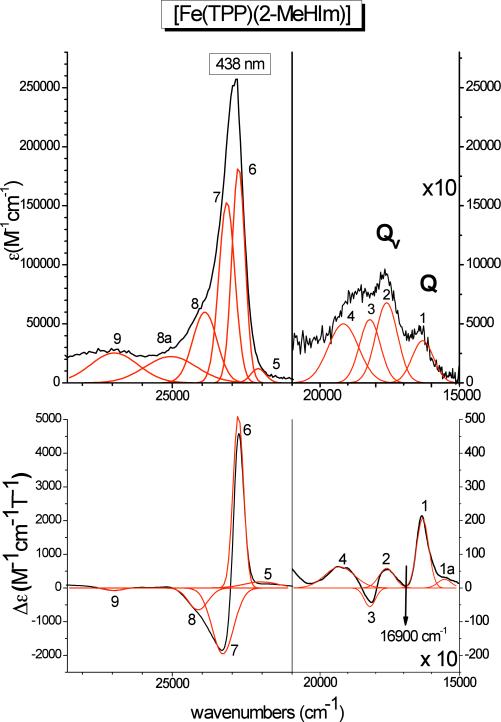
Figure 6 shows the absorption and low-temperature MCD spectra of [Fe(TPP)(2-MeHIm)] (Class N, neutral axial ligand) together with Gaussians obtained from a correlated fit of these data. The obtained band positions are listed in Table 3-A. These spectra show four relatively intense features in the region of the Q and Q_v bands, plus the Soret band around 23000 cm⁻¹, which is resolved into three features in MCD. As shown by one of us previously, the Soret, Q, and Q_v bands of simple metalloporphyrins should give rise to a derivative-shaped C-term signal at low-temperature in MCD due to a low-symmetry splitting of the porphyrin E_g (π*) LUMO of the complexes.³⁸ This causes the Soret, Q, and Q_v excited states, which have E_u symmetry in D_4h, to split into two components, and correspondingly, two bands are observed for the Soret, Q, and Q_v transitions in MCD. Importantly, due to excited state spin-orbit coupling, the two components of these features show opposite signs, and hence, the Soret, Q, and Q_v transitions each give rise to a derivative shaped ‘pseudo-A’ C-term signal in MCD at low (lq. helium) temperature. Additionally, since Q_v is the vibronic band of Q, it should appear about 1250 cm⁻¹ to higher energy of Q as determined by Gouterman.³⁹ With this in mind, the electronic spectra of [Fe(TPP)(2-MeHIm)] can be readily understood. At low energy, one component of the Q band is observed at 16315 cm⁻¹ (band 1). The Q_v band corresponds to the pseudo-A signal at 17608 and 18210 cm⁻¹ (bands 2 and 3). This indicates a relatively large splitting of the two components of the Q excited state of about 600 cm⁻¹ as determined from Q_v. The MCD bands 1 and 2 correspond to the first component of the Q and Q_v exited states, respectively, as evident from (a) their energetic separation of 1293 cm⁻¹, which is very close to the predicted value of ~1250 cm⁻¹, and (b) the fact that both have positive MCD intensity, which means that 2 must be the vibronic band of 1. This raises one question: where is the negative, second component of the Q band located that corresponds to band 3 of Q_v? Using the observed energy difference between bands 2 and 3 of about 600 cm⁻¹, the energy of the negative Q component is estimated to ~16900 cm⁻¹, as indicated in the MCD spectrum in Figure 6. One circumstance that could contribute to the absence of this feature in the MCD spectrum is the large ~600 cm⁻¹ splitting of the Q state, which places this feature just in between the positive bands 1 and 2. Since this feature must be negative, its MCD intensity might then cancel out against these positive features (cf. analysis of the MCD data of [Fe(TPP)(2-MeIm⁻)]⁻ below). In the case of the Soret band, the negative component is split into two bands as shown in Figure 6, which is not unusual, since other porphyrin π → π* transitions appear in this region. These can specifically mix with just one component of the Soret band, and in this way, give rise to the experimentally observed three-band pattern for the Soret transition. This has recently been discussed in detail for [Fe^III(TPP)Cl] by one of us.⁴⁰ The main components of the Soret feature (bands 6 and 7) are located at 22795 and 23310 cm⁻¹, respectively, which is consistent with the observed large energy splitting between the two components of the Q_v band mentioned above. Importantly, the molar MCD intensity of [Fe(TPP)(2-MeHIm)] is surprisingly large, and corresponds to ‘normal’ low-spin ferric hemes as discussed in ref. 40.

Figure 6.

Electronic spectra of [Fe(TPP)(2-MeHIm)] (class N). Top: UV-Vis spectrum measured in CH₂Cl₂ at room temperature. Bottom: MCD C-Term spectrum measured in toluene/CH₂Cl₂ (1:1) at 2 K. The red lines represent a correlated fit of these data (cf. Table 3-A).

Table 3.

Correlated Fit of the UV-Vis Absorption and MCD Spectra Shown in Figures 6–8^a

	MCD		UV-Vis
No.	Position	Δε(M–1cm–1T–1)	Position	ε(M–1cm–1)
A. [Fe(TPP)(2-MeHIm)]
1a	15531	26.0	–	–
1	16315	206.8	16315	3571.4
2	17608	58.5	17608	6785.7
3	18210	–55.5	18210	5357.1
4	19295	62.9	19160	5000.1
5	22031	180.4	22131	12142.9
6	22795	5131.5	22790	183000.0
7	23310	–1956.4	23176	153000.0
8	24134	–649.4	23912	6000.0
8a	–	–	25048	22302.3
9	26932	–77.1	26934	25289.1
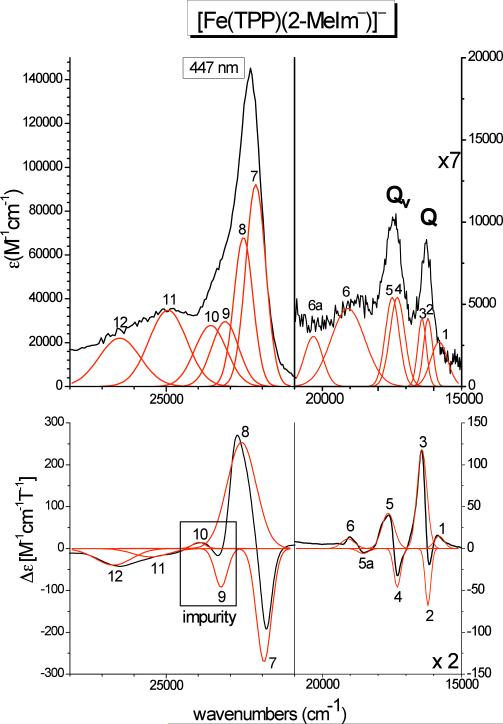
B. [Fe(TPP)(2-MeIm–)]–
1	15807	15.0	15807	2716.0
2	16206	–68.6	16206	4142.9
3	16432	118.51	16432	4142.9
4	17308	–46.3	17308	5428.6
5	17640	42.3	17491	5428.6
5a	18528	–6.0	–	–
6	19082	11.6	19082	4745.9
6a	–	–	20321	3048.8
7	21950	–271.7	22209	92104.2
8	22650	253.7	22592	68100.6
9	23288	–92.9	23162	29607.5
10	23983	14.9	23612	27830.6
11	25482	–20.1	24946	34796.6
12	26642	–39.4	26450	22051.0
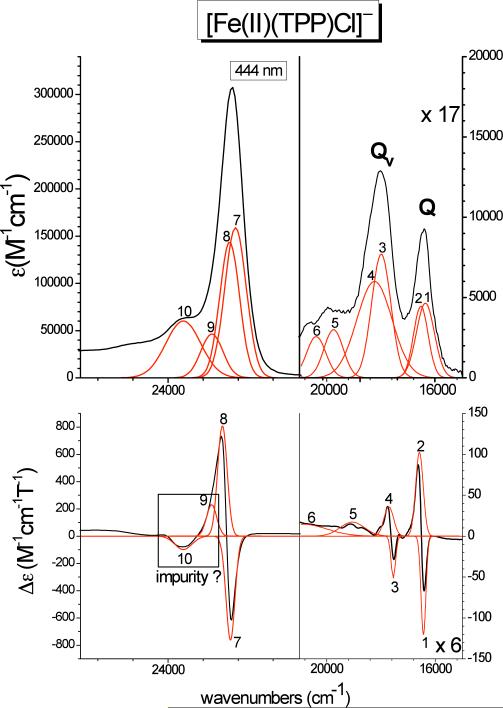
C. [Fe(TPP)Cl]–
1	16438	–120.2	16251	4642.9
2	16587	102.3	16372	4464.3
3	17547	–51.4	17434	7712.8
4	17714	36.2	17614	6000.1
5	19057	17.1	19710	2571.4
6	20864	14.4	20527	2071.4
7	22576	–762.4	22460	159000.0
8	22760	807.7	22595	144000.0
9	23005	233.9	23005	46428.5
10	23652	–98.7	23652	60135.4

^aFor the fit, the minimum number of Gaussians has been used. If a band can be identified from the MCD spectrum, but no corresponding band is necessary to fit the absorption spectrum, then the absorption data is not fit with this feature. Hence, in very few cases, bands appear in the correlated fit of the MCD spectra, but not in the fit of the absorption spectra (or vice versa).

Figure 7 shows the electronic spectra of [Fe(TPP)(2-MeIm⁻)]⁻ (Class A, anionic axial ligand) for comparison. In this case, the Soret, Q, and Q_v features are readily identified from the MCD spectrum via their pseudo-A C-term behavior. Table 3-B summarizes the obtained band positions from a correlated fit of these data. Here, bands 2 and 3, observed at 16206 and 16432 cm⁻¹ in MCD, belong to the Q transition, and bands 4 and 5, located at 17308 and 17640 cm⁻¹ in MCD, are identified with Q_v. The energy differences between the corresponding features 2 and 4 (negative) and 3 and 5 (positive) are 1102 and 1208 cm⁻¹, which is in good agreement with the predicted value of ~1250 cm⁻¹ mentioned above. The relatively low value of 1102 cm⁻¹ is due to the fact that the position of band 2 is not well defined in the fit. Interestingly, the energy splitting between the two components of Q and Q_v is only about 200 – 300 cm⁻¹, which is distinctively smaller than in the case of [Fe(TPP)(2-MeHIm)]. The intensity of the negative band 2 is surprisingly low, but this can be attributed to the fact that this feature is close to the positive bands 1 and 3, and hence, the intensity of band 2 is cancelled out to a large extent, as illustrated by the fit of this feature in Figure 7. This is similar to the case of the missing negative component of the Q band in [Fe(TPP)(2-MeHIm)] discussed above. Due to the lability of [Fe(TPP)(2-MeIm⁻)]⁻ with the imidazolate ligand, it was not possible to prepare MCD samples of this compound without the presence of a slight amount of presumably a ferric impurity. Comparison of different samples shows that bands 9 and 10 actually belong to this impurity. Therefore, the Soret band of [Fe(TPP)(2-MeIm⁻)]⁻ is assigned to bands 7 and 8, observed at 21950 and 22650 cm⁻¹, respectively. Due to the strong overlap of bands 7 – 9, the absolute energies of these features are not well defined. The most striking difference in the MCD spectra of complexes [Fe(TPP)(2-MeHIm)] and [Fe(TPP)(2-MeIm⁻)]⁻ is the significantly lower molar MCD intensity in the case of [Fe(TPP)(2-MeIm⁻)]⁻ by one order of magnitude. This difference relates to the electronic structures of the complexes, and is further analyzed below (cf. DFT Sections). In addition, the signs of the Soret, Q, and Q_v MCD bands are opposite in [Fe(TPP)(2-MeIm⁻)]⁻ compared to [Fe(TPP)(2-MeHIm)], i.e. [Fe(TPP)(2-MeHIm)] shows the sequence +Δε/(−Δε)/+Δε/−Δε/+Δε/−Δε (from lower to higher energy: Q - Q_v - Soret), whereas [Fe(TPP)(2-MeIm⁻)]⁻ (and [Fe(TPP)Cl]⁻, vide infra) exhibits the sequence −Δε/(+Δε)/−Δε/+Δε/−Δε/+Δε. As shown by Michl, this can be explained by a change in the relative HOMO (porphyrin A_1u, A_2u) and LUMO (porphyrin E_g) splitting of the porphyrin ring,⁴¹ where the sequence observed for [Fe(TPP)(2-MeHIm)] is associated with Δ(LUMO) >> Δ(HOMO). [Fe(TPP)(2-MeIm⁻)]⁻ (and [Fe(TPP)Cl]⁻) then correspond to the Δ(HOMO) >> Δ(LUMO) case.

Figure 7.

Electronic spectra of [Fe(TPP)(2-MeIm⁻)]⁻ (class A). Top: UV-Vis spectrum measured in CH₂Cl₂ at room temperature. Bottom: MCD C-Term spectrum measured in toluene/CH₂Cl₂ (1:1) at 2 K. The red lines represent a correlated fit of these data (cf. Table 3-B). .

Finally, Figure 8 shows the absorption and MCD data of complex [Fe(TPP)Cl]⁻ (class A). As in the case of [Fe(TPP)(2-MeIm⁻)]⁻, clean pseudo-A C-term signals are observed for Q, Q_v, and the Soret band, which can therefore readily be identified from the spectra. The Q band corresponds to bands 1 and 2 observed at 16438 and 16587 cm⁻¹, respectively. The vibronic Q_v transition is identified with bands 3 and 4 at 17547 and 17714 cm⁻¹. Therefore, [Fe(TPP)Cl]⁻ shows the smallest splitting between the two components of the Q excited state of only ~150 cm⁻¹. The energy difference between components 1 and 2 of Q and Q_v is 1109 (bands 1 and 3) and 1127 cm⁻¹ (bands 2 and 4), respectively, which is in good agreement with the predicted value of ~1250 cm⁻¹ (vide supra). The main components of the Soret band are assigned to bands 7 and 8 at 22576 and 22760 cm⁻¹, respectively, again reflecting the very small energy splitting between the two components of the E_u excited states as observed for Q. Band 9 could either correspond to a third Soret component as observed for [Fe(TPP)(2-MeHIm)], or an impurity as in the case of [Fe(TPP)(2-MeIm⁻)]⁻. The latter explanation is the most likely, based on the observed pseudo-A behavior of bands 9 and 10 in [Fe(TPP)Cl]⁻, which is very similar to the MCD features of the impurity observed for [Fe(TPP)(2-MeIm⁻)]⁻. Importantly, the molar MCD intensity of [Fe(TPP)Cl]⁻ is again much lower compared to [Fe(TPP)(2-MeHIm)]. This indicates that this difference in the total molar MCD intensity⁴² between Class N and Class A high-spin ferrous hemes constitutes a general trend, and can be employed to distinguish between the two classes of compounds. Correspondingly, these two classes must differ significantly in their electronic structures, which would then explain the apparent difference in total MCD intensity. The experimentally determined order in MCD intensity is: [Fe(TPP)(2-MeHIm)] >> [Fe(TPP)Cl]⁻ > [Fe(TPP)(2-MeIm⁻)]⁻ as evident from Figures 6–8. The electronic structures of these complexes are compared in detail below.

Figure 8.

Electronic spectra of [Fe(TPP)Cl]⁻ (class A). Top: UV-Vis spectrum measured in CH₂Cl₂ at room temperature. Bottom: MCD C-Term spectrum measured in toluene/CH₂Cl₂ (1:1) at 2 K. The red lines represent a correlated fit of these data (cf. Table 3-C).

Density Functional Theory (DFT) Calculations–Geometry Optimizations

In order to determine the electronic structural differences between the two different classes of five-coordinate, high-spin ferrous hemes, we have fully optimized the geometries of the complexes [Fe(TPP)(2-MeHIm)], [Fe(TPP)(2-MeIm⁻)]⁻, and [Fe(TPP)Cl]⁻ using BP86/TZVP without any simplifications. Figures S1–S3 show core diagrams of the fully optimized structures including important bond lengths. In the case of [Fe(TPP)(2-MeHIm)], the Fe–N_p and Fe–N_Im distances of 2.090 (averaged) and 2.183 Å, respectively, are somewhat on the large side of the range of values observed for imidazole complexes (Table 2), but are still in reasonably good agreement with experiment. The out-of-plane displacement, ΔN₄, of iron of 0.35 Å and the orientation of the imidazole relative to the porphyrin plane (dihedral angle ϕ = 18°) are in excellent agreement with the crystal structure of [Fe(TPP)(2-MeHIm)] (exp. values: 0.32 Å and 24°, respectively). The out-of-plane distortions of the TPP ring in both the experimental and calculated structures are complex, and correspond to a combination of different types of distortions⁴³ leading to C₁ symmetries of the cores. As evident from Figure S1, ruffling is more dominant in the calculated structure compared to the experimental result. In comparison, the calculated Fe–N_p and Fe–N_Im distances of 2.119 (averaged) and 2.048 Å, respectively, for the imidazolate [Fe(TPP)(2-MeIm⁻)]⁻ are in excellent agreement with experiment (Table 2). This is also true for the calculated out-of-plane displacement ΔN₄ of iron, which is 0.50 Å (exp. value: 0.56 Å). The largest deviation in the case of [Fe(TPP)(2-MeIm⁻)]⁻ is observed for the orientation of the imidazolate: the calculated value for ϕ = 1° is smaller compared to ϕ = 23° from experiment. We therefore recalculated the structure of [Fe(TPP)(2-MeIm⁻)]⁻ where the angle ϕ was fixed at 23° (Fe(TPP)(2-MeIm⁻)]⁻(fixed)). The structure obtained from this treatment is only +0.7 kcal/mol higher in energy than [Fe(TPP)(2-MeIm⁻)]⁻, and is shown in the Supporting Information, Figure S2. Besides the change in the dihedral angle, the other geometric parameters of [Fe(TPP)(2-MeIm⁻)]⁻(fixed) are very similar compared to the fully optimized structure of [Fe(TPP)(2-MeIm⁻)]⁻. More importantly, the electronic structures of [Fe(TPP)(2-MeIm⁻)]⁻ and [Fe(TPP)(2-MeIm⁻)]⁻(fixed) are similar as discussed below. The nonplanar distortions of the TPP core in the experimental and calculated structures of [Fe(TPP)(2-MeIm⁻)]⁻ are again complex. The experimental core conformation of [Fe(TPP)(2-MeIm⁻)]⁻ shows a clear saddling contribution. In the case of the calculated structures, the imidazolate complexes [Fe(TPP)(2-MeIm⁻)]⁻ and [Fe(TPP)(2-MeIm⁻)]⁻(fixed) show pronounced contributions of the doming distortion, but less saddling. Finally, the calculated Fe–N_p and Fe–Cl distances of 2.119 (averaged) and 2.300 Å, respectively, for the chloride complex [Fe(TPP)Cl]⁻ are again in excellent agreement with experiment (Table 2). The calculated out-of-plane displacement ΔN₄ is 0.51 Å, which also compares well with experiment (exp. value for [Fe(TPP)Cl]⁻: 0.56 Å). As observed before, both the experimental and calculated structures of [Fe(TPP)Cl]⁻ show complex nonplanar distortions of the porphyrin core that differ somewhat between theory and experiment. The distortion observed in the crystal structure corresponds mostly to ruffling and doming, whereas the calculated structure does not predict the ruffling contribution.

Table 2.

Comparison of Observed and Calculated Structural Parameters for High-Spin Iron(II) Porphyrinates

Complex	<Fe–Np >a,b	Fe–Axb	AN4b	ϕ c	ref.
[Fe(TPP)(2-MeHIm)]–Obsd	2.073 (9)	2.127	0.32	24	10
–Calcd	2.090 (8)	2.183	0.35	18.3	twd
[Fe(TPP)(2-MeIm–)]––Obsd	2.118 (13)	2.056	0.56	23.4	12
–Calcd	2.119 (17)	2.048	0.50	1	twd
–Calcd-fixed	2.118 (16)	2.051	0.51	23	twd
[Fe(TPP)Cl]––Obsd	2.113 (19)	2.340	0.56	–	twd
–Calcd	2.119 (19)	2.300	0.51	–	twd

^aAverage value.

^bValue in Å.

^cDihedral angle between imidazole plane and closest Fe–N_p vector, value in degrees.

^dThis work.

In summary, the DFT calculations are able to reproduce the geometries of the high-spin Fe(II) coordination groups well in the three complexes, including Fe–ligand bond lengths, relative orientations of imidazole and imidazolate, and, importantly, the out-of-plane displacement of iron. The cores of the TPP ligands show strong low-symmetry (C₁) distortions, and differences are observed in the core conformations between theory and experiment. However, as a comparison of [Fe(TPP)(2-MeIm⁻)]⁻ and [Fe(TPP)(2-MeIm⁻)]⁻(fixed) shows, the effects of these differences on the electronic structure of the iron(II) center are very small.

Calculation of Zero Field Splitting and Mössbauer Parameters from DFT

As described above, the EPR and Mössbauer measurements have identified dramatic differences in the magnitude and sign of the axial zero field splitting parameter D and the Mössbauer quadrupole splitting ΔE_q between high-spin ferrous heme complexes of classes N and A, as summarized in Table 4. In particular, complexes with neutral imidazole ligands (class N) like [Fe(TPP)(2-MeHIm)] show negative quadrupole splittings ΔE_q and large asymmetry parameters η, whereas complexes with axial anionic imidazolate or chloride ligands (Class A) like [Fe(TPP)(2-MeIm⁻)]⁻ and [Fe(TPP)Cl]⁻ exhibit a positive ΔE_q and a small η. Since ΔE_q reflects the electron distribution of iron in the ground state, these differences indicate that compounds of classes N and A differ in their electronic ground states. DFT calculations on the optimized structures with either BP86/TZVP (see Table S7) or BP86/TZVP using the larger CP(PPP) basis set for iron (see Table 5, left) reproduce this difference in the sign of ΔE_q and the value of η very well. The differences between these two methods are negligible.

Table 4.

Summary of the Experimental EPR and Mossbauer Results for the Investigated High-Spin Ferrous Heme Complexes

	[Fe(TPP)(2-MeHIm)]	[Fe(TPP)(2-MeIm–)]–	[Fe(TpivPP)Cl]–
D (cm–1)	+0.9a	–8b	n/ac
δ (mm/s)	0.85	1.00	1.01
ΔEq (mm/s)	–1.95	+3.60	4.36
η	0.8	0.02	n/ac

^aD = –5.0 cm^–1 had initially been obtained by Lang et al. (J. Chem. Phys. 1979, 71, 4899) from Mössbauer spectroscopy at 6T. This value was later corrected to a positive D of about 5–30 cm^–1 based on variable-field Mössbauer measurements by Scheidt and coworkers (J. Am. Chem. Soc. 2005, 127, 5675). However, Mössbauer fits are not very sensitive to the value of D, and hence, the EPR-based value presented here is much more reliable.

^bDetermined for [Fe(OEP)(2-MeIm^–)]^–.

^cNot available

Table 5.

Summary of the DFT-calculated EPR and Mössbauer Results for High-spin Ferrous Heme Complexes Using Fully Optimized Structures from BP86/TZVP

	BP86/TZVP + CP(PPP) on Fe		B3LYP/TZVP + CP(PPP) on Fe
	[Fe(TPP)(2-MeHIm)]	[Fe(TPP)(2-MeIm–)]–	[Fe(TPP)(2-MeHIm)]	[Fe(TPP)(2-MeIm–)]–
g-values	2.029	2.010	2.041	2.018
	2.036	2.035	2.056	2.047
	2.064	2.050	2.075	2.058
g-iso	2.043	2.032	2.058	2.041
D (cm–1)	–3.74	+2.55	–4.74	–6.21
E/D	0.31	0.21	0.27	0.16
ρ(o) (au–3)	11826.88925	11826.97657	11815.71193	11815.63672
δ (mm/s)	0.738	0.700	0.761	0.789
ΔEq (mm/s)	–2.213	+2.213	2.783	+3.772
η	0.761	0.391	0.992	0.066

Interestingly, our EPR results also show that [Fe(TPP)(2-MeHIm)] and [Fe(OEP)(2- MeIm⁻)]⁻ differ in the sign of the axial zero-field splitting parameter D as shown in Table 4. Because the value of D relates to spin-orbit coupling of the ground state with low-lying excited states, this sign difference in D, however, is much less diagnostic for a difference in ground states than is ΔE_q. Using BP86 calculations on the DFT-optimized structures, the sign change of D is again reproduced, but in the opposite way compared to experiment: whereas experimentally, the imidazole complex has a positive D and for the imidazolate complex D is negative, the DFT calculations predict exactly the opposite trend. In order to determine whether this relates to small structural differences between the experimental (crystallographic) and DFT-optimized structures, we then re-calculated the EPR and Mössbauer parameters for the observed molecular structures. As shown in Table 6, both the trends in ΔE_q and in D are now exactly reproduced in the calculations. In addition, the agreement for η has also distinctively improved. This indicates that the small deviations in the porphyrin structures as described above are significant for the calculation of D, i.e. the excited states energies, whereas the electronic ground state is described well in either case, and ΔE_q is insensitive to this difference.

Table 6.

Summary of the DFT-calculated EPR and Mössbauer Results for High-spin Ferrous Heme Complexes Based on the Experimentally Observed Structures.

BP86/TZVP + CP(PPP) on Fe
	[Fe(TPP)(2-MeHIm)]	[Fe(TPP)(2-MeIm–)]–
g-values	2.0114	2.0002
	2.0409	2.0296
	2.0739	2.0802
g-iso	2.0421	2.0367
D (cm–1)	+3.4077	–2.2767
E/D	0.2917	0.3174
ρ(o) (au–3)]	11827.10921	11827.10552
δ (mm/s)	0.645	0.646
ΔEq (mm/s)	–2.313	+2.335
η	0.751	0.141

Finally, we also tried B3LYP/TZVP calculations (using CP(PPP) on Fe) on the DFT-optimized structures. The results, shown in Table 5, right, do not reproduce the experimental results, i.e. no sign change for either ΔE_q or D is observed. This method is therefore unsuitable. In the following, the electronic structural differences between class N and A high-spin ferrous hemes are therefore analyzed based on BP86/TZVP calculations on the crystal structures. As shown in the Supporting Information, the same conclusions about the electronic ground states of these compounds are drawn from the MO diagrams obtained for the DFT-optimized structures. This again emphasizes that the small structural differences between the experimental and optimized structures of the different compounds do not affect the ground states of these complexes in a significant way, as reflected by the similar ΔE_q values.

Electronic Structure from DFT

In all three complexes, iron(II) is in the high-spin state (S = 2), and hence, the principal d-electron configuration of the metal is [t₂]⁴[e]² or [d_xz, d_yz, d_xy]⁴[d_x²−y², d_z²]. In a spin unrestricted formalism, this means that all α-d orbitals are occupied, and in addition, one of the β-d orbitals is occupied (here, α denotes the majority spin and β the minority spin). Correspondingly, the central questions for the electronic structures of the complexes are (a) which one of the three t₂-type orbitals carries the β-electron, and (b) what is the energy sequence of the remaining two unoccupied β-t₂ orbitals. Because of this, the β-MO diagrams of the three complexes are individually discussed in the following.

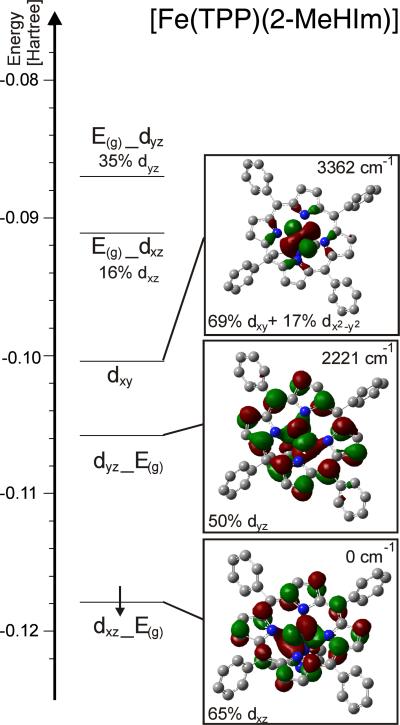
Figure 9 shows the frontier β-MO diagram of [Fe(TPP)(2-MeHIm)], obtained for the observed molecular structure using BP86/TZVP. In this case, the single β-d electron occupies the bonding combination of the d_xz orbital with one component of the unoccupied E_(g) LUMO of the porphyrin ring (cf. Figure S4 for porphyrin orbitals). As can be seen from the contour plot in Figure 9, the ~0.3 Å out-of-plane displacement of iron actually allows for a weak σ backbonding interaction between these orbitals. The resulting MO, labeled d_xz_E_g, has 65% d_xz character. Importantly, the d_xz orbital is located in the plane of the imidazole ligand. The β-d_yz orbital is unoccupied, and is found 2221 cm⁻¹ higher in energy. Again, this orbital shows a σ backbonding interaction with the other component of the E_(g) porphyrin LUMO, and the resulting bonding combination is labeled d_yz_E_g in Figure 9. The d_yz orbital is oriented perpendicular to the imidazole plane, and shows an additional π bonding interaction with an occupied π orbital of the imidazole ligand. The relatively large rhombic splitting between the d_xz and d_yz orbitals is therefore mostly due to the axial imidazole ligand, and not the splitting of the porphyrin E_(g) LUMO caused by the nonplanar distortion of the porphyrin ring (vide supra). Finally, the d_xy orbital is nonbonding, and found at highest energy as shown in Figure 9. This orbital sequence with the d_xz and d_yz orbitals at lower energy than d_xy is uncommon for iron porphyrin complexes, but is consistent with the conclusions drawn earlier from Mössbauer spectroscopy.¹¹ The well-studied low-spin ferric hemes usually show ground states where the d_xy orbital is at lower energy.⁴⁴ But known exceptions of low-spin iron(III) systems where d_xy is at higher energy have π-accepting axial ligands such as weakly basic pyridines^{45, 46} or isocyanides⁴⁷ demonstrating the importance of axial ligation.

Figure 9.

Frontier β-MO diagram of [Fe(TPP)(2-MeHIm)] calculated with BP86/TZVP. The applied coordinate system is chosen such that x and y are located in the porphyrin plane, and z is orthogonal to the porphyrin ring in the direction of the axial ligand. E_(g) refers to the LUMO of the porphyrin as shown in Figure S4 (the index g is put in brackets because of the low symmetry of the porphyrin core). The nomenclature a_b indicates that orbital a interacts with b and that a has a larger contribution to the resulting MO.

The difference in d orbital populations between iron(II) and iron(III) can be rationalized as follows. First, in the ferric oxidation state, the d orbitals are at low energy, and correspondingly, the porphyrin serves mostly as a π donor ligand. This π donation leads to an increase in the energy of the d_xz and d_yz orbitals relative to d_xy. On the other hand, in the ferrous oxidation state, the d orbitals are at high energy, and correspondingly, the porphyrin now serves as a backbonding ligand. This interaction lowers the energy of the d_xz and d_yz orbitals relative to d_xy. Because of the general nature of this effect, we believe that the electronic structure description elaborated for [Fe(TPP)(2-MeHIm)] is in general representative for class N high-spin ferrous porphyrin complexes.

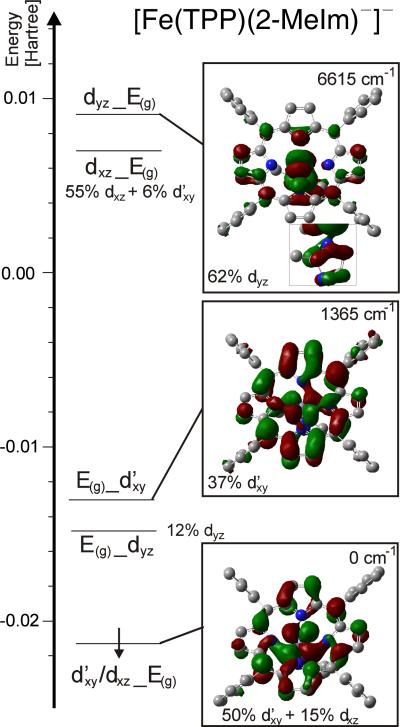
In contrast, the electronic structure of class A complexes shows significant differences. Figure 10 shows the frontier region of the β-MO diagram of [Fe(TPP)(2-MeIm⁻)]⁻, obtained for the observed solid-state structure with BP86/TZVP In this case, the single β-d electron occupies an MO that corresponds to d′_xy with a small admixture of d_xz. This mixing leads to a rotation of the d_xy orbital out of the xy plane. A contour plot of the t₂ type orbital obtained this way is shown in Figure 10. As evident from the contour plot, this rotation of the d′_xy orbital enables a σ backbond with one component of the E_(g) LUMO of the porphyrin. Note that the label d′_xy is used in the following to indicate that this orbital actually corresponds to a combination of the d_xy and d_x²−y² orbitals (~3:1 ratio), which leads to a slight rotation of the d_xy orbital in the xy plane to optimize bonding in the distorted symmetry of the complex. A second combination of d′_xy and the porphyrin E_(g) LUMO is observed only 1365 cm⁻¹ higher in energy than the occupied β-d MO as shown in Figure 10. In summary, the d′_xy orbital is observed at lowest energy in [Fe(TPP)(2-MeIm⁻)]⁻, which is strikingly different from [Fe(TPP)(2-MeHIm)]. This relates to the very large out-of-plane displacement of iron in [Fe(TPP)(2-MeIm⁻)]⁻, which allows for the d′_xy orbital to undergo a backbonding interaction with the E_(g) LUMO of the porphyrin as illustrated by the contour plot of the d′_xy/d_xz_E_(g) MO in Figure 10. In contrast, d_xy is strictly nonbonding in the case of [Fe(TPP)(2-MeHIm)]. Finally, the d_xz and d_yz orbitals are observed at highest energy in the case of [Fe(TPP)(2-MeIm⁻)]⁻, which is due to the fact that imidazolate is a distinctively stronger donor than imidazole. This affects in particular d_yz, which interacts with an occupied π orbital of imidazolate, as evident from the contour plot in Figure 10. This shifts the d_yz orbital to unusually high energy. In contrast, d_xz mixes with an imidazolate (in-plane) σ orbital, which is a weaker interaction, causing the energy splitting between d_xz and d_yz (‘rhombicity’). The principal electronic structure descriptions do not change when the fully optimized structures of these compounds are considered, as evident from Figures S5–S7.

Figure 10.

Frontier β-MO diagram of [Fe(TPP)(2-MeIm⁻)]⁻ calculated with BP86/TZVP. The applied coordinate system is chosen such that x and y are located in the porphyrin plane, and z is orthogonal to the porphyrin ring in the direction of the axial ligand. E_(g) refers to the LUMO of the porphyrin as shown in Figure S4 (the index g is put in brackets because of the low symmetry of the porphyrin core). The nomenclature a_b indicates that orbital a interacts with b and that a has a larger contribution to the resulting MO.

With the electronic structure descriptions of [Fe(TPP)(2-MeHIm)] and [Fe(TPP)(2-MeIm⁻)]⁻ clearly laid out, an interesting question is how the properties of class A complexes change if the anionic axial ligand is an isotropic π donor, such that d_xz and d_yz experience the same level of energetic destabilization. In order to evaluate this case, we consider the chloride complex [Fe(TPP)Cl]⁻. Figure S7 shows the β-MO diagram for this complex in the frontier region, which strikingly supports our previous analysis. In this case, the β-d electron again occupies an orbital that has predominant d_xy character (50% d_xy plus 11% d_xz as shown in Figure S7). Both the d_xz and d_yz orbitals are now high in energy, due to chloride having equivalent 3p_x and 3p_y donor orbitals. This supports the previous conclusion that d_yz in [Fe(TPP)(2-MeIm⁻)]⁻ is high in energy because of imidazolate being a strong π donor.

Based on these results, the two important general differences between the electronic structures of class N and class A five-coordinate high-spin ferrous heme complexes are: (a) d_xy is low in energy in class A compounds due to the large out-of-plane displacement of iron, which allows for a backbonding interaction with the porphyrin E_(g) LUMO, and (b) d_yz and d_xz are high in energy due to the presence of strong anionic (π) donor ligands. As a consequence, the β-d electron occupies the d_xz orbital in class N compounds, and the d_xy orbital in class A complexes. This difference in electronic structure is directly reflected by the molar MCD intensities of these complexes, as further evaluated below.

Electronic Structure and MCD Intensity

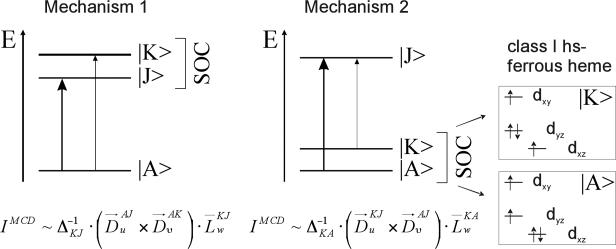
With the electronic structure descriptions of all three complexes in hand, we can now analyze the observed drastic difference in low-temperature MCD intensities between these complexes. In general, MCD C-term intensity is due to two different mechanisms, which require spin-orbit coupling between two energetically close excited states (mechanism 1), or the ground state and a low-lying excited state (mechanism 2). Figure 11 shows illustrations of these mechanisms, together with mathematical expressions for the resulting MCD C-term intensities as derived in Ref. 48. Here, ${\overrightarrow{D}}_u^{AJ}$ is the transition dipole moment for the electronic transition between states |A〉 and |J〉 in direction u (u, v, w = x, y, z), ${\Delta }_{KJ}^{-1}$ is the energy difference between states |K〉 and |J〉, and ${\stackrel{‒}{L}}_w^{KJ}$ is the reduced SOC matrix element between states |K〉 and |J〉 in direction w. These equations show that C-term intensity requires two orthogonal electric dipole allowed transitions, where either the excited states (mechanism 1) or the ground and a low-lying excited state (mechanism 2) are spin-orbit coupled in a direction orthogonal to the plane formed by the two transition dipole moments. Previous work of one of us has shown that for the Soret, Q, and Q_v bands, mechanism 1 leads to a pseudo-A (derivative-shaped) C-term signal in the MCD spectrum.³⁸ This is due to the fact that metalloporphyrins do not show strict four-fold symmetry, leading to a small energy splitting between the two components of the E_(g) LUMO of the porphyrin. Since the Soret, Q, and Q_v bands are mostly in-plane (x, y) polarized, the corresponding excited states can then spin-orbit couple in the z direction (w = z in mechanism 1). Besides this, mechanism 2 becomes important when low-lying (ligand field) excited states are available, for example in the case of low-spin ferric porphyrins. As one of us has shown recently, the two different electron configurations [d_xy]²[d_xz, d_yz]³ (unpaired electron located in the d_xz or d_yz orbital) and [d_xz, d_yz]⁴[d_xy]¹ (unpaired electron located in d_xy) differ significantly with respect to SOC in z direction, and hence, can be distinguished using low-temperature MCD spectroscopy (see Discussion in ref. 40). In a similar fashion, the MCD intensity differences between all three complexes investigated here relate to mechanism 2, i.e. changes in the t₂-type β-d orbitals. Indeed, as described above, all three compounds differ quite strongly in the properties of these orbitals. In the following, we will use the observed Soret band MCD intensity to compare the properties of all complexes.

Figure 11.

MCD C-term mechanisms (left, middle), and example for mechanism 2 for class N five-coordinate high-spin ferrous heme complexes like [Fe(TPP)(2-MeHIm)] (right).

Assuming that state |K〉 in mechanism 2 is a low-lying ligand field excited state, and keeping in mind that the Soret band is x, y polarized, the C-term intensity for this feature is predominantly generated by SOC in the z direction. The corresponding reduced SOC matrix element between the ground state |A〉 and the low-lying excited state |K〉 is defined as (cf. mechanism 2 in Figure 11):

$${\stackrel{‒}{L}}_z^{KA}=\mathrm{Im}\langle K\mid {\mathbf{H}}_{SOC}^z\mid A\rangle ,$$ (1)

where ${\mathbf{H}}_{SOC}^z={\sum }_A\xi \left(r_A\right)l_{A,z}$ (the integrals over the spin functions have already been taken into account in the derivation).⁴⁸ Here, the sum runs over all atoms A of the molecule, ζ(rA) is the radial SOC operator of atom A, and l_A,z is the angular momentum operator l_z on center A. Using the LCAO approximation for molecular orbitals, i.e. $\mid K\rangle ={\sum }_r{c}_r{\varphi }_r$ and $\mid A\rangle ={\sum }_s{c}_s{\varphi }_s$, and neglecting two- and three-center integrals, the total SOC contribution becomes:

$$\frac{\mathrm{Im}\langle K\mid {\mathbf{H}}_{SOC}^z\mid A\rangle }{{\Delta }_{KA}}=\frac{\mathrm{Im}\left[\sum _A{\zeta }^A\sum _{r,s}\langle c_r{\varphi }_r^A\mid l_{A,z}\mid c_s{\varphi }_s^A\rangle \right]}{{\Delta }_{KA}}$$ (2)

where ζ^A is the one-electron spin-orbit coupling constant of atom A. Importantly, the value of this integral is dominated by the contributions of iron d orbitals for two reasons: (a) the SOC constant ζ_3d for iron(II) is about 400 cm⁻¹,⁴⁹ which is much larger than SOC constants for light elements like C and N, and (b) since $l_{A,z}\mid p_z^A\rangle =0$, the integrals in eqn. 2 should all vanish for pure porphyrin π or π* MOs. Although the d orbitals in the complexes all show quite large admixtures of the porphyrin E_(g) LUMO π* orbitals (vide supra), these contributions can therefore be neglected for the SOC matrix elements in eq. 2, which become:

$$\frac{\mathrm{Im}\left[\sum _A{\zeta }^A\sum _{r,s}\langle c_r{\varphi }_r^A\mid l_{A,z}\mid c_s{\varphi }_s^A\rangle \right]}{{\Delta }_{KA}}=\frac{\mathrm{Im}\left[{\zeta }^{Fe}\sum _{r,s}\langle c_r^d{\varphi }_r^{\mathrm{d}}\mid l_z\mid c_s^{\mathrm{d}}{\varphi }_s^{\mathrm{d}}\rangle \right]}{{\Delta }_{KA}}$$ (3)

where the ϕ^d now refer to the principal d orbitals of iron. Equation 3 can be used to obtain qualitative insight into the relative MCD C-term intensities for the three complexes of interest. A quantitative evaluation is prohibited by the fact that the intensity contribution from mechanism 1 is not exactly known, but should at least be quite similar for the three complexes of interest.

For [Fe(TPP)(2-MeHIm)], the four lowest lying excited states (using the nomenclature from Figure 9) give rise to the four contributions:

$$\begin{array}{cc}\mathrm{Im}\left[{\zeta }^{Fe}\langle {\mathrm{d}}_{yz}\_E_{\left(\mathrm{g}\right)}\mid l_z\mid {\mathrm{d}}_{xz}\_E_{\left(\mathrm{g}\right)}\rangle \right]\hfill & \mathrm{Im}\left[{\zeta }^{Fe}\langle {\mathrm{d}}_{xy}\mid l_z\mid {\mathrm{d}}_{xz}\_E_{\left(\mathrm{g}\right)}\rangle \right]=0\hfill \\ \mathrm{Im}\left[{\zeta }^{Fe}\langle E_{\left(\mathrm{g}\right)}\_{\mathrm{d}}_{xz}\mid l_z\mid {\mathrm{d}}_{xz}\_E_{\left(\mathrm{g}\right)}\rangle \right]=0\hfill & \mathrm{Im}\left[{\zeta }^{Fe}\langle E_{\left(\mathrm{g}\right)}\_{\mathrm{d}}_{yz}\mid l_z\mid {\mathrm{d}}_{xz}\_E_{\left(\mathrm{g}\right)}\rangle \right]\hfill \end{array}$$

Since SOC has to be active in the z direction, the matrix elements 〉d_xy|l_z|d_xz〈 and 〉d_xz|l_z|d_xz〈 vanish. Importantly, this means that d_xy cannot contribute to MCD intensity for x, y polarized transitions. In addition, Im〉d_yz|l_z|d_xz〈 = 1.⁴⁹ Using the ground state molecular orbital coefficients, and the orbital energies as a rough approximation for the corresponding excited state energies from Figure 9, one can estimate that the contribution from 〈d_yz_E_(g)|l_z|d_xz_E_(g)〉 will be dominating. (From TD-DFT: d_yz_E(g) excited state = + 1543 cm⁻¹.) The same type of analysis can be applied to [Fe(TPP)(2-MeIm⁻)]⁻, which allows us to approximate the C-term intensity ratio between complexes [Fe(TPP)(2-MeHIm)] and [Fe(TPP)(2-MeIm⁻)]⁻. In the case of [Fe(TPP)(2-MeIm⁻)]⁻, the dominating contribution to MCD intensity comes from the integral 〈d_yz_E_(g)|l_z|d′_xy/d_xz_E_(g)〉. (From TD-DFT: d_yz_E(g) excited state = + 5741 cm⁻¹.) Considering the main d-orbitals of complexes [Fe(TPP)(2-MeHIm)] and [Fe(TPP)(2-MeIm⁻)]⁻, the MCD C-term ratio between complexes [Fe(TPP)(2-MeHIm)] and [Fe(TPP)(2-MeIm⁻)]⁻ is roughly estimated to be ~6:1. (Using TD-DFT excited state energies, the ratio becomes 7:1.) This number is somewhat low compared to experiment, which could be due to the fact that (a) the orbital energies are only crude approximations of the corresponding excited state energies, and more importantly, (b) the occupied β-d orbital of [Fe(TPP)(2-MeIm⁻)]⁻ still shows a distinct d_xz admixture, which might not be the case experimentally.

Discussion

This study began with the idea that there are at least two distinctly different electronic states of high-spin iron(II) porphyrinates. This dichotomy was initially seen from the clear structural differences between five-coordinate species with a neutral nitrogen donor versus species with an anionic axial ligand. These differences are schematically depicted in Figure 2 for the iron(II) derivatives with imidazole and imidazolate as the axial ligand. The values shown for imidazolate are the averages for the structures reported earlier¹² and those for the imidazole averages are drawn from previously defined structures.^{10, 11, 13}−¹⁵ Although both types of species are high-spin (S = 2), the coordination geometry differences are striking. As can be seen in Figure 2, the iron displacement from the four nitrogen atom plane and the Fe–N_p bond distances are both significantly larger in the imidazolate than in the imidazole derivatives. Simply put, in the imidazolate derivatives the size of the iron(II) atom appears to be larger than it is in the imidazole species. The structures for a number of iron(II) species with an axial anionic ligand are similar to those of the imidazolate derivatives as well as that of anionic [Fe(TPP)Cl]⁻ reported herein. The strong correspondence between members of the groups strongly suggested that the origin of these structural differences are the consequence of differing electronic structures.

In exploring this possible dichotomy in this paper, we distinguish between two classes of iron(II) porphyrinate derivatives, which we call Class N, those species with neutral, mostly nitrogen donors, and Class A, those species with an anionic axial ligand. Clearly, the charge on the axial ligand has a strong effect on the electronic structure. Because the d-orbitals are all at relatively high energy in the ferrous state, the π-donating character of the anionic ligands leads to the raising of the d_xz and d_yz orbital energies and concomitant relative lowering of the energy of the d_xy orbital which then becomes the doubly occupied orbital. This effect holds whether the axial ligand has two equivalent π-donor orbitals (p_x and p_y), as in the case of atomic anions (halides, oxyanions), or anisotropic (in-plane and out-of-plane) π donor orbitals, as in the case of imidazolate, hydroxide, or thiolate ligands. Keeping in mind that protonation/deprotonation in the imidazole case occurs at the distant ϵ-N atom, formally sp² hybridized, the strong effect of the protonation state of this N-atom on the electronic structure of the complex is certainly surprising. In contrast, the corresponding change in electronic structures in the cases of water versus hydroxide, or thiol versus thiolate complexes is somewhat less surprising, since in these cases the deprotonation occurs directly at the coordinating donor atom, thereby strongly increasing its π-donor abilities. This increase in π donation strengthens the Fe–(anionic ligand) bonds as evident from the shorter Fe–N bond distance in imidazolate versus imidazole complexes. The basis for the electronic structure differences suggest that a five-coordinate aqua species would be a class N whereas a hydroxo species would be class A. Indeed, de Gracia et al.⁵⁰ describe solution-based Raman and UV-vis spectroscopy for five-coordinate high-spin ferrous aqua and hydroxo complexes, which they conclude have the same electronic structures as the analogous imidazole and imidazolate species, respectively. We believe that these class N and A groupings are broadly applicable and we expect additional data will continue and strengthen the classification. Classification of six-coordinate high-spin ferrous species is somewhat limited. We note that the only well-characterized six-coordinate high-spin iron(II) species are those of bis(tetrahydrofuran) species^{51, 52} that are clearly shown to be members of class N by Mössbauer characterization.⁵¹

As we have outlined in Results and Analysis, we have explored several physical approaches to determine whether the methods provide clear-cut distinctions between the two classes of high-spin iron(II) porphyrinates. In every case, within the necessary limitations of a small number of examples, the result is in the affirmative, and we briefly summarize the strengths and limitations of each approach.

I) X-Ray Analysis

Assigning electronic states from the molecular structure of course requires obtaining an X-ray quality crystal and getting a reasonably precise and accurate structure. With those requirements accomplished, the results needed for assignment to the two classes are fairly unambiguous, based on the coordination group parameters and especially the values of Fe–N_p and the displacement of the iron from the mean planes.⁵³ To our knowledge, only the group of high-spin thiolate-ligated hemes have structural parameters intermediate to those of class N and class A. Cataloguing their behavior with other physical methods is still not complete, but their position as members of class A seems certain based on the available Mössbauer data.²¹ Finally and unfortunately, the X-ray method is not easily applicable to the assignment of the electronic structure of the heme centers of proteins.

II) Mössbauer Spectroscopy

The measurement and fitting of Mössbauer spectra obtained in high field leads to the unequivocal assignment of the sign of ΔE_q. The sign of ΔE_q for all members of class N is negative, whereas for all members of class A it is positive. For small molecule systems, obtaining enough material for an adequate signal to noise ratio is relatively straightforward but may present problems for some heme protein samples. The need for obtaining Mössbauer spectra in high applied magnetic field (and concomitant low temperature) in order to unequivocally determine the sign of the quadrupole splitting constant and somewhat larger sample sizes are the major limitation for the use of this method. The use of ⁵⁷Fe-labeled proteins would clearly aid in making good measurements on proteins.

III) EPR Spectroscopy

As described earlier the integer-spin EPR spectra clearly show that the class N examples have a positive sign for D, whereas those for class A have a negative value of D. Establishing the experimental requirements for integer-spin EPR spectra can be challenging, but the major limitation is the magnitude of D, which if too large will render a sample EPR silent. Although it seems that most samples are within the values needed for the X-band range, measurements at higher frequencies can alleviate this issue. As is well-known, the sensitivity of EPR spectroscopy means that relatively small samples of a heme protein are required for good measurements.

IV) MCD Spectroscopy

The difference in the electronic structures of class N and class A high-spin ferrous hemes is clearly reflected by the absolute molar C-term intensities of the signals, as demonstrated here for the first time. Note that MCD also distinguishes between high-spin and low-spin ferric porphyrins in a similar way.⁴⁰ For practical purposes, comparison of the C-term intensities of the very intense Soret bands is best, which also allows for the usage of quite dilute samples (<100 μM). On the other hand, the observed energies of the transitions, and the overall appearance of the spectra do not show much variation in the case of high-spin ferrous hemes, and hence, cannot be used to distinguish between the two classes. The advantage of MCD spectroscopy is the small amount of sample needed in order to determine the C-term intensity of the Soret band. With sample volumes in the range of 2–3 mL, the total amount of protein required is <0.2 μmol. For the measurement, frozen glasses are needed, which are usually easily achieved for proteins by addition of glycerol. Finding a combination of organic, noncoordinating solvents that glass upon freezing for the small molecule studies is a bigger challenge, and sometimes several attempts are needed to obtain a glass of sufficient quality for measurement.

V) DFT Approaches

DFT calculations on the BP86/TZVP level are able to provide good ground state descriptions that are in overall agreement with experiment if based on known experimental structures. As shown in this paper, and as noticed before,^{54, 40} DFT is challenged when it comes to the prediction of the correct out-of-plane distortion of the porphyrin ring, which affects the accuracy of ground state property (EPR, zero-field splitting, and Mössbauer parameters) predictions. Hence, when only DFT-optimized structures are used, the confidence level of the DFT results is lower. The properties that show the least amount of variation between the experimental and optimized structures are (a) the nature of the MO that carries the single β-electron, and (b) the calculated sign of the Mössbauer quadrupole tensor. These two properties show good agreement with experiment even if the somewhat flawed DFT structures are used for the calculations. Hence, high-level DFT calculations can significantly help predict ground states for high-spin ferrous hemes in new complexes or proteins, particularly when correlated with spectroscopic studies.

The initial recognition of two possible types of high-spin iron(II) electronic structures led to this multimethod study to examine various possible experimental methods for discrimination. We have outlined several methods that we show can be used successfully to make distinctions between the two classes of high-spin d⁶ porphyrinates. The two classes are distinguished by the difference in character of the one doubly occupied d orbital. Although there may be some minor differences within each class, in the class N complexes the doubly occupied orbital is effectively perpendicular to the porphyrin plane. Moreover, this orbital is in the plane of the ligated imidazole as shown by the DFT calculations reported herein. In class A species, on the other hand, the doubly occupied orbital has principally d_xy character. Some variation occurs as the π bonding character of the axial ligand changes and there is some symmetry lowering in imidazolate vs. chloride, but the doubly occupied orbital can be considered effectively parallel to the heme plane. We emphasize that we believe that the distinction of the two groups of high-spin iron(II) porphyrinates is generally applicable to all high-spin iron(II) systems.⁵⁵

Does this recognition of electronic state differences provide new insight into the oft-asked question of the role of the proximal ligand in heme proteins? We believe so. The differences must clearly reflect differences in the function of the heme protein; a tenet of many bioinorganic metalloprotein studies is that electronic structure contributes to function. This clearly is seen in the proteins that can be definitively assigned to one of the two classes. Deoxyhemoglobin and -myoglobin, members of class N, are reversible O₂ binders. The O₂ complex has (partial) ferric-superoxide character;⁵⁶ the location of the unpaired electron in a t_2g-type orbital that overlaps with the incoming O₂ is certainly advantageous for O₂ binding. This is yet another indication of how well fine-tuned the active site of Hb and Mb are for O₂ binding and transport. On the other hand, HRP and potentially cytochrome P450, members of class A, are involved in catalytic oxidations and do not reversibly bind O2. In this case, the link to function is likely due to the fact that stronger donating, anionic proximal ligands promote heterolytic O-O bond cleavage, leading to formation of high-valent ferryl intermediates. This has to be avoided in Mb and Hb, so in these cases, the weaker imidazole donor is preferred over imidazolate as in HRP.

Thus to the extent that data are currently available for proteins, they also follow the classification. Now that the possible significance of electronic state differences are known, we expect that further heme protein classification will be made. Currently the best data are from Mössbauer, but as noted in this paper, MCD may become the most generally useful method for categorizing. From the class N and A classification from spectroscopy it might therefore be possible to predict the likely function of a newly discovered heme protein, i.e. whether it might serve as O₂ binder or sensor, or as an O₂ activating peroxidase, hydroxylase, etc.

Another interpretation of the biological importance of the electronic structure differences has been provided by theoretical studies of Jensen and Ryde, who have studied the effects of hydrogen bonding to imidazole on the properties of histidine-ligated heme proteins.⁵⁷ They have noted that hydrogen bonding leads to large changes in the relative energy differences between the high-spin state and the intermediate-spin state. In the presence of weak, or no, hydrogen bonding, the ferrous state shows very small differences between the two spin states. Indeed, the difficulty of predicting the correct ground state for deoxymyoglobin models is demonstrated by the number of DFT calculations that failed to correctly predict the high-spin ground state.⁵⁸ Jensen and Ryde also showed that in the presence of strong hydrogen bonding to histidine, it is conversely the ferric state that shows the small difference between the intermediate- and high-spin states.⁵⁷ They further suggest that it is this difference that leads to the differences in function. In a subsequent paper,⁵⁹ they suggest that the closeness of varying spin states in the deoxy- derivatives is essential for facile O₂ binding and that this is the solution to the spin-forbidden nature of the reaction and to the differing nature of HRP. We do note, however, that Jensen and Ryde did not suggest differences in the ground state descriptions for the different hydrogen-bonded states, which may simply be a reflection of the difficulty of the calculations.

Where else might the issue of the two electronic states in iron(II) be of biological significance? Although we are unaware of any definitive data on the issue, we suspect that proteins like the gas-sensing heme proteins, such as FixL or soluble guanyl cyclase, will found to be members of class N whereas heme proteins involved in O₂ activation will be found to be members of class A. The differences between the class N and A species are not simply the strength of the ligand field. Although it is known that imidazole is a weaker field ligand that imidazolate,⁶⁰ imidazole is clearly a stronger field ligand than chloride, a class A ligand like imidazolate. Thus the distinction is not simply a ligand field parameter. Further developments in the significance of this dichotomy will wait characterization of more heme proteins in one or the other cases.