Family-School Connections and the Transitions of Low-Income Youth and English Language Learners from Middle School into High School

Abstract

The theoretical and policy focus on parental involvement in education has evolved into a consideration of two-way connections between families and schools. Working from a social capital perspective emphasizing the importance of information in periods and domains of uncertainty, this study tested a specific application of this reconceptualization. Multilevel models of the National Education Longitudinal Study (n = 17,899) revealed that youth started high school in higher-level math when parents, middle school personnel, and high school personnel were in contact with each other and when middle school personnel bridged the other two. The observed effects of other family-school patterns on math and of all family-school patterns on science were driven by selection, including adolescents' characteristics selecting them into different family-school configurations. Importantly, multiple forms of family-school communication were related to reduced income and language disparities in math and science coursework, regardless of their associations with coursework in the general population.

Based on extensive research in developmental psychology and other disciplines (Comer, 2004; Eccles & Harold, 1993; Hill et al., 2004), parental involvement in education is widely viewed as integral to boosting academic progress and reducing academic disparities in American schools. This viewpoint, however, is not without its critics, some of whom argue that it focuses too much on parents at the expense of schools and others who question the underlying assumption of causality (Hoover-Dempsey & Sandler, 1997; Thurston, 2005). Sorting out these issues is of vital importance given the continued centrality of parental involvement in numerous large-scale educational policies, including No Child Left Behind (NCLB) (Organization for Economic Cooperation and Development, 1997; U.S. Department of Education, 2007).

Working from a social capital perspective that emphasizes exchanges of information in a social system (Coleman, 1990), this study takes up this challenge. I view parental involvement in the context of two-way streams of communication between home and school intended to promote the academic prospects of youth, especially those from historically disadvantaged groups, by enabling more informed decision-making by all parties involved. The focus on information in this conceptual framework highlights the domains and stages of schooling—and related developmental considerations—in which information gaps are especially conducive to disparities in long-term educational attainment. Translating this framework into a statistical model, however, requires careful attention to the threats to causal inference that often reduce the policy relevance of developmentally-oriented studies (Duncan, Magnuson, & Ludwig, 2004).

To this end, the National Education Longitudinal Study (NELS) is analyzed to determine whether communication among parents, middle school personnel, and high school personnel reduces discontinuity in math/science coursework as students transition from middle to high school, with special attention to two student populations (low-income youth, English language learners or ELLs) widely considered to be at risk for truncated rates of educational attainment. Because students in this transition are adolescents developmentally capable of providing their own input on curricular positioning (Barber & Olsen, 2004), this study attempts to account for the selection role that youth play in the communication patterns between home and school. To promote causal inference, propensity scores and robustness indices will be coupled in a strategy likely to prove valuable to future developmental research (Frisco, Frank, & Muller, 2007). The goal of this study is to combine theory and methods in ways that inject needed specificity into the often vague parental involvement provisions in major policies by identifying concrete actions that some schools can take to create working models of family-school connections.

Parental Involvement in Education as an Evolving Concept

As an aspect of parenting that shapes and responds to the changing needs of youth, parental involvement in education has long interested developmentalists (Eccles, 1992; Grolnick, Benjet, Kurowski, & Apostleris, 1997; Harvard Family Research Project, 2001; Hill, 2001) and other researchers (Alexander, Entwisle, & Olson, 2007; Hoxby, 1998). Generally, young people achieve more when parents are engaged in their education, including providing cognitive stimulation, meeting with school personnel, and participating in school activities (Alexander et al., 2007; Christenson, 2004; Hoover-Dempsey & Sandler, 1997; Ma, 1999; Raver, Gershoff, & Aber, 2007; Sui-Chu & Willms, 1996). Importantly, these patterns vary by children's age, school level, and social/academic skills (Eccles & Harold, 1993) and are stronger in historically “at-risk” groups (Hill, 2001; Okagaki & Frensch, 1998). This evidence, as well as perceptions that involvement is more amenable to large-scale intervention than other aspects of parenting, contributes to its greater incorporation into educational policy than many other family dynamics studied by developmentalists (Crosnoe & Huston, 2007).

Over time, the prevailing conceptual model of parental involvement has evolved from something that parents do to an exchange between home and school, reflecting awareness that the substance and effectiveness of parental involvement is related to how it is elicited and received by schools (Christenson & Sheridan, 2001; Epstein et al., 2002; Patrikakou, Weisberg, Redding, & Walberg, 2005). This exchange view is advocated by many developmental perspectives on education (Hoover-Dempsey et al., 2005; Pianta & Walsh, 1996), especially those rooted in the larger trend in developmental theory (e.g., Bronfenbrenner, 1979; Sameroff, 1983) towards capturing transactions among contexts.

One perspective, social capital, offers insight into why the exchange dimension of parental involvement matters (Lareau, 2004). Social capital refers to the resources for getting ahead in a system that flow through relationship ties. Information that provides a competitive advantage is one socially traded resource, although certainly not the only one (Coleman, 1988). In the realm of education, such information could pertain to, for example, which schools offer some curriculum, how to secure entry into special programs, or the best strategies for home-based skill development (Furstenberg, Cook, Eccles, Elder, & Sameroff, 1999). When family-school connections are formed, they allow the flow of information in both directions—information to parents about what to do for children, information to schools about a child's special needs, talents, and circumstances. This flow promotes academic progress by constructing a broader information base for the formulation of decisions and plans. To the extent that academic disparities are rooted in differences in parents' pool of practical information about both the stated and unstated rules and expectations of the educational system, not in their values or aspirations, family-school connections will support efforts to achieve a more equitable distribution of academic progress (Bryk & Schneider, 2002; Farkas, 1996; Lareau, 1989).

This conceptualization of family-school connections is evident in the policy arena. As a prominent example, NCLB mandates that school personnel and parents come together to devise compacts—and accompanying organization plans—for accomplishing the twin goals of boosting achievement and reducing achievement disparities (Epstein, 2005; Porter & Polikoff, 2007). The incorporation of family-school connections into policy, the enormous amounts of money involved, and the vagueness of direction that is the norm, however, raise critical questions for research. First, how confident can we be that family-school connections have positive effects? Second, how can the concept of family-school connections be translated into concrete action?

Identifying a Specific Application of the Family-School Connections Concept

The purpose of this study is to answer both of these questions. I do so by using the emphasis on information exchange in the social capital perspective to identify a specific, developmentally appropriate form of family-school connections that might achieve the intended academic goals of the general family-school connections theory and policy strategy.

Accurate information is more likely to support effective and equitable decision-making during periods of uncertainty and when multiple options are available. When rules, expectations, and requirements are unclear or differentially clear across groups, students (and entire groups) can lose ground to peers in ways incommensurate with their actual aptitude (Crosnoe & Huston, 2007; Schneider, 2007). For example, school transitions are periods of uncertainty because they represent entry into new social and organizational environments run by people with little knowledge about students' histories. By virtue of their own educational experiences, personal networks, and social standing, some parents know what is needed to get ahead in the new environment or attract that information from others. This phenomenon contributes to the academic disruptions that occur during transitions and their role in academic disparities (Alexander & Entwisle, 1998; Barber & Olsen, 2004; Benner & Graham, 2008). As another example, coursework decisions are made from a range of options that proliferate across school levels. To make appropriate decisions, school personnel must know students' specific abilities and promise, and parents must know what courses are available, what they represent, and what their short- and long-term consequences may be. Indeed, the availability of choice is directly linked to inequality (Lee, Smith, & Croninger, 1997; Powell, Farrar, & Cohen, 1985). This link is more pronounced in secondary math/science coursework than in other subjects because it becomes increasingly differentiated and optional as schooling progresses, is more hierarchical and cumulative, and is a particularly powerful predictor of college matriculation and completion (Riegle-Crumb, Farkas, & Muller, 2006; Shettle et al., 2007).

Following theory, then, family-school connections may bring returns if they encompass communication about coursework options and consequences during the key secondary school transition: middle school to high school. The optimal situation would involve communication among all three sides of the triangle around this transition—parents learning about the available options for students in high school from high school personnel, high school personnel learning more about incoming students and what they need from parents, and the middle school personnel who are more likely to have established ties to both sides representing high schools and advocating for families. With such triangulation, students would be less likely to experience “slippage” in their initial high school math/science level (e.g., lower than prior history and ability would suggest) that is so important to their curricular pathways into college. Less ideal but still potentially valuable would be one of the three actors bridging the other two; for example, middle school personnel consulting with parents and high school personnel even if the latter two do not consult each other. Most problematic would be no communication at all in this triangle.

Development, Disparities, and Causal Inference

This study, therefore, will assess how patterns of communication among families, middle schools, and high schools predict students' initial math/science course level after the transition into high school. This basic model is further specified in three ways.

First, working down to such a specific application of the family-school connections concept brings up a developmental issue. The young adolescents involved demand more autonomy in their academic pathways than children but still require more guidance and support than older adolescents. This tension is one reason why transitions into and out of middle school can be so difficult (Eccles et al., 1993). Moreover, such adolescents have had longer histories in the system—with more time and opportunity to find their niches, develop talents, create personae, identify trouble spots, and be typed by adults—than children, but, compared to older adolescents, they maintain more flexibility in what their future pathways might be and enjoy greater potential for deflection of their extant trajectories (Alexander et al., 2007; Crosnoe & Huston, 2007). Consequently, this study will account for the potential of youths' academic skills, psychological orientations, behaviors, and future expectations to actively or passively contribute to the communication lines that form between their homes and schools.

Second, both theory and policy highlight the potential for family-school connections to reduce academic disparities. Two such disparities center on low-income youth and ELLs (typically first or second generation immigrants), both of whom are targeted by NCLB as at-risk because of past underachievement, relative to peers, on many academic indicators. Importantly, this pattern extends to the math/science pipeline and the transition into high school (Brooks-Gunn & Duncan, 1997; Crosnoe, Lopez-Gonzalez, & Muller, 2004; Fitzgerald, 1995; McLoyd, 1998; Rumberger & Larson, 1998; Stanton-Salazar, 2001). One oft-discussed mechanism for both disparities is the lesser contact between school personnel (middle class and rarely immigrants themselves) and low-income and immigrant parents, which blocks the flow of information to parents about how to work the system for their children and interferes with parents' expression of their wishes and concerns to schools (Lareau, 1989; Suarez-Orozco & Suarez-Orozco, 1995). Thus, information flowing from school to home is far less likely to be redundant for low-income and immigrant parents, and information flowing from home to school is more likely to bridge cultural differences for these same populations. If so, family-school connections would make more of a difference to youth in these populations (net of prior history). thereby reducing two major math/science disparities. This study will test this possibility.

Third, research on family-school connections is vulnerable to misattributed causality, primarily because the factors that select youth into different types of connections can also affect their academic progress. Although true of developmental research in general (Foster & Kalil, 2005), this problem is heightened in this case because of the scale of investment in family-school connections on the policy level. Unfortunately, causal inferences about family-school connections are still somewhat shaky (Thurston, 2005). In assessing a specific application of the family-school connections concept, therefore, this study will employ multiple techniques to address a range of confounds, both known and unknown.

In sum, this study attempts to make causal inferences about the link between family-school communication patterns and the math/science coursework levels of students transitioning from middle school to high school with different backgrounds and histories, paying special attention to any potential added value for low-income and ELL youth. Doing so will contribute to the case for the continued incorporation of family-school connections into educational policy and offer guidance about a specific form such connections can take.

Methods

Data and Sample

NELS is a representative sample of American 8^th graders in 1988. Following a two-stage sampling frame, the National Center for Education Statistics (NCES) randomly selected youth within 1,052 schools for the base year data collection in 1988. Parents, teachers, school administrators, and adolescents were interviewed, and youth also took achievement tests. This data collection was repeated in 1990 (first follow-up, which corresponded to 10^th grade for most sample members), 1992 (second follow-up, 12^th grade), 1994 (third follow-up, two years out of high school), and 2000 (fourth follow-up, eight years out of high school). Dropouts were followed in a separate survey, and the main sample was freshened over time to maintain representativeness. The sample for the present study contained the 17,899 adolescents who were part of the 1990 NELS data release but not in the dropout or freshened samples. This study sample included roughly 75% of the full base year sample with the same proportion of low-income and ELL youth (both statuses defined below).

Measures

Math/science performance

To capture math/science coursework at the start of high school, this study measured courses completed by the start of 10^th grade. Following NELS conventions (see Schneider, Swanson, & Riegle-Crumb, 1998; Stevenson, Schiller, & Schneider, 1994), I organized enrollment patterns into hierarchical sequences. For math, the sequence had nine points: 0 = none, 1 = Remedial Math, 2 = General Math, 3 = Pre-Algebra, 4 = Algebra I, 5 = Geometry, 6 = Algebra II, 7 = Advanced Math (Pre-Calculus, Trigonometry), 8 = Calculus. For science, the sequence had five points: 0 = none, 1 = basic/remedial, 2 = Physical/Earth science, 3 = Biology, 4 = Chemistry, 5 = Physics or Advanced Science. Mean scores (see Table 1 for descriptive statistics for study variables) indicated that the average adolescent had completed Algebra I (4.16) and Physical/Earth science (2.75) by the start of 10^th grade.

Table 1. Descriptive Statistics for Primary Study Variables (n = 17,899).

	Frequency (%)	Mean	Standard Deviation
Focal Adolescent Groups
Low-income youth	24.44	---	---
ELL youth	2.31	---	---
Academic Indicators
Advanced math program (middle school)	30.69	---	---
Algebra I enrollment (middle school)	34.25	---	---
Math test score (middle school)	---	36.77	12.19
Math course level (high school)	---	4.16	1.84
Advanced science program (middle school)	21.91	---	---
Biology I enrollment (middle school)	14.97	---	---
Science test score (middle school)	---	18.98	4.91
Science course level (high school)	---	2.75	1.13
Family-School Connections
Triangulation	23.00	---	---
Middle school as bridge	5.26	---	---
High school as bridge	30.35	---	---
Family as bridge	2.11	---	---
Disengagement	17.45	---	---
Catch-all category	21.83	---	---
Sociodemographic Characteristics
Gender (female)	50.00	---	---
Age (years)	---	13.81	.55
White	66.41	---
African-American	9.53	---
Latino/a	11.41	---
Asian-American	5.92	---
Other race/ethnicity	1.03	---
Parent education	---	3.10	1.16
Family structure (two-parent)	65.17	---	---
First generation immigration status	5.50	---	---
Second generation immigration status	8.87	---	---
Third-plus generation immigration status	85.64	---	---
School characteristics (8th grade)
Comprehensive school	16.81
School sector
Public	78.28	---	---
Catholic	7.59	---	---
Non-Catholic private	9.17	---	---
School location
Urban	24.81	---	---
Suburban	40.40	---	---
Rural	29.85	---	---
School region
Northeast	18.13	---	---
North central	25.18	---	---
South	32.96	---	---
West	18.78	---	---

Objectively, these measures represent ordered sets of hierarchical categories, not continuous variables. Effectively, however, they tap a linear, quasi-continuous process because of the highly standardized, hierarchical nature of math and science coursework in American schools. Indeed, ample evidence attests that these coursework measures are most accurately analyzed as continuous variables akin to educational attainment scales capturing years of schooling (Riegle-Crumb et al., 2006; Stevenson et al., 1994). Thus, the math/science course-taking variables are used continuously.

In order to create a baseline from which to compare adolescents on math/science coursework in high school, this study controlled for several aspects of middle school math/science status, including standardized test performance, program level, and coursework. In 8^th grade, each adolescent completed tests designed by the Educational Testing Service for math (including items on computation, equations, and word problems) and science (including items on life science, earth science, and chemistry). To reduce floor and ceiling effects, NCES created Item Response Theory (IRT) scores that took into account the difficulty of each test item. Also in 8^th grade, adolescents reported whether, that year, they were enrolled in advanced math and science, Algebra I, or Biology I. See Table 1 for descriptive statistics for these six measures.

Focal adolescent groups

The ratio of total family income in the past year to household size (both parent reported in 1988) was compared to federal poverty thresholds. Following a common strategy among states implementing NCLB, I created a binary marker of low-income status, differentiating youth at 185% of the federal poverty line (24%). Also in 8^th grade, adolescents reported how well they understood, spoke, read, and wrote English, and teachers identified limited English proficient (LEP) adolescents. NCES created a marker of LEP status, differentiating those who responded “not well” to any language item and had a teacher identify them as low proficient (2%) from all others. Following convention in recent developmental research (Uchikoshi, 2005), I have replaced the LEP label with ELL.

Family-school communication

In the base year, parents reported whether they had been contacted by personnel at their adolescents' middle schools about course selection and academic programs at adolescents' future high schools. In the first follow-up, receiving high schools reported whether their counselors, teachers, and administrators met with their middle school counterparts to discuss coursework for incoming freshmen. They also reported whether they had parent orientations and parent-teacher meetings for the parents of these incoming freshmen. These items were collapsed into three binary variables (1 = yes, 0 = no): middle school outreach to families, middle school and high school coordination, and high school outreach to families. Next, I combined these three markers to create a family-school communication typology: 1) triangulation (1 on each variable), 2) middle school as bridge (1 on first and second variables), 3) high school as bridge (1 on second and third variables), 4) family as bridge (1 on first and third variables), and 5) disengagement (0 on each). A sixth dummy variable contained all adolescents whose configuration on the three constituent items did not fit any of these patterns, which was used after tests revealed little extra value of breaking this category into its various subcategories.

Because two of three constituent items were reported by school administrators for all adolescents while the third was reported by parents for specific adolescents, this typology mixed school-level and individual-level measures, which created an imbalance when combining these variables. This imbalance was probably why the one category that was based solely on school-level variables (high school as bridge) was modal in the typology. Paradoxically, it potentially over-weighted the family variable in the typology. At the same time, the two high school measures tap whether an adolescent attended a school in which school outreach to parents or middle schools was possible, not whether any given adolescent in that school actually experienced school outreach to their parents or middle school personnel specifically about them. The interpretation of triangulation, then, is a collection of adolescents whose parents were in contact with their middle schools and who were moving into high schools with a policy of contacting the parents and middle schools of incoming students. Finally, of the three items, two were specifically about coursework discussion, but the third (high school outreach to families) was not specific enough to know for sure whether coursework was covered. Clearly, this is a less than ideal strategy for measuring family-school communication. Yet, these variables were the only available tools for studying three-way communication during this transition in a national sample. Thus, the analyses presented here based on this strategy must be viewed as preliminary, setting the stage for future tests with a more fine-tuned measurement approach.

Sociodemographic characteristics

To account for systematic differences in achievement and social contexts, this study controlled for gender (1 = female, 0 = male), age, race/ethnicity (dummy variables for White, African-American, Latino/a, Asian-American, and other), parent education (maximum level in the household, ranging from a 1 for no high school to a 5 for postgraduate education), family structure (1 = two-parent family, 0 = all other family forms), and immigration status (dummy variables for first, second, and third-plus generation based on reports of birthplace of parents and youth).

School characteristics

Additional controls were measured at the school level, including school type (1 = comprehensive, or a school that included middle school and high school grades together, 0 = separate middle and high schools), sector (public, Catholic, non-Catholic private), urbanicity (rural, urban, suburban), and region (Northeast, North Central, South, West).

Plan of Analyses

Analyses proceeded in four basic steps, which I illustrate with high school math coursework. In the first step, this outcome was regressed on the family-school communication dummy variables and then, in sequence, the low-income and ELL markers, the controls, and the middle school math status and performance markers. Results demonstrated the degree to which adolescents experiencing various family-school communication patterns differed in math coursework, net of middle school background and a large number of co-occurring personal, family, school, and structural factors. These models were estimated with the mixed (multi-level modeling) procedure in SAS (Singer, 1998), with students as level 1 and schools as level 2. This approach allowed for more precise estimates of school-level control variables, the correction of NELS design effects (e.g., deflated standard errors due to school-based clustering of data), and sample weighting. Unconditional models revealed that the intra-class correlation—the ratio of between-school and within-school variance—was .16 for math coursework and .14 for science, indicating a preponderance of variation in the outcomes at the student rather than school level.

In the second step, I used propensity score techniques to address the impact of measurable confounds on any observed associations between the family-school communication categories and math coursework in the multi-level models described above (for more on the logic and mathematics of propensity score techniques, see Heckman, Ichimura, & Todd; Rosenbaum & Rubin, 1983). Basically, logistic regressions were estimated predicting each family-school communication category by a large set of covariates. These covariates included all controls listed above as well as three new categories of potential confounds: 1) adolescent characteristics and statuses (e.g., grades, activity participation, locus of control), 2) parent characteristics and behaviors (e.g., school-based involvement, discussion of coursework), and 3) aspects of middle school and high school student body composition (e.g., size, race/ethnic representation, free lunch rates) and curricular organization (e.g., course offerings, modes of course assignment). The appendix describes all extra variables incorporated into the propensity scores. These logistic regressions generated the predicted probabilities of each adolescent being in the focal category of the dependent variable (e.g., experiencing some type of family-school communication), given her or his values on this set of factors. These predicted probabilities (or propensity scores) measured the average characteristics in one communication category in order to identify adolescents in other categories who “looked” like their peers in that one category.

Traditionally, developmentalists have used propensity scores to match cases—with mean values on an outcome in the sample of treatment cases compared to those in the sample of control cases that had the same or similar propensity scores as the treatment cases (Hill, Waldfogel, Brooks-Gunn, & Han, 2005). An alternative is to use the propensity scores as either model weights or covariates, with control cases over- or under-counted in comparisons with treatment cases according to their propensity to be in the treatment group. Compared to conventional matching, these related strategies allow for the full use of data—unmatchable cases are still retained—and have been proven to significantly increase model efficiency, thereby answering many critiques of the propensity score approach (Hirano, Imbens & Ridder, 2003; Morgan & Harding, 2006). For a recent application of this non-matching propensity technique to a developmental question, see Frisco and colleagues' 2007 study of family structure.

The third step involved the calculation of a post-hoc robustness index, the ITCV. This step was taken to address another problem with propensity scores—they only account for confounds that are known and can be directly observed. Some known confounds (e.g., genetic effects) could not be measured in NELS, and still others may not, as of yet, be known. Rather than attempting to control for the impact of such confounds, as would be done with instrumental variable analysis (see Gennetian, Morris, & Magnuson, 2008), calculating the ITCV quantifies just how powerful those confounds would have to be to negate causal inference. In a sense, it estimates a confidence interval for the inference based on a model coefficient (for a complete description of the ITCV, see Frank, 2000). The equation for the ITCV is: r_xy − r^#_xy / 1 −r^#_xy, where r^#_xy = t / SQRT[(n − q − 1) + t²], t is the critical t-value (usually 1.96), n is the sample size, and q refers to the number of model parameters. When covariates are included in the model, the equation becomes: ITCV_{no covariates} × [SQRT (1 − R²_xg)(1- R²_yg)], where g is the set of covariates, R²_xg is the R² value from a regression predicting the focal independent variable by the covariates, and R²_yg is the R² value from a regression predicting the outcome by the covariates.

The post-hoc calculation of the ITCV gauges the minimum product of the correlation between the predictor and confound and the correlation between the outcome and the confound (r_xc × r_yc) needed to make a focal association from the multi-level model (key predictor → outcome) just statistically significant. If the actual (if unknown) product of these correlations—which represents the impact of the unobserved confound on the regression equation—exceeds this threshold, including that unobserved confound in the regression (if it could be observed) would likely alter the causal inference based on that regression. This information is important because it provides a benchmark for assessing the strength of a focal association—low values invalidate the causal inference, while high values indicate robustness of that inference.

Finally, in the fourth step, all interaction terms between low-income and ELL status on one hand and the family-school communication dummy variables on the other were added to the comprehensive multi-level model. These results indicated whether disparities in math course-taking varied across different family-school connection categories.

Results

The Composition and Implications of Five Family-School Communication Categories

As seen in Table 2, young people in the triangulation category were, in general, more socioeconomically advantaged and had higher math/science achievement than youth in the other categories of the family-school communication typology. In particular, they were less likely to be low-income or ELLs. At the opposite extreme were youth in the disengaged category. In between, youth in the middle school as bridge category more closely resembled their peers in the triangulated category, youth in the high school as bridge category more closely resembled their peers in the disengaged category, and youth in the family as bridge category looked like those in the triangulated and middle school as bridge categories in some ways (e.g., test scores) and those in the disengaged and high school as bridge categories in others (e.g., race, school context).

Table 2. Characteristics of Adolescents in Each Family-School Communication Category.

	Means (standard deviations)
	Triangulation (n = 4,117)	Middle School as Bridge (n = 941)	Family as Bridge (n = 378)	High School as Bridge (n = 5,432)	Disengaged (n = 3,124)
Focal Adolescent Groups
Low-income	.20c (.40)	.24b (.43)	.23b (.42)	.24b (.43)	.32a (.47)
ELL	.01b (.12)	.02ab (.14)	.01b (.11)	.03ab (.16)	.04a (.18)
Sociodemographic Characteristics
Female	.49ab (.50)	.47b (.50)	.50ab (.50)	.53a (.50)	.50ab (.50)
White	.77a (.42)	.80a (.40)	.69b (.46)	.61c (.49)	.56d (.50)
African-American	.08c (.27)	.08c (.26)	.13a (.34)	.09bc (.29)	.11ab (.32)
Latino/a	.08b (.28)	.07b (.26)	.10b (.30)	.12a (.33)	.15a (.36)
Asian-American	.06a (.24)	.03b (.17)	.07a (.24)	.07a (.26)	.06a (.23)
Third-plus generation	.86b (.35)	.91a (.29)	.84b (.37)	.85b (.36)	.85b (.36)
Parent education	3.39a (1.13)	3.26b (1.25)	3.35b (1.16)	2.98c (1.14)	2.79d (1.18)
Family structure (two-parent)	.73a (.44)	.73a (.44)	.69b (.46)	.61c (.49)	.58c (.50)
School Characteristics
Public middle school	.84a (.37)	.82a (.38)	.61c (.49)	.78b (.41)	.77b (.42)
Suburban middle school	.49a (.50)	.40b (.49)	.28c (.49)	.38b (.49)	.38b (.49)
Public high school	.88b (.32)	.84c (.36)	.63d (.48)	.91a (.29)	.85bc (.35)
Suburban high school	.48a (.50)	.38b (.49)	.16c (.37)	.40b (.49)	.37b (.48)
Academic Indicators
Math test score (middle school)	39.35a (12.59)	38.70a (11.92)	38.67a (12.70)	36.01b (11.83)	33.74c (11.31)
Science test score (middle school)	19.86a (5.08)	20.03a (4.95)	18.93b (4.99)	18.62b (4.73)	17.90c (4.66)

Note: Means with different subscripts differed significantly (p < .05), as determined by post-hoc ANOVA tests. An “a” subscript designates the largest mean, with smaller means designated in descending alphabetical order. Statistics for sixth, catch-all, category not shown.

These descriptive statistics suggest that contacts among families, middle schools, and high schools co-occurred with family advantages and academic success. In particular, this pattern was true for adolescents in categories characterized by the parent-reported link—parents noted that they had contact with middle school personnel about adolescents' future coursework—in any combination with other links. This latter pattern could be methodological in nature, in that the parent-reported link was the most concrete (it tapped actual contact, not a policy) and was adolescent-specific (vs. all adolescents in a school). It likely also reflects the well-documented socioeconomic gradient in parent-school interaction.

To investigate these descriptive patterns further, I turned to a multivariate strategy. Preliminary multilevel models—without controls—revealed the basic associations of the family-school communication categories with the math outcome. The results of these preliminary models will be summarized here and not presented in tables.

With the disengaged category as the reference, all communication dummy variables were positively associated with math coursework level at the start of high school. Rotating the reference among the various communication dummy variables provided a test of all pair-wise differences among the different categories. Adolescents in the middle school as bridge category had significantly higher math levels than adolescents in the other categories. Adolescents in the middle school as bridge and family as bridge categories had significantly lower levels than those in the triangulation category but higher levels than those in the high school as bridge category and disengaged categories. Adolescents in the high school as bridge category only had significantly higher levels than adolescents in the disengaged category, who had significantly lower levels than adolescents in all other family-school communication categories.

This preliminary pattern for the family-school communication typology replicated the results when the three items that were used to construct the typology were examined as predictors of the math outcome. Links between middle schools and parents and links between middle schools and high schools both predicted higher math coursework levels, but links between high schools and parents did not. Two- and three-way interactions among these three binary items indicated that adolescents had the highest math coursework level at the start of high school when they had both the middle school-parent link and the middle school-high school link (akin to the middle school as bridge category), followed by adolescents with all three links (akin to triangulation) or with both the middle school-parent link and the high school-parent link (akin to family as bridge), followed by those with the high school-parent link and the middle school-high school link (akin to high school as bridge). Because the results for a set of dummy variables representing the typology are easier to interpret and more accessible to a general audience than three-way interactions, I focus on the typology after this point.

A similar pattern was seen for science coursework at the start of high school, with a few notable deviations. First, the family as bridge partnership category joined the middle school as bridge category in having the greatest association with science course level. Second, looking at the three items used to make the family-school typology revealed no three-way interactions. Main effects and two-way interactions, however, indicated that the high school-family link had the weakest association with the outcome of the three and chipped away at some benefits of the other two links when paired with them.

Looking More Closely at Family-School Communication and Math/Science Outcomes

These basic patterns sketch the parameters of coursework differences by family-school communication patterns, but they do not allow strong conclusions because they are vulnerable to selection and other biases. To address these vulnerabilities and promote causal inference, several additional modeling steps were taken (see Table 3 for math results).

Table 3. Results of Multi-Level Models Predicting Early High School Math Coursework (n = 15, 876).

	Unstandardized b Coefficients (SE)
	1	2	3 d
Focal Adolescent Group
Low-income a	-.22*** (.03)	-.11*** (.03)	-.05 (.03)
ELL	-.66*** (.10)	-.41*** (.09)	-.45*** (.10)
Family/School Connections
Triangulation b	.23*** (.05)	.14** (.05)	.11* (.05)
Middle school as bridge	.40*** (.08)	.28*** (.07)	.26*** (.07)
Family as bridge	.16 (.10)	.03 (.09)	.04 (.09)
High school as bridge	.13** (.05)	.10* (.04)	.11* (.05)
Sociodemographic Characteristics
Gender (female)	.12*** (.03)	.15*** (.02)	.18*** (.02)
Age (years)	-.39*** (.02)	-.19*** (.02)	-.17*** (.02)
African-American c	-.20*** (.05)	-.09 (.05)	.05 (.05)
Latino/a	-.13* (.05)	-.08 (.05)	.11* (.05)
Asian-American	.31*** (.08)	.26*** (.07)	.42*** (.07)
Other race/ethnicity	-.30* (.13)	-.11 (.12)	-.09 (.13)
Parent education	.27*** (.01)	.10*** (.01)	.02* (.01)
Family structure (two-parent)	.23*** (.03)	.16*** (.03)	.12*** (.03)
First generation immigration status	.33*** (.08)	.16* (.07)	.13 (.07)
Second generation immigration status	-.02 (.05)	-.12* (.05)	-.17*** (.05)
Prior Academic Performance
Advanced math program (middle school)	---	.31*** (.03)	.30*** (.03)
Algebra I enrollment (middle school)	---	.41*** (.03)	.39*** (.03)
Math test score (middle school)	---	.05*** (.00)	.04*** (.00)
Intercept	8.23***	3.98***	3.25***
Δ 2 LL	-987 e	-2995	-1339

^*p < .05.

^**p < .01.

^***p < .001.

Note: All models controlled for school type, sector, location, and region.

^aCategory for those missing income information also included in analyses.

^bDisengaged was reference for family-school connections; set of dummy variables also contained a catch-all category.

^cWhite was reference for race/ethnicity, third-plus generation for immigration status.

^dModel 3 added propensity scores cataloging probability of inclusion in each family-school category (including catch-all category).

^eFit statistic for Model 1 relative to a baseline model containing low-income, ELL, and the family-school connection dummy variables only.

First, a full set of basic sociodemographic confounds that could be observed in the data (including low-income and ELL status) were added to the baseline model (Model 1). This addition had a major impact on the basic pattern of results summarized above. Specifically, it substantially attenuated all of the family-school communication coefficients except the high school as bridge coefficient. In particular, the family as bridge coefficient was reduced to marginal significance. Still, the basic pattern of pair-wise differences in math coursework at the start of high school—e.g., middle school as bridge significantly more associated with the outcome than all others, the disengaged category less so—persisted.

Second, various dimensions of middle school math/science status and performance that could influence both family-school communication and high school coursework were controlled (Model 2). As expected, all three middle school math measures significantly predicted initial high school math level, and their addition further attenuated the coefficients for the family-school communication dummy variables. Thus, some of the reason that adolescents with different patterns of family-school communication differed in initial math level in high school was because of corresponding differences in their middle school math classes and achievement. With one exception, however, the same pattern of pair-wise differences among the family-school categories remained the same. The exception was that the family as bridge coefficient no longer differed significantly from the disengaged coefficient.

Third, propensity scores indexing the extent to which adolescents fit the profile of the average adolescent in each family-school communication category were entered in Model 3 as covariates. Among other things (see Appendix), these propensity scores cataloged multiple aspects of adolescent adjustment and behavior that could have selected them into different family-school communication patterns. Once middle school math status was taken into account, the control of these propensity scores had little added impact on the coefficients for the family-school categories or the pair-wise differences among them.

Fourth, the potential for the final pattern of results from Model 3 to be robust to the control of unobserved or unknown confounds was assessed by calculating the ITCV for each family-school communication category that significantly predicted the math outcome. The analyses indicated that the association between the triangulation category and math coursework (ICTV = .06) was the most robust. Assuming that the two correlations (predictor with confound, outcome with confound) were equivalent, this value means that each would have to exceed .24 to reduce the triangulation coefficient to non-significance. The only covariates with a correlation with math coursework exceeding this value were the middle school math measures, and the only covariate matching it was parent education. No covariate had a correlation with the triangulation category of this strength. Although not foolproof, this ITCV boosts confidence that the triangulation coefficient would be robust to the control for other potential confounds. The association between the middle school as bridge category and the outcome was less robust, with an ITCV of .03 requiring that some unknown confound be correlated with both predictor and outcome at .17 to negate the causal inference. The ITCV for the high school as bridge category was less than .01, providing little confidence in causal inference.

The results for science coursework differed (see Table 4). First, basic high school science differences by family-school communication category were attenuated by the control for demographic, family, and school characteristics but persisted in reduced form (Model 1). Second, middle school science status and performance and the propensity to be in each kind of family-school communication category washed out all but one difference among the family-school communication categories (Models 2 and 3). Specifically, adolescents in the family as bridge category—the one category that did not predict math coursework—had marginally higher levels of science coursework at the start of high school than their peers in all other family-school communication categories. Third, the ITCV for this one family-school category that predicted the science outcome was .01, a value indicating a fairly low threshold for the correlations of a confound with predictor and outcome (approximately .10 for each) to reduce the focal association to non-significance. Although this value does not preclude making a causal inference, it does not inspire much confidence either.

Table 4. Results of Multi-Level Models Predicting Early High School Science Coursework (n = 15,876).

	Unstandardized b Coefficients (SE)
	1	2	3 d
Focal Adolescent Group
Low-income a	-.07** (.02)	-.04* (.02)	.01 (.02)
ELL	-.31*** (.06)	-.23*** (.06)	-.23*** (.06)
Family/School Connection
Triangulation b	.07* (.03)	.04 (.03)	.02 (.03)
Middle school as bridge	.14** (.04)	.09* (.04)	.05 (.05)
Family as bridge	.16* (.06)	.16** (.06)	.11 (.06)
High school as bridge	.03 (.03)	.02 (.03)	.01 (.03)
Sociodemographic Characteristics
Gender (female)	.09*** (.02)	.13*** (.02)	.15*** (.02)
Age (years)	-.13*** (.02)	-.08*** (.01)	-.07*** (.02)
African-American c	-.05 (.03)	.05 (.03)	.05 (.03)
Latino/a	-.03 (.03)	.03 (.03)	.07* (.04)
Asian-American	.14** (.05)	.16** (.05)	.26*** (.05)
Other race/ethnicity	-.06 (.08)	.02 (.07)	.10 (.08)
Parent education	.12*** (.01)	.07*** (.01)	.01 (.01)
Family structure (two-parent)	.10*** (.02)	.08*** (.02)	.05** (.02)
First generation immigration status c	.15** (.05)	.11** (.05)	.10* (.05)
Second generation immigration status	-.06+ (.03)	-.09* (.03)	-.13*** (.03)
Prior Academic Performance
Advanced science program (middle school)	---	.19*** (.02)	.16*** (.02)
Biology I enrollment (middle school)	---	.03 (.02)	.03 (.02)
Science test score (middle school)	---	.04*** (.00)	.03*** (.00)
Intercept	4.03***	2.76***	2.31***
Δ 2 LL	-485 e	-615	-1250

^*p < .05.

^**p < .01.

^***p < .001.

Note: All models controlled for school type, sector, location, and region.

^aCategory for those missing income information also included in analyses.

^bDisengaged was reference for family-school connections; set of dummy variables also contained a catch-all category.

^cWhite was reference for race/ethnicity, third-plus generation for immigration status.

^dModel 3 added propensity scores cataloging probability of inclusion in each family-school category (including catch-all category).

^eFit statistic for Model 1 relative to a baseline model containing low-income, ELL, and the family-school connection dummy variables only.

To summarize, any link among families, middle schools, and high schools was associated with higher-level math/science coursework for youth transitioning into high school. Most, but not all, of these apparent benefits were driven by the demographic, family, and school factors selecting youth into family-school communication patterns, especially their prior history in math and science. After controlling for these factors and gauging the robustness of these observed family-school communication effects to the potential control of unknown confounds, young people tended to do better in math when in the middle school as bridge and triangulation categories. Family-school communication, however, was not related to high school science coursework in ways robust enough to make sound causal inferences, at least for the full sample.

Income, Language, and Family-School Communication

Moving beyond main effects, the next step was to assess the degree to which family-school communication patterns moderated income and language disparities in initial high school coursework. In other words, did the associations of low-income and ELL status with the math/science outcomes vary across the different categories in the family-school communication typology? To test for such moderation, I extended the final model from Tables 3 and 4, respectively, to include interaction terms between low-income and ELL statuses on one hand and the family-school typology on the other (Table 5).

Table 5. Selected Results of Multi-Level Models Predicting Early High School Math and Science Coursework with Interactions (n = 15, 876).

	Unstandardized b Coefficients (SE)
	Math	Science
Focal Adolescent Group
Low-income a	-.04 (.06)	.01 (.04)
ELL	-.71*** (.18)	-.45*** (.12)
Family/School Partnership
Triangulation b	.12* (.06)	-.01 (.04)
Middle school as bridge	.32*** (.08)	.06 (.06)
Family as bridge	-.11 (.11)	.05 (.07)
High school as bridge	.14* (.06)	-.01 (.04)
Student × Partnership Interactions
Low-income × triangulation b	.03 (.09)	.00 (.06)
Low-income × middle school as bridge	-.06 (.13)	.01 (.08)
Low-income × family as bridge	.43* (.19)	.22* (.11)
Low-income × high school as bridge	-.14 (.08)	-.06 (.05)
ELL × triangulation b	.66* (.29)	.67* (.20)
ELL × middle school as bridge	.79** (.32)	-.26 (.22)
ELL × family as bridge	1.19 (1.24)	1.07 (.83)
ELL × high school as bridge	.58* (.26)	.40* (.17)
Intercept	3.25***	2.32***
Δ 2 LL (vs. Model 3 in Tables 3-4)	-30	-13

^*p < .05.

^**p < .01.

^***p < .001.

Note: Models controlled for gender, age, race/ethnicity, parent education, family structure, immigration status, school type, school sector, school location, school region, middle school test scores/coursework, and propensity scores cataloging probability of inclusion in each family-school category (including catch-all category).

^aCategory for those missing income information also included in analyses.

^bDisengaged was reference for family-school connections; set of dummy variables also contained a catch-all category, and this category was also interacted with low-income and ELL.

A preliminary model (not shown) including only the income and language markers as predictors revealed a low-income effect size of about one-third of a standard deviation in the math outcome and an ELL effect size of about one-half of a standard deviation. Moreover, each attenuated the association of the other with the math outcome, and the two interacted significantly with each other to predict the math outcome. Basically, that interaction occurred because income-related disparities in math coursework at the start of high school were smaller for ELL youth than non-ELL youth. The same patterns were found for science, although the disparities were smaller in magnitude (one-fifth of a standard deviation in the science outcome for low-income, one-third for ELL). The income and language disparities were not attenuated by the inclusion of the family-school communication dummy variables as predictors of the math/science outcomes, but they were attenuated (entirely so for income) by controls for middle school math status and the propensity scores for each family-school communication category.

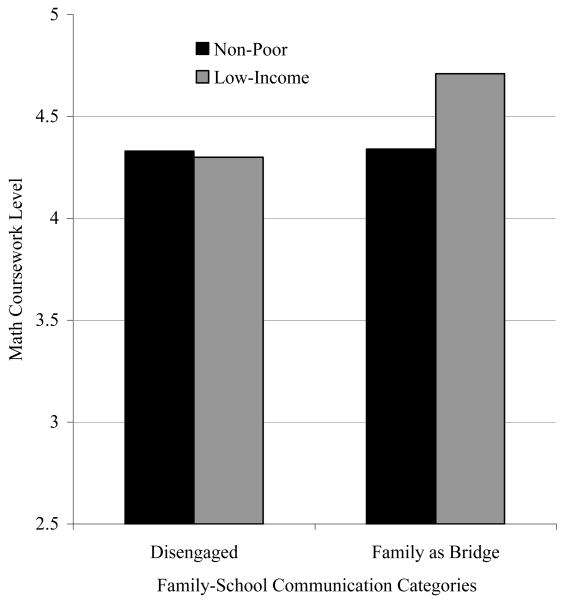
As for the math moderation models (see Table 5), low-income status only interacted with the family as bridge category (b = .43, p < .05). To interpret this interaction term, I calculated the predicted math coursework levels for low-income youth in the family as bridge and disengaged categories (see Figure 1) with all other variables held to their sample means/modes. Low-income youth and their peers had similar math coursework levels when in the disengaged category. Low-income students actually had higher math coursework levels (22% of a standard deviation) than their peers when in the family as bridge category. Thus, the family as bridge communication pattern appeared to have an added benefit for low-income students. This was the only category with a stronger observed benefit for low-income youth and, therefore, the only one that would likely improve the relative math coursework level (vs. higher-income peers), even if other categories would also likely raise the absolute coursework levels of low-income youth.

Figure 1. Predicted Math Coursework Level at Start of High School, by Family Income and Family-School Communication Category.

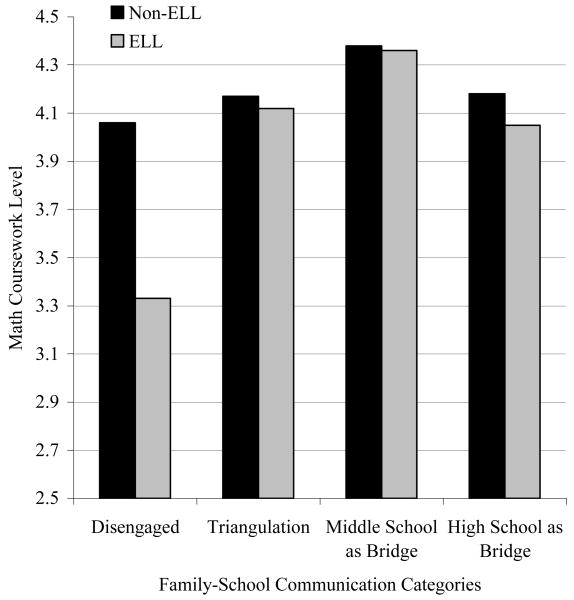
Also in the math model, ELL status interacted with the triangulation (b = .66, p < .05), middle school as bridge (b = .79, p < .01), and high school as bridge (b = .58, p < .05) categories. The number of ELLs in the family as bridge category was extremely small, so that no conclusion could be drawn from the ELL × family as bridge interaction. The predicted math coursework levels derived from these interactions are presented in Figure 2. The language disparities in math coursework were narrower (essentially null) in the triangulation, middle school as bridge, and high school as bridge categories than they were in the disengaged category. This pattern occurred because, although both ELL and non-ELL youth appeared to benefit from all three non-disengaged categories, the benefit was greater for ELL youth. For example, the observed effect size of the triangulation category (vs. disengaged) was 42% of a standard deviation of the math outcome for ELL youth and about 10% for non-ELL youth. The corresponding effect sizes were 60%-17% for middle school as bridge, and 40%-10% for high school as bridge.

Figure 2. Predicted Math Coursework Level at Start of High School, by Language Status and Family-School Communication Category.

For science, a similar pattern of interactions was found. The exception was the absence of a significant interaction between ELL status and the middle school as bridge category.

For the most part, low-income youth and ELLs demonstrated the same observed coursework benefits as their peers with similar demographic, personal, academic, family, and school profiles of having two or three lines of communication among their families, middle schools, and high schools as they transitioned into high school. When they demonstrated differences in these observed benefits, they always appeared to derive greater benefits from having such lines of communication than their peers. Thus, building family-school communication would likely have a bigger impact on these groups (who were less likely to have such communication) than other groups, thereby producing some reduction in income and language disparities in math/science coursework at this point.

Discussion and Conclusion

Developmentalists have done a great deal to shift the conceptualization of parental involvement from a de-contextualized parent behavior to an exchange between families and schools (Hill et al., 2004; Hoover-Dempsey & Sandler, 1997), a shift evident in educational policy, including and especially NCLB. What is needed now are tests of whether this reconceptualization has a real and robust academic payoff as well as guidance on how it can be translated into concrete actions. Questions of form, timing, targets, and developmental appropriateness are paramount. Developmentalists are well-poised to answer these questions.

This study tried to identify an application of the family-school communication concept supported by causal inference. Doing so revealed a potential approach to the family-school compact of NCLB (see Epstein, 2005) that some schools (e.g., secondary schools serving diverse populations) may consider as they try to achieve their performance goals. This application was specific, not universal, in that it only applies to one specific domain of education in a specific time period. Yet, given the dynamic nature of development, parenting, and school, universalism is likely to be an unrealistic standard. Instead, specific recommendations are what are needed to enable more schools to make progress on the NCLB mandate in useful ways, and this study offers such recommendations for one subset of students and school communities.

In looking at family-school communication and its link to math/science coursework across the transition from middle school to high school, this study found that much of the story was really about the selection of young people into different kinds of connections, not the academic significance of the connections themselves. Still, lines of communication between home and sending/receiving schools did appear to come with academic benefits for students in general and did demonstrate potential to reduce key disparities in academic outcomes. In discussing these policy relevant patterns, I focus on the most “trustworthy” results; in other words, observed associations between family-school communication and math/science outcomes that persisted after observable confounds (e.g., middle school status and performance, family and school factors, propensity to have different kinds of family/school communication patterns) were taken into account and after unobservable confounds were assessed with the ITCV.

• In general, triangulated family-school communication was associated with adolescents being in higher-level math coursework at the start of high school. Because this pattern was more pronounced for ELLs and because it extended to science coursework for ELLs only, such communication was associated with smaller language disparities in math and science coursework during this period.

• In general, middle school as bridge communication was associated with adolescents being in higher-level math coursework at the start of high school. Because this pattern was more pronounced for ELLs, such communication was associated with smaller language disparities in math coursework during this period.

• High school as bridge communication was associated with higher-level math/science coursework for ELLs only. As a result, it was associated with smaller language disparities in math/science coursework but not with an higher overall level of such coursework for the full sample.

• Family as bridge communication was associated with higher-level math/science coursework for low-income students only. As a result, it was associated with smaller income disparities in math/science coursework but not with an higher overall level of such coursework for the full sample.

Based on these findings as well as previous research on the link between initial high school placement and eventual credit accumulation and achievement (Baker & Stevenson, 1987; Crosnoe & Huston, 2007), the general conclusion is that building lines of communication among parents, high school personnel, and, especially, middle school personnel may promote progress towards multiple goals—promoting continuity between middle school math/science status in general and reducing disparities in such continuity related to language status. Other kinds of two-way communication among the three actors might promote progress to a single goal—reducing income disparities or language disparities, but not both and not affecting the overall coursework level of students in general. This conclusion brings up several questions.

First, what are the mechanisms involved? Drawing on the social capital perspective, this study postulated that the two-way exchange of new, non-redundant information about coursework and adolescents' histories between home and school was the primary mechanism. This theoretical mechanism, however, could not be tested extensively. This study measured contact and policies of contact between home and sending/receiving schools. Because of how the questions were asked, I know that two of these points of contact were specifically about the high school coursework of incoming middle school students. I could not be sure about the third point of contact (high school-family) because the question was about the transition experience in general. Moreover, even for the two points of contact specifically about coursework, the substance of what was actually said or communicated cannot be known. Clearly, much more needs to be done in this regard, including investigations of other forms of social capital, such as the construction and enforcement of social norms (Coleman, 1990; Furstenberg et al., 1999). Smaller-scale studies (Benner & Graham, 2008) and/or qualitative studies (Lareau 2004) will likely be more valuable in such future endeavors. Unfortunately, such studies also come with the non-negligible disadvantage that they are less equipped to promote generalizability and cover less diverse (and internally diverse) groups of adolescents, families, and schools than analysis of nationally representative data sets, such as NELS. Both establishing generalizable, robust patterns and identifying mechanisms are important from a theoretical and policy standpoint, but they are hard to accomplish at the same time. Thus, coupling studies using different approaches—such as building on the insights gleaned from this study with more intensive investigative approaches—is a way to advance the field and inform policy for now.

Second, why did the results differ for math and science? According to theory, social capital (especially information) matters more in times of uncertainty. To a some extent, the science portion of the math/science pipeline introduces more uncertainty than the math portion. Math is more vertically organized, with one class building on another. Science coursework is not as sequential as math, and some science courses are more easily substituted for others or skipped entirely (Lee et al., 1997; Riegle-Crumb et al., 2006). Thus, family-school communication should have mattered more to science coursework level during the transition into high school than to math coursework, but the opposite pattern was found. At least in the full sample, any observed links between family-school communication and science coursework were completely due to selection on observable (especially, middle school science status as well as other adolescent characteristics indexed in propensity scores) and unobservable factors. Family-school communication appeared to have more independent effects on math coursework. One explanation for this unexpected pattern is that math coursework does have an element of uncertainty but also provides a more limited choice set at each point of uncertainty. For example, parents and schools may still have decisions to make about students' math coursework, but they can make this decision by weighing one or two alternatives (e.g., Algebra I or Geometry after middle school Pre-Algebra) rather the more plentiful alternatives involved in science coursework. Regarding math, therefore, communication between families and schools may have less ground to cover and focus on more specific recommendations. In other words, the exchange of information may matter most in times of uncertainty but not too much uncertainty.

Third, why would different kinds of family-school communication be associated with income and language disparities? When such disparities (e.g., the observed effect of low-income or ELL status on the outcomes) were moderated by family-school communication, it was always in the form of protection (Masten & Coatsworth, 1998). That is, family school communication was often more (or only) predictive of coursework among low-income and ELL youth than among their peers, which suggests that disparities were narrower in the context of certain types of communication even if the overall level of achievement in the sample did not change. Yet, this pattern was less pronounced for income disparities than for language disparities. Moreover, families seemed to be the crucial bridge for low-income youth, the middle school more so for ELLs. A likely explanation concerns differences in parents' familiarity with how American schools work. Most of the low-income parents came up through the American educational system, but a large proportion of the parents of ELL youth (most of whom were immigrants) did not. Moreover, because of language barriers, this latter group of parents faced added obstacles in learning (and working) the system (Suarez-Orozco & Suarez-Orozco, 2001). Thus, information coming from the school to home was more likely to be redundant for low-income parents than immigrant parents, many of whom were also low-income. With more familiarity in schools and generally fewer linguistic obstacles, low-income parents would also be in a better position than immigrant parents to make a case for the children at school. For immigrant parents, having middle school personnel involved was crucial. After all, these personnel typically knew the students better than receiving high school personnel and were also better informed about high school policies and practices than parents themselves. They could make up more of the information gap—which is quite different than a gap in values or motivation—in this population.

Fourth, why was triangulation not always be the most important form of family-school communication? If family-school communication is good, then the maximum lines of communication among families and schools should have predicted the highest level of math/science coursework. Yet, math coursework was typically lower (and language disparities larger) in the triangulation category than in the middle school as bridge category, and income disparities were typically larger in the triangulation category than in the family as bridge category. The science pattern has been addressed above—low-income parents needing to be bridges during transitions so that they can make a case for their children and explain their children's circumstances in ways that overcome institutional barriers (e.g., low expectations, discrimination) and inertia (Lareau, 1989). One possible explanation for the math finding is that the high school to family link (the piece of the triangulation category missing from the middle school as bridge category) was a reaction to historical problems in the math/science pipeline; for example, when slippage between middle schools and high schools in math/science coursework has been a concern for a number of years or when overall performance levels in math/science coursework have been low for some time. In this case, the triangulation pattern might reflect more than predict math/science coursework patterns for students in general, relative to the middle school as bridge pattern.

Fifth, do the findings about the high school as bridge communication pattern suggest that high schools play a less integral role in the process of interest? In general, the high school as bridge category had the weakest associations with math/science coursework of the family-school communication categories, largely because of the strong selection effects associated with this category. This pattern could have been a measurement issue. This category was based solely on school policies (e.g., high school policies about parent outreach and partnering with middle schools), not links specific to any one adolescent. As a result, it was the one category in which the engagement of parents was unknown. Many potentially negative forces could have selected young people into situations in which their parents were absent from the equation, forces that could overwhelm school policies in their educational careers. Still, I want to stress that the weaker findings about the high school as bridge communication category do not let high schools off the hook for managing the transition process. Recall that the triangulation, middle school as bridge, and family as bridge categories could not exist without high school policies about communication with families and/or middle schools. Thus, the findings indicate that high schools need to be involved in the transitions of middle school youth from various populations but need not be the lead actor in these transitions. Parents and middle school personnel, who know the background of young people better, need to be the leaders.

Sixth, how can such an application of family-school connections be implemented? By taking the general concept of family-school connections and the broad family-school compact provision of NCLB to a more specific level, this study can provide more concrete recommendations. At the heart of this study is the unequal distribution of information about the sequence of math/sequence coursework best preparing students for entry into and completion of higher education and how this unequal distribution can create an uneven playing field at the start of high school with a highly cumulative character. The results of this study suggest that this information may be made up by contact among different actors involved in students' transitions into high school. High school counselors could partner with their feeder school counterparts to prepare reports on the math/science history of transitioning students, including a recommendation for high school placement. These reports, which would need to be done for each new group of students each year, would then be shared with adolescents and their families. A more general school-wide report (that would not need to be revised annually) would also be provided with information on the normative math/science sequences of students in the high school, data on the sequences that best predict various educational outcomes (e.g., high school graduation, college matriculation) on the state and national level, and data on the math/science benchmarks that best prepare students for the rigors of higher education. Such state and national data could be culled from extant reports from the U.S. Department of Education (Shettles et al., 2007). Parents would then be required to sign off on the adolescents' report before the start of the high school year. These plans are simple in nature, but they would require some effort and investment from schools. Essentially, what they would do is allow parents, schools, and adolescents to make decisions from a more even playing field about short-term actions that have long-term consequences.

Despite these remaining questions, the need to couple this national analysis with a more in-depth investigation of the substance of communication being exchanged, and the value of investing in even more strategies to determine causality (e.g., instrumental variable analyses; see Gennetian et al., 2008), this study has served a useful purpose by identifying one potential way for schools to act on a concept of developmental research that has been incorporated into educational policy. This strategy is a specific one that applies only to a narrow age range of students in one level of the educational system. As a result, this study needs to be matched by future studies that identify other applications of the family-school connections concept that may be useful for other curricula and other segments of the student population differing in educational and developmental status.

Appendix

Descriptions of Extra Variables for Propensity Scores.

Variable	Description
Adolescent Factors
Grade point average	NCES-constructed measure based on adolescents' 1988 reports of grades in math, science, English, and social studies. This measure takes the form of a standard four point grade point average (M = 2.98, SD = .73).
Locus of control	NCES-constructed measure based on the mean of adolescents' 1988 responses (1 = strongly agree to 4 = strongly disagree) to five items, including “”I don't have enough control over the direction my life is taking” (M = .05, SD = .71). Constituent items were standardized.
Positive self-concept	NCES-constructed measure based on the mean of adolescents' 1988 responses (1 = strongly agree to 4 = strongly disagree) to five items, including “On the whole, I am satisfied with myself” (M = .02, SD = .73). Constituent items were reverse-coded and standardized.
Timing of immigration	In 1988, parents reported when an adolescent born outside the U.S. came to the U.S. Reports were dichotomized into less than five years (1%) or more.
Middle school athletic participation	Adolescent reported involvement with varsity sports in 1988 (57%).
High school athletic participation	Adolescent reported involvement with any of 30 school clubs and extracurricular activities in 1990 (75%).
Middle school activity participation	Adolescent reported involvement with any of 7 school sports in 1988 (51%).
High school activity participation	Adolescent reported involvement with any of 11 school clubs and extracurricular activities in 1990 (61%).
Expectations for high school	Adolescent reported whether they expected to enroll in college-preparatory program in high school (33%).
Future educational expectations	Adolescent reported how far he/she expected to get in the educational system (1 = won't finish high school, 2 = will finish high school, 3 = vocational school, 4 = attend college, 5 = graduate from college, 6 = enter higher school after college) (M = 4.68, SD = 1.23).
Parent/Family Factors
Home language use	NCES-constructed measure, based on adolescent and parent interviews, dichotomized into non-English is primary/sole language (12%) or not.
Parent discussion of coursework	In 1988, adolescents reported how often (1 = never to 3 = often) they talked with their parents about course selection (M = 2.50, SD = .50).
Parent school-based involvement	Sum of adolescents' 1988 reports of whether their parents had attended a school event, spoken with their teacher, visited their classes, or attended a school event (M = 1.90, SD = 1.23).
Extended family structure typology	NCES family structure composite extended to include categories for two-parent (65%), single parent (16%), stepparent (11%), and other family.
Middle School Factors
Size	NCES composite based on 1988 school administrator reports, with categories ranging from 1 (1-99 students) to 7 (1200+) (M = 3.75, SD = 1.76).
% race/ethnic minority students	School administrator reports of percentage of non-Whites in student body (M = 24.27; SD = 28.03).
% students on free/reduced lunch	School administrator reports of percentage of student body receiving free and reduced lunches (M = 22.28; SD = 21.93).
Math/science instruction requirements	School administrator reports of whether full-year instruction in math and science required for all 8th graders in school (M = .86, SD = .34).
Non-English math/science instruction	1988 school administrator reports of whether non-English math and science instruction was available in school (M = .04, SD = .20).
Mode of course assignment	Four variables, based on 1988 school administrator reports of how much influence (1 = none, 4 = a lot) parents (M = 2.12, SD = .82), teachers (M = 2.38, SD = .71), counselors (M = 2.13, SD = .89), and test scores (M = 2.40, SD = .80) had in the assignment and/or selection of high school courses/programs for eighth grade students.
High School Factors
Size	See middle school description (M = 4.71, SD = 2.40).
% race/ethnic minority students	See middle school description (M = 27.05; SD = 26.69).
% students on free/reduced lunch	See middle school description (M = 19.09; SD = 19.67).
Grade structure	Whether school contained an eighth grade (18%) or not, based on school administrator reports.
Number of math/science teachers	School administrators' estimates of how many teachers they had in various departments, ranging from 0 (0-5) to 3 (15+). The sum for math and science was taken (M = 2.20, SD = 1.76)
Math/science course offerings	Proportion of 16 math courses and 17 science courses offered in school, based on responses of school administrator to a set list of courses in each subject (M = .59, SD = .11).
Mode of course assignment	See middle school description (M = 2.12, SD = .82 for parents, M = 2.38, SD = .71 teachers; M = 2.13, SD = .89 for counselors, M = 2.40, SD = .80 for test scores).

Note: All Sociodemographic and school controls also included in propensity scores.