Abstract
Enhancing transdermal delivery of insulin using chemical penetration enhancers (CPEs) has several advantages over other non-traditional methods; however, lack of suitable predictive models, make experimentation the only alternative for discovering new CPEs. To address this limitation, a quantitative structure-property relationship (QSPR) model was developed, for predicting insulin permeation in the presence of CPEs. A virtual design algorithm that incorporates QSPR models for predicting CPE properties was used to identify 48 potential CPEs. Permeation experiments using Franz diffusion cells and resistance experiments were performed to quantify the effect of CPEs on insulin permeability and skin structure, respectively. Of the 48 CPEs, 35 were used for training and 13 were used for validation. In addition, 12 CPEs reported in literature were also included in the validation set. Differential evolution (DE) was coupled with artificial neural networks (ANNs) to develop the non-linear QSPR models. The six-descriptor model had a 16% absolute average deviation (%AAD) in the training set and 4 misclassifications in the validation set. Five of the six descriptors were found to be statistically significant after sensitivity analyses. The results suggest, molecules with low dipoles that are capable of forming intermolecular bonds with skin lipid bi-layers show promise as effective insulin-specific CPEs.
1. Introduction
Non-traditional methods of insulin delivery like insulin pumps, insulin inhalers and insulin pens have obvious advantages over traditional methods of delivery (Patni et al., 2006). Another promising non-traditional alternative is the delivery of insulin through skin. However, human skin provides a very efficient transport barrier (Monteiro-Riviere, 1991, Monteiro-Riviere, 1996) to delivery of protein molecules like insulin, due to their large size (> 3000 Daltons) and weakly hydrophobic nature. Several physical and chemical methods have been developed to improve the permeation of insulin through human skin (Scheuplein and Blank, 1973, Pillai and Panchagnula, 2003a, Rastogi and Singh, 2003, Pillai et al., 2004b). Currently, the most efficient method in enhancing insulin permeation through skin is iontophoresis (Pillai and Panchagnula, 2003a). However, the economic viability and ease of applicability of chemical approaches, such as the use of chemical penetration enhancers (CPEs), makes them an attractive alternative.
Despite the advantages, very few studies involving the use of CPEs for transdermal insulin delivery exist in the literature (Rastogi and Singh, 2003, Pillai et al., 2004b). Further, in these limited studies, CPEs involving either fatty acids or fatty alcohols are employed in tandem with iontophoresis. However, when compared to the physical methods of enhancement like iontophoresis, these ‘traditional’ CPEs have not been effective in enhancing the permeation of large hydrophilic molecules like insulin. Therefore, a need exists to develop new CPEs that can increase the dermal absorption of insulin to therapeutic levels.
The most rigorous means of identifying new CPEs is by estimating experimentally the drug permeability in presence of the CPE; however, practical limitations on time and resources make this method unattractive. Therefore, the scientific community is relying increasingly upon predictive models for estimating the drug permeabilities in the presence of CPEs. Although mechanistic models have been employed in the past to estimate drug permeabilities through skin (Scheuplein and Blank, 1971, Scheuplein and Blank, 1973, Stoughton, 1989), they involve many assumptions, and parameters that cannot be measured easily. In addition, these models do not allow for uncertainties in the experimental data, and as a result, lead to large predictive errors. Semi-empirical modeling approaches like quantitative structure-property relationships (QSPRs) can account for data uncertainties (by employing weighted regression or similar methods) and usually lead to better predictive models. Also, QSPRs are used to model molecular properties based on structural features, which can provide physical insight to the modeled phenomenon.
Most of the available skin permeation QSPR models (Potts and Guy, 1992, Guy and Potts, 1993, Barratt, 1995) in the literature are developed for predicting the passive permeability of chemicals, i.e., the unaided transport of molecules through the skin. However, the permeation of a therapeutic drug in the presence of other chemicals can differ markedly from passive permeation, and in CPE enhanced transdermal drug delivery, the most important property of interest for modeling purposes is the permeability of the drug in the presence of CPEs. Despite the importance of such models, molecular modeling and QSPR studies in the past did not focus on this subject, possibly due to the variations in the structure-activity relationships between different pairs of drugs and enhancers (Iyer et al., 2007). A few recent studies (Li et al., 2003, Ghafourian et al., 2004, Iyer et al., 2007); however, have attempted to model the permeation of different types of drugs in the presence of CPEs.
Like other empirical methods, QSPR models are based on the availability and quality of the data used for model development. A review of the available literature for the pertinent data indicates that insulin has been predominantly delivered through the skin using physical methods like iontophoresis (Rao and Misra, 1994, Pillai et al., 2003a, Pillai et al., 2003b, Pillai and Panchagnula, 2003a, Pillai and Panchagnula, 2003b, Pillai et al., 2004a, Pillai et al., 2004b) and sonophoresis (Mitragotri et al., 1996), with very few reported studies on the use of CPEs. Pillai et al. and Choi et al. (Choi et al., 1999, Pillai and Panchagnula, 2003a, Pillai and Panchagnula, 2003b, Pillai et al., 2004b) have studied the effect of solvents like ethanol, propylene glycol, ethyl acetate and isopropyl myristate on insulin permeation. However, these solvents were used for pre-treatment of the skin before insulin application. A similar study on the effect of CPE pre-treatment on insulin permeation was completed by Choi et al. (Choi et al., 1999). Some common enhancers like Azone, oleic acid and poloxamer have been investigated by Hao et al. (Hao et al., 1995), but these enhancers have been used only after treating the skin with iontophoresis. Priborsky et al. (Priborsky et al., 1988) studied the effects of CPEs without using any physical methods, but the number of CPEs investigated was limited to three. Similar studies on a handful of CPEs have been carried out by others (Rastogi and Singh, 2003, Sintov and Wormser, 2007). This literature review suggests that there is a serious shortage of insulin permeability data in the presence of different CPE classes. In the current work, experiments based on well-established literature procedures were carried out to insure sufficient data exist for modeling analysis. The detailed experimental procedures can be found elsewhere (Yerramsetty et al., 2009).
A total of 48 CPEs with different functional groups were investigated experimentally in the current work, for their effect on insulin permeation. These 48 CPEs were identified with our virtual design algorithm, which combines genetic algorithms (GAs) and quantitative structure-property relationship (QSPR) models for important CPE properties. Details concerning the algorithms and models can be found elsewhere (Godavarthy et al., 2009).
Most literature QSPR models for skin permeation are based on a few, select descriptors that have been established by many researchers in the field. As a result, the number of important descriptors in the field of transdermal delivery is low when compared to other studies, such as drug delivery across the blood-brain barrier (Neumann et al., 2006). Through this work, we attempt to identify additional descriptors that could be important for transdermal delivery. However descriptor pruning is a complex task when developing non-linear QSPR models. Even after removing the highly correlated descriptors, most QSPR data sets retain large numbers of descriptors. Many of these descriptors are redundant or insignificant, and the sheer number can cause difficulties in providing a mechanistic interpretation of the property of interest. Many methods exist for pruning large descriptors sets to smaller sets more amenable to development of practical and useful models. Sensitivity analysis (Turner et al., 2004) is a commonly used technique, in which the sensitivity of the output to random changes in the descriptor values is analyzed. This technique although simple, does not account for descriptor interrelationships. For example, a group of two or more descriptors can provide a significant effect while the same descriptors examined singly are insignificant. Multi-linear regression techniques are also employed commonly (Kang et al., 2007); these techniques are better than sensitivity analysis in their ability to account for the linear relationships between a group of descriptors and the output, but they fail to account for non-linear relationships. Attempts have been made to include genetic algorithms (GA) to search for the best descriptors without imposing any constraints on the types (linear or non-linear) of input-output relationships between the descriptors and the property of interest. However, these algorithms are limited to only a small number of initial descriptors (Agatonovic-Kustrin et al., 2001). In the current work, an evolutionary algorithm called differential evolution (DE) was used for descriptor pruning. This is a two-level algorithm; at the top level, a DE framework searches for the set of best descriptors and at the bottom level neural networks are used to build non-linear models based on the selected descriptors. In addition to the best descriptors, the DE framework has been modified to simultaneously search for the best neural network architecture.
2. Methods
2.1. Experimental Methodology
A brief description of the experimental procedure is provided here. For a detailed description, the readers are referred to Yerramsetty et al. (Yerramsetty et al., 2009) and Rachakonda et al. (Rachakonda et al., 2008).
Resistance measurements
Porcine abdominal skin was placed between the receiver and donor plates of a resistance chamber built in-house, with the stratum corneum facing the donor wells, and the two plates were clamped together tightly. The receiver chambers were filled completely with phosphate buffered saline (PBS, pH – 7.4, phosphate and sodium chloride concentrations of 0.001M and 0.137M, respectively). The resistance of the skin was measured using a common electrode placed beneath the receiver plate and the other placed sequentially into each donor well. All CPEs were tested at a concentration of 5% (wt/v) in 40:60 PBS and ethanol solution with the receiver chambers maintained at 37±1°C. Resistance measurements were taken hourly for a period as long as six hours.
The resistance reduction factor (RF) was calculated as the ratio of the initial resistance (R) of the skin at time 0 to the resistance at time t, as given by:
| (1) |
Permeability measurements
All permeation experiments were carried out using Franz diffusion cells (Permegear Inc., Riegelsville, PA, USA). Porcine abdominal skin was placed between the receiver and donor chambers of the Franz cells. Full thickness porcine skin as the model membrane for insulin permeation has not appeared in the literature; however, Rastogi and Singh (Rastogi and Singh, 2005) have studied the effect of some fatty acids on the permeation of Lispro through porcine epidermis with determined Kp values for the control and oleic acid of 0.0002 and 0.0025, respectively. These values are of the same magnitude as those Kp values calculated in this work, which are 0.0007 and 0.0038 for the control and oleic acid, respectively. Since the majority of the resistance to the permeation of hydrophilic drugs lies in the stratum corneum layer of the skin, we believe that employing full thickness skin for permeation studies should lead to no disadvantages when compared to studies using just the epidermis.
Then, 1.0 mL solutions of 40:60 Lispro (an insulin analog) and ethanol (containing approximately 40 IU of Lispro), and 5% w/v CPE were placed in the donor chambers. Samples of 0.2 mL were withdrawn from the receiver chamber at different time intervals (3, 9, 12, 18, 24, 36 & 48 h), and insulin concentration was analyzed by high-performance liquid chromatography (HPLC). The following steady-state equation was used to calculate permeability of the skin:
| (2) |
where, Am is the exposure area of the skin sample (0.64 cm2), C0 is the initial concentration in the donor chamber in mM, P is the permeability of the membrane and t is time in hours. The permeability is given in terms of the diffusion coefficient (Dm), the partition coefficient (Km), and the thickness of the skin sample (L):
| (3) |
In this study, the amount of drug permeated was calculated as the total amount of drug permeated through skin during the time period of 48 h and the amounts sampled from the receiver chamber during this period.
2.2. QSPR Methodology
The development of a QSPR model involves the following series of steps: (a) data set generation, (b) descriptor calculation, (c) descriptor reduction, (d) model training and (e) model validation.
Data set generation
Insulin permeability data in the presence of 48 CPEs were generated using the experimental procedure discussed in Section 2.1. A data set containing 35 CPEs was used for training the model. The experimental permeability (Kp) values in this data set range from 0.5 cm/h to 7.6 cm/h. Another data set of 25 CPEs was used for validation. This included 12 CPEs that were reported in the literature to be insulin enhancers; eight CPEs that did not significantly reduce the skin resistance when tested in our lab using the resistance procedure described previously in Section 2.1 (permeability values for these CPEs were not measured and therefore are not reported); and five CPEs that were tested in our lab for permeability and were not included in the training set.
Descriptor calculation
Descriptor calculation requires a series of steps common to all QSPR models. ChemBioDraw Ultra 11.0 (CambridgeSoft, 2008) was used to generate the two dimensional (2-D) structures for the CPEs in the data set. These 2-D structures were then used to generate three dimensional (3-D) structures. The molecular energy was minimized using Chem3D Pro 11.0 (CambridgeSoft, 2008) to find the corresponding optimal 3-D conformation. The 3-D structures were further optimized using AMPAC 6.0 (Semichem, 1998a), and the final optimized structures were provided to CODESSA PRO (Semichem, 1998b) for descriptor calculation. CODESSA PRO has the capability to generate over 1200 descriptors. However, due to structural complexity, this number may be lower, and a missing descriptor was assigned a zero.
Descriptor reduction and model training
A non-linear reduction and training strategy was employed in the current work to discover simultaneously the best descriptor set and the best neural network architecture based on these descriptors. An evolutionary algorithm, differential evolution (DE), was used to search for the best descriptors and network architecture, and artificial neural networks (ANNs) were used to build the non-linear models based on these descriptors. Briefly, DE is a stochastic optimization algorithm that finds the global extremes (minimum or maximum) of a function. The method begins with an initial random population of individuals (or independent variables), and through mutation and crossover operations over a number of generations, transforms this initial population into a population that is, on average, much closer to the global minimum (or maximum) of the dependent variable. For a detailed overview of this process, see the description provided by Price et al. (Price et al., 2005). Two essential features of any evolutionary algorithm are (a) genetic representation and (b) the objective function, which are described below.
Genetic representation: A good genetic representation of the solution domain is an important step in developing an efficient DE algorithm. In the current work, the solution space is comprised of all possible molecular descriptors and all possible two hidden-layered neural network architectures. Since a two hidden-layer network is capable of reasonable approximation of any non-linear function, the maximum number of hidden layers was limited to two (Hornik et al., 1989). Guidelines exist in the literature for choosing the maximum number of descriptors for small data sets, and these were applied during QSPR model development (Tropsha et al., 2003). These guidelines limit the maximum number of descriptors in the model to 1/5th the number of data points in the training set. Since 35 training points were available, the number of descriptors used in the modeling effort was limited to six. Therefore, six descriptors form an individual in the solution space and each individual in the population is characterized by this set of six descriptors. As in most evolutionary algorithms, arrays are the most suitable form of representing an individual in the solution space. In the present work, a nine-element integer array, Di, was used to represent the ith individual in the initial population. Each of the first six elements of the array stores an integer that represents a descriptor from the set of all possible descriptors. Therefore, Di,j for j = 1 to 6 represents the jth element (or descriptor) of the ith individual in the initial population. Di, Mi, and Ti, are used to distinguish between the individuals in the initial population, mutated population and the trial population, respectively. In addition to the descriptors, the algorithm also optimizes the network architecture. Therefore, the genetic representation includes elements that denote the number of hidden layers (1 or 2) and also the number of neurons in each of these hidden layers. Employing an analogous representation scheme as used for the descriptors, the seventh element in the arrays Di, Mi, and Ti, was used to represent the number of hidden layers in the network. If this element was set to a value of one, then the corresponding network had a single hidden-layer, and if the value of the element was zero, then the network contained two hidden-layers. Further, the last two elements of the arrays were used to represent the number of neurons in the one or two hidden-layer architectures, respectively. The maximum number of neurons in either hidden layer was set at 25 (denoted as max_neurons in the subsequent discussion).
The objective function: Another major aspect of a DE algorithm is choice of a suitable objective function. In this work, the percent average absolute deviation (%AAD) between the experimental and the predicted Kp values was chosen as the objective function. The algorithm searches for the set of descriptors and the network architecture that result in a neural network with the least %AAD.
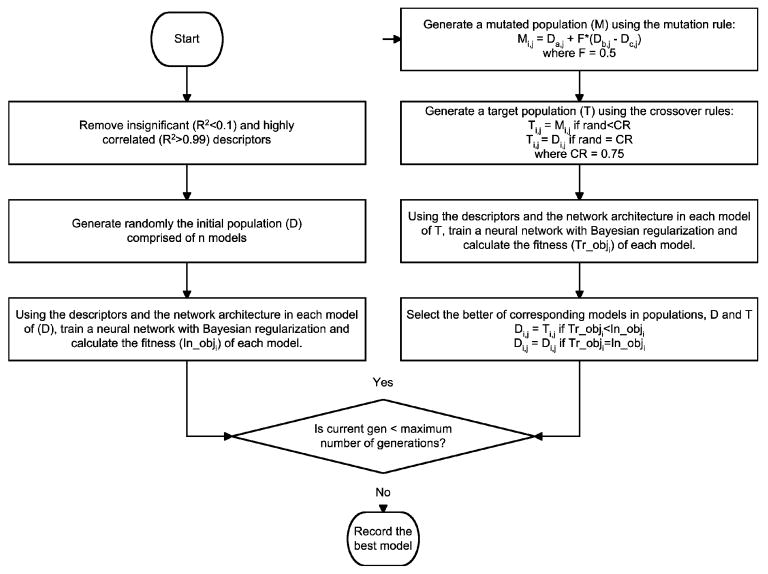
If DE is considered the searching mechanism (or the descriptor reduction mechanism) of the algorithm, artificial neural networks (ANNs) are the non-linear optimization tools of the algorithm. In general ANNs are used to map complex non-linear relations between inputs (or the independent variables) and the outputs (the dependent variables). In this work, a feed-forward neural network with six neurons in the input layer and one neuron in the output layer was used to model the relationships between the six descriptors and the output Kp. The number of neurons in the hidden layers was set based on the last two elements of the representation arrays, Di and Ti. Bayesian regularization was used as the optimization algorithm, because of its advantages for small data sets over other training methods like early stopping (Mathworks, 2005). In addition to limiting the maximum number of neurons in each hidden layer to less than 25, another constraint was imposed on the number of neurons in the hidden layers by maintaining a degree of freedom ratio of at least two. The target values for the network were the logarithmic transformations of the experimental Kp values. In addition, all inputs and target values were normalized to have zero mean and a standard deviation of one. These transformations avoid any bias in the model due to extremely low or high target or input values. A flowchart for the complete algorithm is provided as Figure 1.
Figure 1.
Flowchart for the differential evolution algorithm used.
Model validation
As discussed previously, 25 CPEs were used to validate the model, which consisted of the following: (a) twelve CPEs reported in the literature to be insulin enhancers (literature CPEs), (b) eight CPEs that did not reduce significantly the skin resistance when tested in our lab using the resistance procedure described previously (resistance CPEs), and five CPEs whose Kp values were measured in our lab, but were excluded from the training data (excluded CPEs). Since, the experimental conditions used for the 12 literature CPEs were different from those used in the current study, comparisons between the experimental and predicted values must be made carefully. The same holds true for the 13 resistance CPEs, because of the poor correlation between the experimentally calculated Kp and RF values measured in our lab. In spite of these differences, we expect our model to have the capability of distinguishing effective CPEs from non-effective CPEs. From our experience with a large number of CPEs on insulin permeation, we suggest that any CPE that leads to at least a threefold increase in insulin permeability over that of the control value can be assumed safely to be an effective CPE. Therefore, the predictions for the twelve literature CPEs must be at least 2.0 cm/h, which is three times the control value measured in our lab, and those for the eight resistance CPEs must be lower than this value.
2.3. Statistical Analysis
All experiments were performed a minimum of three times, and single factor one-way analysis of variance (ANOVA) was performed with a 95% confidence interval on the drug permeability data. This was done to determine if the differences among these data at different experimental conditions are greater than the errors due to random effects. A P-value less than 0.05 indicates a significant difference between the two groups of data.
2.4. Sensitivity Analysis
Sensitivity analysis of the final neural network model was performed using four different methods.
Neural interpretation diagram (NID)
A diagram representing the neural network structure, along with the weights between the different neurons can be used to qualitatively interpret the relationships between the output variable and the various input variables. Using this approach, the connections between the neurons will be represented by lines whose thickness depends upon the magnitude of the weights between them. Also, to differentiate between the direction of contribution of the input variables to the output of a neuron, gray lines and black lines will be used for negatively-contributing and positively-contributing inputs, respectively. A NID therefore, provides qualitative information about the magnitude and the direction of the effect of each input on the output. For a detailed discussion on NIDs and their interpretation, the readers are referred to Olden & Jackson (Olden and Jackson, 2002) and Aoki & Kamatsu (Aoki and Komatsu, 1997)
Garson's algorithm
This algorithm was proposed by Garson (Garson, 1991) to evaluate quantitatively the relative importance of each input of a neural network towards the output. In this algorithm, the magnitudes of the weights between each input and hidden neuron are used to calculate the relative importance of the inputs. However, the directions of the effects of the input variables cannot be deduced using this algorithm. A detailed discussion on the exact methodology can be found elsewhere (Garson, 1991, Olden and Jackson, 2002).
Randomized connection weight approach
A randomized connection weight approach was proposed by Olden and Jackson (Olden and Jackson, 2002) to eliminate null-connection weights from the network that do not differ significantly from random values. In brief, the procedure involved randomly generating the output values and constructing neural networks for estimating these random output responses using the same input values that were used to build the optimal final network. All the individual weights were recorded and the connection weights and the overall connection weights for each input were calculated. These weights for each input were calculated in the following manner:
The products of the weights between the particular input and a hidden neuron in the first hidden layer and the weights between this hidden neuron in the first layer and another hidden neuron in the second hidden layer (or output layer if a second hidden layer does not exist) and so on for all the hidden layers, was evaluated. This is called the connection weight of the input.
The sum of these products for each hidden neuron-input connection is called the overall connection weight for each input.
The above procedure was carried out 999 times and the proportion of the connection weights (including the original optimal network) which were larger in magnitude than the corresponding connection weights, and the overall connection weights of the optimal network were recorded. A weight is considered significant if this proportion is lower than 0.05 (for a confidence level of 95 %) and insignificant otherwise.
Using this approach, the NID for the optimal network can be simplified markedly by eliminating the insignificant weights. Also, by using the connection weight approach, the direction of the effect of each input toward the output can be known. If the overall connection weight of an input is positive, then the direction of its effect is also positive and if the overall connection weight is negative, then the direction of its effect is negative. This is advantageous over Garson's algorithm, which does not reveal the directions of the effects of the inputs on the output.
Leave one descriptor out analysis
The relative importance of each descriptor was analyzed by leaving that descriptor out of the model and building a new neural network with the remaining five descriptors. The %AAD of the resulting network, along with the number of misclassifications in the validation set was recorded. A descriptor is considered important, if the network built after excluding this descriptor has a high %AAD and a greater number of misclassifications when compared to the original optimal model.
3. Results
3.1. Training
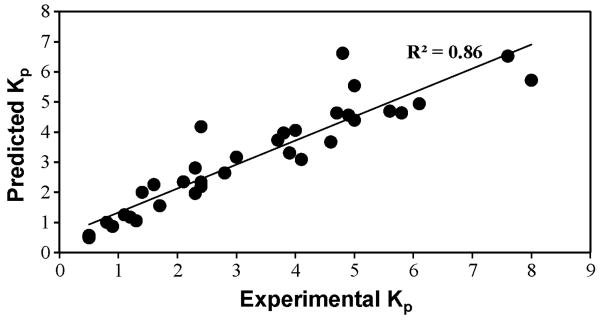
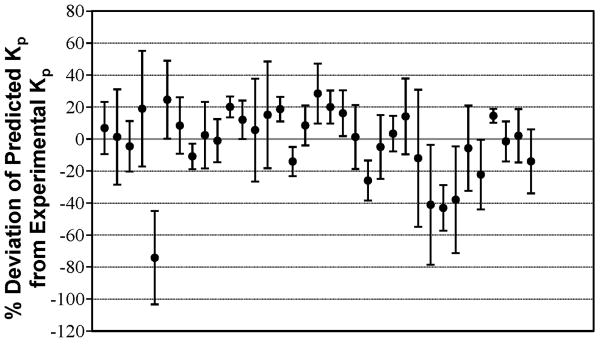
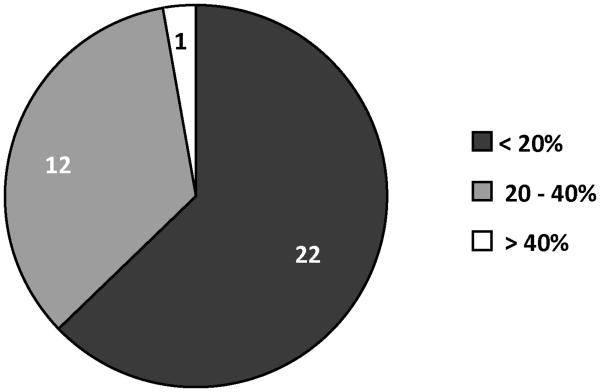
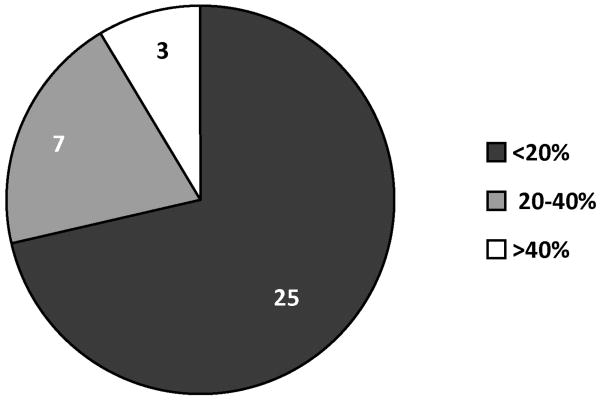
A neural network with one hidden layer was found to result in the least %AAD. Table 1 summarizes the statistical results for this network. The predicted and experimental Kp values and the percent deviations for the predicted values for the 35 CPEs used for training are tabulated in Table 2. A comparison of the experimental and predicted Kp values is shown in Figure 2. Figure 3 provides a graphical representation of the deviations between the predicted and experimental Kp values along with the uncertainties associated with each experimental datum. Figure 4 is a pie-chart for percent uncertainties in the experimental Kp values and Figure 5 presents a pie-chart detailing the ranges of percent deviations between the predicted and experimental Kp values.
Table 1.
The final model and statistical parameters.
| Neural Network architecture | Degrees of Freedom | SSEa | %AADb | RMSEc | (R2)d | |
|---|---|---|---|---|---|---|
| Model | 6-2-1 | 2.33 | 20.86 | 15.88 | 0.77 | 0.86 |
SSE is the sum squared error,
AAD is the average absolute deviation, and
RMSE is the root mean squared error of the predictions.
(R2) is the regression coefficient between the experimental and predicted values.
Table 2.
The experimental and predicted permeability (Kp) values for all 35 CPEs. The percentage deviations between the experimental and predicted values are also shown.
| CPE | Predicted Kp (10-3, cm/hr) | Experimental Kp ± Standard Deviation (10-3, cm/hr) | Deviations (%) |
|---|---|---|---|
| octanoic Acid | 4.56 | 4.9 ± 0.8 | 6.9 |
| decanoic acid | 4.64 | 4.7 ± 1.4 | 1.4 |
| oleic acid | 3.97 | 3.8 ± 0.6 | -4.5 |
| lauric Acid | 4.94 | 6.1 ± 2.2 | 19.0 |
| menthone | 4.18 | 2.4 ± 0.7 | -74.2 |
| 4-octanone | 3.09 | 4.1 ± 1.0 | 24.6 |
| pulegone | 1.56 | 1.7 ± 0.3 | 8.4 |
| cycloundecanone | 5.54 | 5 ± 0.4 | -10.8 |
| cis-4-hexen-1-ol | 2.34 | 2.4 ± 0.5 | 2.5 |
| nonanol | 3.74 | 3.7 ± 0.5 | -1.0 |
| decanol | 3.67 | 4.6 ± 0.3 | 20.1 |
| octanal | 4.40 | 5 ± 0.6 | 12.1 |
| N,N-dimethylisopropylamine | 2.64 | 2.8 ± 0.9 | 5.7 |
| octylamine | 3.31 | 3.9 ± 1.3 | 15.2 |
| 2,4,6-collidine | 1.06 | 1.3 ± 0.1 | 18.7 |
| 1-dodecyl-2-pyrrolidinone | 1.25 | 1.1 ± 0.1 | -14.0 |
| cetyltrimethylammonium bromide | 2.19 | 2.4 ± 0.3 | 8.6 |
| 2-chlorotoluene | 5.72 | 8 ± 1.5 | 28.5 |
| dimethyldisulfide | 4.64 | 5.8 ± 0.6 | 20.0 |
| 2-sec-butylphenol | 4.69 | 5.6 ± 0.8 | 16.2 |
| 3-methyl-2-oxazolidinone | 0.49 | 0.5 ± 0.1 | 1.3 |
| nonane | 1.01 | 0.8 ± 0.1 | -25.9 |
| 2-methyl butane | 0.52 | 0.5 ± 0.1 | -4.9 |
| acetophenone | 0.87 | 0.9 ± 0.1 | 3.4 |
| 1-bromobutane | 6.52 | 7.6 ± 1.8 | 14.2 |
| 1-bromohexadecane | 2.35 | 2.1 ± 0.9 | -11.9 |
| 2-heptanone | 2.26 | 1.6 ± 0.6 | -41.0 |
| 5-methyl-2-hexanone | 2.00 | 1.4 ± 0.2 | -43.0 |
| benzylbromide | 6.62 | 4.8 ± 1.6 | -37.9 |
| ethyl-2-methylpentanoate | 3.17 | 3 ± 0.8 | -5.7 |
| hexachloro-1,3-butadiene | 2.81 | 2.3 ± 0.5 | -22.2 |
| hexanal | 1.97 | 2.3 ± 0.1 | 14.6 |
| methylcaproate | 4.06 | 4 ± 0.5 | -1.4 |
| valeraldehyde | 1.17 | 1.2 ± 0.2 | 2.1 |
| 1-methyl-2-pyrrolidone | 0.57 | 0.5 ± 0.1 | -13.9 |
Figure 2.
Comparison of the experimental and the predicted permeability (Kp) values for insulin in the presence of various CPEs.
Figure 3.
Plot of percentage deviations between predicted and experimental permeability (Kp) values for insulin in the presence of various CPEs. The error bars indicate standard deviations for experimental Kp measurements.
Figure 4.
Range of percentage uncertainties observed in the experimental permeability (Kp) data.
Figure 5.
Range of percentage deviations observed between experimental and predicted permeability (Kp) data.
3.2. Validation
The predictions for the 25 CPEs in the validation set are provided in Table 3. For the 12 CPEs in the literature set, the predicted Kp values were all greater than 4.0 with dimethyl acetamide and limonene being the two exceptions. For the 8 CPEs in the resistance set, the predicted Kp values were considerably lower than 2.0 with 1,2-dichloropropane and azelaic acid being the two exceptions. For the five CPEs in the excluded set, the maximum absolute deviation observed was 32% in the case of 4-hydroxybenzaldehyde. The % AAD for the 5 CPEs in the excluded set was 20%.
Table 3.
Predictions for the validation set. The resistance reduction factors (RF) and the experimental permeability (Kp) values are included wherever available.
| CPE | Predicted Kp (10-3, cm/hr) | Experimental Kp (10-3, cm/hr) | RF = R0/R6 |
|---|---|---|---|
| Resistance set: Predicted Kp value must be lower than 2.0 | |||
| 1,2-dichloropropane* | 4.5 | -- | 3.3 ± 0.8 |
| 1-pentene | 0.5 | -- | 7.0 ± 2.6 |
| 1-pentyne | 0.5 | -- | 3.5 ± 0.3 |
| azelaic acid* | 5.0 | -- | 1.2 ± 0.1 |
| cyclopentane | 0.5 | -- | 3.9 ± 0.1 |
| salicaldehyde | 0.5 | -- | 4.8 ± 0.1 |
| salicylic acid | 1.6 | -- | 5.8 ± 0.4 |
| ethyl acetate | 0.6 | -- | 4.3 ± 0.7 |
| Literature set: Predicted Kp value must be greater than 2.0 | |||
| linoleic acid (6, 55) | 4.0 | -- | -- |
| limonene oxide (19) | 5.0 | -- | -- |
| menthol (19) | 4.5 | -- | -- |
| isopropyl myristate (7) | 4.5 | -- | -- |
| dimethyl acetamide* (7) | 0.5 | -- | -- |
| palmitic acid (55) | 5.4 | -- | -- |
| palmitoleic acid (55) | 4.5 | -- | -- |
| stearic acid (55) | 4.0 | -- | -- |
| linolenic acid (55) | 4.2 | -- | -- |
| limonene* (55) | 0.8 | -- | -- |
| azone (23, 24) | 21.8 | -- | -- |
| dodecyl-L-pyroglutamate (24) | 4.6 | -- | -- |
| Excluded set: Predicted Kp value must be close to experimental Kp value | |||
| 2-methylcyclohexanone | 2.3 | 1.8 ± 0.3 | -- |
| 3-methyl-2-hexanone | 2.0 | 1.6 ± 0.4 | -- |
| 4-hydroxybenzaldehyde | 1.0 | 1.5 ± 0.2 | -- |
| acetanilide | 0.9 | 0.9 ± 0.1 | -- |
| tertbutylacetic acid | 1.8 | 1.5 ± 0.1 | -- |
indicates a CPE that has been misclassified by the model
3.3. Sensitivity Analysis
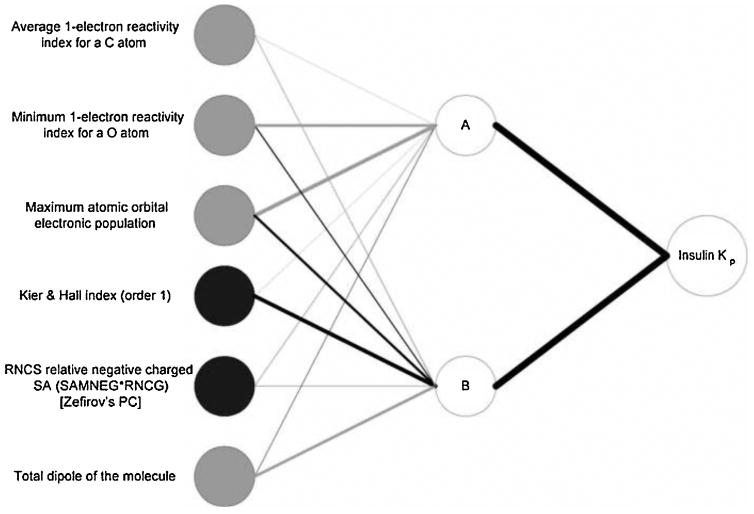
Figure 6 presents the NID for the original optimal network. From this figure, it is clear that the dominant connection weight between the sixth input (total dipole of the molecule) and hidden neuron B is negative, and the connection between this hidden neuron and the output is positive. Therefore, this input has a negative effect on insulin Kp. However, the fourth input (Kier & Hall index (order 1)) has a dominant positive connection weight with hidden neuron B and therefore has a positive effect on insulin Kp values. The connection weights of the fifth input (RNCS relative negative charged SA (SAMNEG*RNCG) [Zefirov's PC]) are both positive, and therefore, the overall effect of this input on the output is positive. For the other three inputs, however, the direction of the effect on the outputs cannot be deduced from the magnitudes of the connection weights alone.
Figure 6.
Neural interpretation diagram (NID) for the optimal neural network. The thickness of the connecting lines is proportional to the magnitude of the weights between the neurons. Black lines indicate positive weights and grey lines indicate negative weights. Black input circles indicate inputs that have an overall positive effect on the output and grey input circles indicate those that have an overall negative effect.
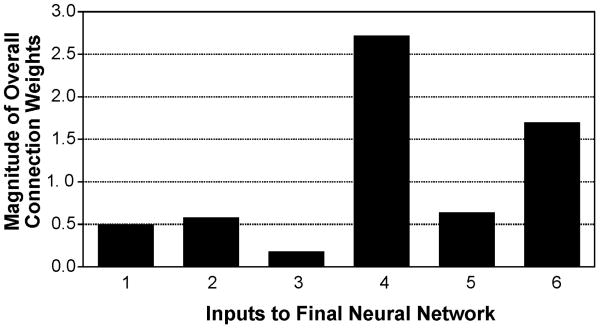
Table 4 lists the descriptors used as inputs in the final optimal network and their physical interpretation. Henceforth in the discussion, these descriptors will be referred to as D1, D2, D3, D4, D5 and D6. Table 5 lists the relative importance (RI %) of these descriptors, calculated using Garson's algorithm. Using the randomized connection weight approach described in Section 2.4, the overall connection weights and the directions of the effects of the inputs on the output are determined and tabulated in Table 5. From this, it is clear that all the inputs except inputs 4 and 5 have a negative effect on the output. Figure 7 presents a bar chart for the magnitudes of the overall connection weights for all the six descriptors. Table 5 also lists the results of the leave one descriptor out analysis. Removing either of the descriptors D4, D2, or D6 resulted in high %AAD values when compared to removing D3, D5 or D1.
Table 4.
The descriptors used in the final model and their physical interpretation.
| Input | Descriptor Name | Descriptor Type | Physical Interpretation |
|---|---|---|---|
| D1 | Average 1-electron reactivity index for a C atom | Quantum-chemical | Reactivity at the site of C atoms |
| D2 | Minimum 1-electron reactivity index for a O atom | Quantum-chemical | Reactivity at the site of O atoms |
| D3 | Max atomic orbital electronic population | Quantum-chemical | Nucleophilicity of the molecule |
| D4 | Kier&Hall index (order 1) | Topological | Molecular branching |
| D5 | RNCS Relative negative charged SA (SAMNEG*RNCG) [Zefirov's PC] | Electrostatic | Nucleophilic portion of the molecule's surface |
| D6 | Tot dipole of the molecule | Quantum-chemical | Charge distribution of the molecule |
Table 5.
The six descriptors in the final neural network, their relative importance (RI %) calculated using Garson's algorithm, their overall connection weights and directions of effect calculated using the randomized connection weight approach by Olden & Jackson (40) and the results from the leave one descriptor out analysis.
| Input | Descriptor | Relative Importance (RI %) | Overall Connection Weight | Direction of Effect | Leave one descriptor out analysis | |
|---|---|---|---|---|---|---|
| %AAD | # of misclassifications | |||||
| D1 | Average 1-electron reactivity index for a C atom | 4.09 | -0.50 | negative | 22.9 | 4 |
| D2 | Minimum 1-electron reactivity index for a O atom | 21.73 | -0.58 | negative | 29.2 | 6 |
| D3 | Max atomic orbital electronic population | 33.29 | -0.18 | negative | 21.3 | 4 |
| D4 | Kier&Hall index (order 1) | 19.64 | 2.72 | positive | 36.9 | 5 |
| D5 | RNCS Relative negative charged SA (SAMNEG*RNCG) [Zefirov's PC] | 6.05 | 0.64 | positive | 23.3 | 4 |
| D6 | Tot dipole of the molecule | 15.20 | -1.70 | negative | 28.0 | 4 |
Figure 7.
Comparison of the overall connection weights of all six inputs to the network.
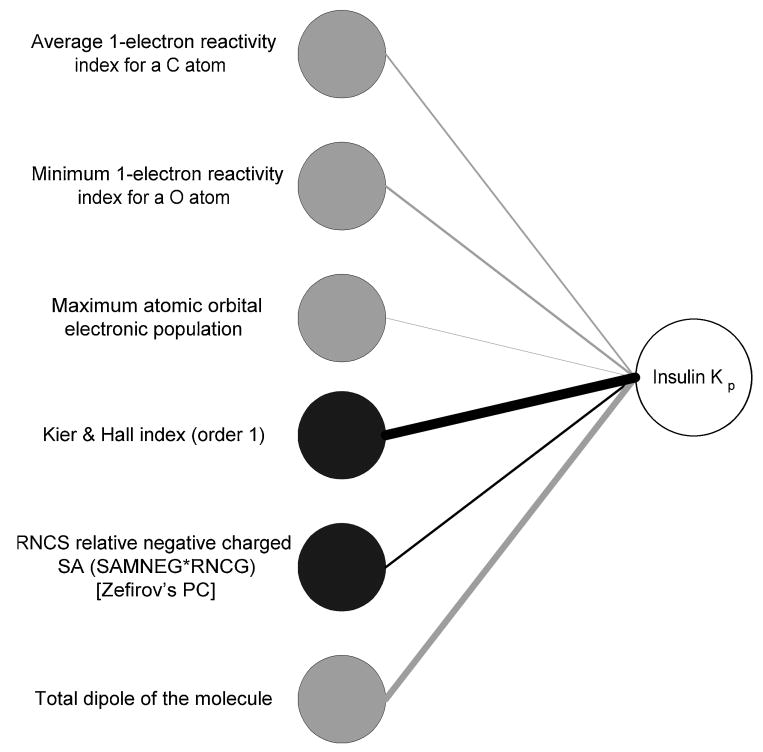
Table 6 lists the all the connection weights and the overall connection weights of the optimal network and their statistical significance values (p-values) calculated using the randomization procedure described in Section 2.4. From the table, it is evident that of the 12 input-hidden-output connections, nine connections are statistically significant, and of the six overall connection weights, five are significant, (i.e. p-values lower than the 0.05) at a 95% confidence level. The overall connection weight of D3 was found to be insignificant. The NID shown as Figure 6 can be simplified by removing the hidden layer and retaining only the significant overall connection weights. The simplified NID is shown in Figure 8.
Table 6.
The statistical significance (P) of the connection weights (WA,i or WB,i) and the overall connection weights (WA,i +WB,i) in the final network determined using the randomized approach proposed by Olden & Jackson (40).
| Input | Descriptor | Hidden Neuron A | Hidden Neuron B | Overall connection weight | |||
|---|---|---|---|---|---|---|---|
| WA,i | P | WB,i | P | WA,i +WB,i | P | ||
| D1 | Average 1-electron reactivity index for a C atom | 0.07* | 0.304 | -0.57 | 0.003 | -0.50 | 0.021 |
| D2 | Minimum 1-electron reactivity index for a O atom | -1.52 | 0.002 | 0.92 | 0.002 | -0.58 | 0.013 |
| D3 | Max atomic orbital electronic population | -2.06 | 0.001 | 1.88 | 0.002 | -0.18* | 0.186 |
| D4 | Kier&Hall index (order 1) | -0.22* | 0.091 | 2.94 | 0.001 | 2.72 | 0.001 |
| D5 | RNCS Relative negative charged SA (SAMNEG*RNCG) [Zefirov's PC] | 0.47 | 0.012 | 0.17* | 0.091 | 0.64 | 0.012 |
| D6 | Tot dipole of the molecule | 0.30 | 0.026 | -2.00 | 0.001 | -1.70 | 0.002 |
indicates insignificant connection weights with 95% confidence level
Figure 8.
Simplified neural interpretation diagram (NID) displaying only the significant overall connection weights, where black and grey indicate positive and negative effects, respectively.
4. Discussion
The optimum model identified in this work was a 6-2-1 network, which was able to account for 86% of the variation in the target property (Figure 2). The six best descriptors identified by the algorithm are tabulated in Table 4. Using Garson's algorithm, the relative importance of these descriptors was calculated to be in the following order: D3 > D2 > D4 > D6 > D5 > D1 (Table 5). In contrast, the overall connection weights (Table 5) when ordered in decreasing order of magnitudes gave rise to the following order: D4 > D6 > D5 > D2 > D1 > D3. Also, the overall connection weight of Descriptor 3 is insignificant (p = 0.186 > α = 0.05 for 95% confidence levels) whereas the other overall connection weights are significant (p < 0.05) when analyzed using the randomization procedure described in Section 2.4. Clearly, RI% values calculated using the Garson' algorithms are in contradiction with the overall connection weights and the significance levels calculated using the randomization analysis. To clarify the issue, the results from leave-one-descriptor-out analysis were evaluated. The larger the error in the network that has been built after leaving out a descriptor, the greater is that particular descriptor's significance. Table 5 summarizes these results for the six networks. As shown, the relative order of importance is D4 > D2 > D6 > D5 > D1 > D3. This is similar to the order calculated using the overall connection weight approach, with the exception of D2, which was calculated to have a lower importance than D6 and D5 (Table 5) using the overall connection weight approach. From the relative orders of importance calculated using the overall connection weight approach and the leave-one-descriptor-out analysis, it is clear that D4 is the most important of the descriptors, and D1 and D3 are the least important. This apparent discrepancy with the RI% values calculated using Garson's algorithm is attributed to the inability of this algorithm to consider the direction of weights. This shortcoming of the Garson's algorithm has been discussed in detail by Olden and Jackson (Olden and Jackson, 2002).
The six descriptors, their types and their physical interpretation are provided in Table 4. D4 (Kier & Hall index (order 1)) is a connectivity index that according to Kier and Hall (Kier and Hall, 2000), “encodes molecular structure in a non-empirical way and does not directly derive from or translate into any particular physical property.” These authors have explained the significance of this property from the view point of intermolecular accessibility. They have reported that atoms with highly branched bonds would have limited access to their environment and therefore would be involved in intermolecular reactions to a lesser degree than atoms that have very little branching at their sites. Therefore, they have suggested that molecules with a low degree of branching, which corresponds to a high value of the first order Kier & Hall connectivity index, would be most likely to participate in intermolecular reactions. Since, this descriptor has been identified as significant by the randomized overall connection weight approach and the leave- one-descriptor-out analysis, and the direction of the overall connection weight from this descriptor to the output is positive (Table 5), it is reasonable to assume that a molecule with relatively little or no branching should greatly enhance the permeation of insulin when compared to molecules that are highly branched.
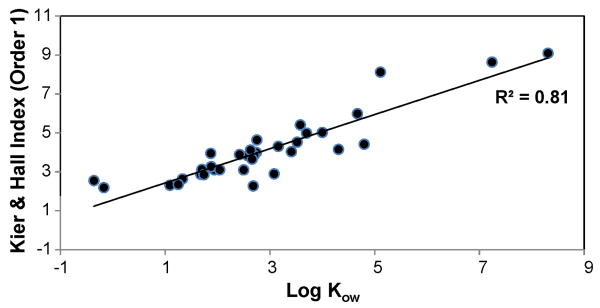
Since most CPEs enhance drug permeation by disruption of the lipid bi-layers, a molecule with a low degree of branching would have its reactive sites well exposed to the bi-layers, and therefore it can induce greater disruption of these layers by forming intermolecular bonds. As opposed to branched molecules which have reactive sites shielded by neighboring atoms and cannot participate sufficiently in chemical reactions. Hrabalek et al. (Hrabalek et al., 2005) have reported significant drug enhancement by 6-aminohexanoic acid derivatives having a small degree of branching. However, they have reported that higher order branching leads to a decrease in enhancement activity. Also, Chantasart et al. (Chantasart et al., 2004) have reported that branched alkanols have significantly lower enhancer potency than their straight chain counterparts. Also, since the first order Kier & Hall index has been used to correlate several physical properties like boiling point (Hall et al., 1975, Kier and Hall, 1976), water solubilities (Hall et al., 1975) and also partition coefficients (Murray et al., 1975), we have tried to correlate this descriptor and the octanol-water partition coefficients, as calculated using Marvin calculator plug-in by ChemAxon (ChemAxon), for all the CPEs in the training set. 1-dodecyl-2-pyrrolidone exhibited a large deviation from the linear trend-line and therefore was excluded from the correlation. The resulting linear correlation between the two properties is shown in Figure 9. Therefore, D4 could be considered as an indicator of the CPE's ability to transport from the donor solution to the skin lipids. When the partition coefficients were compared with the other five descriptors in the model, poor correlations were observed.
Figure 9.
Correlation between the first order Kier & Hall index and the octanol-water partition coefficient (Log Kow) for the various CPEs.
D2 relates to the reactivity at the site of oxygen atoms in the molecule. Since, the direction of the effect of this descriptor is negative, large negative values of this descriptor lead to better insulin permeation. Mathematically, this descriptor is inversely related to the energy gap between the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) of the oxygen atom (Katritzky et al., 1994). Therefore, molecules that have high values of D2 have smaller HOMO-LUMO energy gaps. From a quantum-chemical perspective, a small HOMO-LUMO energy gap indicates the ability of the molecule to exchange electrons and therefore, D2 is a measure of the oxygen atoms in the molecule to participate in chemical reactions. Narishetty & Panchagnula (Narishetty and Panchagnula, 2004a, Narishetty and Panchagnula, 2004b) have performed experimental studies on permeation of Zidovudine in the presence of terpenes and suggested that the oxygen atoms in the terpenes form competitive hydrogen bonds with ceramide molecules in the skin's lipid bi-layers. This leads to the breakup of the compact lamellar network of these bi-layers and results in enhancement of Zidovudine permeation. Assuming a similar mechanism in the current work, the insulin permeation enhancement by molecules with highly reactive oxygen sites can be explained.
While D1 is similar to D2, it describes the average reactivity of all carbon atoms in the molecule. Since the direction of its effect is also negative and using a reasoning strategy analogous to that used for D2, we may suggest that molecules with highly reactive carbon atoms disrupt the skin lipid bi-layers by forming hydrogen bonds and therefore enhance insulin permeation.
D5 relates to the surface area of the molecule that is negatively charged. The positive effect of this descriptor implies that a molecule with a larger negatively charged surface would enhance insulin permeation more than a molecule with relatively smaller or no negatively charged surface. This again conforms to the hydrogen bonding theory proposed in the previous paragraph; greater the charged surface area of a molecule, greater is its chance of reacting with the skin lipid bi-layers to form hydrogen bonds. Therefore, it appears that not only should a molecule have highly reactive oxygen and carbon sites, but also these sites should be sufficiently exposed to the lipid bi-layers to facilitate greater reactivity.
D6 describes the total dipole moment of the CPE. The negative effect of this descriptor on insulin permeability implies that good insulin specific CPEs have low dipoles. It has been reported by some workers that molecules with large dipoles are not easily soluble in lipids (Mazzenga and Berner, 1990), and also ionic forms of a drug fail to permeate through the skin when compared to its non-ionic form, due to the former's low solubility in skin lipids (Abraham and Martins, 2004). Therefore, it may be assumed that a molecule with a high dipole moment would fail to partition into the lipid bi-layers and consequently cannot enhance insulin permeation by disrupting these layers. D3, which again represents the reactivity of the molecule, was found to be insignificant from the randomization analysis for the overall connection weight. Therefore, it is highly likely that this descriptor has no part to play in the mechanism of insulin enhancement and might have been included in the model only as a correction factor for mathematical accuracy.
From the previous discussion concerning the physical interpretation of the descriptors involved in the model, it is apparent that the enhancement effect of the CPEs is interplayed among their structural attributes. On one hand, there are favorable structural features like the first order Kier & Hall index which describes the lipid partitioning ability of the molecule and other electronegative descriptors (reactivity indices of carbon and oxygen atoms and the negatively charged surface area) that describe the ability of the CPE to react with the lipid bi-layers of the skin. On the other hand, there is the total dipole of the molecule, which diminishes the efficacy of a CPE by decreasing its lipid solubility. Therefore, the design methodology for a CPE involves finding structures that account for these different attributes.
The validation for the best model identified was performed on 25 CPEs belonging to varied functional groups. As can be inferred from Table 3, the model performed reasonably well in predicting the permeabilities for new CPEs. However, there were four misclassified CPEs. 1,2-dichloropropane and azelaic acid did not significantly reduce skin resistance and therefore are expected to not disrupt the skin structure upon exposure. However, the model predicts high insulin permeability values in their presence. This could possibly be due to the lack of sufficient diversity in the training set with respect to this particular group of chemical structures. Also, because of the relatively small size of the data set employed in the current work, the number of descriptors in the model was limited to six which might not account for all the descriptors relevant for describing the enhancement mechanism. One of the 12 literature CPEs, dimethyl acetamide has been reported to be an insulin enhancer (Pillai et al., 2004b). In contrast, the current model predicts no insulin permeation enhancement in its presence. This could possibly be explained by the fact that in the work by Pillai et al. (Pillai et al., 2004b), this CPE has been used at 100% concentration as opposed to the 5% w/v solution of CPE used in the current study. Limonene was the other literature CPE that has been reported to enhance insulin permeation in the literature (Rastogi and Singh, 2005), but the model in the current work classifies it as a non-CPE (Table 3). This CPE needs to be investigated experimentally in the future to determine if it enhances insulin permeation using the current experimental set-up. Although Azone has been classified correctly by the current model as an insulin-specific enhancer, the predicted permeability value of approximately 22 cm/h is far greater than the experimental values observed in the current work. This could be due to the fact, that the training set for the model did not include any Azone-like molecules. We seek to improve our model in the future by including derivatives of Azone. As for the predictions for the five CPEs belonging to the excluded set, the percentage absolute average deviation (%AAD) value was 20, which is less than twice the error on the training set. This proves that the model not only classifies the new molecules correctly into working and non-working categories, but also predicts the insulin permeability values with reasonable errors.
Comparison of the elution times of the insulin standards with the other HPLC evaluations of insulin permeated does not reveal any shift in the elution time. This can provide indirect evidence that cluster formation is not occurring; however, we do acknowledge the need for additional biofunctionality and bioavailability analyses to characterize the insulin during transport through the skin. This characterization will involve the performance of in vivo animal testing and is the subject for future research.
5. Conclusions
The results from the current work lead to the following conclusions:
A hybrid algorithm that combines differential evolution algorithms (DE) and artificial neural networks (ANNs) provides a reasonably good predictive model for insulin permeability in the presence of CPEs
Descriptors found to be statistically significant included the following: average 1-electron reactivity index for a C atom, minimum 1-electron reactivity index for a O atom, Kier & Hall index (order 1), RNCS relative negative charged SA (SAMNEG*RNCG) [Zefirov's PC], and total dipole of the molecule
In general, greater hydrophobicity and reactivity increase a CPE's efficacy, and higher dipole moments decrease the efficacy.
Acknowledgments
Financial support for this research was provided by the National Institute of Biomedical Imaging and Bioengineering (1R21EB005749).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abraham MH, Martins F. Human skin permeation and partition: General linear free-energy relationship analyses. J Pharm Sci. 2004;93:1508–1523. doi: 10.1002/jps.20070. [DOI] [PubMed] [Google Scholar]
- Agatonovic-Kustrin S, Beresford R, Yusof AP. ANN modeling of the penetration across a polydimethylsiloxane membrane from theoretically derived molecular descriptors. J Pharm Biomed Anal. 2001;26:241–254. doi: 10.1016/s0731-7085(01)00421-6. [DOI] [PubMed] [Google Scholar]
- Aoki I, Komatsu T. Analysis and prediction of the fluctuation of sardine abundance using a neural network. Oceanologica acta. 1997;20:81–88. [Google Scholar]
- Barratt MD. Quantitative structure-activity relationships for skin permeability. Toxicol in Vitro. 1995;9:27–37. doi: 10.1016/0887-2333(94)00190-6. [DOI] [PubMed] [Google Scholar]
- CambridgeSoft. Chembiooffice 11.0. Cambridge Software 2008 [Google Scholar]
- Chantasart D, Li SK, He N, Warner KS, Prakongpan S, Higuchi WI. Mechanistic studies of branched-chain alkanols as skin permeation enhancers. J Pharm Sci. 2004;93:762–779. doi: 10.1002/jps.10550. [DOI] [PubMed] [Google Scholar]
- ChemAxon. Marvin and Calculator Plugin Demo. ChemAxon 2007 [Google Scholar]
- Choi EH, Lee SH, Ahn SK, Hwang SM. The pretreatment effect of chemical skin penetration enhancers in transdermal drug delivery using iontophoresis. Skin Pharmacol Appl Skin Physiol. 1999;12:326–335. doi: 10.1159/000029894. [DOI] [PubMed] [Google Scholar]
- Garson GD. Interpreting neural-network connection weights. AI expert. 1991;6:46–51. [Google Scholar]
- Ghafourian T, Zandasrar P, Hamishekar H, Nokhodchi A. The effect of penetration enhancers on drug delivery through skin: a QSAR study. J Controlled Release. 2004;99:113–125. doi: 10.1016/j.jconrel.2004.06.010. [DOI] [PubMed] [Google Scholar]
- Godavarthy SS, Yerramsetty KM, Rachakonda VK, Neely BJ, Madihally SV, Robinson RL, Jr, Gasem KAM. Design of improved transdermal drug delivery permeation enhancers. J Pharm Sci. 2009 doi: 10.1002/jps.21940. Accepted. [DOI] [PubMed] [Google Scholar]
- Guy RH, Potts RO. Penetration of industrial chemicals across the skin: a predictive model. Am J Ind Med. 1993;23:711–719. doi: 10.1002/ajim.4700230505. [DOI] [PubMed] [Google Scholar]
- Hall LH, Kier LB, Murray WJ. Molecular connectivity II: Relationship to water solubility and boiling point. J Pharm Sci. 1975;64:1974–1977. doi: 10.1002/jps.2600641215. [DOI] [PubMed] [Google Scholar]
- Hao JS, Zheng JM, Yang WZ. Transdermal iontophoresis of insulin: effect of penetration enhancers on blood glucose level in diabetic rats. Yao Xue Xue Bao. 1995;30:776–780. [PubMed] [Google Scholar]
- Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural networks. 1989;2:359–366. [Google Scholar]
- Hrabalek A, Vavrova K, Dolezal P, Machacek M. Esters of 6-aminohexanoic acid as skin permeation enhancers: The effect of branching in the alkanol moiety. J Pharm Sci. 2005;94:1494–1499. doi: 10.1002/jps.20376. [DOI] [PubMed] [Google Scholar]
- Iyer M, Zheng T, Hopfinger AJ, Tseng YJ. QSAR analyses of skin penetration enhancers. J Chem Inf Model. 2007;47:1130–1149. doi: 10.1021/ci700051e. [DOI] [PubMed] [Google Scholar]
- Kang L, Yap CW, Lim PFC, Chen YZ, Ho PC, Chan YW, Wong GP, Chan SY. Formulation development of transdermal dosage forms: Quantitative structure-activity relationship model for predicting activities of terpenes that enhance drug penetration through human skin. J Controlled Release. 2007;120:211–219. doi: 10.1016/j.jconrel.2007.05.006. [DOI] [PubMed] [Google Scholar]
- Katritzky AR, Lobanov VS, Karelson M. CODESSA User's Manual. University of Florida; Gainsville: 1994. [Google Scholar]
- Kier LB, Hall LH. Molecular connectivity VII: specific treatment of heteroatoms. J Pharm Sci. 1976;65:1806–1809. doi: 10.1002/jps.2600651228. [DOI] [PubMed] [Google Scholar]
- Kier LB, Hall LH. Intermolecular accessibility: the meaning of molecular connectivity. J Chem Inf Comput Sci. 2000;40:792–795. doi: 10.1021/ci990135s. [DOI] [PubMed] [Google Scholar]
- Li CJ, Obata Y, Higashiyama K, Nagai T, Takayama K. Effect of 1-O-ethyl-3-butylcyclohexanol on the skin permeation of drugs with different physicochemical characteristics. Int J Pharm. 2003;259:193–198. doi: 10.1016/s0378-5173(03)00210-2. [DOI] [PubMed] [Google Scholar]
- Mathworks. MATLAB. Novi, Michigan: The Mathworks Inc.; 2005. [Google Scholar]
- Mazzenga GC, Berner B. Transdermal administration of zwitterionic drugs. USA: 1990. [Google Scholar]
- Mitragotri S, Blankschtein D, Langer R. Transdermal drug delivery using low-frequency sonophoresis. Pharm Res. 1996;13:411–420. doi: 10.1023/a:1016096626810. [DOI] [PubMed] [Google Scholar]
- Monteiro-Riviere NA. Comparative Anatomy, Physiology, and Biochemistry of Mammalian Skin. In: Hobson DW, editor. Dermal and Ocular Toxicology: Fundamentals and Methods. 1st. Boca Raton, FL: CRC Press; 1991. [Google Scholar]
- Monteiro-Riviere NA. Anatomical Factors Affecting Barrier Function. In: Marzulli FN, Maibach HI, editors. Dermatotoxicology. 1st. Washington, D.C.: Taylor & Francis; 1996. [Google Scholar]
- Murray WJ, Hall LH, Kier LB. Molecular connectivity III: Relationship to partition coefficients. J Pharm Sci. 1975;64:1978–1981. doi: 10.1002/jps.2600641216. [DOI] [PubMed] [Google Scholar]
- Narishetty STK, Panchagnula R. Transdermal delivery of zidovudine: effect of terpenes and their mechanism of action. J Controlled Release. 2004a;95:367–379. doi: 10.1016/j.jconrel.2003.11.022. [DOI] [PubMed] [Google Scholar]
- Narishetty STK, Panchagnula R. Transdermal delivery system for zidovudine: in vitro, ex vivo and in vivo evaluation. Biopharm Drug Dispos. 2004b;25:9–20. doi: 10.1002/bdd.381. [DOI] [PubMed] [Google Scholar]
- Neumann D, Kohlbacher O, Merkwirth C, Lengauer T. A fully computational model for predicting percutaneous drug absorption. J Chem Inf Model. 2006;46:424–429. doi: 10.1021/ci050332t. [DOI] [PubMed] [Google Scholar]
- Olden JD, Jackson DA. Illuminating the “black box”: a randomization approach for understanding variable contributions in artificial neural networks. Ecological Modelling. 2002;154:135–150. [Google Scholar]
- Patni P, Varghese D, Balekar N, Jain DK. Needle-free insulin drug delivery. Indian Journal of Pharmaceutical Sciences. 2006;68:7–12. [Google Scholar]
- Pillai O, Borkute SD, Sivaprasad N, Panchagnula R. Transdermal iontophoresis of insulin II. Physicochemical considerations. Int J Pharm. 2003a;254:271–280. doi: 10.1016/s0378-5173(03)00034-6. [DOI] [PubMed] [Google Scholar]
- Pillai O, Kumar N, Dey CS, Borkute S, Nagalingam S, Panchagnula R. Transdermal iontophoresis of insulin. Part 1: A study on the issues associated with the use of platinum electrodes on rat skin. The Journal of pharmacy and pharmacology. 2003b;55:1505–1513. doi: 10.1211/0022357022197. [DOI] [PubMed] [Google Scholar]
- Pillai O, Kumar N, Dey CS, Borkute S, Nagalingam S, Panchagnula R. Transdermal iontophoresis of insulin: III. Influence of electronic parameters. Methods Finds Exp Clin Pharmacol. 2004a;26:399–408. [PubMed] [Google Scholar]
- Pillai O, Nair V, Panchagnula R. Transdermal iontophoresis of insulin: IV. Influence of chemical enhancers. Int J Pharm. 2004b;269:109–120. doi: 10.1016/j.ijpharm.2003.09.032. [DOI] [PubMed] [Google Scholar]
- Pillai O, Panchagnula R. Transdermal delivery of insulin from poloxamer gel: ex vivo and in vivo skin permeation studies in rat using iontophoresis and chemical enhancers. J Controlled Release. 2003a;89:127–140. doi: 10.1016/s0168-3659(03)00094-4. [DOI] [PubMed] [Google Scholar]
- Pillai O, Panchagnula R. Transdermal iontophoresis of insulin V. Effect of terpenes. J Controlled Release. 2003b;88:287–296. doi: 10.1016/s0168-3659(03)00065-8. [DOI] [PubMed] [Google Scholar]
- Potts RO, Guy RH. Predicting skin permeability. Pharm Res. 1992;9:663–669. doi: 10.1023/a:1015810312465. [DOI] [PubMed] [Google Scholar]
- Priborsky J, Takayama K, Nagai T, Waitzova D, Elis J, Makino Y, Suzuki Y. Comparison of penetration-enhancing ability of laurocapram, N-methyl-2-pyrrolidone and dodecyl-L-pyroglutamate. Pharm Weekbl Sci. 1988;10:189–192. doi: 10.1007/BF01956869. [DOI] [PubMed] [Google Scholar]
- Price KV, Storn RM, Lampinen JA. Differential evolution: a practical approach to global optimization. Springer Verlag; 2005. [Google Scholar]
- Rachakonda VK, Yerramsetty KM, Madihally SV, Robinson RL, Jr, Gasem KAM. Screening of Chemical Penetration Enhancers for Transdermal Drug Delivery Using Electrical Resistance of Skin. Pharm Res. 2008;25:2697–2704. doi: 10.1007/s11095-008-9696-y. [DOI] [PubMed] [Google Scholar]
- Rao VU, Misra AN. Enhancement of iontophoretic permeation of insulin across human cadaver skin. Die Pharmazie. 1994;49:538–539. [PubMed] [Google Scholar]
- Rastogi SK, Singh J. Passive and iontophoretic transport enhancement of insulin through porcine epidermis by depilatories: permeability and Fourier transform infrared spectroscopy studies. AAPS PharmSciTech. 2003;4:1–9. doi: 10.1208/pt040329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rastogi SK, Singh J. Effect of chemical penetration enhancer and iontophoresis on the in vitro percutaneous absorption enhancement of insulin through porcine epidermis. Pharm Dev Technol. 2005;10:97–104. doi: 10.1081/pdt-49679. [DOI] [PubMed] [Google Scholar]
- Scheuplein RJ, Blank IH. Permeability of the skin. Physiol Rev. 1971;51:702–747. doi: 10.1152/physrev.1971.51.4.702. [DOI] [PubMed] [Google Scholar]
- Scheuplein RJ, Blank IH. Mechanism of percutaneous absorption. IV. penetration of nonelectrolytes (alcohols) from aqueous solutions and from pure liquids. J Invest Dermatol. 1973;60:286–296. doi: 10.1111/1523-1747.ep12723090. [DOI] [PubMed] [Google Scholar]
- Semichem. AMPAC, 6.0. Shawnee, KS: Semichem Inc.; 1998a. [Google Scholar]
- Semichem. CODESSA, 2.7.8. Shawnee, KS: Semichem Inc.; 1998b. [Google Scholar]
- Sintov AC, Wormser U. Topical iodine facilitates transdermal delivery of insulin. J Controlled Release. 2007;118:185–188. doi: 10.1016/j.jconrel.2006.12.006. [DOI] [PubMed] [Google Scholar]
- Stoughton RB. Percutaneous absorption of drugs. Annu Rev Pharmacol Toxicol. 1989;29:55–69. doi: 10.1146/annurev.pa.29.040189.000415. [DOI] [PubMed] [Google Scholar]
- Tropsha A, Gramatica P, Gombar VK. The importance of being earnest: validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb Sci. 2003;22:69–77. [Google Scholar]
- Turner JV, Maddalena DJ, Agatonovic-Kustrin S. Bioavailability prediction based on molecular structure for a diverse series of drugs. Pharm Res. 2004;21:68–82. doi: 10.1023/b:pham.0000012154.09631.26. [DOI] [PubMed] [Google Scholar]
- Yerramsetty KM, Rachakonda VK, Neely BJ, Madihally SV, Gasem KAM. Effect of Different Enhancers on the Transdermal Permeation of Insulin Analog. Submitted to International Journal of Pharmaceutics. 2009 doi: 10.1016/j.ijpharm.2010.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]