Abstract
We present a cellular automaton model of clonal evolution in cancer aimed at investigating the emergence of the glycolytic phenotype. In the model each cell is equipped with a micro-environment response network that determines the behaviour or phenotype of the cell based on the local environment. The response network is modelled using a feed-forward neural network, which is subject to mutations when the cells divide. This implies that cells might react differently to the environment and when space and nutrients are limited only the fittest cells will survive. With this model we have investigated the impact of the environment on the growth dynamics of the tumour. In particular we have analysed the influence of the tissue oxygen concentration and extra-cellular matrix density on the dynamics of the model. We found that the environment influences both the growth and evolutionary dynamics of the tumour. For low oxygen concentration we observe tumours with a fingered morphology, while increasing the matrix density gives rise to more compact tumours with wider fingers. The distribution of phenotypes in the tumour is also affected, and we observe that the glycolytic phenotype is most likely to emerge in a poorly oxygenated tissue with a high matrix density. Our results suggest that it is the combined effect of the oxygen concentration and matrix density that creates an environment where the glycolytic phenotype has a growth advantage and consequently is most likely to appear.
Keywords: Mathematical model, cellular automaton, tumourigenesis, hybrid, evolutionary dynamics, clonal evolution, micro-environment, response network, glycolysis, anaerobic metabolism
1 Introduction
The development of a tumour is a highly complex process involving a multitude of interacting processes such as escaping the host immune response (Dunn et al., 2004), extra-cellular matrix degradation (DeClerck et al., 2004) and angiogenesis (Folkman, 2006). The process in which the cancer cells acquire these capabilities is similar to Darwinian evolution because the cells in a tumour have to compete for space and resources (Alexandrova, 2001). This means that the cancer cells which are best adapted to the tissue environment, in which they are growing, will have a higher chance of survival and thus are more likely to proliferate.
Most of these acquired traits are straightforward to explain from a evolutionary point of view, e.g. cells that are not recognised by the immune system will obviously have a growth advantage, but one typical trait of cancer cells, the reliance on anaerobic metabolism, seems to evade such a simple explanation. The reason for this is that anaerobic metabolism (glycolysis) is more than 10-fold less efficient in producing ATP (the molecule used for energy transport in cells) from glucose compared to the normal aerobic metabolism that utilises oxygen. This means that glycolytic cells need to consume over ten times more glucose to maintain the same energy turn-over. Further, the glycolytic pathway produces an excess of acid, which is harmful for the cells. The growth advantage of cells that rely on glycolysis can therefore not be inferred from a simple cause and effect relationship, but rather seems to be the outcome of complex interactions between the cancer cells and their micro-environment. This is a situation where mathematical modelling can be a useful tool, as it has the capability to capture such complex relationships.
In this paper we will use a mathematical model of clonal evolution to investigate the emergence of the glycolytic phenotype and try to elucidate under which growth conditions this is most likely to occur. Because this phenomenon is tightly linked to clonal evolution, the model presented here is on the level of single cells, allowing cells to posses different phenotypes and behaviours. This is accomplished by letting each cancer cell be equipped with a response network that determines the behaviour of the cells based on the local micro-environment. This naturally introduces a extra layer of complexity to the model, but we believe that the evolutionary origin of the glycolytic phenotype requires this type of detailed modelling and that our model hopefully can increase the understanding of this crucial aspect of carcinogenesis.
1.1 Biological background
The upregulation of glycolysis in tumours was first observed by Warburg (1930), and has therefore been named the ”Warburg effect”. What he observed was not only an increase in anaerobic glycolysis (similar to what occurs during physical exercise), but also sustained glycolysis even in the presence of oxygen. Although no conclusive evidence has been produced, it is hypothesised that the up-regulation of glycolysis is due to the chronic (or sometimes cyclic) exposure to low levels of oxygen that the tumour cells experience. In this competetive environment, where nutrients are scarce, the ability to survive without relying on oxygen presents a growth advantage. On a molecular level this is believed to result from an up-regulation of the hypoxic-inducible-factor HIF1α, which induces the up-regulation of survival specific genes and increases glucose transport across the cell membrane (Semenza, 1998).
The up-regulation of glycolysis is naturally followed by increased glucose uptake, and this can readily be observed with positron emission tomography (PET) using the glucose analogue fluorodeoxyglucose (Hawkins and Phelps, 1988). Using this technique it has been shown that most in vivo human tumours in fact have an increased uptake of glucose (Czernin and Phelps, 2002), which signifies an increased rate of glycolysis. The appearance of tumours relying on glycolysis has also been linked with poor prognosis (Kunkel et al., 2003), which suggests that it may impact on the invasiveness of the tumour cells.
In fact it has been shown that the increased acidity that results from sustained glycolysis has detrimental effects on the surrounding tissue (Schornack and Gillies, 2003), due to acid-induced apoptosis of neighbouring normal cells and increased degradation of the extra-cellular matrix (ECM). Normal cells tend to go into apoptosis when exposed to pH below 7.1 (Casciari et al., 1992), while cancer cells have been observed to proliferate optimally at pH=6.8 (Dairkee et al., 1995). This chronic acidification leads to an acellular gap separating the tumour from the normal tissue, which creates space for the cancerous cells to move into and consequently increases the invasiveness of the tumour (Gatenby and Gawlinski, 1996). Further, it has been reported that low pH also increases invasion through release of matrix degrading enzymes by fibroblasts and macrophages (Rozhin et al., 1994). These enzymes break down the ECM in the peritumoral tissue and similarly promote invasion.
Under normal aerobic metabolism cells convert glucose and oxygen into ATP, which serves as energy for the cell, in a process known as the Krebs-cycle (Alberts et al., 1994a). This process converts each glucose molecule into 36 ATP molecules and can be written in simplified form as:
| (1) |
The glycolytic pathway on the other hand produces ATP, and lactic acid as a by-product, directly from glucose. This reaction can be represented as:
| (2) |
From this we can observe that the anaerobic pathway is 18 times less efficient at creating ATP molecules, which are the energy units in the cell. Further, both metabolic pathways produce hydrogen ions (H+), but the fact that the anaerobic pathway produces 18 times less ATP implies that the hydrogen ion production is much higher for the same energy turn-over. This high hydrogen ion production exceeds the metabolic buffering and in order to maintain a normal intracellular pH cells relying on anaerobic metabolism must transport the excess hydrogen ions to the extracellular space. This is achieved by an increase in the number and activity of the Na+/H+ antiporters on the cell membrane (McLean et al., 2000) and naturally leads to an increased acidity in the surrounding tissue.
In order for the cancer cells to take advantage of the detrimental effects of acidifying the environment they themselves have to be able to survive and proliferate in this harsh environment. This is usually achieved through mutations to the p53-gene, which in its wild-type form induces apoptosis by increased caspase activity at low pH (Park et al., 1999). Tumour cells possessing mutations in p53 can withstand low pH and can make full use of the selective advantage that the low pH presents.
1.2 Previous work
Tumour growth has been subject to extensive mathematical modelling using several different techniques ranging from ordinary differential equations (Enderling et al., 2007; Sachs et al., 2001), level set and boundary-integral methods (Zheng et al., 2005; Macklin and Lowengrub, 2005), fluid dynamic models (Byrne and Chaplain, 1997; Breward et al., 2002) to partial differential equations (Anderson et al., 2000; Swanson et al., 2003). Recently individual based models of tumour growth have gained more attention. This is mainly due to the fact that computational power is now sufficient to run simulations with a large number of individual cells, but also to the fact that the research community has appreciated the impact of single-cell events in tumour growth dynamics. One advantage of modelling tumours on the scale of single cells is that it makes it possible to capture the fact that tumours in general are heterogeneous and consist of a large number of subclones that might behave in different ways. The first work using an individual based cellular automata model in cancer modelling was done by Düchting and Vogelsaenger (1984), who used it to investigate the effects of radiotherapy. More recent work in this direction has investigated the impact of the micro-environment on tumour growth (Ferreira et al., 2002; Anderson, 2005; Anderson et al., 2006). Other studies have focused on how the cell processes information from the environment and how this influences tumour growth dynamics (Gerlee and Anderson, 2007a; Mansury et al., 2006, 2002).
The first attempt at modelling the impact of glycolysis on tumour growth was done by Gatenby and Gawlinski (1996). They used a PDE model of tumour invasion that included an explicit equation for the excess acid in the tissue. Their model predicts a pH gradient extending into the normal tissue, and that a transition from benign to malignant growth occurs depending on the properties of the tissue. For example the model predicts that increased acid production and reduced acid washout increases the aggressiveness of the tumour. Further the model predicts the existence of an acellular gap between the tumour-host interface, a prediction that was verified both in vitro and in vivo.
A similar modelling approach was used in Smallbone et al. (2005), which looked at the growth dynamics of glycolytic tumours in both the avascular and vascular growth regime. Analysis of this model shows that angiogenesis is necessary to sustain tumour growth, as the excess acid produced by the tumour cells otherwise leads to self-acidification. They also identify three key parameters that have an important impact on the growth dynamics: acid production, acid removal and cellular sensitivity to acid, and further suggest treatment strategies based on these findings. One suggested treatment is inducing systemic acidosis, which could halt tumour growth by self-acidosis in the growing tumour.
The impact of glycolysis has also been investigated in a hybrid cellular automaton model (Patel et al., 2001). Using this approach they investigated the role of host tissue vascular density and tumour cell acid production. The results show that a high acid production is favourable for tumour growth and that for a given acid production rate there exists a range of optimal vessel density, which maximises tumour growth. For vessel densities below this range the tumour dies from self-acidification, and above the range the acid is removed at a rate which slows down the tumour growth.
The most recent work in this direction is a hybrid cellular automaton model of tumour growth in an avascular environment separated from the stroma by a basement membrane (Smallbone et al., 2007). The cells in this model are equipped with different phenotypes, and mutations during cell division can change cells from one phenotype into another. This model therefore takes into account the evolutionary origin of the glycolytic phenotype and they show that the progression to an invasive glycolytic phenotype occurs through the competition for space and nutrients in the tissue. These constraints lead to the emergence of hyperplastic, glycolytic and finally acid-resistant phenotypes that have the capability to breach the basement membrane and form an invasive tumour.
The model presented here was previously used to investigate the impact of the tissue oxygen concentration on the growth and evolutionary dynamics of tumour growth (Gerlee and Anderson, 2007a). The results from that study show that a low oxygen concentration gives rise to a tumour with a branched irregular morphology that contains more aggressive phenotypes compared to tumours that grow in a normoxic environment (this was also shown in Anderson et al. (2006)). The model used in that work was a simplified version that disregarded the effect of glucose and acidity on the growth of the tumour. Here we will make use of the full capability of the model and also extend it to take into account the impact of the extra-cellular matrix. In the next section we will give a overview of the model, but for an in-depth description of the model please consider Gerlee and Anderson (2007a).
2 The Model
The tissue under consideration is represented by a two-dimensional grid on which the cells reside. Each grid point holds the local concentration of extra-cellular matrix (ECM), nutrient concentrations and can be either occupied by a cancer cell or be empty. This is of course a highly simplified picture of real tumour-host interactions. The surrounding tissue contains a variety of host cells like fibroblasts, macrophages and blood vessels, all of which have been shown to be important factors in tumourigenesis (Rubin, 2003), but in order to focus on the impact of nutrient concentration and the ECM we have chosen to disregard these aspects of tumour growth. In the current model the vascularity is also modelled in a simplistic way, by incorporating it into the boundary conditions. A natural extension to this would be to explicitly include vessels into the model (Anderson and Chaplain, 1998; McDougall et al., 2006). This would make the model more realistic, but at the same time introduce another level of complexity, which in turn would make the results of the model more difficult to analyse. The trade-off between model simplicity and complexity is always present, and we feel that current model is at level appropriate for the phenomenon we aim at investigating, the emergence of the glycolytic phenotype. The model consists of discrete individual tumour cells, continuous chemical fields (oxygen, glucose, hydrogen ions) and ECM density, which interact with one another in the grid via the cellular automaton. We now discuss each of these variables and processes in more detail in the following sections.
2.1 The Cell
2.1.1 Phenotype
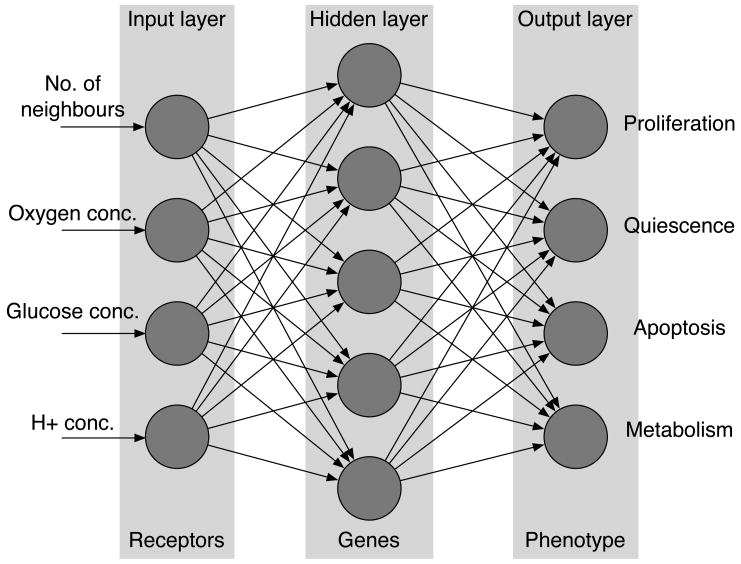
Each cell on the grid is equipped with a decision mechanism, which determines the behaviour of the cell based on the cell genotype and the micro-environment in which it resides. The decision mechanism is modelled using an artificial feed-forward neural network (Haykin, 1999). The input to the network is the number of neighbours of the cell n(x⃗, t), local oxygen concentration c(x⃗, t), glucose concentration g(x⃗, t) and H+ concentration h(x⃗, t). This implies that the input to the network ξ will have four components ξ = (n(x⃗, t), c(x⃗, t), g(x⃗, t), h(x⃗, t)). The phenotype of the cell is then determined by the output of the network.
In our model the output nodes represent the response for proliferation, quiescence, apoptosis and metabolic pathway. As the first three form a group of mutually exclusive behaviours (a cell can not perform these responses simultaneously) the behaviour with the strongest response is chosen from these three, we call this the life-cycle response. If the proliferation node has the strongest response the cell divides and produces a daughter cell, if the quiescence node has the strongest response the cell remains dormant and if the apoptosis node is strongest then the cell dies via apoptosis. A graphical representation of the response network can be seen in fig. 1. The output of the network is deterministic and depends only on the environmental input and the network parameters. These define the strength of connections between the different nodes and are represented as two matrices w, W and threshold vectors θ and ϕ. For further details on the neural network please consider the Appendix.
Fig. 1.
The layout of the response network. The environmental variables are presented to the input layer and then fed through the network. The values of the nodes in the output layer determine the behaviour of the cell.
2.1.2 Metabolism
The network modulates the metabolism of the cell in three separate ways: Firstly the strength of the life-cycle response determines the overall energy consumption of the cell, secondly the nutrient consumption is lowered by a factor q if the cell is quiescent, and finally the network determines the metabolic pathway of the cell. Real cells may rely on a combination of aerobic and anaerobic metabolism (Gatenby and Gillies, 2004), but for simplicity we will let the cells utilise either aerobic or anaerobic metabolism. If the response of the metabolic node is negative the cell uses glycolysis and if the response is positive the normal aerobic pathway is utilised. This choice is modelled by letting the cells utilising the anaerobic pathway consume 18 times more glucose and produce acid whilst not consuming any oxygen.
2.1.3 Mutations
When the cells divide the network parameters are copied to the daughter cell under mutations. The number of mutations that occur in the daughter cell network parameters is chosen from a Poisson distribution with parameter p. These mutations are then distributed equally over the matrices and threshold vectors. The incorrect copying is modelled by adding a normal distributed number s ∈ N(0, σ) to the daughter cell matrix or threshold entry, which means that x → x + s, for those entries x that are chosen for mutation. It should be noted that the mutation rate in this model does not correspond to the somatic mutation rate in human cells, as the amount of information copied by a real cell is approximately 108 orders higher in magnitude. The mutations alter the connection strength between the nodes, which in turn changes how the cells responds to the micro-environment. If for example a mutation occurs in a connection that links the oxygen concentration with the apoptosis node this may allow the cell to survive in low oxygen concentrations.
2.2 Chemical Fields
In the early stages of carcinogenesis the tumour has not yet acquired its own blood supply, and therefore has to rely on diffusion of nutrients from nearby blood vessels. This also applies to metabolic waste products like acid, which have to diffuse from the tumour to the surrounding blood vessels. The metabolism of cancer cells includes a large number of different chemicals that are all needed for maintenance and cell division, but oxygen and glucose concentrations are two key metabolites known to limit the growth of the tumour (Sutherland, 1988). We therefore only choose to focus on these two fields in the model as well as a field for the hydrogen ion concentration, as glycolytic cells produce an excess of acid. For the chemical fields we apply Dirichlet boundary conditions with constant functions, meant to imitate a situation where the tissue is surrounded by blood vessels, with constant nutrient and hydrogen ion concentrations, that supply the tumour with nutrients and remove hydrogen ions from the tissue. The decay rates of the metabolites are known to be considerably smaller than the respective cellular consumption rates and for simplicity we therefore disregard these in the equations. This allows us to develop a minimal model of the chemical fields, similar to those in the models of Patel et al. (2001) and Ferreira et al. (2002). The time evolution of the oxygen (3), glucose (4) and hydrogen ion (5) fields are therefore governed by the following set of partial differential equations,
| (3) |
| (4) |
| (5) |
where Di are the diffusion constants and the fi(x⃗, t) are the individual cell consumption or production functions of the chemical i = c, g, h for the cell at position x⃗ at time t. Note that the hydrogen ion production fh(x⃗, t) is only nonzero if the cell relies on glycolytic metabolism. The solution of the chemical field equations are calculated on a grid of the same step size as the cells using an Alternating Direction Implicit (ADI) scheme for both numerical accuracy and efficiency (Press et al., 1996) (see Appendix). This choice of space step implies that the consumption and production terms in (3)–(5) are determined by each individual cell. The fi(x⃗, t)’s are thus defined in the following way,
| (6) |
where ri are the base consumption/production rates and F (x⃗) is the modulated energy consumption of the individual cell occupying the automaton element at x⃗. This modulation of the consumption is introduced in order to take into account the difference in energy consumption between different subclones, and is modelled as
| (7) |
where k determines the strength of the modulation, R is the response of the network and Tr is the target response. The use of max(•, 0.25) ensures that the cell has a metabolism which is at least a quarter of the base-line consumption rate (Anderson, 2005). Note that this refers to the base-line consumption rate of the metabolic pathway that the cell utilises, and implies that a cell which relies on anaerobic metabolism will have at least a quarter of the anaerobic base-line glucose consumption rate and always a zero oxygen consumption. The use of this function also implies that a cell with a stronger network response will have a higher nutrient consumption.
2.3 The Extra Cellular Matrix
The interactions between cancer cells and the surrounding ECM are known to play an important role in carcinogenesis. The ECM is a complex mixture of macro-molecules, containing collagens, fibronectin etc., but for the sake of simplicity we will represent it as a single concentration. A crucial part of tumour invasion is the ability of cancer cells to degrade the ECM (Liotta et al., 1983; Stetler-Stevenson et al., 1993) and to migrate along gradients of ECM, a phenomenon known as haptotaxis (Lawrence and Steeg, 1996). Degradation of the ECM is accomplished by production of matrix-degrading-enzymes (MDEs) by the cancer cells.
A large number of different MDEs have been identified, of which matrix metalloproteinases (MMPs) constitute a large family (Ennis and Matrisian, 1993). Most of these are soluble, but it has been shown that a considerable part of matrix degradation is accounted for by membrane anchored MMPs (MT-MMPs) (Hotary et al., 2000). This implies that a majority of the ECM degradation has a very short range and can therefore be approximated by contact degradation. We include this effect in the model by letting the ECM be degraded with a rate ec at all grid points adjacent to cancer cells. The ECM also serves as a physical growth restraint of the tumour as cells can not move into regions of the tissue which are too dense, unless they have degraded it sufficiently. This effect is incorporated by introducing a threshold et above which no cells can occupy a grid point. This means that cells at the tumour perimeter have to degrade the ECM to a level below et before they can divide and place a daughter outside the existing tumour boundary.
Another important aspect that is included in the model is acid-induced ECM degradation. The exact dynamics of this process is poorly understood, but has been shown to involve stromal cells, e.g. fibroblasts (Rozhin et al., 1994). For simplicity we will assume that the matrix degradation is proportional to the excess acid concentration and model it by letting the ECM be degraded at a rate eh proportional to the excess acid concentration and matrix concentration. In summary the ECM obeys
| (8) |
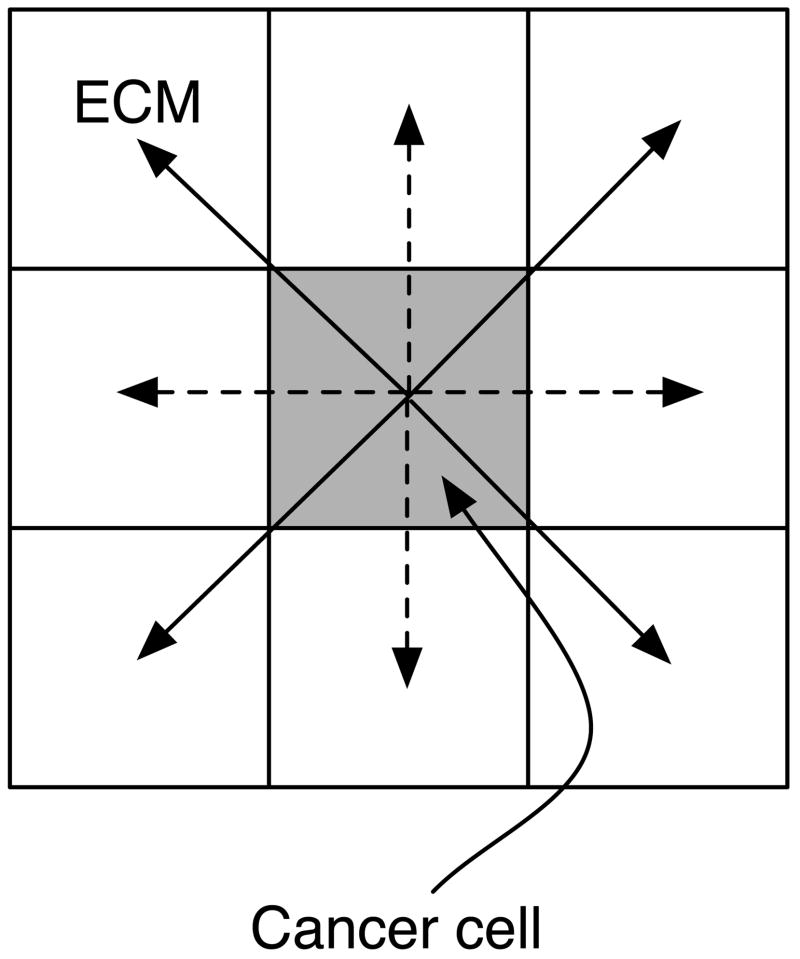
where I(x⃗, t) is an indicator function that returns the number of cancer cells adjacent to site x⃗ and h0 is the normal acid concentration in the tissue. Preliminary simulations showed that an indicator function that used an orthogonal neighbourhood resulted in anisotropic ”diamond-like” growth (data not shown) similar to what is observed in the Eden model (Batchelor and Henry, 1991). In order to avoid this effect of the underlying lattice we allow the cancer cells to alternate between degrading matrix in the orthogonal and diagonal neighbouring sites every time step, which is implemented by letting I(x⃗, t) alternate between orthogonal and diagonal neighbourshoods (see fig. 2).
Fig. 2.
This schematic shows the effect of the alternating neighbourhood in the ECM degradation. At even time steps orthogonal neighbours are degraded (dashed arrow), while at odd time steps the diagonal neighbours are degraded (solid arrows).
2.4 Cellular Automaton
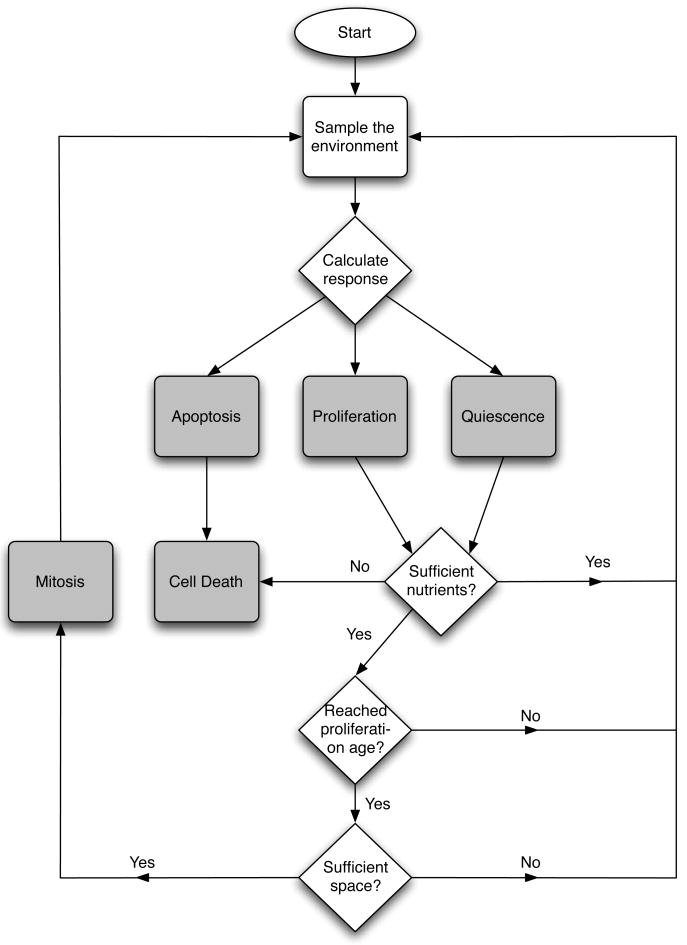
The two-dimensional tissue under consideration is represented by a N×N grid. The grid is characterised by a grid constant Δx = 25 μm, which determines the size of the cells, and gives each square cell an area approximately the same as a real cancer cell (Casciari et al., 1992). The grid points are identified by a coordinate x⃗ = Δx(i, j) i, j = 0, 1,...., N − 1. The chemical concentrations interact with the cells according to cellular production or consumption rates and are given appropriate initial and boundary conditions. Each time step the chemical concentrations are solved using the ADI-scheme (discussed in the Appendix) and all tumour cells are updated in a random order. Every time step each cell is updated according to the flowchart in fig. 3 and as follows:
Fig. 3.
Flowchart describing the life-cycle of a cancer cell.
The input vector ξ is sampled from the local environment (i.e the grid point where the cell resides).
A response R = R(ξ, G) is calculated from the network.
The cell consumes nutrients according to the action taken and the metabolic pathway chosen. If there is not sufficient nutrients present the cell dies from necrosis.
-
The life-cycle action determined by the network is carried out:
If proliferation (P) is chosen, check if the cell has reached proliferation age and if there is space for a daughter cell. If both are true the cell divides and the daughter cell is placed in a neighbouring grid point, if not the cell does nothing.
If quiescence (Q) is chosen the cell becomes quiescent.
If apoptosis (A) is chosen the cell dies.
If a cell dies from either apoptosis or necrosis it is no longer updated. If the cell dies by apoptosis the grid point where it resided is considered empty, but if the cell dies from necrosis (starvation) the cell still occupies the grid point. The reason for this is that the two death processes occur in different ways. When apoptosis occurs the cell membrane collapses and the cell shrinks, while when necrosis occurs the cell keeps it shape and thus still occupies physical space (Alberts et al., 1994b). In order to account for the activity of the immune system, which removes necrotic debris (Kerr et al., 1994), necrotic cells are removed after a given time tN.
2.5 Parameters
The initial network, which is used as a ”seed” in every simulation, is chosen so that the behaviour of the cell resembles that of an initial cancer cell phenotype which has lost normal growth inhibition (for further details on the network parametrisation please see the Appendix). The response of the network therefore has to capture the essential behaviour of real cancer cells. The important features that we want to capture are:
Cells should perform apoptosis if the oxygen concentration c(x⃗, t) falls below a certain threshold cap.
Cells should die if the glucose concentration g(x⃗, t) falls below a certain threshold gap.
Cells should not divide if there is no space for the daughter cell (contact inhibition) i.e if n(x⃗, t) > 3
Cells should perform apoptosis if the acidity h(x⃗, t) is a above a certain threshold hap.
Cells should switch to anaerobic metabolism if the oxygen concentration c(x⃗, t) falls below cm.
The value of cap is difficult to estimate as it depends on the cell type under consideration, but measurement performed in several types of tumours reveal that the oxygen concentration in the necrotic centre of the tumour is 0.5–30% of the concentration in the surrounding tissue (Brown and Wilson, 2004). We therefore estimate cap to be 15 % of the initial oxygen concentration. For high values this parameter is known to have an effect on the morphology of the tumour (Gerlee and Anderson, 2007b; Anderson et al., 2007), but for the relatively small values we consider this effect is negligible. The threshold for glucose induced necrosis is set to 50% of the normal glucose concentration, below which hypoglycemia occurs (Ganong, 1999). The acidity threshold hap is set to match the critical pH = 7.1 below which normal cells go into apoptosis (Casciari et al., 1992). As there is a physical limit to the acidity a cell can survive we also introduce another threshold h̃ap, which is the acid concentration at which a cell will go into apoptosis regardless of the network response, this is estimated to pH=6.5 (Casciari et al., 1992). The metabolic threshold is set to cm = 0, as we are interested in the emergence of cells that utilise the anaerobic pathway. The proliferation age, the time it takes for a cell to move through the entire cell-cycle once has been experimentally measured to lie between 8 and 24 h depending the type of cells (Calabresi and Schein, 1993), we use the intermediate value Ap = 16 h. All cell specific parameters are summarised in Table 1.
Table 1.
A summary of the cell specific parameters in the model.
| Parameter | Meaning | Value | Reference | |
|---|---|---|---|---|
| rc | base oxygen consumption rate | 2.3 × 10−16 mol cells−1 s−1 | (Freyer and Sutherland, 1986) | |
|
|
aerobic glucose consumption rate | 3.8 × 10−17 mol cells−1 s−1 | Calculated from (Freyer and Sutherland, 1986) | |
|
|
anaerobic glucose consumption rate | 6.9 × 10−16 mol cells−1 s−1 | Calculated from (Freyer and Sutherland, 1986) | |
| rh | hydrogen ion production rate | 1.5 × 10−18 mol cells−1 s−1 | (Patel et al., 2001) | |
| cap | hypoxia induced apoptosis threshold | 2.5 × 10−9 mol cm−2 | (Brown and Wilson, 2004) | |
| gap | hypoglycemia threshold | 6.5 × 10−9 mol cm−2 | (Ganong, 1999) | |
| hap | acid induced apoptosis threshold | pH = 7.1 | (Casciari et al., 1992) | |
| h̃ap | maximal acid concentration | pH = 6.5 | (Casciari et al., 1992) | |
| Ap | proliferation age | 16 h | (Calabresi and Schein, 1993) | |
| p | mutation probability | 0.01 | (Anderson, 2005) | |
| q | quiescent metabolism factor | 5 | (Freyer et al., 1984) | |
| Tr | target response | 0.675 | Model specific | |
| k | modulation strength | 6 | Model specific | |
| σ | mutation strength | 0.25 | Model specific |
The diffusion constants for the nutrients and the hydrogen ions have been measured experimentally and are summarised in Table 2. The removal time tN of necrotic debris has not been measured experimentally and we therefore have to resort to an estimate. A reasonable assumption is that this process is of the order of cell cycles and we therefore set it to tN = 5 cell cycles.
Table 2.
A summary of the micro-environment specific parameters in the model in dimensional units.
| Parameter | Meaning | Value | Reference |
|---|---|---|---|
| Dc | oxygen diffusion constant | 1.8 × 10−5cm2 s−1 | (Grote et al., 1977) |
| Dg | glucose diffusion constant | 9.1 × 10−5cm2 s−1 | (Crone and Levitt, 1984) |
| Dc | hydrogen ion diffusion constant | 1.1 × 10−5cm2 s−1 | (Crone and Levitt, 1984) |
| c0 | oxygen background conc. | 1.7 × 10−8 mol cm−2 | (Anderson, 2005) |
| g0 | glucose background conc. | 1.3 × 10−8 mol cm−2 | (Walenta et al., 2001) |
| h0 | hydrogen ion background conc. | 1.0 × 10−13 mol cm−2 (pH = 7.4) | (Patel et al., 2001) |
| n0 | cancer cell density | 1.6 × 105 cells cm−2 | (Casciari et al., 1992) |
| tN | necrotic cell removal rate | 5 cell cycles | Estimated |
In order to simplify the analysis and simulations of the model we nondimensionalise the model in the standard way. Time is rescaled by the typical time of the cell-cycle, t = 16 h (Calabresi and Schein, 1993), and the length by the maximal size of an early stage tumour, L = 1 cm. The chemical concentrations are rescaled using background concentrations (see Table 2) and the tumour cell density n0 = Δx−2 = 0.0025−2 = 1.6 × 105 cells cm−2 (as the cells reside on a 2-dim. grid).
The new non-dimensional variables are thus given by,
| (9) |
For notational convenience we will drop the tildes on the non-dimensional variables.
The degradation rates and threshold density of the ECM have not been measured experimentally and we will therefore use non-dimensional estimates for these parameters. In our simulations we will let et be in the range [0.65, 0.9], which corresponds to 35–10% of the ECM requiring degradation before it can be occupied by a cell. Instead of using this threshold as a measure of the density we introduce an effective matrix density E = 1 − et, which will serve as a measure of the growth constraint imposed by the matrix. For a high matrix threshold we will have a low effective matrix density and vice versa. The matrix degradation of the cells is set to ec = 0.1, which implies that a cell needs 1–4 cell cycles (corresponding to E = 0.1 − 0.35) to degrade the ECM in a neighbouring grid point to a level below et. The combined effect of acid on the matrix is poorly characterised and we therefore set it to eh = 10−3, considerably smaller than the degradation by the cells, in order to make the growth advantage of acid-producing cells small.
The grid size was set to N = 200, which corresponds to a domain size of 0.5 cm, and means that we can simulate a tumour of radius 100 cells, which if we assume radial symmetry in a 3-dimensional setting would correspond to a tumour consisting of approximately 1003 or 1 million cells. The time step in the simulation was set to Δt = 10−1 and the space step to Δx = 0.0025. The mutation probability is set to p = 0.01 (Anderson, 2005) and the mutation strength to s = 0.25. For the full list of parameters and a more detailed discussion on the modelling approach we employ please consult Gerlee and Anderson (2007a).
3 Simulations
Using this model we examine how the tissue architecture and oxygen concentration affects the dynamics of tumour growth. More precisely we investigate how the background oxygen concentration and the density of the ECM impacts upon both the growth and evolutionary dynamics of the system. This was accomplished by systematically varying c0 in the range [0.1, 1] and E in the range [0.1, 0.35], while keeping all other parameters constant. Biologically this corresponds to growing the tumour in a tissue with varying oxygenation and matrix density. In order to characterise the growth dynamics of the tumours we measured the invasive distance as a function of time, examined their morphology and measured the spatial distribution of metabolites. The evolutionary dynamics were also analysed by measuring the fraction of different phenotypes in the population. In particular we focused on cells that have adapted to hypoxic conditions, glycolysis and acid-resistance.
Every simulation was started with a homogeneous concentration of oxygen, glucose and hydrogen ions at background values (c(x⃗, 0) = g(x⃗, 0) = h(x⃗, 0) = 1), and with the boundary conditions c(x⃗, t) = g(x⃗, t) = h(x⃗, t) = 1 for x⃗ ∈ ∂Ω. In order to account for variations in the matrix density the initial condition for ECM was set to m(x⃗, 0) = 1+s, where s ∈ [−0.2, 0.2] is a random variable with a uniform distribution. The grid size was set to N = 200, and each simulation was started with a population of 4 cancer cells at the centre of the grid.
The matrix density naturally imposes different growth rates upon the tumour, as a denser matrix takes longer to invade. In order to compare tumours of the same size the total number of time steps was changed depending on the matrix density. The total number of time steps was scaled such that every tumour would approximately have the same size as one grown for 100 time steps (cell cycles) without any growth restraint from the matrix. The necessary scaling can be found by looking at a simplified local version of the ECM equation (8) at the boundary of the tumour. If we only consider the concentration of ECM in one grid point adjacent to the tumour interface, and further assume that this interface is flat and that the effects of acid degradation are negligible, then the ECM concentration is given by,
| (10) |
with the initial condition m(0) = 1. The factor 3/2 comes from the fact that the cancer cells alternate between degrading orthogonal and diagonal neighbouring sites. At even time steps the ECM in the considered grid point is degraded by one cancer cell, but at odd time steps it is degraded by 2 cancer cells, giving an average of 3/2 neighbouring cancer cells, each degrading at a rate ec (see fig. 2). We are now interested in calculating the time t? it takes for the ECM to reach a level below et, at which point a new cancer cell can occupy the grid point. By solving (10) we find that this time is given by,
| (11) |
For et = 0.9 and ec = 0.1 we get t★ ≈ 0.7 < 1 cell cycle, which implies that the matrix will not pose a growth constraint for the tumour growth. On the other hand for et = 0.65 and ec = 0.1 we have t★ ≈ 2.9, which means that the tumour will grow approximately 3 times slower than in the unconstrained case. The total number of time steps in each simulation was then rescaled with the factor t★ giving tumours of approximately of the same size.
4 Results
4.1 Growth Dynamics
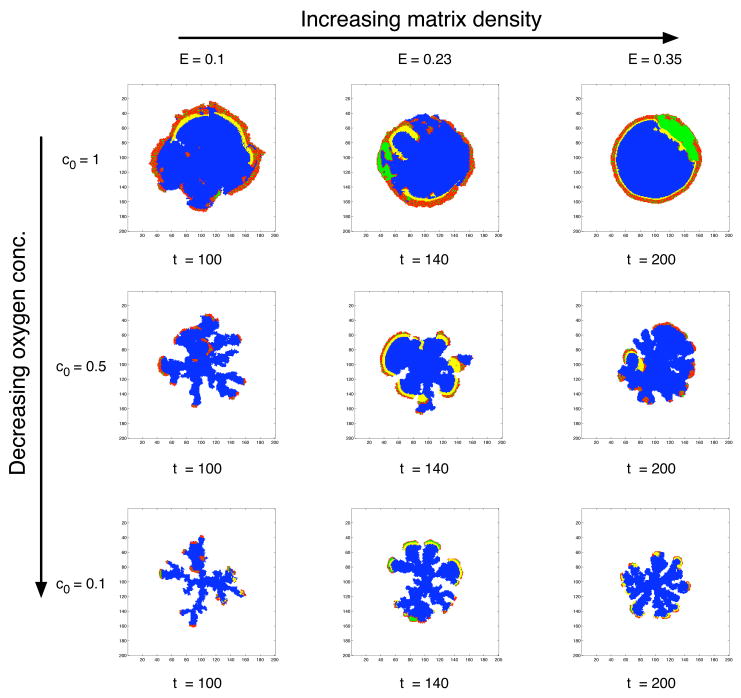
Figure 4 shows the resulting tumour morphologies from simulations using different regions of the two dimensional parameter space (c0, E). These two parameters, that control the background oxygen concentration (c0) and matrix density (E), clearly influence both the growth rate and morphology of the tumour. For a normal oxygen concentration we observe tumours growing with a compact round morphology with a proliferating rim and a core consisting of necrotic and apoptotic cells. In each simulation the tumour starts growing with proliferating cells at the boundary and quiescent cells in the interior, but when the tumour reaches a critical size (r) the diffusion limited supply of oxygen can not support the cells in the interior and we observe the development of a core of dead cells. The time at which this occurs depends on the oxygen concentration, but also on the matrix density. For lower oxygen concentrations this naturally occurs earlier, and for higher density of the matrix it occurs later, because it takes longer for the tumour to reach the critical size in a more dense matrix. For the normal oxygen concentration c0 = 1 this occurs at a radius r = 33 cells, for c0 = 0.5 at r = 13 cells and for c0 = 0.1 at r = 8 cells.
Fig. 4.
Morphology diagram showing the dependence of background oxygen concentration and matrix density. Proliferating cells are coloured red, quiescent green, necrotic yellow and apoptotic blue. For normal oxygen concentration the tumour grows with a smooth boundary, while for low oxygen concentration we observe a branched morphology. The matrix density on the other hand seems to stabilise the morphology giving rise to wider branches in a more dense matrix.
After the development of the necrotic centre the tumour continues to grow, from this point onwards both the population and morphology are intimately dependent upon the two parameters c0 and E. For low oxygen concentration the tumour grows with a fingered morphology similar to those observed in diffusion limited growth processes (Kessler et al., 1988). The tumour mostly consists of dead cells, and the proliferating cells reside on the tips of the growing fingers. The fingering morphology becomes even more pronounced when the oxygen is lowered further. Increasing the matrix density has the opposite effect and leads to a smoother tumour interface with wider fingers. The matrix seems to stabilise the fingered morphology induced by the low oxygen concentration resulting in a less branched morphology.
We can also observe a difference in the distribution of necrotic cells depending on the matrix density. For higher matrix densities there is a rim of necrotic cells lining the proliferating rim. This occurs because here cells have evolved to a glycolytic phenotype that relies on glucose as a source of nutrient. In this case glucose becomes the limiting nutrient and this leads to cell death through necrosis rather than apoptosis, which is the case for oxygen. Because the necrotic cells are removed after tN = 5 cell cycles the necrotic rim follows the proliferating cells like a travelling wave. It should also be noted that making the distinction between apoptotic and necrotic cells has an impact on the general dynamics of the model. If all cells were considered necrotic and the removal time tN was very large, the tumour would have an impenetrable solid core. But because grid points where apoptotic cells reside are considered empty we observe interesting growth dynamics inside the tumour, where subclones adapted to lower nutrient concentrations can spread inwards and exploit the low cell density in the centre of the tumour. This means that the growth is not only confined to the proliferating rim, but can in some cases take place at any location in the tumour mass.
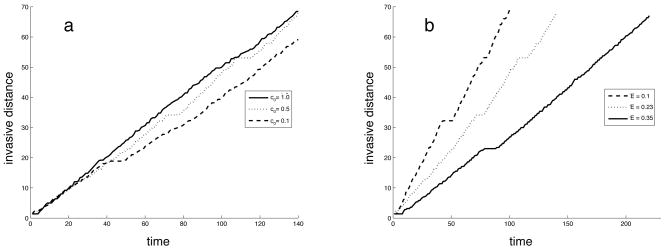
Figure 5 shows the time evolution of the invasive distance of the tumour, which is the distance from the centre of the grid (where the tumour starts growing) to the most distant cancer cell. The figure shows the results from simulations for 3 different values of the oxygen concentration (with the matrix density fixed at E = 0.23) and 3 different values of the matrix density (with the oxygen concentration fixed at c0 = 0.5). As expected the the tumour grows at a lower rate in the denser matrix (higher E), which is due to the fact that the tumour cells need to degrade more of the matrix before they can place a daughter cell outside the existing tumour boundary. Reducing the oxygen concentration on the other hand does not seem to affect the time evolution of the invasive distance. For the simulations presented the tumour grown in the normal oxygen concentration has the largest invasive distance, although the difference is quite small. The total number of cells is larger for higher oxygen concentrations (see fig. 4), but due to the fact that the tumour grows with a branched morphology in the low oxygen means that it still achieves a considerable invasive distance, although the mass of the tumour is smaller.
Fig. 5.
The time evolution of the invasive distance for different (a) oxygen concentrations and (b) matrix densities.
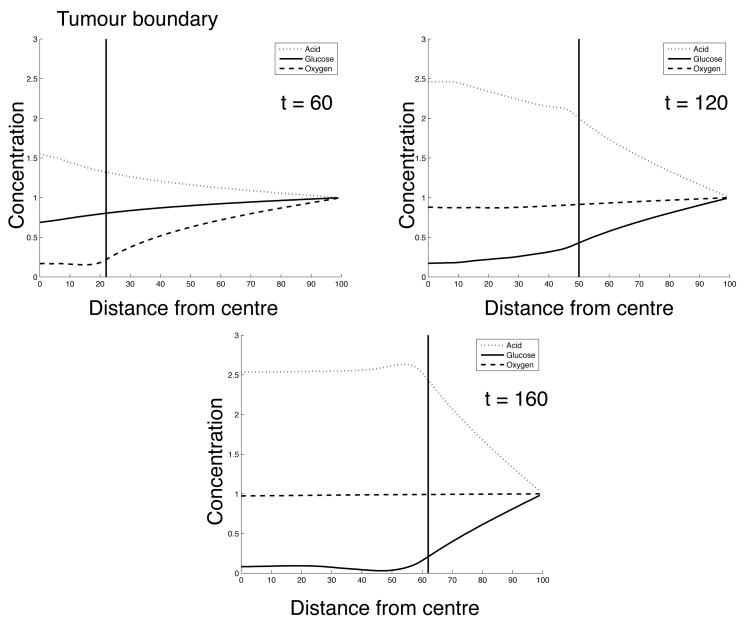
The radial distribution of the metabolites is shown in fig. 6 and corresponds to (c0, E) = (0.5, 0.23) at t = 60, 120 and 160 in fig. 4. In these plots we see a progression from a tumour which almost exclusively contains cells that rely on aerobic metabolism to one which is dominated by glycolytic cells. At t = 60 we observe steep gradient in the oxygen concentration stretching from the boundary of the domain to the tumour interface, while the glucose concentration on the other hand is close to its boundary value even inside the tumour. This suggests that at this point it is the supply of oxygen that limits the growth of the tumour. An increase in excess acid at this point reveals that glycolytic cells already are present in the population. At t = 120 we see almost a reversal in the oxygen and glucose concentration profiles, now the glucose concentration exhibits a gradient while the oxygen has returned to the background concentration in almost the entire domain. The acid concentration has also changed considerably and we can observe a maximum concentration of approximately 2.5 times the background value in the centre of the tumour. In the final plot this phenomenon is even more pronounced and it is clear that it is now the supply of glucose that limits the growth of the tumour.
Fig. 6.
Concentration of metabolites as a function of the distance from the center of the tumour for (c0,E) = (0.5, 0.23) at t = 60, 120 and 160.
4.2 Evolutionary Dynamics
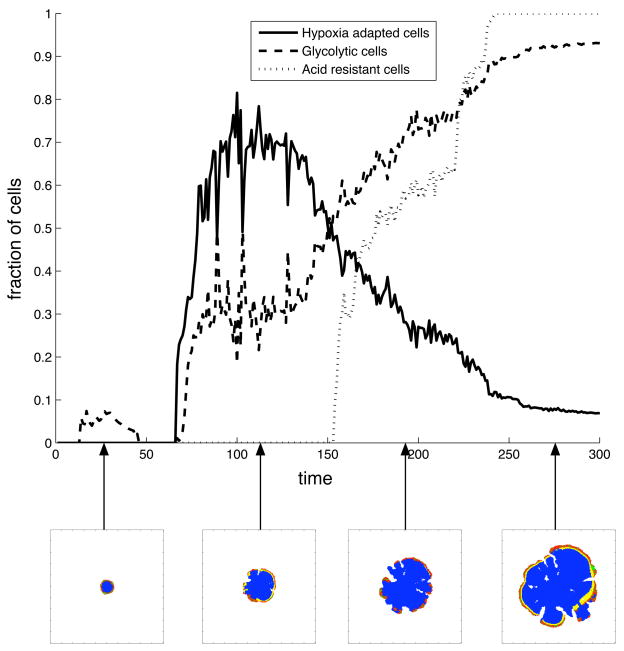
The evolutionary dynamics were characterised by measuring the abundance of certain phenotypes in the population. Because the cells are not confined to a limited number of phenotypes which define all their properties (Anderson, 2005), but instead have behaviours that can vary continuously depending on the environment, we had to cluster cells together that behave in a similar way. This was done by looking at three important phenotypic changes in the cells: (i) the capability to survive in a low oxygen environment using aerobic metabolism (ii) utilising glycolysis (iii) the capability to survive in acidic conditions. The first phenotype, which we term hypoxia adapted cells, was defined as a cell that can survive and proliferate in oxygen concentrations below the initial hypoxic threshold cap, while still using aerobic metabolism. The second one, glycolytic cells, are simply cells that utilise the glycolytic pathway and finally acid resistant cells are those that can survive in acid concentrations above the initial acid threshold hap. We then measured the fraction of the population that each of these phenotypes occupy. The results of a typical simulation (with c0 = 0.5 and E = 0.35) can be seen in fig. 7. At the beginning of the simulation there are no cells with the measured phenotypes. At t ≈ 10 a small fraction of the cells have acquired the glycolytic phenotype, but they quickly die out. However at t ≈ 70 there is a sharp increase in both hypoxia adapted and glycolytic cells. At first the hypoxia adapted cells dominated, but at t = 150 the glycolytic cells starts taking over and at the end of the simulation they occupy almost 90% of the population. The increase in glycolytic cells correlates with the emergence of acid resistant cells, a trait that quickly becomes dominant in the population.
Fig. 7.
The time evolution of phenotypes in the cancer cell population for (c0,E) = (0.5, 0.35). The lower insets show the respective tumour morphology at the different time points.
The phenotype dynamics can also be correlated with the morphology of the tumour. In the early stages of growth (t < 70) the tumour has only recently acquired a necrotic core, which implies that there is only a weak selection pressure for phenotypes that can survive in low nutrient concentrations. This explains why the glycolytic subpopulation that emerged at that point was extinguished. When a hypoxia adapted subclone, that has a growth advantage, emerges in the population it soon dominates the entire population. At first the hypoxia adapted cells are dominant, but the prolonged exposure to low oxygen concentrations favours the glycolytic cells, as they can survive without any oxygen. This also means that they can survive in the hypoxic regions within the proliferating rim, which suggests that the emergence of subclones spreading inwards correlates with the population being glycolytic.
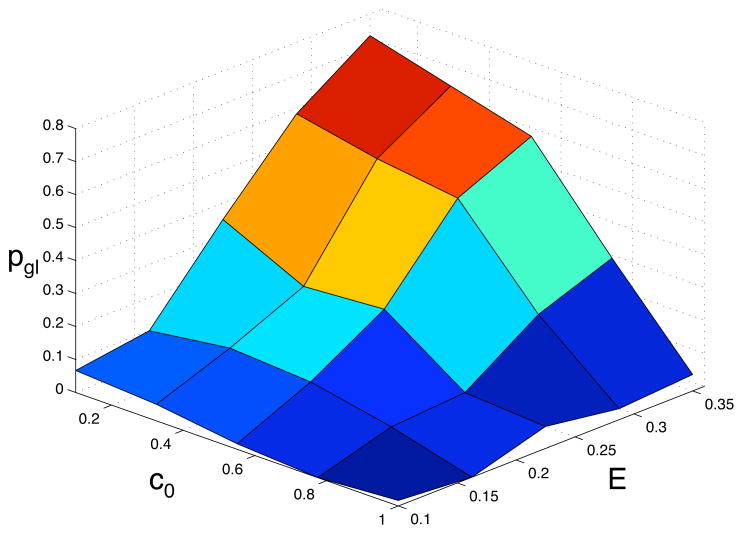
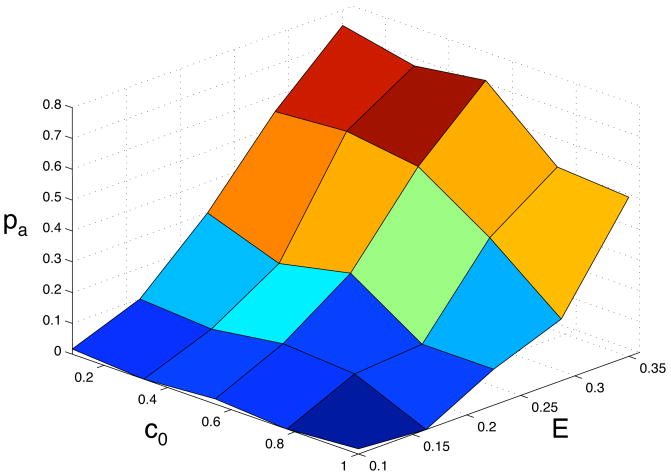
In order to understand how the background oxygen concentration and matrix density influence the phenotypic dynamics we measured the abundance of the above defined phenotypes in 5 × 5 = 25 different points in the (c0, E)-parameter space. The behaviour of the model was averaged over 60 simulations in each point in parameter space, and the outcome was quantified by looking at the probability that the glycolytic and acid resistant phenotypes were dominant in the population. Here we defined a phenotype to be dominant if at least 90% of the population had acquired it. Again we have scaled the number of time steps depending on the matrix density, so that we compare the phenotypic composition of tumour of approximately the same size. The tumour in the least dense matrix was allowed to grow for 100 time steps and in all other matrix densities the total number of time steps were scaled so that the tumours had approximately the same size. The results of this extensive parameter exploration can be seen if fig. 8 and 9. From this we can observe that the emergence of a glycolytic phenotype depends on both the matrix density and oxygen concentration and that it is most likely to appear in a dense matrix (E = 0.35) with low oxygen concentration (c0 = 0.1) where we find the domination probability to be 0.8, and the general trend is that the probability of finding a glycolytic phenotype then decreases when the matrix becomes less dense and when the oxygen concentration is increased. Notable is that only when both the matrix is dense and the oxygen concentration is low do we get a high probability of domination. The lowest domination probability was found for (c0, E) = (1.0, 0.1), where it is close to zero.
Fig. 8.
The probability pgl that the glycolytic phenotype dominates the population as a function of the oxygen concentration c0 and the matrix density E.
Fig. 9.
The probability pa that the acid resistant phenotype dominates the population as a function of the oxygen concentration c0 and the matrix density E.
The results for acid resistance are similar, but we observe an increased probability of acid resistance for high oxygen concentrations and high matrix densities. Here the glycolytic probability is close to zero, but we have a probability of acid resistance of pa ≈ 0.4. The domination probability of the hypoxia adapted phenotype ph was also calculated (data not shown). It correlates strongly with pgl, and for all points in the (c0, E)-parameter space we investigated we have that ph + pgl ≈ 0.8. This means that whenever we have a high probability for glycolytic dominance we have a low probability of hypoxia adapted cells dominating the population and vice versa. This is quite natural, as there is a selection for cells that can survive in low oxygen concentrations, and this can be achieved either by hypoxia adaptation or by switching to glycolysis.
5 Discussion
The tumour morphologies obtained with this model suggest that the shape of the tumour very much depends on its growth conditions, and are similar to those observed in the models of Ferreira et al. (2002), Anderson (2005) and Gerlee and Anderson (2007a). For normal oxygen concentrations we find tumours with a smooth circular morphology, while in low oxygen concentration we observe tumours with invasive fingered shape. The reason why this occurs is because a low oxygen concentration cannot sustain the growth of a smooth tumour boundary. If a cell divides and places a daughter cell outside the existing tumour boundary the daughter cell is closer to the source of oxygen and has a screening effect on cells residing closer to the centre of the tumour. Growth in this region in parameter space is therefore more competitive as cells that do not proliferate will quickly be trapped in the low nutrient regions in the interior of the tumour. For a more in depth study of this phenomena please consider Anderson et al. (2007), where three different models were used to investigate the impact of nutrient supply on tumour morphology.
The similarity between the simulated morphologies and those observed in diffusion limited growth processes like viscous fingers (Daccord et al., 1986) and electro-chemical deposition (Matsushita et al., 1984) occur because the growth dynamics are in fact quite similar. In those processes the interface is advanced at a rate proportional to the gradient of a field u (ν ~ |∇Bu|) that satisfies Laplace equation ∇B2u = 0 outside the structure with the boundary condition u = 0 at the interface. Because the diffusion of oxygen occurs on a much faster time scale than the cell dynamics the oxygen field is in a quasi-stationary state and therefore approximately satisfies ∇B2c = 0 outside the tumour. In the limit of low oxygen concentrations the oxygen approximately satisfies c(x⃗, t) = cap on the boundary of the tumour and only the points where the flux of oxygen ∇c(x⃗, t) is sufficient will the cells survive long enough to divide and expand the tumour. The growth rate of the tumour can therefore be said to be proportional to the gradient of the oxygen field. Seen from this perspective the two systems are quite similar and it is not surprising that they give rise to similar morphologies. In fact it has been shown for a simplified version of the current model (where cells only consume oxygen and without an evolutionary component) that the dynamics are well approximated by a diffusion limited growth process (Gerlee and Anderson, 2007b). Pure diffusion limited growth is inherently unstable (van Saarloos, 1998), but the existence of the proliferating rim stabilises the growth and selects for a typical finger width in the morphology. When the cells rely on aerobic metabolism oxygen is the limiting nutrient and in this case the finger width is proportional to the width dc of the proliferating rim, which is given by
| (12) |
where rc is the oxygen consumption rate and Ap is the proliferation age of the cells. Increasing the consumption rate (or equivalently decreasing the oxygen concentration) gives a smaller dc, which should result in thinner fingers and this is precisely what we observe in this model.
Increasing the matrix density on the other hand seems to stabilise the growth and gives tumours with more compact morphologies. Even for the highest oxygen concentration we observe a rough tumour boundary in the least dense matrix, but when the density is increased we get a smooth circular tumour. The change in finger width is more obvious for the two lower oxygen concentrations, where we can observe a clear shift towards smaller tumours with wider fingers as the matrix density is increased. This can be understood from the fact that the growth of the tumour is not limited by the proliferation age of the cells, but instead by the matrix surrounding the tumour. For the lowest matrix density (E = 0.1) it takes approximately one cell cycle to degrade the matrix in a neighbouring grid point to a level below the threshold, but for higher densities this degradation time exceeds the time of a cell cycle. That means that although a cell is ready to divide it has to wait until the surrounding matrix is degraded before it can go into mitosis. This can be said to reduce the competition at the tumour boundary as cells need to wait longer before they divide. The fact that each cancer cell degrades matrix in a neighbourhood of 8 grid points (alternating between orthogonal and diagonal neighbours) implies that it decreases the matrix concentration in grid points where neighbouring cells can place their daughter cells (see fig. 2). This means that although the degradation is of short range there is a cooperative effect between neighbouring cells in the tissue, which changes the morphology of the tumour.
In the view of diffusion limited growth the matrix density can be viewed as having a negative effect on small wavelength perturbations, thus leading to the selection of wider fingers. The effect of the ECM on tumour growth was also investigated by Anderson (2005). Although the ECM did not directly function as a growth restraint in that model, but rather as a means to stimulate or inhibit migration (via haptotaxis), it was still shown that the structure of the ECM has a profound effect on tumour morphology. In particular tumours grown in a homogeneous ECM exhibited a smooth circular morphology, while a heterogeneous ECM gave rise to branched morphologies.
Measuring how the invasive distance depends on the oxygen concentration and matrix density also reveals some interesting dynamics. Suprisingly the oxygen has little effect on the growth rate of the tumour, while the matrix density has the anticipated impact on the growth rate. The reason why the oxygen has little impact on the growth rate is that although the tumours consists of fewer cells, the fingered morphology allows for a larger invasive distance. This suggests that oxygen does not limit the growth rate of the tumour, but that instead a low oxygen concentration selects for glycolytic cells that can grow independently of the oxygen concentration. These glycolytic cells produce excess acid that has a detrimental effect on the surrounding matrix, which in turn may accelerate the tumour growth. This leads us to conclude that the harshest growth condition (low oxygen, dense matrix) where one would expect to find the smaller tumours in fact gives rise to the most invasive tumours, containing the most aggressive phenotypes.
This is also reflected in the results from the evolutionary dynamics. In fig. 7 we see a progression from an initial cell population, where all three phenotypes are absent, to one that almost exclusively consists of glycolytic cells that can survive in acidic conditions. This seems to occur in an almost step-wise process, where the population first adapts to surviving in hypoxic conditions still relying on oxygen, then adopts a glycolytic phenotype and finally becomes resistant to acid. This is similar to what is seen in the model by Smallbone et al. (2007). They observe a progression from normal to hyperplastic, glycolytic and finally acid resistant cells, due to space and nutrient limitations. In their model hyperplastic cells are those that can proliferate without contact to the basement membrane. Because we consider tumour growth in tissue matrix, the cells in our model do not display that phenotype, but a similar effect can still be observed. Cells from the initial population become quiescent if they are surrounded by other cells, but from fig. 4 we can see that there are few quiescent cells present. What one would expect is only one layer of proliferating cells at the very boundary of the tumour, but in fact the proliferating rim is much wider. These cells have lost contact inhibition and can therefore be said to display a hyperplastic phenotype. This is interesting because although the two models are quite different we still observe a similar evolution of phenotypes in the tumour.
The phenotypic dynamics also depend on the growth conditions of the tumour. The selection for a glycolytic phenotype seems to be strongest in a dense matrix with a low oxygen concentration. The reason why a poorly oxygenated tissue favours a glycolytic phenotype is because glycolytic cells have a clear growth advantage in this environment, but this does not seem to be enough for the glycolytic cells to dominate the population. Even for the lowest oxygen concentration c0 = 0.1 the domination probability is only pgl ≈ 0.1 in the least dense matrix, but when the matrix density is increased the probability increases steadily and for the most dense matrix we get pgl ≈ 0.8. This suggests that the matrix plays an important role in the evolutionary dynamics. The matrix creates a growth constraint that forces the cancer cells to remain in the low oxygen regions instead of growing out of them, which occurs when the matrix density is low.
In the model of Smallbone et al. (2007), the cells are constrained by a basement membrane which they cannot penetrate. In our model this would correspond to a situation where the population grows in a cavity surrounded by a matrix of very high density. Our results predict that the emergence of the glycolytic phenotype is very likely in this situation and the results are therefore in good agreement with theirs. The results from our model suggest that this type of growth constraint is in fact essential for the emergence of the glycolytic phenotype. From the above we can conclude that the progression to a fully adapted glycolytic phenotype requires the following: (i) a hypoxic environment that selects for cells with anaerobic metabolism and (ii) a growth constraint that limits the growth of the tumour. When either the oxygen concentration is high or the matrix has low density the domination probability is much lower, which suggests that it is the combined effect of both these environmental conditions that lead to the emergence and ultimate dominance of a glycolytic phenotype.
The acid resistance domination probability deviates slightly from the glycolytic one. This is especially evident for high nutrient concentration and high matrix densities. One would expect them to be similar, as acid resistance emerges as a response to the excess acid produced by glycolytic cells, but this result suggests that there is a more complex relationship between the two traits. One explanation to this could be that even if only a fraction of the population relies on glycolysis the excess acid produced by these cells will diffuse throughout the tumour and exert a selection pressure for acid resistance on a larger proportion of the cancer cell population. This can be interpreted as a non-local effect, and further highlights the fact that the spatial structure of the population plays an important role in the evolutionary dynamics.
Although the model presented here is simplified compared to the growth of real tumours it can still make some interesting predictions. The observation that it is the low oxygen concentration that drives clonal evolution could explain why in highly vascularised organs (such as kidney and spleen) small tumours are common, but that these often fail to grow to a clinically detectable size (Abrams et al., 1950; Wagle et al., 1975). The high oxygen concentration and effective removal of acid from the tissue could create a relatively mild micro-environment that does not select for aggressive phenotypes, which in turn would lead to less aggressive tumours, failing to invade the tissue. The link between tissue oxygen concentration and tumour morphology is also in qualitative agreement with a study on cervical cancers (Höckel et al., 1996), which showed that hypoxic tumours in general exhibited larger tumour extensions compared to non-hypoxic ones. Hypoxia has also been linked with poor prognosis (Brizel et al., 1997) and metastatic potential (Höckel et al., 1999), which is in line with our results and suggests that nutrient limitation leads to clonal evolution towards more aggressive phenotypes with a larger capability to invade the surrounding tissue (see also Anderson et al. (2006)).
The model also suggests that reducing the oxygen supply of the tumour, by for example anti-angiogenic treatment, might not reduce the growth rate of the tumour. Our results suggest that the growth rate is largely independent of the oxygen concentration, and that in a low oxygen concentration glycolytic and acid resistant cells are more likely to appear. Limiting the oxygen supply could therefore have the opposite effect and lead to a more aggressive tumour. The gradient of acid stretching into the surrounding tissue is also in qualitative agreement with previous theoretical results (Gatenby and Gawlinski, 1996) and those from in vivo studies (Helmlinger et al., 1997; Martin and Jain, 1994). The precise effect of acidification of the peritumoural tissue is still largely unknown, but our results suggest that if it enhances the degradation of the ECM it will increase the selection for glycolytic cells and consequently lead to higher rates of glycolysis and of course further tumour invasion.
6 Conclusions
In this paper we have presented a hybrid cellular automaton model, which has the capability to capture the dynamics of clonal evolution. The model was previously introduced in Gerlee and Anderson (2007a), but in this paper we have made use of the full capabilities of the model and also extended it by introducing interactions between the cancer cells and the extra-cellular matrix. We have investigated the impact of the micro-environment on the growth and evolutionary dynamics of the tumour by varying the oxygen concentration and matrix density in the tissue. In particular we have focused on the emergence of the glycolytic phenotype, which is an important aspect of carcinogenesis. Our results show that environmental conditions affect both the morphology and the evolution of phenotypes in the tumour. While a low oxygen concentration destabilises the growth and leads to a branched tumour morphology a denser matrix gives rise to a more compact tumour with less fingering. On the other hand the combined effect of both these environmental variables leads to the emergence of the glycolytic phenotype, which we found was most likely to appear in a poorly oxygenated and dense tissue. These results are in agreement with our previous investigation, which showed that a low background oxygen concentration gives rise to branched tumours which contain aggressive phenotypes (Gerlee and Anderson, 2007a), and highlights the fact that the tumour micro-environment potentially can have a significant impact on both the morphology and evolutionary dynamics of the tumour. In conclusion our results suggest that the glycolytic phenotype emerges through complex interactions between the cancer cell population and the surrounding tissue, and although this model only takes into account a few of these interactions we were still able to identify key parameters that drive the evolution towards an invasive cancer.
Acknowledgments
The authors would like to thank D.F Griffths for help with implementing the ADI solver. This work was funded by the National Cancer Institute, Grant Number: U54 CA 113007.
Appendix
A.1 Neural Network
The network consists of a number of nodes that can take real number values. The nodes are organised into three layers: the input layer ξ, the hidden layer V, which can be interpreted (for our model) as the processing layer, and the output layer O. The nodes in the different layers are connected via links, of varying connection strengths, which can modify the value of each node via the transfer function (T(x), below). The connections between the input layer and the hidden layer are defined by a connection matrix w, where wij determines the connection strength between node j in the input layer (ξj) and node i in the hidden layer (Vi). Likewise the connections between the hidden layer and the output layer are defined by a connection matrix W, where Wij determines the connection strength between node j in the hidden layer (Vj) and node i in the output layer (Oi). The nodes in the hidden and output layer are also equipped with thresholds, where θi is the threshold of node i in the hidden layer (Vi) and ϕj is the threshold of node j in the output layer Oj. These are real valued parameters used to modulate the impact of the connections to each node.
The response of the network for a given input vector is calculated in the following way: First the values of the input nodes are set to the input vector ξ = (n(x⃗, t), c(x⃗, t), g(x⃗, t), h(x⃗, t)). The node values of the input layer are then fed to the hidden layer using a standard transfer function, T(x), and the connection matrix w.
| (A.1) |
This is a standard function used in neural networks (Haykin, 1999) and guarantees that the resulting node values of the hidden layer are in the range [0, 1]. The value of node j in the hidden layer is given by
| (A.2) |
which is the sum of the input nodes weighted with the connection matrix w and the threshold θj. The same procedure is repeated for the output layer, which means that value of node i in the output layer is given by
| (A.3) |
The behaviour of the cells is then determined by the values of the nodes in the output layer. From (A.3) we can see that the value of each output node is a function of all input nodes and that the impact of each input node depends on the network parameters w, W, θ and ϕ. Therefore the behaviour of the network is determined by these parameters. When a cell divides, to model mutation, we allow these parameters to be copied to the daughter cells with a small variation. The number of parameters to be mutated are chosen from a Poisson distribution with parameter p. For all those parameters x the mutations are modelled by letting x⃗ x + s, where s is random number from a normal distribution N(0, σ), where σ determines the strength of the mutations.
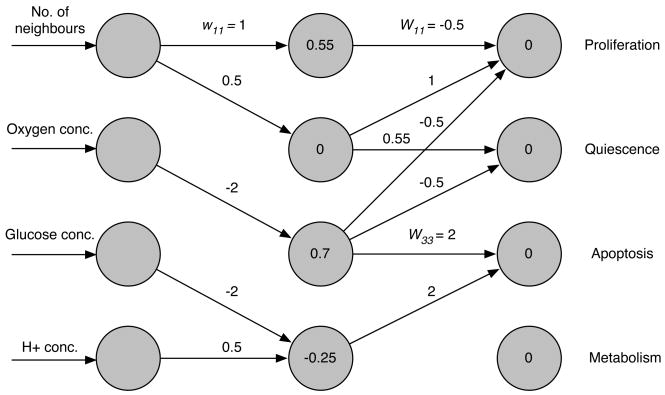
The initial network, which was used as a starting point for every simulation, was constructed by hand to match the cellular behaviour detailed in section 2.5. The network parameters are given by,
| (A.4) |
which results in the network seen in fig. A.1.
Fig. A.1.
The wiring of the initial cell’s network. The weights of the connections are given next to the arrows and the node thresholds are displayed inside the nodes.
A more detailed definition of the model and extended explanation of how it functions can be found in Gerlee and Anderson (2007a).
A.2 Numerical Implementation
The model was implemented in Java (using the JAMA matrix package (Hicklin et al., 2005)) and the partial differential equations (3), (4) and (5) where solved using an alternating direction implicit scheme (ADI) (Press et al., 1996). The use of an implicit scheme decreases computational time as larger time steps can be used compared to explicit methods and also allows us to obtain more accurate solutions compared to the quasi steady-state assumption commonly employed in cancer modelling. The ADI-scheme was implemented with standard five-point finite central difference formulas with space step Δx and time step Δt. Instead of solving the equations with the original boundary conditions we use the boundary condition (c, g, h) = 0, as this simplifies the calculations. The actual solution can then be recovered by simply shifting the solution obtained via the ADI method. The alternating direction means that the discretised equations are first solved in the x-direction for half a time step and then in the y-direction the following half time step. If we let ut represent the discrectised chemical field in matrix notation at time t, then the scheme can be written as
| (A.5) |
where and are matrices that represent second derivatives in the x and y-direction respectively, f(u) represents the consumption/production functions and α = DΔt/Δx2. These equations are then rewritten as
| (A.6) |
where I is the identity matrix and using the fact that and , where T is the matrix representation of the five-point finite central difference formula
| (A.7) |
for the boundary condition u = 0. Each time step the two matrix equations (A.6) are solved and the actual concentrations can easily be recovered by the transformation u → u + 1.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abrams HL, Spiro R, Goldstein N. Metastases in carcinoma; analysis of 1000 autopsied cases. Cancer. 1950;3 (1):74–85. doi: 10.1002/1097-0142(1950)3:1<74::aid-cncr2820030111>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- Alberts B, Bray D, Lewis J, Raff M, Roberts K, Watson J. Ch. 14: Energy Conversion: Mitochondria and Chloroplasts. 3. Garland Publishing; New York: 1994a. The Cell; pp. 660–662. [Google Scholar]
- Alberts B, Bray D, Lewis J, Raff M, Roberts K, Watson J. Ch. 22: Differentiated Cells and the Maintenance of Tissue. 3. Garland Publishing; New York: 1994b. The Cell; pp. 1173–1175. [Google Scholar]
- Alexandrova R. Tumour heterogeneity. Experimental Pathology and Parasitology. 2001;4:57–67. [Google Scholar]
- Anderson A, Chaplain M, Newman E, Steele R, Thompson A. Mathematical modelling of tumour invasion and metastasis. J Theoret Med. 2000;2:129–154. [Google Scholar]
- Anderson ARA. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Math Med Biol. 2005;22:163–186. doi: 10.1093/imammb/dqi005. [DOI] [PubMed] [Google Scholar]
- Anderson ARA, Chaplain M. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Bio. 1998;6:857–899. doi: 10.1006/bulm.1998.0042. [DOI] [PubMed] [Google Scholar]
- Anderson ARA, Rejniak KA, Gerlee P, Quaranta V. Microenviroment driven invasion: A multiscale multimodel investigation. Journal of Mathematical Biology. 2007 doi: 10.1007/s00285-008-0210-2. In Review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson ARA, Weaver AM, Cummings PT, Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell. 2006;127 (5):905–915. doi: 10.1016/j.cell.2006.09.042. [DOI] [PubMed] [Google Scholar]
- Batchelor MT, Henry BI. Limits to eden growth in two and three dimensions. Physics Letters A. 1991;157 (4–5):229–236. [Google Scholar]
- Breward CJW, Byrne HM, Lewis CE. The role of cell-cell interactions in a two-phase model for avascular tumour growth. J Math Biol. 2002;45 (2):125–152. doi: 10.1007/s002850200149. [DOI] [PubMed] [Google Scholar]
- Brizel DM, Sibley GS, Prosnitz LR, Scher RL, Dewhirst MW. Tumor hypoxia adversely affects the prognosis of carcinoma of the head and neck. International Journal of Radiation Oncology Biology Physics. 1997;38 (2):285–289. doi: 10.1016/s0360-3016(97)00101-6. [DOI] [PubMed] [Google Scholar]
- Brown J, Wilson W. Exploiting tumour hypoxia in cancer treatment. Nature. 2004;4:437–447. doi: 10.1038/nrc1367. [DOI] [PubMed] [Google Scholar]
- Byrne H, Chaplain M. Free boundary value problems associated with the growth and development of multicellular spheroids. European Journal of Applied Mathematics. 1997;8:639–658. [Google Scholar]
- Calabresi P, Schein Pe. Medical Oncology. 2. McGraw-Hill; New York: 1993. [Google Scholar]
- Casciari JJ, Sotirchos SV, Sutherland RM. Variation in tumour cell growth rates and metabolism with oxygen-concentration, glucose-concentration and extra-cellular ph. J Cell Physiol. 1992;151:386–394. doi: 10.1002/jcp.1041510220. [DOI] [PubMed] [Google Scholar]
- Crone C, Levitt DG. Handbook of Physiology: A critical, comprehensive presentation of physiological knowledge and concepts. American Physiological Society, Bethesda, Maryland, Ch 2: The Cardiovascular System. 1984;414:434–437. [Google Scholar]
- Czernin J, Phelps ME. Positron emission tomography scanning: current and future applications. Annu Rev Med. 2002;53:89–112. doi: 10.1146/annurev.med.53.082901.104028. [DOI] [PubMed] [Google Scholar]
- Daccord G, Nittmann J, Stanley HE. Radial viscous fingers and diffusion-limited aggregation: Fractal dimension and growth sites. Phys Rev Lett. 1986;56 (4):336–339. doi: 10.1103/PhysRevLett.56.336. [DOI] [PubMed] [Google Scholar]
- Dairkee SH, Deng G, Stampfer MR, Waldman FM, Smith HS. Selective cell culture of primary breast carcinoma. Cancer Res. 1995;55 (12):2516–2519. [PubMed] [Google Scholar]
- DeClerck YA, Mercurio AM, Stack MS, Chapman HA, Zutter MM, Muschel RJ, Raz A, Matrisian LM, Sloane BF, Noel A, Hendrix MJ, Coussens L, Padarathsingh M. Proteases, extra-cellular matrix, and cancer: a workshop of the path b study section. Am J Pathol. 2004;164 (4):1131–1139. doi: 10.1016/S0002-9440(10)63200-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Düchting W, Vogelsaenger T. Analysis, forecasting and control of three-dimensional tumor growth and treatment. J Med Syst. 1984;8:461–475. doi: 10.1007/BF02285258. [DOI] [PubMed] [Google Scholar]
- Dunn GP, Old LJ, Schreiber RD. The three es of cancer immunoediting. Annu Rev Immunol. 2004;22:329–360. doi: 10.1146/annurev.immunol.22.012703.104803. [DOI] [PubMed] [Google Scholar]
- Enderling H, Chaplain M, Anderson A, Vaidya J. A mathematical model of breast cancer development, local treatment and recurrence. J Theor Biol. 2007;264 (2):245–259. doi: 10.1016/j.jtbi.2006.12.010. [DOI] [PubMed] [Google Scholar]
- Ennis BW, Matrisian LM. Matrix degrading metalloproteinases. Journal of Neuro-Oncology. 1993;18 (2):105–109. doi: 10.1007/BF01050416. [DOI] [PubMed] [Google Scholar]
- Ferreira SC, Martins ML, Vilela MJ. Reaction-diffusion model for the growth of avascular tumor. Physical Review E. 2002;65:021907. doi: 10.1103/PhysRevE.65.021907. [DOI] [PubMed] [Google Scholar]
- Folkman J. Angiogenesis. Annu Rev Med. 2006;57:1–18. doi: 10.1146/annurev.med.57.121304.131306. [DOI] [PubMed] [Google Scholar]
- Freyer JP, Sutherland RM. Regulation of growth saturation and development of necrosis in emt6/ro multicellular spheroids by the glucose and oxygen supply. Cancer Research. 1986;46:3513–3520. [PubMed] [Google Scholar]
- Freyer JP, Tustanoff E, Franko AJ, Sutherland RM. In situ consumption rates of cells in v-79 multicellular spheroids during growth. J Cell Physiol. 1984;118:53–61. doi: 10.1002/jcp.1041180111. [DOI] [PubMed] [Google Scholar]
- Ganong W. Ch 19th. 19. Appleton & Lange; New York: 1999. Review of Medical Physiology; p. 329. [Google Scholar]
- Gatenby RA, Gawlinski ET. A reaction-diffusion model of cancer invasion. Cancer Res. 1996;56 (24):5745–5753. [PubMed] [Google Scholar]
- Gatenby RA, Gillies RJ. Why do cancers have high aerobic glycolysis? Nature Review Cancer. 2004;4:891–899. doi: 10.1038/nrc1478. [DOI] [PubMed] [Google Scholar]
- Gerlee P, Anderson ARA. An evolutionary hybrid cellular automaton model of solid tumour growth. Journal of Theoretical Biology. 2007a;246 (4):583–603. doi: 10.1016/j.jtbi.2007.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerlee P, Anderson ARA. Stability analysis of a hybrid cellular automaton model of cell colony growth. Physical Review E. 2007b;75 (5):051911. doi: 10.1103/PhysRevE.75.051911. [DOI] [PubMed] [Google Scholar]
- Grote J, Susskind R, Vaupel P. Oxygen diffusivity in tumor tissue (ds-carcinosarcoma) under temperature conditions within the range of 20–40 degrees c. Pflugers Arch. 1977;372:37–42. doi: 10.1007/BF00582204. [DOI] [PubMed] [Google Scholar]
- Hawkins RA, Phelps ME. Pet in clinical oncology. Cancer Metastasis Rev. 1988;7 (2):119–142. doi: 10.1007/BF00046482. [DOI] [PubMed] [Google Scholar]
- Haykin S. Neural Networks: a comprehensive foundation. 2. Prentice Hall; New Jersey: 1999. [Google Scholar]
- Helmlinger G, Yuan F, Dellian M, Jain R. Interstitial ph and po2 gradients in solid tumors in vivo: High-resolution measurements reveal a lack of correlation. Nature Medecine. 1997;3:177–182. doi: 10.1038/nm0297-177. [DOI] [PubMed] [Google Scholar]
- Hicklin J, Moler C, Webb P. JAMA Matrix Package. 2005 URL http://math.nist.gov/javanumerics/jama/
- Höckel M, Schlenger K, Aral B, Mitze M, Schaffer U, Vaupel P. Association between tumor hypoxia and malignant progression in advanced cancer of the uterine cervix. Cancer Research. 1996;56:4509–4515. [PubMed] [Google Scholar]
- Höckel M, Schlenger K, Höckel S, Vaupel P. Hypoxic cervical cancers with low apoptotic index are highly aggressive. Cancer Res. 1999;59 (18):4525–4528. [PubMed] [Google Scholar]
- Hotary K, Allen E, Punturieri A, Yana I, Weiss SJ. Regulation of cell invasion and morphogenesis in a three-dimensional type i collagen matrix by membrane-type matrix metalloproteinases 1, 2, and 3. J Cell Biol. 2000;149 (6):1309–1323. doi: 10.1083/jcb.149.6.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr JF, Winterford CM, Harmon BV. Apoptosis. its significance in cancer and cancer therapy. Cancer. 1994;73:2013–2026. doi: 10.1002/1097-0142(19940415)73:8<2013::aid-cncr2820730802>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- Kessler DA, Koplik J, Levine H. Pattern selection in fingered growth phenomena. Advances in Physics. 1988;37:255–339. [Google Scholar]
- Kunkel M, Reichert TE, Benz P, Lehr HA, Jeong JH, Wieand S, Bartenstein P, Wagner W, Whiteside TL. Overexpression of glut-1 and increased glucose metabolism in tumors are associated with a poor prognosis in patients with oral squamous cell carcinoma. Cancer. 2003;97 (4):1015–1024. doi: 10.1002/cncr.11159. [DOI] [PubMed] [Google Scholar]
- Lawrence JA, Steeg PS. Mechanisms of tumor invasion and metastasis. World Journal of Urology. 1996;14 (3):124–130. doi: 10.1007/BF00186891. [DOI] [PubMed] [Google Scholar]
- Liotta LA, Rao CN, Barsky SH. Tumor invasion and the extra-cellular matrix. Lab Invest. 1983;49 (6):636–649. [PubMed] [Google Scholar]
- Macklin P, Lowengrub J. Evolving interfaces via gradients of geometry-dependent interior poisson problems: application to tumor growth. J Comput Phys. 2005;203:191–220. [Google Scholar]
- Mansury Y, Diggory M, Deisboeck TS. Evolutionary game theory in an agent-based brain tumor model: exploring the ’genotype-phenotype’ link. J Theor Biol. 2006;238 (1):146–156. doi: 10.1016/j.jtbi.2005.05.027. [DOI] [PubMed] [Google Scholar]
- Mansury Y, Kimura M, Lobo J, Deisboeck T. Emerging patterns in tumor systems: Simulating the dynamics of multicellular clusters with an agent-based spatial agglomeration model. Journal of Theoretical Biology. 2002;219:343370. doi: 10.1006/jtbi.2002.3131. [DOI] [PubMed] [Google Scholar]
- Martin GR, Jain RK. Noninvasive measurement of interstitial ph profiles in normal and neoplastic tissue using fluorescence ratio imaging microscopy. Cancer Res. 1994;54 (21):5670–5674. [PubMed] [Google Scholar]
- Matsushita M, Sano M, Hayakawa Y, Honjo H, Sawada Y. Fractal structures of zinc metal leaves grown by electrodeposition. Phys Rev Lett. 1984;53 (3):286–289. [Google Scholar]
- McDougall SR, Anderson AR, Chaplain MA. Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: Clinical implications and therapeutic targeting strategies. Journal of Theoretical Biology. 2006;241 (3):564–589. doi: 10.1016/j.jtbi.2005.12.022. [DOI] [PubMed] [Google Scholar]
- McLean LA, Roscoe J, Jorgensen NK, Gorin FA, Cala PM. Malignant gliomas display altered ph regulation by nhe1 compared with nontransformed astrocytes. Am J Physiol Cell Physiol. 2000;278 (4):C676–C688. doi: 10.1152/ajpcell.2000.278.4.C676. [DOI] [PubMed] [Google Scholar]
- Park HJ, Lyons JC, Ohtsubo T, Song CW. Acidic environment causes apoptosis by increasing caspase activity. Br J Cancer. 1999;80 (12):1892–1897. doi: 10.1038/sj.bjc.6690617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel A, Gawlinski ET, Lemieux SK, Gatenby RA. A cellular automaton model of early tumor growth and invasion: The effects of native tissue vascularity and increased anaerobic tumor metabolism. J theor Biol. 2001;213:315–331. doi: 10.1006/jtbi.2001.2385. [DOI] [PubMed] [Google Scholar]
- Press W, Teukolsky S, Vetterling WBPF. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University; 1996. [Google Scholar]
- Rozhin J, Sameni M, Ziegler G, Sloane BF. Pericellular ph affects distribution and secretion of cathepsin b in malignant cells. Cancer Res. 1994;54 (24):6517–6525. [PubMed] [Google Scholar]
- Rubin H. Microenvironmental regulation of the initiated cell. Adv Cancer Res. 2003;90:1–62. doi: 10.1016/s0065-230x(03)90001-7. [DOI] [PubMed] [Google Scholar]
- Sachs R, Hlatky LPH. Simple ode models of tumor growth and anti-angiogenic or radiation treatment. Math comput model. 2001;33:1297–1305. [Google Scholar]
- Schornack PA, Gillies RJ. Contributions of cell metabolism and h+ diffusion to the acidic ph of tumors. Neoplasia. 2003;5 (2):135–145. doi: 10.1016/s1476-5586(03)80005-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semenza GL. Hypoxia-inducible factor 1: master regulator of off homeostasis. Curr Opin Genet Dev. 1998;8 (5):588–594. doi: 10.1016/s0959-437x(98)80016-6. [DOI] [PubMed] [Google Scholar]
- Smallbone K, Gatenby RA, Gillies RJ, Maini PK, Gavaghan DJ. Metabolic changes during carcinogenesis: Potential impact on invasiveness. Journal of Theoretical Biology. 2007;244 (4):703–713. doi: 10.1016/j.jtbi.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Smallbone K, Gavaghan DJ, Gatenby RA, Maini PK. The role of acidity in solid tumour growth and invasion. J Theor Biol. 2005;235 (4):476–484. doi: 10.1016/j.jtbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- Stetler-Stevenson WG, Aznavoorian S, Liotta LA. Tumor cell interactions with the extracellular matrix during invasion and metastasis. Annu Rev Cell Biol. 1993;9:541–573. doi: 10.1146/annurev.cb.09.110193.002545. [DOI] [PubMed] [Google Scholar]
- Sutherland R. Cell and environment interactions in tumor microregions: The multicell spheroid model. Science. 1988;240:177–184. doi: 10.1126/science.2451290. [DOI] [PubMed] [Google Scholar]
- Swanson KR, Bridge C, Murray JD, Alvord EC. Virtual and real brain tumors: using mathematical modeling to quantify glioma growth and invasion. J Neurol Sci. 2003;216 (1):1–10. doi: 10.1016/j.jns.2003.06.001. [DOI] [PubMed] [Google Scholar]
- van Saarloos W. Three basic issues concerning interface dynamics in nonequilibrium pattern formation. Physics Reports. 1998;301:9–43. [Google Scholar]
- Wagle DG, Moore RH, Murphy GP. Secondary carcinomas of the kidney. J Urol. 1975;114 (1):30–32. doi: 10.1016/s0022-5347(17)66935-0. [DOI] [PubMed] [Google Scholar]
- Walenta S, Snyder S, Haroon Z, Braun R, Amin K, Brizel D, Mueller-Klieser W, Chance B, Dewhirst M. Tissue gradients of energy metabolites mirror oxygen tension gradients in a rat mammary carcinoma model. Int J Radiation Oncology Biol Phys. 2001;51:840–848. doi: 10.1016/s0360-3016(01)01700-x. [DOI] [PubMed] [Google Scholar]
- Warburg O. The Metabolism of Tumors. Constable Press; London: 1930. [Google Scholar]
- Zheng X, Wise S, Cristini V. Nonlinear simulation of tumor necrosis, neovascularization and tissue invasion via an adaptive finite-element/level-set method. Bulletin of Mathematical Biology. 2005;67:211–259. doi: 10.1016/j.bulm.2004.08.001. [DOI] [PubMed] [Google Scholar]