Numerical Investigation of Coil Configurations That Provide Ultra-High Packing Density of Saccular Aneurysms

Abstract

Background

The long-term outcome of endovascular coiling of cerebral aneurysms is directly related to the packing density at time of treatment. In general, the highest packing density achievable is only about 45% due to the quasi-random distribution of currently available coils within aneurysms. We investigated whether packing densities could be maximized via more ordered coil configurations.

Methods

Three different coil configurations – circular loops, planar spirals, and spherical helices – were investigated. The packing densities achievable in maximally filling the volume of an exemplar human basilar aneurysm with each coil configuration were calculated numerically. Coil packing simulations were also carried out for aneurysms idealized as spheres over diameters ranging from 2 to 30 mm.

Results

The packing densities with the loop, spiral, and spherical helix configurations were 82%, 60%, and 73%, respectively, for the human aneurysm model; the numbers of coils required were 693, 34, and 13, respectively. Simulations within idealized aneurysms suggest that aneurysms cannot be packed to more than 91% with coils of constant circular cross-section. The spherical helix configuration provides a constant packing density (coefficient of variation 0.4%) over the range of aneurysm diameters studied as compared to the two other configurations (coefficients of variation 9% and 8%).

Conclusions

Coil configurations that allow for ordered filling of cerebral aneurysms can potentially provide packing densities that are twice those currently achieved. The spherical helix configuration seems to be the most technically feasible and stable configuration of the three coil types investigated.

Introduction

Endovascular embolization of cerebral aneurysms with metallic micro-coils is currently a widely used treatment modality. The major complication with this modality is re-arrangement of the coil mass within the aneurysm due to repeated pulsatile impingement of blood. Depending on factors such as aneurysm size and location, neck width, or degree of angiographic occlusion at time of treatment, long-term aneurysm recurrence rates due to this coil-compaction phenomenon can be as high as 40% [1]. As the percentage angiographic occlusion immediately after treatment has been found to be an unreliable indicator of long-term outcome, the packing density measure is used to evaluate treatment success [2]. Packing density is calculated as the ratio of the total volume of coils deposited within the aneurysm to the volume of the aneurysm. Studies have shown that higher packing densities protect against the recurrence of aneurysms [2-4]. Higher coil compaction rates in larger aneurysms have been attributed to the lower packing densities that can be achieved in such aneurysms [3,4]. Three-dimensional [5] and complex-shaped [6,7] coil configurations have subsequently been developed to achieve higher packing densities and attest to a direct correlation between packing density and treatment stability [8,9]. In general, the packing densities achievable with bare metallic coils seem to be about 30% with traditional coils, about 40% with complex-shaped coils, with balloon- or stent-assistance providing an additional 5-10% absolute increase [6,7,10].

Although better coil configurations have been developed, it is conceptually interesting that aneurysm packing densities are at most 50% and not closer to 100%. The packing density is a function of the geometrical configuration of a wire (coil) that is to be deposited within a given volume (aneurysm). The low packing densities currently achievable should, therefore, be the result of sub-optimal coil configurations. We attempted to investigate whether aneurysms can be more densely packed, to what extent, and what coil configurations would provide such optimum packing densities. Coil packing simulations with three such configurations are presented here.

Methods

Volume data of a human basilar aneurysm obtained by three-dimensional rotational angiography was used for the coil packing simulations. The contours of the aneurysm were delineated by adapting an algorithm published previously [11]. The neck, width, and height of the aneurysm were 5.3, 11.2, and 10.0 mm, respectively; the volume of the aneurysm was 534 mm³. Horizontal planes were added to close off the top and bottom of the aneurysm. Coil packing simulations were also carried out in spheres representing idealized aneurysms of diameters ranging from 2 mm to 30 mm to investigate trends in maximum packing density with aneurysm diameter. The coil diameter was assumed to be 300 microns (approximately 0.012 inches) for these cases. To evaluate variations in packing density with different coil diameters, simulations were carried out in an idealized aneurysm of 10 mm diameter with coil diameters ranging from 100 to 1000 microns. All simulations were performed in Matlab® (The Mathworks, Natick, MA).

Circular Loops

This configuration was simulated by maximally packing a cross-sectional area of revolution with non-overlapping circles and then revolving the area around the longitudinal axis to get the aneurysm volume filled with circular loops. For the basilar aneurysm, a longitudinal line perpendicular to the aneurysm contours was fitted by linear regression to the centroids of the individual contours (Fig 1A). One point on each individual contour that was farthest away from this perpendicular line was then selected and all such points were joined to form an area of revolution. Revolving this area around the line thus envelops the entire aneurysm. This area of revolution was then filled with circles of diameter 300 microns in a hexagonal lattice without any overlap. The entire lattice was shifted in the four cardinal directions within the area of revolution to locate any further empty space that could be filled. Individual circles were added where empty space was available (Fig 1B). All the circles were then revolved around the perpendicular axis to form loops. Sections of the loops that were outside of the aneurysm surface were removed. The aneurysm volume was thus maximally filled with loops and loop sections. Loop packing simulations in spheres were carried out similarly, by maximally filling a semi-circle with circles of diameter equal to the coil wire diameter and then revolving the semi-circle around its diameter.

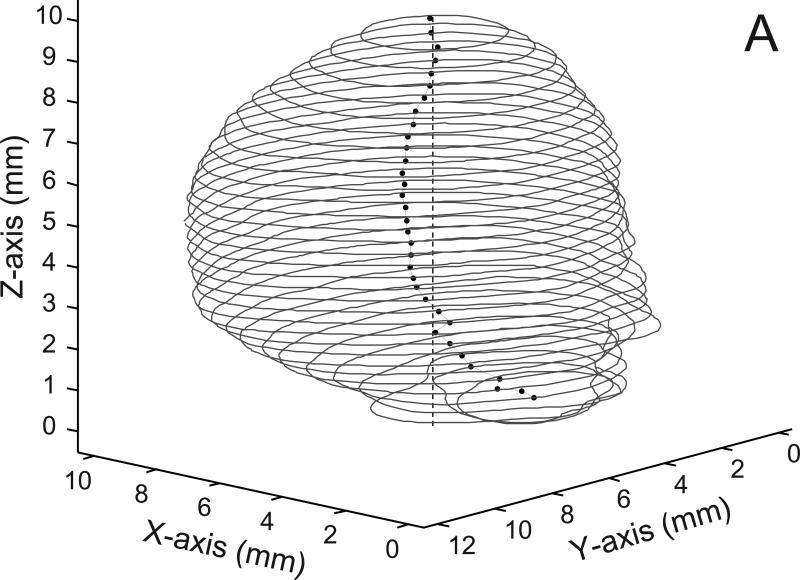
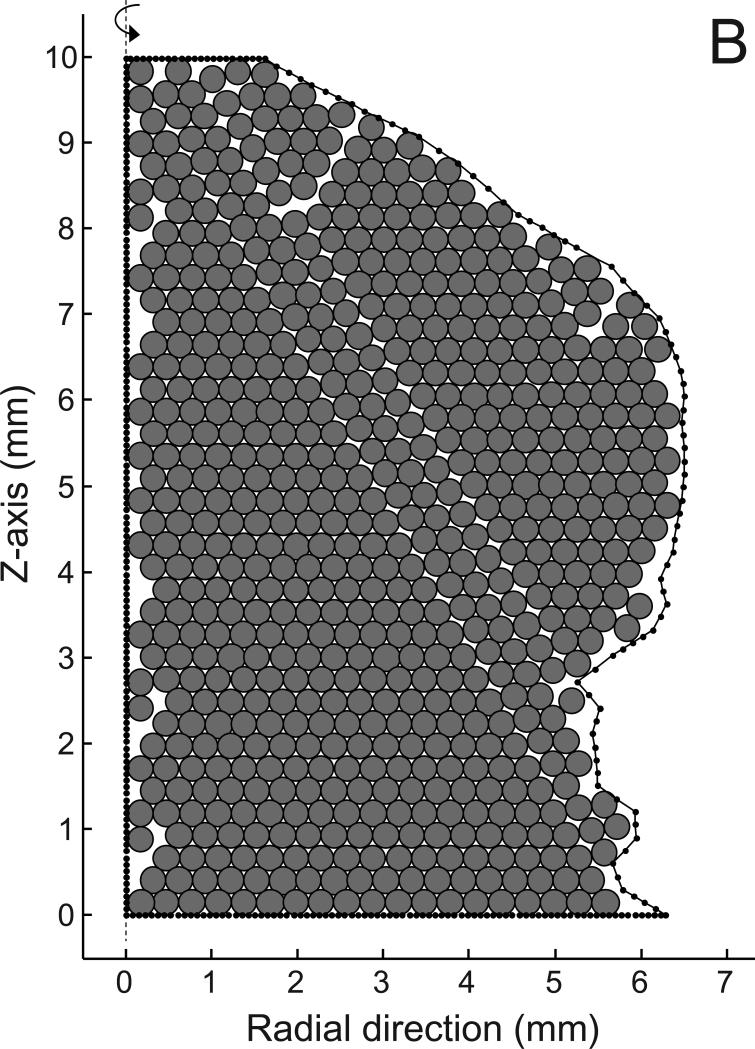
Fig 1.

A) Contours of the basilar aneurysm showing the line joining the centroids (dots) of each contour and the perpendicular line (dashed line) fitted to the centroids by linear regression. B) The area of revolution (bounded by solid dotted line) is maximally filled with circles of 300 micron diameter. There are 646 circles in the packing; the dashed line on the left is the perpendicular axis of revolution from panel A.

Planar Spirals

The aneurysm (basilar or sphere) volume was maximally filled with vertically stacked Archimedes’ spirals of constant wire diameter. At each vertical location, the center coordinates of the largest inner circle that would fit the aneurysm contour at that location was found. The contour was converted to a binary image with 100 pixels/mm resolution and the Matlab ‘bwdist’ function was used to get the minimum distance to the contour for each pixel inside the contour. The pixel with the largest such distance determined the center of the largest inner circle. These center coordinates were then used as the origin of a spiral. The polar equation for the spirals was given as

$$r=\frac{d_c}{2\pi }\theta$$ (1)

where, d_c was the coil wire diameter. The pitch of the spirals was thus equal to the wire diameter ensuring no overlap and tightest packing. The outward end point of each spiral was determined by continuing the spiral until it reached the aneurysm contour.

Spherical Helices

The inner surface of the aneurysm (basilar or sphere) was first covered with a spherical helix having a cross-section equal to the coil wire diameter d_c. The pitch of the spherical helix was set to be equal to d_c for every turn, again ensuring tightest coverage with no overlap. The inner surface of this first helix was then covered with another spherical helix of same cross-section; continuing in the same way, the aneurysm volume was successively filled with concentric spherical helices. The equation used for the spherical helices was

$$\phantom{\{}\begin{array}{c}x=R_s\cos \theta \sin \varphi \hfill \\ y=R_s\sin \theta \sin \varphi \hfill \\ z=R_s\cos \varphi \hfill \end{array}\}\theta =2n\varphi ;0\le \varphi \le \pi$$ (2)

where, R_s was the radius of the spherical helix, ϕ the angle to the z-axis, and n the number of turns in the helix calculated as

$$n=\frac{\pi }{{\cos }^{-1}\left(1-2\frac{r_c^2}{r_i^2}\right)}$$ (3)

where, r_c was the coil wire radius and r_i the average radius of the inner surface to be filled. For the basilar aneurysm, the inner surfaces to be covered were converted to spherical coordinates for use with these equations.

The packing density for each case was calculated as the ratio of the total volume of coils within the aneurysm to the volume of the aneurysm. The dispersion in packing densities over the 2-30 mm range of sphere diameters or over the 0.1 to 1 mm range of coil wire diameters was represented by the coefficient of variation (percentage ratio of standard deviation of maximal packing density to mean maximal packing density).

Results

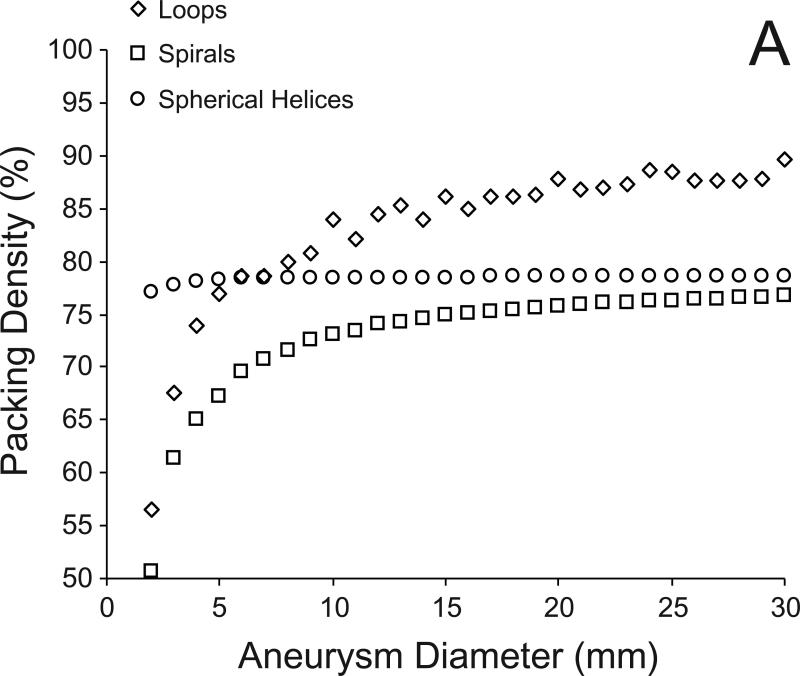
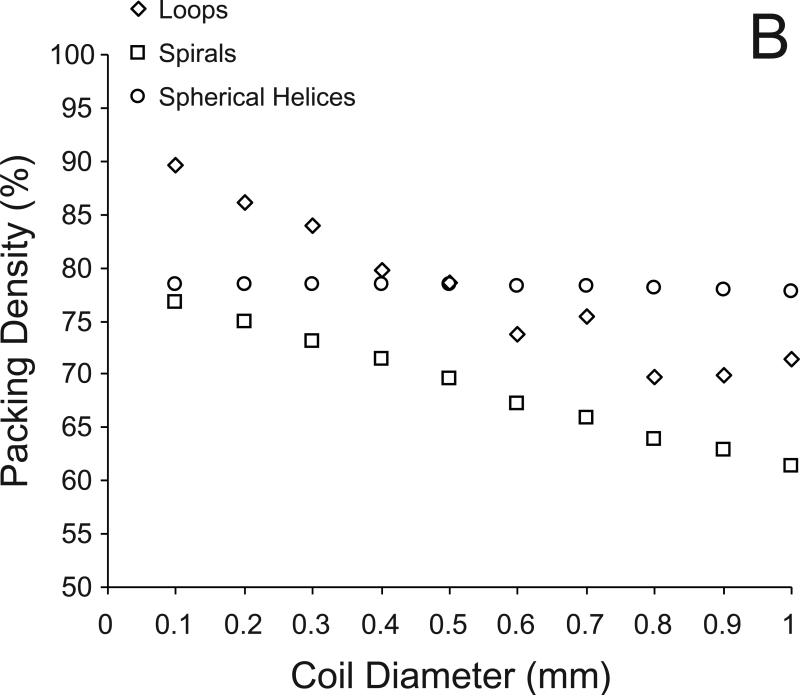
Figure 2 shows examples of coils of each configuration placed within the basilar aneurysm. The packing densities obtained with the loop, spiral, and spherical helix configuration were 82.2%, 59.9%, and 72.7%, respectively. The numbers of coils and coil lengths required to achieve these packing densities are listed in Table 1. Figure 3A shows the changes in maximal packing density with each configuration in filling idealized aneurysms (spheres) of diameters 2 mm through 30 mm. The coefficients of variation for the loop, spiral, and spherical helix configurations were 8.6%, 7.8%, and 0.4%, respectively. Figure 3B shows the maximal packing densities achieved in a 10 mm aneurysm with coils of different diameter. The coefficients of variation for the loop, spiral, and spherical helix configurations were 9.0%, 7.7%, and 0.3%, respectively.

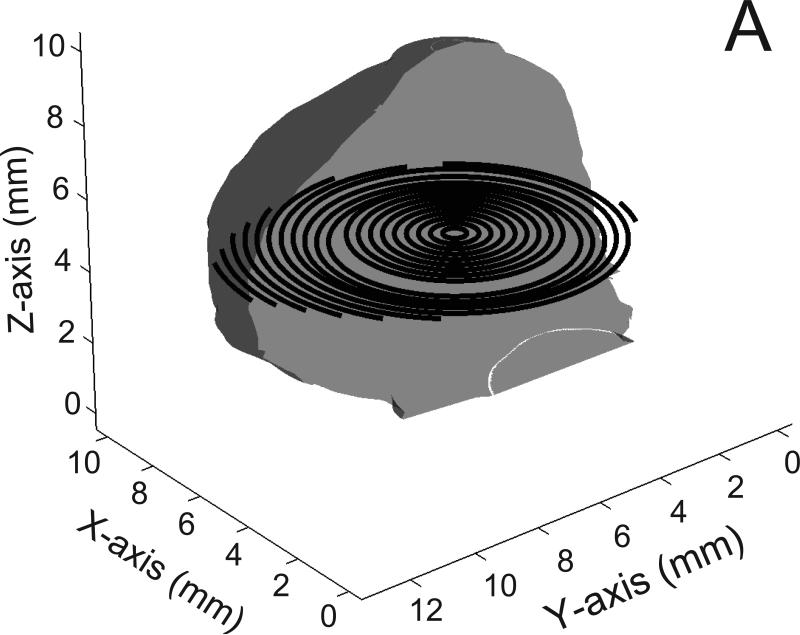
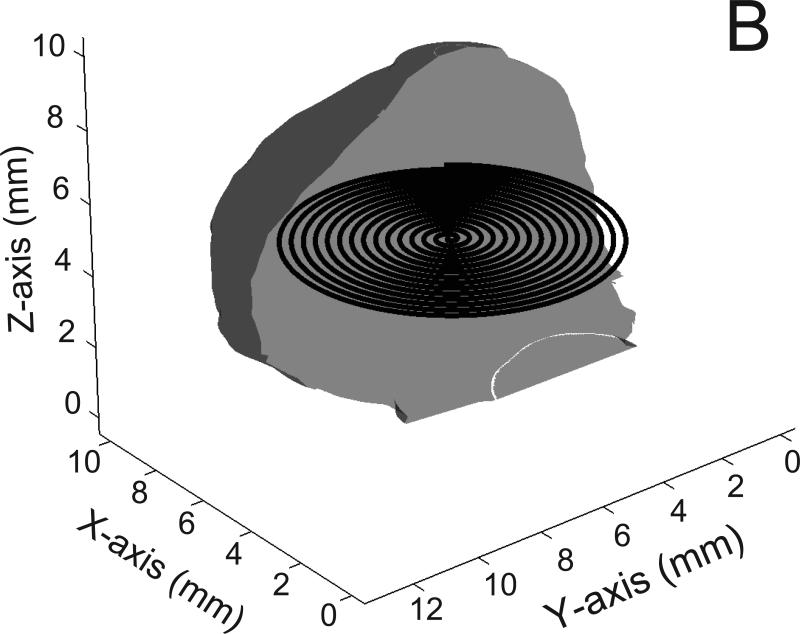
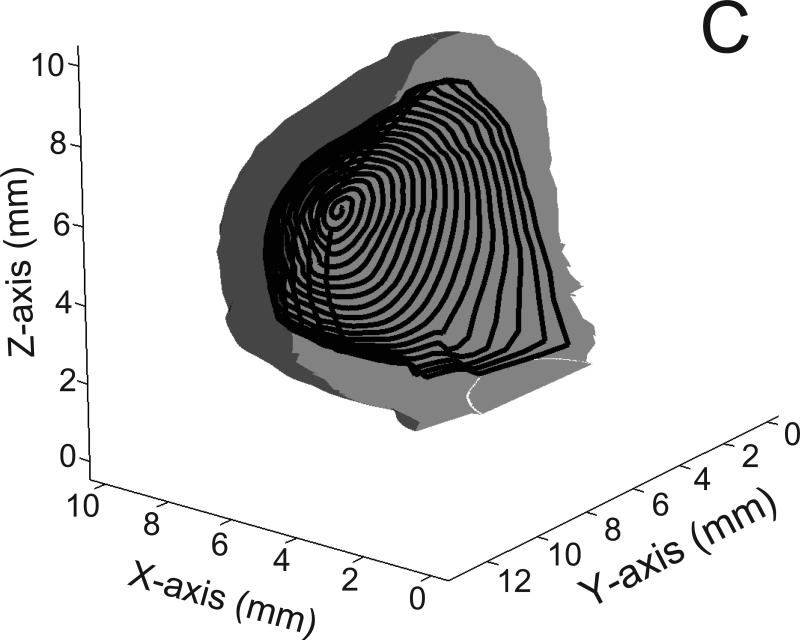
Fig 2.

Examples of coils (300 micron diameter) within the exemplar basilar aneurysm; A) the circular loop configuration; B) the planar spiral configuration; C) the spherical helix configuration; only half of the spherical helix coil is shown for visual clarity. Also for visual clarity, only half of the aneurysm surface is shown and the diameter of the coils is halved; entire aneurysm volume is filled with such coils but all the coils are not shown.

Table 1.

Packing densities and coil dimensions of the three coil configurations in filling a human basilar aneurysm (aneurysm volume = 534 mm³)

Coil Configuration	Number of coils	Length of shortest coil (mm)	Length of longest coil (mm)	Median coil length (mm)	Packing density (%)
Loops	693	0.05	26.7	7.5	82.2%
Spirals	34	14.0	210.2	139.4	59.9%
Spherical Helices	13	68.4	956.9	370.6	72.7%

Fig 3.

A) Variation in maximum packing density with each of the three coil configurations for filling spheres ranging from 2 to 30 mm diameter with coils of 300 micron diameter. B) Variation in maximum packing density for filling a sphere of diameter 10 mm with coils of 100 to 1000 microns diameter.

Discussion

The packing of cerebral aneurysms with micro-coils is mostly governed by the geometric configuration of deposited coils. Based on this realization, we investigated the theoretical maximum packing density that can be achieved within aneurysms and the coil configurations that would provide such optimal packing. Although such an investigation has been called for previously [8], we are unaware of any such studies. One report developing an algorithm for filling volumes with arbitrarily shaped objects used coils configured as tubular sections to fill an aneurysm of about 20 mm size; they report a “volume fill ratio” of 15% [12], which is far from optimal. The reasons for choosing the geometric configurations of coils in use today are unclear. Once deposited, the arrangements are largely random, the goal possibly being to fill as much of the aneurysm volume as possible with each individual coil. A random structure, however, severely limits control over the distribution of dead spaces within the coil mass as more coils are added. A more ordered packing is essential if higher densities are to be achieved. Instead of filling as much as possible of the available volume of the aneurysm, the goal of ordered packing would be to cover as much as possible of the available inner surface area of the aneurysm. Our simulations in a sample human basilar aneurysm show that coil configurations that are concentric and ordered can allow packing densities of 70-80%. Taken together with the packing simulations in spheres, these densities should be achievable in at least any unilobular aneurysm. We should note that we “closed off” the neck of the basilar aneurysm with a plane; our simulations are therefore closer to balloon- or stent-assisted coil embolizations. Configurations of currently developed coils are probably controlled to mitigate coil herniation into the parent artery in the absence of stent-assistance. This, however, should not preclude development of well-structured coil masses.

It is known that the densest possible packing of (non-overlapping, constant diameter) circles on a plane is in a hexagonal lattice, which results in an area coverage of $\frac{\pi }{\sqrt{12}}(90.7\%)$ [13]. Simulations of packing ideal aneurysms with the loop configuration 12 suggest that the maximal packing density approaches this value (90.7%) as the coil diameter becomes small in comparison to the aneurysm diameter (Fig 3). For small ratios of coil to sphere diameter, the semi-circle of revolution approaches an infinite plane as compared to the coil diameter so the area coverage of the semi-circle approaches 90.7%. Also, the semi-circle is more uniformly covered with circles and the volume packing density after revolution approaches the area coverage limit. The densest packing of spheres in a volume is with a face-centered cubic or hexagonal-close packed framework (or other similar arrangements), either (all) of which give a volume packing density of $\frac{\pi }{\sqrt{18}}(74.0\%)$ [13]. Aneurysms, therefore, cannot be embolized to more than 74% with 18 spherical particles of constant diameter irrespective of particle or aneurysm size. The maximal area coverage obtainable by arranging circles in a square lattice on a plane is known to be $\frac{\pi }{\sqrt{16}}(78.5\%)$ [13]. It is interesting to note that packing spherical helices 16 into the idealized aneurysms suggests that the limit of such packing may be the same (78.5 %, Fig 3). These limits are possibly the same because in our simulations, the inner surface of the aneurysm to be covered was successively reduced by the coil wire diameter, i.e., the next (inner) helical layer was wound perpendicularly adjacent to the outer helix. A cross-section of any two successive spherical helices would show circles arranged in a square lattice. Arranging the inner helices to fit into the interstices of the outer helices could result in higher packing densities; however, this arrangement is not geometrically possible for all coil and aneurysm sizes. The limit of packing density with the planar spirals also approaches 78.5% (Fig 3) because in the limit, the spirals represent circles arranged in a square lattice within a semi-circle of revolution. Just as the loop configuration approaches a maximal limit of 90.7% volumetric density (hexagonal lattice packing), the spiral configuration approaches a maximal limit of 78.5% volumetric density (square lattice packing).

Two general conclusions may be drawn from these packing simulations within idealized aneurysms. First, there exists a theoretical limit for packing aneurysms – the packing density of any aneurysm cannot exceed 90.7% with bare coils of constant circular cross-section irrespective of coil or aneurysm dimensions. In other words, the loop configuration simulated here is the (theoretical) optimal configuration for embolizing aneurysms with coils. Second, the packing density increases as the ratio of coil diameter to aneurysm diameter decreases. Contrary to what may be expected [3], thinner coils provide a higher packing density as compared to thicker coils because although the volume of an individual thicker coil is greater, less number of thicker coils can be placed within an aneurysm. As has been suggested previously [2], thinner coils reduce the dead space volume within embolized aneurysms allowing for denser packing. This is assuming that identical coil configurations are being compared; thicker coils with better configurations may provide higher packing densities as compared to thinner coils with poor configurations [8].

As can be noted from Table 1 (and Fig 3), although the loop configuration results in higher packing density the number of coils required to achieve this packing is practically improbable. For example, the number of circular loops required to pack a sphere of 30 mm diameter is about 4500 as compared to about 100 and 50, respectively, for the spiral and spherical helix configurations. Also, the simulations in essence assume that the coils are placed simultaneously within the aneurysm. It would be practically difficult to stably introduce coils of either the loop or spiral configuration into an aneurysm one after the other. The spiral configuration as simulated here is also limited by the fact that large voids are left within the aneurysm volume outside of the stack of coils. Such an arrangement would probably result in high aneurysm recanalization rates.

The spherical helix configuration seems to be the most technically feasible of these three coil types. These coils could easily be manufactured with currently available technology by winding a suitable coil wire on a spherical mandrel of required size. The coil size to be deployed could be based on an estimate of the inner surface area of a given aneurysm to optimize coverage. Steerable microcatheters (such as the Enzo™, Micrus Endovascular, San Jose, CA) may be useful for deploying such coils. The catheter tip could be initially positioned towards one end of the volume to be filled and then gradually steered to the other end while simultaneously pushing the coil out of the catheter thereby ensuring proper layering of the coil. The first coil can be slightly oversized to the aneurysm and form a basket within which successive coils can be deposited. It is generally accepted that filling aneurysms with concentrically layered coils results in a homogenous and more dense packing with less dead space [5,6,8,9]. The spherical helix offers an effective and stable (little possibility of coil shifting during deposition) way to achieve such layering. Moreover, unlike currently available coils this configuration potentially provides a well-ordered structure at the neck of the aneurysm, which may facilitate neointima formation and endothelialization at the artery-aneurysm interface. Figure 3 also suggests that the packing density remains relatively constant with this configuration irrespective of aneurysm diameter (or ratio of coil to aneurysm diameter). This configuration may, therefore, be beneficial for embolizing large to giant aneurysms where the packing densities are currently low or for embolizing basilar tip aneurysms where the coil compaction rates are relatively high [3,14].

Practically, however, there remain two concerns with this structure. First, the pitch of the helices is assumed to be tight so that the entire inner surface is covered. This arrangement would reduce X-ray visibility with each successive coil deposited. However, a material such as Nitinol has much lower radio-opacity as compared to platinum; these coils could be made with Nitinol (or a polymer or some low to negligible X-ray opacity material) and be marked with platinum bands for ease of complete aneurysm embolization. Second, as can be noted in Table 1, the lengths of the individual coils are high with this configuration. If an aneurysm has a volume of 500 mm³ and it is theoretically filled to 100% with a single coil of diameter 300 microns, the length of this coil would be more than 7 meters (π×0.15²×length=500). To achieve higher packing densities, therefore, larger coil lengths have to be deposited within the aneurysm. The first and longest spherical helix that fills the basilar aneurysm in our simulations is close to 1 meter long. It would be practically difficult to stabilize a coil of such length on the table before insertion into the microcatheter and to manually feed it through; longer lengths also imply higher friction within the microcatheter. However, these technical difficulties could probably be overcome given the benefit of high packing densities. The coils could be sectioned into smaller lengths and deployed piece-wise and/or a spool mechanism on the table could feed the coils mechanically into the microcatheter.

Conclusions

There seems to be no theoretical basis for medical device companies choosing the coil configurations currently being manufactured. Although three-dimensional and complex-shaped coils have been produced in order to improve the packing density of aneurysms, the fact that less than half the aneurysm volume can be filled with these coils can only be explained by their more-or-less random distribution within the aneurysm. Our simulations suggest that geometrically ordered coil configurations can provide much higher packing densities than can be achieved with the best of currently available coils. The spherical helix configuration was especially seen to be an effective method of such concentric embolization of aneurysms. Technical hurdles remain with this configuration, but the benefit-to-cost ratio in implementing aneurysm packing of twice the current densities seems high.