Abstract
Instability after slip onset is a key precursor leading to subsequent falls during gait. The purpose of this study was to determine the impact of reactive muscular response from individual lower limb joints on regaining stability control and impeding a novel, unannounced slip during the ensuing single-stance phase. Ten young adults’ resultant moments at three lower limb joints of both limbs, initially derived by an inverse-dynamics approach from empirical data, were optimized to accurately reproduce the original motion before being applied as input to the control variables of their individualized forward-dynamics model. Systematic alteration of the moments of each joint caused corresponding changes in the displacement and velocity of the center of mass (COM) and base of support (BOS) (i.e., their state variables, xCOM, ẋCOM, xBOS, ẋBOS), and in the COM stability. The model simulation revealed that these joints had little influence on ẋCOM, but had substantial impact on ẋBOS reduction, leading to improving the COM stability, mostly from knee flexors, followed by hip extensors, of the slipping limb. Per unit reactive increase in normalized knee flexor or hip extensor moments and per unit reactive reduction in commonly observed plantar-flexor moments could lead to as much as 57.72 ± 10.46 or 22.33 ± 5.55 and 13.09 ± 2.27 units of reduction in normalized ẋBOS, respectively. In contrast, such influence was negligible from the swing limb during this period, irrespective of individual variability.
Keywords: inverse-dynamics, forward-dynamics, joint moments, simulation, optimization, motor control, balance loss, fall prevention
INTRODUCTION
Falls are a major cause of injury and even death in adults 65 years or older. In the United States, over 1.85 million older adults were treated in the emergency room for fall-related injuries in 2004 (Bieryla et al., 2007). Slip-related falls account for about 25% of all falls among older adults (Holbrook, 1984), and frequently cause hip fracture that can have devastating consequences (Kannus et al., 1999). A better understanding of the mechanisms underlying the control of stability during slip-related falls will undoubtedly be an important step towards the prevention of such injuries and reduction of the cost resulted from the slip-related falls.
One of the fall prevention approaches may rely on the adaptive improvements of an individual’s control in dynamic stability following the onset of perturbation (Pai, 2003; Pai and Bhatt, 2007). The center of mass (COM) stability, which can be measured by the shortest distance from the relative motion states (i.e. the instantaneous displacement and its velocity) between the COM and its base of support (BOS) to the dynamic stability limits (Yang et al., 2008b), plays an important role in recovery from a forward slip (Bhatt et al., 2006; Pai, 2003; Pavol and Pai, 2007; You et al., 2001). Four state variables, i.e. the displacement of COM and BOS (xCOM and xBOS) and their corresponding velocity (ẋCOM and ẋBOS), therefore directly dictate the stability during a slip. Empirical evidence indicates that the velocity of the slipping foot (i.e. ẋBOS) is a key factor affecting the recovery outcome following a slip (Bhatt et al., 2006; Cham and Redfern, 2002; Lockhart et al., 2003; Strandberg and Lanshammar, 1981). Yet, the relationship of these four state variables and the COM stability has not been systemically analyzed.
It has been demonstrated that adaptive control of stability can improve the slip recovery outcome to such an extent that successful feedforward control can alleviate or even completely eliminate the need for reactive correction after the onset of a slip (Bhatt et al., 2006; Pai et al., 2000, 1998, 2003). Conversely, following a novel, unannounced slip induced in gait, the COM stability deteriorates rapidly and severely. Such deterioration continues after slip onset during the first ~180 ms of double-stance and during the subsequent ~100 ms single-stance phase, in which only the slipping foot provides the BOS. Little is known how the COM stability is controlled during this crucial period.
The resultant joint moments, especially those from the lower limbs, are responsible for the control of locomotion (Winter, 1980), and they result directly from muscle activation that is governed by a descending motor program initiated from and modulated by various motor centers of the central nervous system. Through comparing the results of slipping trials and those of regular walking trials derived from an inverse-dynamics approach, it has been postulated that increased knee flexor and hip extensor moments at stance limb might be two primary reactive responses required to stabilize human body and to avoid a slip-related fall in gait (Cham and Redfern, 2001). Such comparisons do not in itself reveal the direct causal effect.
A combination of inverse-dynamics analysis and analytical manipulation of a forward-dynamics model to simulate an individual’s performance may reveal the mechanistic underpinning the COM stability control. By systematically altering the joint moments, one at a time while keeping initial motion state of body segments and the other joint moments constant during a forward-dynamics simulation, the exclusive causal relationship between each individual joint moment and stability control may be quantitatively evaluated. Nonetheless, this will lead to a classic paradox here. Namely, the joint moments derived from an inverse-dynamics approach often cannot reproduce original motion when applied as an input to a forward-dynamics model, presumably resulting from error inherent to kinematic and ground reaction force (GRF) data collection (Kuo, 1998). Recent attempts have been taken to reduce this kind of inherent error in the joint moments (Kuo, 1998; Neptune et al., 2001). Such approach is yet to apply to explore causal relationship between the joint moments and the reactive control of the COM stability.
The purpose of this study was to determine the impact of reactive muscular response from individual lower limb joints on regaining stability and impeding a novel and unannounced slip during the ensuing single-stance phase. This objective was achieved by systematically altering the optimally-matched lower joint moments in a forward-dynamics simulation based on personalized individual human models and their actual recorded performance during single-stance phase.
METHODS
The data of ten young adults were randomly selected from an existing database collected during their first encounter of a novel, unannounced slip while walking (Bhatt and Pai, 2009; Bhatt et al., 2006). The mean ± SD body height and mass were 169.4 ±7.0 cm and 64.7 ±15.5 kg, respectively. All subjects have given written informed consent to the experimental protocol approved by the Institutional Review Board. Every one took at least 10 unperturbed walking trials at their self-selected speed in which a passively movable platform was locked and mounted on a low-friction linear bearing on a supporting frame (Yang and Pai, 2007), while they were only told that a slip would be possible (Bhatt et al., 2006). No information was given as to where, when, and how a slip would occur when this slip was actually induced with the release of this platform that was camouflaged by similar decoy structures. In response to this novel and unannounced slip, all subjects experienced backward balance loss by taking a recovery step that landed posterior to the slipping foot. Full body kinematic and kinetic (i.e., GRF) data were collected for this trial (Bhatt et al., 2006), and were included in the following two stages of the present study.
The objective of the first stage was to develop individual human models (Fig. 1) and to derive the resultant joint moments, τ, of the lower limb, first with inverse-dynamics formulation, and then with simulated annealing optimization routine. The resultant joint moments were normalized by the product of the body mass, bm, the gravitational acceleration, g, and the body height, bh. These optimally-matched moments could best replicate, or best fit, each subject’s measured body kinematics and kinetics during gait-slip experiments (Yang and Pai, 2009). Due to the perturbation induced upon the slip trials which alters the kinematics and kinetics of the body segments, the optimally-matched moments differ from the joint moments during regular walking trials (Schwartz et al., 2008). Such differences have been also found by other studies (Cham and Redfern, 2001; Ferber et al., 2002). The objective of the second stage was to apply this individualized model to explore the relationship of these joint moments with these four state variables and with the COM stability. Specifically, with input from experimentally derived initial segment motion state at left liftoff, the time profile of the optimally-matched moment during single-stance phase served as the control variables of forward-dynamics model for this individual subject. The control variables were altered systematically, one joint at a time, by adding or subtracting a fixed increment of 10−4 (bm×g×bh) from their optimally-matched moments throughout the single-stance phase (Fig. 2). This process of augmentation would be terminated until the point at which the left foot contacted the ground before the termination of the perturbed simulation, or at which any joint angle from simulation became anatomically unrealistic, i.e., when it begins to exceed one standard deviation beyond average range of motion for this particular joint (Yang and Pai, 2009).
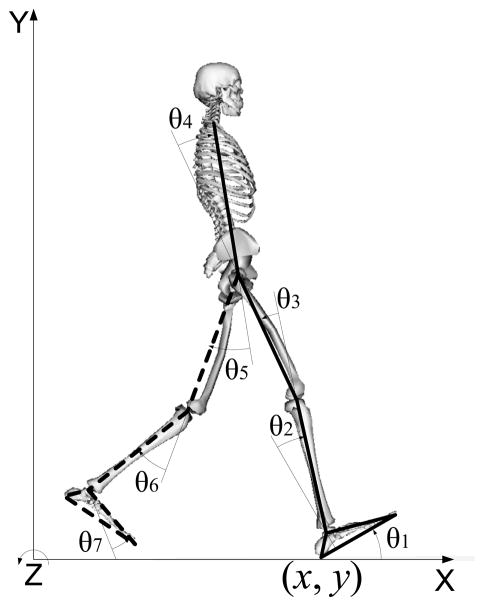
Fig. 1.
Schematic of the 7-link, 9-degree-of-freedom, sagittal-plane model of the human body. The vector q= [x, y, θ1,θ2,…θ7] represents the generalized coordinates of the model. Coordinates x, y, and θ1 specify the position and orientation of the stance (right) foot, which is the base segment of the model following the swing (left) foot liftoff after slip onset, with reference to the inertial reference frame (X, Y, Z). During the single-stance phase, the area under the right foot is the base of support (BOS) of the human model. Joint angles θi (i = 2,3,…,7) correspondingly specify the angles of the ankle, knee, hip of the stance limb (sold line) and the hip, knee, and ankle of the swing limb (dashed line). The segment lengths of an individual model are calculated from the relative distance between pairs of joint centers measured for that individual subject. The location of the center of mass for each segment as well as its moment of inertia are estimated based on the subject’s body mass and the measured segment length (de Leva, 1996). The positive X-axis is in the direction of forward progression, and the positive Y-axis is upward. Positive joint rotation is along the positive Z-axis (counterclockwise) for the stance limb (solid line), and its sign is reversed (clockwise) for the swing limb (dashed line).
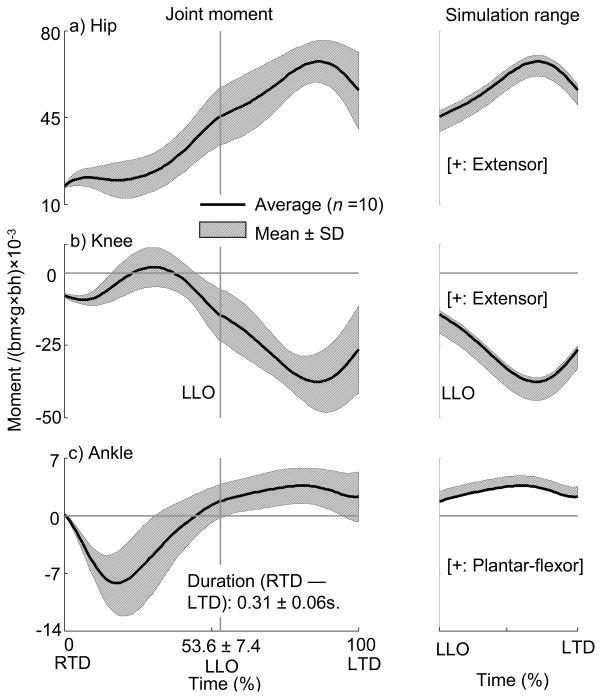
Fig. 2.
Left column: group mean (thick line, n = 10) ± SD (shaded area) profile of optimally-matched joint moments (τ, normalized by the product of the body mass, bm, the gravitational acceleration, g, and the body height, bh) from stance (right) foot touchdown (RTD) to left (swing) foot touchdown (LTD) for (a) stance hip, (b) stance knee, and (c) stance ankle. Hip extensor and knee flexor moments and ankle plantar-flexor moments were found to be the dominant moments that occurred in the stance limb for > 90% of single-stance phase in all subjects. Right column: the averaged simulation range (shaded area) during the single-stance from left liftoff (LLO) to LTD. The joint moments were systematically altered in forward-dynamics simulation by adding to or subtracting a fixed increment of 10−4(bm×g×bh) from each of these 10 subjects’ joint moment profiles. This process of augmentation would be iterated until the point at which the left foot contacted the ground before the termination of the perturbed simulation, or at which any joint angle from simulation became anatomically unrealistic, i.e., when it begins to exceed one standard deviation beyond the average range of motion for this particular joint. It is possible for one subject’s simulation range to be substantially different from the others.
For each alteration in τ, we determined its effect by computing the changes in four state variables (i.e. xCOM, ẋCOM, xBOS, ẋBOS) and in the COM stability (s) at the end of the single-stance phase. Both xCOM and xBOS were normalized to foot length, lBOS; while ẋCOM and ẋBOS were normalized to . Using these ten subjects, the ratios of the leg length and lBOS to bh are respectively 51.58 ± 1.19% (R2 = 0.82, p < 0.001) and 17.43 ± 0.33% (R2 = 0.81, p < 0.001), respectively. As aforementioned, the instantaneous measurement of s was calculated as the shortest distance from the relative COM motion state (i.e. xCOM/BOS and ẋCOM/BOS) to the threshold against backward balance loss under slip condition in gait (Yang et al., 2008a). The model simulation in this previous study predicts that, based on anatomical and physiological limitations and environmental constraints, a backward balance loss must occur when the COM state is located below the threshold (s < 0). Greater stability above the threshold (s ≥ 0) means that a person will less likely experience backward balance loss, because the forward COM momentum is sufficient to prevent that from happening (Pai et al., 2003).
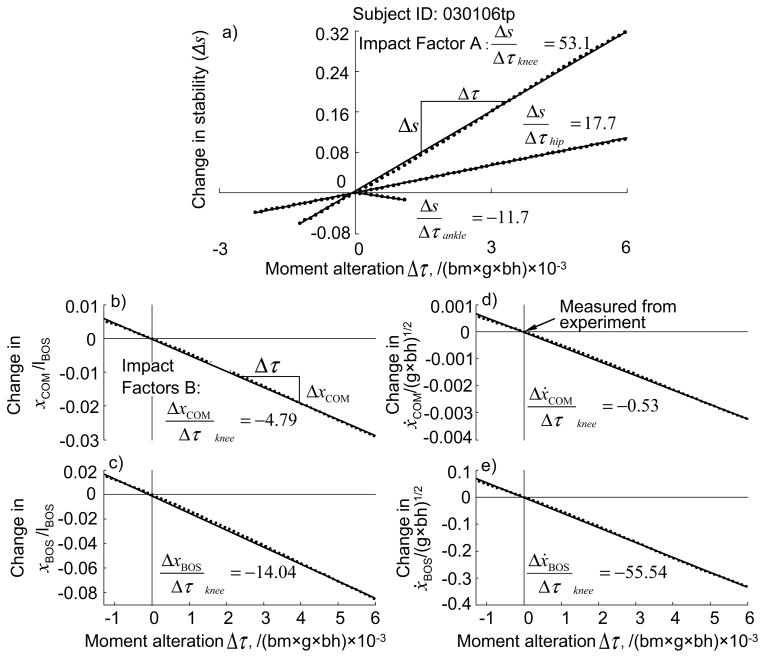
Because we were able to keep everything else in the model unchanged during each simulation, the computed changes in four state variables and in s must result exclusively and directly from the corresponding alterations in τ (Fig. 3 and the mechanistic relationship later illustrated in Fig 7). Linearity of such relationship was examined across the simulation range at each joint (Goldberg et al., 2004). If the linear relationship does exist, the impact of the changes in τ on these variables can be characterized by its constant slope rather than a more complex variable slope associated with a non-linear relationship. The ratios of moment alterations and the resulting changes in four state variables as well as in the COM stability would enable us to determine the exclusive impact of an individual lower limb joint on the COM stability (which is termed as Impact Factor A) and on these four state variables (which are termed as Impact Factors B hereafter).
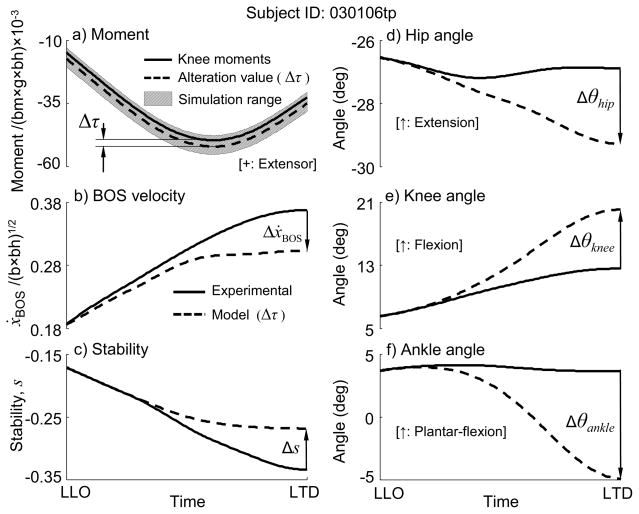
Fig. 3.
One sample of an individual subject’s simulation results showing how the alteration by subtracting 2.6 × 10−3 (bm×g×bh) (dashed line) from the corresponding optimally-matched value (solid line) in (a) knee moments of the stance (right) limb profile leads to changes in (b) the velocity of the base of support (BOS), ΔẋBOS, (c) the center of mass (COM) stability, Δs, (d) the stance hip angle, (e) the stance knee angle, and (f) the stance ankle angle. Here, bm is the body mass, g represents the gravitational acceleration, and bh the body height. The single-stance phase starts from swing (left) foot liftoff (LLO) to its touchdown (LTD). Also shown is the entire simulation range (the shade region) for this subject. The COM stability is determined as the shortest distance from the threshold to the COM state. The COM anterior position and forward velocity are expressed relative to the slipping heel. Positions and velocities of COM are normalized to foot length and , respectively. Flexion increases the knee angle but reduces the hip angle, whereas dorsiflexion reduces the ankle angle. An increase in the stance knee flexor moments in this case causes the hip and knee to flex and the ankle to dorsiflex at stance limb, which jointly lead to a reduction in ẋBOS and an increase in COM stability.
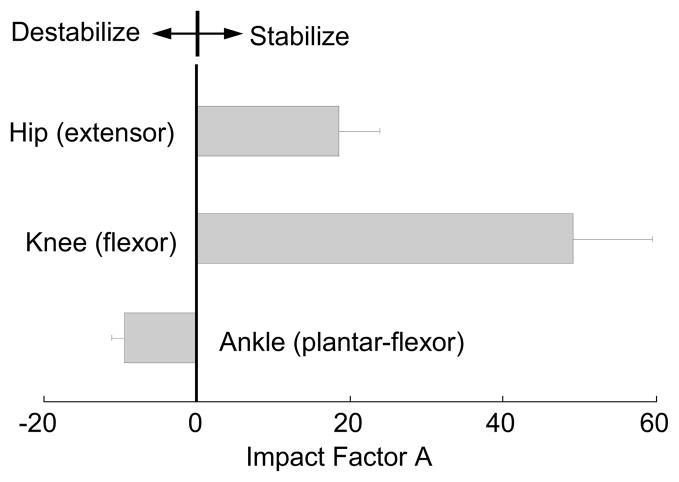
Fig. 7.
The mean (length of the bar) and standard deviation (the error bar, n = 10) of the Impact Factor A, which is the change in the stability (Δs) caused by a per unit increment in the hip extensor, knee flexor, and ankle plantar-flexor moments of the stance limb (Δτ, one bm×g×bh Nm, bm represents the body mass, g indicates the gravitational acceleration, and bh the body height), and is measured by the slope of the line best fitting the simulation results as shown in Fig 4.
These impact factors of 10 subjects were then applied as dependent variables in one-way analyses of variance to determine different functions in the control of stability served by the joints (with hip, knee, and ankle joints as independent variables) and by the limbs (with stance and swing limbs as independent variables). Post hoc analyses employed t-test with a Bonferroni correction. Analyses were performed using SPSS 15.0 (Chicago, IL). A significance level of 0.05 was used for all analyses.
RESULTS
The changes in the resultant joint moments led to changes in the motion of their residing joint and other joints (Fig. 3) and led to proportional changes in state variables in a near-perfect linear relationship with correlation coefficient R2 > 0.99, whereby their slopes (i.e., the Impact Factors B listed in Table 1) remained constant throughout the simulation range (Fig. 4b–e) and throughout all joints. Similar relationship existed between the joint moments and the COM stability, where the Impact Factor A was also a constant (Fig. 4a). The joints of the stance limb had significantly greater impact than those of the swing limb in controlling the BOS velocity and the COM stability (Table 1). For instance, the average impact factor of stance knee on the BOS velocity was 48.9 times great than that of its counterpart of the swing limb (Table 1). Moreover, the average impact factor of the ankle joint on the BOS velocity, which was the smallest among the joints of stance limb, was still 3.6 times greater than that of the swing hip, which was the greatest among the joints of swing limb (Table 1). Therefore, the rest of this text would be focused primarily on the stance limb.
Table 1.
Mean (SD, n =10) of the impact of each lower limb joint moment on the COM stability s (Impact Factor A), and the state variables (Impact Factors B): center of mass (COM) position, xCOM; its velocity, ẋCOM; base of support (BOS) position xBOS, and its velocity, ẋBOS. The impact factor is measured by the change at the end of the single-stance phase in these variables (ΔxCOM and ΔxBOS normalized by foot length, lBOS, ΔẋCOM and ΔẋBOS normalized by , where g is the gravitational acceleration and bh the body height; and Δs dimensionless) caused by one unit increment in joint moments (i.e., when Δτ = 1bm×g×bh Nm, bm represents the body mass) or by the slope of the simulated results for these relationship depicted in Fig 4, which had a near-perfect linear fit across the simulation range (R2 > 0.99). Positive slope means a unit of increase in these dominant moments will bring an increase in the state variables or in the COM stability, and vice versa for a negative slope. Hip extensor, knee flexor, and ankle plantar-flexor moments were found to be the dominant moments that occurred in stance limb for > 90% of single-stance phase in all subjects, meanwhile the swing limb was dominated by hip flexor and knee extensor moments and ankle dorsiflexor moments (Fig 2).
| Joints | Sides | Impact Factor A | Impact Factors B | |||||
|---|---|---|---|---|---|---|---|---|
| s | xCOM/lBOS | xBOS/lBOS | ||||||
| Hip | Stance (Extensor)a | 18.57 (6.08)b | −1.08 (1.54) | −0.14 (0.25) | −4.98 (4.72)b | −22.33 (5.55)b | ||
| Swing (Flexor) | 3.29 (0.81)b | −0.26 (0.41)b | −0.02 (0.07)b | −0.98 (0.92)b | −3.69 (1.46)b | |||
| Knee | Stance (Flexor)a | 49.12 (9.85)b | −3.13 (5.64)b | −0.53 (0.73)b | −18.57 (7.75)b | −57.72 (10.46)b | ||
| Swing (Extensor) | −0.99 (0.66) | 0.10 (0.10) | 0.01 (0.02) | 0.36 (0.21)b | 1.18 (0.41)b | |||
| Ankle | Stance (Plantar-flexor)a | −9.36 (1.97)b | 0.62 (2.67) | 0.10 (0.06) | 2.10 (1.03)b | 13.09(2.27)b | ||
| Swing (Dorsiflexor) | −0.33 (0.16) | 0.005 (0.05) | 0.004 (0.004) | 0.10 (0.09)b | 0.41 (0.24)b | |||
p < 0.001 vs. swing limb;
p < 0.001 vs. the other two joints on the same side.
Fig. 4.
(a) Derivation of Impact Factor A of the stance knee flexor and hip extensor, and right ankle plantar-flexor for a sample subject (body mass, bm = 54.5kg, body height, bh = 1.64m). During the single-stance phase, the hip extensors, knee flexors, and ankle plantar-flexors produce dominant moments. The Impact Factor A is defined by the change in stability (Δs) measured at the end of the single-stance phase caused by a per unit increment in joint moment (Δτ, one bm×g×bh Nm, g represents the gravitational acceleration), i.e., the slope of the thick line that can best fit the simulation results (where each simulation yields an individual dot here). Also shown is the derivation of the Impact Factors B of stance knee flexor moment for (b) center of mass (COM) position, (c) base of support (BOS) position, (d) COM velocity, and (e) BOS velocity for the same subject during single-stance phase. The Impact Factors B are the change in the variables (displacements of COM, ΔxCOM and BOS, ΔxBOS, normalized by foot length, lBOS; velocities of COM, ΔẋCOM and BOS, ΔẋBOS, normalized to ) due to a per unit increment in joint moment, and is measured by the slope of the thick line that best fits the simulation results.
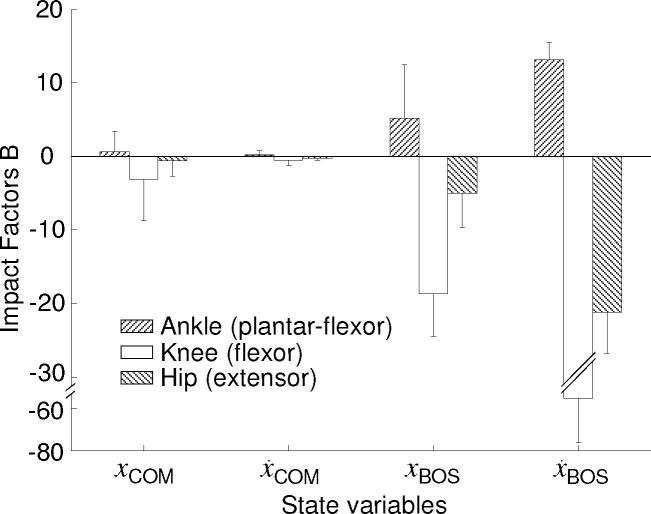
The changes in all three joint moments of the stance limb had the greatest impact on the BOS velocity in comparison with their influences on other three state variables (Fig. 5), regardless whether such influence is to decrease (e.g., by increasing hip extensor or knee flexor moments) or to increase its velocity (e.g., by increasing ankle plantar-flexor moments or by conversely decreasing hip extensor or knee flexor moments). During entire single-stance phase, all subjects, without exception, displayed hip-extensor, knee-flexor, and ankle-plantar-flexor dominancy (i.e., flexor or extensor moments that appeared in longer than 90% of the entire single-stance phase) at the stance limb (Fig. 2). An increase in such dominancy at both hip and knee, but not at ankle, caused a decrease in the BOS velocity (Figs. 4 and 5). An increase of one unit (bm×g×bh Nm) in normalized hip extensor or knee flexor moments led to a reduction in the normalized BOS velocity by as much as 57.72 ± 10.46 or 22.33 ± 5.55, respectively, whereby a decrease of the same moments caused the opposite effect (Fig. 5). An increase of one unit in plantar-flexor moments can cause an increase in the BOS velocity by 13.09 ± 2.27 (Fig. 5).
Fig. 5.
The Impact Factors B of the lower limb joint moments of the stance limb on four state variables at the end of the single-stance phase following slip onset in gait. The state variables consist of the position and velocity of the center of mass (COM, xCOM and ẋCOM) and of the base of support (BOS, xBOS and ẋBOS). The Impact Factors B of a joint moment on state variables are the change in these variables (ΔxCOM, ΔxBOS, normalized by foot length, lBOS; ΔẋCOM, ΔẋBOS, normalized by , where g is the gravitational acceleration and bh the body height) caused by a one unit increment in joint moment (Δτ, one bm×g×bh Nm, bm represents the body mass), and is measured by the slope of the line best fitting the simulation results as shown in Fig 4.
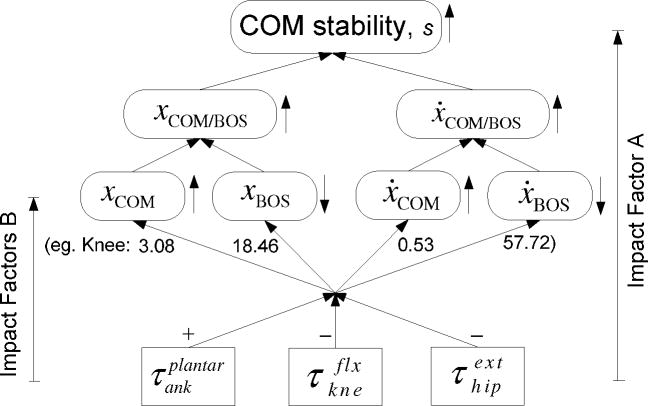
A reduction in the BOS velocity led directly to an increase in the COM stability at the end of the single-stance phase (Figs. 4, 6, and 7). The changes in the stance knee joint moment had the greatest impact on the BOS velocity, and the ankle had the least (Figs. 3 and 5, Table 1). Therefore, the knee also had the greatest impact on the COM stability (Fig. 7, Table 1). Numerically, all three joints’ impact on the BOS velocity was greater than theirs on the COM stability (Table 1), by a uniform ratio of −0.82 ± 0.06 between Impact Factors A and B across these three joints. For instance, the magnitude of Impact Factor B for the knee was 57.72 ± 10.46 on altering the BOS velocity and it was 1.18 ± 0.35 times greater than its magnitude of Impact Factor A on altering the COM stability.
Fig. 6.
Causal diagram shows the change in the joint moments of the stance (right) limb and the resulting change in the center of mass (COM) stability (Δs), each quantified by Impact factor A, and measured at the end of the single-stance phase corresponding to a per unit change in the joint moments during this phase. The solid line indicates the impact of the variable at the tail end of the arrow on the variable at the head of the arrow based on the forward-dynamics formulation. The diagram also shows the impact of these moments on four state variables consisting of the position and velocity of the center of mass (COM, xCOM and ẋCOM) and of the base of support (BOS; xBOS and ẋBOS) as Impact Factors B. An arrow “↑” or “↓” respectively implicate the increment or decrement in these variables and in their composite variables, xCOM/BOS and ẋCOM/BOS, that leads to an increase “↑” in the stability. The sign “+” or “−” indicates that the effort caused by an increase in the optimally-matched moment profile shown in Fig two on the change in these four state variables. For example, “−”indicates that one unit of increase in the knee flexor moments causes a reduction in all these four variables by the amount indicated by the corresponding numbers which were averaged across 10 subjects.
DISCUSSION
Aided by forward-dynamics simulation, the present study was able to elucidate the exclusive causal mechanisms underlying the muscular response generated at individual joints in order to regain the control of the COM stability during the single-stance phase in a person’s reaction to a novel, unannounced slip in gait. An increase in flexor moments at the stance knee, which is consistent with the motor programming in regular, unperturbed gait, characterized by a switch from extensor to flexor moments (Yang and Pai, 2009), would improve the COM stability. This is achieved primarily through the reduction of the velocity of the traveling BOS, rather than directly altering the COM velocity. In contrast, the rapidly rising plantar-flexor moments often observed during this period of regular gait would only be further destabilizing; thus the slip response requires the drastic alteration of the motor programming of regular gait for the reduction of plantar-flexor moments. Similarly, the extensor moments at the stance hip necessary for reducing the BOS velocity are somewhat contrary to the regular switch during the same period from extensor to flexor moments of unperturbed gait. Based on the same per unit change in the resultant joint moments, the knee flexors had the greatest stabilizing effect, followed by the hip extensors. Notably, the swing limb produces only relatively negligible effect on the control of stability during this period, although its effect on improving stability after its landing can still be dominant, potentially overriding preceding advantage of the stance limb during this period.
Based on the empirical design and the comparison of the joint moments between the slip and the regular trials, it was concluded that increased hip extensor and knee flexor moments of the stance limb are two primary reactions in response to a forward slip perturbation in gait (Cham and Redfern, 2001). These findings have now been confirmed. Moreover, the analytical approach can offer at least two distinctive advantages to the elucidation of these mechanisms. First, because our model is individualized, the findings are unaffected by the naturally existing inter-subject variability in their initial motion state, which can profoundly affect the results of the joint moments. Under this pretext, however, the present study has verified that the findings derived from the inverse-dynamic approach are indeed robust and are generalizable in this sample (Figs 5 and 7). Second, this approach can quantify, beyond the capability of the inverse-dynamic approach, their relative impact amongst the joints on the stability control (Figs 5 and 7).
Previously, studies have suggested that the control of COM stability is achieved primarily through the control of the BOS velocity after the onset of a slip induced during walking (Bhatt et al., 2006; Cham and Redfern, 2002; Lockhart et al., 2003; Strandberg and Lanshammar, 1981). Our study was able to verify these observations (Figs 5 and 7). In addition, the current study revealed for the first time that all lower limb joints had relatively little impact on the absolute displacement and velocity of the COM during this single-stance phase (Fig 5). In fact, increases in hip extensors and knee flexors of the stance limb achieve the opposing (destabilizing) effect, by reducing its absolute forward COM displacement and velocity, and therefore reducing overall stability against backward balance loss (Yang et al., 2008a). The potential of the knee flexors to retard COM forward progression during single-stance phase in gait-slip appears to be in agreement with previous findings that knee flexors generate backward COM acceleration during single-stance phase under regular gait by using the induced-acceleration analysis (Kepple et al., 1997).
The concept of the stability control of the COM with respect to the BOS is originally developed by Borelli for static condition (Borelli, 1680) and has recently been extended to dynamic condition (Pai and Patton, 1997). The basic static concept has been widely accepted (Maki and McIlroy, 1996; Nashner, 1987; Winter et al., 1990; Wolfson et al., 1986), and the dynamic stability concept has been verified across a range of different activities, including bimanual pull (Patton et al., 2000; Patton et al., 1999), waist pull (Pai et al., 1998), standing on movable platform (Pai et al., 2000), chair-rise and slip (Pai et al., 2003), and gait (Bhatt and Pai, 2009; Bhatt et al., 2006). The stability limits have very high predictability (~100% accuracy) of backward balance loss when the relative COM motion states reside outside of the feasible stability region (Bhatt et al., 2006; Yang et al., 2008a). Based on this concept, a novel, unannounced slip induced in walking can severely destabilize a person. From liftoff (stability value: −0.22 ± 0.08) to the instant immediately prior to touchdown of the trailing limb (−0.33 ± 0.09), the COM stability deteriorated as much as 0.11 ± 0.08 among 53 subjects as a group (Yang et al., 2009). Of these subjects, the difference in the COM stability was a significant factor at the end of the single-stance phase that differentiates those who fell (−0.45 ± 0.11) and those who recovered (−0.29 ± 0.12). To advance this concept, the present study revealed the mechanisms these people have applied to gain better stability during this crucial period of recovery from a slip.
The present study also showed that the joints of the swing limb had almost negligible effect on stability control during the single-stance phase (Table 1). The effects of the hip, knee, and ankle of the stance limb were 5.64, 49.62, and 28.36 times greater than were their counterpart of the swing limb, respectively. Although the swing limb’s impact was very little, its subsequent contribution at touchdown led to profound improvement in the COM stability (Yang et al., 2009). Instead of taking a forward step, without exception, everyone was able to modify his/her ongoing motor program governing regular gait. As result of the successful execution of protective stepping, the swing limb all landed posterior to the slipping limb in this novel, unannounced slip (Bhatt et al., 2006; Yang et al., 2008a). This success restored the COM stability in these young adults, such that the significant differences in the COM stability between the fallers and those who recovered diminished upon touchdown (Yang et al., 2009). Among the same individuals, the protective stepping could improve the COM stability by an average of 1.22 ± 0.28 (i.e., from −0.33 ± 0.09 at the instant immediately prior to its touchdown to 0.89 ± 0.21 at its touchdown) (Yang et al., 2009). It is unclear whether individuals with musculoskeletal or neuromuscular impairment can achieve similar success in their protective stepping.
The present study has several limitations. First, the human model and simulation were confined in the sagittal plane, and the pelvic rotation was all eliminated. The extent to which motion in the sagittal plane may interact with that in the mediolateral direction is unclear and so is the contribution from pelvic rotation. Second, constant value of an alteration was applied uniformly to the optimally-matched moment-time history during single-stance phase. Such simplification neglects the possibilities of other forms of changes in joint moments. Further, simulation in the present study focused on manipulating one joint at a time, whereby the coordinated changes among all the lower limb joints were ignored. While the present analysis is essential to the identification of each primary muscle group’s exclusive role on each joint (Fig. 3), it shed little light on the interactive influence from concerted inter-joint muscular coordination. This limitation can be address in future when the computing power can be expanded so effectively to overcome the enormous computational demand.
Finally, the findings may be altered with repeated exposure to slips and ensuing adaptation. Perceivably, in comparison with this novel experience, the knee or hip moment profile could become similar to that of regular walking as individuals become adapted due to the proactively improved COM stability before slip onset (Bhatt et al., 2006). Such proactive control improves the COM stability with feedforward control, and is often achieved by anteriorly shifting the COM relative to the BOS with flat foot and augmented knee angle at the landing. The adjustments are often sufficient to avoid a backward balance loss, despite the forward slip of the stance limb observed among individuals who employed the “skate-over” strategy (Bhatt et al., 2006). The corrective (reactive) control of lower limb joint moments could then become unnecessary or inconsequential. This hypothesis is still to be verified.
In summary, the study has demonstrated how forward-dynamics simulation can be applied to determine the function of each lower limb joint in regaining stability after the onset of a novel, unannounced forward slip induced in gait. The results have revealed the basic causal relationships between the control of joint moments and resulting stability against slip-related backward balance loss. Because the control of COM stability is an essential component of recovery response, the current approach can provide analytical understanding for a successful fall prevention strategies (Pai and Bhatt, 2007).
Acknowledgments
This work was funded by NIH 2R01-AG16727. The authors thank Dr. Frank C. Anderson for his software platform and consultation applied for model construction.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bhatt T, Pai YC. Immediate and latent interlimb transfer of gait stability adaptation following repeated exposure to slips. Journal of Motor Behavior. 2009;40:380–390. doi: 10.3200/JMBR.40.5.380-390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhatt T, Wang E, Pai YC. Retention of adaptive control over varying intervals: prevention of slip- induced backward balance loss during gait. Journal of Neurophysiology. 2006;95:2913–2922. doi: 10.1152/jn.01211.2005. [DOI] [PubMed] [Google Scholar]
- Bieryla KA, Madigan ML, Nussbaum MA. Practicing recovery from a simulated trip improves recovery kinematics after an actual trip. Gait and Posture. 2007;26:208–213. doi: 10.1016/j.gaitpost.2006.09.010. [DOI] [PubMed] [Google Scholar]
- Borelli GA. De Motu Animalium. Berlin, New York: Springer-Verlag; 1680. (Translated by Maquet, P., 1989) [Google Scholar]
- Cham R, Redfern MS. Lower extremity corrective reactions to slip events. Journal of Biomechanics. 2001;34:1439–1445. doi: 10.1016/s0021-9290(01)00116-6. [DOI] [PubMed] [Google Scholar]
- Cham R, Redfern MS. Heel contact dynamics during slip events on level and inclined surfaces. Safety Science. 2002;40:559–576. [Google Scholar]
- de Leva P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. Journal of Biomechanics. 1996;29:1223–1230. doi: 10.1016/0021-9290(95)00178-6. [DOI] [PubMed] [Google Scholar]
- Ferber R, Osternig LR, Woollacott MH, Wasielewski NJ, Lee J-H. Reactive balance adjustments to unexpected perturbations during human walking. Gait and Posture. 2002;16:238–248. doi: 10.1016/s0966-6362(02)00010-3. [DOI] [PubMed] [Google Scholar]
- Goldberg SR, Anderson FC, Pandy MG, Delp SL. Muscles that influence knee flexion velocity in double support: implications for stiff-knee gait. Journal of Biomechanics. 2004;37:1189–1196. doi: 10.1016/j.jbiomech.2003.12.005. [DOI] [PubMed] [Google Scholar]
- Holbrook TL. The frequency of occurrence, impact and cost of musculoskeletal conditions in the United States. American Academy of Orthopedic Surgeons 1984 [Google Scholar]
- Kannus P, Parkkari J, Koskinen S, Niemi S, Palvanen M, Jarvinen M, Vuori I. Fall-induced injuries and deaths among older adults. The Journal of the American Medical Association. 1999;281:1895–1899. doi: 10.1001/jama.281.20.1895. [DOI] [PubMed] [Google Scholar]
- Kepple TM, Siegel KL, Stanhope SJ. Relative contributions of the lower extremity joint moments to forward progression and support during gait. Gait and Posture. 1997;6:1–8. [Google Scholar]
- Kuo AD. A least-squares estimation approach to improving the precision of inverse dynamics computations. Journal of Biomechanical Engineering. 1998;125:864–874. doi: 10.1115/1.2834295. [DOI] [PubMed] [Google Scholar]
- Lockhart TE, Woldstad JC, Smith JL. Effects of age-related gait changes on the biomechanics of slips and falls. Ergonomics. 2003;46:1136–1160. doi: 10.1080/0014013031000139491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maki BE, McIlroy WE. Postural control in the older adult. Clinics in Geriatric Medicine. 1996;12:635–658. [PubMed] [Google Scholar]
- Nashner L. A systems approach to understanding and assessing orientation and balance. NeuroCom International; Clackamas, OR: 1987. [Google Scholar]
- Neptune RR, Kautz SA, Zajac FE. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. Journal of Biomechanics. 2001;34:1387–1398. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
- Pai YC. Movement termination and stability in standing. Exercise and Sport Sciences Reviews. 2003;31:19–25. doi: 10.1097/00003677-200301000-00005. [DOI] [PubMed] [Google Scholar]
- Pai YC, Bhatt T. Repeated slip training: An emerging paradigm for prevention of slip-related falls in older adults. Physical Therapy. 2007;87:1478–1491. doi: 10.2522/ptj.20060326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pai YC, Maki BE, Iqbal K, McIlroy WE, Perry SD. Thresholds for step initiation induced by support-surface translation: a dynamic center-of-mass model provides much better prediction than a static model. Journal of Biomechanics. 2000;33:387–392. doi: 10.1016/s0021-9290(99)00199-2. [DOI] [PubMed] [Google Scholar]
- Pai YC, Patton J. Center of mass velocity-position predictions for balance control. Journal of Biomechanics. 1997;30:347–354. doi: 10.1016/s0021-9290(96)00165-0. [DOI] [PubMed] [Google Scholar]
- Pai YC, Rogers MW, Patton J, Cain TD, Hanke TA. Static versus dynamic predictions of protective stepping following waist-pull perturbations in young and older adults. Journal of Biomechancis. 1998;30:347–354. doi: 10.1016/s0021-9290(98)00124-9. [DOI] [PubMed] [Google Scholar]
- Pai YC, Wening JD, Runtz EF, Iqbal K, Pavol MJ. Role of feedforward control of movement stability in reducing slip-related balance loss and falls among older adults. Journal of Neurophysiology. 2003;90:755–762. doi: 10.1152/jn.01118.2002. [DOI] [PubMed] [Google Scholar]
- Patton JL, Lee WA, Pai YC. Relative stability improves with experience in a dynamic standing task. Experimental Brain Research. 2000;135:117–126. doi: 10.1007/s002210000500. [DOI] [PubMed] [Google Scholar]
- Patton JL, Pai YC, Lee WA. Evaluation of a model that determines the stability limits of dynamic balance. Gait and Posture. 1999;9:38–49. doi: 10.1016/s0966-6362(98)00037-x. [DOI] [PubMed] [Google Scholar]
- Pavol MJ, Pai YC. Deficient limb support is a major contributor to age differences in falling. Journal of Biomechanics. 2007;40:1318–1325. doi: 10.1016/j.jbiomech.2006.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz MH, Rozumalski A, Trost JP. The effect of walking speed on the gait of typically developing children. Journal of Biomechanics. 2008;41:1639–1650. doi: 10.1016/j.jbiomech.2008.03.015. [DOI] [PubMed] [Google Scholar]
- Strandberg L, Lanshammar H. The dynamics of slipping accidents. Journal of Occupational Accidents. 1981;3:153–162. [Google Scholar]
- Winter DA. Overall principle of lower limb support during stance phase of gait. Journal of Biomechanics. 1980;13:923–927. doi: 10.1016/0021-9290(80)90162-1. [DOI] [PubMed] [Google Scholar]
- Winter DA, Patla AE, Frank JS. Assessment of balance control in humans. Medical Progress Through Technology. 1990;16(1–2):31–51. [PubMed] [Google Scholar]
- Wolfson LI, Whipple R, Amerman P, Kleinberg A. Stressing the postural response: A quantitative method for testing balance. Journal of the American Geriatrics Society. 1986;34:845–850. doi: 10.1111/j.1532-5415.1986.tb07256.x. [DOI] [PubMed] [Google Scholar]
- Yang F, Anderson FC, Pai YC. Predicted threshold against backward balance loss following a slip in gait. Journal of Biomechanics. 2008a;41:1823–1831. doi: 10.1016/j.jbiomech.2008.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F, Bhatt T, Pai YC. Role of stability and limb support in recovery against a fall following a novel slip induced in different daily activities. Journal of Biomechanics. 2009;42:1903–1908. doi: 10.1016/j.jbiomech.2009.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F, Pai YC. Correction of the inertial effect resulting from a plate moving under low-friction conditions. Journal of Biomechanics. 2007;40:2723–2730. doi: 10.1016/j.jbiomech.2006.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F, Pai Y-C. Understanding recovery from a novel slip in gait: Inverse and forward- dynamic modeling. Annals of Biomedical Engineering. 2009 (under review) [Google Scholar]
- Yang F, Passariello F, Pai YC. Determination of instantaneous stability against backward balance loss: Two computational approaches. Journal of Biomechanics. 2008b;41:1818–1822. doi: 10.1016/j.jbiomech.2008.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You J, Chou Y, Lin C, Su F. Effect of slip on movement of body center of mass relative to base of support. Clinical Biomechanics. 2001;16:167–173. doi: 10.1016/s0268-0033(00)00076-0. [DOI] [PubMed] [Google Scholar]