Abstract
Previously we introduced an automated high-dimensional non-linear registration framework, CVS, that combines volumetric and surface-based alignment to achieve robust and accurate correspondence in both cortical and sub-cortical regions [[28]]. In this paper we show that using CVS to compute cross-subject alignment from anatomical images, then applying the previously computed alignment to diffusion weighted MRI images, outperforms state-of-the-art techniques for computing cross-subject alignment directly from the DWI data itself. Specifically, we show that CVS outperforms the alignment component of TBSS in terms of degree-of-alignment of manually labeled tract models for the uncinate fasciculus, the inferior longitudinal fasciculus and the corticospinal tract. In addition, we compare linear alignment using FLIRT based on either fractional anisotropy or anatomical volumes across-subjects, and find a comparable effect. Together these results imply a clear advantage to aligning anatomy as opposed to lower resolution DWI data even when the final goal is diffusion analysis.
Keywords: tractography alignment, volumetric registration, diffusion imaging
1. Introduction
The analysis of diffusion weighted MRI (DWI) data has become increasingly important in neuroimaging. DWI images contain information about the anatomy essential for quantifying white matter architecture and connectivity patterns. DWI images reveal details about the connectional and microstructural anatomy of the living human brain that are inaccessible to any other in vivo imaging modality. Diffusion tensor images (DTI), in particular, describe the local diffusion process or the 3D probability profile of water diffusion in tissue using a 3×3 symmetric positive definite matrix at each voxel.
The analysis of white matter integrity in brain development, aging, and neurological conditions is a relatively new and active area of neuroscientific and clinical research [[20]]. One approach to quantifying white matter anatomy with DWI data is to compute scalar summaries of the diffusion weighted images such as fractional anisotropy (FA), trace, and apparent diffusion coefficient (ADC). A more complex alternative is to examine reconstructed fiber tractography, which reveals systems-level information not directly contained in the voxel measures [[6]].
Tract-based analysis of populations allows one to quantify the effects of natural and disease processes using a rich set of information, including diffusion values along the tracts, integrity of the fiber bundles, as well as shape and deformation quantification of tract geometry [[7,22,25]]. One of the most frequently cited group analysis streams in neuroimaging is tract-based spatial statistics (TBSS) [[32]] available as part of the FSL software suite from the FMRIB group at Oxford. This analysis pipeline projects the FA data from all subjects onto a mean FA tract skeleton, before applying voxel-wise cross-subject statistics.
For group studies and for labeling the anatomy of an individual subject it is frequently important to establish inter-subject correspondence, either directly or through a common coordinate system. Since structural MRI images such as T1- and T2-weighted acquisitions contain little information about the interior of the cerebral white matter, it is reasonable to base cross-subject alignment in these regions on properties of the DWI data, either directly or indirectly. As an example of the former, several algorithms have been introduced that make use of information directly derived from the DTI images. One way to define such a framework is to extract scalar-valued summaries from the DTI tensors at each voxel (trace, fractional anisotropy,…) and define a similarity metric on these quantities. Guimond et al. suggested a modified version of the demon’s algorithm for aligning T2 and DTI datasets by using transformation-invariant tensor characteristics (eigenvalues) extracted from the diffusion tensors [[16]]. Alexander et al. build upon a more complete set of diffusion information and their alignment of structural and DTI scans is proposed via an elastic matching algorithm using the tensor difference as a similarity metric [[1]]. Ruiz-Alzola et al. proposed a template matching algorithm, where a similarity function derived from the generalized correlation matrix is computed directly from the diffusion tensors [[30]]. The inclusion of information beyond the scalar metrics has also been shown to be advantageous in some studies. For example Park et al. found that considering all six components of the diffusion tensors resulted in improved alignment accuracy [[26]]. In the TBSS framework, the spatial alignment of the input data is based on computing an affine and nonlinear warp combination to align the fractional anisotropy volume of each subject with an atlas coordinate system. Another approach is to use the reconstructed fiber tracts themselves as a basis of spatial normalization. Objective functions can be constructed that ensure that the size, shape and spatial location of white matter fiber tracts from different individuals are in corresponding locations [[36,23,27,37]]. Even though in the case of these approaches correspondence between subjects is established based upon (some portion of) the diffusion data and thus more information about the white matter is considered, the lower spatial resolution, contrast-to-noise ratio (CNR) and geometric distortions of diffusion images often limit the accuracy and robustness of the outcomes.
In indirect registration approaches, structural acquisitions such as T1- and T2-weighted scans of corresponding subjects are used to compute image correspondence. As DWI acquisitions are typically acquired in the same session as the structural images, the alignment of structural and DTI images of the same subject usually involves just rigid or linear motion correction (as long as a separate EPI distortion correction precedes this registration in the diffusion image preprocessing pipeline). The composition of these registrations then allows one to transform the DWI data into a common coordinate system. As mentioned above, the advantage of these methods is inherently related to the significantly higher spatial resolution, contrast-to-noise ratio and far less geometric distortion of the structural acquisitions. However, these images contain little information about the architecture of the interior of the white matter, and thus the alignment in these regions might be somewhat arbitrary when based only on structural scans. Significant research effort has been devoted to incorporating diffusion derived measurements into nonlinear cross-subject alignment with the goal of improving the alignment of these areas [[26,1,21]]. Recently, various similarity metrics (quantifying the level of similarity of diffusion features at corresponding spatial locations) have been suggested for use in nonlinear cross-subject DWI alignment [[2,3]].
In this paper we evaluate the performance of our combined volume and surface (CVS) algorithm [[28]] for the purposes of fiber bundle alignment and show that high accuracy cross-subject registration based on structural MRI images can provide improved alignment compared to methods directly aligning DWI-derived scalar volumes, such as the widely used FA volumes. In the past, we established that our technique, using structural acquisitions, accurately and robustly aligns both cortical and non-cortical regions of the brain anatomy, and at present we demonstrate that when its results are applied to corresponding diffusion data, it also achieves superior accuracy. For our analysis, we compare the performance of CVS to the FA-FNIRT registration (registration component from the TBSS preprocessing) as well as linear alignment FLIRT [[18]] computed from either the anatomical or the DWI data. We evaluate, both qualitatively and quantitatively, the resulting alignments by analyzing the correspondence of a set of manually labeled fiber bundles. The results demonstrate that there is a clear advantage to aligning the anatomy, when available, as opposed to relying only on the lower resolution, distorted diffusion information, even if the goal of the registration is the analysis of the diffusion properties of the brain.
2. Methods
In this section we introduce our image preprocessing stream and the four image registration methods whose performance we later compare in Sec. 3 and 4. For each registration method we describe the processing steps and the underlying implementation details.
2.1. Data Processing
All the data sets in our experiments were subjected to the following preprocessing steps. The structural MRI acquisitions were analyzed by the FreeSurfer reconstruction pipeline [[15]] that produces intensity normalized T1-weighted parameter maps, automatic segmentation and parcellation labels, and white and pial surfaces separating the white matter/gray matter and gray matter/CSF regions respectively [[12,8,10,14,11]]. For the diffusion images, the preprocessing of the balanced-echo diffusion data involves motion, B0 and eddy-current correction. First, the individual direction scans are unwarped using the phase-unwrapping and B0 correction algorithms developed and distributed as part of the FMRIB Software Library (FSL) package [[17,19,33]]. Next, each unwarped DW image is registered to the T2-weighted low-b image (i.e. the image with no diffusion encoding).
Note that for the balanced echo sequences the eddy current distortions are small, and in our experience the 12 parameter transforms are sufficient to remove both motion artifacts and residual eddy-current distortions. Finally, the diffusion tensor image and several scalar maps including fractional anisotropy are computed in the preprocessed diffusion domain. The data processing stream for FA-FNIRT is slightly different from the above and is detailed in Sec 2.3.
In addition to the above, a rigid transform is computed that maximizes the mutual information between the T1-weighted anatomical and the unwarped T2-weighted low-b image. This is to establish a correspondence between the structural and diffusion spaces.
2.2. FLIRT
FLIRT is a robust and accurate automated linear (affine) registration tool based around a multi-start, multi-resolution global optimization method [[18]]. It is available as part of the FSL software package and it can be used for inter- and intra-modal registration with 2D or 3D images. In addition, it can be run with a number of different transformation models (degrees of freedom) and it implements a general cost function weighting scheme for all cost functions. In our experiments, we specified the objective function to be correlation ratio and computed a 12 component affine registration matrix. We ran this algorithm on both the T1-weighted structural images and the FA volumes computed from the corresponding diffusion weighted images. Below, we refer to the former framework as FLIRT and the latter as FA-FLIRT.
2.3. FA-FNIRT
Tract-Based Spatial Statistics [[32]] has been the most cited NeuroImage article since its publication1. It describes a framework from the FSL group performing voxel-wise statistical analysis of fractional anisotropy data. In the current paper, the algorithm that we call FA-FNIRT, in fact, refers to the preprocessing steps of this analysis pipeline. After brain extraction (using BET [[31]]), the FA volumes of all subjects are computed and aligned into a common space by using first the affine registration step FLIRT and then the nonlinear registration FNIRT [[4]] [[5]]. The latter registration tool uses a B-splines representation of the registration warp field [[29]] and optimizes the sum of squared differences (SSD) as its objective function. More precisely, after the FA computations, we executed the tbss_1_preproc and tbss_2_reg steps from the TBSS pipeline. For our experiments, we used the default parameter settings of TBSS to process the diffusion images of our dataset and after the warps were computed, we applied them to the manually specified tracts.
Additionally, we also attempted to run the non-linear registration component of this pipeline between the anatomical data for each pair of subjects. FNIRT, however, is not typically run in a subject-to-subject setting; it is optimized for subject-to-template registrations and the corresponding configuration file is not ideal, at present, to achieve high quality subject-to-subject correspondence. Our results (presented below) imply that when such optimized configuration files are developed for generating subject-to-subject registration based on the anatomy, the accuracy of the FA-FNIRT pipeline will be further improved.
2.4. Combined Volumetric and Surface-based Registration
Combined Volumetric and Surface-based Registration is our brain image registration method that maximizes the alignment of both cortical and subcortical structures. It consists of three image processing steps. First, a surface registration algorithm finds correspondences between the input surfaces from two brain scans [[13]] and these correspondences are transformed into a sparse displacement field in Euclidean space. This morph is then diffused into a dense displacement field in the volume using a nonlinear elastic model. Finally, a nonlinear volumetric registration algorithm refines the alignment, bringing subcortical and ventricular structures, which are not near the surfaces used in the first step, into accurate alignment. This technique has been shown to produce state-of-the-art alignment of cortical folding patterns, architectonics and subcortical structures [[28]]. In the present paper, we quantify how well it aligns white matter fiber tracts computed from DWI data.
3. Experiments
We compared the registration accuracy of our registration tool with respect to three other literature standards. We experimented with FLIRT on both structural and diffusion images, FA-FNIRT, and CVS. We then computed the symmetric mean Hausdorff distance between a set of manually selected fiber bundles morphed into the common coordinate spaces.
In this section, we detail our data processing stream and present how the manually identified fiber bundles, that are later used for our quantitative analysis of registration performance, are extracted from the diffusion weighted images using both automatically and manually specified ROIs.
3.1. Data Acquisitions Protocol
Our experiments were run on data provided to us through our collaboration with Dr. Randy Gollub and the Mental Illness and Neuroscience Discovery (MIND) Institute. Fifty-three data sets were selected for this study all of which have been acquired by our collaborators using an identical MRI sequence on a Siemens scanner. The structural data is of 256×256×256 size with 1 mm3 voxel resolution and TR =12ms, TE=4.76ms, TI=4.76ms, flip angle=20. The diffusion data scans use single shot echo planar imaging, and a twice-refocused spin echo pulse sequence, optimized to minimize eddy current-induced image distortions (TR/TE=7400/89 ms, b=700 s/mm2, 256×256 mm FOV, 128×128 matrix, 2 mm (0 mm gap) slice thickness, 10 T2 + 60 DWI, total acquisition time 8 min 38 sec). Sixty four slices were acquired in the AC-PC plane. The 60 diffusion-encoding gradient directions were determined using the electrostatic shell method, and result in a high signal-to-noise diffusion volume. In addition to taking advantage of the built-in distortion minimization of this sequence, the acquisitions also included B0 field maps that could be used for further distortion correction. These corrections allow us to register DWI images with the high-resolution anatomical images.
3.2. Visually-guided Fiber Bundle Generation
In order to identify a set of fiber bundles for our quantitative registration performance analysis, we propose to use the validated manual tract segmentation procedure defined in [[35]]. In this approach, all tract solutions are computed for the entire brain, then regions of interest (ROIs) are used to remove fibers that are not part of the desired tract, or to restore fibers removed by previous ROIs. These ROIs interact with the full set of tract solutions using Boolean operators AND, OR and NOT. In this section, we use the corticospinal tract (CST) to illustrate the procedure, with the full set tracts described in Sec. 3.3.
The CST is an extensive white matter bundle that begins in primary motor cortex (Brodmann’s area 4, frontal lobe) and ends at various levels of the anterior spinal cord. The procedure for modeling the fibers in the CST is illustrated in Figure 1 using the Trackvis utility [[34]]. Figure (a) shows the results of running the Fiber Assignment by Continuous Tracking (FACT) [[24]] deterministic tractography algorithm using every voxel in the brain as a seed for a tract solution. Images (b) and (c) show only tracts that intersect the left or right precentral gyrus white matter and the brainstem respectively, where these ROIs were automatically generated by FreeSurfer [[15]]. We then combine the precentral gyrus ROIs with the brainstem one using an AND operator to obtain only solutions connecting them. Any fibers that appear in this solution that are not actually part of the CST anatomy are removed using a NOT operator. Thus, the final set of tracts, shown on image (d), represents those that traverse brainstem AND precentral gyrus white matter via the internal capsule but NOT any extraneous fiber tracts.
Figure 1.
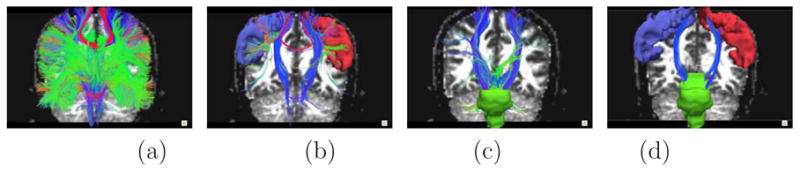
Labeling the CST: (a) deterministic tractography seeded in the whole brain (b) tracts going through the precentral gyri ROIS (c) tracts going through the brainstem ROI (d) tracts going through both the precentral gyri and brainstem ROIs.
3.3. Three Tracts of Interest
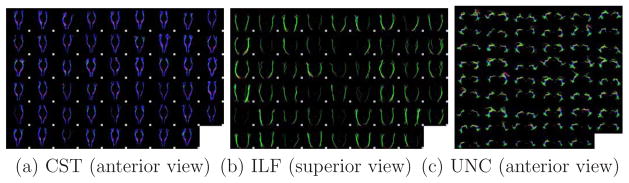
In this paper we use three different tracts for the validation of the registration experiments. Besides the CST, we generated models of the inferior longitudinal fasciculus and the uncinate. Even though we mostly relied on the fiber definitions presented in a recent paper by Wakana et al. [[35]], in this section, we give a brief description of the key ROIs and segmentation rules that we used to identify them. Figure 2 illustrates the resulting fiber tracts from the population of 53 subjects used as a gold standard in this study.
Figure 2.
The three tracts of interest manually selected from 53 subjects.
3.3.1. Cortico-spinal tract (CST)
The CST extends from the precentral gyrus to the spinal cord at varying levels. Cortically, it runs from the superior part of the brain fanning out laterally in order to represent leg, trunk, hand, and face, with leg being the most medial and face being the most lateral. It travels down through the posterior limb of the internal capsule and through the cerebral peduncles in the midbrain. We defined the start and end ROI for this region to be the white matter of the precentral gyrus and the brainstem respectively, both being available to us from the FreeSurfer processing pipeline. We removed fibers, using exclusion ROIs, that were projecting to the cerebellum and the thalamus and heading in the lateral or frontal directions. Additionally, corticopontine fibers that were crossing in the pons were also eliminated.
3.3.2. Inferior longitudinal fasciculus (ILF)
The ILF travels from the temporal lobe and fans out toward the occipital lobe. We defined the anterior ROI as the temporal white matter in the posterior-most coronal slice in which the temporal lobe is not yet connected to the frontal lobe. The posterior ROI was the white matter region of the entire hemisphere on a coronal slice selected at that edge of the cingulum on a parasagittal slice. We eliminated any fibers that went through the putamen or that ran far too medially.
3.3.3. Uncinate fasciculus (UNC)
The uncinate fasciculus travels between the temporal and the frontal lobe making a C shape. We defined the anterior ROI of the uncinate to include all frontal projections from the temporal lobe, usually localized inferior to the putamen. The posterior ROI was drawn to include the temporal white matter in the posterior most coronal slice in which the temporal lobe was not connected to the frontal lobe similar to the ROI for the ILF (see above). Any fibers that headed sharply medially were excluded.
3.4. Reliability
Some interaction with the data is required in order to generate an accurate set of fibers, which naturally raises the issue of reliability of the manually generated training set. We tested the reliability of these segmentations using both intra-rater and inter-rater experiments. Three raters each generated uncinate representations for both hemispheres of ten subjects using the procedure detailed above and one rater repeated the segmentations several weeks later. The results of this study are given in Figure 3, showing the symmetric mean Hausdorff distance (HD) of the inter- (a) and intra- (b) rater reliability. The classic HD is the maximum of the minimum distances of each point in one labeling to the other labeling. The symmetric mean HD is the mean of the minimum distances of each set to the other. As can be seen, the intra-rater error has a mean of around 1.15 mm, or N = 0.6 diffusion voxel, and even the inter-rater error is only a modest 2mm, indicating that the procedure is stable and reliable.
Figure 3.
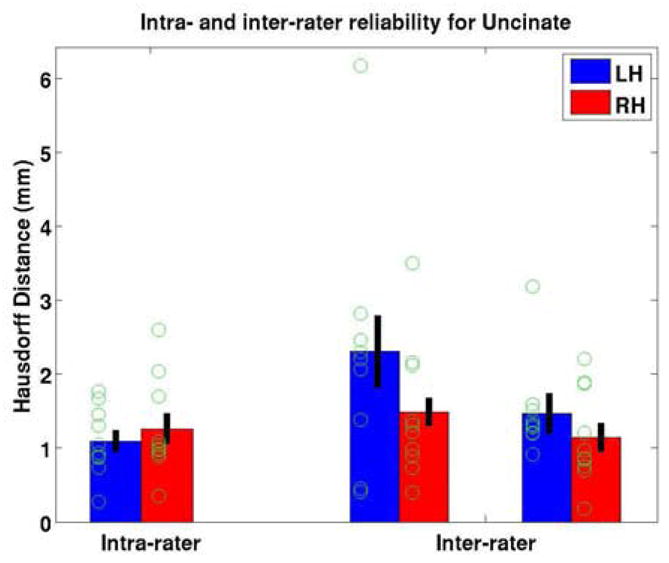
Reliability scores computed on the uncinate fiber bundle on ten subjects by three raters. The green circles correspond to individual measurements, while the red and blue bars are their mean and the black line indicates the corresponding standard error.
3.5. Experiment Setup
For all the registration methods besides FA-FNIRT, we randomly selected one subject from the input data set to be the template and registered the rest of the data to it. For FA-FNIRT the subjects are registered into an FSL template space. In order to characterize the registration performance of the different measures, we aligned the fiber bundles using the resulting morphs and then computed the maximum and mean Hausdorff distance among them in the new space.
4. Results
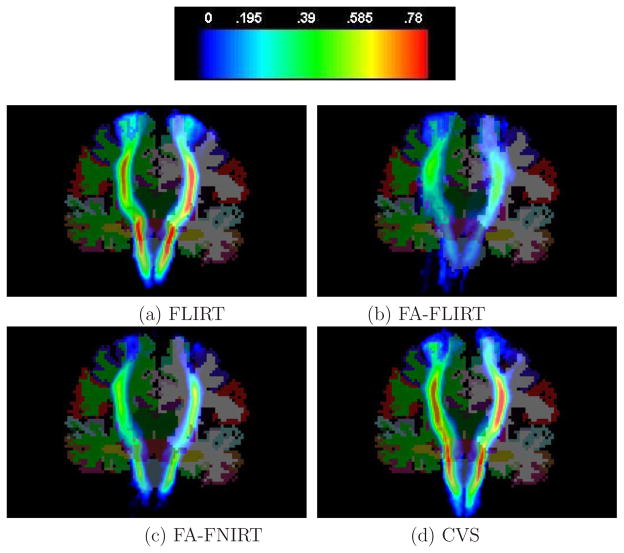
First, we present qualitative results from our registration experiments. In Figure 4 we illustrate the alignment of the CST fibers on the template brain. Specifically, the CST from each subject was transformed into the template brain coordinate system using the previously computed registration from each of the 4 techniques. We then computed the probability of occurrence of the CST at each point in space. As can be seen, in the case of CVS, the mean reaches higher values and is less diffuse both in the cortical and subcortical regions as compared to the other methods, indicating that this registration technique groups the individual subject CSTs more tightly.
Figure 4.
The average CST tracts after registration mapped to the template.
Figure 5 presents the probability maps in 3D using isosurfaces. We thresholded the maps at 0.1 (at least 10 % agreement between the manually labeled and registered fiber tracts) and constructed isosurfaces to visualize their spatial content. Note the accuracy with which the purely anatomical registration using CVS predicts the location of both the CST and ILF, resulting in significantly tighter and more accurate estimates of the spatial location of the fiber bundles. Additionally the sharpening of the distributions yielded by the nonlinear CVS warps relative to FA-FNIRT and FLIRT, provides evidence that the alignment of anatomy does also align the underlying fascicles.
Figure 5.
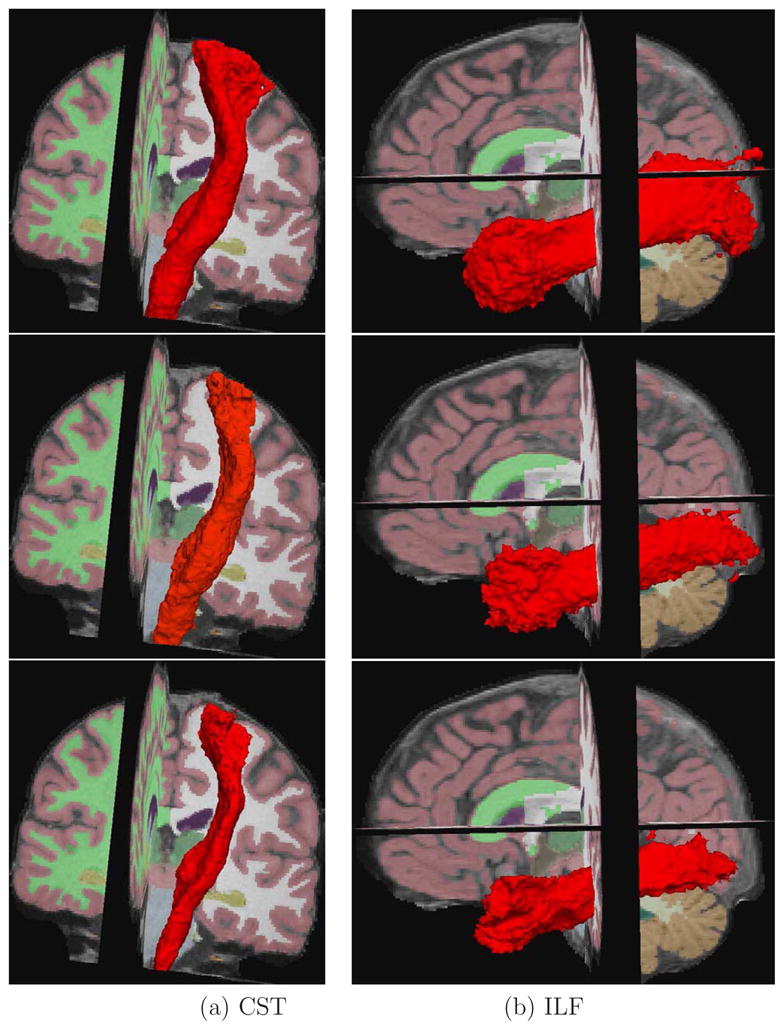
Average tracts after registration mapped to the template displayed with isosurfaces: (top) FLIRT, (middle) FA-FNIRT, (bottom) CVS
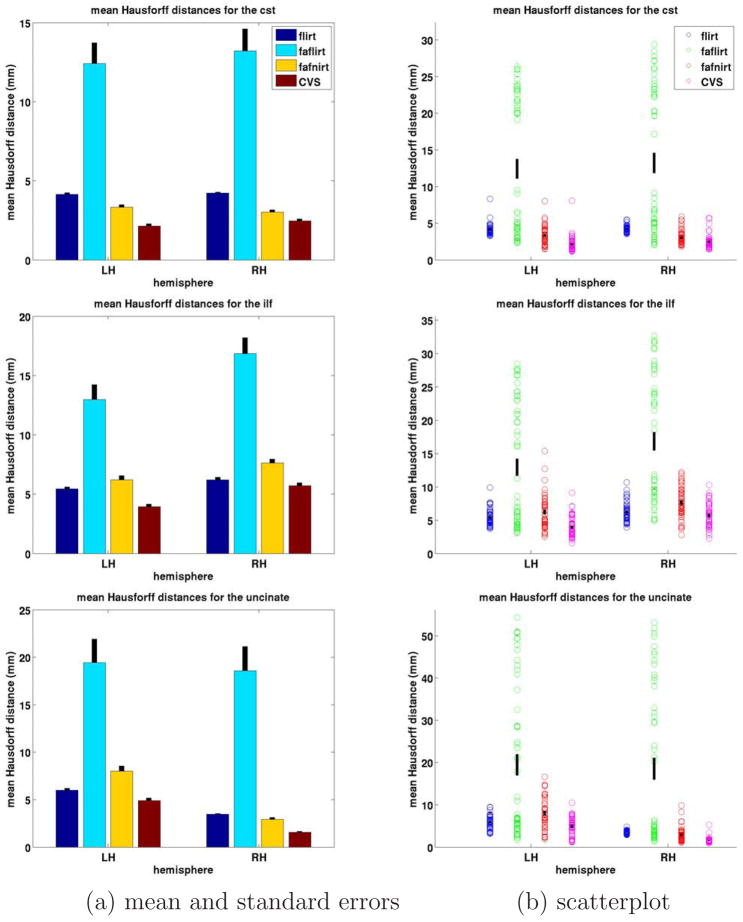
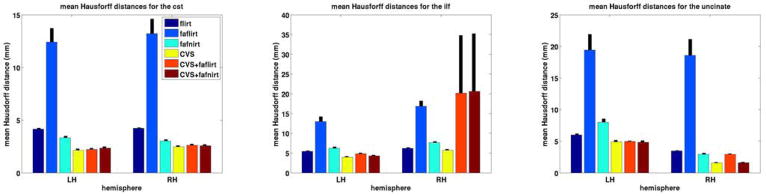
For a quantitative evaluation, we computed the mean Hausdorff distance measures for each registration method for each of the tracts, as shown in Figure 6. In summary, for all three tracts and both hemispheres, we found that CVS outperformed FLIRT, FA-FLIRT and FA-FNIRT in a statistically significant manner. In addition, FA-FLIRT was outperformed by all other three methods in a statistically significant manner. FLIRT was outperformed also by FA-FNIRT in all cases in a statistically significantly manner except for lh UNC and lh ILF where FLIRT outperformed FA-FNIRT. It is interesting to note that the accuracy of the linear registration computed by FLIRT increased substantially when using the structural data (FLIRT) over the DWI data (FA-FLIRT), even though the gold standard we use for assessing accuracy is derived from the DWI data. For the above quantitative comparison, p-values were computed using the Student T-test with α < .0025.
Figure 6.
Mean Hausdorff distance measures for the three fiber bundles: (top) CST, (middle) ILF, (bottom) UNC
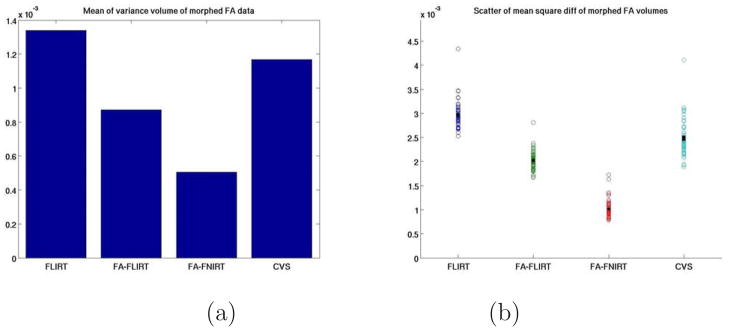
Finally, in order to verify that FLIRT and FNIRT were performing as expected, we estimated cross-subject FA variability for each registration technique. The results of this study are given in Figure 7. The left-hand plot in Figure 7 shows the mean value of the variance volumes, and the right-hand one is a scatterplot of the mean squared difference of morphed FA volumes for each registration algorithm. As expected, FA-FNIRT and FA-FLIRT both accomplish their goal of reducing the cross-subject variance of the FA volumes, indicating that they are functioning properly, and providing evidence that alignment of FA volumes does not imply tract alignment.
Figure 7.
For all four registration methods: (a) mean of the variance volume of the morphed FA volumes (b) scatter plot of the mean squared difference of morphed FA volumes per subject
5. Conclusion
In this paper, we have presented results that suggest that cross-subject registration based on structural MRI images can provide improved alignment of fiber architecture compared to directly aligning DWI-derived scalar volumes, such as the widely used FA volumes.
We compared the accuracy of the CVS structural registration method with other widely used techniques for aligning diffusion weighted images. More specifically, we tested the performance of various registration methods with respect to the alignment of fiber bundles. Our conclusion is that the utility of using high resolution structural data sets for the alignment of diffusion data sets should not be underestimated, as they provide significant advantages even when the goal is diffusion analysis. We emphasize that this is not to suggest that the DWI data should not be used, only that initializing the registration with a good alignment of the anatomy helps achieve significantly increased accuracy in the alignment of the underlying tracts.
In the future we intend to extend our study of tract alignment by (i) enhancing CVS to incorporate diffusion information and quantifying the increased performance provided by this additional data, (ii) considering registration algorithms that make use of higher dimensional diffusion information, as opposed to scalar measures such as FA, (iii) validating our results on probabilistic tractography outcomes (iv) and investigating what coordinate system is optimal for a tract-based analysis.
It is worth stressing the superior cross-subject alignment of tracts that was obtained even when a linear transform was computed from the structural data as opposed to the DWI data directly. This is strong evidence that the alignment of structure removes many of the degrees of freedom in aligning tracts. These results imply that the relationship between the location of the tracts and the surrounding anatomy is consistent across subjects. The increased accuracy provided by CVS would then stem from the fact that it provides state-of-the-art alignment of cortical, subcortical and ventricular structures, and that once these are all aligned, the tracts are largely aligned as well. In addition, recent work has revealed a strong relationship between cortical folding patterns and architectonic borders [[9]]. Since one would expect that a given fiber bundle terminates in a specific and consistent set of cytoarchitectural regions across subjects, it is reasonable to also expect more accurate tract registration with improved alignment of the folding patterns and by extension, the underlying architectonics.
A final important contributing factor to point out is the difference in image quality between the structural and the DWI data. The fast encoding necessary to acquire multiple directions in DWI results in image distortions that are only partially correctable [[17,19]]. In addition, the goal of the DWI acquisition is obtaining orientation information, not maximizing tissue CNR, and thus there is significantly reduced contrast between anatomical structures in DWI relative to typical anatomical acquisitions. Finally, the need to acquire multiple diffusion directions makes it difficult to obtain the types of resolutions that are standard in anatomical imaging, and in fact the typical resolution of anatomical MRI is approximately an order of magnitude finer than DWI in terms of voxel volume, implying that finer spatial co-registration is achievable using the anatomy rather than the DWI. As noted above, we would not be surprised to find that the accuracy of the FNIRT-FS alignment increases substantially if it were optimized for registering anatomical images, and perhaps using this to initialize an FA-based registration. Unfortunately, a simple sequential combination of the structural registration and an FA alignment postprocessing step is not powerful enough to obtain such improvement. As a quick experiment, we ran two sets of further experiments: CVS+flirtfa and CVS+fnirtfa. After completing our CVS registration framework we added an additional registration step using FA information from the diffusion images. The former method just used 12 DOF affine and the latter a non-linear transformation model. As shown in Fig. 8, such a step did not improve the alignment, but actually slightly made it worse in all three bundle cases. Therefore, we believe that relying on a combination of such multi-modal data sources will necessitate a more careful evaluation.
Figure 8.
Mean Hausdorff distance measures for the three fiber bundles: (left) CST, (middle) ILF, (right) UNC
In summary, we anticipate that cross-subject registration of connectional anatomy will be improved when techniques are developed that employ all the available information provided by the imaging data, including measurements derived from the DWI data such as tensors or orientation density functions, intensity information from structural acquisitions, and geometric features provided by cortical models.
Acknowledgments
Support for this research was provided in part by the NCRR (P41-RR14075, R01 RR16594-01A1 and the NCRR BIRN Morphometric Project BIRN002, U24 RR021382), the NIBIB (R01 EB001550, R01EB006758), the NINDS (R01 NS052585-01) as well as the MIND Institute, and is part of NAMIC, funded by the National Institutes of Health through the NIH Roadmap for Medical Research, Grant U54 EB005149. We also acknowledge Ruopeng Wang and Van J. Wedeen (Martinos Center for Biomedical Imaging, Massachusetts General Hospital) for Trackvis and Diffusion Toolkit, Jean Augustinack for our long discussions about neuroanatomy and Steve Smith for his suggestions about the methodological section of our work.
Footnotes
Smith et al.’s paper has been the most cited paper published in NeuroImage since 2006, the year of its publication. It has a total of 176 citations registered in the “ISI Web of Science” (http://www.isiwebofknowledge.com/) database. This number is more than a 50 % higher than the citation numbers for any of the second-most cited papers published between 2006 and present (128, 111, 36 and 17 respectively).
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Alexander D, Gee J. Elastic matching of diffusion tensor images. Computer Vision and Image Understanding. 2000;77(2) [Google Scholar]
- 2.Alexander D, Pierpaoli C, Basser P, Gee J. Techniques for spatial normalisation of diffusion tensor image. SPIE Conference on Medical Imaging (Image Processing); Feb, 2000. pp. 470–79. [Google Scholar]
- 3.Alexander D, Pierpaoli C, Basserand P, Gee J. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Transactions on Medical Imaging. 2001 November;20 (11):1131–1139. doi: 10.1109/42.963816. [DOI] [PubMed] [Google Scholar]
- 4.Andersson J, Jenkinson M, Smith S. Non-linear optimisation. Tech Rep TR07JA1, FMRIB 2007a [Google Scholar]
- 5.Andersson J, Jenkinson M, Smith S. Non-linear registration, aka spatial normalisation. Tech Rep TR07JA2, FMRIB 2007b [Google Scholar]
- 6.Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using dt-mri data. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 2000 October;44(4):625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. URL http://view.ncbi.nlm.nih.gov/pubmed/11025519. [DOI] [PubMed]
- 7.Corouge I, Fletcher P, Joshi S, Gilmore J, Gerig G. Fiber tract-oriented statistics for quantitative diffusion tensor mri analysis. MICCAI. 2005:131–139. doi: 10.1007/11566465_17. [DOI] [PubMed] [Google Scholar]
- 8.Dale A, Fischl B, Sereno M. Cortical surface-based analysis i: Segmentation and surface reconstruction. NeuroImage. 1999;9 (2):179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 9.Fischl B, Rajendran N, Busa E, Augustinack J, Hinds O, Yeo B, Mohlberg H, Amunts K, Zilles K. Cortical folding patterns and predicting cytoarchitecture. Cerebral Cortex. 2008;18 (8):1973–80. doi: 10.1093/cercor/bhm225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fischl B, Salat D, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale A. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- 11.Fischl B, Salat D, van der Kouwe A, Makris N, Ségonne F, Dale A. Sequence-independent segmentation of magnetic resonance images. NeuroImage. 2004a;23:S69–S84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 12.Fischl B, Sereno M, Dale A. Cortical surface-based analysis ii: Inflation, flattening, and a surface-based coordinate system. NeuroImage. 1999a;9 (2):195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- 13.Fischl B, Sereno M, Tootell R, Dale A. High-resolution inter-subject averaging and a coordinate system for the cortical surface. Human Brain Mapping. 1999b;8:272–284. doi: 10.1002/(SICI)1097-0193(1999)8:4<272::AID-HBM10>3.0.CO;2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fischl B, van der Kouwe A, Destrieux C, Halgren E, Segonne F, Salat D, Busa E, Seidman L, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale A. Automatically parcellating the human cerebral cortex. Cerebral Cortex. 2004b;14:11–22. doi: 10.1093/cercor/bhg087. [DOI] [PubMed] [Google Scholar]
- 15.FreeSurfer. 2009 http://surfer.nmr.mgh.harvard.edu/
- 16.Guimond Guttmann, Warfield Westin. Deformable registration of dt-mri data based on transformation invariant tensor characteristics. ISBI. 2002 July 7-10;:1–4. [Google Scholar]
- 17.Jenkinson M. Improved unwarping of epi volumes using regularised b0 maps. Proceedings of International Conference on Human Brain Mapping; 2001. [Google Scholar]
- 18.Jenkinson M, Smith SM. A global optimisation method for robust affine registration of brain images. Medical Image Analysis. 2001 June;5 (2):143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- 19.Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from b0 field variations. Mag Res Med. 1995;34:65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 20.Johansen-Berg H, Behrens T. Diffusion MRI: From quantitative measurement to in-vivo neuroanatomy. Academic Press; New York: 2009. [Google Scholar]
- 21.Jones D, Griffin L, et al. Spatial normalization and averaging of diffusion tensor mri data sets. NeuroImage. 2002;17 (2):592–617. [PubMed] [Google Scholar]
- 22.Maddah M, Grimson W, Warfield S, Wells W. A unified framework for clustering and quantitative analysis of white matter fiber tracts. Medical Image Analysis. 2008;12 (2):191–202. doi: 10.1016/j.media.2007.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mayer A, Greenspan H. Bundles of interest based registration of white matter tractographies. ISBI. 2008:919–922. [Google Scholar]
- 24.Mori S, Crain B, Chacko V, van Zijl P. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45:265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 25.O’Donnell L, Westin CF, Golby A. Tract-based morphometry for white matter group analysis. NeuroImage. 2009;45 (3):832–844. doi: 10.1016/j.neuroimage.2008.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Park H, Kubicki M, Shenton M, Guimond A, McCarley R, Maier S, Kikinis R, Jolesz F, Westin C. Spatial normalization of diffusion tensor mri using multiple channels. NeuroImage. 2003;20:1995–2009. doi: 10.1016/j.neuroimage.2003.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Petrovic A, Smith S, Patenaude B, Jbabdi S, Zarei M, Jenkinson M. Tractography-driven registration for improved within-surface correspondence in brain structures. Neuroimage. 2009 July;47 (S1):122. [Google Scholar]
- 28.Postelnicu G, Zöllei L, Fischl B. Combined volumetric and surface registration. IEEE Transactions on Medical Imaging. 2009;28 (4):508–522. doi: 10.1109/TMI.2008.2004426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Non-rigid registration using free-form deformations: Application to breast mr images. IEEE Transactions on Medical Imaging. 1999;18 (8):712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- 30.Ruiz-Alzola Westin, Warfield Alberola, Maier Kikinis. Non-rigid registration of 3d tensor medical data. Medical Image Analysis. 2002;6:143–161. doi: 10.1016/s1361-8415(02)00055-5. [DOI] [PubMed] [Google Scholar]
- 31.Smith S. Fast robust automated brain extraction. Human Brain Mapping. 2002 November;17 (3):143–155. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Smith S, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols T, Mackay C, Watkins K, Ciccarelli O, Cader M, Matthews P, Behrens T. Tract-based spatial statistics: Voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31:1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- 33.Smith S, Jenkinson M, Woolrich M, Beckmann C, Behrens T, Johansen-Berg H, Bannister P, De Luca M, Drobnjak I, Flitney D, Niazy R, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady J, Matthews P. Advances in functional and structural mr image analysis and implementation as fsl. Neuroimage. 2004;23 (S1):208–219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 34.Trackvis. 2009 http://www.trackvis.org/
- 35.Wakana S, Jiang H, Nagae-Poetscher LM, van Zilj P, Mori S. Fiber tract-based atlas of human white matter anatomy. Radiology. 2003 November;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- 36.Ziyan U, Sabuncu MR, O’Donnell L, Westin C-F. MICCAI. Springer; 2007. Nonlinear registration of diffusion mr images based on fiber bundles; pp. 351–358. [DOI] [PubMed] [Google Scholar]
- 37.Zvitia O, Mayer A, Shadmi R, Miron S, Greenspan H. Co-registration of white matter tractographies by adaptive-mean-shift and gaussian mixture modeling. IEEE Trans Med Imaging. 2010 Jan;29 (1):132–45. doi: 10.1109/TMI.2009.2029097. [DOI] [PubMed] [Google Scholar]