Unsupervised White Matter Fiber Clustering and Tract Probability Map Generation: Applications of a Gaussian Process framework for white matter fibers

Abstract

With the increasing importance of fiber tracking in diffusion tensor images for clinical needs, there has been a growing demand for an objective mathematical framework to perform quantitative analysis of white matter fiber bundles incorporating their underlying physical significance. This paper presents such a novel mathematical framework that facilitates mathematical operations between tracts using an inner product based on Gaussian processes, between fibers which span a metric space. This metric facilitates combination of fiber tracts, rendering operations like tract membership to a bundle or bundle similarity simple. Based on this framework, we have designed an automated unsupervised atlas-based clustering method that does not require manual initialization nor an a priori knowledge of the number of clusters. Quantitative analysis can now be performed on the clustered tract volumes across subjects thereby avoiding the need for point parametrization of these fibers, or the use of medial or envelope representations as in previous work. Experiments on synthetic data demonstrate the mathematical operations. Subsequently, the applicability of the unsupervised clustering framework has been demonstrated on a 21 subject dataset.

1. Introduction

Diffusion MRI non invasively recovers the in vivo effective diffusion of water molecules in biological tissues. This information characterizes tissue micro-structure and its architectural organization (Basser and Pierpaoli, 1996) by modeling the local anisotropy of the diffusion process of water molecules, providing unique biologically and clinically relevant information not available from other imaging modalities. Once the diffusion information has been recovered within each voxel, it can be synthesized in the form of a diffusion tensor (Basser et al., 1994). Brain connectivity can then be assessed by assembling the tensors into tracts using tractography methods (Mori et al., 1999; Koch et al., 2002; Descoteaux et al., 2009). Among these methods, streamline tractography (Mori et al., 1999) recovers white matter fiber tracts from a seed voxel by following the principal direction of the diffusion tensor. Using this technique, white matter fiber tracts are represented as points sampled from a three-dimensional curve. Finally, these fibers can then be grouped into fiber bundles based on anatomic knowledge (O’Donnell and Westin, 2007; Maddah et al., 2008a). The Cortico Spinal Tract (CST) or the Corpus Callosum (CC) are prominent examples of the latter.

In this paper, we address the important problem of developing a mathematical framework for the quantitative analysis of fiber bundles, which has become a very active research area, with the aim of facilitating subsequent clustering and group-based statistical analysis on the bundles. The effects of pathology on tracts is evident, as in the case of brain tumors that grossly displace tracts, or can be subtle, as in the case of neuropsychiatric disorders, such as schizophrenia, which can manifest as changes in the tracts (Kubicki et al., 2007; Ciccarelli et al., 2008). We propose a framework for tract analysis based on a novel metric between bundles that serves as a probabilistic measure of inclusion of a fiber tract into a bundle. This framework is then used to develop a method for automated clustering of bundles, which are now quantifiable on the basis of membership and ready for statistics based on the distances between bundles. Once obtained, the clusters can be mapped to tract probability maps (Hua et al., 2008) enabling tract-based statistics on the cerebral white matter.

2. Materials and Methods

2.1. Prior work

The clustering of different fiber tracts into an anatomically coherent bundle, like the CC or the CST, is a challenging task for several reasons. In the first place, as seen in Figure 1, axons composing a bundle can diverge from it connecting cortical and subcortical areas. This renders approaches that quantify similarity among white matter fibers using the whole fiber instead of analyzing partial overlaps like shape statistics or rigid transformations (Veltkamp, 2001) unsuited for the clustering task. Take for instance the cingulum bundle, whose constituent fibers only partially overlap among themselves, with many diverging to innervate the cortex, as shown in Figure 1. These divergent fibers can have quite different shapes, calling into question the utility of shape-based metrics for subsequent tensor statistics. Even if current streamline tractography techniques are reproducible (Wakana et al., 2007), fiber tracts obtained through tractography do not recover the whole underlying axonal trajectory (Lenglet et al., 2009). This behaviour can be observed clearly in complex bundle configurations like crossings or fannings (Savadjiev et al., 2008), the crossing area of the CC and the CST for example (Wiegell et al., 2000). In order to overcome this problem, streamline tracking techniques that are more sensitive to complex bundle configurations have been developed (Qazi et al., 2009; Descoteaux et al., 2009). These produce better local approximations of axonal distribution by exploiting more complex models of the underlying water diffusion in a voxel (Tuch, 2004; Peled et al., 2006; Descoteaux et al., 2007). Still, results are far from being reliable after the streamline tracking procedure traverses a region with complex bundle configuration. In clustering tracts into a bundle, a common workaround for this problem consists of seeding all over the brain and performing a dense whole brain tractography. This algorithm produces fiber tracts that could later be grouped through clustering techniques (O’Donnell and Westin, 2007). This highlights the need for a similarity metric that can quantify the closeness of two fibers or the degree to which a tract belongs to a bundle; both of these are challenging problems, critical to automatic bundle identification.

Figure 1.

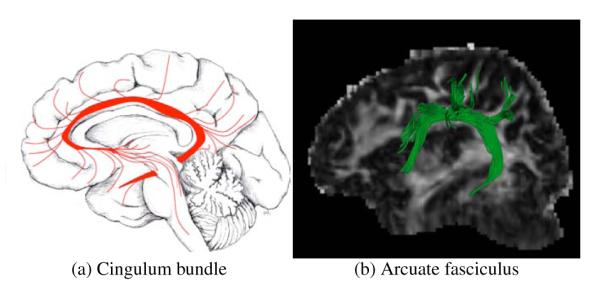
Axons enter and leave anatomical bundles. Image (a) reproduced from O’Donnell (2006) with permission of Jimmy Fallon, UCI. Image (b) manually selected Arcuate fasciculus after full brain tractography.

Quantifying fiber similarity is a fundamental part of fiber clustering that has been addressed in different ways. Recent works (Batchelor et al., 2006; Corouge et al., 2006; Leemans et al., 2006) quantify fiber similarity with different flavors of shape statistics. However, partial overlapping of fibers is not taken into account as a similarity feature. Thus, the previous approaches are unsuited for automatic classification of fibers in the brain. There is a separate set of works (Ding et al., 2003; O’Donnell and Westin, 2007; Wassermann and Deriche, 2008; Maddah et al., 2008a), which uses different clustering algorithms based on the Hausdorff or Chamfer distances among the sequence of points parametrizing each fiber tract. This family of similarity metrics deals with sets of points instead of curves, hence they discard continuity or directionality information. Moreover, similarity tends to decrease very fast in cases of partial overlapping, failing to include fibers diverging from the bundle in the correspondent cluster. In particular, Ding et al. (2003) only analyze fibers whose seed points are spatially close together. This is not suited for a whole brain analysis because different fiber seed points from the same bundle may have been scattered all over the white matter. This seeding technique is frequently used in order to overcome limitations of streamline tracking in regions with complex bundle configurations (O’Donnell and Westin, 2007). Manifold learning techniques are used by O’Donnell and Westin (2007) and Wassermann and Deriche (2008) to generalize these distances from small sets of similar fibers to a bigger more diverse set of fibers. These approaches embed the fibers into Euclidean or topological spaces that can be handled more easily.

O’Donnell and Westin (2007) start by generating an atlas of white matter fibers, fibers from new subjects are then classified according to this atlas. Even though these automatically grouped bundles are anatomically coherent, the process to generate the atlas requires heavy user interaction and fine parameter tuning. The level of manual interaction needed renders the approach difficult to reproduce. Wassermann and Deriche (2008) use a publicly available anatomical atlas in conjunction with the fiber similarity metric. This work requires a smaller number of parameters, nevertheless situations of partial fiber overlapping generate non-anatomically coherent bundles. This strategy has proved to be useful for single individuals but lacks the necessary parameter stability needed for group studies: the parameters of the algorithm must be fine-tuned individually for each subject in order to obtain the same white matter bundle. Maddah et al. (2008a) enhances the Hausdorff similarity with Mahalanobis distance between fiber points. In order to handle partial overlapping, an ad-hoc penalty term is added to this distance. This approach requires user initialization, by selecting a fiber which is known to be in the desired bundle. Their subsequent work (Maddah et al., 2008b) incorporated atlas information to increase accuracy, however an initial fiber representing each bundle is still required. From all the presented approaches, only O’Donnell and Westin (2007) succeed in the task of semi-automated classification of the whole ensemble of white matter fibers, however this is achieved with a great deal of user interaction and parameters tuning.

Once bundles have been found, quantitative analysis can be performed. This analysis is useful to monitor pathological conditions (Ciccarelli et al., 2008; Kubicki et al., 2007). Most of the works performing bundle statistics (Goodlett et al., 2009; Hua et al., 2008; O’Donnell et al., 2007; Maddah et al., 2008a) rely on the use of medial representations for bundles. These representations are only appropriate for bundles which can be modeled as convex envelopes. Thus, their methodology is not entirely appropriate at the extremes of the bundles, an area where the axons fan-out inervating cortical or subcortical structures. Other works (Oh et al., 2007) use a mesh approach over ROIs and perform statistics on the surface. However, automated transition from a set of fibers to the mesh is unclear. There is recent evidence that tract probability maps can be used in order to perform bundle-oriented statistics in diffusion MRI (Hua et al., 2008) and histological images (Bürgel et al., 2006). However, in these two approaches the process to obtain the tract probability maps must be performed manually by experts. Overall, statistical models of white matter bundles which rely on medial representations are insufficient. Moreover, for models which are more appropriate for a wider spectra of bundles, the transition from automatically obtained bundles to these statistical models is not straightforward.

2.2. A Mathematical framework for white matter fibers and bundles

The goal of this work is to introduce a novel mathematical framework for performing statistical analysis of fiber tracts and bundles. Our model includes diffusion information and relates the bundles with an ROI in the volume, mapping every voxel to degree of membership to the bundle, the bundle’s blurred indicator function. It provides a similarity measure for fiber bundles and fiber tracts, which are considered as single-fiber bundles. Its linear combination operation between fiber bundles seamlessly generates new bundle configurations and allows for the volume-based statistics of fiber bundles. In addition, the similarity measure handles cases of partial fiber overlap naturally. The previously mentioned characteristics facilitate statistical analysis and classification/clustering tasks. Finally, we present a clustering application based on our mathematical framework and on anatomical information in the shape of a volumetric atlas. The output of this application is a set of automatically obtained white matter bundles like the Arcuate Fasciculus or the Cingulum. For each bundle, we are also able to produce an ROI which maps every voxel to its probability of belonging to the bundle, referred in previous work as tract probability map (Hua et al., 2008; Bürgel et al., 2006). This map is an appropriate tool to perform bundle-based statistics on the cerebral white matter. We validate this clustering algorithm by applying it to 21 healthy subjects and then performing statistical analysis on the results using our mathematical framework.

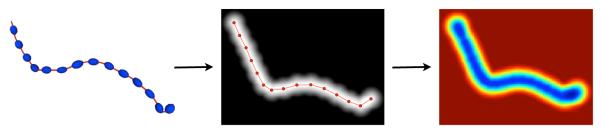
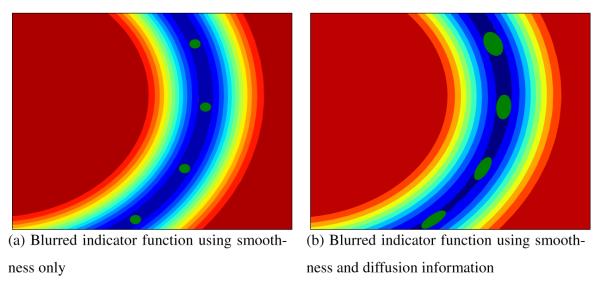
As a first step, we need to provide a mathematical model for each fiber. Each fiber tract $\mathcal{F}$ is modeled as a blurred indicator function $y_{\mathcal{F}}:\mathbf{p}\in {\mathbb{R}}^3\to \mathbb{R}$. This blurred indicator function has a maximal level set which corresponds to $\mathcal{F}$. Moreover, $y_{\mathcal{F}}$ is blurred in accordance with the information provided by the underlying diffusion tensor field, i.e. along the fiber direction and not across it. This is illustrated on Figure 2.

Figure 2.

Gaussian Process representation of the fiber: We model each fiber as a blurred indicator function. Each fiber obtained by tractography is constituted as a sample of points over a line, which is shown in red line on the left side of the figure, and its corresponding diffusion tensor field, indicated by the blue tensors over the red fiber. The sampled points are then used to generate a blurred indicator function with a maximal level set which corresponds to the fiber (central image of the figure). Then, the fiber is blurred in accordance with the information provided by the underlying diffusion tensor field. The resulting representation, on the right side of the figure, is a smooth indicator function blurred along the fiber direction.

Then, we need to govern the properties of our fibers/functions while subsequently simplifying a certain number of sophisticated operations between the fibers like similarity quantification and combination into bundles. Gaussian Processes (GP) (Seeger, 2004), as we show in Appendix A, provide the right framework to integrate spatial and diffusion tensor MRI information for $y_{\mathcal{F}}$ and to perform these operations between the fibers. A Gaussian Process can be seen as a generalization of the classical Gaussian probability distribution to describe properties of functions and not only properties of random variables such as scalars or vectors. More precisely, we model the blurred indicator function $y_{\mathcal{F}}\left(\mathbf{p}\right)$ by the GP

$$y_{\mathcal{F}}\left(\mathbf{p}\right)~\mathcal{GP}\left(y_{\mathcal{F}}^{\ast }\right(\mathbf{p}),c_{\mathcal{F}}(\mathbf{p},{\mathbf{p}}^{\prime }\left)\right),$$ (1)

where the mean function $y_{\mathcal{F}}^{\ast }\left(\mathbf{p}\right)$ and covariance function $c_{\mathcal{F}}(\mathbf{p},{\mathbf{p}}^{\prime })$ are the parameters of this stochastic process. These two functions are inferred from the tractography of each fiber. That is, from the sequence of points f = {f₁,…,f_∣f∣} estimated by tractography of the anatomical bundle $\mathcal{F}$ and from the corresponding sampling on its diffusion tensor field Σ(f₁),…,Σ(f_∣f∣). The inference process of the GP corresponding to a white matter fiber is developed in Appendix A.1. It is important to point out that such framework provides also adequate computational tractability. Through closed form operations on the parameters of the GPs, it allows us to measure bundle similarity with partial fiber overlap without relying on point correspondences and to combine different fibers into a bundle by simply averaging the fibers’ GPs. Now that we have a Gaussian Process representation of white matter fiber bundles, we can express similarity, combination and tract probability maps in terms of this representation.

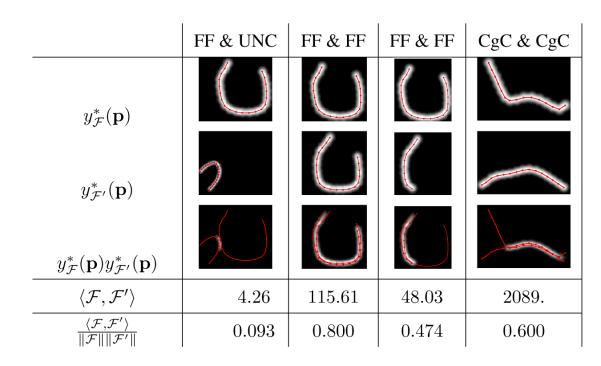
Firstly, we implement a similarity measure between bundles. Our measure quantifies the overlapping as of two bundles as illustrated in Figure 4 . This is done with an inner product operation developed in detail in Appendix A.3. If the mean function representing a bundle $\mathcal{F}$, $y_{\mathcal{F}}^{\ast }\left(\mathbf{p}\right)$, is square integrable and has finite support, the inner product between two bundles $\mathcal{F}$ and ${\mathcal{F}}^{\prime }$ is defined as

$$\langle \mathcal{F},{\mathcal{F}}^{\prime }\rangle ≔{\int }_{{\mathbb{R}}^3}{y}_{\mathcal{F}}^{\ast }\left(\mathbf{p}\right)y_{{\mathcal{F}}^{\prime }}^{\ast }\left(\mathbf{p}\right)d\mathbf{p},$$ (2)

along with its induced norm

$$\Vert \mathcal{F}{\Vert }^2≔\langle \mathcal{F},\mathcal{F}\rangle .$$ (3)

Moreover, we can define a similarity measure, bounded by 1 when $\mathcal{F}$ and ${\mathcal{F}}^{\prime }$ are exactly the same and by 0 when there is no intersection, as the inner product normalized by its induced norm,

$$\langle \mathcal{F},{\mathcal{F}}^{\prime }{\rangle }_N≔\frac{\langle \mathcal{F},{\mathcal{F}}^{\prime }\rangle }{\Vert \mathcal{F}\Vert \Vert {\mathcal{F}}^{\prime }\Vert }.$$ (4)

Examples of these two similarity measures are shown in Figure 4.

Figure 4.

Examples of the product of blurred indicator functions for different fiber pairs, the value of our inner product operation $\langle \mathcal{F},{\mathcal{F}}^{\prime }\rangle$, defined in Equation 2, and of our inner product normalized by its natural norm, $\Vert \mathcal{F}\Vert =\sqrt{\langle \mathcal{F},\mathcal{F}\rangle }$. Inner product quantifies the overlapping of blurred indicator functions. A larger inner product means that fibers are more similar and relates to the volume of the overlapping. The inner product normalized by its norm quantifies similarity ranging from 0 when overlapping is null to 1 when the two fibers are identical. The compared fibers have been extracted from different anatomical tracts of a diffusion MRI image, the Frontal Forceps (FF), the Uncinate Fasciculus (UNC) and the Cingulate Cortex section of the Cingulum (CgC).

Using our framework, we are able to combine N fibers into a bundle by simply averaging the GPs corresponding to these fibers. The GP which corresponds to the indicator function of a fiber bundle $\mathcal{B}$, is obtained through the mean Gaussian Processes of single fibers or smaller bundles composing it,

$$\begin{array}{c}\hfill y_{\mathcal{B}}\left(\mathbf{p}\right)=\frac{1}{N}\sum _{i=1}^N{y}_{{\mathcal{F}}_i}\left(\mathbf{p}\right)~\mathcal{GP}\left(y_{\mathcal{B}}^{\ast }\right(\mathbf{p});c_{\mathcal{B}}(\mathbf{p},{\mathbf{p}}^{\prime }\left)\right),\hfill \\ \hfill \text{where}{y}_{\mathcal{B}}^{\ast }\left(\mathbf{p}\right)=\frac{1}{N}\sum _{i=1}^N{y}_{{\mathcal{F}}_i}^{\ast }\left(\mathbf{p}\right)\text{and}{c}_{\mathcal{B}}(\mathbf{p},{\mathbf{p}}^{\prime })=\frac{1}{N^2}\sum _{i=1}^N{c}_{{\mathcal{F}}_i}(\mathbf{p},{\mathbf{p}}^{\prime }).\hfill \end{array}$$ (5)

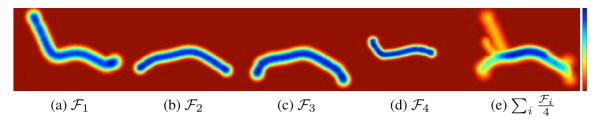
An example of this is shown in Figure 3, where blurred indicator functions for four fiber tracts and the obtained function for the bundle combining them can be seen.

Figure 3.

Mean indicator function for four fiber tracts (a-d) and mean indicator function for the bundle formed by averaging them according to our framework (e). Blue color means that the bundle is more likely to cross that voxel while red color means it is not likely that the bundle traverses that voxel. Fibers were manually selected from a full brain tractography and belong to the Cingulate Cortex section of the Cingulum (CgC).

It is worth noting that the combination of fibers bundles, which is a linear combination operation, and the similarity measure, which is an inner product operation, constitute an inner product space. As we will show later, this space is an appropriate support to perform statistical analyses such as clustering of fiber bundles.

We mentioned previously the importance for bundle statistics of the tract probability map, the probability that a point p in ${\mathbb{R}}^3$ is contained in a bundle $\mathcal{B},\mathbb{P}\{\mathbf{p}\in \mathcal{B}\}$. As we show in Appendix A.4, having calculated the GP for a bundle $\mathcal{B},y_{\mathcal{B}}(\cdot )$, by means of Equation 5, we can define the tract probability map from the parameters of the GP as

$$\mathbb{P}\{\mathbf{p}\in \mathcal{B}\}\propto \frac{1}{2\sqrt{\pi (h^2+{\sigma }_{\mathcal{B}}^2(\mathbf{p}\left)\right)}},$$ (6)

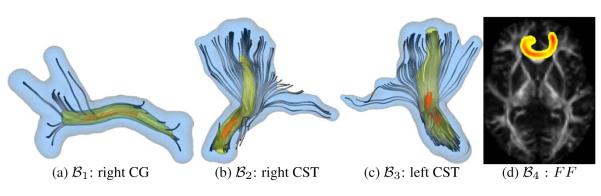
where h is a parameter that diffuses the tract probability map in space and ${\sigma }_{\mathcal{B}}^2\left(\mathbf{p}\right)$ is calculated from the parameters of $y_{\mathcal{B}}(\cdot )$. In order to illustrate the tract probability map calculated from a GP for a bundle, color-coded surfaces and a probability map over an FA image for anatomical bundles are shown in Figure 5.

Figure 5.

Iso-probability surfaces for manually selected fiber bundles, fig. (a-c), and tract probability map over FA for an automatically obtained bundle, fig. (d), see section 2.3. The probability at each voxel is calculated using Equation 6. Color code for fig. (a-c) is as follows, Blue: $\mathbb{P}\{\mathbf{p}\in {\mathcal{B}}_i\}=.01$, Yellow: $\mathbb{P}\{\mathbf{p}\in {\mathcal{B}}_i\}=.2$, Red: $\mathbb{P}\{\mathbf{p}\in {\mathcal{B}}_i\}=.6$.

Up to this point, we have introduced our GP-based framework for white matter fiber bundles and its three main operations: combination of fibers into a bundle, similarity quantification and calculation of the tract probability map. Thus, in this section we provide all the right and necessary tools to perform a quantitative statistical analysis of white matter fiber bundles. In the following sections, we use these tools in order to perform automatic white matter bundle identification by means of white matter fiber clustering and we assess the quality of this clustering by performing inter-subject statistical analysis of white matter fiber bundles using our framework.

2.3. Clustering Algorithm

Taking advantage of the mathematical framework for fiber bundles presented in section 2.2, we propose a stochastic process-based agglomerative clustering algorithm. This algorithm is executed over a full brain tractography, a set of densely sampled fibers from the whole white matter. Once executed, our algorithm generates a dendrogram, a tree structure where each joint is a candidate cluster, this is illustrated in Figure 6. Then, this dendrogram can be interactively explored in order to choose the desired granularity of the clustering without reprocessing the data. Being a hierarchical agglomerative algorithm it has several desirable properties: To begin with, convergence is guaranteed by the finite number of elements to cluster. Next, the number of clusters does not have to be known a priori. Also, it handles the clustering of outliers. These are incorporated to clusters during the late stages of the clustering algorithm if at all, which makes easy to identify them (Jain et al., 1999). All of these characteristics make our clustering algorithm effective and robust in order to classify white matter fibers from a full brain tractography into anatomically coherent bundles.

Figure 6.

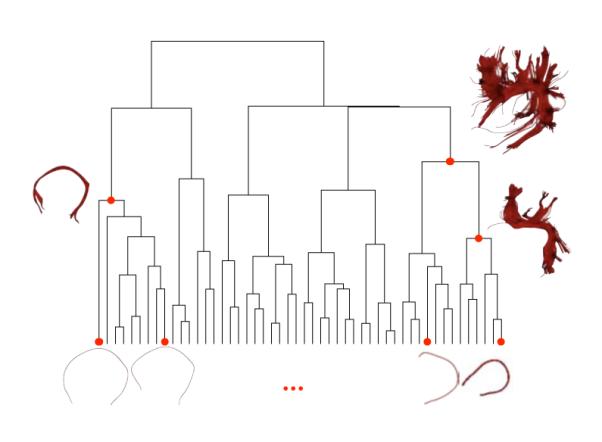
Illustration of our clustering algorithm defined in section 2.3. The algorithm starts from all the single-fiber bundles obtained by a full brain tractography, shown at the bottom of the figure, and joins them into multi-fiber bundles according to our similarity measure (Equation 2). This generates a tree structure called dendrogram. Finally every joint is a candidate cluster. Sample clusters are shown on the side of the dendrogram and their positions on the dendrogram are marked with red dots.

Our clustering algorithm applied to a full brain tractography is as follows,

• Step 1. Given a full brain tractography $F=\left\{{\mathcal{F}}_i\right\}$, with 1 ≤ i ≥ ∣F∣, calculate the set of stochastic processes representing each fiber $Y=\left\{y_{{\mathcal{F}}_i}\right(\mathbf{p}\left)\right\}$.

• Step 2. Initialize the clustering as the set of single fiber bundles $B=\left\{{\mathcal{B}}_i\right\}$, where ${\mathcal{B}}_i$ is a set (bundle) formed by a single fiber, ${\mathcal{F}}_i$, and 1 ≤ i ≥ ∣F∣.

• Step 3. Initialize the set of edges in the dendrogram: T = ∅

• Step 4. While there is a pair of different bundles $\mathcal{B},{\mathcal{B}}^{\prime }$ in B, s.t. $\langle \mathcal{B},{\mathcal{B}}^{\prime }\rangle >0$

  • Step 4.1. Select two different bundles $\mathcal{B},{\mathcal{B}}^{\prime }$ such that $\langle \mathcal{B},{\mathcal{B}}^{\prime }\rangle ={\max }_{\mathcal{C},{\mathcal{C}}^{\prime }\in B}\langle \mathcal{C},{\mathcal{C}}^{\prime }\rangle$.
  • Step 4.2. Remove the bundles $\mathcal{B}$ and ${\mathcal{B}}^{\prime }$ from B and add the bundle $\{\mathcal{B}+{\mathcal{B}}^{\prime }\}$.
  • Step 4.3. Add the edge $(\mathcal{B},{\mathcal{B}}^{\prime })$ to the dendrogram T.

The output of this algorithm is a dendrogram T, more precisely a set of trees where joint edge represents the joining of two bundles such as the one shown in Figure 6.

A main advantage of our framework within this clustering algorithm is that the most important operation in step 4, the inner product among bundles described in section 2.2, is fast and simple to compute as we show in Appendix A.4. Once we have calculated the matrix of inner products for every pair of fibers in the full brain tractography $\mathcal{F}$, the algorithm works by simply performing linear operations on the rows of this matrix.

2.4. Tract Querying: Automatic cluster selection based on anatomical knowledge

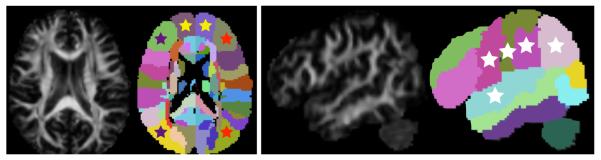
Once our clustering algorithm generates the dendrogram for a full brain tractography, section 2.3, the main problem is how to select the joints in the dendrogram so that they are anatomically correct clusters. In order to do this, we introduce a query system based on volumetric information, the result of this query will be a cluster selected from joints of the dendrogram. In this work we use a publicly available atlas which has a parcellation of the brain gyri on the grey and white matter (Wakana et al., 2004) as anatomically-aware volumetric information. Then, an anatomical query is defined by a set of grey or white matter regions that the tract must traverse, for example, the Inferio Fronto Occipital tract must connect the inferio-frontal gyrus and the medial-occipital gyrus. Images of the white matter atlas parcellation and queries for various tracts are shown in Figure 7. After setting an anatomical query Q traversing K labeled regions on the atlas, Q = {r₁,…,r_K, we use the tract probability map of each bundle, Equation 6, to select the bundle $\mathcal{B}$ on the dendrogram T with maximal joint probability of traversing all the regions:

$$\mathcal{B}=\underset{{\mathcal{B}}^{\prime }\in T}{\mathrm{argmax}}\prod _{r\in Q}{\int }_{\mathbf{p}\in r}\mathbb{P}\{\mathbf{p}\in {\mathcal{B}}^{\prime }\}d\mathbf{p}.$$ (7)

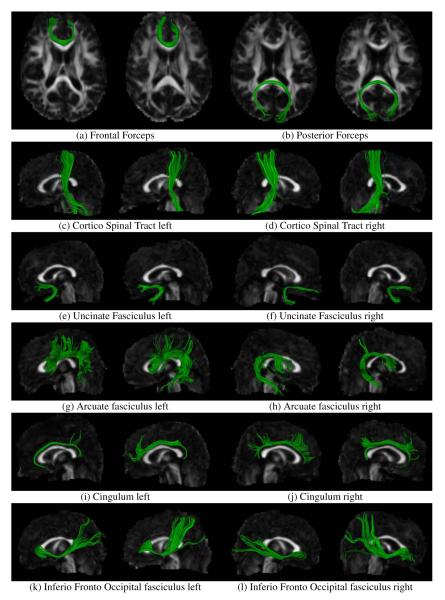
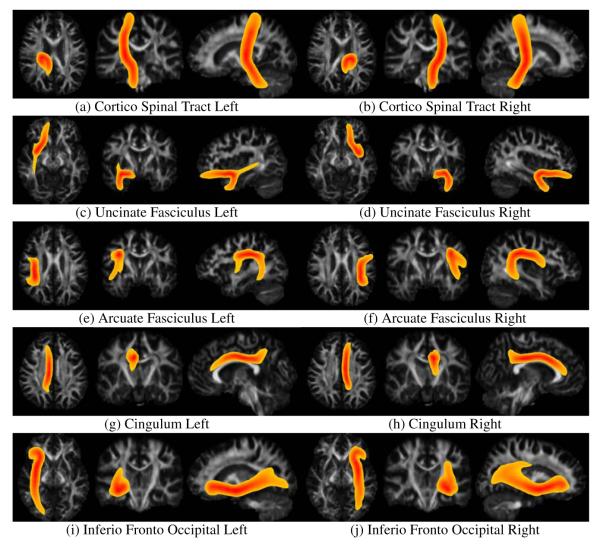
The results of queries for 13 different white matter tracts, Table 1, on 4 subjects are exhibited in Figures 9 to 9 and tract probability maps of the mean bundles across subjects are shown in Figures 10 and 11.

Figure 7.

Illustration of anatomical queries based on volumetric information. A Fractional Anisotropy image and an image of a parcellation of the white matter are shown. The colored stars indicate the anatomical queries. On the left: Purple and red stars tag the inferio-frontal gyrus and middle-occipital gyrus on the left and right sides respectively, this query corresponds to the inferio-fronto-occipital fasciculus on the left and right hemispheres. Yellow stars tag the left and right middle-frontal-orbital gyrus, this query corresponds to the frontal forceps. On the right: white stars tag the pre and post central gyri, the angular, supra-marginal and superio-temporal gyri, this query corresponds to the arcuate fasciculus. The results of this queries on 4 subjects are exhibited in Figures 9 to 9 and tract probability maps for the mean bundles for every subject are shown in Figures 10 and 11.

Table 1.

Queries applied to a set of 21 registered subjects in order to automatically extract major white matter fiber bundles using the algorithm presented in section 2.3. The results of this queries on 2 subjects are exhibited in Figure 9 and tract probability maps for the tract probability maps corresponding to the population-averaged bundles for every subject are shown in Figures 10 and 11

White matter tract to extract	Tract queries
frontal forceps	middle frontal orbital left gyrus, middle frontal orbital right gyrus
posterior forceps	medial occipital left gyrus, medial occipital right gyrus
fornix (left-section)	fornix left, medial temporal left gyrus
cortico spinal tract (post-central)	midbrain, post central gyrus
uncinate fasciculus	middle frontal orbital gyrus, medio temporal gyrus
arcuate fasciculus	post central gyrus, pre central gyrus,angular gyrus, supra marginal gyrus, superio temporal gyrus
cingulum bundle	cingulate gyrus
inferio fronto occipital tract	medial occipital gyrus, inferio frontal gyrus

Figure 9.

White matter fiber bundles automatically clustered from a database of 21 subjects using the clustering algorithm presented in section 2.3. The subjects where previously registered to a white matter fiber atlas and full brain tractography was performed by densely seeding on the whole cerebral white matter. Two subjects are shown.

Figure 10.

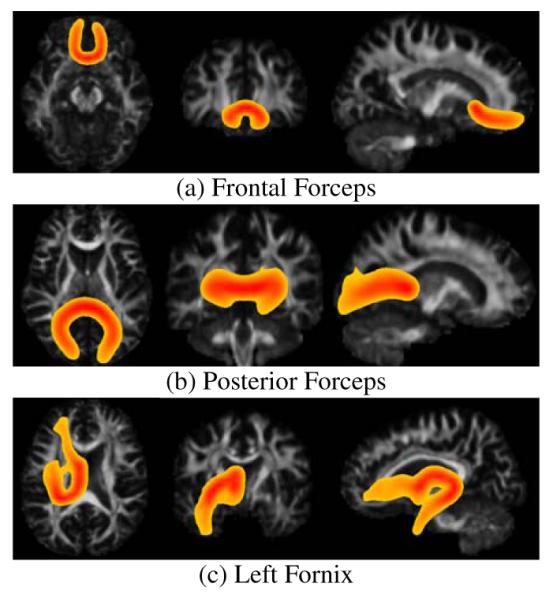
Tract probability maps for the averaged white matter fiber bundles over 21 subjects. The bundles have been automatically extracted from each subject individually using the clustering algorithm presented in section 2.3 and the queries presented in Table 1. The subjects where previously registered to a white matter atlas and full brain tractography was performed by densely seeding on the whole cerebral white matter. Maximum intensity projection is used for the color intensity. Color code ranges from red, when the probability of the voxel belonging to the bundle is 1.0 to yellow, when the probability of the voxel belonging to the bundle is 0.2.

Figure 11.

Tract probability maps for the averaged white matter fiber bundles over 21 subjects. The bundles have been automatically extracted from each subject individually using the clustering algorithm presented in section 2.3 and the queries presented in Table 1. The subjects where previously registered to a white matter atlas and full brain tractography was performed by densely seeding on the whole cerebral white matter. Maximum intensity projection is used for the color intensity. Color code ranges from red, when the probability of the voxel belonging to the bundle is 1.0 to yellow, when the probability of the voxel belonging to the bundle is 0.2.

2.5. Subjects, Imaging and Data Processing

Whole-brain DWI datasets were acquired from 21 healthy volunteers (30.05 +− 7.05 years, 10 Male ) on a Siemens Trio 3T scanner with 1.71 × 1.71mm² in-plane resolution, 2mm thick slices, six unweighted images and 64 diffusion weighted images (b=1000s/mm²) acquired with non-collinear diffusion sensitizing gradients.

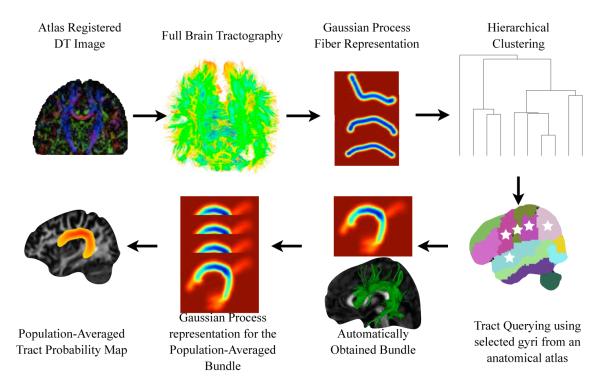
DTI images for each subject were computed and deformably registered, using DTI-DROID (Yang et al., 2008), to a DTI atlas (Wakana et al., 2004). Full brain tractography was performed following (O’Donnell and Westin, 2007), streamline tractography was performed by seeding in sub-voxel resolution by taking every voxel with linear anisotropy higher than .3, dividing it into 0.25 × 0.25 × 0.25mm³ sub-voxels and seeding from each sub-voxel. In average, 10.000 fiber tracts where obtained for each subject. Then, the previously presented clustering algorithm was applied to every subject individually. In order to extract major white matter tracts on every subject individually we performed set of queries, shown in Table 1, over the dendrogram obtained from the clustering of each subject using the tract querying algorithm we introduced. The whole process is shown in Figure 8

Figure 8.

The procedure used to cluster white matter fibers into anatomical bundles and produce the tract probability maps for each bundle: We registered 21 Diffusion Tensor MR images using (Yang et al., 2008). We performed full brain tractography obtaining around 10.000 fibers per brain. We produced the Gaussian Process representation for each fiber as we describe in section 2.2. We identified anatomical bundles like the arcuate or the uncinate fasciculus by applying our clustering and tract querying algorithms to each subject individually as we describe in section 2.3. Finally we produced a population-averaged Gaussian Process for each identified bundle and the corresponding tract probability map with the methodology described in section 2.2

3. Results

We applied the clustering and tract-querying procedure to a 21 subject database. In order to provide qualitative assessment, we show the results of our clustering and tract querying algorithms for 2 different selected subjects in Figure 9. In this figures, we note that tracts obtained by means of our clustering-querying procedures, are consistent with manually obtained tracts by experts in diffusion MRI images (Wakana et al., 2004, Figures 3, 4, and 5) and macroscopical preparations (Lawes et al., 2008, Figures 5iii and 6ii). Furthermore, since our similarity measure handles partial overlap of fibers, we are able to correctly cluster fibers diverging from complex tracts like the arcuate fasciculus and the cingulum which innervate cortical and subcortical regions. This is observable in Figure 9.

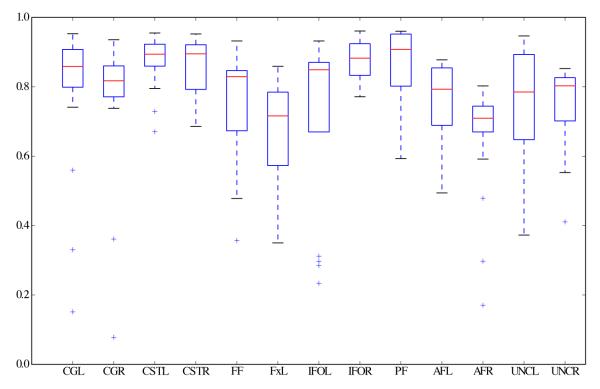
Then, we calculated the population-averaged tract probability maps for each bundle in order to evaluate cluster coherence across subjects. As the first step of this process we calculated the GP representation of the population-averaged bundle across the 21 subjects for each automatically extracted tract: For each queried white matter tract, the GP corresponding to the population-averaged bundle across subjects was calculated using Equation 5. Then, we used Equation 6 to calculate the tract probability map for each for each population-averaged bundle. We show the results of this step in Figures 10 and 11, these maps are in atlas space, over fractional anisotropy images. Visual inspection of these tract probability maps shows that the population-averaged bundles are in agreement with probability maps obtained by manual selection of the bundles in Hua et al. (2008, Figure 3) and chemical staining on post-mortem brains (Bürgel et al., 2006). Finally, in order to provide quantitative evaluation, for each bundle extracted from each subject we quantified its similarity with respect to the corresponding population-averaged bundle using our normalized similarity metric, Equation 4. The result is plotted in Figure 12. In this plot, the boxes span between the second and third quartiles of the similarity with the population-averaged bundle, the red bar is the median similarity. Moreover, the whiskers indicate the bundles whose similarity value with the population-averaged bundle is the smallest and largest within within 1.5 times the interquartile distance of the population-averaged similarity and the ‘+’ symbols indicate outliers. The high mean similarity with low dispersion on the cingulum, the cortico spinal tract and the inferior fronto-occipital fasciculus is consistent with histological studies (Bürgel et al., 2006). Additionally, the relatively lower and more disperse mean similarity on the arcuate and uncinate fasciculus is also consistent with previously cited histological studies.

Figure 12.

Quantitative assessment of bundle coherence among subjects. For each automatically extracted bundle, the similarity between the mean bundle across all subjects and the bundle extracted from each subject individually was calculated by means of the normalized inner product, Equation 4. Similarity ranges from 1, bundles are identical, to 0, bundles are completely different. Boxes span between the second and third quartiles of the similarity with the mean bundle, the red bar is the median similarity. Moreover, the whiskers indicate the bundles whose similarity value with the mean bundle is the smallest and largest within 1.5 times the interquartile distance of the mean similarity and the ‘+’ symbols indicate outliers.

4. Discussion

Results showed that our clustering and tract querying method automatically differentiates white matter fiber bundles consistently across subjects. Furthermore, results demonstrate that we are able to identify white matter structures that agree with several works which manually perform white matter fiber bundle identification. Firstly, results of individual subjects are consistent with manually obtained tracts by experts (Wakana et al., 2004) and macroscopical preparations (Lawes et al., 2008). Next, population-averaged tract probability maps match previously reported results obtained manually (Hua et al., 2008) and through chemical staining (Bürgel et al., 2006). Finally, inter-subject tract variability measured through similarity with the population-averaged bundle is consistent with histological studies (Bürgel et al., 2006). Thus, thanks to our mathematical framework we are able to build an algorithm which performs automatic identification of white matter structures given a full-brain tractography.

In recent years tractography has become a popular means of performing white matter studies through diffusion MRI (Ciccarelli et al., 2008). Tractography results are visually appealing and recent developments produced means to perform analyses of diffusion-derived measures such as the fractional anisotropy. Still, statistical analysis on the fibers themselves has not been performed in sound ways due to the lack of an appropriate mathematical framework. Several examples of statistical analysis of white matter bundles including fiber clustering (O’Donnell and Westin, 2007; Wassermann and Deriche, 2008; Maddah et al., 2008a) and tract probability maps (Hua et al., 2008) have been reported. However, clustering approaches were either not suited for largescale clinical studies or required a great deal of parameter tuning. With regards to tract probability maps, they were calculated by averaging binary masks obtained by manually extracted white matter fibers from tractography or by chemical staining.

This paper proposes a mathematical framework that provides the necessary tools to perform automatic clustering and identification of white matter fibers and subsequent statistics on them. Automatic clustering of white matter fibers into bundles which produces consistent results between subjects is a fundamental tool for clinical studies. In this work we provide the tools to solve these issues. First, we develop a mathematical model for handling white matter bundles which includes spatial and diffusion tensor information and provides the grounds for their statistical analysis. Finally, we use it to develop a clustering algorithm and automatically obtain white matter structures which we then applied to 21 subjects.

4.1. Mathematical framework for white matter bundles

Our mathematical framework sets the foundation for statistical analysis of white matter fiber bundles including applications like clustering and tract-based quantification of scalar quantities amongst others. We provide three important operations for white matter bundle statistics: 1) the first operation to linearly combines white matter fibers into a bundle, see Figure 3; 2) the second quantifies bundle similarity based on their overlap in space, see Figure 4; and 3) the third calculates the probability that a point in space belongs to a bundle, called the tract probability map of the bundle.

Within our model, we represent white matter fibers and bundles as blurred indicator functions; Gaussian Processes are a parametrical representation of these functions. It is important to note that any GP representation of the blurred indicator functions will be able to implement the same operations as ours. These different GP representations are characterized by their covariance functions, which we present in detail in Appendix A. Particularly, our choice of covariance functions contains our smoothness hypothesis about the fibers and enables us to perform efficient calculation of bundle similarity and tract probability maps. We chose a combination of two covariance functions to represent white matter bundles: one representing the smoothness of the bundles and a second changing blurring characteristics according to diffusion tensor information.

The smoothness covariance function allows us to infer the value of the blurred indicator functions from the sequences of points which represent each fiber. Three main characteristics led us to the choice of this covariance function. To begin with, it enforces the least wiggled representations of the fibers which has a smoothing effect on their trajectory. Secondly, it only enforces differentiability up to the second derivative, the minimum necessary to perform this smoothing. These characteristics lead to a covariance function equivalent of a compact support thin-plate spline function, that accurately models smooth spatial data (Wahba, 1990). Other choices of smoothing covariance functions, like the widely used squared exponential function (Rasmussen and Williams, 2006), may lead to infinitely differentiable blurred indicator functions. It has been argued that covariance functions with this characteristic have undesirable geometric effects when representing implicit curves (Williams and Fitzgibbon, 2007) and are unrealistic for modelling many physical processes (Stein, 1999). Finally, an important characteristic of our choice of covariance function is that it has compact support. This is not only more efficient computationally, but also leads to compact support blurred indicator functions which has an important effect on our similarity measure. Our operation quantifies the volume of the overlapping region between two fibers and can be normalized in order to provide a similarity index ranging from 1, when fibers overlap completely, to 0, when they are completely different. Compactness allows the similarity of two blurred indicator function which are sufficiently separated in space to be 0.

We combined the diffusion associated covariance function with that of smoothness in order to alter the blurring of the indicator function. Hence, the blurring is adapted according to diffusion tensor information without changing the compact support characteristic. Such covariance function is based on the diffusion tensor model, however in further work it would be simple to change it in order to make this model appropriate for more descriptive representations of the diffusion propagator (Tuch, 2004; Descoteaux et al., 2007). This would be done by simply changing Equation 13 to suit the chosen representation.

As a final word on the covariance functions, it is important to note that this model is flexible. In further work, a different analysis of white matter fibers and bundles could require a representation of the white matter bundles with a different set of hypotheses. In this case, a different set of covariance functions can be chosen or combined with the ones used in this work in order to retain most of the properties of our proposed framework while expressing different characteristics of the white matter bundles.

4.2. Applications

We presented two applications of our Gaussian Process framework: clustering of white matter bundles and tract probability maps.

With regards to the clustering, we began by creating a dendrogram (see Figure 6) from a full brain tractography. The dendrogram is a versatile tool for representing represent clustering results, given that is a precomputed tree structure where each joint is a candidate cluster. Among other advantages, it allows for interactive exploration of the clustering results at different scales and is resilient to outliers. Moreover, clusters can be selected at different scales using different postprocessing methodologies. In particular, we take advantage of this feature using the tract probability map for each cluster and a volumetric atlas with a parcellation of the cerebral gyri. We combine both of these tools with the dendrogram in order to produce a tract query algorithm.

Tract probability maps were recently introduced as a tool to perform bundle-specific quantification of scalar quantities by Hua et al. (2008). The cited work provides an example of this by analyzing fractional anisotropy (FA) of a multiple sclerosis Patient in comparison with a normal population. Another example of this could be found by calculating the expected FA of a bundle, the weighted average of the FA using the values of the tract probability map as the weights. Tract probability maps have a wide range of applications. For instance, in this work we use them to relate the results of our clustering algorithm to anatomical information given by a white matter atlas enabling us to perform consistent identification of white matter structures among subjects. Although the clustering method is fully automated, it depends on the atlas parcellation and the method used to produce the tracts. We noticed two cases where non-anatomically coherent low probability regions (yellow) are present: the left section of the fornix, Figure 10c, and the left uncinate fasciculus, Figure 11c. In the case of the left side of the fornix, Figure 10c, even though the high probability region (red) is consistent with the previously cited anatomical studies, there is a low probability region corresponding to the optical nerve that can be seen in this map. Careful analysis of the clustered fibers generating this region shows that this artifact comes from the tractography techniques used; these fibers go all the way from the posterior column of the fornix to the frontal sections of the optical nerve. This is not anatomically correct and is the source of the high variability exhibited by this tract in the quantitative analysis, Figure 12. In the case of the left uncinate fasciculus, Figure 11c, there is a high probability region (red) which is consistent with the previously cited anatomical studies. There is however, a low probability region corresponding to a section of the inferior-longitudinal fasciculus. This increases the variability of the clusters corresponding to the left uncinate fasciculus region, Figure 12. Analysis of the clustered fibers constituting this bundle and the query used to obtain the cluster corresponding to the uncinate fasciculus, Table 1, shows that this artifact is produced by the white matter parcellation used to create the tracts. The absence of a parcel corresponding to the temporal pole in the atlas leads us to use the medial temporal gyrus for the corresponding query, shown in Figure 7 right side in light green. This allows fibers fully contained within the medial temporal gyrus to be incorporated in the uncinate fasciculus as a result of the corresponding query. In the future, we will investigate the use of alternate atlases or expert-corrected ROIs to remedy this problem.

In further work, we plan to expand the applications of our framework. One of the most important potential applications is the use of tract probability maps as a probabilistic prior for streamline tractography. This would take advantage of the fact that Gaussian Processes are a generative model, thereby recovering tracts in the case of pathologies where the course of a white matter bundle might be interrupted. In turn, this would enable the comparison of a white matter structure predicted using control data to a pathological one.

5. Conclusion

We presented a mathematical framework to perform statistical operations on white matter fibers obtained from diffusion tensor MRI tractography. In doing so, we showed that this framework constitutes an inner product space which is appropriate for performing statistical operations among white matter bundles. We used this framework to build a clustering algorithm and a tract querying algorithm which allow automatic fiber bundle identification with the white matter queries as a sole parameter. Then, we applied these algorithms to 21 subjects registered to a publicly available atlas with a parcellation of the white matter gyri that we used as a priori anatomical information. Finally, we showed that the results of our clustering were consistent with studies carried by dissection macroscopical preparations and chemical staining. Thus, our framework has proved suitable to perform group studies of the cerebral white matter with minimal user interaction.

Appendix

A. Gaussian Process framework for white matter fibers

Gaussian Processes (GP) are a rich mathematical framework that has been used in a wide variety of research fields. Examples of this being machine learning (MacKay, 1998; Seeger, 2004; Rasmussen and Williams, 2006), spatial statistics (Stein, 1999) and modeling of observational data (Wahba, 1990). They are also related to kernel machines and radial basis functions (Wahba, 1990; Rasmussen and Williams, 2006). In this work, we use GPs to produce a parametric representation of fiber bundles. Particularly, we take advantage of the capability to incorporate different types of hypotheses into the model. This representation provides a simple way to linearly combine fibers into bundles and to measure similarity through an inner product operation which we develop in section A.3. Moreover, it provides a natural method to calculate tract probability maps, developed in section A.4.

A.1. Single fibers as Gaussian Processes

Our parametric representation of a single fiber bundle is based on two hypotheses. Firstly, smoothness: due to the fact that fiber bundles in the brain do not have sharp angles (Basser et al., 2000), we consider that the least wiggled trajectory joining the sample points of a fiber represents that fiber in a most probable manner. Secondly, diffusion associated blurring : The decay of the blurred indicator functions at each point on the bundle can be modeled using the water diffusion profile at that position. This relates the width of the bundle with the two smallest eigenvalues and their eigenvectors.

Using these two hypotheses, we write $y_{\mathcal{F}}\left(\mathbf{p}\right)$, the GP for the indicator function of fiber $\mathcal{F}$, y(p) for clarity, as the combination of two other GPs, y_s(p) and y_d(p). The process y_s(p) represents the smoothness of the trajectory in space, its parameters are inferred from the point sequence obtained through the tractography of a fiber: $\mathbf{f}=\{{\mathbf{f}}_1,\dots ,{\mathbf{f}}_{\mid \mathbf{f}\mid }\}\subset {\mathbb{R}}^3$. The process y_d(p) represents the diffusion information, adds a variability to the fiber at p using full diffusion information and it is inferred from the tensor field over the fiber Σ(f₁),…,Σ(f_∣f∣). We now show that y_s(p) and y_d(p) can be modelled as GPs by characterizing them through covariance functions.

A.1.1. Smoothness

We show that GPs are a fit parametrical model for the blurred indicator functions, by stating a smoothness constraint and, in the first place, showing that functions abiding to this constraint are representable by GPs. Secondly, we proceed to fully characterize the corresponding GP, which consists of deriving the appropriate covariance function.

We formulate a prior for the probability of a function y_s(·) being the indicator function of a fiber. From the hypotheses that an indicator function with smaller curvature is a more probable representation of a given trajectory and that the original trajectory $\mathcal{F}$ is C². We express these hypotheses as the probabilistic prior

$$-\log \left(\mathbb{P}\right\{y_s(\cdot )\left\}\right)=\frac{1}{2}{\int }_{\Omega }{\mid D^2{y}_s\left(\mathbf{p}\right)\mid }^{2}d\mathbf{p}+\mathit{const},\Omega \subset {\mathbb{R}}^3$$ (8)

where the linear operator D maps y_s(·) to its derivative. Then, we characterize y_s(·) from this prior: To begin with, we rewrite the prior over a finite sampling {p_i}_i⊂Ω. Thus, letting [y_s(p_i)]_i be the column vector of values of y_s(·) at each sampled point, we reformulate Equation 8 as

$$-\log \left(\mathbb{P}\right\{{\left[y_s\right({\mathbf{p}}_i\left)\right]}_i\left\}\right)=\frac{1}{2}{\left[y_s\right({\mathbf{p}}_i\left)\right]}_i^T{D}^2{\left(D^2\right)}^T{\left[y_s\right({\mathbf{p}}_i\left)\right]}_i+\mathit{const}$$ (9)

which is the p.d.f of a multivariate Gaussian with covariance matrix

$$C_s={\left(D^2{\left(D^2\right)}^T\right)}^{-1}={\left(D^4\right)}^{-1}.$$ (10)

Hence, due to the Kolmogorov consistency theorem (Kolmogorov, 1956), the function y_s(·) may be represented by the GP,

$$y_s\left(\mathbf{p}\right)~\mathcal{GP}\left(y_s^{\ast }\right(\mathbf{p}),c_s(\mathbf{p},{\mathbf{p}}^{\prime }\left)\right).$$

We now proceed to the characterization of the GP by deriving the covariance function, c_s(·,·), from the probabilistic prior in Equation 9

In order to fully characterize the GP for y_s(p), we need to find an explicit formulation for c_s(p, p’). We do this by first rewriting Equation 10 as D⁴C_s = I. Taking this to a continuous formulation, it reveals c_s(p, p’) to be the Green function of the fourth derivative operator (Williams and Fitzgibbon, 2007; Wahba, 1990)

$${\int }_{\Omega }{D}^4(\mathbf{u},\mathbf{w})c_s(\mathbf{w},\mathbf{v})d\mathbf{w}=\delta (\mathbf{u}-\mathbf{v}).$$

Finally, the solution for the previous equation inside a sphere in ${\mathbb{R}}^3$ of radius R is

$$c_s(\mathbf{p},{\mathbf{p}}^{\prime })≔\psi (\Vert \mathbf{p}-{\mathbf{p}}^{\prime }\Vert ),\psi \left(r\right)=\{\begin{array}{cc}2{\mid r\mid }^3-3R{r}^2+R^3\hfill & r\le R\hfill \\ 0\hfill & r>R\hfill \end{array}\phantom{\}},$$ (11)

where the constants have been chosen such that c_s(p, p’) is a positive semi-definite symmetric function.

Up to this point, we have fully characterized the probabilistic space of functions which describes the blurred indicator function for a smooth trajectory as the family of GP whose covariance function is given by Equation 11. In section A.2 we show how this is useful to infer the value of y_s(·) at an arbitrary point in space from a finite set of samples. The result of this inference process is shown on Figure 13a.

Figure 13.

Segment of two blurred indicator functions for the same fiber. On the left, the green dots represent the samples of the fiber f, only the smoothness-related Gaussian Process is used to generate the blurred indicator function. On the right smoothness and diffusion associated blurring, the green ellipses denote the diffusion tensors. It can be seen how, the decay from the fiber to the background is even along the fiber on the left, while on the right depends on the directional diffusion intensity represented by the diffusion tensors.

A.1.2. Diffusion associated blurring

Until now, we have only used the points which constitute a fiber, to build the blurred indicator function. This function has a maximal value for points with high probability of being at the fiber and decays to 0, meaning no probability of belonging to the fiber, at an even speed across the fiber as seen in Figure 13a. Within this section, we develop the means to perform the blurring using full tensor information. This means that on every direction, the intensity of the blurring depends on the intensity of the diffusion of water molecules. This diffusion is modelled by the diffusion tensors associated with the fiber which were obtained through diffusion tensor MRI. This will enhance the blurring of the blurred indicator function along the fiber and relate the decay across it to the width of the diffusion tensors as depicted in Figure 13b.

We now represent the diffusion information of a point in the trajectory by a blurring GP at that point. The usual practice in GP literature is to perform isotropic blurring on every sampled point of the function (MacKay, 1998). In our case, we use anisotropic blurring at every given point sampled from fiber by means of a second covariance function based on diffusion tensor MRI information. This covariance function is built with convolution kernels: Let g(·) be the GP of an isotropic blurring function, then its convolution with a kernel k(·),

$$y_d\left(\mathbf{p}\right)=\int k(\mathbf{w};\mathbf{p})g\left(\mathbf{w}\right)d\mathbf{w}$$

is a GP with covariance function (Paciorek and Schervish, 2006),

$$c_d(\mathbf{p},{\mathbf{p}}^{\prime })=\int k(\mathbf{w};\mathbf{p})k(\mathbf{w};{\mathbf{p}}^{\prime })d\mathbf{w}.$$ (12)

Thus, the anisotropic blurring of a smooth function with a kernel k(·; p) is representable as a GP with covariance function c_d(·;·).

In order to apply an anisotropic blurring at a point p using diffusion tensor information, we need to encode this information into a blurring kernel k(·; p). To this end, we take the kernel as the probability of a particle going from p to w in a time τ in terms of the Diffusion Tensor Σ(p) (Basser et al., 1994):

$$\begin{array}{cc}\hfill k(\mathbf{w};\mathbf{p})=\mathbb{P}\{\mathbf{w}\mid \mathbf{p},& \tau ,\Sigma \left(\mathbf{p}\right)\}=\hfill \\ \hfill & \frac{1}{\sqrt{{\left(4\pi \tau \right)}^3\mid \Sigma \left(\mathbf{p}\right)\mid }}\exp \left(-\frac{1}{4\tau }{(\mathbf{w}-\mathbf{p})}^T{\left(\Sigma \right(\mathbf{p}\left)\right)}^{-1}(\mathbf{w}-\mathbf{p})\right).\hfill \end{array}$$ (13)

Finally, by performing the integral in Equation 12, we characterize the covariance function for the anisotropic blurring process as,

$$c_d(\mathbf{p},{\mathbf{p}}^{\prime })=\frac{1}{\sqrt{{\left(4\pi \tau \right)}^3\mid \Sigma \left(\mathbf{p}\right)+\Sigma \left({\mathbf{p}}^{\prime }\right)\mid }}\exp \left(-\frac{1}{4\tau }{(\mathbf{p}-{\mathbf{p}}^{\prime })}^T{\left(\Sigma \right(\mathbf{p})+\Sigma ({\mathbf{p}}^{\prime }\left)\right)}^{-1}(\mathbf{p}-{\mathbf{p}}^{\prime })\right).$$

To conclude this section, having characterized the covariance function of the anisotropic blurring process, the blurring at each point is represented by a zero mean GP,

$$y_d\left(\mathbf{p}\right)~\mathcal{GP}(0,c_d(\mathbf{p},{\mathbf{p}}^{\prime }\left)\right).$$

This GP, as seen on the following section, combined with the GP representing the smooth blurred indicator function, y_s(p), produces a smooth function blurred in accordance to diffusion tensor MRI information as shown in Figure 13b.

A.1.3. Gaussian Process representation of a fiber

We are now in position to write the GP formulation for the blurred indicator function of the fiber:

$$y\left(\mathbf{p}\right)~\mathcal{GP}\left(y^{\ast }\left(\mathbf{p}\right)=y_s^{\ast }\left(\mathbf{p}\right);c(\mathbf{p},{\mathbf{p}}^{\prime })=c_s(\mathbf{p},{\mathbf{p}}^{\prime })+c_d(\mathbf{p},{\mathbf{p}}^{\prime })\right).$$ (14)

Up to this point we have a Gaussian Process-based model for the white matter fibers. This model incorporates spatial and diffusion information. Moreover, within this model we can linearly combine fibers into bundles as show in Equation 5 and quantify similarity as shown in Equation 2. In the remainder of this appendix we show how to characterize the value of the indicator function y(p) at any test point $\mathbf{p}\in {\mathbb{R}}^3$, how to effectively calculate the similarity between two fibers and finally, how to calculate the tract probability map for a bundle.

A.2. Calculating the indicator function value distribution for a test point

We want to calculate a p.d.f. for the value of y(·) at a test point $\mathbf{p}\in {\mathbb{R}}^3$. This is a simple operation as we have a GP representation of the indicator function y(·) for a trajectory $\mathcal{F}$, see Equation 14. The p.d.f. of y(p), given the tracked point sequence $\mathbf{f}=\{{\mathbf{f}}_1,\dots ,{\mathbf{f}}_{\mid \mathbf{f}\mid }\}\subset {\mathbb{R}}^3$ and its corresponding diffusion tensor field Σ = {Σ(f₁),…,Σ(f_∣f∣)}⊂SPD(3) are characterized as Gaussian-distributed random variable. More precisely, y(p) is the Gaussian distribution,

$$\left(y\right(\mathbf{p})\mid \mathbf{f},\Sigma ,\mathbf{p})~\mathcal{G}\left(y^{\ast }\left(\mathbf{p}\right),{\sigma }^2\left(\mathbf{p}\right)\right)$$ (15)

due to marginalization properties of the GPs (MacKay, 1998). Setting y(p) to take the constant value l when p is a point that belongs to the fiber trajectory $\mathcal{F}$, the mean and covariance functions can be calculated in the following way (MacKay, 1998):

$$y^{\ast }\left(\mathbf{p}\right)=S_{\mathbf{f}}{\left(\mathbf{p}\right)}^T{C}_{\mathbf{ff}}^{-1}1l{\sigma }^2\left(\mathbf{p}\right)=c_s(\mathbf{p},\mathbf{p})-S_{\mathbf{f}}{\left(\mathbf{p}\right)}^T{C}_{\mathbf{ff}}^{-1}{S}_{\mathbf{f}}\left(\mathbf{p}\right),$$ (16)

where [S_f(p)]_i = [c_s(f_i, p)]_i, [C_ff]_ij = [c(f_i, f_j)]_ij with 1 ≤ i, j ≤ ∣f∣ and 1 is the vector with all ones; the functions c_s(·,·) and c(·,·) were defined in Equation 11 and Equation 14. This formulation is equivalent to “train” a Gaussian Process-based regression with values l at the sampled fiber points and 0 everywhere else. We set the parameter R such that we guarantee that the blurred indicator function is compact, as the maximal distance between two consecutive points in f. The parameter τ modulates the scale of the diffusion associated covariance function by setting a diffusion time. We set it as the maximal time needed to traverse the maximal distance between two consecutive sampled points, R. More precisely, letting λ₁(Σ) be the largest eigenvalue of the tensor Σ, the parameter is

$$\tau =\underset{i=1..\mid \mathbf{f}\mid }{\max }\frac{R}{\sqrt{{\lambda }_1\left(\Sigma \right({\mathbf{f}}_i\left)\right)}}$$

Examples of blurred indicator functions can be seen in figures 3, 4 and 13.

A.3. Calculating the deterministic inner product between two fiber bundles

In order to produce an inner product space for fiber bundles, we must provide an inner product operation. We have previously introduced this operation in Equation 2. In this section we give a more formal definition and show how to calculate it efficiently.

We look for an inner product that quantifies fiber bundle overlapping in a deterministic manner. This simplifies the mathematical treatment of our inner product space, hence its applicability for large scale computations such as clustering of densely sampled full brain tractographies. In order to provide a deterministic inner product, we need to make a decision about the value of y(p) defined in Equation 16. We do this by employing decision theory (De Groot, 2004): To make a decision about the value of y(p) at p, we use a point-like prediction, y⁺(p). This prediction is taken in order to minimise the error in the squared norm induced by our inner product (Equation 3),

$$\underset{y^{+}\left(\mathbf{p}\right)}{\mathrm{argmin}}\int {\left(y^{+}\left(\mathbf{p}\right)-y\left(\mathbf{p}\right)\right)}^2\mathbb{P}\left\{y\right(\mathbf{p})\mid \mathbf{f},\mathbf{t},\mathbf{p}\}dy\left(\mathbf{p}\right)=y^{\ast }\left(\mathbf{p}\right).$$ (17)

Thus letting the mean value of y(p), y*(p), be an appropriate estimator of the value of y(p) at p. Then, as y*(p) is square integrable due to its definition in Equation 16,

$$\langle \mathcal{F},{\mathcal{F}}^{\prime }\rangle ≔{\int }_{{\mathbb{R}}^3}{y}_{\mathcal{F}}^{\ast }\left(\mathbf{p}\right)y_{{\mathcal{F}}^{\prime }}^{\ast }\left(\mathbf{p}\right)d\mathbf{p}$$

is an inner product (Schmidt, 1908). Furthermore, it can be easily computed by replacing Equation 16 in the previous formula:

$$\langle \mathcal{F},{\mathcal{F}}^{\prime }\rangle ≔{\int }_{{\mathbb{R}}^3}{\left(S_{\mathbf{f}}{\left(\mathbf{p}\right)}^T{C}_{\mathbf{ff}}^{-1}1l\right)}^T\left(S_{{\mathbf{f}}^{\prime }}{\left(\mathbf{p}\right)}^T{C}_{{\mathbf{f}}^{\prime }{\mathbf{f}}^{\prime }}^{-1}1l\right)d\mathbf{p}$$

Finally, we simplify the previous expression using that S_f (p) and S_f’ (p) are the only vectors depending on p, see section A.2:

$$\langle \mathcal{F},{\mathcal{F}}^{\prime }\rangle ≔{\left(C_{\mathbf{ff}}^{-1}1l\right)}^T\left({\int }_{{\mathbb{R}}^3}{S}_{\mathbf{f}}\left(\mathbf{p}\right)S_{{\mathbf{f}}^{\prime }}{\left(\mathbf{p}\right)}^{T}d\mathbf{p}\right)C_{{\mathbf{f}}^{\prime }{\mathbf{f}}^{\prime }}^{-1}1l$$ (18)

where

$${\left[{\int }_{{\mathbb{R}}^3}{S}_{\mathbf{f}}\left(\mathbf{p}\right)S_{{\mathbf{f}}^{\prime }}{\left(\mathbf{p}\right)}^{T}d\mathbf{p}\right]}_{ij}={\int }_{{\mathbb{R}}^3}{c}_s({\mathbf{f}}_i,\mathbf{p})c_s({\mathbf{f}}_j^{\prime },\mathbf{p})d\mathbf{p}$$ (19)

can be calculated analytically.

Indeed, Equation 18 gives us a way to calculate the similarity between two fibers without recurring to point-to-point correspondences. Moreover, the fact that Equation 19 can be calculated analytically provides a closed formula for the similarity calculation. Examples of the deterministic inner product of two fibers and of the product of two mean indicator functions are shown in Figure 4. It can be noted that the inner product quantifies partial fiber overlapping.

An interesting outcome of the inner product space property of our framework is the simple calculation of similarity between fiber bundles. We are able to calculate this similarity among two bundles of white matter fibers, $\mathcal{B}=\{{\mathcal{F}}_1,\dots ,{\mathcal{F}}_N\}$ and ${\mathcal{B}}^{\prime }=\{{\mathcal{F}}_1^{\prime },\dots ,{\mathcal{F}}_N^{\prime }\}$,

$$\langle \mathcal{B},{\mathcal{B}}^{\prime }\rangle =\langle \frac{1}{N}\sum _{i=1}^N{y}_{{\mathcal{F}}_i}\left(\mathbf{p}\right),\frac{1}{M}\sum _{j=1}^M{y}_{{\mathcal{F}}_j^{\prime }}\left(\mathbf{p}\right)\rangle ,$$

by using the linearity and symmetry properties of the inner product operation. Then, the previous equation becomes

$$\langle \mathcal{B},{\mathcal{B}}^{\prime }\rangle =\frac{1}{NM}\sum _{i=1}^N\sum _{j=1}^M\langle y_{{\mathcal{F}}_i}\left(\mathbf{p}\right),y_{{\mathcal{F}}_j^{\prime }}\left(\mathbf{p}\right)\rangle .$$ (20)

This provides a quick and simple way to calculate the similarity between to fiber bundles using the fiber-to-fiber similarities. In section 2.3 we use this advantage to perform clustering of fiber bundles.

A.4. Calculation of the tract probability map

Having characterized y(·) as a GP in section A.1, we can express the probability that a point p in ${\mathbb{R}}^3$ is contained in a bundle $\mathcal{F}$, this map is called the tract probability map. We do this by calculating the probability of y(p) = l or, equivalently the expected concentration of the random value y(p) around l,

$$\mathbb{P}\{\mathbf{p}\in \mathcal{F}\}≔\mathbb{P}\left\{y\right(\mathbf{p})=l\mid \mathbf{f},\Sigma ,\mathbf{p}\}\propto \mathbb{E}\left[\theta \right(y\left(\mathbf{p}\right)-l)\mid \mathbf{f},\mathbf{t},\mathbf{p}].$$ (21)

where $\theta :\mathbb{R}\to [0,1]$ is a symmetric kernel. To ease the equations and the computation time, we take Θ(·) as a Gaussian kernel, with standard deviation h,

$$\theta \left(y\right(\mathbf{p})-l)=\frac{1}{2\sqrt{\pi h}}\exp \left(-{\left(\frac{y\left(\mathbf{p}\right)-l}{h}\right)}^2\right).$$

Then, we calculate Equation 21 as

$$\mathbb{E}\left[\theta \right(y\left(\mathbf{p}\right)-l)\mid \mathbf{f},\mathbf{t},\mathbf{p}]=\int \theta \left(y\right(\mathbf{p})-l)\mathbb{P}\left\{y\right(\mathbf{p})\mid \mathbf{f},\mathbf{t},\mathbf{p}\}dy\left(\mathbf{p}\right)$$

which leads to

$$\mathbb{P}\{\mathbf{p}\in \mathcal{F}\}\propto \mathbb{E}\left[\theta \right(y\left(\mathbf{p}\right)-l)\mid \mathbf{f},\mathbf{t},\mathbf{p}]\frac{1}{2\sqrt{\pi (h^2+{\sigma }^2(\mathbf{p}\left)\right)}}.$$ (22)

where h is a bandwidth parameter and σ²(p) is defined in Equation 16. Then, the tract probability map for a bundle $\mathcal{F}$ on a domain Ω, is calculated by evaluating $\mathbb{P}\{\mathbf{p}\in \mathcal{F}\}$ at every point p ⊂ Ω. In order to illustrate the probabilistic map for a bundle, colorcoded surfaces and a probability map over an FA image for anatomical bundles are shown in Figure 5. These tract probability maps are highly similar to the hand-obtained ones by Hua et al. (2008) on DTI images and Bürgel et al. (2006) by means of chemical staining. These two previous works have shown that these tract probability maps are an appropriate tool to perform statistics on white matter fiber bundles.