Speed, Spatial, and Temporal Tuning of Rod and Cone Vision in Mouse

Abstract

Rods and cones subserve mouse vision over a 100 million-fold range of light intensity (−6 to 2 log cd m⁻²). Rod pathways tune vision to the temporal frequency of stimuli (peak, 0.75 Hz) and cone pathways to their speed (peak, ∼12°/s). Both pathways tune vision to the spatial components of stimuli (0.064–0.128 cycles/°). The specific photoreceptor contributions were determined by two-alternative, forced-choice measures of contrast thresholds for optomotor responses of C57BL/6J mice with normal vision, Gnat2^cpfl3 mice without functional cones, and Gnat1^−/− mice without functional rods. Gnat2^cpfl3 mice (threshold, −6.0 log cd m⁻²) cannot see rotating gratings above −2.0 log cd m⁻² (photopic vision), and Gnat1^−/− mice (threshold, −4.0 log cd m⁻²) are blind below −4.0 log cd m⁻² (scotopic vision). Both genotypes can see in the transitional mesopic range (−4.0 to −2.0 log cd m⁻²). Mouse rod and cone sensitivities are similar to those of human. This parametric study characterizes the functional properties of the mouse visual system, revealing the rod and cone contributions to contrast sensitivity and to the temporal processing of visual stimuli.

Introduction

Visual sensitivity is tuned in both space and time. It is generally greatest for intermediate spatial and temporal frequencies and attenuated at higher and lower frequencies. Such tuning characterizes vision in humans, monkeys, and cats. All yield characteristic bandpass functions that relate visual contrast sensitivity to the spatial and temporal frequencies of the stimulus when tested under relatively high (photopic) levels of illumination. At lower (scotopic) levels, sensitivity decreases for high spatial frequencies, and contrast sensitivity functions (CSFs) have a low-pass profile (humans, van Nes et al., 1967; cats, Pasternak and Merigan, 1981). The intensity-dependent changes in contrast sensitivity reflect the transition from rod to cone vision (Hess and Nordby, 1986).

We report here that mouse contrast sensitivity has features in common with the contrast sensitivities of human, monkey, and cat. It changes with light intensity and has a characteristic bandpass shape at photopic levels. The intensity-dependent changes are not restricted to spatial contrast sensitivity. Temporal tuning preference is also intensity dependent. Under photopic conditions, mouse vision is tuned to stimulus speed, whereas under scotopic conditions, it is tuned to the temporal frequency of the stimulus. Such speed versus temporal tuning appears to reflect differential processing of visual inputs by rod and cone pathways.

Our study of mouse vision uses a behavioral assay of reflexive optomotor responses. We used a two-alternative, forced-choice psychophysical procedure (Umino et al., 2006a,b) to measure response thresholds for computer-generated, moving sine-wave gratings (Prusky et al., 2004). Our overall approach is similar to those developed by others for testing vision in humans (Kelly, 1972; Teller et al., 1974), monkeys (De Valois et al., 1974), and cats (Pasternak and Merigan, 1981). This study establishes the spatiotemporal properties of contrast sensitivity of rod and cone vision in mice, revealing the temporal tuning of rod vision and speed tuning of cone vision. The results should prove useful for the functional characterization of the nature and progression of retinopathies in mouse models of disease.

Materials and Methods

Animals.

We tested the vision of mice having normal rod–cone function, mice without rod function, and mice without cone function. For this purpose, we selected the following four mouse models: C57BL/6J (n = 8), Gnat1^−/− (n = 10), Gnat2^cpfl-3 (n = 8), and ALR/LtJ mice. C57BL/6J wild-type pigmented mice served as controls for Gnat1^−/− mice. The Gnat2^cpfl3 mutation is found in the ALS/LtJ strain, and ALR/LtJ mice serve as controls for the ALS/LtJ mutants (Chang et al., 2006). We selected Gnat1^−/− mice because the null mutation in the rod transducin α-subunit gene Gnat1 blocks the phototransduction cascade (Calvert et al., 2000), leading to a loss of rod function. We tested Gnat1^−/− mutant mice between 4 and 10 weeks of age because they show mild retinal degeneration by 13 weeks (Calvert et al., 2000). We selected Gnat2^cpfl-3 mice because they have a missense mutation in the Gnat2 gene that encodes the cone-specific transducin α-subunit and blocks cone function. They have a normal rod-mediated electroretinogram (ERG) but lack a cone-mediated ERG from 4 weeks to 9 months of age (Chang et al., 2006). The C57BL/6J, Gnat2^cpfl-3 and ALR/LtJ mice were shipped from The Jackson Laboratory (Bar Harbor, ME). Breeding pairs of Gnat1^−/− mice were provided by J. Lem (Tufts University, Boston, MA), and offspring were reared at State University of New York (SUNY) Upstate Medical University. Except for Gnat1^−/− mice, ages of the animals tested ranged from 2 to 4 months old. Mice were fed Purina Formulab Diet (catalog #5008; Purina Mills, St. Louis, MO) ad libitum and maintained on a 14/10 h light/dark cycle. Mice were dark-adapted 14 h before testing and were tested during their subjective day. Experimental protocols were approved by the Institutional Animal Care and Use Committee at SUNY Upstate Medical University. In Figures 7–9, we refer to wild-type C57BL/6J mice with normal retinas as “rod–cone vision” mice, to Gnat1^−/− mice with only functional cones as “cone vision” mice, and to Gnat2^cpfl-3 mice with only functional rods as “rod vision” mice.

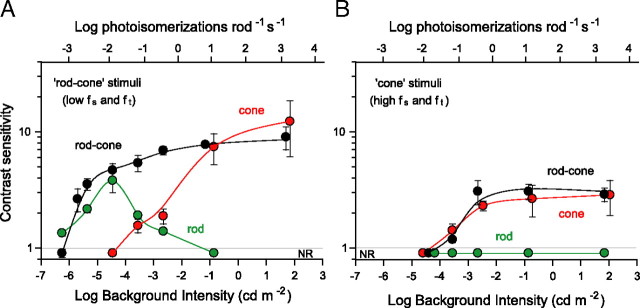
Figure 7.

Spatial contrast sensitivity of rod (Gnat2^cpfl-3), cone (Gnat1^−/−) and rod–cone (C57BL/6J) vision mice plotted as a function of background intensity. A, Comparison of the sensitivities of three genotypes for a grating visible under both scoptopic and photopic conditions (f_s = 0.031 cycles/°; f_t = 0.4 Hz). B, Comparison of contrast sensitivities for a grating under photopic conditions (f_s = 0.383 cycles/°; f_t = 3 Hz). NR, No optomotor response. Top abscissa indicates the photoisomerizations rod⁻¹ s⁻¹, accounting for pupil contraction (Pennesi et al., 1998).

Figure 8.

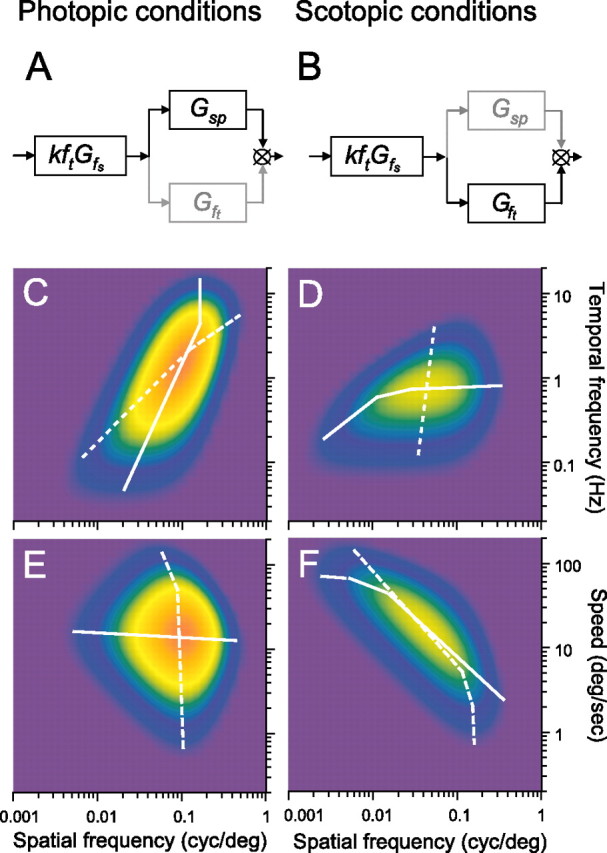
Schematic diagram of the linear model indicating the shift in tuning preference under photopic (A) and scotopic (B) conditions. Contour plots of the contrast sensitivities of wild-type C57BL/6J mice computed with Equation 2 for rotating gratings of different spatial and temporal frequencies under photopic (C, E) and scotopic (D, F) conditions (Table 1 parameters). Color scale from blue to orange encodes contrast sensitivity from low to high. White lines plot maximal sensitivities at constant temporal (dashed) and spatial (continuous) frequencies in C and D and maximal sensitivities at constant speed (dashed) and spatial frequency (continuous) in E and F.

Measuring visual sensitivity from optomotor responses.

We measured visual CSFs of mice by observing their optomotor responses to moving sine-wave gratings [OptoMotry (Prusky et al., 2004)]. Mice reflexively respond to rotating vertical gratings by moving their head in the direction of grating rotation. To observe these head movements, we placed mice (one at a time) on a pedestal situated in the center of a square array of computer monitors that display stimulus gratings. We monitored the mouse using an overhead infrared television camera placed on top of the testing chamber. The camera allowed the observer to observe only the mouse and not the rotating grating. Once the mouse became accustomed to the pedestal with the monitors displaying a 50% gray uniform field, the observer initiated a 5 s trial of a rotating sine-wave stimulus with the direction of rotation randomly selected by the computer-controlled protocol. Using a two-alternative, forced-choice protocol (Teller et al., 1974; Bilotta and Powers, 1991; Solessio et al., 2004; Umino et al., 2006a), the observer selects the direction of grating rotation based on the animal's optomotor response and receives an auditory feedback indicating correct or incorrect response. The monitors return to 50% gray after the 5 s trial. Based on the observer's responses, the computer changes grating contrast using a staircase paradigm and converges on a threshold that we defined as 70% correct observer responses. Contrast sensitivity is the inverse of the grating contrast at threshold. Choice of threshold as 70% correct was arbitrary but is commonly used in two-alternative forced-choice paradigms (Prusky and Douglas, 2004). We measured CSFs over an 8-log unit range of luminance, with the maximum mean luminance of the monitors equal to 70 cd m⁻² (1.8 log cd m⁻²). Light levels were attenuated with cylindrical neutral density filters that surrounded the pedestal. We measured contrast sensitivity at spatial frequencies ranging from 0.014 to 0.511 cycles/° and at speeds of rotation ranging from 0.5 to 48 °/s that corresponds to temporal frequencies ranging from 0.04 to 12 Hz.

Statistical analysis.

In all plots, the error bars indicate the SD of the means. Figure legends give the number of animals tested and fit of model calculations (Eq. 2) to the data (R²). We performed a two-way ANOVA to determine differences (p < 0.05) in optimal speeds under scotopic and photopic conditions (see Fig. 5).

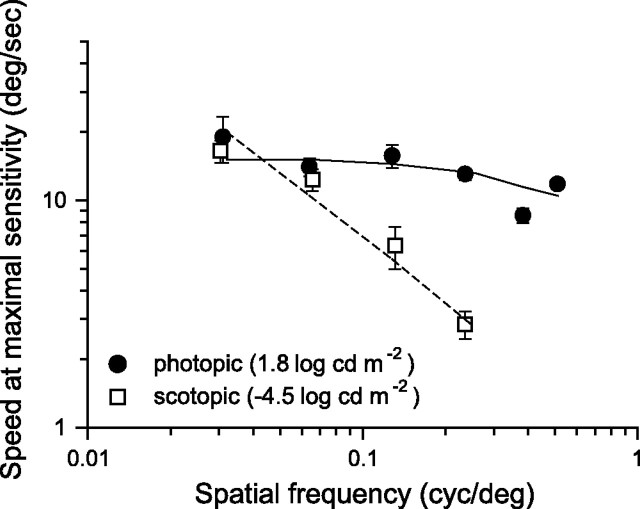
Figure 5.

Speeds eliciting maximal contrast sensitivity plotted as a function of spatial frequency of the rotating sine-wave pattern under photopic (1.8 log cd m⁻²) and scotopic (−4.5 log cd m⁻²) illumination conditions. Equation 2 calculated the continuous and broken lines using the parameters in Table 1. The speed eliciting the maximal sensitivity was determined by fitting the (normalized) speed CSFs with the product of Equations A9 and A10 after substituting f_t = s_p f_s for each mouse under photopic conditions. Likewise, for scotopic conditions, we determined the speed for maximum sensitivity by fitting the (normalized) speed CSFs with the product of Equations A3 and A4.

Linear systems analysis.

We applied linear systems theory to the analysis of contrast sensitivity after the treatment of human vision by Watson (1986). Our rationale for this approach is that the CSFs we measured for mice have inverted U shapes characteristic of electrical filters and of primate vision (for review, see De Valois and De Valois, 1980). This approach models visual information processing with a series of spatiotemporal filters having bandpass and/or low-pass characteristics. We represent the overall CSF of a mouse (G) by the product of these filters:

where k is a scaling factor, and f_t is the temporal frequency of the stimulus. G_fs, G_ft, and G_sp are low-pass filter functions relating contrast sensitivity to spatial frequency (f_s, cycles per degree), temporal frequency (f_t, cycles per second), and grating speed (s_p, degrees per second). The speed of grating rotation, s_p, relates the two independent variables f_s and f_t as f_t = s_p f_s. We multiply the filter functions by kf to account for the observed direct proportionality between sensitivity and temporal frequency. We derive in Appendix the following expression for contrast sensitivity:

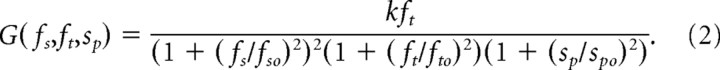The parameters k, f_so f_to, and s_p0 are determined empirically. Table 1 summarizes the values for scotopic and photopic conditions. Unless otherwise noted, Equation 2 generated the curves in Figures 1, 3–5, and 8.

Table 1.

Model parameters for photopic and scotopic conditions

Conditions	Luminance (cd m−2)	k(Hz−1)	fso(cycles/°)	fto(Hz)	spo(°/s)
Photopic	70	16.3	0.18	12.0	15
Scotopic	3.5 × 10−5	34.4	0.3	0.8	80

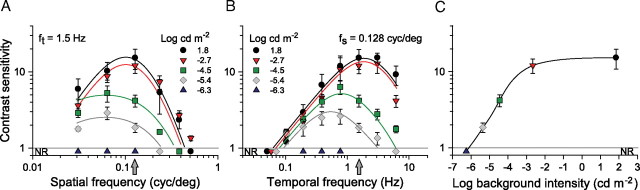
Figure 1.

CSFs of C57BL/6J mice for rotating sine-wave gratings measured over a wide range of background light intensities. A, Spatial CSFs measured at a fixed temporal frequency of 1.5 Hz for which the mice are maximally sensitive (peak in B). The 1.5 Hz frequency was maintained by adjusting the speed of the rotating grating according to the relationship f_t = s_p f_s. Equation 2 calculated the curves for background intensities 1.8 and −6.5 log cd m⁻² using the parameters in Table 1. The curves for −2.7 and −5.4 log cd m⁻² were calculated with Equation 2 using parameters adjusted for best fit (R² > 0.8). B, Temporal CSFs measured at a fixed spatial frequency of 0.128 cycles/° for which the mice are maximally sensitive (peak in A). Experimental limitations precluded measurements of responses to frequencies >6 Hz. C, Spatial contrast sensitivity as a function of background illumination for the sine-wave grating parameters (arrows; f_s = 0.128 cycles/°; f_t = 1.5 Hz) that yielded maximal sensitivity at the highest intensity tested (1.8 log cd m⁻²). A background intensity of −6.0 log cd m⁻² is equivalent to 0.001 photoisomerizations rod⁻¹ s⁻¹. NR, No optomotor response.

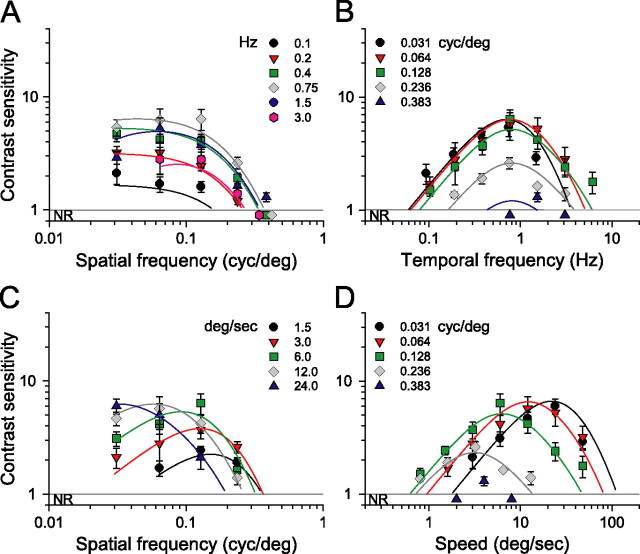
Figure 3.

Scotopic CSFs for C57BL/6J mice (light intensity, −4.5 log cd m⁻²). A, Family of spatial CSFs measured at six temporal frequencies (legend). B, Family of temporal CSFs measured at five spatial frequencies (legend) shows that sensitivity is tuned to temporal frequency of 0.75 Hz. C, Family of spatial CSFs measured at five speeds of rotation. D, Family of speed CSFs measured at the same spatial frequencies as in B. Continuous lines are sensitivity functions calculated with Equation 2 and parameter values listed in Table 1; R² > 0.9 (n = 8 mice). NR, No optomotor response.

Figure 4.

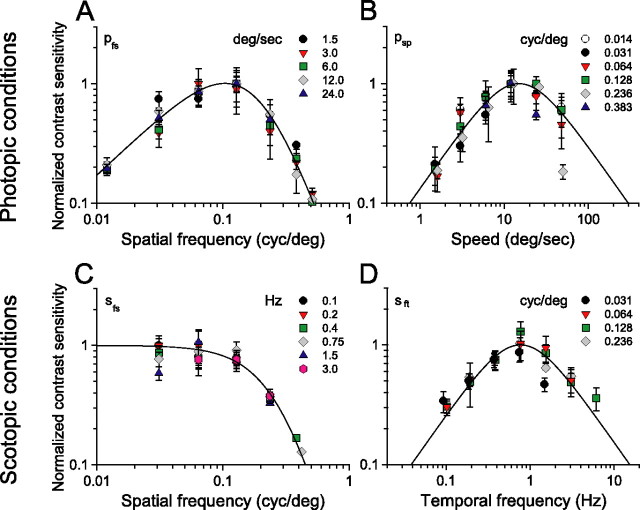
Normalized CSFs for photopic (A, B) and scotopic (C, D) illumination conditions. The fitted continuous curves are used to estimate the parameters in Table 1 (see Appendix). A, Spatial CSF at the same rotation speeds as in Figure 2C and fitted with Equation A8; R² = 0.91 (n = 4). B, Speed CSF for the fixed spatial frequencies in Figure 2D and fitted with Equation A9; R² = 0.9 (n = 4). C, Spatial CSF at the temporal frequencies in Figure 3A and fitted with Equation A2; R² = 0.85 (n = 8). D, Temporal CSF at four spatial frequencies and fitted with Equation A3; R² = 0.98 (n = 8).

Visual acuity.

We define visual acuity as the spatial frequency at the contrast sensitivity of 1.0 that corresponds to gratings having 100% contrast. Operationally, we determine acuity as the point of intersection of an extrapolated spatial CSF with the abscissa at the ordinate value of 1.0.

Converting luminance to rate of photoisomerization in rods and cones.

We measured average luminance of the monitors at the corneal surface using a Graseby Optronics (Orlando, FL) Model 370 Optometer equipped with photometric filter and lumilens. Luminance values (L_v) are expressed in terms of photometric candelas m⁻². To estimate R*, the number of photoisomerizations rod⁻¹ s⁻¹, we applied the following formula (adapted from Wyszecki and Stiles, 1982):

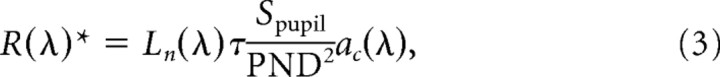where L_n(λ) is the spectral radiance (sr) (photons s⁻¹ m⁻² sr⁻¹ nm⁻¹) of the test monitors measured using a PR-650 SpectraScan portable spectroradiometer (Photo Research, Chatsworth, CA). τ accounts for transmission loss through the ocular media and has a value of 0.7 (Lyubarsky et al., 2002). The area of the pupil S_pupil has a maximal value of 2.4 mm² under dark-adapted conditions and decreases with light adaptation (Pennesi et al., 1998). The posterior nodal distance (PND) is 1.6 mm (Remtulla and Hallett, 1985). The maximal collecting area of a rod is 0.87 μm² (Lyubarsky et al., 2004), and that of a cone is 2.5 μm² (Lyubarsky et al., 1999). We define the maximal effective collecting area, a_c(λ), as the product of the physical collecting area and the normalized absorption spectra of rods and cones derived from visual pigments templates (Govardovskii et al., 2000) and the peak absorptions of rods (λ_max of 498 mn) and cone (λ_max of 508 nm) (Nikonov et al., 2006). Contributions of UV cones (λ_max of 360 nm) are negligible because of the insignificant radiance of the test monitors below 400 nm. The total rate of photoisomerizations per rod (or cone) was estimated by evaluating Equation 3 at each wavelength and integrating across the spectrum. Illumination values in the literature expressed in terms of irradiance at the cornea (E_n(λ)) were converted to photoisomerization rates by applying the following:

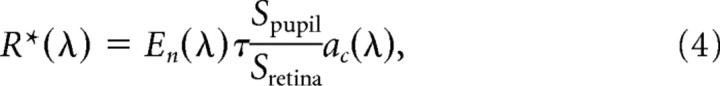where area of the retina S_retina is 18 mm² (Lyubarsky et al., 2002).

Results

Spatial contrast sensitivity increases with luminance

Figure 1A shows that increasing luminance levels increases contrast sensitivity of control C57BL/6J mice and shifts their peak sensitivity to higher spatial frequencies. The mice did not elicit detectable optomotor responses (NR) at the lowest light intensity tested (−6.3 log cd m⁻², blue triangles) but did so at −5.4 log cd m⁻² (gray diamonds) with low sensitivity (2.9 ± 0.6), requiring 34.5% grating contrast to reach threshold. Their sensitivity increased to 5.3 ± 1.3 at −4.5 log cd m⁻², with a peak at 0.064 cycles/°. Increasing luminance to −2.6 log cd m⁻² increased sensitivity to 12.0 ± 2.6, but an additional 30,000-fold increase to 1.8 log cd m⁻² only had a modest effect, incrementing sensitivity to a peak value of 15.3 ± 4.5 (6.5% contrast). Visual acuity also increased with luminance from ∼0.22 cycles/° at −5.4 log cd m⁻² to a maximal value of ∼0.6 cycles/° at 1.8 log cd m⁻². In addition, increasing luminance levels changed the shape of the CSF from low-pass (less than −4.5 log cd m⁻²) to bandpass (more than −2.6 log cd m⁻²). Together, the data in Figure 1A show that both spatial contrast sensitivity and acuity of mice increase with luminance.

Temporal contrast sensitivity increases with luminance

Figure 1B plots a family of temporal CSFs that parallel the spatial CSFs in Figure 1A. They were measured from the same mice, and, as was the case in Figure 1A, the mice first elicited detectable optomotor responses at a background of −5.4 log cd m⁻². Their contrast sensitivity then increased with background intensity to a maximum value of 15.3 ± 4.5 at 1.8 log cd m⁻². Remarkably, in the low-frequency range, background luminance has no effect on contrast sensitivity. Contrast sensitivity increases in proportion to temporal frequency, along an asymptote of unity slope, diverging from it and decreasing monotonically at high temporal frequencies. Contrast sensitivities are highest near the divergence from the asymptote and, with increasing background intensity, shift to higher temporal frequencies (3 Hz). Sensitivity is highest at high background intensities and relatively high temporal frequencies and then decreases for frequencies >3 Hz. The data in Figure 1B show that increasing luminance increases temporal contrast sensitivity, accompanied by small shifts in temporal tuning.

Mice can see over an ∼100 million-fold range of light intensity

Figure 1C plots contrast sensitivities from Figure 1, A and B, as a function of light intensity. Plotted are the data for the grating parameters that yielded maximum contrast sensitivity at the highest intensity tested (Fig. 1A,B, arrows). As noted above, the mice did not respond (NR) at −6.3 log cd m⁻² but did so at −5.4 log cd m⁻² with an average sensitivity of 1.9 ± 0.3 (52.6% contrast) and reached a maximum value of 15.3 ± 4.5 at 1.8 log cd m⁻², the highest intensity tested. As described below in experiments with functional rod-less and cone-less mice (see Figs. 6, 7), we found that this approximate 8-log unit range of intensity encompasses both scotopic and photopic vision with a mesopic range separating the scotopic (<4.0 log cd m⁻²) and photopic (>2.0 log cd m⁻²) ranges.

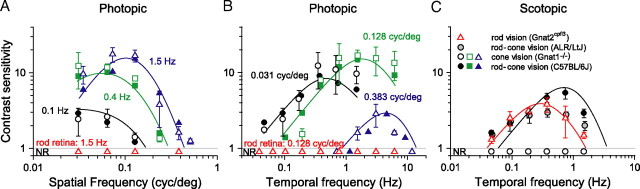
Figure 6.

Comparison of CSFs for knock-out and control mice under photopic and scotopic conditions. A, Spatial CSFs for C57BL/6J mice (filled symbols and continuous curves) and for Gnat1^−/− mice (unfilled symbols) measured for three temporal frequencies under bright photopic conditions of 1.8 log cd m⁻². B, Temporal CSFs for C57BL/6J and Gnat1^−/− mice for three spatial frequencies. Gnat2^cpfl-3 mice did not respond under the photopic conditions (NR, red triangles). C, Temporal CSFs for Gnat2^cpfl-3 (red triangles) and their control ALR/LtJ albino mice (gray circles) measured under scotopic conditions (−4.5 log cd m-2). Gnat1^−/− mice did not respond (NR, white circles). Spatial frequency is 0.031 cycles/°. Red curve through the red triangles is calculated with Equation 2 using the following parameters: f_to = 0.4 Hz, f_so = 0.03 cycles/°, f_sp = 80°/s, and k = 23 Hz⁻¹. The black curve in C and all curves in A and B were calculated with the parameters in Table 1.

Mouse photopic vision is tuned to speed

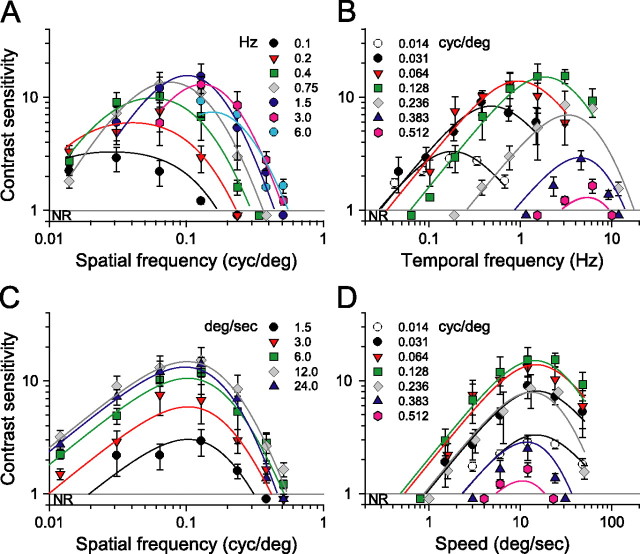
To better understand the spatiotemporal properties of photopic vision, we performed a parametric study under bright light conditions (1.8 log cd m⁻²). Figure 2A shows a family of spatial CSFs measured at seven temporal frequencies adjusted by changing the speed of the rotating grating. It is apparent that grating speed affects the shape of the spatial CSFs. Contrast sensitivity is relatively low, and the functions are low pass in shape and limited in bandwidth (0.2 cycles/°) at the lowest temporal frequencies tested (0.1–0.2 Hz). Sensitivity increases and the functions acquire a bandpass characteristic at higher temporal frequencies. That is, contrast sensitivity nearly doubled as temporal frequency increases from 0.4 to ∼1.5 Hz, suggesting improved “spatial resolution.” A temporal frequency of 0.75 Hz yielded peak sensitivity of 13.1 ± 3.4 at 0.064 cycles/°, and a temporal frequency of 1.5 Hz gave a peak sensitivity of 15.3 ± 4.5 at 0.128 cycles/°. Additional increases in temporal frequency (>3 Hz) attenuated contrast sensitivity. Increases in spatial frequency also attenuated sensitivity with no responses detectable for frequencies >0.5 cycles/°.

Figure 2.

Photopic contrast sensitivity of C57BL/6J mice (light intensity, 1.8 log cd m⁻²). A, Family of spatial CSF measured at seven temporal frequencies (legend). B, Family of temporal CSF measured at seven spatial frequencies (legend). C, Family of spatial CSF measured at five speeds of rotation. D, Family of speed CSF measured at the same spatial frequencies as in B. Note that sensitivity is tuned to the speed of 15°/s. Continuous lines are calculated with Equation 2 and parameter values listed in Table 1; R² > 0.86 in all plots (n = 4 mice). NR, No optomotor response.

The family of temporal CSFs in Figure 2B plots contrast sensitivity as a function of temporal frequency for fixed spatial frequencies. Unlike the sensitivity functions in Figure 2A, the shapes of those in Figure 2B do not change significantly with spatial frequency. All are bandpass with similar attenuation of sensitivity at low and high temporal frequencies, but they shift to the right along the abscissa as spatial frequency increases. In essence, they behave much like a bank of narrow bandpass filters with the envelope covering wide range of temporal frequencies extending from 0.04 to ∼12 Hz.

Remarkably, holding grating speed constant yields sensitivity functions with identical bandpass profiles (Fig. 2C). That is, replotting the CSFs in Figure 2A for given grating speeds produces similarly shaped functions, all having peak sensitivities at 0.128 cycles/°. The CSFs are displaced along the sensitivity axis, i.e., changes in grating speed merely scale the sensitivities. Normalizing the CSFs (see Fig. 4A) demonstrates that their shape is indeed invariant and well described by a bandpass filter function, p_fs (Eq. A8). Analogously, plotting the CSFs in Figure 2B in terms of grating speed with spatial frequency held constant produces similarly shaped functions peaking at 12°/s (Fig. 2D). These speed CSFs maintain a characteristic bandpass shape, but unlike the temporal CSFs (Fig. 2B), they are not spread along the abscissa. Rather they are centered about a grating speed of 12°/s, the speed evoking maximal sensitivity. Function shape does not change with spatial frequency, and the normalized functions (Fig. 4B) are well fit by a bandpass filter function, p_sp (Eq. A9). The independence of spatial frequency and speed indicates that contrast sensitivity is “spatial-speed” separable under photopic conditions. In other words, mouse spatial contrast sensitivity is “speed tuned” because the grating speed for which mice are maximally sensitive does not depend on spatial frequency.

Based on the separability of spatial frequency and speed, we describe photopic contrast sensitivity as the product of two functions, one dependent on grating speed and the other dependent on grating spatial frequency. As described in Materials and Methods (see also Appendix), we derive a single expression, P(f_s, s_p) (Eq. A12) for photopic contrast sensitivity of mice based on separate spatial and speed filter functions, p_sp and p_s. We calculated all curves in Figure 2 with Equation 2 based on p_fs, p_sp, and a third function, p_ft (Eq. A10), that accounts for the attenuation of sensitivity at high temporal frequencies (f_t > 10 Hz).

Mouse scotopic vision is tuned to temporal frequency

Whereas photopic contrast sensitivity is speed tuned (Fig. 2), scotopic contrast sensitivity is temporally tuned (Fig. 3). Figure 3A shows a family of spatial CSFs measured from wild-type mice under scotopic conditions (−4.5 log cd m⁻²), with each function measured at a constant temporal frequency. Sensitivity is 2.1 ± 0.4 at 0.1 Hz, increases to a maximum of 6.4 ± 1.3 at 0.75 Hz, and then declines progressively at higher temporal frequencies. The conspicuous tuning characteristic of the photopic CSFs (Fig. 2A) is absent. Sensitivity is approximately constant for gratings with spatial frequencies <0.128 cycles/° and declines sharply for spatial frequencies >0.128 cycles/°. The functions are displaced vertically along the sensitivity axis, that is, changing temporal frequency merely scales the sensitivities. Normalizing the functions (Fig. 4C) reveals that shape is indeed invariant with temporal frequency and is well described by a low-pass filter (s_fs in Eq. A2). Under these low scotopic intensities, the mice did not respond to spatial frequencies >0.25–0.3 cycles/°, limiting the bandwidth to approximately half that measured under photopic conditions.

The temporal CSFs measured from wild-type mice under scotopic conditions are bandpass in shape and centered around 0.75 Hz (Fig. 3B). Unlike the photopic temporal CSFs, the scotopic functions are not displaced along the abscissa. Indeed, the functions peak at 0.75 Hz temporal frequency and are scaled vertically along the sensitivity axis with spatial frequency. Mice responded with maximal sensitivity of ∼6.0 to gratings of intermediate spatial frequencies (0.031–0.128 cycles/°). Contrast sensitivity then decreases with spatial frequency to 2.6 ± 0.3 at 0.236 cycles/°. Shapes of the CSFs do not change significantly with spatial frequency and are well described by a bandpass filter centered at a temporal frequency of 0.75 Hz, as is apparent in the normalized CSFs plotted in Figure 4D (s_ft in Eq. A3).

Invariance of the spatial and temporal CSFs suggests that mouse scotopic sensitivity can be expressed as the product of two functions, one dependent on temporal frequency and the other on spatial frequency. We calculated all curves in Figure 3 with a single expression for scotopic contrast sensitivity (Eq. 2), based on s_fs and s_ft in Figure 4, C and D, and the parameter values listed in Table 1. Second-order effects observed with speed >24°/s are accounted for by s_sp (Eq. A4).

A corollary of “temporal” tuning is the absence of “speed” tuning. When plotted as a function of speed, the bandpass spatial CSFs shift along the abscissa (Fig. 3C) and likewise for the speed sensitivity functions (Fig. 3D). The position of each function along the abscissa decreases in direct proportion to the spatial frequency. Figure 5 plots the speed of rotation eliciting maximal sensitivity as a function of spatial frequency. Under photopic conditions, the speeds eliciting maximal sensitivity are nearly constant at 15°/s. The continuous line represents speeds estimated from the model (Eq. 2). The predicted break at spatial frequencies >0.24 cycles/° appears to match the speed reduction. Under scotopic conditions, the speed decreases in proportion to the spatial frequency of the grating (Fig. 5, open squares). Speed is ∼15°/s at 0.031 cycles/° and decreases at a constant rate to 2.8°/s at 0.236 cycles/°. A two-way ANOVA (Tukey's test) indicates that optimal speeds are statistically different under scotopic (p < 0.05) but not photopic conditions. Additional pairwise comparisons confirm differences in optimal speed between conditions for f_s >0.064 cycles/°. The dashed line with unitary slope represents the velocities predicted by the model (Eq. 2) using the scotopic parameters in Table 1. There is good agreement between measured and predicted speeds.

Rod and cone contributions to contrast sensitivity

To specify the ranges of rod and cone vision and their contributions to contrast sensitivity, we tested mice having only functional cones (Gnat1^−/− mice; termed cone vision mice), mice having only functional rods (Gnat2^cpfl-3 mice; termed rod vision mice), as well as mice with normal rod–cone vision (wild-type C57BL/6J mice; termed rod–cone vision mice). We measured their spatial and temporal CSFs under dim and bright background conditions. Using a bright background of 1.8 log cd m⁻², we found that the spatial CSFs of cone vision mice match well those of wild-type mice (Fig. 6A). Both genotypes have equal contrast sensitivities and similarly shaped spatial CSFs at temporal frequencies of 0.1 and 0.4 Hz but not at the higher1.5 Hz at which cone vision mice are somewhat more sensitive to low spatial frequencies. Both genotypes also have similar temporal CSFs (Fig. 6B). Note that no optomotor behavior was detected in rod vision mice (Fig. 6A,B, red triangles). The high background intensities of these tests likely saturated the rods or other elements downstream along the rod pathway, leaving the rod vision mice functionally blind. The close match of the spatial and temporal CSFs of cone vision mice with those of wild-type mice in Figure 6, A and B, indicates that cones mediate vision at a background of 1.8 cd m⁻² and that this intensity is within the photopic range. The similar visual functions in mutant and wild-type mice suggest that the retinas of cone vision mice are not degenerate and possess no abnormalities.

Under dim light conditions (−4.5 log cd m⁻²), rod vision and wild-type mice exhibit similar temporal contrast sensitivities, and cone vision mice appear functionally blind (Fig. 6C). The temporal CSF of rod vision Gnat2^cpfl3 mice (red triangles) matches closely that of ALR/LtJ albino mice (gray circles) that serve as controls for the rod vision mice (Chang et al., 2006). The overlapping sensitivities of Gnat2^cpfl3 and albino control mice are inconsistent with circuitry abnormalities or degeneration in the retinas of the Gnat2^cpfl3 rod vision mice.

The CSFs of both Gnat2^cpfl3 and albino control mice match that of wild-type C57BL/6J mice (filled black circles) at low temporal frequencies (<0.4 Hz). Note that no optomotor responses (NR) were detected from cone vision mice under these dim illumination conditions (Fig. 6C, open circles). The close match of the CSFs of rod vision mice to those of wild-type mice points to exclusive rod function at a background of −4.5 cd m⁻², which lies within the scotopic range. The close match also supports use of the Gnat2^cpfl-3 mice as an adequate model for studying rod-mediated vision.

To specify more precisely the scotopic and photopic ranges and the rod and cone contributions to contrast sensitivity within them, we tested the same null mutants and wild-type mice over a wide range of background intensities. Figure 7A compares contrast sensitivities of all three genotypes for a rotating grating detectable by both rod and cone systems. We selected grating parameters based on the spatiotemporal frequencies that yielded similar sensitivities for C57BL/6J and Gnat2^cpfl-3 mice in Figure 6. Note that rod vision (green symbols) and rod–cone vision (black symbols) mice have about the same low-contrast sensitivity at the dimmest light levels tested (−6.2 to −5.8 log cd m⁻²). We determined absolute threshold for rod vision by extrapolating the data to a contrast sensitivity of 1.2. We selected a contrast sensitivity of 1.2 (83% grating contrast) because it is the highest contrast for which we can derive reliable thresholds (70% correct) with our computer-controlled staircase paradigm. This criterion yields approximately equal thresholds for rod vision and rod–cone vision mice of −6.0 log cd m⁻² that we designate as rod threshold. Above rod threshold, the sensitivities of both genotypes increase together as luminance is increased, reaching a sensitivity of ∼4.0 (25% grating contrast) at −4.5 log cd m⁻². The sensitivity of rod–cone vision mice continues to increase with light intensity but that of rod vision mice does not. It decreases with increases in light intensity, becoming negligible at more than −2.6 log cd m⁻².

Shifting attention to cone vision Gnat1^−/− mice in Figure 7A (red symbols), we find that these null mutants reach a contrast sensitivity of 1.2, the criterion for cone threshold, at approximately −4.0 log cd m⁻², which is 100-fold higher than rod threshold. The sensitivity of cone vision mice increases with intensity over the next 4 log units, reaching 7.4 ± 2.3 at −0.9 log cd m⁻² and matching the sensitivity of wild-type mice at the same intensity. Additional increases in background intensity (−0.9 to 1.8 log cd m⁻²) yielded relatively constant contrast sensitivity for both cone and rod–cone vision mice in accordance with Weber's law.

Cone vision mice (Fig. 7B, red symbols) are as sensitive as wild-type mice to a test grating of high spatial and temporal frequencies that favors cone-mediated vision. Rod vision mice (green symbols) did not respond to the grating (NR). The close match between the data for cone vision and rod–cone vision mice indicates that cone pathways mediated the contrast sensitivities in Figure 7B. The lower contrast sensitivities in Figure 7B relative to those in Figure 7A are expected from a test grating having such high spatial and temporal frequencies (Fig. 1).

Together, the data in Figure 7 underscore the role of rods at low scoptopic levels and of cones at high photopic levels. Rods alone mediate mouse vision at luminance levels less than −4.0 log cd m⁻², defining the scotopic range, and cones do so at luminance levels more than −2.0 log cd m⁻² defining the photopic range. Rod and cone responses combine to provide vision in the intermediate range of −4.0 to −2.0 log cd m⁻², indicating the mesopic range. Rod and cone sensitivities do not sum in the mesopic range to yield that of wild-type mice, indicating nonlinear contributions from both rods and cones.

Discussion

Spatial vision of mice shares features with that of cats (Pasternak and Merigan, 1981), monkeys (De Valois et al., 1974), and humans (Kelly, 1972). All have frequency-dependent contrast sensitivity, bandpass-shaped CSFs, and relatively constant contrast sensitivity (Weber-like behavior) over the photopic range of vision. Weber-like behavior breaks down in the mesopic and scotopic ranges at which sensitivity and bandwidth decline steadily with decreasing luminance. Although humans and mice share some vision properties, humans have ∼10 times greater contrast sensitivity (0.5 vs 5% contrast) and ∼100 times greater acuity (60 vs 0.5 cycles/°). Our measure of mouse acuity of 0.48 ± 0.03 cycles/° (n = 4) under photopic conditions is similar to the value of 0.4 cycles/° reported by others (Prusky et al., 2004; Douglas et al., 2005; Pinto et al., 2007) using the same behavioral apparatus (OptoMotry) but different behavioral methodologies. Interestingly, acuities of 0.51–0.56 cycles/° were measured using a different behavioral apparatus (water maze) but a similar two-alternative, forced-choice method (Prusky et al., 2000; Prusky and Douglas, 2004). Our measure of mouse contrast sensitivity under photopic conditions agrees in general with the results of Prusky et al. (2004) and Pinto et al. (2007) with the exception that we detected peak contrast sensitivities at higher spatial frequencies than Prusky et al. (2004) but did not detect the plateau in spatial CSF they report. There are no comparable measures of mouse contrast sensitivity in the mesopic or scotopic intensity ranges as determined by tests of knock-out mice in Figures 6 and 7.

Mice and humans also share some properties of temporal vision. For example, increasing light intensity increases contrast sensitivity and the bandwidth of the temporal CSFs of both mice and humans. However, there are differences. Mice have relatively poor sensitivity and temporal resolution compared with humans. Under photopic conditions, contrast sensitivity in mice peaks at 1.5 Hz, approximately fivefold below human performance (Kelly, 1972). Also, contrast sensitivity is constant over a 10⁶-fold range of light intensity (−4.0 to 1.8 log cd m⁻²) for low temporal frequencies, a clear example of Weber-like light adaptation.

A remarkable consequence of light adaptation is a shift in tuning preference. Adapted to photopic conditions, mouse contrast sensitivity is tuned to the spatial frequency and speed of the rotating grating (Fig. 2). That is, because the grating speed for maximum sensitivity is the same for all spatial frequencies (Fig. 8E, continuous line), the temporal frequency for maximum sensitivity (Fig. 8C, dashed line) must vary as a function of spatial frequency. A mouse's sensitivity cannot be tuned to one of the grating parameters (speed, spatial, and temporal frequency) independent of the other two because the grating speed equals temporal frequency divided by spatial frequency. The orthogonal relationship in Figure 8E underscores the separability of speed and spatial frequency under photopic conditions. The lumped linear model (Fig. 8A) represents this separability as dominance of the contributions of the low-pass filters G_fs and G_sp relative to G_ft. Discarding the nondominant stage, G_ft reduces the sensitivity functions to the product of two independent functions, G_fs and G_sp. Similarly, under scotopic conditions, contrast sensitivity is tuned to spatial and temporal frequencies of the grating (Fig. 3). Specifically, the near orthogonal relationship between temporal and spatial frequencies for maximum sensitivities in Figure 8D (continuous and dashed lines) points to separable tuning for spatial and temporal frequency under scotopic conditions. Because temporal frequency for maximum sensitivity varies little with spatial frequency (Fig. 8D), grating speed must be approximately proportional to spatial frequency (Fig. 8F), and thus scotopic contrast sensitivity has separable tuning for spatial and temporal frequency. The lumped linear model in Figure 8B represents scotopic conditions as dominant contributions from G_fs and G_sp and minimal from G_sp. The physiological mechanisms underlying spatial, temporal, and speed tuning are unknown in mouse. They could originate in the retina, in higher levels, or be distributed across all levels of the visual system. Indeed, different cortical pathways may exhibit different spatial and temporal tuning. Interestingly, changes in tuning speed versus temporal preference have been detected in the midtemporal visual area of macaque visual cortex (Priebe et al., 2006). Neurons in this part of the primate brain are tuned to the spatial and speed dimensions of high-contrast gratings and to the spatial and temporal frequencies of low-contrast gratings. If the mouse visual system possesses analogous neurons, their tuning preference would be shifted by luminance level rather than contrast.

Humans and mice have similar thresholds for rod and cone vision. The dark-adapted threshold of rod vision Gnat2^cpfl3 equals that of wild-type C57BL/6J mice and is approximately −6.0 log cd m⁻² (Fig. 7A), which converts to 0.001 photoisomerizations rod⁻¹ s⁻¹ (estimated from Eq. 3, and shown in Fig. 7) and is same as the thresholds measured using a water maze of 0.001–0.002 photoisomerizations rod⁻¹ s⁻¹ (Sampath et al., 2005; Nathan et al., 2006). The similarity of dark-adapted thresholds determined from dissimilar methods is remarkable. The human dark-adapted threshold for detecting sinusoidal gratings is 0.5 milliTrolands (van Nes et al., 1967; Hess and Howell, 1988), which converts to 0.001 photoisomerizations rod⁻¹ s⁻¹ and agrees with our psychophysical measure of rod threshold in mouse. Interestingly, thresholds for human cone vision measured psychophysically (Shapley and Enroth-Cugell, 1984) range from 1.4 to 140 photoisomerizations cone⁻¹ s⁻¹ depending on method. The lowest threshold of 1.4 is slightly higher than the value of 0.4 photoisomerizations cone⁻¹ s⁻¹ that we calculated with Equation 3 from our cone threshold of −4.0 log cd m⁻² for cone and rod–cone vision mice (Fig. 7). Also, the mouse cone thresholds of 50–70 photoisomerizations cone⁻¹ s⁻¹ derived from water-maze measurements of Nathan et al. (2006) and Sampath et al. (2005) are >100 times higher than those we calculate from the data in Figure 7.

Mouse scotopic (rod) and photopic (cone) vision bracket a transition “mesopic” region of overlapping rod and cone vision. Rod and cone signals combine to sustain a high-contrast sensitivity in the mesopic range (−4.0 to −2.0 log cd m⁻²) (Fig. 7A). Rod contributions begin to decline at approximately cone threshold (−3.6 log cd m⁻²) and are negligible in the photopic range (more than −2.0 log cd m⁻²). Cone contributions, conversely, increase throughout the mesopic range, reaching near maximal levels at approximately −1.0 log cd m⁻². The contrast sensitivities of rod vision and cone vision mice do not sum linearly to produce the contrast sensitivity of rod–cone wild-type mice. Such lack of additivity in the mesopic range points to interactions between rods and cones such as those detected in human vision (Goldberg et al., 1983).

Lack of rod-mediated vision above approximately −2.0 log cd m⁻² cannot be attributed to saturation (Nikonov et al., 2006) or loss of gain (Dunn et al., 2006) of rod photoreceptors because both physiological effects occur at significantly higher light intensities (>2–100 photoisomerizations rod⁻¹ s⁻¹). However, the gain of synapses between rod bipolar and AII-type amacrine cells (Dunn et al., 2006) and the scotopic threshold response (Saszik et al., 2002) decrease at intensities as low as 0.01–0.03 photoisomerizations rod⁻¹ s⁻¹, which corresponds to approximately −4.4 log cd m⁻², the intensity at which the contrast sensitivity of rod vision mice begins to decrease (Fig. 7). Rod-mediated visual sensitivity thus appears to be controlled by neurons postsynaptic to rod photoreceptors rather than the rods themselves. Our finding of blindness of cone-less (rod vision) mice for luminance levels above −2.0 log cd m⁻² that converts to 1 photoisomerization rod⁻¹ s⁻¹ contrasts with reports of cone-less mice behaving in a water maze (Nathan et al., 2006) and responding to incremental light paradigms (Williams et al., 2005) at levels up to 3 × 10³ photoisomerizations rod⁻¹ s⁻¹.

In summary, the methodology and results presented here will be useful in characterizing mouse models of retinal disease. The spatiotemporal properties of rod- and cone-mediated vision should aid in assessing the precise effects of degeneration and efficacy of treatment of individual mice. Discovery of the effect of light adaptation on temporal tuning preference underscores the power of rigorous animal psychophysical testing.

Appendix

A model of contrast sensitivity in mouse

The overall CSFs are expressed as the product of individual spatial, temporal, and speed CSFs. Thus, under scotopic conditions, the overall contrast sensitivity can be expressed as follows:

where A_max is a scaling constant, and s_fs, s_ft, and s_sp are the normalized filter functions relating contrast sensitivity to f_s, the spatial frequency, to f_t, the temporal frequency, and sp, the speed of the rotating gratings. The normalized functions are designed to fit the empirical data and are defined as follows:

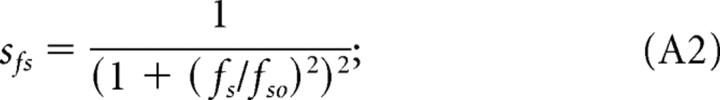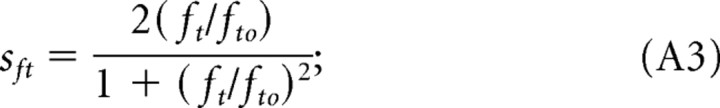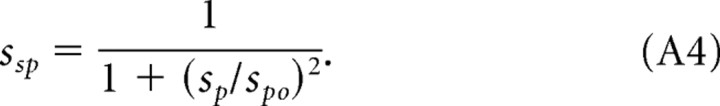Combining Equations A1–A4, we can rewrite the scotopic CSF (S) as follows:

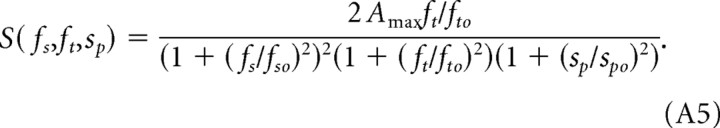The values of f_so and f_to are determined directly by fitting the normalized spatial and temporal sensitivity functions in Figure 4, C and D, with Equations A2 and A3 using the Marquardt–Levenberg algorithm (SigmaPlot Software; Systat Software, Port Richmond, CA). Having established the values of the parameters f_so = 0.3 cycles/° and f_to = 0.8 Hz, we estimated A_max = 6.5 by fitting the spatial CSFs with Equation A5 (Fig. 3). Assigning s_po = 80°/s accounts for the attenuation observed at very high rotation speeds. For s_p ≪ s_po, the effects of speed are negligible, and Equation A5 simplifies to

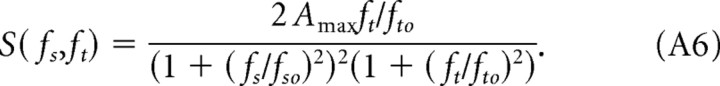Under these conditions, spatial and temporal frequencies are separable or independent variables, meaning that changes in spatial frequency will scale temporal sensitivities without altering the shape of the temporal CSF. Likewise, changes in temporal frequency scale the spatial sensitivity function.

Under photopic conditions, the CSF is

where the normalized filter functions are

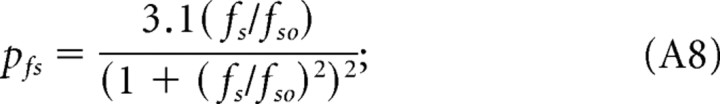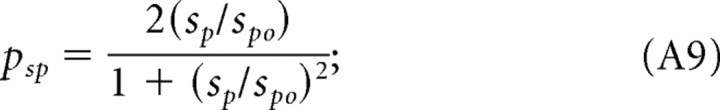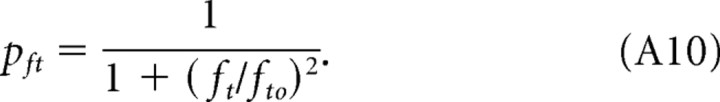Combining Equations A7–A10, the CSF under photopic conditions is

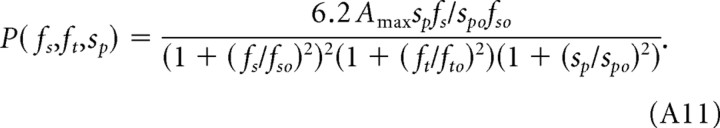The values of the parameters f_so = 0.18 cycles/° and s_po = 15°/s were determined by fitting the normalized spatial and speed CSFs (Fig. 4A,B) with Equations A8 and A9. The value of A_max = 15 was determined by fitting the temporal CSFs in Figure 2 with Equation A11. The temporal frequency cutoff of f_to = 12 Hz accounts for the attenuation observed at high temporal frequencies (Fig. 2B). At temporal frequencies f_t ≪ f_to, contrast sensitivity can be expressed in terms of two independent variables, f_s and s_p:

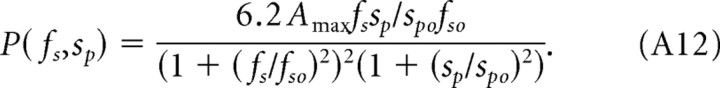A canonical expression

By definition, f_t = s_p f_s, and, after substituting the numerator in Equation A11, both Equations A5 and A11 acquire a similar form, differing only by their scaling constants. Thus, both photopic and scotopic visual CSFs in mice can be expressed in terms of the following canonical equation:

where k is a constant that depends on luminance levels, and the functions G_i are as follows:

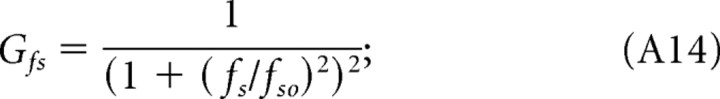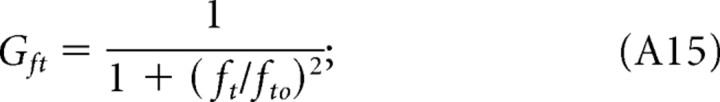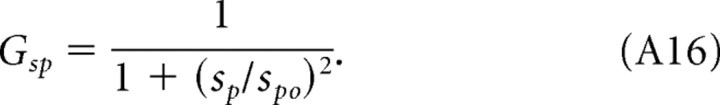Temporal versus speed tuning

The temporal CSF (Eq. 2) can be rewritten in the following terms after substituting for s_p = f_t/f_s:

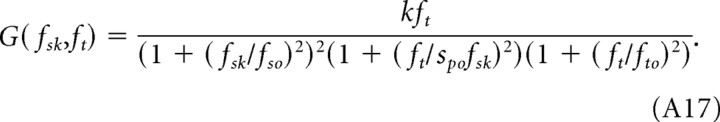The first term in the denominator is a vertical scaling factor that depends on spatial frequency of the sinusoidal grating, f_s = f_sk. The second and third terms express the attenuation in terms of temporal frequency. According to this equation, sensitivity declines sharply when

and/or

The smaller term in Equations A18 and A19 determines the temporal frequency at which attenuation begins, and we refer to it as the dominant cutoff frequency. Under scotopic conditions, f_to is 0.8 Hz (see Table 1), whereas the product s_po f_sk is 10.2 Hz (assuming f_sk = 0.128 cycles/°). As shown in Figure 3B, each curve represents the sensitivity to a different spatial frequency (f_sk). The lower limb of the sensitivity functions increases in proportion to f_t. At the dominant cutoff frequency (f_to = 0.8 Hz), the function diverges from the asymptote as attenuation begins. The second break is predicted to occur at much higher temporal frequencies (between 5 and 50 Hz), when temporal frequency is equal to s_po f_sk.

Under photopic conditions, the value of the critical parameters changes (Table 1). f_to is 12 Hz, and the product s_po f_sk is 1.9 Hz (again for f_sk = 0.128 cycles/°). In this case, s_po f_sk is the dominant frequency. However, the value of the product s_po f_sk is not unique, changing in proportion to the spatial frequency of the pattern. Therefore, the first break for each function occurs at different temporal frequencies (Fig. 2B), and the family of functions is not tuned to a particular temporal frequency. The second break occurs at 12 Hz.

Analogously, the CSF (Eq. 2) can be expressed in terms of speed rather than temporal frequency:

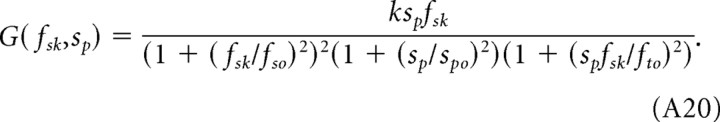Under photopic conditions, s_po is significantly smaller than the ratio f_to/f_sk (Table 1), and the first break occurs at s_p = 15°/s (Fig. 2D). Thus, the photopic sensitivity functions are tuned to speed. In contrast, under scotopic conditions, the ratio f_to/f_sk is dominant and the first break in each function changes with f_sk. The functions are not tuned to a particular speed.