A Novel Application of a Bivariate Regression Model for Binary and Continuous Outcomes to Studies of Fetal Toxicity

Summary

Public health concerns over the occurrence of birth defects and developmental abnormalities that may occur as a result of prenatal exposure to drugs, chemicals, and other environmental factors has led to an increasing number of developmental toxicity studies. Because fetal pups are commonly evaluated for multiple outcomes, data analysis frequently involves a joint modeling approach. In this paper, we focus on modelling clustered binary and continuous outcomes in the setting where both outcomes are potentially observable in all offspring but, due to practical limitations, the continuous outcome is only observed in a subset of offspring. The subset is not a simple random sample (SRS) but is selected by the experimenter under a prespecified probability model.

While joint models for binary and continuous outcomes have been developed when both outcomes are available for every fetus, many existing approaches are not directly applicable when the continuous outcome is not observed in a SRS. We adapt a likelihood-based approach for jointly modelling clustered binary and continuous outcomes when the continuous response is missing by design and missingness depends on the binary trait. The approach takes into account the probability that a fetus is selected in the subset. Through the use of a partial likelihood, valid estimates can be obtained by a simple modification to the partial likelihood score. Data involving the herbicide 2,4,5-T are analyzed. Simulation results confirm the approach.

1. Introduction

Growing concern over the occurrence of birth defects and developmental abnormalities that may occur as a result of prenatal exposure to drugs, chemicals and other environmental factors has led to agencies such as the U.S. Environmental Protection Agency (EPA) and the Food and Drug Administration (FDA) to place emphasis on setting exposure limits in order to protect the public from the adverse effects of these substances. Because data on humans are often unavailable, information from controlled animal experiments accounts for a large proportion of the data on the effects of toxins.

Fetal toxicity studies often involve exposing a pregnant dam to the study agent at the peak of fetal organogenesis. Experiments known as segment II studies, intended to evaluate dose response, follow federal testing guidelines and have been described in detail elsewhere (Manson, 1994). Briefly, these experiments typically involve 3–4 dose groups including a control group, with each dose group containing 20-30 dams. Just prior to normal delivery, the dams are sacrificed and the uterine contents are examined. Typically, offspring are evaluated on multiple outcomes which may include a mix of discrete and continuous responses. Outcomes include prenatal loss (i.e., resorptions and fetal deaths), and among viable offspring, a number of outcomes including fetal weight, externally visible malformations, and malformations of internal organs and the skeleton. In addition, as it is well known that offspring from the same dam tend to respond more similarly than those from different dams, possibly due to genetic similarity and a shared maternal environment during gestation, clustering within litter is a common characteristic of data from these experiments. The statistical challenges involved have been discussed by others (Ryan, 1992; Aerts et al., 2002).

While much is known about a number of toxins, the biological mechanisms involved are usually not well established. Another area of fetal toxicity studies involves experiments that are intended to evaluate specific mechanisms of the developmental processes that may be interrupted by prenatal exposure to a toxin. Often, these studies require detailed assessments of offspring involving a continuous response, that may reflect minute changes that are not easily determined by gross examination of the fetus. These studies extensively evaluate a small number of animals and are often restricted to two groups, exposed and unexposed. For example, in studies of ocular development, Inagaki & Kotani (2003) reported the rate of microphthalmia and conducted detailed morphometric evaluation of the embryos of rats exposed to soft X-ray irradiation. Examination by stereo-microscope revealed reduced growth of the optic cup in exposed offspring. Others have included detailed evaluation in studies of lung maturation, development of the eye and of the liver (Grasty et al., 2005; Martins et al., 2005; Rogers & Hurley, 1987).

Although these types of studies differ somewhat in their objectives, they have some shared characteristics which includes evaluating multiple outcomes. Some outcomes may be cheap and quick to assess, such as malformation determined by gross examination, while others, such as the size of the ocular cup, are time-consuming and expensive to measure. While there may be sufficient resources to evaluate all offspring in small toxicity studies, in large studies, cost constraints limit the extent to which detailed assessments can be made, so collecting detailed measures on all subjects is unrealistic. To overcome this limitation, some studies evaluate a fixed number of pups per litter (Rogers & Hurley, 1987; Grasty et al., 2005) while others select pups from a fixed number of litters (Kennedy & Elliott, 1986).

If exposure-related changes in the detailed measure are more likely to occur in affected offspring, the experimenter might preferentially select affected offspring in which to observe the detailed measure. While there might be resources to do detailed assessment among a fraction of offspring, a simple random sample (SRS) might not be the best use of limited resources and therefore, selecting a SRS may not be optimal. One approach to selecting a subset is to oversample the affected offspring. Oversampling has arisen before in evaluating eye size and malformation of the eye (Weller et al., 1999).

We consider a case in which a binary trait, such as malformation, is observed in all offspring while a continuous outcome, corresponding to the detailed assessment, is observed in a subset of offspring selected from the main study. The subset is not a SRS in the sense that the probability of selecting an affected offspring is not equal to that of an unaffected offspring. We were motivated by the idea that a probability-based subsample that is not a SRS might be obtained, and sought an approach to analyze these data. Our approach pairs existing methods for mixed effects models, which have been previously applied to analyze fetal toxicity data (Gueorguieva & Agresti, 2001; Dunson, 2000), with the concept of two-phase sampling, which has been used in screening and surveys in psychiatry (Deming, 1977; Shrout & Newman, 1989). In our approach, the screening variable, which is the variable at the first phase of sampling (i.e., malformation), does not necessarily reflect the same phenomenon as the variable at the second phase (the detailed assessment), though the two are expected to be correlated. Our intent, in the application of two-phase sampling, differs somewhat from the screening context in that malformation status itself is of interest because it carries information on exposure. Thus, we were concerned with analyzing the variable at the first phase as well as the variable at the second phase. We refer to the sampling procedure at the second phase as subsampling to reflect this difference in intent. While the application to toxicology is presented as a working example, our approach can be applied more generally to analyze a mix of binary and continuous outcomes when the continuous response is missing by design. We apply our approach to a segment II study involving a number of doses that also allows for estimation of a joint dose response curve.

We begin with a bivariate regression model in Section 2. The model is an extension of the clustered ordinal regression approach of Hedeker & Gibbons (1994) that includes the continuous outcome. To handle subsampling, we then derive a partial likelihood (PL) that is based on the bivariate model, and give an expression for the PL score in Section 3. We show that consistent estimates can be obtained by adjusting the PL score via a simple weighting scheme that accounts for the sampling design. Results from a data analysis involving the herbicide 2,4,5-T are presented in Section 4 and a simulation study confirms the PL approach in Section 5. Some of the technical details are relegated to a separate technical report available from the authors.

2. Bivariate random effect regression model (BRM)

Our approach follows the method of Hedeker & Gibbons (1994) for modelling clustered ordinal outcomes. Central to the model are a normally distributed unobservable latent trait and fixed but unknown threshold values which generate the observed ordinal outcomes. In extending the model of Hedeker & Gibbons (1994) to account for a continuous outcome, the latent trait and continuous outcome are assumed to have a bivariate normal distribution. For the purpose of modelling fetal malformation, attention is restricted to clustered binary outcomes. The bivariate random effect model (BRM) accounts for a binary and a continuous outcome. We assume that mean fetal response depends only on fixed effects so a one-dimensional mean zero random effect for litter is assumed. As the latent trait and the continuous outcome may not be in the same scale, a parameter for each outcome is used to scale the random effect. In addition, consistent with assumptions typical for fetal toxicity studies, no fetus-specific effects are assumed so that only litter-level covariates are considered. Finally, the latent trait and the continuous outcome are assumed to be positively correlated, so that small values of the latent variable, corresponding to malformation, are correlated with lower values of the continuous outcome. We first assume there is a latent variable for malformation, $M_{\mathit{\text{ik}}}^{\ast }$, with unknown latent variance ${\sigma }_1^2$, and a continuous outcome, S_ik, for fetus k in litter i. The joint model for ${(M_{\mathit{\text{ik}}}^{\ast }{S}_{\mathit{\text{ik}}})}^T$ is written

$$\begin{array}{cc}{M}_{\mathit{\text{ik}}}^{\ast }& ={\mathbf{\text{w}}}_{1i}^T{\stackrel{\sim }{\alpha }}_1^{\ast }+{\stackrel{\sim }{\sigma }}_{b1}{\theta }_i+{\stackrel{\sim }{\epsilon }}_{1\mathit{\text{ik}}}\\ S_{\mathit{\text{ik}}}& ={\mathbf{\text{w}}}_{2i}^T{\alpha }_2+{\sigma }_{b2}{\theta }_i+{\epsilon }_{2\mathit{\text{ik}}}\end{array}$$

where the random effect, ${\theta }_i\stackrel{\mathit{\text{iid}}}{\sim }N(0,1)$, is independent of the vector of error terms (ε̃_1ik ε_2ik) where (ε̃_1ik ε_2ik)^T ∼ N (0, Σ̃) and

$$\sum ^{\sim }=\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_1{\sigma }_2\rho \\ {\sigma }_1{\sigma }_2\rho & {\sigma }_2^2\end{array}\right).$$

As $M_{\mathit{\text{ik}}}^{\ast }$ is unobservable, the unknown latent variance ${\sigma }_1^2$ is not uniquely identifiable. $M_{\mathit{\text{ik}}}^{\ast }$ can be rescaled by the unknown latent variance producing a second latent variable, $Y_{\mathit{\text{ik}}}^{\ast }$, with variance 1. Denoting $Y_{\mathit{\text{ik}}}^{\ast }$ and S_ik for latent malformation and the continuous outcome, respectively, for fetus k in litter i, the joint model for ${(Y_{\mathit{\text{ik}}}^{\ast }{S}_{\mathit{\text{ik}}})}^T$, for a single fetus is written

$$\begin{array}{cc}{Y}_{\mathit{\text{ik}}}^{\ast }& =z_{1\mathit{\text{ik}}}+{\epsilon }_{1\mathit{\text{ik}}}\\ S_{\mathit{\text{ik}}}& =z_{2\mathit{\text{ik}}}+{\epsilon }_{2\mathit{\text{ik}}}\end{array}$$

where $z_{1\mathit{\text{ik}}}={\mathbf{\text{w}}}_{1i}^T{\alpha }_1^{\ast }+{\sigma }_{b1}{\theta }_i$, $z_{2\mathit{\text{ik}}}={\mathbf{\text{w}}}_{2i}^T{\alpha }_2+{\sigma }_{b2}{\theta }_i$, ${\alpha }_1^{\ast }={\stackrel{\sim }{\alpha }}_1^{\ast }/{\sigma }_1$. σ_b1 = σ̃_b1/σ₁, and ε_1ik = ε̃_1ik/ σ₁. ε_ik = (ε_1ik ε_2ik)^T is a mean zero bivariate normal random variable with covariance matrix

$$\sum =\left(\begin{array}{cc}1& {\sigma }_2\rho \\ {\sigma }_2\rho & {\sigma }_2^2\end{array}\right).$$

We assume ρ > 0 so that malformations are correlated with lower values of the continuous outcome.

A malformation occurs when the latent variable falls below the fixed threshold, γ₁. The observable pair of variables is (O_ik, S_ik) where O_ik = 1, a fetal malformation, if ${\gamma }_0<Y_{\mathit{\text{ik}}}^{\ast }\le {\gamma }_1$ and O_ik = 2 (no malformation) if ${\gamma }_1<Y_{\mathit{\text{ik}}}^{\ast }\le {\gamma }_2$. We take γ₀ = −∞ and γ₂ = ∞. When a binary outcome is generated from the unobservable latent variable, it is well known that the unknown threshold is not individually estimable. Therefore, while ${\alpha }_1^{\ast }$ is not estimable, a parameter, α₁, that is a transformation of ${\alpha }_1^{\ast }$ that depends on γ₁ can be estimated. For example, in the simplified case where there is no clustering, if the latent mean is ${\alpha }_{11}^{\ast }+{\alpha }_{12}^{\ast }d$, only ${\alpha }_{11}={\gamma }_1-{\alpha }_{11}^{\ast }$ and ${\alpha }_{12}=-{\alpha }_{12}^{\ast }$ are estimable since only the probability of malformation can be estimated from the data. For the data analysis, we were primarily interested in modeling the dose effect of a toxin. For convenience, we chose to set γ₁ = 0, although other values could be chosen, which would result in shifting the intercept term for malformation.

Supressing the subscript for litter, i, temporarily, the marginal between-fetus and within-fetus correlations are found to be

$$\begin{array}{l}{\rho }_Y=\text{cor}(Y_k^{\ast },Y_{k^{\prime }}^{\ast })=\frac{{\sigma }_{b1}^2}{{\sigma }_{b1}^2+1}\\ {\rho }_S=\text{cor}(S_k,S_{k^{\prime }})=\frac{{\sigma }_{b2}^2}{{\sigma }_{b2}^2+{\sigma }_2^2}\\ {\rho }_{YS}=\text{cor}(Y_k^{\ast },S_k)=\frac{{\sigma }_2\rho +{\sigma }_{b1}{\sigma }_{b2}}{\sqrt{({\sigma }_{b1}^2+1)({\sigma }_{b2}^2+{\sigma }_2^2)}}\\ {\rho }_{Y{S}^{\prime }}=\text{cor}(Y_k^{\ast },S_{k^{\prime }})=\frac{{\sigma }_{b1}{\sigma }_{b2}}{\sqrt{({\sigma }_{b1}^2+1)({\sigma }_{b2}^2+{\sigma }_2^2)}}.\end{array}$$

This marginal correlation structure is represented in Figure 1. The marginal joint distribution is

Fig. 1.

Marginal correlation structure of the bivariate model.

$$\left(\begin{array}{c}{\mathbf{\text{Y}}}^{\ast }\\ \mathbf{\text{S}}\end{array}\right)\sim {\text{N}}_{\text{2}n}\left(\left(\begin{array}{c}{\mathbf{\text{w}}}_1^T{\alpha }_1{\mathbf{1}}_n\\ {\mathbf{\text{w}}}_2^T{\alpha }_2{\mathbf{1}}_n\end{array}\right),V=\left(\begin{array}{cc}{V}_{11}& V_{12}\\ V_{21}& V_{22}\end{array}\right)\right)$$

where $V_{11}=I_n+{\sigma }_{b1}^2{J}_n$, $V_{21}=V_{12}={\sigma }_2\rho I_n+{\sigma }_{b2}^2{J}_n$, and $V_{22}={\sigma }_2^2{I}_n+{\sigma }_{b2}^2{J}_n$. V can be rewritten

$$V=\left(\begin{array}{cc}{\sigma }_Y^2[(1-{\rho }_Y)I_n+{\rho }_Y{J}_n]& {\sigma }_Y{\sigma }_S[({\rho }_{YS}-{\rho }_{Y{S}^{\prime }})I_n+{\rho }_{Y{S}^{\prime }}{J}_n]\\ {\sigma }_Y{\sigma }_S[({\rho }_{YS}-{\rho }_{Y{S}^{\prime }})I_n+{\rho }_{Y{S}^{\prime }}{J}_n]& {\sigma }_S^2[(1-{\rho }_S)I_n+{\rho }_S{J}_n]\end{array}\right).$$

where ${\sigma }_Y^2={\sigma }_{b1}^2+1$ and ${\sigma }_S^2={\sigma }_{b2}^2+{\sigma }_2^2$. Of interest is to estimate η = (α₁ α₂ σ_b1 σ_b2 σ₂ ρ)^T. The mean parameters, α₁ and α₂, and the within-litter variance for fetal weight, σ₂, are uniquely identifiable as they can be estimated by analyzing the outcomes separately. As the marginal correlations, ρ_Y, ρ_S, and ρ_{Y S} can be individually estimated, σ_b1, σ_b2, and ρ are also uniquely identifiable which is seen by rewriting the expressions relating model parameters and the marginal correlations (see Appendix A).

2.1. Estimation for complete data pairs

If (o_ik, s_ik) are observed for every fetus k = 1, ⋯, n_i and litter i = 1, ⋯, N, the marginal joint likelihood is given by

$$L(\eta )=\prod _{i=1}^{N}h({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i;\eta )=\prod _{i=1}^N\int P({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i|{\theta }_i)g({\theta }_i)d{\theta }_i$$ (1)

where $P({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i|{\theta }_i)={\prod }_{k=1}^{ni}P(o_{\mathit{\text{ik}}},s_{\mathit{\text{ik}}}|{\theta }_i)$. Estimation proceeds via Fisher scoring in a fashion similar to the univariate ordinal model. Estimates are obtained by solving the score equation

$$U(\eta )=\sum _{i=1}^{N}h{({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i;\eta )}^{-1}\frac{\partial }{\partial \eta }h({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i;\eta )$$

where derivatives of the log likelihood are obtained by directly differentiating the log of (1)

$$\frac{\partial h({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i;\eta )}{\partial \eta }=\int \sum _{k=1}^{n_i}\left[\frac{\frac{\partial }{\partial \eta }P({\mathit{\text{s}}}_{\mathit{\text{ik}}}|{\theta }_i)}{P(s_{\mathit{\text{ik}}}|{\theta }_i)}+\sum _{j=1}^{2}1({\mathit{\text{o}}}_{\mathit{\text{ik}}}=j)\frac{\frac{\partial }{\partial \eta }P(O_{\mathit{\text{ik}}}=j|s_{\mathit{\text{ik}}},{\theta }_i)}{P(O_{\mathit{\text{ik}}}=j|s_{\mathit{\text{ik}}},{\theta }_i)}\right]P({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i|{\theta }_i)g({\theta }_i)d{\theta }_i$$ (2)

where $P(s_{\mathit{\text{ik}}}|{\theta }_i)=\varphi (s_{\mathit{\text{ik}}}^{\prime })/{\sigma }_{2i}$, P (O_ik = 1∣s_ik, θ_i) = Φ(v_ik), P (O_ik = 2∣s_ik, θ_i) = 1 − Φ(v_ik), $v_{\mathit{\text{ik}}}=-m_{\mathit{\text{ik}}}/\sqrt{1-{\rho }^2}$, m_ik = z_1ik + ρ(s_ik − z_2ik)/σ₂, and $s_{\mathit{\text{ik}}}^{\prime }=(s_{\mathit{\text{ik}}}-z_{2\mathit{\text{ik}}})/{\sigma }_2$. φ() and Φ() denote, respectively, the probability density function and cumulative distribution function of the normal distribution. Substituting terms, the right hand side of (2) is written

$$\int \sum _{k=1}^{n_i}\left[\frac{\partial }{\partial \eta }logP({\mathit{\text{s}}}_{\mathit{\text{ik}}}|{\theta }_i)+\left(\frac{1({\mathit{\text{o}}}_{\mathit{\text{ik}}}=1)}{\Phi (v_{\mathit{\text{ik}}})}-\frac{1(o_{\mathit{\text{ik}}}=2)}{1-\Phi (v_{\mathit{\text{ik}}})}\right)\frac{\partial \Phi (v_{\mathit{\text{ik}}})}{\partial \eta }\right]P({\mathbf{\text{o}}}_i,{\mathbf{\text{s}}}_i|{\theta }_i)g({\theta }_i)d{\theta }_i.$$ (3)

Standard error estimates are based on the inverse observed information. Marginal quantities are approximated by numerical quadrature (Najita, 2006).

3. Partial likelihood approach

To account for subsampling, the mechanism generating the observed data is viewed in terms of two steps: a sampling step and an additional selection step. In the sampling step, a fetus potentially observable for the data pair, (o, s), is sampled at random from the population, depicted on the left in Figure 2. This step corresponds to viable offspring observed when the uterine contents are examined. The sampled data pair falls in one of two strata, based on malformation status. At the selection step, a subsample is obtained where offspring are selected from stratum 1 (abnormality or affected) with probability p₁ and from stratum 2 (healthy or unaffected) with probability p₂. The continuous outcome, S, is observed only for pups selected at the second step. Thus, in affected pups, a data pair is observed with probability p₁ while in unaffected pups, the data pair is observed with probability p₂. For pups not selected at the second step, only malformation status is observed.

Fig. 2.

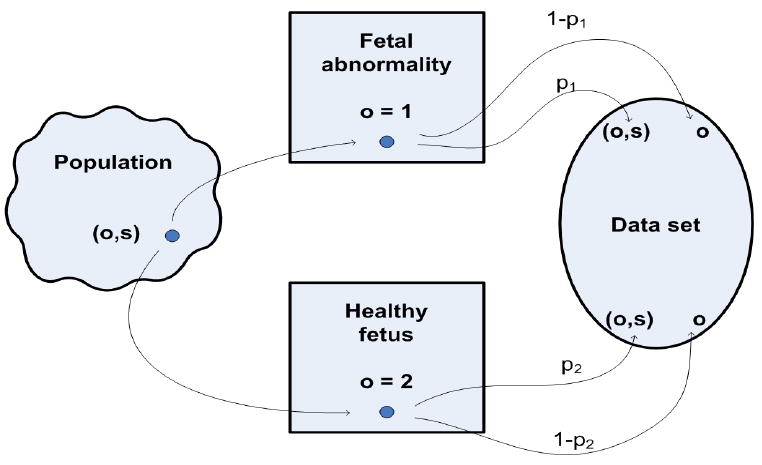
Selection model in the subsampling setting.

The case p₁ = p₂ = 1 corresponds to the complete data setting where the selection step is absent. p₁ = p₂ = p < 1 corresponds to the SRS case where the population-based relative frequencies are retained in the subsample. p₁ > p₂ corresponds to oversampling malformations while p₁ < p₂ corresponds to undersampling. When there is subsampling, the likelihood involves a normalizing constant that depends on the unknown probability of malformation, so the full likelihood is complex. We base inference on a PL in which the selection process is not formally modeled.

3.1. Partial likelihood under subsampling

We now derive expressions for the PL and the PL score. Let, Δ_ik be the variable indicating whether the continuous outcome is observed for the k^th fetus where $P({\Delta }_{\mathit{\text{ik}}}=1|O_{\mathit{\text{ik}}}=o_{\mathit{\text{ik}}})=p_1^{1(o_{\mathit{\text{ik}}}=1)}{p}_2^{1(o_{\mathit{\text{ik}}}=2)}$. Write the data available for the k^th fetus as ${\mathbf{\text{d}}}_{\mathit{\text{ik}}}^{\prime }=(o_{\mathit{\text{ik}}},{\delta }_{\mathit{\text{ik}}})$ if δ_ik = 0 and ${\mathbf{\text{d}}}_{\mathit{\text{ik}}}^{\prime }=(o_{\mathit{\text{ik}}},s_{\mathit{\text{ik}}},{\delta }_{\mathit{\text{ik}}})$ if δ_ik = 1. Conditional on the random effect for litter, the distribution of the observed data for a single fetus is $P({\mathbf{\text{d}}}_{\mathit{\text{ik}}}^{\prime }|{\theta }_i)=P{(o_{\mathit{\text{ik}}},{\delta }_{\mathit{\text{ik}}}|{\theta }_i)}^{1-{\delta }_{\mathit{\text{ik}}}}P{(o_{\mathit{\text{ik}}},s_{\mathit{\text{ik}}},{\delta }_{\mathit{\text{ik}}}|{\theta }_i)}^{{\delta }_{\mathit{\text{ik}}}}$ which we write as

$$P({\mathbf{\text{d}}}_{\mathit{\text{ik}}}^{\prime }|{\theta }_i)=\prod _{j=1}^2{[(1-p_j)P(O_{\mathit{\text{ik}}}=j|{\theta }_i)]}^{d_{0j\mathit{\text{ik}}}}{[p_{j}P(O_{\mathit{\text{ik}}}=j,s_{\mathit{\text{ik}}}|{\theta }_i)]}^{d_{1j\mathit{\text{ik}}}}$$ (4)

where d_ℓjik = 1(δ_ik = ℓ, o_ik = j), ℓ = 0, 1 and j = 1, 2. Setting $P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)={\prod }_{k=1}^{n_i}P({\mathbf{\text{d}}}_{\mathit{\text{ik}}}^{\prime }|{\theta }_i)$ and integrating over the random effect gives the PL

$$\text{PL}(\eta )=\prod _{i=1}^N\int P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)g({\theta }_i)d{\theta }_i.$$ (5)

Setting ${\text{PL}}_i=\int P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)g({\theta }_i)d{\theta }_i$, the PL score is obtained by substituting (4) in (5) and directly differentiating the log PL:

$$U(\eta )=\sum _{i=1}^N\frac{1}{{\text{PL}}_i}\int D_1({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,\eta )P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)g({\theta }_i)d{\theta }_i,$$ (6)

where

$$D_1({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,\eta )=\sum _{k=1}^{n_i}\sum _{j=1}^2\left[d_{0j\mathit{\text{ik}}}\frac{\frac{\partial }{\partial \eta }P(O_{\mathit{\text{ik}}}=j|{\theta }_i)}{P(O_{\mathit{\text{ik}}}=j|{\theta }_i)}+d_{1j\mathit{\text{ik}}}\frac{\frac{\partial }{\partial \eta }P(O_{\mathit{\text{ik}}}=j,s_{\mathit{\text{ik}}}|{\theta }_i)}{P(O_{\mathit{\text{ik}}}=j,s_{\mathit{\text{ik}}}|{\theta }_i)}\right].$$ (7)

Writing P(O_ik = j∣θ_i) = Φ(u_ik)^{1(j =1)} (1 − Φ(u_ik))^1(j=2) where u_ik = −z_1ik, the derivatives in (7) can be expressed as

$$\begin{array}{ccc}\frac{\frac{\partial }{\partial \eta }P(O_{\mathit{\text{ik}}}=j|{\theta }_i)}{P(O_{\mathit{\text{ik}}}=j|{\theta }_i)}& =& \frac{{(-1)}^{1(j=2)}\frac{\partial }{\partial \eta }\Phi (u_{\mathit{\text{ik}}})}{\Phi {(u_{\mathit{\text{ik}}})}^{1(j=1)}{[1-\Phi (u_{\mathit{\text{ik}}})]}^{1(j=2)}}\hfill \\ \frac{\frac{\partial }{\partial \eta }P(O_{\mathit{\text{ik}}}=j,s_{\mathit{\text{ik}}}|{\theta }_i)}{P(O_{\mathit{\text{ik}}}=j,s_{\mathit{\text{ik}}}|{\theta }_i)}& =& \frac{{(-1)}^{1(j=2)}\frac{\partial }{\partial \eta }\Phi (v_{\mathit{\text{ik}}})}{\Phi {(v_{\mathit{\text{ik}}})}^{1(j=1)}{[1-\Phi (v_{\mathit{\text{ik}}})]}^{1(j=2)}}+\frac{\partial }{\partial \eta }logP(s_{\mathit{\text{ik}}}|{\theta }_i)\end{array}$$

with P(s_ik∣θ_i) and v_ik as defined in Section 2.1. Substituting terms, (7) can be written as

$$\begin{array}{l}{D}_1({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,\eta )=\sum _{k=1}^{n_i}\sum _{j=1}^2[\frac{d_{0j\mathit{\text{ik}}}{(-1)}^{1(j=2)}\frac{\partial }{\partial \eta }\Phi (u_{\mathit{\text{ik}}})}{\Phi {(u_{\mathit{\text{ik}}})}^{1(j=1)}{[1-\Phi (u_{\mathit{\text{ik}}})]}^{1(j=2)}}\\ +d_{1j\mathit{\text{ik}}}\left(\frac{{(-1)}^{1(j=2)}\frac{\partial }{\partial \eta }\Phi (v_{\mathit{\text{ik}}})}{\Phi {(v_{\mathit{\text{ik}}})}^{1(j=1)}{[1-\Phi (v_{\mathit{\text{ik}}})]}^{1(j=2)}}+\frac{\partial }{\partial \eta }logP(s_{\mathit{\text{ik}}}|{\theta }_i)\right)].\end{array}$$ (8)

It can be shown that when selection occurs at rates that differ by malformation status, the expected value of (6) is non-zero for α₂, the component corresponding to the mean continuous outcome. To correct for bias, the PL score is modified by sampling weights. The weighted PL score, Ũ(η), can be written $\stackrel{\sim }{U}(\eta )={\sum }_{i=1}^N{\stackrel{\sim }{U}}_i(\eta )$, where

$${\stackrel{\sim }{U}}_i(\eta )=\frac{1}{{\text{PL}}_i}\int D_w({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,\eta )P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)g({\theta }_i)d{\theta }_i.$$ (9)

D_w has the form of D₁ in (7) with w_ℓjd_ℓjik substituted for d_ℓjik where w_1j = 1/p_j and w_0j = 1/(1 − p_j), j = 1, 2. It is straightforward to show that the weighted PL score equation is an unbiased estimating equation by conditioning on the random effect and taking expectations (Najita, 2006). PL estimates (PLE's) are obtained by solving the weighted score equation Ũ(η) = 0.

Standard error estimates are based on the robust sandwich estimator. To obtain an expression for the robust SE, we write the estimating function $G_N(\eta )=\frac{1}{N}{\sum }_{i=1}^N\Psi ({\mathbf{\text{d}}}_i^{\prime },\eta )$ where $\Psi ({\mathbf{\text{d}}}_i^{\prime },\eta )={\stackrel{\sim }{U}}_i(\eta )$. Expansion of G_N around η₀ gives, for large N,

$$\sqrt{N}(\widehat{\eta }-{\eta }_0)\approx -{\dot{G}}_N({\eta }_0)\sqrt{N}{G}_N({\eta }_0)$$

where Ġ_N(η₀) denotes $\frac{\partial G_N}{\partial {\eta }^T}=\frac{\partial }{\partial {\eta }^T}\frac{1}{N}{\sum }_{i=1}^N{\stackrel{\sim }{U}}_i(\eta )$ evaluated at η = η₀. Following general results for M-estimators (Huber, 1967), PL estimates are asymptotically normal, so, for large N, η̂ ≈ N (η₀, 1/N A(η₀)⁻¹B(η₀) [A(η₀)⁻¹]^T) where $A({\eta }_0)=\text{E}\left[-\frac{\partial }{\partial {\eta }^T}{\stackrel{\sim }{U}}_i({\eta }_0)\right]$ and B(η₀) = E [Ũ_i(η₀)Ũ_i(η₀)^T]. Therefore, we estimate the robust sandwich variance by

$${\left(\frac{1}{N}\sum _i\frac{\partial {\stackrel{\sim }{U}}_i}{\partial \eta }\right)}^{-1}\frac{1}{N}\sum _i{\stackrel{\sim }{U}}_i(\eta ){\stackrel{\sim }{U}}_i{(\eta )}^T{{\left[{\left(\frac{1}{N}\sum _i\frac{\partial {\stackrel{\sim }{U}}_i}{\partial \eta }\right)}^{-1}\right]}^T|}_{\eta =\widehat{\eta }}.$$ (10)

Expressions for the derivatives are obtained by direct differentiation (see Appendix B).

4. Application to 2,4,5-T data

We have confirmed the PL method via extensive simulations (Najita (2006) and summarized in Section 5 below) and here we show results from an analysis of a large toxicity study. For the data analysis, we wanted to evaluate the PL approach by comparing PLE's to MLE's as we wanted to directly compare differences due only to subsampling. Our motivation in this approach was to compare MLE's obtained from an “expensive” study, in which all offspring are evaluated, with PLE's that could be obtained had the study been implemented by oversampling affected offspring, a potentially less expensive study.

In order to evaluate the PLE's directly against MLE's, we focused on live outcomes. We believe that limiting the analysis to live outcomes was the simplest approach to make the comparison as the subsampling is intended for live outcomes only. Thus, our analysis excludes non-live outcomes and while experimenters who are interested in risk assessment (evaluating safe doses) may eventually wish to include non-live outcomes, existing approaches to augment the likelihood can be easily applied to the PL as well (Catalano & Ryan, 1992; Regan & Catalano, 1999).

For live outcomes, we focused on malformation and fetal weight which are typical primary endpoints for live offspring. Given a subsampling of fetal weight, we wanted to show that valid estimates could still be obtained when the subsample is not a SRS, and because fewer pups would be evaluated, there is potential for cost-saving. For continuous outcomes that are more expensive to measure than fetal weight, such as the size of the ocular cup or eye size, the potential for cost-savings would be greater.

In applying the PL approach, we sought a single data set in which we could compare MLEs with PLE's. To make the comparison, we began with data containing information on all offspring (complete pairs). A second data set was derived by oversampling malformations from the complete pairs data set (subsampling data set). Because we were interested in making a direct comparison between the MLE's and PLE's, a subsampling data set alone was not sufficient for our purposes. We chose to analyze data from a large developmental toxicity study of the herbicide 2,4,5-tricholorophenoxyacetic acid (2,4,5-T) in C57BL/6 mice (Holson et al., 1992).

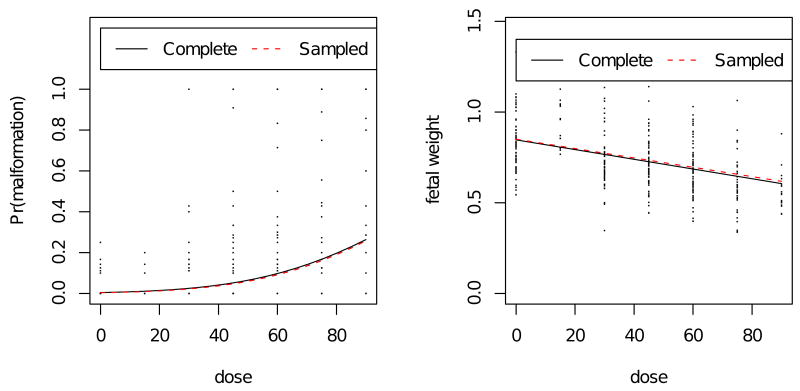
Between gestational days 4–16, dams were exposed to 2,4,5-T at one of seven dose levels (0, 15, 30, 45, 60, 75, 90 mg/kg/day). The number of pregnant dams at each dose level varied by dose group by design (13-66 dams per dose). The main study was comprised of 367 litters and we focus on the 337 litters containing at least one viable pup. While the most pronounced effects were reduction in fetal weight and the incidence of cleft palate, our analysis involved malformation of any type. Fetal weight and malformation status were available for 2,295 fetuses, which comprise the complete pairs data set of 337 litters. Dose effects of 2,4,5-T were evident in fetal weight and malformation. The proportion of fetal malformations increased steadily with dose ranging from a background rate of approximately 1% to 37% at the highest dose (see left panel, Figure 3). A plot of malformation rate transformed on a normal quantile scale suggested a linear trend in dose.

Fig. 3.

Estimated dose response for fetal malformation and mean fetal weight based on fitting the joint model to the complete data set and the sampled data set. Left panel: litter-specific proportion of fetal malformation plotted by dose. Right panel: litter-specific mean fetal weight in grams plotted by dose. Estimate based on the complete data set (MLE) is indicated by the solid line. Estimate based on the sampled data set (PLE) is indicated by the dashed line.

Fetal weight declined with dose, from 815 mg at the control dose to 548 mg at the highest dose. As there appeared to be some deviation from this trend at 15 mg/kg (see right panel, Figure 3), attempts were made to fit a quadratic term for dose in a univariate model for fetal weight in order to determine whether non-linear terms were appropriate before fitting the bivariate model. While the linear term for dose was significant, the quadratic term was not significant (possibly due to a smaller number of litters at the 15 mg/kg dose level). We fit the regression model

$$Y_{\mathit{\text{ik}}}^{\ast }={\alpha }_{11}+{\alpha }_{12}{d}_i+{\sigma }_{b1}{\theta }_i+{\epsilon }_{1\mathit{\text{ik}}}$$ (11)

$$S_{\mathit{\text{ik}}}={\alpha }_{21}+{\alpha }_{22}{d}_i+{\sigma }_{b2}{\theta }_i+{\epsilon }_{2\mathit{\text{ik}}}$$ (12)

$$var({\epsilon }_{\mathit{\text{ik}}})=\left(\begin{array}{cc}1& {\sigma }_2\rho \\ {\sigma }_2\rho & {\sigma }_2^2\end{array}\right)$$ (13)

where σ_b1, σ_b2, σ₂, and ρ were included as fixed constants. A summary of dose levels, malformation rates and fetal weight are presented in Table 1.

Table 1.

Summary of malformation rate and fetal weight observed in C57BL/6 mice in the 2,4,5-T study. All viable litters (litters with at least one live pup) were included. Number of viable pups per litter refers to the average number over all litters at the specified dose. Malformation rate refers to the proportion of malformation over all pups at the given dose. Mean fetal weight per litter (in grams) refers to the mean fetal weight in the litter averaged over all litters at the given dose.

	2,4,5-T dose level (mg/kg/day)
Response	0	15	30	45	60	75	90	Total
Total litters	71	13	56	75	73	47	32	367
Viable litters	71	13	54	74	69	37	19	337
Viable pups	494	95	364	526	463	247	106	2295
# Viable pups per litter	7.13	7.31	7.2	7.28	6.97	6.83	6.8
# Malformations	7	3	24	50	69	64	38
% Malformation	0.014	0.032	0.067	0.095	0.150	0.260	0.373
Mean fetal weight per litter	0.81	0.94	0.73	0.71	0.67	0.61	0.55
SD	0.07	0.12	0.06	0.06	0.06	0.06	0.05

To apply the PL approach, the subsampling data set was created from the complete data set by oversampling malformations (p₁=0.9, p₂=0.6). The subsampling data set consisted of data on fetal malformation (n=2295) and fetal weight (n=1469) for pups from the 337 litters. Seven litters contained no fetal weight observations while fetal weight was observed for a single pup in 21 litters. Among the remaining 309 litters, there was information on both outcomes for at least two pups. As a result of oversampling malformations, mean fetal weight in the subsampling data set was generally lower than that in the complete data set. MLE's were obtained from the complete data set and PLE's were obtained from the subsampling data set. The regression estimates were used to calculate marginal fetus-level correlations as described in Section 2.

A comparison of parameter estimates is presented in Table 2. Overall, regression estimates were similar (see Figure 3). MLE's of the within litter variance of fetal weight and the PLE's were similar (MLE: σ₂ = 0.073 versus PLE: σ₂ = 0.072). Estimates of the random effect SD's were also similar (MLE: σ_b1=0.48, σ_b2=0.09 versus PLE: σ_b1=0.54, σ_b2=0.10). As a result, there was very good agreement in estimates of marginal correlations within litter (MLE: ρ_Y=0.19, ρ_S=0.62 versus PLE: ρ_Y=0.23, ρ_S=0.67). In addition, the within-fetus correlations between fetal weight and latent malformation were also similar (MLE: ρ=0.40 versus PLE: ρ=0.39) and this led to similar estimates of the marginal within-fetus correlations between outcomes (MLE: ρ_{Y S}=0.56 versus PLE: ρ_{Y S}=0.59). Between-fetus correlations between outcomes were comparable (MLE: ρ_{Y S′}=0.34 versus PLE: ρ_{Y S′}=0.39). As expected, robust SE's tended to be larger than ML SE's. Although robust SE's for latent malformation were twice that of the ML SE's and the robust SE's for fetal weight were 3–4 times the ML SE's, all model parameters remained highly significant and qualitatively, the overall conclusions were unaffected by the larger robust SE's. The smaller sample size of fetal weight may be one explanation for the larger robust SE's.

Table 2.

Comparison of MLE's and PLE's for the complete data set and the subsampling data set in the 2,4,5-T study. RE SD refers to the SD of the random effect for litter. Fetal weight SD refers to the SD in fetal weight within a litter. The within-fetus correlation refers to the correlation between latent malformation and fetal weight conditional on the litter.

		complete pairs n= 2295		sampled fetal weight n= 1469
Term	Parameter	Est	SE×102	Est	Robust SE ×102
Malformation
Int	α 11	2.626	8.63	2.697	16.31
Dose	α 12	-0.0222	0.13	-0.0227	0.25
Fetal weight
Int	α 21	0.8465	0.24	0.850	0.73
Dose	α 22	-0.0027	0.005	-0.0026	0.02
SD	σ 2	0.0730	0.06	0.0722	0.24
RE SDY *	σ b1	0.4848	2.41	0.5390	8.02
Within-fetus corr	ρ	0.3958	2.65	0.3922	6.52
RE SDS	σ b2	0.0930	0.10	0.1020	0.29

We chose to model the variance and correlation terms, σ_b1, σ_b2, σ₂, and ρ, as constants because this is frequently assumed in developmental toxicity studies and because it is consistent with a prior analysis of the data (Holson et al., 1992). In other toxicity studies, the experimenter's prior knowledge of the test agent's effects on the animal species selected for testing is expected to play a large role in specifying a model for these second order terms. The model is generalizable in the sense that analysts who may not want to assume homogeneity in the variances and correlations can specify dose-dependence. This is possible when studies involve a small number of doses and many replicates at each dose level, however, the precision of estimates would be limited by the sample size at each dose level.

In developmental toxicity studies, litter size often carries information about the live outcomes. For example, for fetal weight, it is well known that weight can be inversely related to litter size as there are fewer pups competing for a fixed amount of nutritional resources when the litter size is smaller. The dose effect can be underestimated if the test agent induces embryolethality and therefore smaller litters. This bias has been described previously by Romero et al. (1992). Approaches have proposed adjusting for litter size by including it as a covariate (Catalano & Ryan, 1992; Regan & Catalano, 2000; Gueorguieva & Agresti, 2001; Chen, 1993) while others have proposed jointly modeling litter size and the live outcomes (Dunson et al., 2003; Catalano et al., 1993). In the data analysis, we focused on modelling live outcomes, and therefore condition on the litter size. Thus, there is the potential for biased inference of the dose effect. However, here we found that estimates of the dose effect did not change when litter size was included in the model, hence we chose to fit the simpler model including only dose effects in our bivariate model. The model we fit is also consistent with a prior analysis of the data.

5. Simulation Study

In applying the PL approach to the 2,4,5-T data, application was limited to the oversampling case (p₁ > p₂). In this section, we give results from a simulation study where we compared MLE's and PLE's under a range of subsampling scenarios. For the purpose of the study, simulations involved binary and continuous outcomes with characteristics similar to the 2,4,5-T data and while there are differences in some of the details, the simulated data are consistent with data commonly seen in practice. Specifically, simulated experiments included four doses and a control, assuming the rate of malformation, transformed by the inverse probit function, increased linearly with dose while mean fetal weight decreased linearly with dose. The malformation rate ranged from 7% (background) to 69% at the highest dose. Comparing controls and those exposed to the highest dose, mean fetal weight was reduced by 300 mg. For each outcome, within-litter correlations were modest (ρ_Y=0.10, ρ_S=0.10) while a moderately high within-fetus correlation was assumed (ρ_{Y S}=0.60). Correlations were held constant over dose. Therefore, we fit the models in Equations (11)–(13) with α₁w_1i=1.5-2d_i, α₂w_2i=5-3di, σ_b1=0.33, σ_b2=0.33, σ₂=1.0, and ρ=0.56. Dose levels were spaced equally between the control dose and the maximum (i.e., set to 0, 0.25, 0.50, 0.75, and 1.0). The number of live offspring in each litter was fixed at 10 and the number of dams assigned to each dose level was fixed at 30, corresponding to study sizes of 1,500 pups.

Subsampling scenarios were achieved by varying the sampling rates in malformation strata (p₁ and p₂). Specifically, for the SRS case, we sampled fetal weight from 90% of fetuses (p1 =0.9, p₂ =0.9). For the oversampling case, we sampled fetal weight from 90% affected offspring while only 60% of healthy fetuses were sampled (p₁=0.9, p₂ = 0.6). These sampling rates were exchanged (p₁ =0.6, p₂ =0.9) for the undersampling case. To demonstrate the robustness of PLE's over a range of subsampling rates, we also sampled fetal weight at rates with greater discrepancy as we expected bias to occur only when subsampling rates were different, and that the size of the bias would increase as the difference in sampling rates increased. We fixed the sampling rate at 0.90 for one stratum (e.g., affected offspring) and sampled at lower rates in the other (p=0.30, 0.40, 0.50). While our intent was to confirm the PL method for bias correction, we also calculated robust SE's for comparison with simulation-based estimates.

To evaluate the PL approach, we compared the PLE's to the true parameter values under oversampling and undersampling. To understand the potential bias in the over- and undersampling cases, in addition to PLE's, we also calculated uncorrected estimates for the oversampling and undersampling cases, which were obtained by maximizing the PL without adjustment by sampling weights. Finally, for comparison purposes, we calculated MLE's when there were complete data or the subset was a SRS. For each case, 100 experiments were simulated.

Parameter estimates are summarized in Tables 3, 5 and 6. Simulations confirmed MLE's when fetal malformation and weight were available for all fetuses. When fetal weight was available in an SRS, evidence of bias was not observed. However, as expected for the unweighted PL, dose response was overestimated when malformations were oversampled (see uncorrected estimates, Table 3). Similarly, with the unweighted estimates, the dose effect was underestimated when malformations were undersampled, demonstrating the importance of including sampling weights. The magnitude of bias in the unweighted estimates increased as the discrepancy between the sampling rates increased and was greatest when the sampling rate was 0.30 (Tables 5 and 6). Agreement between PLE's and the true parameter values was very good. Model-based SE's agreed well with empirical estimates when there were complete data or the subsample was a SRS (Table 4). Robust SE's were similar to empirical estimates and robust SE's increased as the discrepancy in sampling rates increased (see Tables 7 and 8).

Table 3.

Simulation results: comparison of MLE's and PLE's. Uncorrected estimates refer to parameter values that maximize the PL without accounting for sampling weights. Estimates were averaged over 100 replications.

		Complete	SRS	Oversampling		Undersampling
		(p1=p2=1)	(p1=p2=0.90)	(p1=0.90, p2 =0.60)		(p1=0.60, p2 =0.90)
parameter	true	MLE	MLE	uncorrected	PLE	uncorrected	PLE
α 11	1.50	1.5005	1.5098	1.1801	1.4933	1.7508	1.4882
α 12	-2.00	-2.0077	-2.0167	-2.0980	-1.9886	-1.8391	-1.9892
α 21	5.00	4.9934	4.9982	4.8472	4.9875	5.0830	4.9896
α 22	-3.00	-2.9950	-2.9969	-3.1008	-2.9785	-2.8262	-2.9861
σ b1	0.33	0.3221	0.3296	0.3320	0.3210	0.3052	0.3190
σ 2	1.00	0.9994	0.9992	1.0039	0.9991	0.9926	0.9987
ρ	0.56	0.5597	0.5615	0.5659	0.5619	0.5543	0.5600
σ b2	0.33	0.3196	0.3224	0.3409	0.3318	0.3131	0.3276

Table 5.

Simulations results: comparison of uncorrected estimates and PLE's when oversampling over a range (p₁=0.90 and p₂=0.30, 0.40, 0.50).

	Oversampling
		(p1=0.9, p2=0.50)		(p1=0.90, p2=0.40)		(p1=0.90, p2=0.30)
parameter	true	uncorr	PLE	uncorr	PLE	uncorr	PLE
α 11	1.50	1.0454	1.5093	0.8317	1.5013	0.5771	1.4918
α 12	-2.00	-2.1495	-2.0175	-2.1465	-2.0205	-2.1227	-2.0168
α 21	5.00	4.7817	5.0024	4.6743	4.9957	4.5195	4.9947
α 22	-3.00	-3.1337	-3.0056	-3.1425	-3.0074	-3.0921	-3.0019
σ b1	0.33	0.3281	0.3193	0.3289	0.3170	0.3153	0.3133
σ 2	1.00	1.0013	0.9989	0.9995	0.9965	1.0006	0.9946
ρ	0.56	0.5662	0.5635	0.5689	0.5618	0.5761	0.5649
σ b2	0.33	0.3275	0.3222	0.3217	0.3182	0.3155	0.3213

Table 6.

Simulations results: comparison of uncorrected estimates and PLE's when undersampling over a range (p₁=0.30, 0.40, 0.50 and p₂=0.90).

	Undersampling
		(p1=0.50, p2=0.90)		(p1=0.40, p2=0.90)		(p1=0.30, p2=0.90)
parameter	true	uncorr	PLE	uncorr	PLE	uncorr	PLE
α 11	1.50	1.8865	1.5150	2.0014	1.5260	2.1615	1.5583
α 12	-2.00	-1.7850	-2.0008	-1.7083	-2.0261	-1.5962	-2.0676
α 21	5.00	5.1232	4.9976	5.1433	5.0008	5.1575	5.0127
α 22	-3.00	-2.7662	-2.9895	-2.6768	-3.0000	-2.5467	-3.0159
σ b1	0.33	0.3001	0.3225	0.2896	0.3157	0.2827	0.3165
σ 2	1.00	0.9863	0.9980	0.9820	0.9995	0.9742	0.9976
ρ	0.56	0.5518	0.5643	0.5492	0.5660	0.5411	0.5677
σ b2	0.33	0.3003	0.3231	0.2922	0.3231	0.2787	0.3231

Table 4.

Simulation results: comparison of model-based and robust standard error estimates with empirical estimates. Robust standard error estimates are based on bias-corrected PL approach.

	Complete		SRS		Oversampling		Undersampling
	(p1=p2=1)		(p1=p2=0.90)		(p1=0.90, p2=0.60)		(p1=0.60, p2=0.90)
parameter	model SE	emp SE	model SE	emp SE	robust SE	emp SE	robust SE	emp SE
α 11	0.092	0.090	0.122	0.143	0.103	0.107	0.117	0.110
α 12	0.142	0.140	0.186	0.251	0.167	0.172	0.175	0.171
α 21	0.066	0.064	0.080	0.098	0.076	0.082	0.074	0.076
α 22	0.107	0.112	0.128	0.181	0.126	0.143	0.123	0.134
σb	0.058	0.054	0.089	0.081	0.063	0.063	0.064	0.062
σ 2	0.020	0.020	0.029	0.028	0.023	0.023	0.020	0.023
ρ	0.029	0.027	0.042	0.043	0.032	0.033	0.033	0.032
σ b2	0.040	0.041	0.059	0.057	0.044	0.043	0.042	0.040

Table 7.

Oversampling simulations. Robust SE estimates.

	Oversampling
	(p1=0.9, p2=0.50)		(p1=0.90, p2=0.40)		(p1=0.90, p2=0.30)
parameter	robust SE	emp SE	robust SE	emp SE	robust SE	emp SE
α 11	0.109	0.106	0.114	0.112	0.126	0.123
α 12	0.181	0.196	0.194	0.190	0.223	0.243
α 21	0.081	0.077	0.086	0.086	0.098	0.101
α 22	0.133	0.152	0.143	0.145	0.163	0.184
σ b1	0.071	0.071	0.073	0.073	0.082	0.077
σ 2	0.025	0.025	0.027	0.028	0.030	0.031
ρ	0.034	0.036	0.036	0.036	0.038	0.039
σ b2	0.048	0.046	0.052	0.052	0.058	0.058

Table 8.

Undersampling simulations. Robust SE estimates.

	Undersampling
	(p1=0.50, p2=0.90)		(p1=0.40, p2=0.90)		(p1=0.30, p2=0.90)
parameter	robust SE	emp SE	robust SE	emp SE	robust SE	emp SE
α 11	0.133	0.131	0.146	0.155	0.170	0.190
α 12	0.194	0.205	0.212	0.196	0.244	0.236
α 21	0.078	0.079	0.082	0.085	0.090	0.099
α 22	0.130	0.152	0.139	0.138	0.155	0.160
σ b1	0.073	0.076	0.079	0.076	0.087	0.080
σ 2	0.023	0.023	0.025	0.025	0.027	0.027
ρ	0.035	0.039	0.038	0.037	0.042	0.040
σ b2	0.045	0.045	0.047	0.050	0.052	0.057

We elected not to sample at rates lower than 0.30 for practical reasons. First, it was thought to be unlikely that experimenters would choose rates lower than 0.30 as there might be interest in evaluating the continuous outcome alone and a small subsample might be viewed as having limited utility on its own. Second, while the simulations were designed to estimate the dose effect assuming all data pairs were available, subsampling at lower rates was thought to impact sample size sufficiently to reduce power. Hence subsampling at rates lower than 0.30 was not thought to be of practical interest. Third, simulation runs became impractical at rates lower than 0.30 because convergence was substantially slower so fitting the data required many more iterations than when p₂=0.50 or 0.60. Although infrequent, when fitting the simulated data, we observed sensitivity to the starting value when the sampling rate was 0.30. While we hypothesize this sensitivity to become more frequent with subsampling rates lower than 0.30, futher study would be needed to determine whether our results are unique to the experiment we have simulated.

6. Discussion and Future Work

Accounting for multiple endpoints may be appropriate for characterizing overall toxicity compared with approaches that focus on the most sensitive outcome thus motivating a joint modelling approach. In this paper, we have presented a joint model for binary and continuous outcomes that are clustered within litter and, using a PL, an approach when the continuous outcome is missing by design. To account for the non-representative subsample, the approach weights fetus-level terms by the inverse of subsampling probabilities. As methods that specify the joint distribution directly are limited by the lack of a natural joint distribution for a mix of discrete and continuous outcomes, a latent variable framework provides a convenient means with which to model this mix of outcomes, as others have done (Catalano & Ryan, 1992; Regan & Catalano, 1999; Gueorguieva & Agresti, 2001; Faes et al., 2004; Dunson, 2000). In contrast to approaches in which estimates depend on a litter-level statistic (Ochi & Prentice, 1984; Regan & Catalano, 1999), the mixed model formulation naturally lends itself to incorporating fetus-specific sampling weights because estimators can be expressed in terms of fetus-level responses. For segment II studies, prior approaches have incorporated non-live outcomes such as prenatal loss in evaluating dose response (Catalano & Ryan, 1992; Ryan, 1992; Dunson, 2000; Gueorguieva, 2005; Faes et al., 2006). While others have incorporated non-live outcomes, we were interested in modeling the live outcomes because we were interested in evaluating the PL approach, an approach intended for live outcomes. Although our method does not handle non-live outcomes, adjustments described by Regan & Catalano (2000) are possible. The PL approach is easily paired with a model for prenatal loss because our approach conditions on the number of live offspring. This can be accomplished by fitting a separate model for non-live outcomes followed by the PL approach for live outcomes.

In our model, outcomes within offspring are linked through a one-dimensional random effect corresponding to a random intercept model. We chose to analyze the 2,4,5-T data assuming a random intercepts model as a prior analysis found this assumption to be appropriate because with C57BL/6 mice, doses in this range had only a small negative effect on net maternal weight gain that was not statistically significant and decrement in maternal weight gain had a relatively small effect on fetal weight (Holson et al., 1992). In other experiments, a toxin could adversely impact dams and therefore, the maternal environment. In this case, it would be reasonable to include a multivariate random effect in order to account for a random intercept and random slope. One way to link outcomes with a multivariate random effect is to include a linear combination of random effects for each outcome, where the random effect components are related through a joint normal distribution, as suggested by Gueorguieva & Agresti (2001). In our approach, because the estimation requires integrating over the random effect, there would be practical limits as approximating the integral by numerical quadrature can become computationally challenging as the dimension of the random vector increases.

While we apply the PL approach to data from a segment II study, the method can be used in other settings as well. The PL approach might aid researchers who wish to conduct experiments in order to understand the complex processes involved in fetal development and the role that toxins play in disrupting normal development during organogenesis. If the continuous outcome is important for understanding the processes that lead to affected offspring, such as malformations, and affected offspring are relatively less common, then oversampling the affected pups may confer cost savings compared with approaches that assess all pups or a fixed proportion of pups. For example, if 10% of pups are affected, sampling 90% of affected pups and 30% of unaffected pups would lead to evaluating slightly more than one-third of all offspring, compared with approaches that sample one-half of all fetuses, for example. Greater savings are achievable by reducing the fraction of unaffected pups that are sampled. Our approach might also be of interest in the context of epidemiologic investigations. For example, in studies of respiratory health in children, the impact of indoor environmental exposures on childhood asthma may be of interest. Measures of respiratory health in children who share the same household environment may be correlated so that accounting for clustering within household when exposure occurs at the household level may be important. While self-reported information on physician-diagnosed asthma may be easily obtained for all subjects, it may not be feasible to do detailed assessment for every participant if the assessments involve the use of tissue or serum.

In the PL approach, essential parameters are the subsampling probabilities which are specified at the time of study design. Future work with this approach would include a method for choosing the probabilities in order to achieve a desired precision for a parameter of interest or an overall cost requirement. While we have presented simulation results for one experiment with several choices of p₁ and p₂, further study is needed to understand more generally how to choose sampling rates during the planning phase of a study.

Appendix A Estimability of parameters in the joint model

As the mean parameters and the variance for fetal weight are estimable, it remains to show that the remaining parameters, σ_b1, σ_b2, and ρ are uniquely identifiable. Estimability of these parameters can be seen by rewriting the expressions relating the marginal correlations to the model parameters as follows:

$${\sigma }_{b1}=\sqrt{{\rho }_Y/(1-{\rho }_Y)}$$ (14)

$${\sigma }_{b2}=\sqrt{{\rho }_S{\sigma }_2^2/(1-{\rho }_S)}$$ (15)

$$\rho =\left({\rho }_{YS}\sqrt{({\sigma }_{b1}^2+1)({\sigma }_{b2}^2+{\sigma }_2^2)}-{\sigma }_{b1}{\sigma }_{b2}\right)/{\sigma }_2$$ (16)

The marginal correlation ρ_Y can be estimated from the data by fitting the binary outcome alone. The estimate for σ_b1 is obtained by substituting the estimate for ρ_Y in (14). Similarly, the estimate for σ_b2 is obtained by substituting estimates for ρ_S and σ₂ in the expression for σ_b2 in (15). Finally, as the marginal correlation σ_{Y S} is also estimable from the data, estimates of parameters on the right-hand side of (16) can be substituted to estimate ρ.

Appendix B BRM partial likelihood robust standard error estimates

Let $G_N(\eta )=\frac{1}{N}{\sum }_{i=1}^N{\stackrel{\sim }{U}}_i(\eta )$ be the scaled modified PL score function. The derivative of the estimating function is given by

$${\dot{G}}_N(\eta )=\frac{\partial }{\partial \eta }\frac{1}{N}\sum _{i=1}^N{\stackrel{\sim }{U}}_i({\eta }^T)=\frac{1}{N}\sum _{i=1}^N\frac{1}{L_i}\frac{{\partial }^2{\stackrel{\sim }{L}}_i}{\partial \eta \partial {\eta }^T}-\frac{1}{L_i^2}\frac{\partial L_i}{\partial \eta }\frac{\partial {\stackrel{\sim }{L}}_i}{\partial {\eta }^T}.$$

Writing the derivative $\frac{\partial {\stackrel{\sim }{L}}_i}{\partial \eta }=\int D_w({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,\eta )P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)g({\theta }_i)d{\theta }_i$ and recalling $\frac{\partial }{\partial \eta }P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)=D_1({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,\eta )P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)$, the second derivative is obtained by direct differentiation

$$\begin{array}{ll}\frac{{\partial }^2{\stackrel{\sim }{L}}_i}{\partial \eta \partial {\eta }^T}& =\frac{\partial }{\partial \eta }\int D_w({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,{\eta }^T)P({\mathbf{\text{d}}}_i^{\prime }|{\theta }_i)g({\theta }_i)d{\theta }_i\\ & =\int \left[\frac{\partial }{\partial \eta }{D}_w({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,{\eta }^T)+D_1({\mathbf{\text{d}}}_i^{\prime };\eta )D_w({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,{\eta }^T)\right]P(d_i^{\prime }|{\theta }_i)g({\theta }_i)d{\theta }_i\end{array}$$

where

$$\begin{array}{l}\frac{\partial }{\partial \eta }{D}_w({\mathbf{\text{d}}}_i^{\prime };{\theta }_i,{\eta }^T)=\sum _{k=1}^{n_i}[-\left(\frac{w_{01}{d}_{11\mathit{\text{ik}}}}{\Phi {(u_{\mathit{\text{ik}}})}^2}+\frac{w_{02}{d}_{12\mathit{\text{ik}}}}{{[1-\Phi (u_{\mathit{\text{ik}}})]}^2}\right)\frac{\partial \Phi (u_{\mathit{\text{ik}}})}{\partial \eta }\frac{\partial \Phi (u_{\mathit{\text{ik}}})}{\partial {\eta }^T}\\ +\left(\frac{w_{01}{d}_{01\mathit{\text{ik}}}}{\Phi (u_{\mathit{\text{ik}}})}-\frac{w_{02}{d}_{02\mathit{\text{ik}}}}{1-\Phi (u_{\mathit{\text{ik}}})}\right)\frac{{\partial }^2\Phi (u_{\mathit{\text{ik}}})}{\partial \eta \partial {\eta }^T}-\left(\frac{w_{11}{d}_{11\mathit{\text{ik}}}}{\Phi {(v_{\mathit{\text{ik}}})}^2}+\frac{w_{12}{d}_{11\mathit{\text{ik}}}}{{[1-\Phi (v_{\mathit{\text{ik}}})]}^2}\right)\frac{\partial \Phi (v_{\mathit{\text{ik}}})}{\partial \eta }\frac{\partial \Phi (v_{\mathit{\text{ik}}})}{\partial {\eta }^T}\\ +\left(\frac{w_{11}{d}_{11\mathit{\text{ik}}}}{\Phi (v_{\mathit{\text{ik}}})}-\frac{w_{12}{d}_{12\mathit{\text{ik}}}}{1-\Phi (v_{\mathit{\text{ik}}})}\right)\frac{{\partial }^2\Phi (v_{\mathit{\text{ik}}})}{\partial \eta \partial {\eta }^T}+(w_{11}{d}_{11\mathit{\text{ik}}}+w_{12}{d}_{12\mathit{\text{ik}}})\frac{{\partial }^{2}logP(s_{\mathit{\text{ik}}}|{\theta }_i)}{\partial \eta \partial {\eta }^T}]\end{array}$$ (17)

Expressions for derivatives of Φ(u_ik), Φ(v_ik) and log P (s_ik∣ θ_i) are provided in Appendix C.

Appendix C Derivatives useful for robust standard error estimates

The derivatives in (17) take the form

$$\begin{array}{c}\frac{{\partial }^2\Phi (v_{\mathit{\text{ik}}})}{\partial \eta \partial {\eta }^T}=-v_{\mathit{\text{ik}}}\mathit{\varphi }(v_{\mathit{\text{ik}}})\frac{\partial v_{\mathit{\text{ik}}}}{\partial \eta }\frac{\partial v_{\mathit{\text{ik}}}}{\partial {\eta }^T}+\mathit{\varphi }(v_{\mathit{\text{ik}}})\frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial \eta \partial {\eta }^T},\\ \frac{{\partial }^2\Phi (u_{\mathit{\text{ik}}})}{\partial \eta \partial {\eta }^T}=-u_{\mathit{\text{ik}}}\mathit{\varphi }(u_{\mathit{\text{ik}}})\frac{\partial u_{\mathit{\text{ik}}}}{\partial \eta }\frac{\partial u_{\mathit{\text{ik}}}}{\partial {\eta }^T}\end{array}$$

because the second derivatives of u_ik are zero. In addition, with

$$\frac{\partial }{\partial {\eta }_r}logP(s_{\mathit{\text{ik}}}|{\theta }_i)=-\frac{1}{{\sigma }_{2i}}\frac{\partial {\sigma }_{2i}}{\partial {\eta }_r}-s_{\mathit{\text{ik}}}^{\prime }\frac{\partial s_{\mathit{\text{ik}}}^{\prime }}{\partial {\eta }_r},$$

we have

$$\frac{{\partial }^{2}logP(s_{\mathit{\text{ik}}}|{\theta }_i)}{\partial \eta \partial {\eta }^T}=\frac{1}{{\sigma }_{2i}^2}\frac{\partial {\sigma }_{2i}}{\partial \eta }\frac{\partial {\sigma }_{2i}}{\partial {\eta }^T}-\frac{1}{{\sigma }_{2i}}\frac{{\partial }^2{\sigma }_{2i}}{\partial \eta \partial {\eta }^T}-\frac{\partial s_{\mathit{\text{ik}}}^{\prime }}{\partial \eta }\frac{\partial s_{\mathit{\text{ik}}}^{\prime }}{\partial {\eta }^T}-s_{\mathit{\text{ik}}}^{\prime }\frac{{\partial }^2{s}_{\mathit{\text{ik}}}^{\prime }}{\partial \eta \partial {\eta }^T}.$$

The non-zero first derivatives are

$$\begin{array}{cccc}\frac{\partial u_{\mathit{\text{ik}}}}{\partial {\alpha }_1}=-{\mathbf{\text{w}}}_{1i},& \frac{\partial u_{\mathit{\text{ik}}}}{\partial {\sigma }_{b1}}=-{\theta }_i,& \frac{\partial v_{\mathit{\text{ik}}}}{\partial {\alpha }_1}=-{(1-{\rho }^2)}^{-1/2}{\mathbf{\text{w}}}_{1i},& \frac{\partial v_{\mathit{\text{ik}}}}{\partial {\alpha }_2}=\rho {\sigma }_2^{-1}{(1-{\rho }^2)}^{-1/2}{\mathbf{\text{w}}}_{2i},\end{array}$$

$$\begin{array}{ll}\frac{\partial v_{\mathit{\text{ik}}}}{\partial {\sigma }_{b1}}=-{(1-{\rho }^2)}^{-1/2}{\theta }_i,& \frac{\partial v_{\mathit{\text{ik}}}}{\partial {\sigma }_{b2}}=\rho {\sigma }_2^{-1}{(1-{\rho }^2)}^{-1/2}{\theta }_i,\\ \frac{\partial v_{\mathit{\text{ik}}}}{\partial \rho }=-s_{\mathit{\text{ik}}}^{\prime }{(1-{\rho }^2)}^{-1/2}-\rho {(1-{\rho }^2)}^{-3/2}{m}_{\mathit{\text{ik}}}.& \frac{\partial v_{\mathit{\text{ik}}}}{\partial {\sigma }_2}=\rho {(1-{\rho }^2)}^{-1/2}{s}_{\mathit{\text{ik}}}^{\prime }{\sigma }_2^{-1}\\ \frac{\partial s_{\mathit{\text{ik}}}^{\prime }}{\partial {\alpha }_2}=-{\sigma }_2^{-1}{\mathbf{\text{w}}}_{2i},& \frac{\partial s_{\mathit{\text{ik}}}^{\prime }}{\partial {\sigma }_{b2}}=-{\sigma }_2^{-1}{\theta }_i,\\ \frac{\partial s_{\mathit{\text{ik}}}^{\prime }}{\partial {\sigma }_2}=-{\sigma }_2^{-1}{s}_{\mathit{\text{ik}}}^{\prime }.\end{array}$$

In addition, non-zero second derivatives of v_ik are

$$\begin{array}{ll}\frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {\alpha }_1\partial {\rho }^T}=-\rho {(1-{\rho }^2)}^{-3/2}{\mathbf{\text{w}}}_{1i},\hfill & \frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {\alpha }_2\partial {\sigma }_2^T}=-\rho {\sigma }_2^{-2}{(1-{\rho }^2)}^{-1/2}{\mathbf{\text{w}}}_{2i},\hfill \\ \frac{{-}^2{v}_{\mathit{\text{ik}}}}{\partial {\alpha }_2\partial {\rho }^T}=\left({\rho }^2{(1-{\rho }^2)}^{-3/2}+{(1-{\rho }^2)}^{-1/2}\right){\sigma }_2^{-1}{\mathbf{\text{w}}}_{2i},\hfill & \frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {\sigma }_{b1}\partial {\rho }^T}=-\rho {(1-{\rho }^2)}^{-3/2}{\theta }_i,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {\sigma }_{b2}\partial {\sigma }_2^T}& =& {-\rho (1-{\rho }^2)}^{-1/2}{\sigma }_2^{-2}{\theta }_i,\hfill \\ \hfill \frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {\sigma }_{b2}\partial {\rho }^T}& =& \left({(1-{\rho }^2)}^{-1/2}+{\rho }^2{(1-{\rho }^2)}^{-3/2}\right){\sigma }_2^{-1}{\theta }_i\hfill \\ \hfill \frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {\sigma }_2\partial {\rho }^T}& =& \left({\rho }^2{(1-{\rho }^2)}^{-3/2}+{(1-{\rho }^2)}^{-1/2}\right){\sigma }_2^{-1}{s}_{\mathit{\text{ik}}}^{\prime }\hfill \\ \hfill \frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {{\sigma }_2}^2}& =& {-2\rho (1-{\rho }^2)}^{-1/2}{\sigma }_2^{-2}{s}_{\mathit{\text{ik}}}^{\prime }\hfill \\ \hfill \frac{{\partial }^2{v}_{\mathit{\text{ik}}}}{\partial {\rho }^2}& =& -2s_{\mathit{\text{ik}}}^{\prime }{\rho (1-{\rho }^2)}^{-3/2}-m_{\mathit{\text{ik}}}{(1-{\rho }^2)}^{-5/2}-3m_{\mathit{\text{ik}}}{\rho }^2{(1-{\rho }^2)}^{-5/2}\hfill \end{array}$$

The non-zero second derivatives of $s_{\mathit{\text{ik}}}^{\prime }$ are

$$\begin{array}{ccc}\frac{{\partial }^2{s}_{\mathit{\text{ik}}}^{\prime }}{\partial {\sigma }_{b2}\partial {\sigma }_2}={\sigma }_{2i}^{-2}{\theta }_i,& \frac{{\partial }^2{s}_{\mathit{\text{ik}}}^{\prime }}{\partial {\alpha }_2\partial {\sigma }_2}={\sigma }_{2i}^{-2}{\mathbf{\text{w}}}_{2i},& \frac{{\partial }^2{s}_{\mathit{\text{ik}}}^{\prime }}{\partial {\sigma }_2^2}=2{\sigma }_{2i}^{-2}{s}_{\mathit{\text{ik}}}^{\prime }\end{array}.$$