RB69 DNA Polymerase Mutants with Expanded Nascent Base-Pair-Binding Pockets Are Highly Efficient but Have Reduced Base Selectivity

Abstract

We have investigated the effect of systematically enlarging the nascent base-pair-binding pocket (NBP) of a replicative DNA polymerase from bacteriophage RB69 (RB69 pol) on the incorporation efficiency (k_pol/K_d,app) for both correct and incorrect dNMPs. Accordingly, we replaced residues L561, Y567, and S565 in the NBP with Ala, Ala, and Gly, respectively. We combined L561A and Y567A to give a double mutant and then introduced the S565G mutation to give a triple mutant. The efficiency of incorrect dNMP insertion increased markedly relative to the wild type with the single mutants and increased further as the number of substitutions in the NBP increased. The difference in incorporation efficiency for mispairs between the mutants and the wild-type RB69 pol was due mainly to k_pol. Unexpectedly, enlarging the NBP had a minimal effect on the incorporation efficiency of correct dNMPs. Our kinetic data suggest that replicative DNA pols exert base discrimination via “negative selection” against mispairs by using residues in the NBP, particularly the three residues analyzed in this study, to allow rapid incorporation of only correct base pairs. This proposal differs from how geometry and “tightness of fit” of the NBP is often invoked to account for rapid incorporation of correct base pairs, namely, that a tighter fit within the NBP leads to an increase in insertion rates [Kool, E. T. (2002) Annu. Rev. Biochem. 71, 191–219]. We related our findings to that of a model translesion DNA pol, Sulfolobus solfataricus Dpo4. We concur with the main conclusion of a previous study [Mizukami, S., et al. (2006) Biochemistry 45, 2772–2778], namely, that lesion bypass pols exhibit low incorporation efficiencies for correct dNMPs (leading to relative promiscuity) not because of a more open NBP but because of a loose fit of substrates bound in the catalytic centers. This is a property not shared by RB69 pol and its mutants.

High-fidelity DNA replication is essential for maintaining genomic integrity. This is accomplished principally by DNA polymerases (pols),¹ the central component of the replisome. When replication fidelity is perturbed, mutations that occur as a consequence, if not removed, are usually deleterious. Under normal circumstances many of these errors are corrected by an exonuclease editing function inherent in the pol or by a separate exonuclease associated with the replisome. To ensure the integrity of the genome throughout subsequent cycles of cell division, repair enzymes exist that restore the DNA to a functionally intact state after it has suffered postreplication damage (for reviews see refs (1–3)).

It has been generally accepted that the high level of base discrimination exhibited by replicative pols cannot be explained solely by the free energy differences between Watson-Crick (W–C) and non-W–C base pairing (4, 5). Although hydrogen bonding between the templating base and the base of the incoming dNTP clearly contributes to base selectivity, a tight complementary fit between the nascent base pair and the nascent base-pair-binding pocket (NBP) in pols is thought to markedly enhance the level of base selectivity and incorporation efficiency (6, 7). There also appears to be a correlation between the rates of nucleotide incorporation and Watson–Crick (W–C) ideal geometry as reported k_pol values of correct dNMP insertions are several orders of magnitude higher than that found for incorrect dNMPs (3, 8). DNA pols of the Y family (translesion pols) insert correct dNMPs with markedly lower efficiency and incorporate mispaired dNMPs with higher frequency than replicative pols, presumably because their NBPs are less rigid and relatively open (8–11).

In a previous report we presented evidence that questioned the generality of the relationship between the “tightness of fit” and fidelity by showing that reducing the size of the L561 side chain of the replicative DNA polymerase RB69 pol, a residue lining the NBP (Figure 1), did not alter the pre-steady-state kinetic parameters for incorporation of correct dNMPs but did reduce base selectivity (12). In another study, Zhong et al. reported that replacing L415 in the NBP of RB69 pol with Phe or Gly increased misinsertion but left the specific activity of the enzyme unaltered (13). The results of these studies led us to propose an alternative to the “tightness of fit” hypothesis, namely, that the geometry of the nascent base pair and the spatial complementarity with the NBP, rather than serving to enhance the efficiency of dNMP insertion, instead act as a key determinant that strongly disfavors misincorporation. In this study we wanted to distinguish between the two competing hypotheses that attempt to account for base selectivity: one claiming that high efficiency of base insertion depends on the “tightness of fit” between the nascent base pair and the residues in the polymerase that envelope it and the other proposing that the size and shape of the NBP determine whether misincorporation will occur. We attempted to do this by testing whether the proposed relationship between the “tightness of fit” of the nascent base pair in the NBP and rates of correct dNMP incorporation would be maintained if we systematically expanded the size of the NBP in a replicative DNA pol (Figure 1). Our choice of RB69 pol as a model pol was based on several considerations: (i) since there is extensive kinetic and structural information on RB69 pol and its close relative T4 pol (12, 14–25), a valuable resource was available for interpreting the results obtained in this study; (ii) this pol is representative of B family DNA polymerases, a class that includes human replicative polymerases α and δ; and (iii) large quantities of this enzyme and its mutants can be obtained from plasmids harboring RB69 pol cDNA in Escherichia coli, making it possible to carry out experiments that would be difficult to perform with other B family replicative pols that can only be obtained in limited amounts.

Figure 1.

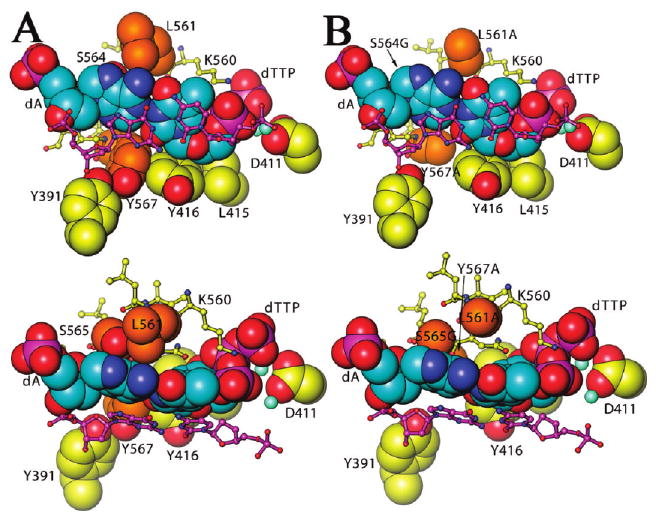
Crystal structures of the ternary complexes of wt RB69 pol (16) and the triple mutant (M. Wang and J. Wang, personal communication) showing the added volume of the NBP upon substitution of L561, S565, and Y567 with Ala, Gly, and Ala, respectively. Pertinent residues are labeled and shown in space-filling form. Other molecules that are a part of the NBP are shown in stick form (including the penultimate base pair of the DNA duplex shown mostly in purple with blue nitrogen atoms and orange oxygen atoms). (A) Orthogonal views of the NBP of wt enzyme. (B) Orthogonal views of the NBP of the triple mutant. All graphic figures were made using Ribbons (50).

In addition to the L561A mutant (12), we decided to replace Y567 and S565 with Ala and Gly, respectively, then combined Y567A with L561A to obtain the L561A/Y567A double mutant, and finally added S565G to give the L561A/Y567A/S565G triple mutant (Figure 1) (12, 22). All of these mutants had pre-steady-state K_d,app and k_pol values for the incorporation of correct dNMPs that were comparable to or exhibited k_pol values that were somewhat greater than wild-type RB69 pol. The mutants displayed a correlation between an increased NBP volume and loss of base selectivity. The implications of these results for replication fidelity are discussed.

Materials and Methods

Materials

T4 polynucleotide kinase and dNTPs were obtained from New England Biolabs, [γ-³²P]ATP was from Perkin-Elmer Life Science, Inc., and electrophoresis reagents were from American Bioanalytic Corp. Oligonucleotides were synthesized by the W. M. Keck Foundation Biotechnology Resource Laboratory at Yale University. The F and Q phosphoramidites were a gift from the Glen Research Corp. RB69 pol, referenced hereafter as wt, and all the variants used for the kinetic studies carried the D222A/D327A double replacement that eliminated the 3′–5′ exonuclease activity of the polymerase.

Protein Expression and Purification

After sequences of the coding region of the RB69 pols containing the intended mutations had been verified, plasmids containing the RB69 pol cDNA were transformed into E. coli BL21(DE3) competent cells. Protein expression, purification, and storage was performed as previously described (12).

Primer-Template DNA Sequences

The nucleotide sequence of 13/20mer primer-templates (P/Ts) used for these experiments are shown in Table 1 together with the incoming dNTPs that were paired with the corresponding P/Ts. These combinations were designed so that the base 5′ to the templating base would not favor further extension for a given incoming dNTP. As anticipated, the products were extended by only a single nucleotide residue.

Table 1.

Pre-Steady-State Kinetic Parameters for Wild-Type and Single, Double, and Triple Mutants of RB69 Pol^a

	Kd,app (μM)					kpol (s−1)
dNTP/dN	wt	Y567A	L561A	double	triple	wt	Y567A	L561A	double	triple
dGTP/dC	66	27	26	40	60	160	130	89	220	>300b
dATP/dT	50	30	30	62	60	220	220	110	230	>300b
dCTP/dG	70	68	42	48	50	200	210	110	220	>300b
dTTP/dA	42	21	51	58	55	270	270	120	190	>300b
dATP/dC	1800	210	370	240	300	0.08	1.6	0.8	22	82
dCTP/dC	NDc	1200	2000	860	960	NDc	0.05	0.03	0.4	1.1
dTTP/dC	1700	460	510	800	850	0.09	1.7	0.8	45	77
dGTP/dT	730	280	250	370	300	0.04	0.43	0.18	15	35
dCTP/dT	NDc	760	1500	510	590	NDc	0.24	0.14	0.86	5.2
dTTP/dT	1400	360	210	290	300	0.015	0.18	0.13	2.1	6.7
dGTP/dG	NDc	500	160	450	900	NDc	0.02	0.11	1.0	13
dATP/dG	910	470	310	1000	640	0.004	0.05	0.03	3	15
dTTP/dG	NDc	65	28	40	50	NDc	0.18	0.05	1.7	8.7
dGTP/dA	780	250	230	230	450	0.003	0.05	0.01	0.2	1.2
dATP/dA	810	370	160	250	240	0.13	0.5	0.03	1.1	4.1
dCTP/dA	NDc	850	540	900	1100	NDc	1.2	0.26	3.2	10

^aThe double mutant had the L561A/Y567A substitutions, and the triple mutant had the L561A/Y565G/Y567A substitutions. The data for L561A were reported previously (12). The primer sequence was 5′-CCGACCACGGAAC-3′. The template sequences had various nucleotides in the templating position and a 5′-overhang for making all 12 combinations of base pairs: 3′-GGCTGGTGCCTTGX(N)_m-5′, where m = 5 or 6. Two different 5′-overhanging (N)_m were used for each templating nucleotide X for four incoming dNTPs as follows: dATP and dCTP, X = C and (N)_m = AAAAAA; dGTP and dTTP, X = C and (N)_m = GGTTT; dATP and dGTP, X = G and (N)_m = AAAAAA; dCTP and dTTP, X = G and (N)_m = CCCCCC; dATP and dCTP, X = A and (N)_m = CCCCCC; dGTP and dTTP, X = A and (N)_m = GGTTT; dATP and dCTP, X = T and (N)_m = CCCCCC; dGTP and dTTP, X = T and (N)_m = GGTTT. The standard deviation for the K_d,app values was (10% when K_d,app values were <100 μM, (20% when K_d,app values were between 100 and 900 μM, and ±30% when K_d,app values were >900 μM. The standard deviation for k_pol values was ±15%. Most of the experiments to determine the kinetic parameters were done in duplicate.

^bBecause k_obs at saturating concentrations of correct dNTP had a t_1/2 ∼ 2 ms using the triple mutant, the actual values cannot be determined with high precision, so we have put a lower limit of 300 s⁻¹ for the values of k_pol in these cases.

^cND = not determined. Generally, K_d,app values >2000 μM could not be determined with sufficient accuracy due to solubility issues of dNTPs at concentrations required to approach saturation. However, because the specificity constant k_pol/K_d,app can be found from the slope of the k_obs versus dNTP concentration plot, we obtained the k_pol/K_d,app values at low [dNTP] for the dNTP/dN combinations in question: dCTP/dC, 3 × 10⁻⁷; dCTP/dT, 6 × 10⁻⁶; dGTP/dG, 1 × 10⁻⁵; dTTP/dG, 7 × 10⁻⁵; dCTP/dA, 1.7 × 10⁻⁴.

Rapid Chemical Quench Assays

Rapid chemical quench experiments were carried out using the KinTek rapid quench instrument (Model RQF-3; KinTek Corp., University Park, PA) as previously described (12). Single turnover experiments were performed under conditions in which the enzyme concentration was five times that of the P/T. Unless otherwise noted, each reaction mixture contained 66 mM Tris-HCl, pH 7.5, and was performed at 25 °C by mixing equal volumes of the preincubated complex of 400 nM 5′-³²P-labeled P/T and 2 μM RB69 pol (exo⁻) enzyme (or its mutants) with 20 mM MgCl₂ and varying concentrations of dNTPs to give final concentrations of 200 nM P/T and 1 μM enzyme. The polymerase reaction mixture was quenched with 0.5 M EDTA at defined time intervals. For slower reactions, requiring sampling at time intervals longer than 20 s, aliquots of the reaction mixtures were quenched manually. Products and substrates were separated by electrophoresis in 20% acrylamide gels containing 8 M urea and identified by radioactive bands in the gel resulting from ³²P-labeling of the primer strand using phosphorimaging plates (Molecule Dynamics) and quantified using NIH Imaging software. For assays requiring excess unlabeled P/T to sequester free enzyme during the reaction, a final concentration of 20-fold excess unlabeled P/T (of the same sequence as labeled) over enzyme was added to the syringe containing dNTP and MgCl₂. Low temperature assays were performed using an LKB/Bromma thermostatic circulator to keep the temperature at 4 °C within the rapid quench instrument.

Stopped-Flow Fluorescence Measurements

Transient kinetic fluorescence experiments were performed using an Applied Photophysics SX18MV-R instrument at 25 °C as described previously (24). Briefly, fluorescence emission was monitored through a 345 nm long-pass glass filter upon excitation of 2-aminopurine (2AP) at 313 nm. Final concentrations of the reaction components after mixing were 66 mM Tris-HCl (pH 7.5), 200 nM primer-template with 2AP as the templating base, 1 μM RB69 pol triple mutant, 10 mM MgCl₂, and various concentrations of dNTPs. Time courses were fit to a sum of exponentials using Pro-K software provided with the instrument as described previously (24).

Data Analysis

Data from most of the single turnover experiments fit best to the equation for a single exponential, [product] = A[1 − exp(−k_obst)], with the exception of when the triple mutant encountered correct dNTPs and several dNTP/dN mispairs. In these cases the data fit best to a double exponential equation, [product] = A[1 − exp(−k_obs,1t)] + B[1 − exp(k_obs,2t)]. The apparent dissociation constant, K_d,app, for dNTP binding to the RB69 pol P/T complex was calculated by fitting data from the k_obs versus dNTP concentration [S] (see Figure 2 for two examples) to the hyperbolic equation k_obs = k_pol[S]/(K_d,app + [S]), where k_pol is the maximum rate of dNMP incorporation. With the wt enzyme, the k_obs versus [dNTP] plots were nearly linear for many of the mispairs so that only k_pol/K_d,app ratios could be determined (Table 1).

Figure 2.

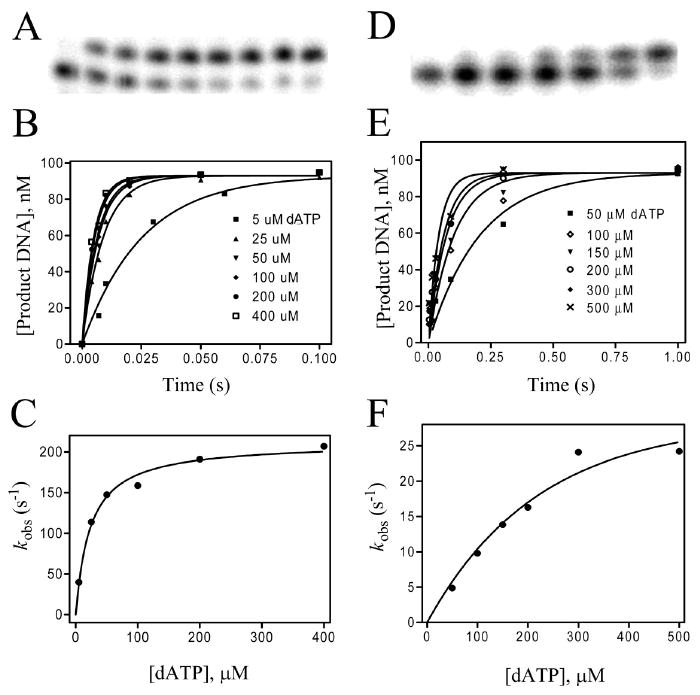
Determination of pre-steady-state kinetic parameters. (A–C) Incorporation of dAMP opposite dT with the Y567A mutant of RB69 pol. (D–F) Incorporation of dAMP opposite dF with the triple mutant. (A) Time course for the reaction at 0.004, 0.007, 0.01, 0.02, 0.05, 0.1, 0.25, and 0.5 s with 50 μM dATP showing the formation of product DNA over time. (B) Plots of [product DNA] versus time with varying [dATP]s. (C) Plot of k_obs versus [dATP] fit to a hyperbola to obtain the kinetic parameters k_pol = 220 s⁻¹ and K_d,app = 30 μM. (D) Time course for the reaction at 0.003, 0.006, 0.015, 0.03, 0.09, 0.3, and 1.0 s with 100 μM dATP showing the formation of product DNA over time. (E) Plots of [product DNA] versus time with varying [dATP]s. (F) Plot of k_obs versus [dATP] fit to a hyperbola to obtain the kinetic parameters k_pol = 28 s⁻¹ and K_d,app = 150 μM.

Results

Characterization of RB69 Pol Mutants with Enlarged NBPs

The aim of this study was to investigate the consequence of enlarging the volume of the NBP on the kinetic parameters for correct and incorrect dNMP incorporation. Highly conserved residues in motif B were candidates for substitution since they comprised part of the NBP as determined from the crystal structures of RB69 pol ternary complexes (16). We used site-directed mutagenesis to replace these conserved residues with Ala or Gly with the expectation that the resulting mutants would have an enlarged NBP and could more easily accommodate non-W–C base pairs. We had previously reported results obtained with the L561A mutant that included pre-steady-state kinetic parameters for a complete set of 4 correct and 12 incorrect dNTPs. We also had preliminary data for the Y567A mutant (22). With both single mutants, there was a loss in base selectivity. We then combined the two single replacements to give the L561A/Y567A double mutant. Pre-steady-state kinetic parameters for the double mutant were determined using all 16 base-pair combinations. As shown in Table 1, there was a further decrease in base discrimination compared to the mutants with single site replacements, but the k_pol and K_d,app values for incorporation of correct dNMPs were comparable to the values obtained with the wt. We also constructed several other single site mutants in this region of the NBP, one of which was S565G. Similar to the other single site mutants, the S565G mutant showed reduced base discrimination while maintaining comparable efficiencies for incorporation of correct nucleotides as the wt. On the basis of these results, we introduced the S565G substitution into the double mutant to give the L561 A/S565G/Y567A triple mutant. Again, we used this triple mutant to obtain the pre-steady-state kinetic parameters for all 16 base-pair combinations. As shown in Table 1, there was a further decrease in base discrimination for the triple mutant compared to mutants with single and double site replacements without much change in k_pol and K_d,app values for insertion of correct dNMPs. Table 2 shows the calculated discrimination values for each mispair by the wt and the mutant pols.

Table 2.

Discrimination between Correct and Incorrect dNMP Incorporation by wt RB69 and Its Mutants

		discriminationa
dNTP	template	wt	Y567A	L561A	double	tripleb
dGTP	C	1	1	1	1	1
dATP		54000	630	1600	60	18
dCTP		8200000	110000	230000	12000	4400
dTTP		45000	1300	2200	98	55
dATP	T	1	1	1	1	1
dGTP		80000	2400	5100	92	43
dCTP		710000	12000	39000	2200	570
dTTP		410000	7400	5900	510	220
dCTP	G	1	1	1	1	1
dGTP		270000	78000	3800	2100	420
dATP		650000	29000	27000	1500	260
dTTP		41000	1100	1500	110	34
dTTP	A	1	1	1	1	1
dGTP		1700000	65000	54000	3800	2000
dATP		40000	9500	13000	750	320
dCTP		38000	9100	4900	920	600

^aDiscrimination values were calculated using the equation: k_pol/K_d,app (correct)/k_pol/K_d,app (incorrect). Discrimination values for incorporation of correct dNMPs were unity by definition.

^bDiscrimination values for the triple mutant were calculated using correct dNTP incorporation k_pol values of 300 s⁻¹ (Table 1).

Pre-Steady-State Kinetic Parameters for Primer Extension Using Correct and Incorrect dNTPs

Pre-steady-state experiments were performed under single turnover conditions using a 5:1 ratio of enzyme:P/T, where the [RB69 pol] was 1 μM. This ensured that about 92% of the P/T was in a binary complex based on the DNA ground state dissociation constant of 30 nM (H. Lee, unpublished results), a value comparable to that obtained for T4 pol (70 nM) (26). Product formation as a function of time followed a single exponential for all base-pair combinations, [product] = A[1 − exp(−k_obst)], except for the triple mutant with correct dNTPs and some dNTP/dN mispairs where the data fit best to a double exponential equation of the form [product] = A[1 − exp(−k_obs,1t)] + B[1 − exp(k_obs,2t)]. It appears that the triple mutant differs from the wt and the other NBP mutants in that it initially forms a significant amount (∼50%) of unproductive complexes with the P/T that subsequently dissociates and rebinds productively with the enzyme to yield product. This conclusion was based on experiments using excess unlabeled P/T DNA to trap free enzyme during the rapid chemical quench. We found that excess unlabeled DNA virtually eliminated the second phase (see Supporting Information and Figure 3C for further details). Mispairs that were incorporated with lower rates (<5 s⁻¹k_pol) by the triple mutant did not display two phases.

Figure 3.

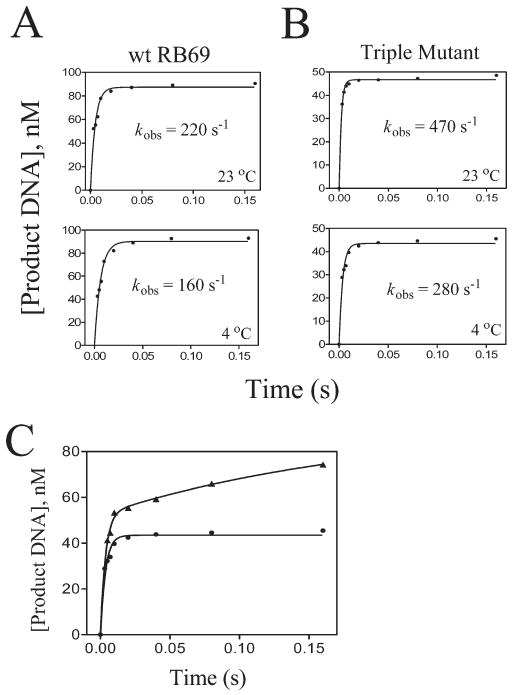
k_obs of phosphodiester bond formation at saturating [dATP] (1 mM) opposite a templating dT using wt and triple mutant RB69 pol under single turnover conditions. The concentrations of ³²P-labeled primer-template and enzyme were 100 nM and 1 μM, respectively. (A) Time course for incorporation of dAMP at 23 and 4 °C using wt enzyme. (B) Time course for incorporation of dAMP at 23 and 4 °C using the triple mutant. For the latter studies, a 20-fold excess of unlabeled P/T over enzyme to trap excess enzyme was used. (C) The data from the lower panel of (B) (●) is shown superimposed with the results of a parallel experiment where an unlabeled P/T trap was not included (▲).

To determine the overall apparent K_d (K_d,app), defined as the [dNTP] that supports the half-maximal rate of phosphodiester bond formation, the k_obs values were plotted versus [dNTP]. Most of the plots fit best to a hyperbola of the form k_obs = k_pol[dNTP]/([dNTP] + K_d,app) (Figure 2). For this relationship to be valid, we had to assume that the EDN collision complex was in rapid equilibrium with ED + N, where E stands for enzyme, D for DNA, and N for dNTP. Lending support to this assumption was the lack of any lag phase even at low [dNTP] in both the chemical quench and stopped-flow fluorescence experiments (24, 27). It must be noted that the K_d,app value is a product of several steps in the catalytic cycle, up through the chemistry step, and thus is not necessarily the same value as the true ground state dissociation constant for dNTP binding (27). Therefore, we cannot make direct comparisons between the K_d,app values we obtained in this study from the chemical quench and stopped-flow assays to those obtained from assays that did not include as many kinetic steps, e.g., the apparent K_d values obtained in the absence of chemistry using the fluorescence changes of 2AP in a P/T for RB69 pol (24) or a dye-labeled T7 DNA polymerase (28). The results of these assays for all dNTP/dN combinations are shown in Table 1 and summarized in a bar graph (Figure 4). There are several issues that should be mentioned with respect to this data: (i) When the K_d,app values exceeded 2 mM, as they do with the wt and some incorrect dNTPs, the values were only rough estimates based on computer-generated plots that were greatly dependent on the k_obs values determined at the highest [dNTP]. For this reason these K_d,app values had very large errors. As a consequence we could only obtain accurate k_pol/K_d,app ratios. (ii) Because of the high k_pol values for correct insertions, significant product formation occurred within the 2 ms dead time (t_1/2 ∼ 3 ms for a k_pol value of 250 s⁻¹) of the Kintek chemical quench instrument, creating uncertainty about the maximum value of k_pol for the wt and the mutants. We therefore determined k_pol for dATP opposite dT for both the wt and the triple mutant at 4 °C, and we found that the k_pol for both were reduced to about the same extent going from 25 to 4 °C (30% for wt and 40% for the triple mutant) (Figure 3A,B), an indication that these high k_pol values are reasonable estimates. However, we are hesitant to assign a precise number to k_pol values >300 s⁻¹ because these values have half-times within the dead time of the Kintek chemical quench instrument (Table 1).

Figure 4.

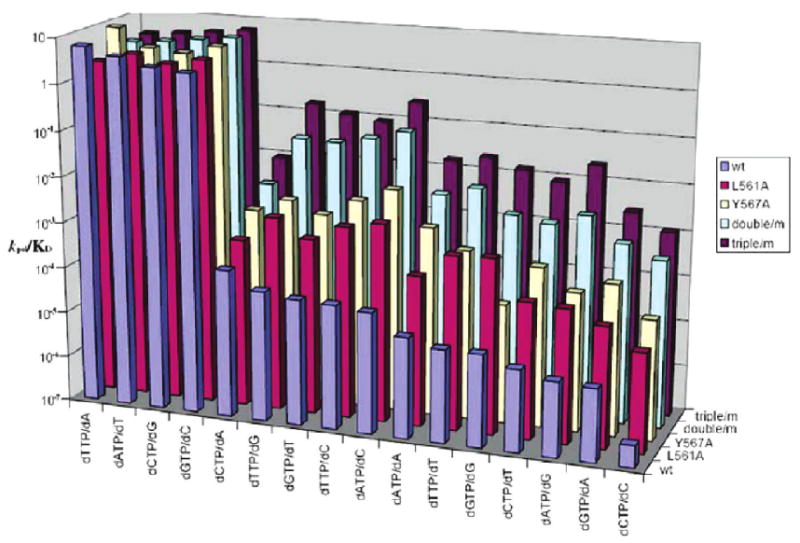
Graphic representation of kinetic parameters for correct and incorrect dNMP incorporation by wt RB69 pol and the four NBP mutants. The logarithm of incorporation efficiencies (vertical axis) plotted against the 4 correct dNTPs (left 4 groups of bars) and the 12 mispaired dNTPs (right 12 groups of bars) in descending order of incorporation efficiency with respect to the wt enzyme. The third dimension shows results for the wt and the L561A, Y567A, L561A/Y567A, and L561A/Y567A/S565G mutants, respectively.

To determine whether the rate-limiting step for incorporation of correct dNMPs was the same for the wt and the triple mutant, we carried out stopped-flow fluorescence experiments with the triple mutant using increasing [dTTP] opposite 2AP as the templating base. As shown in Figure 5, two phases were observed. The very rapid phase of 2AP fluorescence quenching occurred within the 2 ms dead time of the instrument, and its amplitude increased with increasing [dTTP]. This was almost identical to our previous results with wt where the very rapid phase reflected the rate of fingers closing (24). The second, slower phase had a quench rate equal to that determined from the rapid chemical quench. The rate constants (k_obs), derived from the second phase, when plotted as a function of [dTTP], fit a rectangular hyperbola that extrapolated to a k_pol of 380 s⁻¹ and gave a K_d,app of 22 μM (Figure 5). These parameters were comparable to the dTMP insertion rate k_pol of >300 s⁻¹ and the K_d,app of 55 μM obtained from the rapid chemical quench (Table 1), suggesting that these transitions were monitoring the same process with the triple mutant and the wt. Thus with both the wt and the triple mutant, the rate of phosphodiester bond formation, or a kinetically invisible step just prior to chemistry, appeared to be rate-limiting. We were restricted to examining dNTP/dAP pairs because we could only get a significant change in 2AP fluorescence when 2AP was the templating base. We assumed however that all of the correct dNTP/dN pairs would have behaved in a similar fashion if we could have monitored them by fluorescence.

Figure 5.

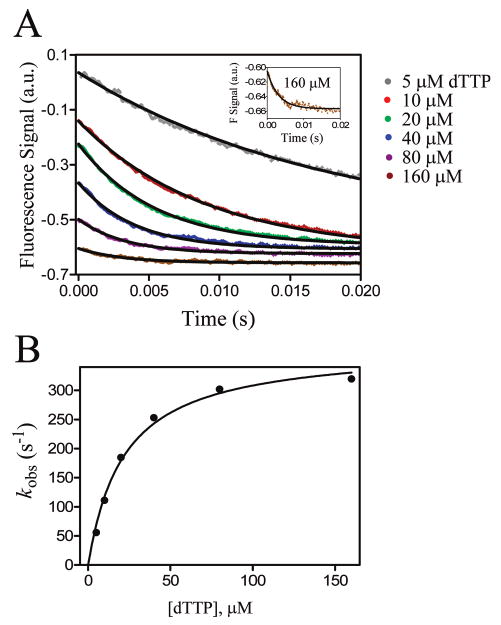
Stopped-flow data for fluorescence of dTTP binding opposite a templating 2-aminopurine in a triple mutant ternary complex. (A) Transient plots of fluorescence emission changes of 2-aminopurine upon addition of various [dTTP]s. Two phases were observed showing [dTTP] dependence was observed; a rapid quenching phase that occurred within the dead time of the stopped-flow instrument (t_1/2 < 2 ms) followed by a second quenching phase. The second phase was fit to a single exponential decay equation for each of the six [dTTP]s. The inset shows an expanded view of the 160 μM dTTP time versus fluorescence amplitude plot. (The amplitude was very low, resulting in high background noise, but the fit to the single exponential decay was still satisfactory.) (B) k_obs values from (A) were plotted as a function of [dTTP] and fit to a hyperbola to obtain a K_d,app of 22 μM and a maximum rate k_pol of ≅ 380 s⁻¹. Conditions are described in the Materials and Methods section.

Analysis of the Kinetic Data for Correct and Incorrect dNTPs

There are a number of ways of analyzing and interpreting this large set of kinetic data. One approach is to compare the averaged kinetic parameters k_pol and K_d,app as well as the averaged efficiency for correct and incorrect nucleotide incorporation with the wt and each mutant to see if a correlation exists between the NBP volume and the observed kinetic parameters. The results are presented in the Supporting Information. A second approach, complementary to the first, is to examine the variation in individual kinetic parameters among different mispairs with each of the mutants and attempt to correlate them with structures of ternary pol complexes containing the corresponding mispairs. It was also of interest to compare the relative base selectivity of the various mutants with the wt. We define selectivity as (k_pol/K_d,app)_correct/(k_pol/K_d,app)_incorrect. From the wt to the triple mutant there was a large decrease in base selectivity, up to an average of 3 orders of magnitude (Table 2). For example, the maximum selectivity exhibited by the wt RB69 pol was 1.3 × 10⁷ against the dCTP/dC mispair, which was reduced 2000 times to about 5.5 × 10³ with the triple mutant.

There Is No Direct Correlation between Mispair Geometry and the Volume of the NBP and K_d,app Values for Incorrect dNTPs

With the exception of the dGTP/dG mispair, which has a very high K_d,app with wt RB69 pol (only k_pol/K_d,app could be determined), the K_d,app values for the remaining three purine–purine (Pu–Pu) mismatches are lower than, or similar to, purine–pyrimidine (Pu–Py) mismatches such as dTTP/dG or dCTP/dA mispairs (Table 1). The dCTP/dA mispair has one of the highest estimated K_d,app when tested with wt RB69 pol, but the K_d,app for this mispair was lower with the L561A mutant but it increased again with the double and triple mutants (Table 1). This was also true for the dATP/dG mispair. Thus, there is no apparent correlation between the nature of the mispair, the volume of the NBPs, and the K_d,app values for incorrect dNTPs. These results raise questions about the size-based discrimination hypothesis, Pu–Pu mismatches being too large and Py–Py mismatches being too small to fit snugly into the NBP of the wt or its mutants (6, 10). However, it has been pointed out that solvation of the pyrimidines, giving them more bulk, could provide a strong basis for their exclusion from the NBPs on steric grounds (29).

Asymmetry in the Kinetic Parameters for Incorporation of Mispairs with Reciprocally Related Bases

The kinetic parameters for the dTTP/dG versus the dGTP/dT mispair differed substantially with both the wt and the NBP mutants (Table 1). For example, with the L561A mutant, the K_d,app was 28 μM for dTTP opposite dG, whereas the K_d,app was 250 μM for dGTP opposite dT (12). Kinetic asymmetry of this type was the rule rather than the exception and was likely due to structural asymmetry for any given set of mispairs (Figure 6) (30–32).

Figure 6.

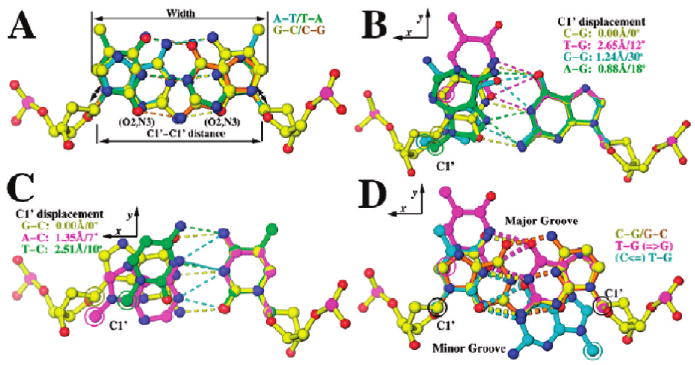
Geometry of Watson–Crick (W–C) base pairs and some non-W–C base pairs of known structure as determined by X-ray crystallography within DNA duplexes (31). (A) W–C base pair, superimposed using ribosyl atoms of both strands. (B) Mispairs opposite dG, superimposed using all atoms of dG in the templating nucleotide position. Deviations in the C1′ position and the orientation of the glycosidic bonds are indicated. (C) Mispairs opposite dC, superimposed using all atoms of dC. (D) Asymmetric geometry with reciprocally swapped bases, superimposed using all atoms of dG (magenta) or all equivalent atoms of dC onto dT (cyan) with reference dG-dC base pairs in yellow and gold.

Kinetics of Nucleotide Incorporation Opposite the Templating Isosteres dF and dQ

The observation that the triple mutant can incorporate W–C base-paired dNTPs as efficiently as the wt prompted us to evaluate the contribution of interbase hydrogen bonding to incorporation efficiency. We used two nonpolar isosteres as templates, dF and dQ (Figure 7), which have the same size and shape as dT and dA, to direct incorporation of dAMP and dTMP, respectively. For dF, the replacement of carbonyl oxygen atoms with fluorine and nitrogen with carbon in thymine completely abolished its ability to form interbase hydrogen bonds with dATP. Similarly, For dQ, the isosteric analogue of dA, no hydrogen bonds are formed with dTTP (33–35).

Figure 7.

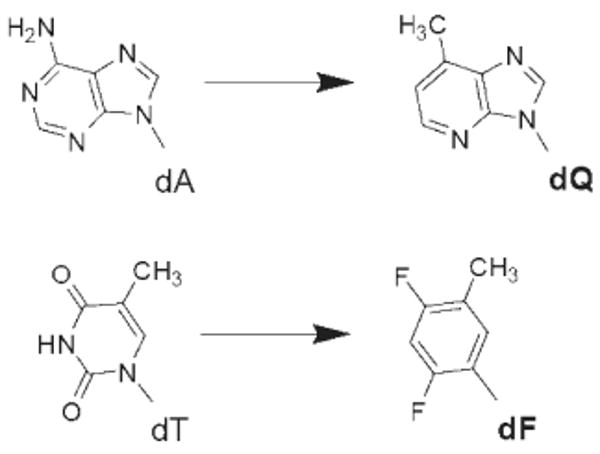
Structures of the templating base isosteres used. dQ is isosteric to dA, and dF is isosteric to dT. Both isosteres are unable to form hydrogen bonds with their complementary dNTPs, dTTP and dATP, respectively.

A representative set of kinetic data for incorporation of dAMP opposite dF is shown in Figure 2D–F, where formation of the 14-mer product by the triple mutant is plotted against time with increasing [dATP]. The k_obs were then plotted as a function of [dATP] (Figure 2F). The pre-steady-state kinetic parameters, K_d,app and k_pol, for incorporation of dAMP opposite dF by the wt were 400 μM and 0.25 s⁻¹ (Table 3). In contrast, the K_d,app and k_pol values for dAMP incorporation opposite dF by the triple mutant were 150 μM and 28 s⁻¹. Misincorporation of dGMP opposite dF by the triple mutant gave a K_d,app of ∼ 1500 μM and a k_pol of 0.46 s⁻¹, compared to 780 μM and 0.003 s⁻¹ for the wt. When dQ was used as the templating residue, there was no observable incorporation of dTMP by the wt even after 30 min, but with the triple mutant, we obtained a K_d,app of 780 μM and a k_pol of 3.4 s⁻¹.

Table 3.

Pre-Steady-State Kinetic Parameters for Incorporation of dNMPs Opposite Templating Isosteres with wt and the RB69 Pol Triple Mutant^a

	Kd,app (μM)		kpol (s−1)		kpol/Kd,app (μM−1 s−1)
dNTP/dN	wt	triple	wt	triple	wt	triple
dATP/dF	400	150	0.25	28	6 × 10−4	0.14
dGTP/dF	780	1500	0.003	0.46	4 × 10−6	3 × 10−4
dTTP/dQ	nob	780	no	3.4	no	4 × 10−3

^aBecause we had limited quantities of the templating isosteres, the reported parameters were based on a single set of experiments for each isostere. The standard deviation for the K_d,app and k_pol values were approximately the same as reported in Table 1.

^bno = not observable within 30 min.

Discussion

There are several reports that ascribe the “tightness of fit” between the correct nascent base pairs and the corresponding NBP to the high level of accuracy and efficiency of correct dNMP incorporation exhibited by many pols (6, 7). This conclusion was based on the inverse correlation observed between incorporation efficiency (as well as base discrimination) and the size of the NBP (6, 36, 37). Replicative pols with the smallest NBPs, i.e., NBPs that fit most snugly around a correct nascent base pair, have the highest incorporation efficiencies and base selectivity, while lesion bypass pols with the largest NBP have much lower incorporation efficiencies and base selectivity (9, 38). This correlation appears to be valid for rat pol β, where amino acid substitutions that enlarged the NBP decreased the efficiency of correct dNMP incorporation (39, 40). However, these studies were limited to single site substitutions. Expanding the NBP volume of RB69 pol, a high-fidelity pol, using multiple site substitutions, provided us with the opportunity to test the scope of this correlation. Our results show that as the NBP increases in volume, from the introduction of one to three amino acid substitutions, base discrimination decreases up to 3 orders of magnitude (Table 2). This study expands on and extends the results of previous studies which focused on single site substitutions in RB69 pol (12, 13).

Unexpectedly, we found that for one particular mispair, dTTP/dG, K_d,app values for dTMP incorporation averaged ∼45 μM for all four mutants examined, not far from the 70 μM K_d,app for insertion of dCMP opposite dG. This should be compared to a value of >2 mM for wt (Table 1). We relied on crystal structures of the triple mutant complexes containing dTTP/dG and dCTP/dG to rationalize these results (M. Wang et al., unpublished results).

Wobble dTTP/dG Base Pairing Allows NBP Mutants To Efficiently Insert dTMP Opposite dG

Wobble geometry exists within DNA duplexes bound to some DNA pols. For example, Johnson and Beese (29) observed that the dT/dG mispair can form either wobble or inverted wobble base pairs within the BstI pol ternary complex, depending on the location of the mispair in the DNA duplex (Figure 8). Because wobble pairing optimizes hydrogen bonding between the base of the incoming dNTP and the templating base, a correlation likely exists between wobble pairing and a reduction of K_d,app values (41). Wild-type RB69 pol binds both dGTP opposite dT and dTTP opposite dG with high K_d,app values, indicating that wobble pairing is not occurring (Table 1). Upon wobble pairing, the dG of a dTTP/dG mispair would be displaced toward the minor groove to form hydrogen bonds with T, and according to our computer modeling with wt, this geometry would lead to a steric clash between dG and the side chain of Y567. In the case of an inverted wobble, the templating dG would be displaced toward the major groove, resulting in a steric clash with the side chain of L561. The Y567A and L561A single mutants may allow wobble and inverted wobble geometry to form with the dTTP/dG mispair, respectively, by eliminating steric clashes and could explain the resulting low K_d,app values for dTTP with each of these mutants (Table 1). With the reciprocal situation, dGTP opposite dT, the K_d,app values did not change appreciably as the NBP volume increased, perhaps due to an alternate positioning of the incoming dGTP relative to the mutated residues, limiting its ability to make wobble pairings with T.

Figure 8.

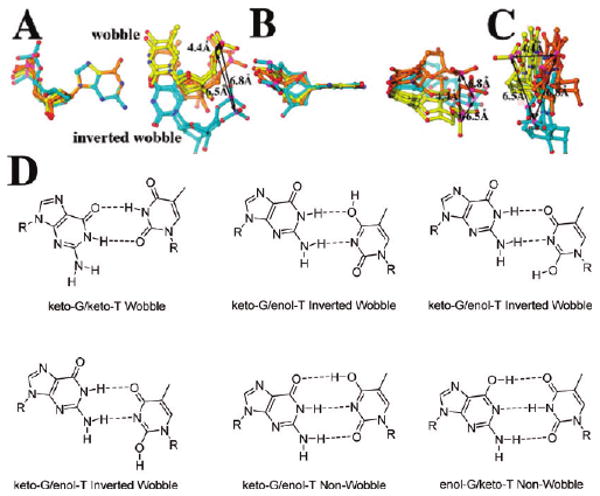
Observed geometries of dTTP/dG and dGTP/dT mispairs within DNA duplexes of the ternary complexes of Bst pol I (30). (A) The maximal displacements of the phosphous atoms of dT are indicated by a triangle when the dG bases are superimposed. This suggests possible displacements for the α-phosphorus atom in the dTTP/dG mispair. (B, C) Orthogonal views of (A). (D) Geometry of six possible configurations of dTTP/dG and dGTP/dT mispairs.

Because the dTTP/dG mispair can assume either wobble or inverted wobble geometry in the NBP of the mutants, there was no additive effect on the K_d,app for dTMP incorporation going from the single to the double or to the triple mutant where both L561 and Y567 are replaced by Ala. Of note, wobble pairing can result in six possible geometric conformations of the dTTP/dG mispair (Figure 8D). Each could have a distinct set of kinetic parameters for dTMP incorporation, which might be resolvable using single molecule procedures (42).

Structural Features of Pols That Are Relevant to Base Selectivity

Transition state stabilization of incorrect dNTPs would be expected to be greatly reduced with wt RB69 pol because the α-phosphorus atoms of mismatched dNTPs are misaligned with respect to the 3′-terminal OH of the priming nucleotide residue. The enlarged volume in the NBP mutants could allow realignment of mispaired dNTPs resulting in increased transition state stabilization and lower energy barriers for misincorporation compared to wt RB69 pol, assuming that the rate-limiting steps are the same for the triple mutant and wt. Evidence that the rate-limiting steps are indeed the same, for incorporation of correct dNMPs, was provided by the stopped-flow fluorescence results with the triple mutant, which showed that the fingers closing conformation step, before chemistry, was not rate-limiting (Figure 5). These findings were identical to those observed with wt (24). Preliminary structural work showed that the ternary complexes of both wt and triple mutant containing correct dNTPs were nearly identical, further indicating that the three substitutions introduced in the triple mutant did not alter the rate-determining step (M. Wang et al., unpublished data) (Figure 9). The details of the structural features of the triple mutant will be reported elsewhere.

Figure 9.

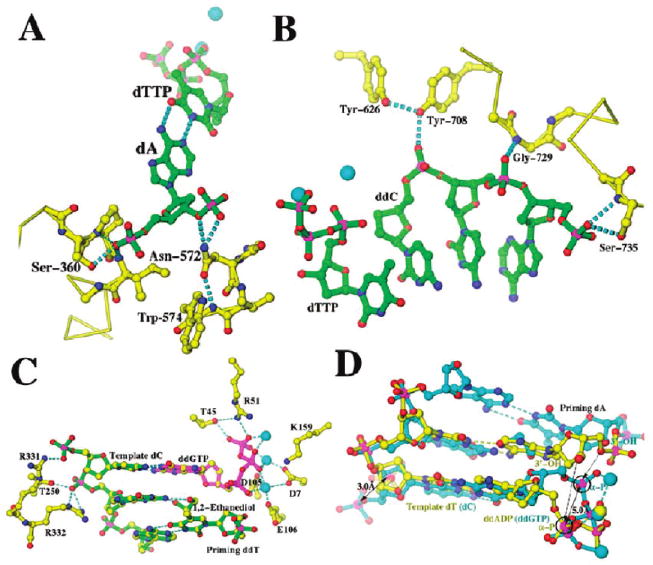
Structural features required for rigid binding of substrates in wt RB69 pol and the triple mutant (16) (M. Wang, personal communication) and nonrigid binding in Dpo4 (43). (A) Rigid interactions for the templating nucleotides in wt RB69 pol and in the triple mutant. (B) Rigid interactions for the primer strand in RB69 pol. (C) Nonrigid binding sites for the template and primer strands in Dpo4, namely, long side chains with positive charges R331, R332, R51, and K159. (D). Superimposition of normal (yellow) and slippage (cyan) replication complexes of Dpo4. The α-phosphorus atoms (Pα) are circled, and displacements in Pα and its distance to the 3′-OH of the primer terminal nucleotides are indicated.

In contrast to wt RB69 pol, translesion DNA pols, including those in the DinB superfamily such as Dpo4, have relatively spacious and flexible NBPs that effectively expose nascent base pairs to solvent (43). In crystal structures of Dpo4 ternary complexes, the DNA:Dpo4 contacts are not sufficient to prevent “slippage”, which lead to base deletions during replication, a common occurrence with this enzyme (43). The positively charged residues, R51, K159, R331, and R332 (among others), reorient the DNA backbone of the template strand and the triphosphate tail of the incoming dNTP by several angstroms prior to formation of a complex capable of skipping the templating base in favor of the neighboring 5′ base (Figure 9C, D). Thus the low-fidelity, low-efficiency Dpo4 not only has an enlarged NBP but also has flexible binding sites for key substrate components. These structural features suggest that Dpo4 likely provides less extensive stabilization of its substrates in the transition state than RB69 pol and may account for why Dpo4 has much lower k_pol values than RB69 pol (9, 10, 44).

Contribution of Hydrogen Bonding and Other Factors to Catalysis

The hydrophobic isosteres, F and Q, lack the ability to hydrogen bond, which was reported to be an important contributor to the low efficiency of dAMP incorporation opposite dF and dTMP incorporation opposite dQ with human mitochondrial DNA polymerase (pol γ), a family A DNA polymerase (32). Our results with incorporation of “correct” dNMPs opposite templating dF and dQ differ from those found with pol γ and with the Klenow fragment (KF), where only dTMP incorporation opposite dQ was inefficient (32, 45). There was a striking loss of efficiency (∼2000-fold) for dAMP insertion opposite dF with wt RB69 pol compared to the DNA pols mentioned above. Previous attempts to rationalize the rapid incorporation of dAMP opposite dF, but not dTMP opposite dQ, were based on the idea that Q is not a “perfect” isostere of A (32, 45). The bulk of a hydrogen atom within the hydrogen-bonding face (Q having a C–H instead of N at the purine N-1 position, Figure 7) makes Q slightly larger than A. The fact that F, a “perfect” shape mimic of T, is a poor template for insertion of dAMP by wt RB69 pol is not consistent with this explanation. We speculate that the difference in efficiencies may be due to the fact that RB69 pol, a member of the B family, has different NBP residues from family A pols. Future studies are needed to address this issue.

Solvation and stacking effects are also thought to be important factors that affect incorporation efficiencies of dNMPs (6, 29). The expulsion of water within the NBP, upon binding of a dNTP, has an energy cost that has a negative effect on dNMP incorporation efficiency, but this energy cost is offset by formation of hydrogen bonds between the bases of the nascent base pair, resulting in a positive entropic effect due to the release of bound water molecules, and stacking between the nascent base pair and the bases in the DNA duplex. In the case of the templating isosteres mentioned above, although some desolvation would occur during insertion of the incoming base, the benefit gained from stacking would apply to the isostere itself and would likely confer a relatively large energy gain because these isosteres are more hydrophobic than natural nucleobases. Overall, because of the complex combination of energy gains and losses, it is difficult to deconvolute the contribution of stacking and desolvation effects on the efficiency of base insertion. For the remainder of this discussion, we will focus only on how hydrogen bonds and the size and shape of the NBP affect dNMP incorporation efficiencies.

It can still be argued that dNMP insertion efficiency depends on geometry and “tightness of fit”, given that these isosteres pair with their natural canonical counterparts more efficiently than with mispairs (32). Insertion efficiencies of mispairs increased dramatically relative to wt upon expanding the NBP (i.e., the requirement for “ideal” base-pair geometry within the mutated NBP had been relaxed), consistent with the “tightness of fit” hypothesis. However, with the triple mutant, there was a dramatic increase in insertion efficiency of “correct” dNMPs opposite the two hydrophobic isosteres (Table 3). This is just the opposite of what would have expected from the “tightness of fit” hypothesis because the size and shape constraint is relaxed in the NBP of the triple mutant (Figure 1). A proposal consistent with our data posits geometry as a negative selector with regard to insertion efficiency of mispaired dNMPs. Our proposal has fundamental similarities with the recent concept advanced by Kuchta and colleagues (46–48). Using steady-state V_max and k_cat/K_M parameters, they suggested that human pol α (also a B family pol) discriminates against insertion of incorrect dNMPs by “recognizing” specific chemical features of incoming nucleobases and that geometry of the nascent base pair was “essentially irrelevant” with respect to insertion of correct dNMPs (46). The latter point is clearly illustrated by the fact that pol α achieves facile and rapid insertion (within an order of magnitude of correct dNMP insertion) of dNTPs containing unnaturally large, hydrophobic incoming nucleobases (e.g., 5,6-dinitrobenzimidazole) (47).

Our data support the conclusion that certain chemical features are critical for the fidelity mechanism (i.e., with wt, the lack of hydrogen bonding between the incoming dATP and templating dF virtually abolished chemistry (Table 3)). We would like to point out, however, that the geometry of the NBP plays an indirect role in preventing the insertion of incorrect dNMPs. Intuitively, it seems obvious that geometric constraints are needed to force opposing functional groups close together, e.g., the N-1 hydrogen of guanine and the N-3 hydrogen of thymine during mispair formation. These interactions (between the two bases and between the bases and the NBP) would create highly unstable conformations of the nascent base pair.

We would like to emphasize the difference between the two proposals regarding the influence of geometry on fidelity: one states that a tighter fit within the NBP leads to an increase in the insertion rate and the other, favored by us, states that the size and shape of the NBP are primarily responsible for preventing misinsertion. Both proposals have some overlapping features but are fundamentally distinct. Both predict that misinsertion rates would increase with an expanded NBP but differ in how they account for the rapid insertion rates of correct dNMPs.

We should point out that the L561A/Y567A double mutant studied here is only one of the three combinations of the single site substitutions in double mutants. We have to consider that one of the other possible double mutants, i.e., Y567A/S565G, might behave differently with respect to misincorporation efficiency. Another point to consider is that all of our kinetic data were obtained using the exonuclease-deficient form of RB69 pol so that any influence of these replacements on pol to exo switching would be masked. This issue will have to be considered when comparing these in vitro kinetic results with in vivo mutation frequencies exhibited by these NBP mutants.

In summary, we have determined the pre-steady-state kinetic parameters for incorporation of all correct and incorrect dNMPs catalyzed by wt RB69 pol and its NBP-expanded mutants. By comparing pre-steady-state kinetic parameters for incorporation of correctly paired and mispaired dNMPs, we have shown that the “tightness of fit” of the nascent base pair in the NBP of RB69 pol and its NBP mutants is not strictly coupled to the incorporation efficiency of correct or incorrect dNMPs. Our kinetic results, in combination with computer modeling, have prompted us to propose that the highly conserved L561, S565, and Y567 side chains of RB69 pol function not to optimize geometry for rapid insertion of correct dNMPs but rather to minimize insertion of incorrect dNMPs. This proposal does not concur with the notion of geometric selection as it pertains to the “tightness of fit” hypothesis (6, 7, 49), which posits that these three residues contribute to the spatial complementarity between the polymerase and the nascent base pair leading to incorporation of correct dNTPs with very high efficiency.