Efficient framework for automated classification of subcellular patterns in budding yeast

Abstract

Fluorescent-tagging and digital imaging are widely used to determine the subcellular location of proteins. An extensive publicly available collection of images for most proteins expressed in the yeast S. cerevisae has provided both an important source of information on protein location but also a testbed for methods designed to automate the assignment of locations to unknown proteins. The first system for automated classification of subcellular patterns in these yeast images utilized a computationally expensive method for segmentation of images into individual cells and achieved an overall accuracy of 81%. The goal of the present study was to improve on both the computational efficiency and accuracy of this task. Numerical features derived from applying Gabor filters to small image patches were implemented so that patterns could be classified without segmentation into single cells. When tested on 20 classes of images visually classified as showing a single subcellular pattern, an overall accuracy of 87.8% was achieved, with 2330 images out of 2655 images in the UCSF dataset being correctly classified. On the 4 largest classes of these images, 95.3% accuracy was achieved. The improvement over the previous approach is not only in classification accuracy but also in computational efficiency, with the new approach taking about 1 h on a desktop computer to complete all steps required to perform a 6-fold cross validation on all images.

INTRODUCTION

Green Fluorescent Protein (GFP) and its variants are widely used in biological imaging because they can be linked with virtually any protein to visualize location in vivo. GFP-tagging is used both to confirm conjectured localizations and to determine them for previously uncharacterized proteins (although the localization can potentially be altered by the tagging). Traditionally, the assignment of a location is done by visual inspection. However, it is often difficult to insulate against the influence of prior experience or hypotheses on those assignments in order to rely exclusively on the tagged protein images themselves. In addition, visual inspection is not well suited to efficiently handling proteome-scale tasks such as classifying thousands of different GFP-tagged protein images.

Automated classification of subcellular patterns in such images is a viable alternative, and a number of systems for this task have been described (1–3). These typically start by calculating numerical features from the microscope image that are designed to capture essential characteristics of the pattern without being sensitive to the position, orientation and brightness of individual cells. Machine learning algorithms are then trained to predict subcellular location labels from the numerical features. The classification problem generally consists of four steps: 1) image preprocessing, 2) feature extraction, 3) feature selection, and 4) classifier training and evaluation. Among these steps, the first two steps are commonly most important because the steps decide essential qualities of features that influence the entire process. In order to provide information on subcellular location for the many proteins about which little is known, efforts to create proteome-scale image collections have been described (4–7). The most comprehensive coverage to date has been of the yeast proteome, for which Huh et al. (4) collected images of over 4,000 GFP-tagged proteins encoded by cDNAs (a more recent collection for over 1,000 proteins was created by chromosomal tagging with GFP by Hayashi et al. (8)). The Human Protein Atlas (9) has collected images for over 6,000 proteins to date using mono-specific antisera.

The availability of such collections has permitted automated classification systems to be applied on a scale not previously possible. In the first such application, Chen et al. (10) developed an automated system capable of recognizing the patterns in the UCSF yeast image collection. The system used a graphical model method (11) to segment each image into single cell regions (using parallel images of differential image contrast images (DIC) and a DNA-binding probe). For each cell, a feature set containing Zernike moment features, morphological features, wavelet features, DNA overlap features, edge features, and Haralick texture features was calculated. The system showed 81% agreement with visual assignments for proteins having a single location. Results using this approach depend on the accuracy of cell segmentation, and additional methods for segmentation of yeast cells have since been presented (12,13). Systems for performing other kinds of analyses of yeast images have also been described, including systems for analyzing cell morphology (14), counting peroxisomes (15), quantifying protein and RNA expression (16), and carrying out image-based screens (17,18). Some approaches to classifying subcellular patterns do not require segmentation into single cell regions (3,19,20), but while these approaches offer reduced computation time they often sacrifice some accuracy of classification.

In this paper, we present a framework for subcellular pattern classification in yeast that shows both improved accuracy and computational efficiency compared to the previously reported results for this image collection. The approach does not require segmentation of images into single cell regions, eliminating the need for parallel DIC and DNA images. This makes it applicable to datasets for which images of only a single (protein) channel are available.

METHODS

UCSF yeast GFP fusion localization database

The UCSF yeast GFP fusion localization database contains 4156 sets of three 535×512 grayscale images (for DIC, DAPI, and GFP) where yeast cells in each set express different GFP-tagged proteins (4). The DAPI channel reflects the DNA distribution, and the DIC channel shows the boundaries of the cells. The original web site through which the images were made available, http://yeastgfp.ucsf.edu, is not currently online; therefore the images are currently being made available at http://murphylab.web.cmu.edu/data.

One or more labels have been assigned to each GFP image by visual examination (and in some cases using additional information) by two evaluators; a total of 22 labels were used (4). As in the previous work (10), we restricted our automated analysis to 2655 images by selecting images assigned to a single location but eliminating those labeled as “ambiguous” and “composite punctate” which do not correspond to any particular subcellular location. In the resulting set, each image belongs to one of 20 classes such as nucleus, cytoplasm and mitochondrion. The number of images in each class is uneven, ranging from 6 to 823. The names and sizes of the 20 classes are shown in Table 1.

Table 1.

Images with a unique subcellular location in the UCSF dataset

Class	Number of images	Class	Number of images
Cytoplasm	823	Endosome	34
Nucleus	496	Late_Golgi	33
Mitochondrion	485	Actin	27
ER	267	Peroxisome	21
Vacuole	121	Lipid_particle	19
Nucleolus	69	Golgi	15
Cell_periphery	57	Bud_neck	15
Vacuolar_membrane	54	Early_Golgi	11
Nuclear_periphery	53	Microtubule	10
Spindle_pole	39	ER_to_Golgi	6

Intensity adjustment

Due to the different levels of tagged protein expression and varying positions of cells relative to the focal plane, the intensities of yeast cells with the same class label can vary significantly. Thus, we applied intensity adjustment to reduce the intra-class variance. To do this, we first took the 0.05th percentile of intensity distribution as the lowest intensity and the 99.95th percentile as the highest intensity. Then, we linearly adjusted each intensity between 0.05th percentile and 99.95th percentile to the percentile of the entire intensity range. We also mapped every intensity lower than 0.05th percentile to the minimum value and every intensity higher than 99.95th percentile to the maximum value of the entire intensity range. The rationale for using the 0.05th percentile and 99.95th percentiles instead of maximum and minimum was to avoid outlier pixels (e.g., resulting from dust particles or fluorescent debris).

After intensity adjustment, we smoothed each image with a 3×3 rectangular average convolution filter (3×3 matrix with all elements 1/9) without zero padding. We then subtracted the most common pixel value as background and applied a global threshold for each image using the Ridler-Calvard method as described previously (1).

Rotation-invariant feature extraction

Yeast cells float freely and thus it is possible for them to rotate in the media. Different cells in a given field are therefore expected to show different orientations. Features to describe the patterns in such images should therefore be invariant to local rotation. A simple approach to doing this is to calculate texture features in different orientations and average them. This approach was used in the previous automated analysis of the yeast images. Several alternative methods to achieve rotation invariant features have been described.

For example, Varma and Zisserman (21) presented the maximum response (MR) filter sets. The main idea of this filtering method is to apply multiple orientation filters but use only the maximum filter response across all orientations. Though this method is computationally cheap and extracts a small number of features, it achieved high classification accuracy on the Columbia-Utrecht reflectance and texture database (21,22).

Another method to gain rotation-invariant features is to use rotationally invariant filters such as Gaussian filters or Laplacian of Gaussian filters (23). In recent work, Lazebnik et al. (24), also introduced rotationally invariant descriptors, i.e., SPIN and RIFT. Although these descriptors extract rotation-invariant features, they sacrifice the spatial information that may be important to distinguish different classes (25).

Lowe (26) suggested a method to find the dominant gradient orientation of each patch or region. SIFT descriptors with this method showed higher classification accuracies than rotation-invariant descriptors (25); however, the method to find the dominant gradient is computationally expensive (24).

In order to extract local patterns, we used Gabor filters that can catch local frequency and orientation information in the given image. We defined a non-background patch as a 7×7 pixel region that does not include any background pixels and applied Gabor filters with 20 scales and 16 orientations. We obtained rotation invariant features by applying the method discussed in detail in the next paragraph. Then, we calculated the mean and the variance of the energy distribution corresponding to each filter. These means and variances are used to construct 2×20×16=640 Gabor features for each image. The patch size, the number of scales and the number of orientations were determined empirically to obtain the highest cross-validation accuracy, and the other variables of the Gabor filter bank were set to reduce redundant information (27).

We added rotation invariance to the Gabor features as follows. First, we find the first major orientation and the second major orientation corresponding respectively to the maximum value and the second maximum value among all 20×16 filtered values from each patch. After finding these two major orientations, each patch is rotated to have its first major orientation align toward the same direction as all the other patches (Figure 2a). Then, each patch is flipped along the first major axis if needed, to align its second major orientation to form an acute angle on the counterclockwise side from its first major orientation (Figure 2b).

Fig. 2.

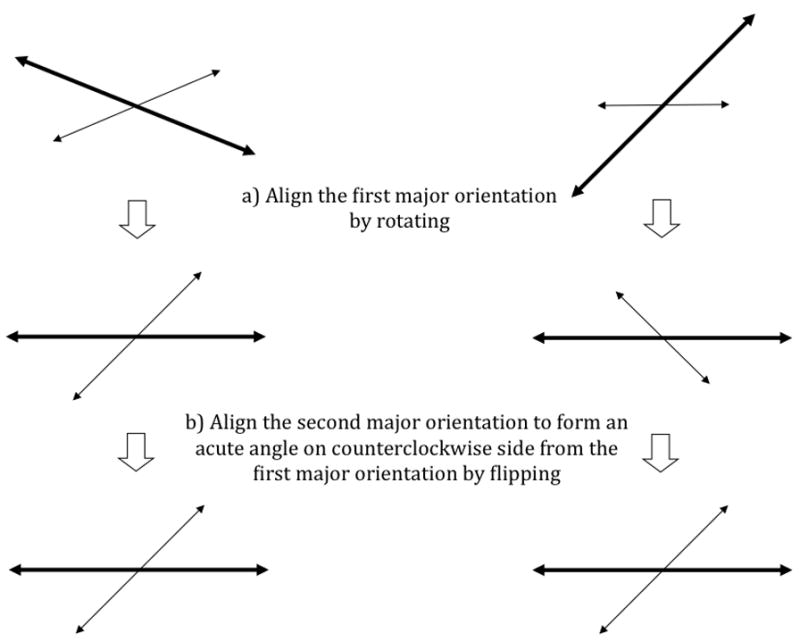
Illustration of the orientation adjustment scheme. The long thick arrows represent the major orientation and the short thin arrows represent the second major orientation.

Directly convolving all possible patches with Gabor filters is often wasteful when a significant number of pixels belong to background. Thus, we first partition the image into rectangular regions, and test whether each region contains any non-background patches. Only when at least one non-background patch is found, the rectangular region is convolved with Gabor filters. We reduce the computation time significantly by using 30×30 rectangular regions.

To evaluate the performance of our rotation invariance method, we implemented a maximum response method and a dominant gradient orientation method as well. The maximum response method adopts the main idea suggested by Varma and Zisserman (21). After convolving all 7×7 patches with 20×16 Gabor filters, we adopt only the maximum response for each scale; then calculate the mean and the variance of the energy distribution of the maximum response corresponding to each scale. As a result, we obtain 40 rotation invariant features for each image.

For the gradient orientation method, we apply the same 20×16 Gabor filters, extract Gabor features, and apply an adaptation of Lowe’s method used for SIFT features (26) to obtain the major orientations with which orientation adjustment is performed. We precompute the gradient magnitude m(x,y) and orientation θ(x,y) for each pixel as

$$\begin{array}{l}m(x,y)=\sqrt{{(I(x+1,y)-I(x-1,y))}^2+{(I(x,y+1)-I(x,y-1))}^2}\\ \theta (x,y)={tan}^{-1}((I(x,y+1)-I(x,y-1))/(I(x+1,y)-I(x-1,y)))\end{array}$$

where I(x,y) is the intensity of a pixel. Then for each patch, we form an orientation histogram that has 32 bins. Each sample added to the histogram is weighted by its gradient magnitude, and then a Gaussian circular weight is applied. We find the orientation whose bin has the maximum weight and the second maximum weight, and set them as the major orientation and the second major orientation. Then, these two orientations are applied to adjust the Gabor features’ orientation in the same manner outlined above to obtain rotation invariance.

Feature Selection

To create a compact set of features for use in classification, we used a state-of-the-art extension to Linear Discriminant Analysis, Spectral Regression Discriminant Analysis (SRDA) (28). SRDA is known to save both time and memory compared with other Linear Discriminant Analysis extensions. We used the SRDA source code provided by Cai et al. (28) with regularization and with the default value for the regularization parameter (0.1).

When the number of classes is small compared to the number of images, SRDA tends to overreduce features so that classification does not work well. Thus, when considering only 4 classes, we did not apply feature selection.

Support vector machine classification

We used the LIBSVM implementation of a support vector machine (SVM) classifier (http://www.csie.ntu.edu.tw/~cjlin/libsvm) with a radial basis function (RBF) kernel. Since SVMs are binary classifiers, we adopted the one-against-one approach (29) so that the most frequently predicted class from all possible one-versus-one classifiers is selected to be the predicted class of each image. We evenly split the data into six folds (since the smallest class contains only six samples). Using each fold in turn as a test set, we used four of the remaining folds for training and the last fold as an internal test set for choosing optimal SVM parameters (the slack penalty and the RBF kernel parameter) for the training folds by a grid search. The test accuracy was calculated by aggregating the predictions on all six test sets using the independently chosen parameters.

We measure the confidence of each prediction by calculating the sum of decision values of the prediction. For each prediction, LIBSVM can generate a decision value that is proportional to the distance from decision boundary, and each prediction gets n−1 decision values in an n-class classification. For each image, the n−1 decision values are summed up, representing how confident the prediction is. Varying values of a threshold on this confidence were used to determine the dependence of classification accuracy (precision) on confidence.

Implementation and Availability

All components of our approach were implemented in Matlab except the LIBSVM package which was invoked through a Matlab interface. The source code and data used in this study will be made available upon publication at http://murphylab.web.cmu.edu/software.

RESULTS AND DISCUSSION

Classification Performance

As described in the Methods, our approach consists of image preprocessing (intensity adjustment, background correction), rotation-invariant feature extraction, feature selection, and classification using a support vector machine with a radial basis function kernel. We applied our approach to the 2655 images from the UCSF collection that show proteins assigned to a single location by visual examination. Our system classified 2330 images correctly, an overall accuracy of 87.8%. This is a 6.8% improvement from our previous work that achieved 81.0% accuracy (10). The confusion matrix obtained from 6-fold cross validation is shown in Table 2. Table 3 shows the comparison of the accuracies for each class with the previous work. Significant improvement is observed for some of the classes that were poorly recognized previously, and endosome, late Golgi and actin are now recognized with greater than 50% accuracy. As a result of improvements in the lower frequency classes, the accuracy when weighting by class (rather than by image) is significantly higher than it was previously.

Table 2.

The confusion matrix for the full system described in the text. The order of classes is from the largest to the smallest.

	Cytoplasm	Nucleus	Mitochondirion	ER	Vacuole	Nucleolus	Cell periphery	Vacuolar membrane	Nuclear periphery	Spindle pole	Endosome	Late Golgi	Actin	Peroxisome	Lipid particle	Golgi	Bud neck	Early Golgi	Microtubule	ER to Golgi
Cytoplasm	97.0	0.0	0.9	1.1	0.2	0.4	0.5	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Nucleus	0.4	93.5	1.6	0.0	1.8	1.6	0.0	0.0	0.4	0.0	0.2	0.0	0.2	0.0	0.0	0.0	0.2	0.0	0.0	0.0
Mitochondrion	1.6	0.8	94.2	1.0	0.0	0.4	0.0	0.0	0.0	0.4	0.6	0.4	0.0	0.0	0.2	0.0	0.2	0.0	0.0	0.0
ER	8.2	0.0	0.4	87.3	1.1	0.0	1.5	0.0	1.1	0.0	0.0	0.0	0.0	0.0	0.0	0.4	0.0	0.0	0.0	0.0
Vacuole	8.3	4.1	0.8	5.0	75.2	0.0	1.7	5.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Nucleolus	0.0	13.0	1.4	0.0	1.4	82.6	0.0	0.0	0.0	0.0	1.4	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Cell periphery	1.8	0.0	3.5	10.5	0.0	3.5	80.7	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Vacuolar membrane	0.0	0.0	5.6	3.7	11.1	0.0	0.0	66.7	7.4	1.9	3.7	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Nuclear periphery	1.9	0.0	0.0	3.8	3.8	1.9	0.0	3.8	81.1	0.0	3.8	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Spindle pole	0.0	0.0	7.7	0.0	0.0	12.8	0.0	0.0	0.0	64.1	12.8	0.0	0.0	2.6	0.0	0.0	0.0	0.0	0.0	0.0
Endosome	0.0	2.9	11.8	5.9	0.0	0.0	0.0	0.0	0.0	8.8	61.8	2.9	0.0	2.9	0.0	2.9	0.0	0.0	0.0	0.0
Late Golgi	3.0	3.0	15.2	3.0	0.0	0.0	0.0	0.0	0.0	0.0	9.1	57.6	0.0	0.0	3.0	3.0	0.0	3.0	0.0	0.0
Actin	0.0	0.0	7.4	22.2	0.0	0.0	0.0	0.0	0.0	0.0	0.0	3.7	55.6	7.4	0.0	0.0	0.0	0.0	0.0	3.7
Peroxisome	0.0	0.0	19.0	4.8	0.0	0.0	0.0	0.0	0.0	9.5	14.3	0.0	4.8	33.3	14.3	0.0	0.0	0.0	0.0	0.0
Lipid particle	0.0	0.0	21.1	10.5	0.0	0.0	0.0	0.0	0.0	0.0	10.5	15.8	5.3	5.3	31.6	0.0	0.0	0.0	0.0	0.0
Golgi	0.0	0.0	0.0	13.3	0.0	0.0	0.0	0.0	0.0	0.0	6.7	20.0	0.0	0.0	13.3	26.7	0.0	20.0	0.0	0.0
Bud neck	6.7	0.0	33.3	13.3	0.0	6.7	0.0	0.0	0.0	0.0	6.7	0.0	0.0	0.0	0.0	0.0	33.3	0.0	0.0	0.0
Early Golgi	0.0	0.0	9.1	18.2	0.0	0.0	0.0	9.1	0.0	0.0	0.0	27.3	0.0	0.0	0.0	36.4	0.0	0.0	0.0	0.0
Microtubule	0.0	20.0	60.0	0.0	0.0	20.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
ER to Golgi	0.0	0.0	0.0	50.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	50.0

Table 3.

Comparison of accuracy with previous results.

	Accuracy Chen et al. 2007 (%)	Accuracy this work (%)
Cytoplasm	94.4	97
Nucleus	88.6	93.5
Mitochondrion	90.9	94.2
ER	70.2	87.3
Vacuole	73.6	75.2
Nucleolus	73.5	82.6
Cell periphery	75.4	80.7
Vacuolar membrane	51.9	66.7
Nuclear periphery	77.4	81.1
Spindle pole	64.1	64.1
Endosome	47.1	61.8
Late Golgi	12.1	57.6
Actin	22.2	55.6
Peroxisome	14.3	33.3
Lipid particle	0	31.6
Golgi	6.7	26.7
Bud neck	0	33.3
Early Golgi	0	0
Microtubule	0	0
ER to Golgi	0	50
Average by class for 20 classes	43.1	58.6
Average by image for 20 classes	81.0	87.8
Average by image for 4 major classes	92.7	95.3

We also report the accuracies of classifying just the four major classes in Table 3. For the four-major-class task, both our approach and the previous approach were configured slightly differently compared with the 20-class task. In our approach, we did not use SRDA because it induces over-reduction for such a small number of classes. Our approach achieves a higher accuracy, approximately halving the error rate.

Given that our approach does not involve segmentation, it was of interest to determine whether classification accuracy showed dependence on cell density. The number of cells per image (as determined using the graphical model segmentation approach used previously) was as high as 51, with a mean of 18.7 and a standard deviation of 7.8. Images of all densities were correctly classified, and the few incorrectly classified images showed a similar distribution of cell density as the whole collection.

Computational Efficiency

Table 4 reports the running time of each component on a computer with a 2.66 GHz Intel CPU and 2 GB of RAM. As can be seen in the table, our approach takes about one hour to perform the entire process. This is a great improvement over the previous system, which takes several days. The improved speed is achieved primarily because segmentation of each image to find cell boundaries is avoided and feature calculation is more rapid. In addition, SRDA significantly reduces classification time through finding only 19 combinations of features among 640 features in the 20-class task. For example, after SRDA feature selection, SVM classification time was reducesd to approximately 1/25 of the time required for all features. This computational efficiency allows investing more effort to find proper parameters in the SVM classification so that the classification accuracy can be improved.

Table 4.

Running time of each component.

Component	Running time
Image preprocessing	646 sec
Rotation-invariant feature extraction	49 min
Feature selection using SRDA	15 sec
Classification using an SVM with the RBF kernel	230 sec

Contributions of System Components to Overall Accuracy

Table 5 shows the performance drops in terms of overall accuracy in our method when each of three processes that characterize our approach is disabled. Note that in this analysis only one process is disabled, leaving the other two functional. When the intensity adjustment process is disabled, the overall accuracy drops from 87.8% to 80.1%, showing a performance drop of 7.7%. In the cases that disable orientation adjustment and linear discriminant analysis, 5.3% and 2.8% performance drops are observed respectively.

Table 5.

Contributions of system components to accuracy. Performance drop is calculated as the difference between the original accuracy (87.8%) and the accuracy when each part of the approach is not applied.

Process disabled	Overall accuracy (%)	Performance drop (% points)
Intensity adjustment	80.1	7.7
Orientation adjustment	82.5	5.3
Linear discriminant analysis	85.0	2.8

Rotation Invariance Comparison

The comparison of three different methods to achieve rotation-invariance is show in Table 6. As can be seen, our method shows the best performance in terms of overall accuracy. The maximum response method may negatively impact the performance because important spatial information is lost in the process of achieving rotation invariance. In addition, the number of features may be too small to distinguish different classes effectively. The reason that the dominant gradient orientation method performs poorly may be due to the incompatibility of this method with Gabor features. The dominant gradient orientation method is originally devised for the SIFT descriptor which produces the gradient orientation histogram. The resulting major orientations from the histogram are not likely to correlate perfectly with the major orientations from the Gabor filter responses. Also, using the gradient orientation histogram to determine the major orientations does not reflect relative spatial information found among the patches from the same yeast cell. Therefore, rotations based on the dominant gradient orientation method may jumble up the Gabor features patch by patch.

Table 6.

Comparison of rotation invariance methods

Rotation invariance method	Accuracy (%)
Local orientation	87.8
Maximum response	82.1
Dominant gradient orientation	82.4
No orientation adjustment	82.5

Analysis of Prediction Confidence

It is possible to return the predictions sorted in terms of confidence. Figure 3 shows the behavior of prediction accuracy as predictions are made with varying threshold on that confidence. Note that an accuracy of approximately 92% can be achieved when only the most confident 50% of predictions are considered.

Fig. 3.

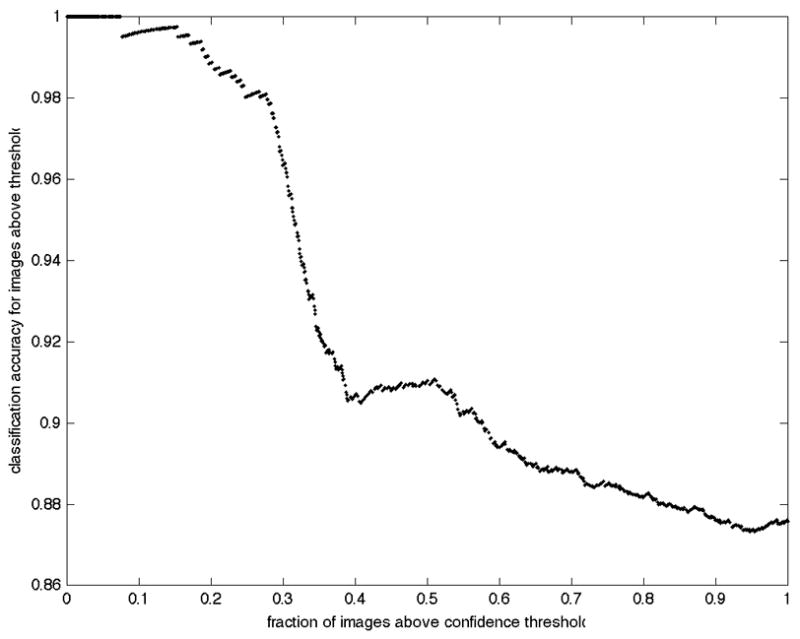
Improved accuracy for high confidence predictions. The overall accuracy of only those predictions with confidence above a given threshold is displayed as a function of the fraction of images whose confidence was greater than that threshold.

Conclusion

In this paper, we have introduced a framework for yeast image classification that outperforms previously reported results. We anticipate that this framework can also be successfully applied to other fluorescence microscope images depicting subcellular patterns. In addition, utilizing more recent and efficient descriptors such as SIFT might be expected to improve classification accuracy. Future work will be required to test these expectations.

The automated classification framework described here is computationally efficient and reduces potential human biases in making assignments. Therefore, we anticipate that its natural applications include proteome-scale high-throughput analysis of subcellular location in which computational efficiency may be an important consideration.

Fig. 1.

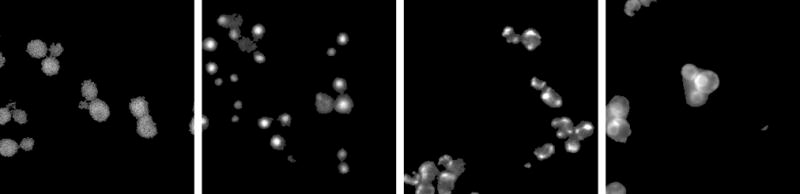
Example GFP images from the four major classes in the UCSF yeast GFP fusion database. Each panel shows a 256 × 256 pixel region in the center of the original image for a randomly chosen protein from a given class. From left to right, the proteins shown (and their subcellular locations) are YNL267W (Cytoplasm), YPL011C (Nucleus), YDL120W (Mitochondrion), and YOR254C (Endoplasmic Reticulum). The images were scaled and background-corrected as described in the methods.