Skip to main content
NCBI home page
Genome Research logoLink to Genome Research
. 2010 Apr;20(4):496–502. doi: 10.1101/gr.102095.109

Pronounced inter- and intrachromosomal variation in linkage disequilibrium across the zebra finch genome

Jessica Stapley 1,1, Tim R Birkhead 1, Terry Burke 1, Jon Slate 1
PMCID: PMC2847752  PMID: 20357051

Abstract

The extent of nonrandom association of alleles at two or more loci, termed linkage disequilibrium (LD), can reveal much about population demography, selection, and recombination rate, and is a key consideration when designing association mapping studies. Here, we describe a genome-wide analysis of LD in the zebra finch (Taeniopygia guttata) using 838 single nucleotide polymorphisms and present LD maps for all assembled chromosomes. We found that LD declined with physical distance approximately five times faster on the microchromosomes compared to macrochromosomes. The distribution of LD across individual macrochromosomes also varied in a distinct pattern. In the center of the macrochromosomes there were large blocks of markers, sometimes spanning tens of mega bases, in strong LD whereas on the ends of macrochromosomes LD declined more rapidly. Regions of high LD were not simply the result of suppressed recombination around the centromere and this pattern has not been observed previously in other taxa. We also found evidence that this pattern of LD has remained stable across many generations. The variability in LD between and within chromosomes has important implications for genome wide association studies in birds and for our understanding of the distribution of recombination events and the processes that govern them.

Linkage disequilibrium (LD), which refers to the nonrandom association of alleles at two or more loci, plays an important role in evolutionary biology and gene mapping (Coop et al. 2008; Slatkin 2008). LD can reveal much about population demography and, because the extent of LD is approximately inversely proportional to the recombination rate, LD can also uncover variability in recombination rates across genomes and chromosomes (Hedrick 1988; Miyashita and Langley 1988; Daly et al. 2001; Jeffreys et al. 2001; Gabriel et al. 2002; Arnheim et al. 2007). Importantly, LD determines the power and precision of association mapping studies, directly influencing our ability to localize genes and/or loci responsible for traits and diseases (Kruglyak 1999; Weiss and Clark 2002).

Studies of LD are dependent on the availability of genomic resources, and across vertebrates comprehensive genome-wide studies have been restricted to model species, in particular mammals. Studies in other organisms, however, are likely to reveal extensive variation in patterns of LD not seen in humans (Slatkin 2008), and organisms with different genomic architecture to mammals may provide novel insight into patterns of LD and genome evolution. Birds are interesting in this respect as most bird genomes are composed of many small (micro) chromosomes and relatively few large (macro) chromosomes. Linkage mapping studies have shown that microchromosomes have a higher recombination rate than their larger counterparts (International Chicken Genome Sequencing Consortium 2004; Stapley et al. 2008). Increased recombination rate is expected to reduce the amount of background LD; however, to date there has been no comprehensive analysis of how LD varies with chromosome length and across macrochromosomes and microchromosomes. With respect to LD in birds, the chicken Gallus gallus has received the most attention; studies have quantified LD in several breeds of domestic chicken but have only focused on relatively few chromosomes (Heifetz et al. 2005; Aerts et al. 2007; Andreescu et al. 2007; Wahlberg et al. 2007; Rao et al. 2008; Abasht et al. 2009). In chickens, LD extends very short distances, which reflects the high recombination rate and relatively large effective population size of domestic fowl relative to other livestock species. Passerines, which make up around half of all birds species, and diverged from chickens at least 80 million yr ago, are beginning to receive attention; however, all studies to date have either investigated single chromosomes (Backström et al. 2006), a few genomic regions (Balakrishnan and Edwards 2008), or have low marker coverage (Li and Merilä 2009).

The zebra finch, the second bird to have its genome sequenced, can provide a useful target for a comprehensive LD study. In addition to having the two types of chromosomes (macro- and microchromosomes) characteristic of most birds, the zebra finch genome exhibits an unusual pattern of crossing over. Cytogenetic studies have revealed that the location of meiotic crossover events on the macrochromosomes is highly nonrandom, mostly occurring at the ends of the macrochromosomes (Pigozzi and Solari 2005; Calderón and Pigozzi 2006). This suggests there is a large recombination desert on all macrochromosomes, corresponding with the center of the metacentric chromosomes and the center of the long arm of the acrocentric chromosomes (Calderón and Pigozzi 2006). The suppressed recombination in the middle of the chromosomes is not necessarily related to the position of the centromere, nor to the presence of heterochromatin (Calderón and Pigozzi 2006), which is thought to suppress recombination. It is unknown how stable this pattern of recombination is or if this is characteristic of other zebra finch populations. If it is a persistent phenomenon of zebra finch chromosomes, it is likely to affect the extent of LD across macrochromosomes and generate extensive heterogeneity across and between chromosomes. Interestingly, this pattern has not been reported in chickens (Calderón and Pigozzi 2006; Groenen et al. 2009).

Patterns of LD may also co-vary with other sequence features that are correlated with recombination rate, such as heterozygosity, GC content, and the number of genes. Recombination rate is expected to increase heterozygosity (Begun and Aquadro 1992; Nachman 2001), although this pattern may be obscured by the action of other forces such as selection and biased gene conversion (Maynard Smith and Haigh 1974; Ohta 1999). Recombination rate is also positively related to GC content and other sequence features known to co-vary with GC content, e.g., gene density, intron length, CpG motifs (Kong et al. 2002; Meunier and Duret 2004; Groenen et al. 2009). It is unknown how LD and these sequence features will co-vary in the presence of highly nonrandom recombination.

The aim of this study was to construct genome-wide LD maps of the zebra finch in order to examine (1) whether LD extended further on macro- than microchromosomes, as predicted by previously described differences in recombination rate; (2) whether LD varied across macrochromosomes, corresponding to the biased location of crossing-over events on chromosome spreads; and (3) whether patterns of LD co-vary with heterozygosity, GC content, and the number of genes; and (4) to assess the stability of patterns in LD, by examining whether contemporary genome-wide variation in recombination rates, as detected by linkage mapping, is consistent with historical recombination rate variation, as inferred from LD maps.

Results

Across all chromosomes pairwise LD (r2) declined as a function of distance between markers (Supplemental Fig. S4). There was less variation in r2 when plotted against genetic distance (cM) than when it was plotted against physical distance (Supplemental Fig. S4). This reflects the fact that, although LD declines with recombination distance (genetic distance cM), recombination distance is not necessarily equivalent to physical distance.

Interchromosomal variation in LD

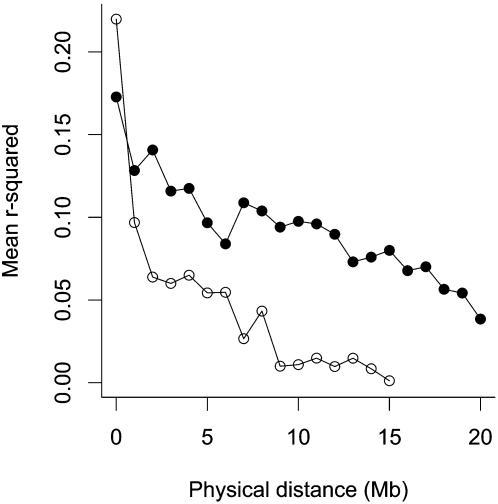
Comparisons of macro- and microchromosomes indicate that r2 extends further on the macrochromosomes (Supplemental Fig. S4). The longer-range LD on the macrochromosomes is clearly visible when the mean r2 for 1-megabase (Mb) bins is plotted (Fig. 1). The extent of useful LD (defined as r2 > 0.3) ± standard error for the whole genome was 0.43 ± 0.13 Mb (0.40 ± 0.04 cM); for the microchromosomes useful LD extended 0.09 ± 0.07 Mb (0.03 ± 0.04 cM), and for the macrochromosomes it extended 0.46 ± 0.11 Mb (0.37 ± 0.04 cM).

Figure 1.

Figure 1.

Open in a new tab

Mean r2 for distance bins of 1 Mb for macrochromosomes and microchromosomes plotted against physical distance (Mb).

Fitting Malêcot's equation to each individual chromosome reveals considerable variation in parameter estimates between chromosomes (Table 1), suggesting that the relationship between LD and physical distance varies between chromosomes. The mean length of 1 LD unit (LDU) (swept radius) across all chromosomes was 15.10 Mb (median = 4.16 Mb; range, 0.163–108.37 Mb). The total length of the LD map was 150.69 LDU. There was a positive relationship between the length of 1 LDU and chromosome length (F(1,25) = 77.96, P < 0.001; Fig. 2), demonstrating that LD declines faster on the microchromosomes than on the macrochromosomes. Concurrently, there was a negative relationship between 1 LDU and recombination rate (cM/Mb) (F(1,25) = 46.72, P < 0.001; Fig. 2).

Table 1.

Summary table of results for each chromosome

graphic file with name 496tbl1.jpg

Open in a new tab

The length of the chromosome, the number of markers, the recombination rate (cM/Mb), the length of 1 LDU, the Malécot model parameter estimates (L, M), and the slope estimate and significance of the relationship between LDU and cM position (see text for details). NA, Not available.

aBackground LD.

bProportion monophyletic.

cSlope of relationship between LDU and genetic distance (linear model LDU ∼ physical distance (kb) + genetic distance [cM]) . **P-value < 0.001; *P-value < 0.05.

Figure 2.

Figure 2.

Open in a new tab

The extent of useful LD was negatively related to chromosome length and positively related to recombination rate. Observed and fitted relationship between the swept radius and recombination rate (left) and chromosome length (right).

Intrachromosomal variation in LD

On macrochromosomes, 1 LDU covers a physically shorter region at the chromosome ends than in central regions (Fig. 3; Supplemental Figs. S5.1–S5.4), indicative of higher recombination rates at the ends and deserts of low recombination in the middle of the macrochromosomes (regardless of whether they are metacentric or acrocentric). Therefore, there are many markers in the center of the macrochromosome that are separated by large physical distances (1–10 Mb) but are in strong LD (Fig. 3; Supplemental Figs. S5.1–S5.4). This pattern was much weaker for microchromosomes, where recombination events appear to be more evenly distributed. As a result there was a positive relationship between LDU distance and standardized distance from the center of the macrochromosomes, but no such relationship on microchromosomes (macro: χ21 = 39.18, P < 0.001; micro: χ21 = 0.46, P = 0.49; Fig. 4).

Figure 3.

Figure 3.

Open in a new tab

LD maps (LDU) and genetic maps (cM) plotted against physical distance along four macrochromosomes (Tgu1, Tgu2, Tgu4, and Tgu5) and four microchromosomes (Tgu15, Tgu17, Tgu19, and Tgu20). (Solid circles and black lines) LD map; (open gray squares and gray lines) genetic map. This figure demonstrates large regions of extended LD on the macrochromosomes, corresponding to low recombination in the center and high recombination at the ends. In contrast, this pattern is not consistently evident on the microchromosomes, where the relationship between LD and physical distance is mostly linear. See Supplemental Figs. S5.1–S5.4 for all chromosomes.

Figure 4.

Figure 4.

Open in a new tab

Observed (filled circles) and fitted (lines) relationship of LD distance between adjacent markers and standardized distance from the center of the chromosome (Mb). Recombination is localized on the ends of the macrochromosomes, whereas it is more uniformly distributed on the microchromosomes.

Plots of LD map distances and linkage map distances as a function of physical map also show that regions with historically high recombination rates also have high contemporary recombination rates (Fig. 3; Supplemental Figs. S5.1–S5.4). On all macrochromosomes positive relationships were found between LDU and cM positions, even after accounting for physical map position (Table 1).

Covariance between LD and sequence features

On macro- and microchromosomes the LDU per Mb was positively correlated with the number of genes and GC content, but not mean heterozygosity per Mb (genes: Kendall's tau = 0.21, P < 0.001; GC content: tau = 0.32, P < 0.001; heterozygosity: tau = −0.04, P = 0.06; Supplemental Fig. S6). This covariation along the chromosome is evident in plots of LDU, heterozygosity, GC content, and number of genes (per Mb) along the chromosomes (Fig. 5; all chromosomes, Supplemental Figs. S7.1–S7.2). Sequence features varied between macro- and microchromosomes; on microchromosomes the GC content and the number of genes per Mb was higher (mean [±SE] GC content: macro = 41.74 (±0.14), micro = 47.84 (±0.36), F(1,391) = 315.84, P ≤ 0.001; number of genes: macro = 11.25 (±0.53), micro = 22.67 (±0.99), F(1,391) = 226.99, P < 0.001), but mean heterozygosity per Mb was slightly lower (macro = 0.36 (±0.01), micro = 0.32 (±0.32), F(1,391) = 8.21, P = 0.004).

Figure 5.

Figure 5.

Open in a new tab

The total number of linkage disequilibrium units (LDU), GC content, number of genes, and heterozygosity per megabase (Mb) for two macrochromosomes (Tgu2, Tgu3) and two microchromosomes (Tgu12, Tgu13). See Supplemental Figs. S7.1–S7.3 for all chromosomes.

Discussion

Here, we presented the most comprehensive genome-wide analysis of linkage disequilibrium and LD maps for a bird. LD between markers decays with distance, and our estimates of the extent of LD based on r2 = 0.3 were comparable to estimates in chickens (0.01–0.82 Mb, Aerts et al. 2007) and greater than those obtained for humans (0.01 Mb, Khatkar et al. 2008). We found that LD declined much faster with physical distance on microchromosomes than macrochromosomes (Fig. 1), which reflects the greater recombination rate of these chromosomes. The most striking finding of this study was the unusual pattern of LD on the macrochromosomes, with LD extending much further at the center of the macrochromosomes compared to the ends (Fig. 3; Supplemental Figs. S5.1–S5.4). The pattern of LD is relatively stable, as it was evident on both the LD maps constructed using information about historical recombination events and the linkage maps, which were constructed from present day recombination.

This notable intrachromosomal variation in LD was not evident on the microchromosomes and differs dramatically from patterns in other species. In other taxa, where comparable data are available (De La Vega et al. 2005) the relationship between physical distance and LDU is more linear. In contrast, in the zebra finch the relationship is more akin to a Logit relationship (Fig. 3; Supplemental Figs. S5.1–S5.4). Suppression of recombination immediately around the centromere and the telomeres is common in many organisms; however, suppression is usually localized to a very small region of the chromosome (e.g., Sherman and Stack 1995; de Massy 2003; Groenen et al. 2009). We observed suppression of recombination extending tens of megabases, and this is not simply an extended suppression of recombination around the centromere, because in some cases (i.e., acrocentric chromosomes Tgu4, and Tgu5) the area of extended LD does not involve the centromere.

We also found that LD covaries with GC content and number of genes per Mb, but not heterozygosity (Fig. 5; Supplemental Figs. S6, S7.1–S7.2). These results are consistent with the results of previous studies that have found a positive relationship between GC content and recombination (Myers et al. 2005; Groenen et al. 2009) and, because GC content is also positively correlated with gene density (e.g., Kong et al. 2002), it is not surprising to see a positive relationship between gene density and LDU. With respect to differences between micro- and macrochromosomes, our results demonstrate higher GC content and higher gene density on the microchromosomes, which is consistent with results from chicken (International Chicken Genome Sequencing Consortium 2004). We detected slightly lower heterozygosity on the microchromosomes, which is somewhat unexpected because they had a higher recombination rate, and previous studies have found positive correlations between the number of polymorphisms and recombination rate (Begun and Aquadro 1992; Nachman 2001). In chicken no relationship between chromosome size and single nucleotide polymorphism (SNP)/indel rates was found (Wong et al. 2004). It is likely that many other factors, such as selection, demographic history, mutation, and hitchhiking, may be acting to affect levels of heterozygosity.

The localization of recombination observed on zebra finch macrochromosomes has not been observed in chromosomal spreads of chicken and quail (Galliformes) or pigeons (Columbiformes) (Calderón and Pigozzi 2006). Whether this pattern will be found in other Passerines (which represent around half of all bird species) is unknown. There was no evidence of greater recombination rate at the ends of the macrochromosomes in linkage maps of either the Blue tit (Cyanistes caeruleus) or the Siberian Jay (Perisoreus infaustus), which we visualized by plotting the genetic distance (cM) against predicted physical positions (bp) (in zebra finch or chicken; Hansson et al. 2009; Jaari et al. 2009). However, this pattern may be obscured because in the absence of whole-genome sequences the true physical positions of the markers are unknown. There was some evidence of a greater number of SNPs at the ends, compared to the center of the macrochromosomes in the great tit (Parus major) (van Bers et al. 2010), consistent with the pattern of greater recombination rate at the ends of the macrochromosomes observed here. Variability in the distribution of recombination events across a chromosome, within a genome (between macro and micros) and between different bird species, will have important implications for our understanding of processes governing recombination events, as well as practical consequences for genetic mapping. What maintains this distribution of recombination and how it influences our understanding of various genetic processes such as hitchhiking, co-adapted gene complexes, and genetic correlations warrants further study.

Accuracy of LD estimates and implications for genetic mapping

The amount of LD that is useful for mapping studies is often referred to as the amount of “useful LD” in a region or across the genome (Kruglyak 1999; Pritchard and Przeworski 2001). The estimate of useful LD obtained from this study was 0.4 Mb (microchromosomes: 0.1 Mb; macrochromosomes: 0.4 Mb). Estimates of useful LD based on r2 can be sensitive to marker density. The slope of the relationship between LD and distance gets shallower with increasing distance, but if there are few pairs of markers close together on the steepest part of the slope, the rate at which LD declines may be underestimated. Therefore, we do not attempt to extrapolate and estimate exactly how many SNPs will be required for future genome-wide association scans (GWAS) because estimates based on greater than 900 SNPs may not be robust. However, it is clear that higher marker densities will be required on microchromosomes and it is possible that a SNP chip with a few thousand markers will be informative for most GWAS, especially for QTL located at the center of macrochromosomes. Despite any possible inaccuracies in estimates of useful LD based on r2 caused by a modest marker density, the broad patterns reported here (intra- and interchromosomal variation in LD) are likely to be robust. This is because broad patterns of low and high LD can be distinguished at coarse marker densities and because these patterns are consistent with the distribution of recombination events observed in cytogenetic studies (Pigozzi and Solari 2005; Calderón and Pigozzi 2006). Furthermore, the analysis is based on parameters from the Malécot's equation and LD maps, which are less sensitive to marker density (Ke et al. 2004) than pairwise LD measures.

In summary, a genome-wide analysis of LD revealed close agreement between contemporary and historical patterns of recombination rate across the genome. However, the most striking feature of this analysis is how the relationship between LD and physical distance differs, both between the macro- and microchromosomes, and within individual macrochromosomes. The localized pattern of recombination rate along the macrochromosomes creates large blocks of markers in very close LD, a pattern absent from the microchromosomes. The distribution of LD has important implications for future GWAS mapping studies, and also for our understanding of the mechanisms governing recombination.

Methods

The individuals used in this study are a subpopulation of a larger captive population maintained at the University of Sheffield since 1985 (by TRB) and have been described elsewhere (Stapley et al. 2008). The pedigree contains 60 grandparents, 43 parents, and 251 offspring.

SNPs and genotyping

A detailed description of SNP discovery and genotyping is provided elsewhere (Stapley et al. 2008) and briefly described in the Supplemental material. Analysis was restricted to markers with minor allele frequencies (MAF) of >0.05 (838 markers) and individuals that were genotyped at ≥75% of loci (all 354 individuals).

Calculation of linkage disequilibrium

Estimating linkage disequilibrium metrics is easiest and most accurate when haplotype phase is inferred using statistical procedures (Weir 1979; Stephens et al. 2001; Slatkin 2008). Pedigree-based phasing is usually more accurate than approaches based on population data (Bonizzoni et al. 2003; Li and Jiang 2005) and we employed Markov chain Monte Carlo and associated algorithms implemented in SimWalk v2.91 (Sobel and Lange 1996) to infer haplotype phase for the autosomes. SimWalk for biallelic markers (simwalk2snp) was run once for each chromosome. Prior to running SimWalk the pedigree was split into 14 subfamilies using the command CRIGEN, which is implemented in a version of CriMap (Green et al. 1990) modified by Xueu Liu (Monsanto). Splitting the pedigree in this way was necessary for SimWalk to efficiently infer haplotypes from our relatively complex pedigree.

The phased haplotypes of founders only were then imported into GOLD (Abecasis and Cookson 2000) and LD statistics were calculated. Haplotype phase on the Z chromosome was known for all females (heterogametic sex), so LD statistics for the Z chromosome were calculated directly for founder females using GOLD. A discussion of the methodology and a comparison of LD statistics and LD maps for phased and unphased haplotypes are provided in the Supplemental material.

Modeling linkage disequilibrium

To model the decline in LD, we used the pairwise estimate r2 (Pritchard and Przeworski 2001; Ardlie et al. 2002; Weiss and Clark 2002). The decline of LD was modeled using Sved's equation,

graphic file with name 496equ1.jpg

where β is the decline in LD with distance d (Sved 1971) and 1/n accounts for small sample sizes (Hill 1981). The extent of useful LD for mapping can be defined as r2 = 0.3 (Ardlie et al. 2002). In this study we use mean r2 for nonoverlapping 1-Mb bins to fit Sved's equation. In addition LD was modeled using the Malécot's equation (Malécot 1948),

graphic file with name 496equ2.jpg

where ɛ is the rate of exponential decline in allelic association (ρ) with distance d (kb), the asymptote L is the background level of association between unlinked loci, and M is the proportion of the youngest haplotype that is monophyletic (M ∼ 1 is consistent with a monophyletic origin and relatively short history, M < 1 suggests polyphyletic origin of haplotypes in founders). The metric ρ has a strong theoretical foundation and ɛ has been shown to be relatively insensitive to allele frequencies, less confounded by sample sizes than other metrics and relatively insensitive to low marker density (Morton et al. 2001; Maniatis et al. 2002; Shete 2003; Collins et al. 2004; Ke et al. 2004). The “swept radius” describes the extent of LD and is given by 1/ɛ. The swept radius is therefore the distance over which M is reduced by e−1. The swept radius is also referred to as 1 LD unit (LDU). For additional details of this approach refer to Supplemental material.

Assessing the stability in the pattern of LD across chromosomes

The LD map reflects historical recombination events whereas a genetic linkage map (cM) is constructed using recombination events observed in the pedigree. To test whether ancestral and contemporary recombination rates were colocalized on each chromosome the following linear model was used:

graphic file with name 496equ3.jpg

where LDUi is the map position of the ith marker in LD units, di is the physical position (Mb), GDi is the genetic map position (cM), and ei residual error. Because both the LD map and the linkage map increase cumulatively with physical position along a chromosome, it is first necessary to fit the physical position of each marker. If the linkage map position is a significant model term, even after fitting the physical position, ancestral and contemporary recombination events have occurred in the same chromosomal regions. Because LD was estimated in the founders (and reflects recombination in their ancestors) and linkage distances were obtained from their progeny, the LDU maps and linkage maps are statistically independent. This means any correspondence between LD maps and linkage maps is suggestive that regions of relatively high (and low) recombination rate have remained constant over time. Models were only fitted to chromosomes with at least 10 markers.

Analysis of inter- and intrachromosomal variation in LD

Linear models were used to test for a relationship between the LDU map length and both chromosome length (measured in Mb) and recombination rate (cM/Mb). Variables were transformed using Box Cox power transformations to meet assumptions of normality.

To investigate if LD varied across the macrochromosomes as predicted from the biased location of crossing-over events observed in chromosomal spreads (Calderón and Pigozzi 2006), we test for a relationship between standardized distance from the center of the chromosome (midi) and LD for macrochromosomes (Tgu1–9 and Tgu1a, TguZ) and microchromosomes (Tgu4a and Tgu10–15, Tgu17–21, Tgu23–28) using a generalized (Poisson error) linear model. The LDU distance (dij) for each kth SNP was calculated as the distance between it and the previous (jth) SNP using:

graphic file with name 496equ4.jpg

For the ith chromosome, distance from the center of the chromosome (dmid) was standardized relative to the longest chromosome (lmax) using:

graphic file with name 496equ5.jpg

Analysis of inter- and intrachromosomal variation in other sequence features

To investigate how the pattern of LD covaried with other sequence features we also quantified heterozygosity, GC content, and number of genes per Mb across the zebra finch genome (see Supplemental material for details). CpG motifs (CCTCCT, CTCTCCC, CCCCCCC, CTCF consensus [CCNCCNGGNGG]) previously shown to be related to recombination (Myers et al. 2005; Shifman et al. 2006; Groenen et al. 2009) are highly correlated with GC content (Supplemental Fig. S3), so we only present data for GC content in this analysis. To test for a correlation between LDU per Mb and mean heterozygosity, GC content, and number of genes per Mb, we used nonparametric correlations (Kendall's Tau). Correlations were used instead of linear models because it was not clear which variable was the explanatory and which was the response. To test for differences in the quantities of these sequence features between macrochromosomes and microchromosomes we used linear and generalized linear models. Unless otherwise stated, all analysis was carried out in R 2.7.1 (R Development Core Team 2006).

Acknowledgments

We thank The Genome Center, Washington University School of Medicine, and the International Zebra Finch Genome Sequencing Consortium for making the Taeniopygia guttata genome sequence publicly available prior to publication. We thank Jayne Pellatt for maintaining and arching the zebra finch mapping panel. We also thank Alex Ball, Deborah Dawson, Andy Krupa, and Sarah Follet for preparing DNA/RNA samples. Karine Viaud (Illumina) coordinated SNP genoypting and assay design. The work was funded by the United Kingdom Biotechnology and Biological Sciences Research Council (BBSRC) under grant no. BBE0175091.

Footnotes

[Supplemental material is available online at http://www.genome.org.]

Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.102095.109.

References

  1. Abasht B, Sandford E, Arango J, Settar P, Fulton J, O'Sullivan N, Hassen A, Habier D, Fernando R, Dekkers J, et al. Extent and consistency of linkage disequilibrium and identification of DNA markers for production and egg quality traits in commercial layer chicken populations. BMC Genomics. 2009;10:S2. doi: 10.1186/1471-2164-10-S2-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Abecasis GR, Cookson WO. GOLD—graphical overview of linkage disequilibrium. Bioinformatics. 2000;16:182–183. doi: 10.1093/bioinformatics/16.2.182. [DOI] [PubMed] [Google Scholar]
  3. Aerts J, Megens HJ, Veenendaal T, Ovcharenko I, Crooijmans R, Gordon L, Stubbs L, Groenen M. Extent of linkage disequilibrium in chicken. Cytogenet Genome Res. 2007;117:338–345. doi: 10.1159/000103196. [DOI] [PubMed] [Google Scholar]
  4. Andreescu C, Avendano S, Brown SR, Hassen A, Lamont SJ, Dekkers JCM. Linkage disequilibrium in related breeding lines of chickens. Genetics. 2007;177:2161–2169. doi: 10.1534/genetics.107.082206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ardlie KG, Kruglyak L, Seielstad M. Patterns of linkage disequilibrium in the human genome. Nat Rev Genet. 2002;3:299–309. doi: 10.1038/nrg777. [DOI] [PubMed] [Google Scholar]
  6. Arnheim N, Calabrese P, Tiemann-Boege I. Mammalian meiotic recombination hot spots. Annu Rev Genet. 2007;41:369–399. doi: 10.1146/annurev.genet.41.110306.130301. [DOI] [PubMed] [Google Scholar]
  7. Backström N, Qvarnström A, Gustafsson L, Ellegren H. Levels of linkage disequilibrium in a wild bird population. Biol Lett. 2006;2:435–438. doi: 10.1098/rsbl.2006.0507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Balakrishnan CN, Edwards SV. Nucleotide variation, linkage disequilibrium and founder-facilitated speciation in wild populations of the Zebra Finch (Taeniopygia guttata) Genetics. 2008;181:645–660. doi: 10.1534/genetics.108.094250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Begun DJ, Aquadro CF. Levels of naturally occurring DNA polymorphism correlate with recombination rates in D. melanogaster. Nature. 1992;356:519–520. doi: 10.1038/356519a0. [DOI] [PubMed] [Google Scholar]
  10. Bonizzoni P, Della Vedova G, Dondi R, Li J. The Haplotyping problem: An overview of computational models and solutions. J Comput Sci Technol. 2003;18:675–688. [Google Scholar]
  11. Calderón P, Pigozzi M. MLH1-focus mapping in birds shows equal recombination between sexes and diversity of crossover patterns. Chrom Res. 2006;14:605–612. doi: 10.1007/s10577-006-1059-0. [DOI] [PubMed] [Google Scholar]
  12. Collins A, Lau W, De La Vega F. Mapping genes for common diseases: The case for genetic (LD) maps. Hum Hered. 2004;58:2–9. doi: 10.1159/000081451. [DOI] [PubMed] [Google Scholar]
  13. Coop G, Wen XQ, Ober C, Pritchard JK, Przeworski M. High-resolution mapping of crossovers reveals extensive variation in fine-scale recombination patterns among humans. Science. 2008;319:1395–1398. doi: 10.1126/science.1151851. [DOI] [PubMed] [Google Scholar]
  14. Daly MJ, Rioux JD, Schaffner SF, Hudson TJ, Lander ES. High-resolution haplotype structure in the human genome. Nat Genet. 2001;29:229–232. doi: 10.1038/ng1001-229. [DOI] [PubMed] [Google Scholar]
  15. De La Vega FM, Isaac H, Collins A, Scafe CR, Halldórsson BV, Su X, Lippert RA, Wang Y, Laig-Webster M, Koehler RT, et al. The linkage disequilibrium maps of three human chromosomes across four populations reflect their demographic history and a common underlying recombination pattern. Genome Res. 2005;15:454–462. doi: 10.1101/gr.3241705. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. de Massy B. Distribution of meiotic recombination sites. Trends Genet. 2003;19:514–522. doi: 10.1016/S0168-9525(03)00201-4. [DOI] [PubMed] [Google Scholar]
  17. Gabriel SB, Schaffner SF, Nguyen H, Moore JM, Roy J, Blumenstiel B, Higgins J, DeFelice M, Lochner A, Faggart M, et al. The structure of haplotype blocks in the human genome. Science. 2002;296:2225–2229. doi: 10.1126/science.1069424. [DOI] [PubMed] [Google Scholar]
  18. Green P, Falls K, Crooks S. CRI-MAP Documentation. 1990. http://linkage.rockefeller.edu/soft/crimap/.
  19. Groenen MAM, Wahlberg P, Foglio M, Cheng HH, Megens H-J, Crooijmans RPMA, Besnier F, Lathrop M, Muir WM, Wong GK-S, et al. A high-density SNP-based linkage map of the chicken genome reveals sequence features correlated with recombination rate. Genome Res. 2009;19:510–519. doi: 10.1101/gr.086538.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hansson B, Ljungqvist M, Dawson DA, Mueller JC, Olano-Marin J, Ellegren H, Nilsson JA. Avian genome evolution: Insights from a linkage map of the blue tit (Cyanistes caeruleus) Heredity. 2009;104:67–78. doi: 10.1038/hdy.2009.107. [DOI] [PubMed] [Google Scholar]
  21. Hedrick PW. Inference of recombinational hotspots using gametic disequilibrium values. Heredity. 1988;60:435–438. doi: 10.1038/hdy.1988.61. [DOI] [PubMed] [Google Scholar]
  22. Heifetz EM, Fulton JE, O'Sullivan N, Zhao H, Dekkers JCM, Soller M. Extent and consistency across generations of linkage disequilibrium in commercial layer chicken breeding populations. Genetics. 2005;171:1173–1181. doi: 10.1534/genetics.105.040782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hill WG. Estimation of effective population-size from data on linkage disequilibrium. Genet Res. 1981;38:209–216. [Google Scholar]
  24. International Chicken Genome Sequencing Consortium. Sequence and comparative analysis of the chicken genome provide unique perspectives on vertebrate evolution. Nature. 2004;432:695–716. doi: 10.1038/nature03154. [DOI] [PubMed] [Google Scholar]
  25. Jaari S, Li M-H, Merila J. A first-generation microsatellite-based genetic linkage map of the Siberian jay (Perisoreus infaustus): Insights into avian genome evolution. BMC Genomics. 2009;10:1. doi: 10.1186/1471-2164-10-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jeffreys AJ, Kauppi L, Neumann R. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat Genet. 2001;29:217–222. doi: 10.1038/ng1001-217. [DOI] [PubMed] [Google Scholar]
  27. Ke X, Hunt S, Tapper W, Lawrence R, Stavrides G, Ghori J, Whittaker P, Collins A, Morris AP, Bentley D, et al. The impact of SNP density on fine-scale patterns of linkage disequilibrium. Hum Mol Genet. 2004;13:577–588. doi: 10.1093/hmg/ddh060. [DOI] [PubMed] [Google Scholar]
  28. Khatkar M, Nicholas F, Collins A, Zenger K, Cavanagh J, Barris W, Schnabel R, Taylor J, Raadsma H. Extent of genome-wide linkage disequilibrium in Australian Holstein-Friesian cattle based on a high-density SNP panel. BMC Genomics. 2008;9:187. doi: 10.1186/1471-2164-9-187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kong A, Gudbjartsson DF, Sainz J, Jonsdottir GM, Gudjonsson SA, Richardsson B, Sigurdardottir S, Barnard J, Hallbeck B, Masson G, et al. A high-resolution recombination map of the human genome. Nat Genet. 2002;31:241–247. doi: 10.1038/ng917. [DOI] [PubMed] [Google Scholar]
  30. Kruglyak L. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat Genet. 1999;22:139–144. doi: 10.1038/9642. [DOI] [PubMed] [Google Scholar]
  31. Li J, Jiang T. Computing the minimum recombinant haplotype configuration from incomplete genotype data on a pedigree by integer linear programming. J Comput Biol. 2005;12:719–739. doi: 10.1089/cmb.2005.12.719. [DOI] [PubMed] [Google Scholar]
  32. Li MH, Merilä J. Extensive linkage disequilibrium in a wild bird population. Heredity. 2009 doi: 10.1038/hdy.2009.150. [DOI] [PubMed] [Google Scholar]
  33. Malécot G. Les Mathematiques de l'Heredite. Maison et Cie; Paris: 1948. [Google Scholar]
  34. Maniatis N, Collins A, Xu CF, McCarthy LC, Hewett DR, Tapper W, Ennis S, Ke X, Morton NE. The first linkage disequilibrium (LD) maps: Delineation of hot and cold blocks by diplotype analysis. Proc Natl Acad Sci. 2002;99:2228–2233. doi: 10.1073/pnas.042680999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Maynard Smith J, Haigh J. The hitch-hiking effect of a favourable gene. Genet Res. 1974;23:23–35. [PubMed] [Google Scholar]
  36. Meunier J, Duret L. Recombination drives the evolution of GC-content in the human genome. Mol Biol Evol. 2004;21:984–990. doi: 10.1093/molbev/msh070. [DOI] [PubMed] [Google Scholar]
  37. Miyashita N, Langley CH. Molecular and phenotypic variation of the white locus region in Drosophila melanogaster. Genetics. 1988;120:199–212. doi: 10.1093/genetics/120.1.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Morton NE, Zhang W, Taillon-Miller P, Ennis S, Kwok PY, Collins A. The optimal measure of allelic association. Proc Natl Acad Sci. 2001;98:5217–5221. doi: 10.1073/pnas.091062198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Myers S, Bottolo L, Freeman C, McVean G, Donnelly P. A fine-scale map of recombination rates and hotspots across the human genome. Science. 2005;310:321–324. doi: 10.1126/science.1117196. [DOI] [PubMed] [Google Scholar]
  40. Nachman MW. Single nucleotide polymorphisms and recombination rate in humans. Trends Genet. 2001;17:481–485. doi: 10.1016/s0168-9525(01)02409-x. [DOI] [PubMed] [Google Scholar]
  41. Ohta T. A note on the correlation between heterozygosity and recombination rate. Genes Genet Syst. 1999;74:209–210. doi: 10.1266/ggs.74.209. [DOI] [PubMed] [Google Scholar]
  42. Pigozzi M, Solari A. The germ-line-restricted chromosome in the zebra finch: Recombination in females and elimination in males. Chromosoma. 2005;114:403–409. doi: 10.1007/s00412-005-0025-5. [DOI] [PubMed] [Google Scholar]
  43. Pritchard JK, Przeworski M. Linkage disequilibrium in humans: Models and data. Am J Hum Genet. 2001;69:1–14. doi: 10.1086/321275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2006. [Google Scholar]
  45. Rao YS, Liang Y, Xia MN, Shen X, Du YJ, Luo CG, Nie QH, Zeng H, Zhang XQ. Extent of linkage disequilibrium in wild and domestic chicken populations. Hereditas. 2008;145:251–257. doi: 10.1111/j.1601-5223.2008.02043.x. [DOI] [PubMed] [Google Scholar]
  46. Sherman JD, Stack SM. Two-Dimensional spreads of synaptonemal complexes from solanaceous plants. VI. High-resolution recombination nodule map for tomato (Lycopersicon esculentum) Genetics. 1995;141:683–708. doi: 10.1093/genetics/141.2.683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Shete S. A note on the optimal measure of allelic association. Ann Hum Genet. 2003;67:189–191. doi: 10.1046/j.1469-1809.2003.00025.x. [DOI] [PubMed] [Google Scholar]
  48. Shifman S, Bell JT, Copley RR, Taylor MS, Williams RW, Mott R, Flint J. A high-resolution single nucleotide polymorphism genetic map of the mouse genome. PLoS Biol. 2006;4:e395. doi: 10.1371/journal.pbio.0040395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Slatkin M. Linkage disequilibrium understanding the evolutionary past and mapping the medical future. Nat Rev Genet. 2008;9:477–485. doi: 10.1038/nrg2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Sobel E, Lange K. Descent graphs in pedigree analysis: Applications to haplotyping, location scores, and marker-sharing statistics. Am J Hum Genet. 1996;58:1323–1337. [PMC free article] [PubMed] [Google Scholar]
  51. Stapley J, Birkhead TR, Burke T, Slate J. A linkage map of the Zebra Finch Taeniopygia guttata provides new insights into avian genome evolution. Genetics. 2008;179:651–667. doi: 10.1534/genetics.107.086264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Stephens M, Smith NJ, Donnelly P. A new statistical method for haplotype reconstruction from population data. Am J Hum Genet. 2001;68:978–989. doi: 10.1086/319501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Sved JA. Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor Popul Biol. 1971;2:125–141. doi: 10.1016/0040-5809(71)90011-6. [DOI] [PubMed] [Google Scholar]
  54. van Bers NEM, van Oers K, Kerstens HD, Dibbits BW, Crooijmans PMA, Visser ME, Groenen AM. Genome-wide SNP detection in the great tit Parus major using high throughput sequencing. Mol Ecol. 2010;19 (Suppl. 1):89–99. doi: 10.1111/j.1365-294X.2009.04486.x. [DOI] [PubMed] [Google Scholar]
  55. Wahlberg P, Stromstedt L, Tordoir X, Foglio M, Heath S, Lechner D, Hellstrom AR, Tixier-Boichard M, Lathrop M, Gut IG, et al. A high-resolution linkage map for the Z chromosome in chicken reveals hot spots for recombination. Cytogenet Genome Res. 2007;117:22–29. doi: 10.1159/000103161. [DOI] [PubMed] [Google Scholar]
  56. Weir BS. Inferences about linkage disequilibrium. Biometrics. 1979;35:235–254. [PubMed] [Google Scholar]
  57. Weiss KM, Clark AG. Linkage disequilibrium and the mapping of complex human traits. Trends Genet. 2002;18:19–24. doi: 10.1016/s0168-9525(01)02550-1. [DOI] [PubMed] [Google Scholar]
  58. Wong GK, Liu B, Wang J, Zhang Y, Yang X, Zhang Z, Meng Q, Zhou J, Li D, Zhang J, et al. A genetic variation map for chicken with 2.8 million single-nucleotide polymorphisms. Nature. 2004;432:717–722. doi: 10.1038/nature03156. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES