Abstract
Site-specific 15N chemical shift anisotropy (CSA) tensors have been derived for the well-ordered backbone amide 15N nuclei in the B3 domain of protein G (GB3) from residual chemical shift anisotropy (RCSA) measured in six different mutants that retain the native structure but align differently relative to the static magnetic field when dissolved in a liquid crystalline Pf1 suspension. This information is complemented by measurement of cross-correlated relaxation rates between the 15N CSA tensor and either the 15N-1H or 15N-13C′ dipolar interaction. In agreement with recent solid state NMR measurements, the 15N CSA tensors exhibit only a moderate degree of variation from averaged values, but have larger magnitudes in α-helical (−173 ± 7 ppm) than in β-sheet (−162 ± 6 ppm) residues, a finding also confirmed by quantum computations. The orientations of the least shielded tensor component cluster tightly around an in-peptide-plane vector that makes an angle of 19.6±2.5° with the N-H bond, with the asymmetry of the 15N CSA tensor being slightly smaller in α-helix (η=0.23±0.17) than in β-sheet (η=0.31±0.11). The residue-specific 15N CSA values are validated by improved agreement between computed and experimental 15N R1ρ relaxation rates measured for 15N-{2H} sites in GB3, which are dominated by the CSA mechanism. Use of residuespecific 15N CSA values also results in more uniform generalized order parameters, S2, and predicts considerable residue-by-residue variations in the magnetic field strengths where TROSY line narrowing is most effective.
Keywords: CSA, GB3, liquid crystal, NMR, RDC, residual chemical shift anisotropy
Introduction
Chemical shifts play an increasingly important role in NMR analyses of protein structure and dynamics.1–6 Although the structural dependence of 1H and 13C chemical shifts is known reasonably well, both on the basis of empirical and computational studies,7–13 backbone amide 15N chemical shifts are less well understood and many factors have been reported to impact them, including residue type, backbone torsion angles, hydrogen bonding, the intraresidue χ1 angle, and the sidechain of the preceding residue.14–21 The isotropic 15N shift corresponds to the trace of its anisotropic chemical shielding tensor, and a quantitative analysis of factors impacting the isotropic shift hinges on an understanding of the role each of the structural parameters has on the six independent variables that make up the symmetric part of this tensor.
For solid state NMR applications, valuable structural information is encapsulated in the 15N chemical shielding anisotropy. In particular, when studying oriented peptide or protein samples, the observed chemical shift provides information on the orientation of the peptide group relative to the magnetic field, which becomes a particularly powerful structural restraint when combined with the orientation of the 15N-1H bond, contained in its dipolar coupling.22–24 For solution NMR, interference between the 15N CSA and 15N-1H dipolar relaxation mechanisms forms the basis for the all-important TROSY experiment, which dramatically enhances resolution in protein NMR spectroscopy.25 Quantitative analysis of 15N relaxation rates, which depends on the 15N CSA tensor, can provide detailed information on internal dynamics of the protein backbone.26–28 To date, nearly all analysis have been carried out under the assumption of a uniform value for the 15N CSA tensor, often assumed to be axially symmetric with a magnitude, Δσ, of −160 or −170 ppm.27,29 However, early single crystal solid state NMR measurements by Hiyama et al. on Boc-glycylglycyl[15N]glycine benzyl ester showed large variations in the CSA asymmetry, from nearly axially symmetric in a monoclinic lattice form, to quite asymmetric (η = 0.44) in a triclinic lattice.30 Numerous subsequent studies have aimed to better characterize the 15N CSA tensor in peptide bonds and its variability and structural dependence.21,31–44 However, the degree of intrinsic variability in the 15N CSA tensor remains the subject of considerable debate. Although Hiyama’s CSA asymmetry parameter was very different for the two crystal forms, the CSA magnitude (Δσ) was nearly unchanged (−164 vs −161 ppm).30 Solution relaxation data recorded for ubiquitin pointed to a high degree of variability, but similar data recorded for ribonuclease H, after removal of outliers, indicated a much smaller spread.35 A subsequent analysis of ubiquitin cross-correlated transverse and longitudinal relaxation data, combined with R1, R2, and 15N-{1H} NOE data, indicated a point-to-point variability estimate of only 5.3 ppm, with a 95% confidence interval spanning from 1.4 to 9.4 ppm,39 even somewhat lower than the spread seen in ribonuclease H,35 and considerably smaller than the variability reported originally for ubiquitin33 and more recently for GB3.44 However, it is important to note that the site-to-site variability hinges on the estimate for the experimental measurement error; the actual best-fitted CSA data show a much larger spread, part of which is attributed to experimental measurement error. A recent elegant study of cross-correlated relaxation data in ubiquitin shows that the extracted CSA values weakly depend on the motional model assumed during the analysis.40 This ubiquitin study finds a relatively large average CSA asymmetry parameter, η, of 0.28 and notes that an increase in η correlates with a downfield change in the isotropic 15N shift. However, with a Pearson’s correlation coefficient, RP, of 0.36 these tensor parameters showed little correlation with those of Damberg et al.39 Another recent solid state NMR study utilized slow magic angle spinning to obtain residue-specific 15N and 13C′ CSA tensors in polycrystalline GB1.43 That study finds a moderate degree of variability in the magnitude of the CSA tensor (−164±9 ppm) but substantial variations in its asymmetry (η = 0.19 ± 0.16), which lack the significant correlation with isotropic shift, previously deduced from solution NMR cross-correlated relaxation studies on ubiquitin.40
Here, we use several enhanced NMR techniques to study the 15N CSA of the backbone amides in protein GB3, which has very high sequence and structural similarity to GB1, using both liquid crystal and cross-correlated relaxation NMR. In order to eliminate the effect of a change in solvent conditions between isotropic and aligned samples, we utilize magic angle spinning (MAS) of the same solution to remove the effect of protein alignment,38,45 thereby allowing the accurate measurement of the small contribution of residual chemical shift anisotropy (RCSA)41,46–48 on the chemical shifts observed in the liquid crystalline state. These measurements are carried out for six conservative mutants,49 which align differently with respect to the liquid crystalline matrix consisting of the filamentous bacteriophage Pf1.47,50 These measurements, as well as the cross-correlated relaxation measurements, are carried out on perdeuterated protein, with the backbone amides back-exchanged to become protonated, thereby removing small effects resulting from remote protons that can interfere with the precise measurement of chemical shifts and relaxation rates. CSA tensors derived in this manner for GB3 result in much improved predictions of the GB3 relaxation rates of 15N-{2H} groups, compared to using a uniform CSA tensor, thereby validating the accuracy of the results derived by our approach.
Materials and Methods
Sample expression and purification
Six 15N/13C/2H labeled mutants of the 56-residue third IgG-binding domain of protein G, GB3, were made by expression in Escherichia coli BL21 (DE3*) cells, transformed with a pET-11 vector containing the mutated GB3 gene. These include K19AV42ED47K, T11KK19AV42E, K19ED40NV42E, K4AK19EV42E, K4AK19EV42E-N-His6, and K4AK19EV42E-C-His6. Preparations were grown in M9 minimal media, containing 15NH4Cl and uniformly 13C-enriched glucose (3 g/L), as well a 1 g/L 15N/13C Celtone growth medium (Martek Biosciences, Columbia, MD). A high level (~85%) of deuteration of the non-exchangeable protons was achieved by using 99% D2O during the entire process. Protein expression was induced by 0.5 mM IPTG. Cultures were centrifuged and resuspended in 20 ml PBS buffer. The cells were lysed by heating to 80 °C for 10 minutes and centrifuged again. The supernatant was loaded on a Superdex 75 HiLoad 26/60 (Amersham Biosciences) column, equilibrated with NMR buffer (25 mM sodium phosphate, 50 mM NaCl, 0.05% w/v NaN3, pH 6.5).
For measurement of the residual chemical shift anisotropy, mutant GB3 NMR samples contained ca 4 mM 15N/13C/2H protein and an amount of Pf1 that yielded a suitable degree of alignment for each mutant corresponding to 2H quadrupole splittings of the lock solvent of 16 Hz (K19AV42ED47K), 31 Hz (T11KK19AV42E), 50 Hz (K19ED40NV42E), 56 Hz (K4AK19EV42E), 18 Hz (K4AK19EV42E-N-His6), and 40 Hz (K4AK19EV42E-C-His6). For each mutant, two samples were prepared from the same Pf1-containing stock solution: one sample in a 300 μL volume Shigemi microcell, the other in a 40 μL volume Bruker magic angle spinning (MAS) rotor. Isotropic samples at concentrations of 0.8 mM for K4AK19EV42E and 4.0 mM for K19AV42ED47K 15N/13C/2H were prepared and used to measure cross-correlated relaxation rates between 15N CSA and 15N-13C′ dipolar, as well as between 15N CSA and 15N-1HN dipolar mechanisms. A sample of 2.5 mM T11KK19EV42E 13C/15N-GB3 dissolved in 100% D2O buffer containing 13 mM sodium phosphate, pH 6.9, and 25 mM NaCl was used to measure the R1 and R1ρ relaxation rates of backbone amide 15N-{2H} moieties.
NMR spectroscopy
All NMR experiments were carried out on Bruker Avance 500, 600 and 800 MHz spectrometers, equipped with z-axis gradient, triple resonance, cryogenic probeheads and on a Bruker Avance 600 MHz spectrometer equipped with a room-temperature MAS probehead that included a z-axis gradient coil. All experiments were performed at 298 K unless explicitly stated.
A three-dimensional HNCO spectrum was recorded for each 15N/13C/2H-labeled aligned sample. In order to obtain simultaneously the chemical shifts and the one-bond 15N-1H and 13C′-13Cα splittings, which were used to determine the alignment tensors, the HNCO experiments were performed (at 500 MHz 1H frequency) in the absence of 1H decoupling during 15N evolution, and with 13Cα decoupling omitted during 13C′ evolution. The acquisition times were 112 (13C′), 90 (15N), and 64 ms (1H) with the data matrices consisting of 56* × 128* × 512* data points, where N* indicates N complex points. In these 3D HNCO spectra, each correlation was split into four multiplet components, separated by 1JHN + 1DHN in the 15N dimension and by 1JC′Cα + 1DC′Cα in the 13C′ dimension. The frequencies of the four components were averaged to obtain the chemical shift, δaligned, in the liquid crystalline phase. The isotropic chemical shifts, δisotropic, for each mutant were obtained from a regular HNCO experiment with heteronuclear decoupling in all dimensions, carried out on the samples under MAS conditions, spinning at a slow rate of ~620 Hz which effectively removed alignment. For several samples, spinning at higher rates (ca 3 kHz) resulted in the absence of a 2H solvent quadrupole splitting after the MAS spinner was stopped following several days of spinning, presumably due to precipitation of the Pf1 under the relatively high g forces operative under these conditions. Following slower (620 Hz) MAS conditions, no such loss of quadrupole splitting was observed. The acquisition times for the 3D HNCO experiments were 94 (13C′), 94 (15N), and 106 ms (1H) with the data matrix consisting of 47* × 94* × 1024* data points. The effect of very small temperature differences between the static and MAS samples on the difference in chemical shift for any given mutant was accounted for during data analysis by measurement of the temperature coefficients of each nucleus, which allowed for an accurate estimate of the difference in effective sample temperatures between aligned and isotropic samples (to within ~0.1 °C), and subsequent removal of the temperature dependent contribution. The temperature coefficients of the 1HN, 15N and 13C′ nuclei were derived from HNCO experiments carried out on mutant K19AV42ED47K in an isotropic solution at 298 K and at 306 K, and these temperature coefficients (SI Table S1) were assumed to be the same for all six mutants. The residual chemical shift anisotropy (RCSA) is then derived from the difference between the chemical shifts measured for the aligned and MAS samples, after the above mentioned correction for minor differences in temperature.
15N relaxation rates were measured for the mutant K4AK19EV42E, including longitudinal (R1), spin-locked transverse (R1ρ), transverse 15N CSA/N-H dipolar cross-correlated (ΓCSA,NH), and transverse 15N CSA/N-C′ dipolar cross-correlated (ΓCSA,NC′) relaxation, using the set of experiments described below, all based on the 1H-detected 1H-15N HSQC pulse sequence, 51 and closely related to experiments by Loth et al.40
For the R1ρ measurement, carried out using standard methods52 at 600 MHz 1H frequency, spin-lock durations were 3, 10, 40, 80, 120, 150, 175 and 200 ms. A 15N spin-lock field strength of 2.4 kHz was used with the carrier frequency positioned in the center of the 15N spectrum. A single 1H composite pulse 90°x-210°y-90°x was applied at the midpoint of the spin-lock period to suppress the effect of 15N CSA/N-H dipolar cross-correlation. A 500 μs hyperbolic secant 180° 13C′/13Cα pulse53 was utilized in a similar way to suppress 15N CSA/N-C′ as well as 15N CSA/N-Cα dipolar cross-correlation. The acquisition times were 80 (15N) and 61 ms (1H), with the data matrices consisting of 160* × 512* points. A 2-s water saturation pulse with a RF field strength of 37 Hz was applied during the delay between scans, and 15N RF heating compensation pulses were utilized to ensure the temperature of the R1ρ experiment to remain constant.54
For the R1 measurement, carried out at 600 MHz 1H frequency, the longitudinal relaxation delays were 50.6, 151.8, 253, 354.2, 455.4, and 506 ms. A 1H composite pulse 90°x-210°y-90°x and a hyperbolic secant 180° 13C pulse were applied every 50 ms during the R1 relaxation delay to remove the effect of longitudinal 15N CSA/N-HN and 15N CSA/C′(Cα) dipolar cross-correlation. The acquisition times were 56 (15N) and 80 (1H) ms, with data matrices consisting of 140* × 768* points.
Transverse 15N CSA/N-HN dipolar cross-correlated relaxation rates, ΓCSA,NH, were measured using a constant-time 15N evolution HSQC experiment (Supporting Information, Fig. S2). This experiment, and the analogous measurement of the 15N CSA/N-C′ dipolar cross-correlated relaxation rates, ΓCSA,NC′, are based on measurement of the relative intensities of 15N doublet components after a constant-time evolution period lacking 1H (or 13C′) decoupling, and are fully analogous to methods described previously for this purpose55,56 (SI Fig. S2). The value of ΓCSA,NH then directly follows from the intensity ratio of the up- and downfield components of the 15N doublets.55,56 The ΓCSA,NH measurement was performed at 600 MHz 1H frequency using constant-time durations 2T of 81.6 ms and 161.6 ms, and at 500 MHz with 2T 81.6 ms. The delay between scans was 1.5 s. The ΓCSA,NC′ dipolar cross-correlated relaxation rate was measured in the same way, but with the pulse sequence modified to decouple 1H during constant-time 15N evolution by means of two composite 90°x-210°y-90°x 1H pulses, and to decouple 13Cα and other aliphatic carbons by using two band-selective 2.0-ms hyperbolic secant 180° pulses53 during 15N constant-time evolution (Figure S3). The experiment was carried out at both 500 and 600 MHz 1H frequency, using a constant-time duration, 2T, of 165.1 ms. Resonance overlap was observed for the correlations of E24 and T25 in the 15N-CSA/N-HN dipolar cross-correlated relaxation spectrum. To solve this problem, a 15N-CSA/N-HN cross-correlated experiment (at 600 MHz) was performed on the K19AV42ED47K mutant, where these resonances are slightly shifted relative to one another, using a constant-time duration 2T of 81.6 ms. By linearly fitting the rates of residues measured for K4AK19EV42E to those measured for the five times more concentrated sample of K19AV42ED47K, a scaling factor of 1.086 was determined with a Pearson’s correlation coefficient RP = 0.993, allowing the ΓCSA,NH rates of E24 and T25 to be taken from this second measurement.
Longitudinal (R1) and spin-locked transverse (R1ρ) 15N relaxation rates were also measured for the mutant T11KK19EV42E dissolved in 100% D2O, using a modified HA(CACO)N sequence57 (SI Figure S4). The R1 measurement was performed at 600 MHz 1H frequency with delays of 0.101, 0.303, 0.505, 0.707, 0.808, 0.909 and 1.01s, and at 800 MHz field with delays of 0.050, 0.100, 0.300, 0.501, 0.701, 0.901, and 1.00 s. R1 experiments were performed at 283 K. The R1ρ was measured at 600 MHz 1H frequency, using a spin lock field strength of 2.0 kHz, and carried out both at 283 K and at 298 K, in order to identify residues affected by temperature-dependent conformational exchange. All spectra were processed and analyzed using the software package NMRPipe.58 Peak positions and intensities were determined by parabolic interpolation. R1 and R1ρ rates were determined from two-parameter exponential fits of peak intensities. The R2 rate was calculated by eliminating the R1 contribution from the measured R1ρ rate.59 The cross-correlated relaxation rates Γ were calculated from the intensity ratio of the up- and down-field 15N doublet components.56
Quantum Chemical Calculations
The model compound N-methyl acetamide (NMA) was used to calculate the difference in the effective length of N-D and N-H bonds. The molecular geometry was optimized using the Gaussian 03 program for B3LYP/6-31G** density functional calculations in a continuum solvent model (dielectric constant 78.4).60 To explore the 15N CSA differences between α-helix and β-strand conformations, alanine dipeptide models (HCO(NHCH(CH3)CO)2H) were built with backbone φ, ψ angles set equal to typical α-helix (T25-A26) and β-strand (F52-T53) conformations of the NMR-refined X-ray structure (PDB entry 2OED).61 One alanine dipeptide model was also built with φ, ψ angles corresponding to T49-K50 while another Ala-Gly model was built with φ, ψ angles equal to those of N37-G38. The models were optimized at the B3LYP/6-311+G** level while keeping all the dihedral angles fixed, and the chemical shielding tensors were calculated using the GIAO method62,63 at the B3LYP/aug-cc-pvtz level. The chemical shift tensor was computed as δii = δ0 − σii (i = X,Y,Z), where δ0 is 244.6 ppm, the absolute chemical shift of liquid ammonia at 298 K, and σii are the calculated CSA tensor principal components.
Results
Theoretical background
The change in chemical shift for a given nucleus upon switching from the isotropic to the liquid crystalline phase is commonly referred to as the residual chemical shift anisotropy, or RCSA, and is given by:
| (1) |
where P2(α) = (3 α2−1)/2, σXX, σYY and σZZ are the principal components of the traceless CSA tensor, while θ1, θ2, and θ3 are the angles between the principal axes of the CSA tensor and the magnetic field orientation. The angular brackets, <…>, refer to ensemble averaging. By applying the spherical harmonics addition theorem, eq 1 can be rewritten as
| (2) |
where b and a are vectors of the same form:
| (3a) |
| (3b) |
where (xi, yi, zi) are the Cartesian coordinates of the CSA principal axis bi and (x, y, z) are the Cartesian coordinates of the magnetic field in the molecular frame, and <a> represents the alignment tensor. If internal motion is assumed to be isotropic and affects all three CSA principal components in the same way, a single order parameter is sufficient to describe such motion. Eq 2 then can be rewritten as
| (4) |
where SRCSA is the order parameter. Assuming a uniform order parameter for the backbone amide 15N nuclei in the highly ordered regions of GB3, eq 4 can be rewritten in matrix format for the case where RCSAs are measured under N different alignment tensors,
| (5) |
where Λ is a L×N matrix, Bσii (i=X, Y, Z) is a L×5 matrix, <A> is a 5×N matrix and L is the number of nuclei. 15N-1H RDCs measured under multiple alignments can be expressed as:64
| (6) |
where DM is the L×N RDC matrix and B is an L×5 matrix, each row of which is a dipole internuclear vector of the same form as b described earlier and <A> is the alignment matrix. is a constant, defined as
| (7) |
where μ0 is the magnetic permittivity of vacuum, ħ is the reduced Planck’s constant, γH is the 1H gyromagnetic ratio, rNH is the internuclear distance, and <…> denotes averaging over the zero-point vibrational motion (including N-H bond stretching and librational motions). In our earlier study, using multiple RDCs in six alignments, we found when only considering the bond stretching motion.65 In addition, quantum calculations for the model compound N-methylacetamide (NMA) indicate that the zero-point librational motions reduce the 15N-1H dipolar coupling by 7.6%, equivalent to lengthening the effective bond by 0.025 Å to reff = 1.040 Å.65,66 By assuming a group of residues with only isotropic motions of uniform amplitude, described by an order parameter SRDC, eq 6 can be written as
| (8) |
with the apparent alignment matrix Amat given by:
| (9) |
The alignments, Amat, can be determined from the RDCs, either by means of singular value decomposition (SVD) if atomic coordinates are known,67 or if coordinates are unknown but three or more alignment orientations are available, by direct interpretation of dipolar couplings (DIDC)64,68 , or by other approaches that minimize the alignment error caused by structural noise.69 As seen from eq 9, knowledge of is prerequisite for determining the <A> matrix, and therefore for determining the CSA tensor (eqs 4,5). Entering the reff value and those of the other constants into eq 9 yields,
| (10) |
As seen from eq 10, the absolute amplitude of alignment depends on the motional amplitude of the N-H bond vectors. Eq 5 then can be rewritten as,
| (11) |
where Λ represents the experimental RCSA values, and Amat is obtained from RDCs, as described above. Therefore SRDC R/S CSA Bσii/ (i =X, Y, Z) follows from eq 11. The apparent CSA tensor for a given nucleus, obtained from RCSAs, scales relative to the static CSA tensor according to:
| (12) |
Information on the 15N CSA tensor can also be derived from relaxation data, in particular the R1, R2, and the CSA/dipolar cross-correlated relaxation rate ΓCSA,DD. It is well recognized that zero-point backbone motions scale down both the N-H dipole interaction and the 15N CSA, σii. However the applicable scaling factors (order parameters caused by zero point motions) for the two types of interactions are different, with the 15N CSA rescaling resulting from such motions being much weaker than that for the dipolar interaction, and the scaling of ΓCSA,DD falling in between.70 It is also worth noting that the scaling due to zero point motions of ΓCSA,DD for 15N CSA and N-C′ dipole cross-correlation is complicated by the large angle between the main principal axis of the nearly axially symmetric 15N CSA tensor, σZZ, and the N-C′ bond vector (ca 100°). This intrinsic complexity can be greatly reduced if the zero-point motion of the entire peptide plane, which may be assumed to be quite uniform and very small for all peptide bonds, is excluded from the relaxation data analysis. For isotropic internal motion, the dipole-dipole order parameter will be the same as the CSA order parameter in both relaxation and RCSA data analysis, i.e. S RDC = S RCSA and (order parameters derived from relaxation for CSA and dipole tensors), and the cross-correlated relaxation rate . As a result, the 15N CSA σii value determined in this study corresponds to the effective CSA averaged over zero-point motions, equivalent to what would be measured in a static solid-state NMR experiment in the absence of thermally activated motions, i.e., for a sample temperature approaching 0 K.
The 15N CSA and N-H (or N-C′) dipole cross-correlated relaxation rate for an isotropically tumbling system is described by,71
| (13) |
where B0 is the magnetic field strength, the subscript A represents the second nucleus, H or C′, and α1, α2, α3 are angles between the N-H or N-C′ bond vector and the X, Y, Z principal axes of the 15N CSA tensor, respectively. The N-C′ bond length of 1.329 Å is accurately known from high resolution X-ray structures on small peptides.72
R1 and R2 relaxation rates also are affected by CSA and therefore carry information on its magnitude. However, at the commonly used magnetic field strength of 14.1 T (600 MHz 1H frequency), the CSA relaxation mechanism is much smaller than the 15N-1H dipolar contribution and accounts for only ~27% of the R1 and R2 rates.73 Thus, these rates are dominated by the 15N-1H dipolar interaction. The fractional contribution of CSA to the relaxation rate can be greatly increased by exchanging the amide protons for deuterons, simply accomplished by dissolving the protein sample in 100% D2O. Due to the smaller magnetogyric ratio of 2H compared to 1H, its dipolar contribution to 15N relaxation is greatly diminished and the relative effect of CSA on 15N relaxation therefore is considerably larger for 15N-{2H} groups. To increase the otherwise very slow and more difficult to measure transverse relaxation rates of 15N-{2H} groups, the rotational correlation time can be increased by lowering the temperature (to 283 K in this study). The R1 and R2 relaxation rates for 15N-{2H} in an isotropically tumbling system are described by (Goldman, 1984),
| (14) |
| (15) |
where . R1p, R2p are the dipolar relaxation contributions resulting from nuclei other than the attached 2H, including the adjacent 13C′ and 13Cα spins, and remote 13C and 1H nuclei; Rex is the transverse relaxation contribution resulting from conformational exchange. The rotational diffusion tensor of GB3 protein is anisotropic and therefore more general forms of eqs 13–15 are used in this study (SI, eqs S2–S4).
Determination of alignment tensors
Each of the six GB3 mutants was aligned in a liquid crystalline suspension of Pf1, adjusted to a concentration that yielded a degree of GB3 alignment that was suitable for measuring 15N-1H RDCs at high relative accuracy, with values in the −25 to +45 Hz range. Note that this degree of alignment is somewhat stronger than commonly used for protonated proteins. Together, these six mutants provide a very good mapping of the five-dimensional alignment space.49 The isotropic chemical shifts, δisotropic, for each mutant were obtained from a regular HNCO experiment with heteronuclear decoupling in all dimensions, carried out on the samples under MAS conditions, spinning at a slow rate of ~620 Hz which effectively removed alignment (Figure 1). Singular value decomposition (SVD) fitting67,74 of the experimental RDCs to the N-H orientations obtained in our previous study (SI table S8) was used to determine the alignment tensors, Amat, for each of the six mutants (Table 1). The vector orientations were also used for fitting the relaxation data and the RCSA values, in order to determine the rotational diffusion tensor and the site-specific 15N CSA tensors.
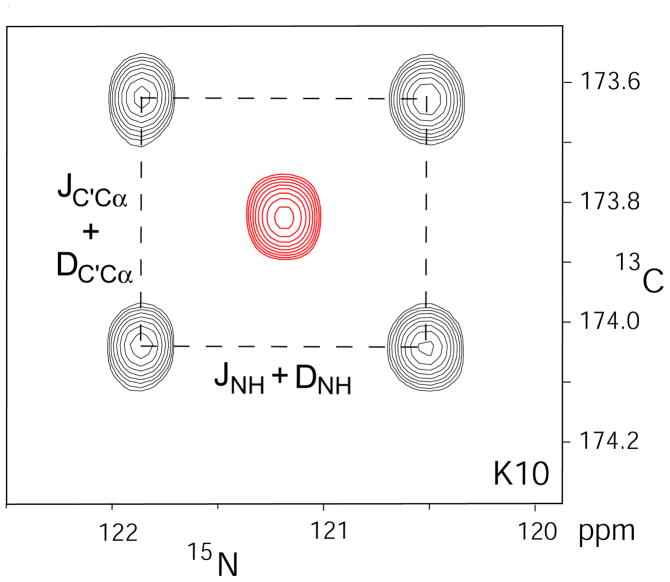
Figure 1.
Superposition of 13C-15N cross sections taken at the 1HN frequency of residue K10 through the HNCO 3D spectra recorded for aligned (black contours) and magic angle spinning (red contours) samples of GB3 mutant K19AV42ED47K. The spectrum on the aligned sample was recorded without 13Cα decoupling during 13C′ evolution, and without 1HN decoupling during 15N evolution; the isotropic data were recorded in the presence of decoupling, yielding a single resonance.
Table 1.
Alignment tensors for the GB3 mutants in liquid crystalline Pf1.a
| Da (Hz) | R | αb | βb | γb | |
|---|---|---|---|---|---|
| K19AV42ED47K | 24.0 | 0.253 | 82.7 | 94.2 | 294 |
| K19ED40NV42E | −12.4 | 0.222 | 89.9 | 336 | 133 |
| K4AK19EV42E-C-histag | 8.61 | 0.461 | 162 | 258 | 213 |
| K4AK19EV42E-N-histag | 18.5 | 0.179 | 123 | 256 | 184 |
| T11KK19AV42E | 20.0 | 0.300 | 102 | 246 | 220 |
| K4AK19EV42E | 10.3 | 0.551 | 162 | 251 | 23.0 |
The RDCs are fitted to the N-H orientations determined previously 65 that were aligned relative to the molecular frame of PDB entry 2OED61 (SI, Table S8).
The angles reported are z-y-z convention Euler angles needed to rotate the molecular frame to the alignment tensor frame.75
Residual chemical shift anisotropy
Owing to the weak alignment of the protein in the dilute liquid crystalline Pf1 suspension, a small amount of residual chemical shift anisotropy contributes to the observed chemical shifts. Just like the dipolar couplings, the RCSA is scaled down relative to its static CSA value by about three orders of magnitude, and RCSA effects for 15N then typically fall in the ±100 ppb range, considerably larger than the estimated RCSA random measurement error of ±5 ppb. Accurate measurement of such small chemical shift differences between isotropic and aligned samples also requires the absence of systematic effects that might perturb these chemical shifts. Such effects may include the difference in solvent composition, including small differences in ionic strength, pH, or molecules associated with the liquid crystalline matrix. These “solvent effects”, together with possible small differences in experimental sample temperature between the recordings of the separate spectra, previously were significant concerns in determining highly accurate RCSA values, and a number of methods have been devised to minimize them.37,41,76 For example, it is relatively easy to generate an isotropic bicelle solution that is similar in composition to the liquid crystalline bicelle sample, causing the effect of the change in medium to nearly cancel. Alternatively, by changing the temperature across the nematic to isotropic phase boundary, the same sample can be studied under isotropic and aligned conditions, but this increases the effect of uncertainty in the temperature coefficients of the chemical shifts.37 For the highly robust and popular alignment medium of filamentous bacteriophage Pf1,50 it is not readily possible to introduce a switch between isotropic and aligned phases for a static sample. Instead, we here study two Pf1-containing samples, prepared from the same stock solution with one sample contained in a regular Shigemi NMR microcell and the other in a 4-mm outer diameter magic angle spinning rotor (40 μL volume). Depending on Pf1 concentration and ionic strength, static liquid crystalline Pf1 samples require between seconds and minutes to align once placed in an external magnetic field. Slow spinning around the magic angle axis is therefore efficient at removing magnetic field alignment of the Pf1, analogous to what was used previously for bicelles.38,77,78 The slowest stable MAS spinning rate achievable on our Bruker NMR probehead was ca 620 Hz, and this rate was used for measurement of chemical shifts under isotropic conditions. Besides the effect of random noise, the main uncertainty introduced when comparing chemical shifts recorded for the static and MAS samples then relates to small differences in temperature. Temperature control of the MAS probe is relatively crude, and the effective sample temperature was determined a posteriori, in the manner described below, followed by small corrections of these chemical shifts using their experimentally established temperature coefficients (Table S1).
To determine the temperature difference between the aligned and MAS samples, we calculated the 1HN RCSA values predicted for a uniform CSA tensor of the magnitude determined previously37 for each of the alignment tensors determined above. By plotting the difference between predicted RCSA and experimental values against the proton chemical shift temperature coefficients (SI Figure S5), a precise measure for the temperature difference between the MAS and static samples is obtained, and this procedure will also reveal any potential problems with chemical shift referencing between the two measurements. MAS spectra for the six different mutants were recorded over the time span of more than a year, and differences between the MAS and static sample temperatures ranged from +0.45 to +1.3 °C. The experimental amide 15N RCSA were corrected as follows:
| (16) |
where Δδ and Δδexp are the corrected and raw RCSA respectively, c is the 15N linear temperature coefficient (SI Table S1), and ε accounts for small problems with the chemical shift referencing, resulting from the fact that the water resonance position, used for indirect referencing of the 1H and 15N chemical shifts, can vary with the precise electronic tuning of the cryogenic probehead used;79 ΔT is the temperature difference as listed in SI Table S2. Based on reproducibility of both the static and MAS 15N chemical shift measurements, the experimental random uncertainty in Δδ is estimated at ±0.3 Hz, or ±5 ppb.
Rotational diffusion tensor determination
The rotational diffusion tensor for the 2H/15N/13C-labeled K4AK19EV42E GB3 mutant in H2O was determined by optimizing its trace, degree of axial asymmetry, and orientation relative to the NMR-refined GB3 structure (PDB entry 2OED)61 such that it yielded a best fit of the experimental R2/R1 ratios. R2 and R1 rates were calculated using expressions for both axially symmetric and asymmetric diffusion tensors75,80,81 but, as found previously,73 ,83 the fully asymmetric diffusion tensor did not result in an improvement of the fit that statistically warranted the introduction of two additional parameters needed to describe this deviation from axial symmetry. The dipolar contributions from all atoms within 4 Å from the 15N nucleus were included in these R2 and R1 rate calculations. Although to first order the results are insensitive to the precise values of the CSA tensor components and N-H-bond length, uniform values based on a previous best estimate of (−109, 46, 63 ppm and 19° β angle) for the CSA tensor37 and 1.040 Å for the zero-point motion adjusted effective N-H bond length65 were used.
The thus obtained diffusion tensor values (Table 2), corresponding to an effective rotational correlation time tc = 3.19 ns and a diffusion anisotropy of D///D⊥ = 1.36, are in close agreement with results reported previously73,82 and yield an excellent correlation between observed and predicted R2/R1 ratios (RP = 0.97; Fig. S6). The diffusion tensor parameters are essentially indistinguishable from results obtained when using the analytic equations developed for the axially symmetric diffusion tensor83 (data not shown).
Table 2.
Rotational diffusion tensor for the K4AK19EV42E mutant of GB3a
| DXXb (×107s−1) | DYY (×107 s−1) | DZZ (×107 s−1) | θ(°) | φ(°) |
|---|---|---|---|---|
| 4.67 | 4.67 | 6.34 | 60.3 | 96.6 |
Values correspond to 95% H2O, 5% D2O at 298 K. The principal components of the diffusion tensor for T11KK19EV42E in 100% D2O, 283 K, are scaled down by 0.481 relative to values listed for K4AK19EV42E.
The DXX and DYY values are restrained to be the same, and θ and φ are polar coordinates for the unique axis of the tensor in the coordinate frame of PDB entry 2OED with the N-H orientations defined by our previous RDC analysis65 (SI, Table S8).
The rotational diffusion tensor asymmetry and principal axes orientations of the 15N/13C--labeled mutant T11KK19EV42E in D2O at 283 K were assumed to be the same as those in H2O, but the tumbling time under these higher viscosity conditions is much longer, and only the trace of the diffusion tensor was treated as a variable in the fit of the 15N-2H relaxation rates. Best fitting of the 15N-{2H} R1 and R2 rates, while excluding residues for which the temperature dependence of R2 was indicative of an exchange broadening process (see below), yielded an effective correlation time of 6.63 ns (see SI for details). This value is somewhat larger than the value of 5.94 ns expected on the basis of the increased viscosity at this lower temperature of D2O, comparing to the value of 3.19 ns measured at 25 °C in H2O. The longer correlation time is likely caused by the higher protein concentration of the sample used in D2O (2.5 mM) than in H2O (0.8 mM). In fact, if the prediction were based on relaxation data measured for another mutant (K19AD47K) at 4.0 mM, an effective correlation time of 6.43 ns was obtained. When deriving the rotational correlation time from five residual amide 15N-1H sites (E27, F30, T44, T51, and F52) in T11KK19EV42E, whose protons had not back-exchanged to 2H after several weeks, a restrained fit of their R2/R1 ratios (keeping the orientation and asymmetry of the diffusion tensor again fixed at the values measured in H2O solution) yields τc = 6.5±0.2 ns.
Cross-correlated relaxation rates
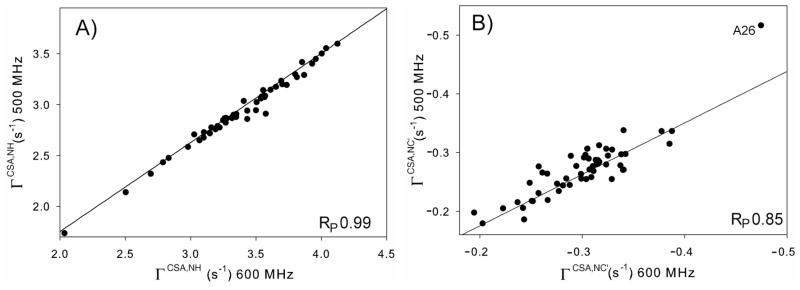
The 15N CSA/N-H dipole cross-correlation rates, ΓCSA,NH, were measured at 600 MHz 1H frequency from the relative 15N-{1H} doublet intensities, obtained in a constant-time 1H-15N HSQC experiment (Figure S2, S10). Analysis of data recorded with constant-time evolution periods of 81.6 ms and 161.6 ms yielded essentially the same rates (SI Figure S7). The ΓCSA,NH cross-correlation rates were also measured at 500 MHz 1H frequency, using a 81.6 ms constant-time duration. The rates derived from the measurements at the two fields correlate very well with each other (Pearson’s correlation coefficient RP = 0.99) and the slope of 0.87 falls very close to the theoretical value of 0.88 calculated for a protein with a tumbling time of 3.19 ns (Figure 2A). Based on the pairwise root mean square deviation (RMSD) from the expected linear correlation, the error in the 600 MHz cross correlation rates was estimated to be ~0.05 s−1, i.e., <2% of the observed rates. As described in the Materials and Methods section, due to peak overlap the cross-correlated relaxation rates of E24 and T25 were measured from a different mutant, K19AV42ED47K, and scaled by 1.086 to account for tumbling time differences between the samples. The need for a scaling factor raises the concern that transient intermolecular interactions in this mutant, responsible for the apparent increase in rotational correlation time, could also impact the diffusion tensor anisotropy and orientation. However the RMSD between the 15N CSA/15N-1H ΓCSA,DD values measured for the two samples (after rescaling by 1.086) equals 0.05 s−1, and therefore is completely dominated by the experimental error. This indicates that the impact of transient intermolecular interactions on the diffusion tensor orientation and anisotropy falls well below the detection limit of our measurements.
Figure 2.
Correlation of transverse 15N CSA/15N-1H dipole cross-correlation rates (A) and transverse 15N CSA/15N-13C′ dipole cross-correlation rates (B), measured at 500 and 600 MHz 1H frequency. The solid lines correspond to the theoretical rate ratio of 0.88 for a 3.19 ns tumbling time. The outlier value measured for A26 in (B) is not included in the calculation of RP.
The 15N CSA/N-C′ dipole cross-correlation rates, ΓCSA,NC′, measured at both 600 and 500 MHz 1H frequency using the constant-time HSQC experiment of Figure S3, are much smaller than the ΓCSA,NH rates and therefore show considerably more scatter (RP = 0.85). However, the slope of 0.90 agrees well within experimental error with the ratio of 0.88 expected for a molecule tumbling with τc = 3.19 ns (Figure 2B). Based on the scatter observed in Figure 2B, the random measurement error was estimated to be 0.02 s−1, or 5–10% of the observed rates. Outlier ΓCSA,NC′ values measured for residue A26 were not included in calculating RP nor in the subsequent CSA fitting procedure. We attribute this outlier to the nearly identical chemical shifts of T25 13Cα and 13Cβ atoms (at 66.9 ppm), which result in incomplete decoupling of the 13C aliphatic carbons during the constant-time 15N evolution period to an extent that depends on the T25 13C′ spin state.
Relaxation of backbone amide 15N-{2H}
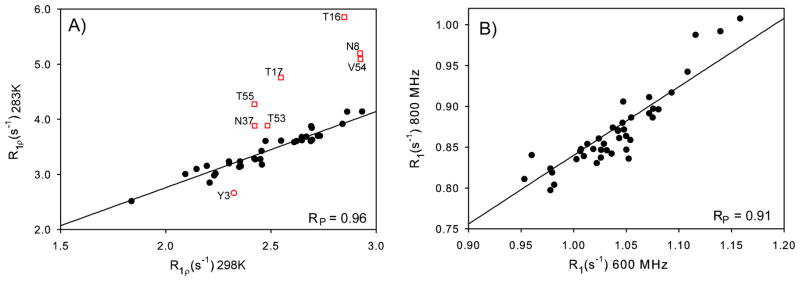
R1 and R1ρ relaxation rates of the T11KK19EV42E mutant, dissolved in 100% D2O, were measured at 600 MHz 1H frequency and 283 K, using detection of 1Hα resonances in a modified H(CACO)N experiment (SI Figure S4). To identify residues that may be affected by conformational exchange contributions to the R1ρ rates, which are expected to be temperature dependent, R1ρ rates were also measured at 298 K. A comparison of these rates (Figure 3A) shows outliers for N8, T16, T17, N37, T53 and T54, identifying these residues as potentially having substantial Rex contributions to their R1ρ rate at 283 K, but which due to the faster rates of these processes at 298 K become much smaller at the higher temperature. The estimated measurement error based on the scatter observed in Fig. 3A (excluding the outliers) is 0.10 s−1, or 3–5% of the observed rates. The slope of 1.38±0.07 is consistent with the factor of 1.36 expected for the change in D2O viscosity with temperature.
Figure 3.
Correlation between relaxation rates measured for 15N-{2H} groups. (A) 15N R1ρ rates, measured at 600 MHz 1H frequency, for T11KK19EV42E in 100% D2O at 283 K and 298 K, both at 600 MHz 1H frequency. Values from residues affected by conformational exchange are plotted as red squares; the rate measured for Y3 at 283 K was affected by overlap of its 1Hα chemical shift with the residual water signal. The solid line is the best linear fit and has a slope of 1.38. (B) 15N R1 rates of the same sample at 283 K, measured at magnetic fields corresponding to 600 and 800 MHz 1H frequencies. The solid line corresponds to the theoretical ratio of 0.84 for a tumbling time of 6.6 ns.
The 15N-{2H} R1 rates of the same sample were also measured at 800 MHz and 283 K, and correlate well with the 600 MHz data (Figure 3B). The scatter observed in that figure indicates a random measurement error of 0.018 s−1, which corresponds to ca 2%. We note that the correlation between R1 rates measured at different fields is not expected to be completely linear for 15N nuclei with different CSA tensors, with varying contributions from remote protons and a non-isotropic diffusion tensor, and therefore the scatter relative to a linear correlation provides an upper limit for the random error in R1.
Due to the mass difference between 1H and 2H, the effective bond lengths of N-H and N-D are affected differently by their zero-point motions. The effect of zero point motions on the 15N-1H dipolar coupling, often expressed as a change in effective N-H bond length, previously has been studied by both quantum chemical calculations66 and experimentally derived RDCs.65 Here, we assume the equilibrium bond length of N-D, the length corresponding to the electron energy minimum, to be the same as that of the N-H bond since the electron energy is independent of the atomic mass. The amplitude of bond stretching motions is inversely proportional to the square root of the reduced mass of N-H or N-D, indicating a 27% reduction in the amplitude of N-D zero point bond stretching motions compared to N-H, reducing the increase in effective bond length, reff = <rNH−3>−1/3, from 0.007 for N-H to 0.005.
The change in effective dipolar coupling resulting from zero-point librational motion was estimated for the model compound NMA using normal mode analysis, in the manner previously utilized by Case,66 resulting in a 4.9% decrease in dipolar coupling, or an increase of 0.017 Å to 1.030 Å for the effective 15N-2H bond length, slightly shorter than the effective bond length of 1.040 Å for 15N-1H (Table 3). This 1.030 Å N-D bond length was used in all subsequent analyses. In principle, the substitution of 1H by 2H also perturbs the 15N CSA value. However, as found by Tang and Case in their quantum computational analysis,70 the 15N CSA tensor orientation fluctuations are dominated by the adjacent heavier carbon atoms and not by motions of the amide proton or deuterium relative to the peptide bond, suggesting that the effect of zero-point motions on the CSA tensor is comparable for 15N-2H and 15N-1H sites. Therefore, this difference has been ignored in the fitting of the 15N-2H relaxation data.
Table 3.
Effective N-H and N-D bond lengths of backbone amide groups
| reqa (Å) | Δrstrb (Å) | Δrlibc (Å) | reffd (Å) | |
|---|---|---|---|---|
| N-H | 1.008 ± 0.006 | 0.007e | 0.025e | 1.040e ± 0.006 |
| N-D | 1.008 ± 0.006 | 0.005 | 0.017 | 1.030 ± 0.006 |
Equilibrium bond length determined from RDCs.65
Effective bond length increase due to zero point bond stretching motion, obtained from B3LYP/6-31G** QM calculations on N-methylacetamide in a water continuum solvent.
Effective bond length increase due to zero point bond librational motion, obtained from normal mode analysis.
Effective bond length defined as reff = req + Δrstr + Δrlib.
from reference 66
Extracting residue-specific 15N CSA tensors
In our analysis, we simultaneously fit the 15N RCSAs under six different alignment orientations, the 15N CSA/N-H and 15N CSA/N-C′ cross-correlated transverse relaxation rates, and the R1 rates of the 15N-2H groups at two magnetic fields, 14.1 and 18.8 T. Under the common assumption that the 15N CSA tensor is symmetric with respect to the peptide plane,40 one of its principal components must be oriented orthogonal to this plane, and the orientation of the tensor is then defined by a single angle, β, between the N-H bond and its nearest in-plane principal component, which corresponds to the least shielded component, σZZ, of the tensor (SI, Scheme S1). With the restriction that σXX + σYY + σZZ = 0, two parameters suffice to define its principal components, and a total of three parameters therefore suffice to fully define the tensor. In the fit of the experimental data, two global parameters are optimized as well: the tumbling time of 15N-2H groups and a uniform generalized order parameter, S2, describing all internal motions other than the zero-point librations and vibrations.
The backbone dynamics of GB3 and its nearly identical homolog GB1 previously has been studied extensively by both relaxation44,73,82 and RDC-based methods64,65,84–89. Overall, the protein is found to be relatively rigid with the exception of a number of residues located in turn and loop regions, connecting elements of secondary structure. After excluding the residues found to have the lowest order parameters in the earlier relaxation study by Hall and Fushman,73 including Q2, K10-E15, A20, D40-G41 and A48, a uniform order parameter, S2 = 0.903, provided a best fit to all experimental data, well within their respective measurement errors. Although use of residue-specific S2 values in the fitting procedure slightly lowers the χ2 of the fit, introduction of such additional adjustable parameters proved unwarranted on the basis of F statistics, and also resulted in a slightly larger spread of the extracted CSA parameters and worse cross validation statistics. Use of a uniform order parameter in our analysis is conceptually equivalent to the assumption of uniform backbone dynamics by Wylie et al.43 when deriving CSA values from the spinning side-band analysis observed for polycrystalline protein under slow magic angle spinning conditions.
In principle, the spectral density terms resulting from internal backbone dynamics also contributes to the relaxation rates, in particular to R1. However, as reported by Hall and Fushman,73 the longest internal correlation time τe in the well-structured region of the protein used for our analysis is 56 ps. For an average S2 value of 0.903, this corresponds to an R1 contribution less than 1.2% compared to that from overall tumbling.90 For R1 relaxation of 15N-{2H} nuclei in the protein dissolved in D2O at 10 °C (τc = 6.6 ns), the fractional contribution from internal dynamics becomes even smaller (<0.6%) due to the relatively large R1 contribution resulting from the overall tumbling 6J(ωN+ωD) term (taking into account the opposite signs of ωN and ωD). These contributions are smaller than the experimental measurement error, and therefore have been neglected.
Overall, for N residues, our fitting procedure then uses 3N+2 adjustable parameters, with nearly 10N experimental observables (a few residues lack one or two observables due to resonance overlap). Details of the data fitting procedure are presented in the Supporting Information.
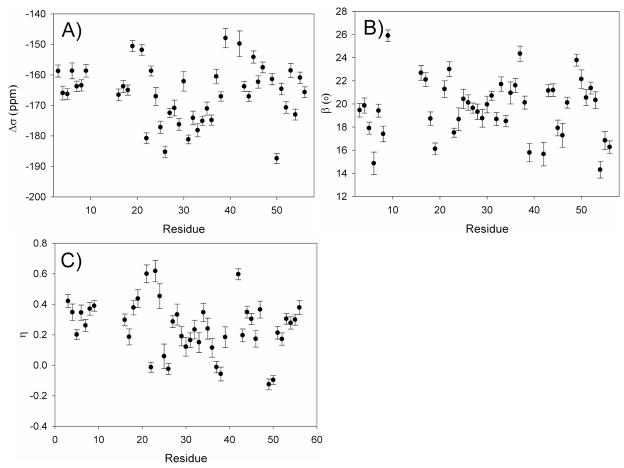
Residue-specific 15N CSA parameters are shown in Figure 4 (Table S3). The shielding anisotropy, Δσ defined as σZZ − (σXX + σYY)/2,91 shows an average value of −166 ppm with a standard deviation of 9 ppm over all residues included in the analysis. This average is very close to the value of −165 ± 7 ppm, determined by slow magic angle spinning solid state NMR for the closely homologous protein GB143 (averaged over the 33 amides for which values are obtained in both studies). With a correlation coefficient, RP = 0.8, the Δσ values extracted from our data correlate fairly well with these values too (SI, Figure S8), but less well with values derived by the same group using the ROCSA method (RP = 0.5), which also are systematically smaller.42 We note, however, that neither set of solid-state NMR values accounts for the effect of backbone internal dynamics. Assuming that the amplitude of such dynamics is comparable in solution and in the solid state, our solution values which correspond to the absence of thermal motions, need to be scaled by the average order parameter, S =√0.903, prior to comparison to the solid state NMR data and the average Δσ (158 ppm) then falls in between the ROCSA and slow MAS results.
Figure 4.
Residue specific 15N CSA parameters derived from RCSA and relaxation data: (A) Δσ = σZZ − (σXX + σYY)/2; (B) the angle β between σZZ and the N-H bond vector, while σXX and σZZ are forced to fall in the C′-N-HN plane; (C) the CSA asymmetry, η, defined as (σYY − σXX)/σZZ. Error bars correspond to the results of 100 Monte Carlo calculations, where Gaussian noise with an amplitude corresponding to the estimated root-mean-square error was added to the experimental input data.
The average CSA value obtained from our study falls close to the value of −164 ± 19 obtained by Hall and Fushman from auto- and cross-relaxation rates measured for the same protein at five magnetic field strengths (this average extends over the same group of residues evaluated in our study and has been scaled by 1.06 to eliminate the zero-point librational contribution). Site-to-site variations are considerably smaller in our study, suggesting that RCSA and R1 rates of 15N-{2H} provide useful independent additional constraints for CSA fitting, thereby reducing the effect of random and systematic measurement errors.
Our solution NMR measurements also yield the orientation of the 15N CSA tensor relative to the peptide group. With β = 19.6 ± 2.5°, we find tight clustering of the orientations of the least shielded σZZ axis relative to the N-H bond. However, considerable variation in the shielding asymmetry parameter η, defined as (σYY − σXX)/σZZ,91 is observed: η = 0.23 ± 0.17 for α-helix, and η = 0.31 ± 0.11 for β-sheet. Interestingly, for six residues (five of them outside regions of regular secondary structure, SI Table S3) we find that the most shielded CSA component is orthogonal to the peptide plane, and following IUPAC nomenclature the X and Y axis of the CSA tensor would need to be interchanged.91 However, in order to facilitate comparison of the different amide CSA tensors, we retain the same orientation, resulting in negative η values for these residues.
Significant correlations between the CSA parameters and the type of secondary structure are observed in our study. For β-strand residues, we find <Δσ> = −162 ± 6 ppm, whereas considerably larger CSA is observed for α-helical amide groups: <Δσ> = −173 ± 7 ppm. Statistically significant differences between CSA parameters in β-strand and α-helical residues pertain to all three components (Table 4). By including the variation in isotropic chemical shift, we can now evaluate which components of the shift tensor are affected most by secondary structure. Using δii = δisotropic − σii, yields average values of δZZ = 230 ± 7, δXX = 52 ± 8, δYY =85 ± 9 ppm for β-sheet and 236 ± 6, 49 ± 8, 76 ± 10 ppm for the α-helix, indicating that the 15N nucleus in β-strand, on average, is more shielded in the Z direction, and less shielded in X (3 ppm) and Y directions (9 ppm) (scheme S1). These data indicate that the, on average, downfield isotropic 15N shift in β-sheet relative to α-helix results from decreased shielding in the X and Y directions, which outweigh an actual increase in shielding in the Z direction.
Table 4.
Fitted CSA tensors for α-helix, β-strand and overall protein.
| σZZ (ppm) | σXX (ppm) | σYY (ppm) | β(°) | Δσ (ppm) | η | |
|---|---|---|---|---|---|---|
| α-helixa | −115±5 | 71±8 | 44±11 | 19.8±1.2 | −173±7 | 0.23±0.17 |
| β-stranda | −108±4 | 71±4 | 38±7 | 18.8±2.4 | −162±6 | 0.31±0.11 |
| Alla | −111±8 | 69±11 | 42±9 | 19.6±2.5 | −166±9 | 0.25±0.17 |
Average and standard deviation for CSA tensor components experimentally derived for the backbone amide 15N nuclei in GB3. Values apply to the absence of thermal motions, i.e., Δσ values observed by solid state NMR are expected to be scaled down by √(S2) ≈ 0.95 relative to values reported in the table. Three parameters (Δσ, η, β) are fitted for each 15N site. The root-mean-square deviations from the reported averaged values reflect the CSA variability in α-helix, β-strand, and all residues.
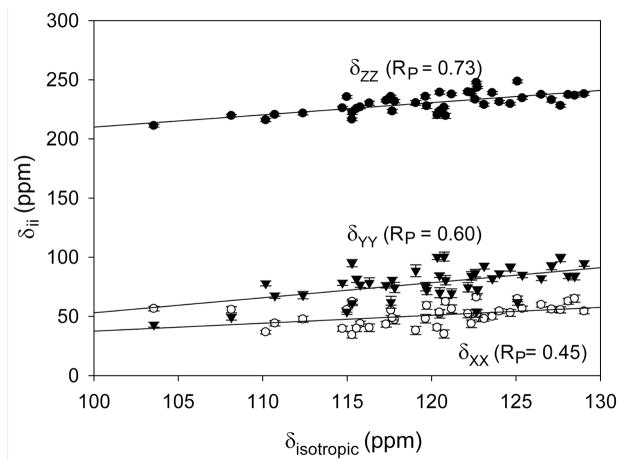
Previously, a correlation between δii values and isotropic chemical shifts was noted for backbone amides in ubiquitin.40 Somewhat stronger correlations are found in our present study of GB3 (Figure 5) where, for example, the correlation coefficient RP between δZZ and δisotropic equals 0.73, versus 0.41 for ubiquitin.
Figure 5.
Correlation between the principal components of the chemical shift tensor δii (i=X,Y,Z) and the isotropic chemical shift δisotropic. The three best fitted lines correspond to δZZ = 1.03δisotropic + 107 ppm, δYY = 1.33δisotropic − 82 ppm and δXX = 0.63δisotropic − 25 ppm.
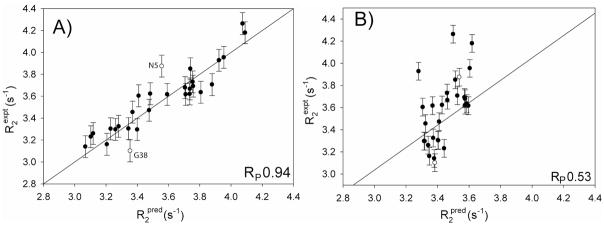
Validation of CSA parameters
To validate the quality of the residue-specific CSA values, derived in our study, the R2 rates of 15N-{2H} backbone amides, which are dominated by CSA relaxation, were calculated on the basis of the above derived CSA tensors and compared to the experimental values. Note that these experimental 15N-{2H} R2 rates were not included at any stage in deriving the CSA values. A strong correlation (RP = 0.94) between observed and predicted rates is obtained, compared with RP = 0.53 when a uniform CSA (average of the residue-specific CSA values) tensor is used (Figure 6). For an isolated 15N-{2H} two-spin system subject to isotropic tumbling, the predicted R2 rates are uniform when a uniform CSA tensor is utilized. The small variation in predicted R2 rates, even for a uniform CSA tensor (Figure 6B) results from anisotropic molecular tumbling, and also from small contributions from passive 1H and 13C nuclei. The correlation coefficient of 0.94 is also higher than the corresponding value of 0.84 obtained when correlating the experimental and predicted R2 rates using the solid state CSA values of the homologous GB1 protein (SI, Figure S9A). These latter data lack information on the orientation of the CSA tensor within the peptidyl frame, and therefore a uniform value β = 19.6° was assumed.
Figure 6.
Correlation between experimental and predicted R2 rates of 15N-{2H} groups. Predicted rates were calculated from (A) experimental site-specific 15N CSA values, or (B) from using a uniform, averaged CSA tensor. The solid line in panel A represents the best linear fit with zero intercept and has a slope of 1.00 (excluding two outliers, N5 and G38).
Considering that the root-mean-square variation in β angle in our residue-specific CSA values is only 2.5°, it is interesting to explore the impact of fixing this parameter rather than letting it vary on a residue-by-residue basis. Therefore, we also carried out a fit of all experimental data (excepting again the 15N-2H R2 data) while fixing β at 19.6°, while allowing Δσ and η to vary residue by residue. When using the CSA parameters resulting from this approach to predicted the 15N-2H R2 rates, a somewhat lower correlation with the experimental rates is observed (RP = 0.90; SI Figure S9B). Even though the R2 value to first order is not sensitive to the orientation of the CSA tensor, restricting β during the fitting procedure results in small changes of the best fitted principal components of the CSA tensors. The lower agreement between experimental and predicted R2 values obtained with a fixed β angle confirms that the small β variations obtained when letting this parameter float do not result from random measurement error.
For the vast majority of residues, the most shielded CSA tensor component is located in the peptide plane, nearly parallel to the N-C′ bond, but the difference in magnitude relative to the component orthogonal to the peptide plane is modest. To assess the significance of permitting asymmetry as a variable parameter in the fit, we also carried out the entire CSA fitting procedure while fixing the tensor to be axially symmetric, i.e. η = 0, and use the resulting CSA tensors again to predict the R2 values. Pearson’s correlation coefficient RP between the experimental and predicted R2 values then drops to 0.86 (SI Figure S9C), again significantly lower than the RP = 0.94 value obtained when η is a fitted parameter. The effect of asymmetry of the CSA tensor on relaxation rates scales with (1+η2/3), and in this case the lower correlation appears to be dominated by the neglect of the η2/3 component, rather than the small changes in Δσ caused by the η = 0 restriction during the fit.
Orientation of 15N CSA tensor
Above, the principal axes of σXX and σYY were restrained in our fitting such that one component is orthogonal to the peptide plane. Removal of this restriction increases the number of adjustable parameters to five, but more importantly makes it difficult to establish the precise orientations of the σXX and σYY axes when the difference between σXX and σYY is small, as applies for many of the backbone amide 15N nuclei in GB3. Therefore, in order to validate the assumption that the CSA tensor is symmetric with respect to the peptide plane, we forced the CSA tensor values and orientations relative to their respective peptide plane to be uniform within each type of secondary structure. This latter clause reduces the ratio of the number of fitted parameters over the number of experimental observables and thereby increases the robustness of the analysis.
Three angles, together with Δσ and η, are fitted simultaneously for all helical residues, and similarly for all β-strand residues. For the fit, the generalized order parameter S2 is fixed at the above derived value of 0.903, and the tumbling time for the protein in D2O (required for analysis of the 15N-{2H} R1 data) is fixed at the above derived value of 6.63 ns. The principal components and orientations obtained when following this procedure (SI Table S6) confirm that the CSA amplitudes and β angles are consistent with the averages obtained from their respective site specific values (Table 4). The fitting procedure also confirms that the orientation of σYY remains nearly perpendicular to the peptide plane, deviating from orthogonality by 2.5° and 0.6° for α-helix and β strand, respectively, while σXX essentially remains in the peptide plane. This result supports the validity of the assumption made in our site-specific 15N CSA analysis that the CSA tensor to a very good approximation is symmetric with respect to the peptide plane, despite the chiral nature of the adjacent Cα carbons. Note, however, that the average orientation of the Y axis of the CSA tensor, determined for each type of secondary structure, is dominated by residues with the largest η value, for which the χ2 is far more sensitive to this orientation than for small η values, with the definition of its orientation in the XY plane becoming arbitrary for η=0. Larger deviations from orthogonality to the peptide plane for small η values are therefore not excluded by our data.
Origin of 15N CSA variations
The ca 10 ppm larger 15N CSA observed in α-helix compared to β-strand (Table 4) confirms the effect of the backbone torsion angles on the CSA tensor, and agrees closely with the 9 ppm difference found by slow-spinning solid state NMR.92 This value is opposite in sign and much smaller than the average −24 ppm difference obtained from vacuum calculations on partially geometry-optimized peptide fragments19 but close to the +4 ppm difference obtained from lower basis set calculations on hydrated dipeptide models by Cai et al.20 In order to further evaluate the factors underlying the differences in CSA, which are known to be impacted by a wide variety of factors, we carried out additional DFT calculations for closely related fragments at a high level of theory. Even though the effect of hydration then cannot easily be included, these calculations are aimed to evaluate the trends behind the experimentally observed differences in CSA.
Our DFT calculations on formyl-(Ala)2 yields chemical shift tensor components (δXX, δYY and δZZ) of 219, 30, 97 ppm for the helical conformation (using ψ and φ torsion angles of T25 and A26) and 218, 36, 98 ppm for a β-strand (ψ and φ angles of F52-T53 in GB3) conformation (Table S7). Even though the calculated values deviate substantially from the experimental ones, likely caused by the simplicity of the model, the difference between α-helix and β-strand geometries points in the same direction as the experimental results.
Two GB3 residues, V21 and A23, show exceptionally high η values, 0.62 and 0.60 respectively (Table S3). Interestingly, DFT calculations on formyl-(Ala)2 with φ, ψ angles of A20-V21 and D22-A23 also yield larger η values, 0.84 and 0.86, than computed for α-helical (0.64) and β-strand (0.61) conformations. The (φ, ψ) angles are (−154°, 159°) for A20, (−77°,−24°) for V21, (−152°, 168°) for D22, and (−67°, −36°) for A23, suggesting that an extended followed by an α-helical conformation peptide linkage tends to result in larger η values. Exceptionally low experimental η values are found for G38 (−0.06) and K50 (−0.10). DFT calculations on formyl-(Ala)2 with the backbone torsion angles of T49-K50 and formyl-Ala-Gly with the N37-G38 backbone torsion angles yield η values of 0.23 and 0.28, suggesting that (φ, ψ) combinations of (−112°, 3°), (51°, 43°) for T49-K50 and similarly (−101°, 10°), (72°, 21°) for N37-G38 generate small η values. It is worth noting that the DFT calculations in this study are oversimplified as other effects such as sidechain types and torsion angles, long range electrostatics, solvent interaction, etc., are ignored. Instead of attempting to reproduce the experimental CSA values, these calculations aim to simply explore the importance of the backbone (φ, ψ) angles. The close correspondence between trends seen in calculated CSA values and experimentally observed values points to a dominant effect from the backbone torsion angles on the CSA magnitude and asymmetry (SI Table S7).
Discussion
The value of the 15N backbone amide chemical shift anisotropy tensor affects both solid state NMR structural studies, in particular those based on analysis of 15N chemical shifts in oriented membrane proteins as studied by PISEMA analysis, as well as the quantitative evaluation of protein dynamics from 15N relaxation rates measured by solution NMR. The precise eigenvalues and orientation of the 15N CSA also affect the degree of cancellation between dipolar and CSA interactions which underlies the important TROSY experiment,25 and determines the field strength at which the minimum 15N TROSY line width is reached, as well as the maximum degree of cancellation of dipolar and CSA contributions possible for an isolated 15N-1H spin pair. Below, we briefly discuss the impact of 15N CSA variations on these latter two areas.
Impact on 15N relaxation studies
Most prior analyses of protein backbone dynamics from 15N relaxation data assume an axially symmetric 15N CSA tensor with a Δσ value of either −160 or −170 ppm. A second important parameter includes the length of the N-H bond vector, often assumed to be 1.02 Å. However, when factoring out the nearly uniform attenuation of the 15N-1H dipolar coupling caused by zero-point librations of the N-H bond, this becomes equivalent to using a 1.04 Å effective N-H bond length,66,93 accompanied by a concomitant increase in the order parameters, S2, extracted from NMR relaxation rates.
When using a 1.04-Å effective N-H bond length, our data correspond to an average 15N Δσ value of −166 ppm, which represents the effective CSA averaged over the zero-point backbone motions, i.e., the CSA that would be measured at 0 K, in the absence of thermally activated motions. Considering that the difference between α-helical and β-sheet residues is quite pronounced, approximately two standard deviations, a better choice in 15N relaxation analysis is the use of secondary structure-specific CSA tensors, with Δσ = −162 ppm and η = 0.31 for β-sheet residues, and Δσ = −173 ppm, η = 0.23 for helical residues. If instead the non-librationally-corrected N-H bond length of 1.015 Å were used, this should be accompanied by an average Δσ value of −179 ppm, and will then result in a uniform 7% reduction in derived order parameters (13.5% for S2). It is important to note that this −179 ppm CSA value does not correspond to the CSA of the protein at 0 K and has no direct physical meaning; instead it is an artificial number used to match the CSA order parameter with the dipole-dipole order parameter if one were to use a non-librationally-corrected rNH =1.015 Å value.
Prior analyses of NMR relaxation data and their field dependence alternately have been interpreted as indicative of rather large residue-by-residue variations in the 15N CSA tensor,33,44 or as evidence for much higher CSA uniformity.35,39 Much of the difference in the conclusions from the very similar experimental data appears to relate to the magnitude of the experimental errors assumed in the relaxation measurements, with larger experimental errors requiring less variation in the CSA parameters to fit the experimental data. Although the random measurement error is easily estimated from reproducibility of experimental results, quantitative estimates of systematic errors are difficult to make as their origins in many cases are unknown, and neither conclusion appears definitive in the absence of such information.
Cross-correlated relaxation measurements yield additional information on the orientation of the CSA tensor. Provided that relaxation interference between the CSA and multiple dipolar interactions can be measured separately, such measurements also can yield the deviation from axial symmetry of the 15N CSA tensor. Measurements for ubiquitin by Loth et al, for example, show a correlation between the tensor asymmetry, η, and the isotropic 15N chemical shift.40 On the other hand, two separate sets of solid state NMR measurements of the 15N CSA tensors in polycrystalline GB1, one using the recoupling of chemical shift anisotropy or ROCSA method,42,94 and a more recent one that uses slow magic angle spinning sideband analysis,43 do not show any such correlation between η and δiso (Figure S1). Although these latter two sets of measurements correlate fairly well with one another (RP = 0.77), the ROCSA method Δσ values are systematically smaller than the more recent values by nearly 10%, and therefore don’t quite answer the question about how large the 15N CSA truly is. Our current measurements on GB3 agree most closely with the slow magic angle spinning results on the homologous GB1 protein, and also lack any significant correlation between η and δiso. Instead, it appears η is dominated by backbone torsion angles. In particular, the only non-Gly residue with positive values for its φ backbone torsion angle shows an inverted sign for η, when keeping σYY oriented orthogonal to the peptide plane. Similarly, the measurements by Loth et al. also yield η values much below average for all three non-Gly residues in ubiquitin with positive φ angles.
The effect of asymmetry of the CSA tensor on the R1 and R2 relaxation rates scales with (1+η2/3), equivalent to scaling the magnitude of the CSA by (1+η2/3)1/2. For most residues, η≤0.4, and the asymmetry increases the effective magnitude of the CSA by less than 2.6%, or ~4 ppm. However, for some residues, such as V21 and A23 in GB3, η>0.6 and the tensor asymmetry increases the effective magnitude by as much as 10 ppm.
As was the case for the prior solid-state NMR studies of 15N CSA in polycrystalline proteins, our analysis assumes that the observed RCSA values are scaled uniformly by a generalized order parameter, S, which has a uniform value (√0.903) for all residues considered. Residues that clearly exhibit elevated internal dynamics based on prior relaxation measurements therefore were excluded from our analysis. As expected, if in addition to the CSA tensor, S2 is treated as a residue-specific adjustable parameter, a better fit to the NMR data is obtained. However, the nearly 30% improvement in terms of χ2 statistics is insufficient to warrant inclusion of these extra variables in the fitting procedure (F value equals 2.57, smaller than the critical value of F(1, 6, 0.05) = 5.99).95 Notably, the spread in the extracted CSA values increases from ±9 to ±16 ppm, and for most residues then correlates inversely with the value of S (data not shown). Because such an inverse correlation clearly points to overfitting of the experimental data, use of a residue-specific S2 value is not warranted for the well-ordered regions of GB3. However, true variations in S2 will contribute to the variability of the observed CSA magnitude, and the variability in Δσ extracted from our data, as well as that seen in the solid state NMR results, therefore provides an upper limit for the true variability.
It previously has been shown from both NMR relaxation measurements and molecular dynamcis simulations96 as well as RDC measurements.61,64,84 that motions of the N-H vector are axially asymmetric, with largest amplitudes around the Cα-Cα axis (so-called γ motions in the Gaussian axial fluctuation or GAF model). In contrast to isotropic motion, anisotropic motion scales the CSA components σXX, σYY, σZZ differentially. However, in practice, it is very difficult to separate isotropic from anisotropic motions for two reasons: First, zero-point librations, though anisotropic, scale σXX, σYY, σZZ more uniformly than thermal motions,70 but separating anisotropic zero point motion from thermally activated motions is experimentally difficult. Second, while in the fitting of the relaxation and RCSA data, the anisotropic internal motion effectively makes the dipole-dipole interaction tensor asymmetric, whereas the contribution to the CSA tensor is virtually indistinguishable from a change in asymmetry (and magnitude) of the already asymmetric CSA tensor. When imposing uniform motional asymmetry of all peptide plane motions using the GAF model84,96 while restraining the total order parameter S2 at 0.903, essentially no change of the total fitting error is obtained, even though the magnitudes of σZZ and σYY increase slightly with increasing amplitudes of the γ motions around the Cα-Cα axis (and decreasing amplitudes of motions orthogonal to this axis to keep S2 = 0.903; data not shown).
It also is worth pointing out that random experimental errors in any of our measurements will generally increase the spread in the extracted CSA values. Therefore, even disregarding the effect of variations in S2, the true spread in CSA values is expected to be somewhat smaller than the standard deviation of ±9 ppm reflected in the values shown in Figure 4A (±6–7 ppm within sheet or helix).
As highlighted by Damberg et al.,39 the modelfree generalized order parameters extracted from NMR relaxation measurements vary with the value of the assumed Δσ parameter, and in particular at high magnetic field strengths (e.g. 800 or 900 MHz 1H frequency) extracted S2 values are quite sensitive to Δσ.
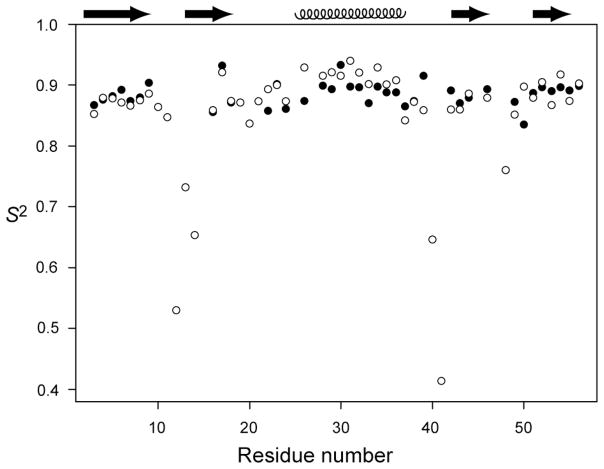
To explore the impact of our experimental CSA variation on S2, we performed the standard model-free analysis90,97 using our site-specific 15N CSA values to fit experimental R1(15N-1H) and R2(15N-1H) values and the NOE data from Hall and Fushman 83 with two parameters, the local internal motion time constant, τe and S2. The values obtained for the 30 residues located in GB3’s β-sheet and α-helix, determined using site-specific 15N CSA values, are highly homogeneous, yielding S2 = 0.888±0.017. For the purpose of comparison, when performing the same model-free analysis on the same set of amides, but using a uniform, averaged 15N CSA tensor, considerably more variation is seen: S2 = 0.892±0.025 (Figure 7). The nearly 50% increase in S2 variation when using uniform instead of site-specific 15N CSA strongly suggests that variations in the extracted S2 values among the well structured residues are significantly affected by variations in CSA. We note that the remaining small spread of ±0.017 in S2 includes contributions from random measurement errors in the 15N R1 and R2 rates, as well as from residual uncertainty in the CSA values extracted in our present study. For example, the rmsd value when using site-specific CSA values is dominated by the high order parameter obtained for F30, for which a far below average value of Δσ is obtained. However, we note that for this residue no 15N-{2H} R1 input data were available, and its CSA value is therefore less well determined than for most other residues. The S2 spread of ±0.017 therefore represents an upper estimate for the true variation in backbone order, indicating that dynamic backbone behavior on the fast time scale in secondary structure regions of GB3, and presumably of many other proteins too, is considerably more homogeneous than indicated by previous NMR relaxation studies. At the same time, the small degree of variation observed for S2 (1.9%, or 1% for S) confirms that the assumption of a uniform S value is not unreasonable, and that the derived 15N CSA variation 5.4% is dominated by true site-to-site differences, and not by variations in dynamics.
Figure 7.
Order parameters, S2, from model-free analysis using uniform CSA (open circles) and site-specific CSA (filled circles) values. Site specific CSA values are only available for residues previously identified as rigid (see text). For the sake of completeness, the results obtained for the more flexible residues (using uniform CSA) are also shown.
Impact on 15N TROSY spectra
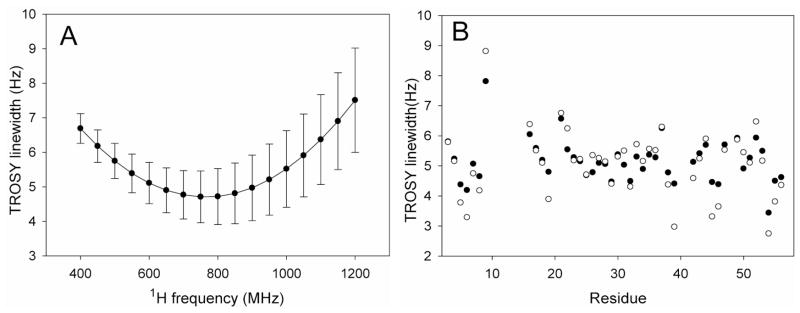
Most predictions of 15N resolution enhancement attainable with transverse relaxation optimized spectroscopy (TROSY)25 are based on the assumption of a uniform, axially symmetric 15N CSA tensor. Variations in the magnitude, asymmetry, and orientation of the 15N CSA tensor will impact the TROSY 15N line width, however, as well as the optimal field strength where the line width is narrowest. Indeed, considerable variation in the TROSY line widths, calculated when using the CSA values derived for GB3, manifests itself in a standard deviation that represents a significant fraction of the line width (Figure 8A). To eliminate small contributions from diffusion anisotropy or variations in order parameter, values are calculated under the assumption of isotropic diffusion with a tumbling time of 50 ns and a uniform S2 = 0.903. On average, the minimum line width is obtained at ca 800 MHz 1H frequency, well below the value of ca 1 GHz predicted when using earlier CSA parameter values,25 and as anticipated the variation in intrinsic line width increases with field strength. For example the standard deviation of the calculated line widths increases from 0.6 Hz (or 12%) at 600 MHz to 0.95 Hz (19%) at 900 MHz. The residue-specific TROSY peak line widths calculated for field strengths corresponding to 600 and 900 MHz 1H frequency show that for some residues the 15N TROSY line width is narrower at 600 MHz (e.g., V54 and T55), whereas for others predicted line widths are narrowest at 900 MHz (Figure 8B). Note that these intrinsic line widths neglect mechanisms that add a nearly field-independent contribution from dipolar couplings to 13C, 2H, and residual remote 1H nuclei, as well as the non-zero R1 relaxation rate of 1HN. As can be seen, the largest line width is predicted for the amide of G9 which is 53% (77%) larger than the average value at 600 (900) MHz 1H frequency, while the smallest one is found for V54, which is 33% (55%) below the average value predicted at 600 (900) MHz. G9 has the largest β angle 25.9° and V54 has the smallest β angle 14.3° (Figure 4B), highlighting the fact that the cancellation of dipolar and CSA contributions, which underlies the TROSY experiment, is more affected by variations in the angle β than by differences in the magnitude or asymmetry of the CSA tensor. For example, if the β angle is set to 19.6°, but the site-specific CSA values are used to calculate the TROSY line widths, the rms variation in line width drops from 0.6 to 0.41 Hz at 600 MHz or from 0.95 to 0.46 Hz at 900 MHz, and residues G9, and V54 are no longer outliers. The remaining line width variation then results from residue by residue variation in the CSA magnitude and asymmetry.
Figure 8.
Calculated TROSY line widths for 15N nuclei in GB3, assuming isotropic rotational diffusion with a correlation time of 50 ns, and idealized two-spin approximations for each amide group (i.e., ignoring the presence of other spins and relaxation mechanisms other than 15N CSA and 15N-1H dipolar), using experimentally derived CSA tensors and uniform S2 = 0.903 values. (A) Average TROSY line widths and standard deviations as a function of field strength. (B) Residue specific 15N TROSY line widths calculated for magnetic field strengths corresponding to 1H frequencies of 600 MHz (filled symbols) and 900 MHz (open symbols).
Supplementary Material
Acknowledgments
We thank Dennis A. Torchia and Jinfa Ying for helpful discussions, and Werner Maas and Jochem Struppe (Bruker Instruments) for help with the MAS measurements. This work was supported in part by the Intramural Research Program of the NIDDK, NIH, by the Intramural AIDS-Targeted Antiviral Program of the Office of the Director, NIH, and by NIH grants P41RR02301 (BRTP/NCRR) and P41GM66326 (NIGMS) to GC.
Footnotes
Supporting Information Available: A detailed description of the equations and protocols used for analysis of the relaxation and dipolar coupling data, three figures with pulse diagrams used for the measurement of cross-correlated relaxation and 15N-{2H} R1 and R2 relaxation rates; two figures comparing η and Δσ with solid state values reported for GB1, 6 figures correlating the difference between observed and expected Δδ(1H) with the 1H temperature coefficients; one figure comparing observed with best-fitted R2/R1 ratios; one figure comparing ΓCSA,NH values measured with two different transverse evolution delays; 3 figures correlating 15N-{2H} R2 experimental and predicted values; 2 figures showing experimental data used for deriving ΓCSA,NH and ΓCSA,NC′ values; one table with apparent 1H temperature coefficients; one table with the temperature differences for cryogenic and MAS probes; one table with experimentally derived Δσ, η, and β values; one table with experimental RCSA values; one table with experimental 15N-{1H} R1, R2, ΓCSA,NH and ΓCSA,NC′ values; one table listing the CSA tensors. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Berjanskii MV, Wishart DS. J Am Chem Soc. 2005;127:14970–14971. doi: 10.1021/ja054842f. [DOI] [PubMed] [Google Scholar]
- 2.Cavalli A, Salvatella X, Dobson CM, Vendruscolo M. Proc Natl Acad Sci U S A. 2007;104:9615–9620. doi: 10.1073/pnas.0610313104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.London RE, Wingad BD, Mueller GA. J Am Chem Soc. 2008;130:11097–11105. doi: 10.1021/ja802729t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vila JA, Aramini JM, Rossi P, Kuzin A, Su M, Seetharaman J, Xiao R, Tong L, Montelione GT, Scheraga HA. Proc Natl Acad Sci U S A. 2008;105:14389–14394. doi: 10.1073/pnas.0807105105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Villegas ME, Vila JA, Scheraga HA. J Biomol NMR. 2007;37:137–146. doi: 10.1007/s10858-006-9118-6. [DOI] [PubMed] [Google Scholar]
- 6.Shen Y, Delaglio F, Cornilescu G, Bax A. J Biomol NMR. 2009;44:213–223. doi: 10.1007/s10858-009-9333-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Saito H. Magn Reson Chem. 1986;24:835–852. [Google Scholar]
- 8.Wishart DS, Sykes BD, Richards FM. J Mol Biol. 1991;222:311–333. doi: 10.1016/0022-2836(91)90214-q. [DOI] [PubMed] [Google Scholar]
- 9.Case DA. J Biomol NMR. 1995;6:341–346. doi: 10.1007/BF00197633. [DOI] [PubMed] [Google Scholar]
- 10.Wagner G, Pardi A, Wuthrich K. J Am Chem Soc. 1983;105:5948–5949. [Google Scholar]
- 11.Williamson MP, Asakura T. J Magn Reson B. 1993;101:63–71. [Google Scholar]
- 12.Bim J, Poon A, Mao Y, Ramamoorthy A. J Am Chem Soc. 2004;126:8529–8534. doi: 10.1021/ja049879z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Birn J, Poon A, Ramamoorthy A. Biophys J. 2004;86:73A–73A. [Google Scholar]
- 14.Le HB, Oldfield E. J Phys Chem. 1996;100:16423–16428. [Google Scholar]
- 15.Brender JR, Taylor DM, Ramamoorthy A. J Am Chem Soc. 2001;123:914–922. doi: 10.1021/ja001980q. [DOI] [PubMed] [Google Scholar]
- 16.Wang YJ, Jardetzky O. J Am Chem Soc. 2002;124:14075–14084. doi: 10.1021/ja026811f. [DOI] [PubMed] [Google Scholar]
- 17.Xu XP, Case DA. Biopolymers. 2002;65:408–423. doi: 10.1002/bip.10276. [DOI] [PubMed] [Google Scholar]
- 18.Wang YJ, Jardetzky O. J Biomol NMR. 2004;28:327–340. doi: 10.1023/B:JNMR.0000015397.82032.2a. [DOI] [PubMed] [Google Scholar]
- 19.Poon A, Birn J, Ramamoorthy A. Journal of Physical Chemistry B. 2004;108:16577–16585. doi: 10.1021/jp0471913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cai L, Fushman D, Kosov DS. J Biomol NMR. 2008;41:77–88. doi: 10.1007/s10858-008-9241-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Waddell KW, Chekmenev EY, Wittebort RJ. J Am Chem Soc. 2005;127:9030–9035. doi: 10.1021/ja044204h. [DOI] [PubMed] [Google Scholar]
- 22.Gu ZTT, Opella SJ. J Magn Reson. 1999;140:340–346. doi: 10.1006/jmre.1999.1825. [DOI] [PubMed] [Google Scholar]
- 23.Marassi FM, Opella SJ. J Magn Reson. 2000;144:150–155. doi: 10.1006/jmre.2000.2035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Opella SJ, Marassi FM. Chemical Reviews. 2004;104:3587–3606. doi: 10.1021/cr0304121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pervushin K, Riek R, Wider G, Wuthrich K. Proc Natl Acad Sci USA. 1997;94:12366–12371. doi: 10.1073/pnas.94.23.12366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dellwo MJ, Wand AJ. J Am Chem Soc. 1989;111:4571–4578. [Google Scholar]
- 27.Kay LE, Torchia DA, Bax A. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- 28.Peng JW, Wagner G. J Magn Reson. 1992;98:308–332. [Google Scholar]
- 29.Tjandra N, Wingfield P, Stahl S, Bax A. J Biomol NMR. 1996;8:273–284. doi: 10.1007/BF00410326. [DOI] [PubMed] [Google Scholar]
- 30.Hiyama Y, Niu CH, Silverton JV, Bavoso A, Torchia DA. J Am Chem Soc. 1988;110:2378–2383. [Google Scholar]
- 31.Lumsden MD, Wu G, Wasylishen RE, Curtis RD. J Am Chem Soc. 1993;115:2825–2832. [Google Scholar]
- 32.Fushman D, Cowburn D. J Am Chem Soc. 1998;120:7109–7110. [Google Scholar]
- 33.Fushman D, Tjandra N, Cowburn D. J Am Chem Soc. 1998;120:10947–10952. [Google Scholar]
- 34.Lee DK, Wittebort RJ, Ramamoorthy A. J Am Chem Soc. 1998;120:8868–8874. [Google Scholar]
- 35.Kroenke CD, Rance M, Palmer AG. J Am Chem Soc. 1999;121:10119–10125. [Google Scholar]
- 36.Boyd J, Redfield C. J Am Chem Soc. 1999;121:7441–7442. [Google Scholar]
- 37.Cornilescu G, Bax A. J Am Chem Soc. 2000;122:10143–10154. [Google Scholar]
- 38.Kurita J, Shimahara H, Utsunomiya-Tate N, Tate S. J Magn Reson. 2003;163:163–173. doi: 10.1016/s1090-7807(03)00080-6. [DOI] [PubMed] [Google Scholar]
- 39.Damberg P, Jarvet J, Graslund A. J Am Chem Soc. 2005;127:1995–2005. doi: 10.1021/ja045956e. [DOI] [PubMed] [Google Scholar]
- 40.Loth K, Pelupessy P, Bodenhausen G. J Am Chem Soc. 2005;127:6062–6068. doi: 10.1021/ja042863o. [DOI] [PubMed] [Google Scholar]
- 41.Burton RA, Tjandra N. J Biomol NMR. 2006;35:249–259. doi: 10.1007/s10858-006-9037-6. [DOI] [PubMed] [Google Scholar]
- 42.Wylie BJ, Franks WT, Rienstra CM. Journal of Physical Chemistry B. 2006;110:10926–10936. doi: 10.1021/jp060507h. [DOI] [PubMed] [Google Scholar]
- 43.Wylie BJ, Sperling LJ, Frericks HL, Shah GJ, Franks WT, Rienstra CM. J Am Chem Soc. 2007;129:5318–5319. doi: 10.1021/ja0701199. [DOI] [PubMed] [Google Scholar]
- 44.Hall JB, Fushman D. J Am Chem Soc. 2006;128:7855–7870. doi: 10.1021/ja060406x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Grishaev A, Yao LS, Ying JF, Pardi A, Bax A. J Am Chem Soc. 2009;131:9490–9492. doi: 10.1021/ja903244s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sanders CR, Hare BJ, Howard KP, Prestegard JH. Prog Nucl Magn Reson Spectrosc. 1994;26:421–444. [Google Scholar]
- 47.Cornilescu G, Marquardt JL, Ottiger M, Bax A. J Am Chem Soc. 1998;120:6836–6837. [Google Scholar]
- 48.Hansen AL, Al-Hashimi HM. J Magn Reson. 2006;179:299–307. doi: 10.1016/j.jmr.2005.12.012. [DOI] [PubMed] [Google Scholar]
- 49.Yao LS, Bax A. J Am Chem Soc. 2007;129:11326–11327. doi: 10.1021/ja073937+. [DOI] [PubMed] [Google Scholar]
- 50.Hansen MR, Mueller L, Pardi A. Nat Struct Biol. 1998;5:1065–1074. doi: 10.1038/4176. [DOI] [PubMed] [Google Scholar]
- 51.Bodenhausen G, Ruben DJ. Chem Phys Lett. 1980;69:185–189. [Google Scholar]
- 52.Mulder FAA, de Graaf RA, Kaptein R, Boelens R. J Magn Reson. 1998;131:351–357. doi: 10.1006/jmre.1998.1380. [DOI] [PubMed] [Google Scholar]
- 53.Silver MS, Joseph RI, Hoult DI. Nature. 1984;310:681–683. doi: 10.1038/310681a0. [DOI] [PubMed] [Google Scholar]
- 54.Wang AC, Bax A. J Biomol NMR. 1993;3:715–720. doi: 10.1007/BF00198374. [DOI] [PubMed] [Google Scholar]
- 55.Fischer MWF, Zeng L, Pang YX, Hu WD, Majumdar A, Zuiderweg ERP. J Am Chem Soc. 1997;119:12629–12642. [Google Scholar]
- 56.Tjandra N, Bax A. J Am Chem Soc. 1997;119:8076–8082. [Google Scholar]
- 57.LiWang AC, Bax A. J Magn Reson. 1997;127:54–64. doi: 10.1006/jmre.1997.1187. [DOI] [PubMed] [Google Scholar]
- 58.Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. J Biomol NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 59.Davis DG, Perlman ME, London RE. J Magn Reson Ser B. 1994;104:266–275. doi: 10.1006/jmrb.1994.1084. [DOI] [PubMed] [Google Scholar]
- 60.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JJA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03, Revision C.02. Gaussian Inc; Wallingford CT: 2004. [Google Scholar]
- 61.Ulmer TS, Ramirez BE, Delaglio F, Bax A. J Am Chem Soc. 2003;125:9179–9191. doi: 10.1021/ja0350684. [DOI] [PubMed] [Google Scholar]
- 62.Ditchfield R. Mol Phys. 1974;27:789–807. [Google Scholar]
- 63.Wolinski K, Hinton JF, Pulay P. J Am Chem Soc. 1990;112:8251–8260. [Google Scholar]
- 64.Yao L, Vogeli B, Torchia DA, Bax A. J Phys Chem B. 2008;112:6045–6056. doi: 10.1021/jp0772124. [DOI] [PubMed] [Google Scholar]
- 65.Yao L, Voegeli B, Ying JF, Bax A. J Am Chem Soc. 2008;130:16518–16520. doi: 10.1021/ja805654f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Case DA. J Biomol NMR. 1999;15:95–102. doi: 10.1023/a:1008349812613. [DOI] [PubMed] [Google Scholar]
- 67.Losonczi JA, Andrec M, Fischer MWF, Prestegard JH. J Magn Reson. 1999;138:334–342. doi: 10.1006/jmre.1999.1754. [DOI] [PubMed] [Google Scholar]
- 68.Tolman JR. J Am Chem Soc. 2002;124:12020–12030. doi: 10.1021/ja0261123. [DOI] [PubMed] [Google Scholar]
- 69.Lakomek NA, Walter KFA, Fares C, Lange OF, de Groot BL, Grubmuller H, Bruschweiler R, Munk A, Becker S, Meiler J, Griesinger C. J Biomol NMR. 2008;41:139–155. doi: 10.1007/s10858-008-9244-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Tang S, Case DA. J Biomol NMR. 2007;38:255–266. doi: 10.1007/s10858-007-9164-8. [DOI] [PubMed] [Google Scholar]
- 71.Goldman M. J Magn Reson. 1984;60:437–452. [Google Scholar]
- 72.Engh RA, Huber R. Acta Crystallogr A. 1991;47:392–400. [Google Scholar]
- 73.Hall JB, Fushman D. J Biomol NMR. 2003;27:261–275. doi: 10.1023/a:1025467918856. [DOI] [PubMed] [Google Scholar]
- 74.Sass J, Cordier F, Hoffmann A, Rogowski M, Cousin A, Omichinski JG, Lowen H, Grzesiek S. J Am Chem Soc. 1999;121:2047–2055. [Google Scholar]
- 75.Spiess HW. NMR, Basic Princip Progr. 1978;15:55–214. [Google Scholar]
- 76.Burton RA, Tjandra N. J Am Chem Soc. 2007;129:1321–1326. doi: 10.1021/ja066835c. [DOI] [PubMed] [Google Scholar]
- 77.Zandomeneghi G, Williamson PTF, Hunkeler A, Meier BH. J Biomol NMR. 2003;25:125–132. doi: 10.1023/a:1022244025351. [DOI] [PubMed] [Google Scholar]
- 78.Zandomeneghi G, Tomaselli M, Williamson PTF, Meier BH. J Biomol NMR. 2003;25:113–123. doi: 10.1023/a:1022236217018. [DOI] [PubMed] [Google Scholar]
- 79.Torchia DA. J Biomol NMR. 2009 in press. [Google Scholar]
- 80.Woessner DE. The Journal of Chemical Physics. 1962;36:1–4. [Google Scholar]
- 81.Ying JF, Grishaev AE, Bax A. Magn Reson Chem. 2006;44:302–310. doi: 10.1002/mrc.1762. [DOI] [PubMed] [Google Scholar]
- 82.Stone MJ, Gupta S, Snyder N, Regan L. J Am Chem Soc. 2001;123:185–186. doi: 10.1021/ja003094l. [DOI] [PubMed] [Google Scholar]
- 83.Fushman D, Xu R, Cowburn D. Biochemistry. 1999;38:10225–10230. doi: 10.1021/bi990897g. [DOI] [PubMed] [Google Scholar]
- 84.Bouvignies G, Bernado P, Meier S, Cho K, Grzesiek S, Bruschweiler R, Blackledge M. Proc Natl Acad Sci U S A. 2005;102:13885–13890. doi: 10.1073/pnas.0505129102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Markwick PRL, Bouvignies G, Blackledge M. J Am Chem Soc. 2007;129:4724–4730. doi: 10.1021/ja0687668. [DOI] [PubMed] [Google Scholar]
- 86.Bouvignies G, Markwick PRL, Blackledge M. Chem Phys Chem. 2007;8:1901–1909. doi: 10.1002/cphc.200700353. [DOI] [PubMed] [Google Scholar]
- 87.Bouvignies G, Markwick P, Brueschweiler R, Blackledge M. J Am Chem Soc. 2006;128:15100–15101. doi: 10.1021/ja066704b. [DOI] [PubMed] [Google Scholar]
- 88.Vogeli B, Yao L, Bax A. J Biomol NMR. 2008;41:17–28. doi: 10.1007/s10858-008-9237-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Vogeli B, Ying JF, Grishaev A, Bax A. J Am Chem Soc. 2007;129:9377–9385. doi: 10.1021/ja070324o. [DOI] [PubMed] [Google Scholar]
- 90.Lipari G, Szabo A. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- 91.Harris RK, Becker ED, De Menezes SMC, Granger P, Hoffman RE, Zilm KW. Pure Appl Chem. 2008;80:59–84. [Google Scholar]
- 92.Wylie BJ, Rienstra CM. J Chem Phys. 2008:128. doi: 10.1063/1.2834735. [DOI] [PubMed] [Google Scholar]
- 93.Ottiger M, Bax A. J Am Chem Soc. 1998;120:12334–12341. [Google Scholar]
- 94.Chan JCC, Tycko R. J Chem Phys. 2003;118:8378–8389. [Google Scholar]
- 95.Bevington PR, Robinson DK. Data reduction and error analysis for the physical sciences. McGraw-Hill; New York: 1992. [Google Scholar]
- 96.Lienin SF, Bremi T, Brutscher B, Bruschweiler R, Ernst RR. J Am Chem Soc. 1998;120:9870–9879. [Google Scholar]
- 97.Mandel AM, Mikael A, Palmer AG. J Mol Biol. 1995;246:144–163. doi: 10.1006/jmbi.1994.0073. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.