A Comparison of the Quasi-static Mechanical and Nonlinear Viscoelastic Properties of the Human Semitendinosus and Gracilis Tendons

Abstract

Background

Over fifty-percent of anterior cruciate ligament reconstructions are performed using semitendinosus and gracilis tendon autografts. Despite their increased use, there remains little quantitative data on their mechanical behavior. Therefore, the objective of this study was to investigate the quasi-static mechanical and nonlinear viscoelastic properties of human semitendinosus and gracilis tendons, as well as the variation of these properties along their length.

Methods

Specimens were subjected to a series of uniaxial tensile tests: one-hour static stress-relaxation test, 30-cycle cyclic stress-relaxation test and load to failure test. To describe the nonlinear viscoelastic behavior, the quasi-linear viscoelastic theory was utilized to model data from the static stress relaxation experiment.

Findings

The constants describing the viscoelastic behavior were similar between the proximal and distal halves of the gracilis tendon. The proximal half of the semitendinosus tendon, however, had a greater viscous response than its distal half, which was also significantly higher than the proximal gracilis tendon. In terms of the quasi-static mechanical properties, the properties were similar between the proximal and distal halves of the semitendinosus tendon. However, the distal gracilis tendon showed a significantly higher tangent modulus and ultimate stress compared to its proximal half, which was also significantly higher than the distal semitendinosus tendon.

Interpretation

The results of this study demonstrate differences between the semitendinosus and gracilis tendons in terms of their quasi-static mechanical and nonlinear viscoelastic properties. These results are important for establishing surgical preconditioning protocols and graft selection.

Introduction

The anterior cruciate ligament (ACL) is the most frequently injured knee ligament during sports and work related activities, with tears occurring in approximately 150,000 to 200,000 people in the United States each year (Beaty, 1999). Because midsubstance tears fail to heal and the long-term results of conservative treatments are poor, most ACL ruptures in young and active people require surgical reconstruction using tissue grafts. In recent years, autografts consisting of the semitendinosus and/or gracilis tendons have become more popular being utilized in approximately one half of ACL reconstruction procedures (Forssblad et al., 2006). The primary reasons for their use include less reported donor site morbidity when compared to other autografts (Aglietti et al., 1993, Kartus et al., 2001, Pinczewski et al., 2002), as well as adequate initial stiffness and strength when compared to the native ACL (Pinczewski et al., 2002, Steiner et al., 1994, Hamner et al., 1999).

Graft constructs can consist of a single tendon, either the semitendinosus or gracilis tendon, looped over on itself (double-strand), or both tendons looped and combined to form a quadrupled semitendinosus and gracilis (QSTG) graft. A number of studies have investigated the structural properties of the doubled and quadrupled semitendinosus and gracilis tendon grafts in terms of load to failure and stress relaxation experiments and found several variables influence these measurements including graft preparation, fixation to bone, temperature, and preconditioning protocols (Hoher et al., 2000, Nurmi et al., 2004, Ciccone et al., 2006, Steiner et al., 1994, Hamner et al., 1999). These studies have provided valuable information on the structural properties of graft constructs, which reflect the size, length, and quality of the tendons collectively.

The mechanical properties, on the other hand, describe soley the properties of the material or tissue quality and are independent of the size or amount of tissue. These data are important because they are intimately related to the composition and micro-architecture of a tissue. In addition, the data can be utilized within computational models to more accurately predict the behavior of constructs in response to clinically relevant loading conditions that cannot be simulated experimentally. Despite the importance of such data, relatively few studies have characterized the mechanical properties of individual semitendinosus and gracilis tendons, especially in terms of their viscoelastic behavior (Noyes et al., 1984, Butler et al., 1984, Donahue et al., 2001).

Previous studies have demonstrated that mechanical properties can vary significantly from tendon to tendon (Butler et al., 1984). These properties have also been shown to vary significantly along the length of tendons, with the tangent modulus generally increasing toward the distal attachment (Arruda et al., 2006). On the other hand, greater amounts of stress relaxation are observed near the muscle attachment (Eliasson et al., 2007). This variation is believed to be related to the function of tendons, i.e. to provide a transition between compliant muscle and stiff bone (Paxton and Baar, 2007). At the region near the bone (bone-tendon), the maximum tangent modulus of the tibialis anterior tendon was reported to be 2.1-fold higher than that of either the midsection (mid-tendon) or the tendon near the muscle (muscle-tendon) (Arruda et al., 2006). Such differences for a looped graft construct could result significant inhomogeneties of stress through the cross-section of an ACL graft.

Thus, a more complete description of the semitendinosus and gracilis tendons is not only important for graft selection and surgical decisions, but can also serve as inputs to finite element models for both ACL reconstruction and for modeling the mechanics of the lower extremity. From a basic science perspective, these data would provide insight into the potential disparity in mechanical behavior of two tendons from similar anatomical locations within the human body. More specifically, quantitative data on the quasi-static mechanical and nonlinear viscoelastic properties between tendons and along their length is important to further understand structure function relationships of these tissues.

Thus, this study had two objectives. The first was to measure and compare the quasi-static mechanical and nonlinear viscoelastic properties of human semitendinosus and gracilis tendons, while the second was to compare the properties of their respective proximal and distal halves. Since a larger percentage of the semitendinosus tendon’s length resides in the musculotendinous junction, which is known to have less compact fibers that deviate from the longitudinal direction of the tendon (Paxton and Baar, 2007), we hypothesized that its proximal half (i.e. towards the musculotendinous junction) would demonstrate inferior mechanical properties and an increased viscous response compared to its distal half and to the corresponding proximal half of the gracilis tendon. Conversely, since a smaller percentage of the gracilis tendon’s length resides in the musculotendinous junction, we further hypothesized that its mechanical behavior would be more homogenous throughout its length, with the distal portions of both tendons behaving similarly.

To test these hypotheses, the quasi-linear viscoelastic (QLV) theory was used to curve fit the experimental data from stress-relaxation tests to obtain the five constants describing the instantaneous elastic response and reduced relaxation function (A, B, C, τ₁, and τ₂). These constants were utilized to predict the experimental peak stresses of a separate cyclic stress-relaxation experiment. The constants were then utilized for comparisons between the proximal and distal halves of the semitendinosus and gracilis tendons. Stress-strain curves were obtained from load to failure tests and utilized for comparisons of the quasi-static mechanical properties of the tissue samples. Parameters describing these properties were tangent modulus, ultimate stress, ultimate strain and strain energy density.

Materials and Methods

Experimental

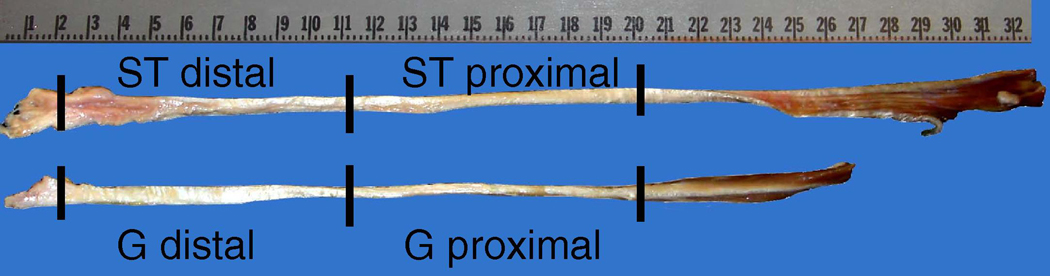
Ten independent fresh-frozen, intact human cadaveric knee specimens were used in this study (mean 56, SD 8 years). The knee specimens were thawed at room temperature overnight before dissection. The semitendinosus and gracilis tendons were harvested from the tibial insertion site of the knees using a closed tendon stripper (Wolf Instruments, Knittlingen, Germany) and examined to ensure that there were no visible signs of damage. The tendons were then wrapped in saline-soaked gauze, placed into an airtight plastic bag and kept frozen at −20°C until the day of testing (4–6 months later), (Moon et al., 2006). Before testing, the tendons were allowed to thaw at room temperature and cleaned to remove the muscle and fatty tissues. The most distal 2 cm of the tendon (bony attachment) was removed and the proximal 18 cm of the tendon was taken for testing. Any remaining tissue towards the proximal end (muscle attachment) of the tendon was discarded. The entire 18 cm portion of the tendon was cut into two 9 cm long halves, which were referred to as the proximal and distal half of the tendon (Fig. 1).

Fig. 1.

A diagram defining the location of the proximal and distal halves of ST and G tendons at dissection. (The major unit of the scale is cm)

The initial cross-sectional area of each tendon half was measured with a laser micrometer system (accurate to 0.1 mm²) at three locations, i.e., distally, mid, and proximally along the longitudinal axis (Lee and Woo, 1988). Each half was then placed in a custom guide (width of the narrow portion was 3 mm) and cut into a dog-bone shape with an aspect ratio of approximately 10. The length of the narrow portion (30 mm) of the dog-bone was placed at the middle third along the length of each tendon half. A second series of cross-sectional area measurements of the dog-bone shaped tendon were taken at three locations along the axis of the narrow portion of each tendon half. The three measurements were averaged to serve as the cross-sectional area of the tendon half for Lagrangian stress calculations. Following cross-sectional area measurement, two round reflective markers about 20 mm apart along the long axis of the tendon were glued on the narrow portion of each tendon half for strain measurement. The motion of these reflective markers was recorded during testing using a video analysis system (Motion Analysis™ VP320, Willamette Valley, Oregon, USA). Prior tests revealed that the errors in the accuracy of strain measurement with this system are less than 0.2% (Smutz et al., 1996).

Each end of the tendon halves was clamped with a set of customized soft-tissue clamps with a thin piece of gauze placed on each inner side to increase roughness of the clamp to prevent slippage during testing. The entire construct was submerged in a saline bath, which was fixed to the base of a materials testing machine (model 4502; Instron, Canton, MA, Load Cell 2518–103). Each tendon half was maintained at 33 °C (the body temperature in the knee) for the entirety of the testing protocol. The remaining cadaveric knee joint was subsequently utilized in a robotic study on ACL function that required the ACL to be transected. Thus, the ACL from these specimens could not be tested and compared to the results of the semitendinosus and gracilis tendons. This is a limitation of this study.

After allowing each tendon half to equilibrate to the environment for 1 hour, a preload of 2 N was applied and the cross-head displacement of the testing system was set to zero. Then, preconditioning was applied by elongating each tendon half between 0 and 1.5 mm for 10 cycles at 10 mm/min. After preconditioning, all tension was removed and each tendon half was allowed to recover for 1 hour (Woo et al., 1981). Subsequently, each each tendon half was returned to the zero position and a stress-relaxation test was performed by elongating each tendon half to 1.5 mm at an elongation rate of 10 mm/min and holding for a period of 60 min. The elongation rate resulted in loading phase that was t₀ = 9.2 s. This was chosen to avoid the potential experimental errors associated with fast strain rates (i.e. overshoot, vibrations, and inaccurate measurements of tissue strain) (Funk et al., 2000). In addition, the elongation of 1.5 mm corresponded to a strain level of 2.2% (SD 0.6%), which allows for significant loading without extending beyond the toe region of the stress-strain curve. Our testing system does not allow for a strain-controlled experiment. Thus, the variability in the resulting peak strains is a consequence of biologic variation in that the relationship between displacement and surface strain varied from tendon half to each tendon half. The tendon half was considered to be completely relaxed after 1 hour because the stress relaxation during the last 10 minutes of the test was less than 1% of the peak stress. Following the static stress-relaxation test, all tension was again removed and each specimen was allowed to recover for 1 hour. Subsequently, a second test was performed to measure the cyclic stress relaxation behavior of the tendon half. Each tendon half was returned to the zero position and was subjected to 30 cycles of elongation between 0 and 1.5 mm at the same elongation rate. Finally, each tendon half was loaded to failure at an elongation rate of 10 mm/min and the failure mode of each tendon half was recorded.

Viscoelastic Properties

The QLV theory proposed by Professor Fung (1972) has been widely utilized to model the time- and history-dependent viscoelastic behavior of soft tissues, and has been proven to be very successful for characterizing viscoelastic properties of ligaments and tendons (Johnson et al., 1994, Woo et al., 1981, Abramowitch and Woo, 2004, Funk et al., 2000). The QLV theory assumes a separation of an instantaneous elastic response σ^e(ε) and a reduced relaxation function G(t), for a step change in strain. The stress in response to an arbitrary strain history at some time, t, can then be described as the convolution of these two functions,

$$\sigma (\epsilon ,t)={\displaystyle {\int }_0^{t}G(t-\tau )\cdot \frac{\partial {\sigma }^e(\epsilon )}{\partial \epsilon }\cdot \frac{\partial \epsilon }{\partial \tau }\cdot d\tau }$$ (1)

The reduced relaxation function, G(t), formulated by Fung (1972) was chosen for this study. It was developed to model soft tissues that are relatively insensitive to strain rate and, therefore, describes a continuous relaxation spectrum in which the magnitude of the viscous response, C, is constant between the frequencies bounded by 1/τ₂ and 1/τ₁ (Fung, 1972):

$$G(t)=\frac{1+C(E_1[(t-\tau )/{\tau }_2]-E_1[(t-\tau )/{\tau }_1])}{1+C\text{ln}({\tau }_2/{\tau }_1)}$$ (2)

where $E_1(y)={\displaystyle {\int }_y^t\frac{e^{-z}}{z}dz}$ is the exponential integral, and C, τ₁, and τ₂ are material constants. The physical significance of these constants has been examined in terms of their relation to stress relaxation (Sauren and Rousseau, 1983). The dimensionless constant C determines the magnitude of viscous effects and is related to the total percentage of stress relaxation. The time constants τ₁ and τ₂ govern early and late relaxation, respectively, relating to the slope of the stress-relaxation curve at early and late time periods. An exponential approximation has been chosen to describe the instantaneous elastic response:

$${\sigma }^e(\epsilon )=A(e^{B\epsilon }-1)+k$$ (3)

where A and B are material constants and k accounts for the effect of a preload by adding a non-zero stress value at t=0 (Fisher et al., 2006). The physical significance of B and the product A×B are the nonlinearity of the stress–strain curve and the initial slope of the curve, respectively. The constants allow a quantitative comparison of the viscoelastic behavior between different tissues (Abramowitch and Woo, 2004, Fisher et al., 2006).

Our research center has established a novel methodology to determine the constants of this theory based on the strain history of stress-relaxation experiments that utilize slow strain rates and by accounting for the effects of preload (Fisher et al., 2006, Abramowitch and Woo, 2004). This approach allows for reliable results from specimen to specimen and has been demonstrated to work very well in describing and comparing the viscoelastic behaviors of the normal and healing medial collateral ligament from the goat and rabbit (Abramowitch and Woo, 2004, Fisher et al., 2006). Details of the approach can be found in the provided references. Briefly, for a constant strain rate, α, applied from 0 < t < t₀ , σ_k(t) can be combined with the stress resulting from the initial loading phase of the stress relaxation experiment, found by substituting Eqs. (2) and (3) into Eq. (1), to obtain:

$$\sigma (t)={\sigma }_k(t)+\frac{AB\alpha }{1+C\text{ln}(\frac{{\tau }_2}{{\tau }_1})}{\displaystyle {\int }_0^t\{1+\mathrm{C}({\mathrm{E}}_1[\frac{(\mathrm{t}-\tau )}{{\tau }_2}]-{\mathrm{E}}_1[\frac{(\mathrm{t}-\tau )}{{\tau }_1}])\}{e}^{\mathrm{B}\alpha \tau }\partial \tau }$$ (4)

Similarly, for the stress relaxation phase for t₀ < t at a constant strain of α*t₀, the stress is

$$\sigma (t)={\sigma }_k(t)+\frac{AB\alpha }{1+C\text{ln}(\frac{{\tau }_2}{{\tau }_1})}{\displaystyle {\int }_0^{t_0}\{1+\mathrm{C}({\mathrm{E}}_1[\frac{(\mathrm{t}-\tau )}{{\tau }_2}]-{\mathrm{E}}_1[\frac{(\mathrm{t}-\tau )}{{\tau }_1}])\}{e}^{\mathrm{B}\alpha \tau }\partial \tau }$$ (5)

Using Eqs. (4) and (5), the ramping and relaxation data can then be curve-fit simultaneously utilizing a modified Levenberg-Marquardt non-linear optimization algorithm to obtain A, B, C, τ₁, and τ₂. This method has been shown to yield a unique solution that is minimally sensitive to systematic and random experimental noise. It has been shown that parameters A and τ₁ become correlated. Since parameter A is not required to describe the reduced relaxation following ramping at a constant strain rate, it was held fixed and determined, along with k, by an initial curve-fit of the ramping phase data with the exponential function (Eq. 3).

To demonstrate the ability of the QLV theory to predict data for the semitendinosus and gracilis tendons for the peak strain level utilized in this study, predictions of a different experiment, i.e. the cyclic stress-relaxation test, were made on the basis of the obtained constants. The theoretical peak stresses at each cycle were determined on the basis of a previously described approximated cyclic strain-time history. Details regarding this method to determine the peak stresses of a cyclic stress-relaxation experiment and a figure of the approximated cyclic strain-time history are presented in the referenced publication (Woo et al., 1981). These peak stresses were then compared to those obtained experimentally during the cyclic stress-relaxation test.

Quasi-Static Mechanical Properties

Stress-strain curves were generated by dividing the load data by the CSA measurement of the sample to calculate Lagrangian stress. The change in the marker distance was divided by the marker distance when the specimen was at the zero position to calculate strain. Parameters describing the mechanical properties of the tissue sample were tangent modulus, ultimate stress, ultimate strain and strain energy density. The tangent modulus of each sample was calculated by fitting a line to the linear portion of the stress-strain curve between 3% and 6% of strain. The ultimate stress was defined as the highest stress value reached during the load to failure test and the point when catastrophic failure occurs. The ultimate strain was the strain value corresponding to the ultimate stress. The strain energy density was defined as the area under the stress-strain curve from the beginning of the load to failure test until failure. It was computed using an interpolation subroutine within the software package Mathematica™ (Wolfram Research, Inc., Champaign, IL, USA) to generate a function describing the stress-strain data, which was then integrated from 0 to the ultimate strain.

Statistics

For statistical analysis, a one-sample Kolmogorov-Smirnov test was first used to test the normality of the measured variables and obtained constants. Since all were found to be normally distributed, a two-factor repeated measures analysis of variance (ANOVA) was utilized, with the type of tendon (semitendinosus & gracilis) and the tendon half (proximal & distal) as the factors. This design was chosen because all the measured variables and obtained constants were compared within tendons from the same knee specimen. A Bonferroni post-hoc test was utilized to determine differences between individual groups with a significance level set at p<0.05.

Results

Grossly, the semitendinosus and gracilis tendons showed geometrical variation along their length. The middle part of the semitendinosus and gracilis tendons were round and uniform in cross-sectional area. At the distal end (toward the bony attachment), the tendons were more elliptical in shape, with compact collagen fibers. At the proximal end (toward the muscle attachment), the tendons took on a more flat, feather-like appearance, with the collagen fibers appearing to fan out while remaining connected by a thin film of connective tissue. It was also observed that the semitendinosus tendon had a longer percentage of the overall tendon length residing in the musculotendinous junction than the gracilis tendon. The initial cross-sectional areas of the whole tendons confirmed these observations and are displayed in Table 1. The semitendinosus tendon displayed a larger cross-sectional area than the gracilis tendon and the proximal halves of both tendons were approximately 32% (semitendinosus) to 46% (gracilis) larger than their distal halves (p<0.05). The cross-sectional areas of the specimens after they were cut into dog-bone shapes were uniform with an average of 4.2 mm² (SD 1.3 mm²) for all tendons.

Table 1.

The variation of the initial cross-sectional area of proximal and distal halves of the ST and G tendons. Data reported as mean (SD).

	Average Area
ST proximal(n=10)	22.4 (9.4) mm2 *,**
ST distal(n=10)	15.3 (5.5) mm2 *
G proximal(n=10)	15.8 (8.1) mm2 **
G distal(n=10)	8.6 (1.8) mm2

^*indicates a statistically significant difference between tendons, i.e. ST versus G tendon;

^**indicates a statistically significant difference within tendons, i.e. proximal versus distal halves (p < 0.05).

During the loading phase of the stress-relaxation test, the surface strain was found to increase linearly with time. The elongation rate of 10 mm/min was equivalent to a surface strain rate of 0.24%/s (SD 0.06%/s) for all specimens, achieving a peak strain of 2.2% (SD 0.6%) at 9.2 sec. The corresponding peak stresses, however, revealed some differences, reaching a value of 5.64 MPa (SD 1.71 MPa) for the proximal semitendinosus tendon, 5.97 MPa (SD 2.39 MPa) for the distal semitendinosus tendon, 7.96 MPa (SD 2.51 MPa) for the proximal gracilis tendon, and 10.24 MPa (SD 3.02 MPa) for the distal gracilis tendon. These peak stresses were only significantly different between the distal semitendinosus and the distal gracilis (p=0.002). At 60 minutes, the total amount of stress relaxation was found to be 34.0% (SD 8.2%) for the proximal semitendinosus tendon, 25.4% (SD 5.9%) for the distal semitendinosus tendon, 26.8% (SD 6.4%) for the proximal gracilis tendon, and 24.8% (SD 4.0%) for the distal gracilis tendon, with a significant difference found between the proximal semitendinosus tendon and the distal semitendinosus tendon (p=0.009).

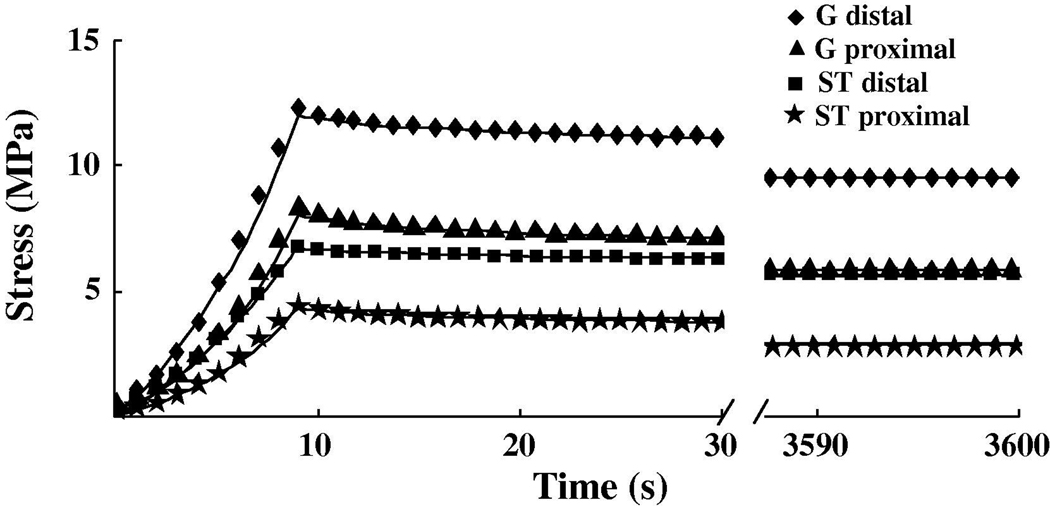
Figure 2 shows a typical curve-fit of the experimental data demonstrating an accurate description of these data by QLV theory. Curve fits of the data of each individual specimen were of good quality with coefficient of determination R² greater than 0.95. The obtained constants describing the instantaneous elastic response and viscous response for proximal and distal halves of the semitendinosus and gracilis tendon are shown in Table 2. For constants describing the instantaneous elastic response, there were no significant differences found in constant A (p>0.05), which scales the elastic response, or constant B (p>0.05), which describes the nonlinearity of the elastic response. However, their product, A×B, which describes the initial slope of the elastic response, was significantly less for the proximal semitendinosus (35.1% smaller A×B, p=0.012) compared with the proximal gracilis tendon. The distal semitendinosus tendon also showed a significantly lower initial slope (42.0% smaller A×B, p=0.020 ) of the elastic response than distal gracilis tendon.

Fig. 2.

Typical curve-fits of the experimental data with the QLV theory for the ST proximal tendon (*), ST distal tendon (■), G proximal tendon (▲), G distal tendon (◆). The discrete symbols of ◆, ▲, ■, *, represent the experimental data and the solid line is the curve-fit to these data.

Table 2.

Constants describing the instantaneous elastic response (upper) and reduced relaxation function (lower) for the proximal and distal halves of ST and G tendons. Data reported as mean (SD).

QLV Constant	ST proximal(n=10)	ST distal(n=10)	G proximal(n=10)	G distal(n=10)
A (MPa)	2.78 (1.98)	2.51 (2.63)	5.19 (3.89)	3.78 (2.33)
B	77.7 (54.0)	80.3 (50.1)	70.7 (46.1)	65.0 (22.5)
A×B (MPa)	163.3 (88.2) *	119.3 (70.1) *	251.5 (112.0)	205.8 (80.7)
C	0.083 (0.031) *,**	0.051 (0.017)	0.054 (0.021)	0.048 (0.014)
τ1(s)	0.366 (0.106)	0.380 (0.183)	0.378 (0.078)	0.342 (0.077)
τ2 (s)	2444 (1764)	3267 (2517)	3831 (2654)	2352 (1445)

^*indicates a statistically significant difference between tendons, i.e. ST versus G;

^**indicates a statistically significant difference within tendons, i.e. proximal versus distal (p < 0.05).

For constants describing the viscous response, there were no significant differences found for constant τ_1, which governs the early relaxation (p>0.05), and constant τ_2, which governs the late relaxation (p>0.05). However, the proximal semitendinosus tendon had a greater viscous response (53.7% larger constant C, p=0.007) than the proximal gracilis tendon. There were also significant differences found between the proximal semitendinosus and distal semitendinosus tendons (p=0.023), with proximal semitendinosus tendon having a significantly larger (65%) constant C than the distal semitendinosus tendon. The gracilis tendon, on the other hand, showed consistent viscoelastic properties along its length as no significant differences were found between its proximal and distal halves for all five constants (p>0.05).

In terms of the ability to predict results using the obtained constants, the predicted peak stresses agreed with the experimentally measured peak stresses very well for all tendons. The predicted peak stresses were within 8.4% (SD 4.4%) error of the experimental measured peak stresses for all specimens. The close agreement confirmed the ability of the QLV theory to predict results for the strain levels investigated in this study.

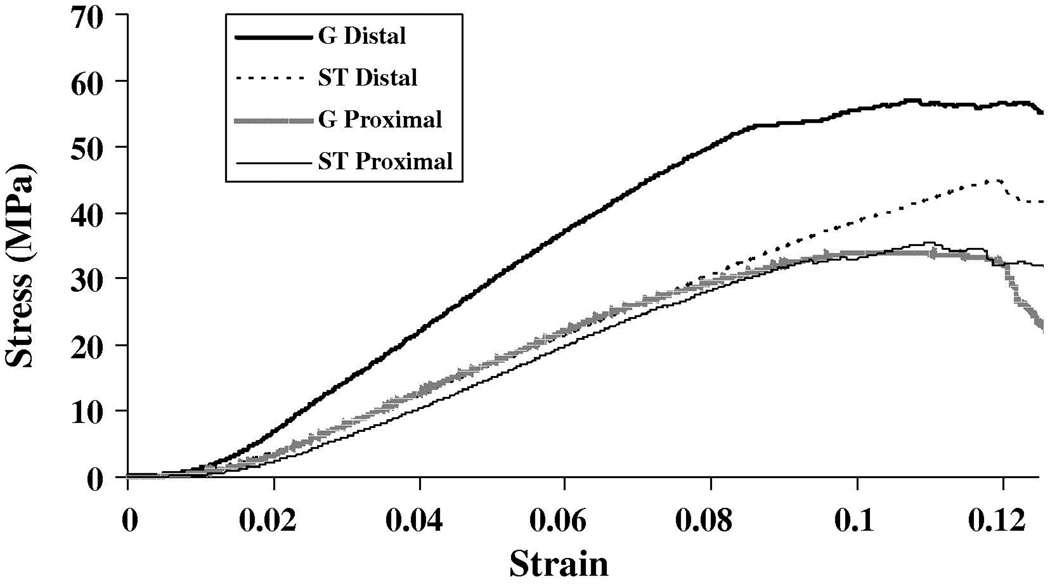
For the load to failure test, all of the specimens failed in the narrow portion of the sample between the strain markers. The stress-strain curves displayed a typical shape, including a nonlinear toe region followed by a linear region and failure region. Typical curves for the proximal and distal halves of the semitendinosus and gracilis tendons are shown in Figure 3. When comparing between the semitendinosus and gracilis tendons (Table 3), no significant differences were found between the proximal halves. In the distal half, however, the semitendinosus tendon showed a 22% lower tangent modulus than that of the gracilis tendon, which was found to be statistically significant (p<0.05). In addition, the ultimate stress of the semitendinosus tendon was 23% lower than that of the gracilis tendon, which was significant (p<0.05). However, the strains at which this failure occurred were not significantly different for the two tendons. Consequently, the strain energy density of the semitendinosus tendon was 20% lower than that of the gracilis tendon, although this was not a significant difference (p=0.43).

Fig. 3.

Representative stress-strain curves resulting from load-to-failure tests of the proximal and distal halves of the ST and G tendons.

Table 3.

The variation of the mechanical properties of proximal and distal halves of the ST and G tendons. Data reported as mean (SD).

Mechanical Properties	ST proximal(n=10)	ST distal(n=10)	G proximal(n=10)	G distal(n=10)
Tangent Modulus (MPa)	446.5 (315.7)	484.5 (124.8)	467.5 (210.5)	625.5 (148.0) *,**
Ultimate Stress (MPa)	37.2 (17.8)	48.5 (11.8)	34.7 (12.0)	63.0 (13.3) *,**
Ultimate Strain (%)	13.4 (6.3)	14.1 (2.0)	11.3 (5.8)	13.6 (2.1)
Strain Energy Density (MPa)	2.6 (1.9)	3.4 (1.0)	2.2 (1.3)	4.3 (0.9) **

^*indicates a statistically significant difference between tendons, i.e. ST versus G;

^**indicates a statistically significant difference within tendons, i.e. proximal versus distal (p < 0.05).

When the proximal halves of the tendons were compared to the distal halves of the same tendons, the semitendinosus tendon showed similar mechanical properties throughout (Table 3). However, the gracilis tendon showed some difference along its length, with the tangent modulus for the proximal gracilis tendon measuring 25% lower than that of the distal gracilis tendon (p<0.05). In addition, the ultimate stress of the proximal gracilis tendon was almost half (45% lower) of that for the distal gracilis tendon, which was significant (p<0.05). No differences were observed for the ultimate strains. Thus, the strain energy density for the proximal gracilis tendon was 50% lower than that of the distal gracilis tendon, which was also significant (p<0.05).

Discussion

In this study, the quasi-static mechanical and nonlinear viscoelastic properties of paired human semitendinosus and gracilis tendons were quantified. The major findings of this study were that the semitendinosus tendon displayed significantly different viscoelastic behavior compared with the gracilis tendon, and that the semitendinosus tendon showed significantly different viscous responses between its proximal and distal halves. On the other hand, in terms of the quasi-static mechanical properties, the semitendinosus tendon was more homogeneous throughout its length, while the distal gracilis tendon displayed up to 2-fold higher mechanical properties (i.e. tangent modulus, ultimate stress, and strain energy density) compared to its proximal half.

The viscoelastic findings supported our hypothesis that variations along the tendon length would be more apparent for the semitendinosus tendon since a greater percentage of its overall length resides in the musculotendious junction. The proximal semitendinosus tendon had a larger value of constant C, which correlated with increased stress relaxation compared to its distal half. Collagen fibers have been found to be less compact in this region of the tendon with a higher ground substance to collagen ratio; thus, this may allow for easier fluid flow in and out of the tissue (Paxton and Baar, 2007). Therefore, it would dissipate more energy and have a longer recovery time upon removal of load. In terms of the other estimated constants of the QLV theory, they were consistent with previous results for other human ligaments and tendons (Johnson et al., 1994).

The viscoelastic behavior of the semitendinosus and gracilis tendons is well recognized by surgeons as intra-operative preconditioning and tensioning protocols aim to minimize viscoelastic effects (Conteduca et al., 2003, Yasuda et al., 1997, Boylan et al., 2003). Thus, the question of the length of the preconditioning protocol is clinically relevant. In this study, more than 90% of the stress relaxation of all tendon halves occurred in the first 10 minutes (i.e. as reflected by similar values of τ₁ across all groups). In addition, no significant differences were observed for τ₂ indicating that the long-term relaxation for all tendon halves reaches a plateau at approximately the same time (approximately 40–60 minutes). However, it should be noted that for some specimens the value of τ₂ exceeded the length of the experiment (1 hour) even though the rate of relaxation had achieved our stoppage criteria. This suggests that relaxation had not fully plateaued on a log-scale and that a longer stress-relaxation test may be necessary to determine a more accurate value for this constant. Nevertheless, our predictions of the separate cyclic stress-relaxation experiment accurately predicted peak stresses to 30 cycles indicating that this model was describing the majority of stress relaxation.

While the viscoelastic behavior, with the semitendinosus tendon varying along its length and little change observed between the gracilis tendon halves, supported our hypothesis, the quasi-static mechanical properties refuted it as differences were observed for the gracilis tendon halves and not for the semitendinosus tendon halves. For the gracilis tendon, the variation in tangent modulus is consistent with previous studies that demonstrated increased collagen cross-linking toward the distal attachment of tendons (Curwin et al., 1994). However, why the same observation was not made for the semitendinosus tendon is not entirely clear. This might reflect architectural differences; however, the two tendons have been shown to have a similar parallel fibered arrangement (Makihara et al., 2006). On the other hand, it may reflect our choice to define the proximal and distal halves of both tendons based on the distance from tibial insertion and not as a percentage the tendon’s overall length. Nevertheless, the disparity in the variation of these properties demonstrates that the mechanisms responsible for viscoelastic behavior are not the same as those governing the quasi-static mechanical properties.

Compared to previously reported values on the quasi-static mechanical properties of the semitendinosus and gracilis tendons, the data presented here are consistent with previous literature when differences in methodology for cross-sectional area and strain measurements are considered along with specimen age (Noyes et al., 1984, Butler et al., 1984, Donahue et al., 2001). In terms of ACL reconstruction, these tendons have a much higher (2–3 times) tangent modulus compared to those measured for sections of the ACL, for which the anterior portion had a 2-fold higher modulus than the posterior portion (Butler et al., 1992), In addition, the quasi-static mechanical properties obtained in this study are roughly similar to those reported for human patellar tendon (Johnson et al., 1994). In terms of the viscoelastic behavior, the human patellar tendon appears to stress relax to a much greater degree compared to all of the tendon halves (Johnson et al., 1994), which appears to be more similar to that of the native ACL (Kwan et al., 1993). Thus, at the time of surgical reconstruction, these tendons likely exceed the requirements for ACL replacement from a material standpoint. However, if one considers the subsequent remodeling process that ensues in which replacement grafts deteriorate in terms of their mechanical properties and display increased viscous behavior, a materially stiffer (i.e. higher tangent modulus) and stronger graft with less stress relaxation at time zero may actually be preferable with everything else being equal (graft cross-sectional area, length, fixation, etc.).

Of course, from a structural standpoint, graft failure remains a primary reason for revision surgery with some studies suggesting that hamstring tendon grafts are more likely to fail than patellar tendon grafts (Freedman et al., 2003). Still others have suggested that graft tension may influence the remodeling process of the ACL graft (Tohyama and Yasuda, 1998, Weiler et al., 2001). While there are clearly many factors that influence graft failure and remodeling, it may also be important to consider the nonuniform stress distributions in multiple stranded grafts that would result from variations in both quasi-static mechanical and viscoelastic properties between the semitendinosus and gracilis tendons, as well as the variations along their length. Future healing studies using animal models would be necessary to delineate these effects and the potential clinical significance of this result.

This study is not without some limitations. First, the cadaveric knees from which the tendons were obtained were utilized in a separate study to evaluate the function of the ACL, in which the ACL was transected. Thus, the ACL from these knees could not be tested for a direct comparison to the data obtained in the study. Second, the data obtained on the viscoelastic behavior of the tendons was measured within the toe region of the stress-strain curve. It is important to recognize that the actual functional range of strain that these tendons experience when utilized for ACL replacement may be beyond the range tested here. Third, it should be recognized that graft selection should not be solely based on the quasi-static mechanical and viscoelastic data presented in this study alone as these data are only one factor that can impact the structural integrity of a graft construct. The quantity of the material, length of the construct, and method of fixation will also contribute significantly to a graft’s structural properties in-vivo. Lastly, in order to obtain accurate quasi-static mechanical properties it was necessary to cut each specimen into a dog-bone shape. Previously, it has been suggested that changing the dimensions of a specimen may influence its viscoelastic behavior. In this study, the cross-sectional areas of all specimens after they were cut into a dog-bone shape were approximately equal. Thus, the general trends found between proximal and distal ends as well as between tendons likely reflect actual differences in viscoelastic behavior; yet, comparisons to previous literature should always consider this and other methodological differences.

In conclusion, the data obtained in this study provides the fundamental biomechanical properties of the semitendinosus and gracilis tendons, and the variation of these properties along their length. Based on the findings of this study, further investigations into the morphology and biochemistry of these tendons are suggested to explain the differences observed between tendons as well as along their length. In addition, as the age of human donors tends to be older for cadaveric studies, future work should aim to determine whether the mechanical and viscoelastic properties of semitendinosus and gracilis tendons vary with age.