Application of the continuity equation to a breathing motion model

Abstract

Purpose: To quantitatively test a breathing motion model using the continuity equation and clinical data.

Methods: The continuity equation was applied to a lung tissue and lung tumor free breathing motion model to quantitatively test the model performance. The model used tidal volume and airflow as the independent variables and the ratio of motion to tidal volume and motion to airflow were defined as $\vec{\alpha }$ and $\vec{\beta }$ vector fields, respectively. The continuity equation resulted in a prediction that the volume integral of the divergence of the $\vec{\alpha }$ vector field was 1.11 for all patients. The integral of the divergence of the $\vec{\beta }$ vector field was expected to be zero.

Results: For 35 patients, the $\vec{\alpha }$ vector field prediction was 1.06±0.14, encompassing the expected value. For the $\vec{\beta }$ vector field prediction, the average value was 0.02±0.03.

Conclusions: These results provide quantitative evidence that the breathing motion model yields accurate predictions of breathing dynamics.

INTRODUCTION

A novel free breathing lung motion model proposed by Low et al.¹ hypothesized that the breathing motion of lung tissues and lung tumors can be modeled as a function of five independent parameters: The three-dimensional positions of the tissue at the reference conditions of zero tidal volume and zero airflow, the tidal volume, and the airflow. The tidal volume metric was a surrogate for the general inhalation and exhalation motion while the airflow was a surrogate for the hysteresis behavior, where the lung tissues move in different paths during inhalation and exhalation.

This model was formulated such that the volume and airflow were functions of time, rather than have time as an explicit variable in the model. The time dependence did not explicitly exist within the model equation, allowing the complex time dependence to reside within the variables rather than explicitly within the model equation. This work examines some of the consequences of the model and validates predictions with patient data.

MATERIALS AND METHODS

Derivation of divergence relationship

The breathing motion model was proposed with a linear relationship between tidal volume, airflow, and the subsequent tissue displacement. The position $\vec{X}$ of tissue was modeled as

$$\vec{X}\left(v,f:{\vec{X}}_0\right)={\vec{X}}_0+\vec{\alpha }\left({\vec{X}}_0\right)v+\vec{\beta }\left({\vec{X}}_0\right)f,$$ (1)

where ${\vec{X}}_0$ was the position of the tissue under the conditions of tidal volume v=0 and airflow f=0, $\vec{\alpha }\left({\vec{X}}_0\right)$ characterized the displacement of lung tissues from air filling, and $\vec{\beta }\left({\vec{X}}_0\right)$ characterized the hysteresis motion. $\vec{\alpha }$ had units of distance per tidal volume (mm l⁻¹ in this work) and $\vec{\beta }$ had units of distance per airflow (mm s l⁻¹ in this work). Equation 1 does not have time explicitly included. The time dependence is imbedded in v and f.

This first-order model was assumed to accurately represent breathing motion under the conditions of quiet respiration, which was typically characterized by smooth changes in tidal volume and airflow. In this model, the physical processes that were modeled by the tidal volume and airflow were assumed to be independent of one another, so the hysteresis behavior occurred independently of lung filling. For example, if the hysteresis component of motion for a specific piece of tissue (located at ${\vec{X}}_0$) was $\vec{\beta }\left({\vec{X}}_0\right)$, the hysteresis motion was the same whether the tidal volume was at inhalation, exhalation, or in between.

The model accuracy has been studied by Low et al.¹ and investigations are ongoing to evaluate the consistency of model parameters both in the case of irradiated and unirradiated lungs.

The objective of this manuscript was to examine whether the model behaved correctly when applied to the continuity equation. The continuity equation stated that the relationship between a velocity field $\vec{U}$ and density ρ was

$$\vec{\nabla }\cdot \rho \vec{U}=-\frac{\partial \rho }{\partial t},$$ (2)

where t was time and the velocity vector field $\vec{U}=d\vec{X}∕dt$. Expanding the left side of Eq. 2,

$$\vec{\nabla }\rho \cdot \vec{U}+\rho \vec{\nabla }\cdot \vec{U}=-\frac{\partial \rho }{\partial t}.$$ (3)

Equation 3 states that the change in lung tissue density, as a function of time, at a point in space is due to two causes. The first term of Eq. 3 is the inner product of the gradient of the tissue density and the tissue velocity. When there is a gradient in the tissue density and the tissue moves past the point of observation, the density at the point of observation will change in time. The second term describes the change in density due to expansion or contraction of the velocity field. The local expansion and contraction of lung tissue was likely to be a physiologically relevant quantity to study, so the first term was subtracted from both sides of the equation. This resulted in

$$\rho \vec{\nabla }\cdot \vec{U}=-\frac{d\rho }{dt}.$$ (4)

In the proposed breathing motion model, time was not the dependent variable, so the chain rule was employed to change the variable from t to v and f, yielding terms with the derivatives dv∕dt and df∕dt. In order to simplify the equation, the constraint of a constant airflow df∕dt=0 was applied. This yielded

$$\rho \frac{dv}{dt}\left\{\frac{\partial }{\partial x}\frac{\partial x}{\partial v}+\frac{\partial }{\partial y}\frac{\partial y}{\partial v}+\frac{\partial }{\partial z}\frac{\partial z}{\partial v}\right\}=-\frac{\partial \rho }{\partial v}\frac{dv}{dt}.$$ (5)

Equation 1 provided the relationship between the tidal volume, airflow, and the tissue position. Taking the partial derivatives of the position vectors and dividing both sides by ρ dv∕dt lead to

$$\vec{\nabla }\cdot \vec{\alpha }=-\frac{1}{\rho }\frac{\partial \rho }{\partial v},$$ (6)

where the equation was valid under conditions of constant airflow. This equation was obtained by dividing both sides by ρ dv∕dt, so in principle it was not valid when either the density or the airflow were zero, but it was valid in the limit that they went to zero.

Evaluation equations

Equation 6 showed that under conditions of constant airflow, the relative local density changed as a function of tidal volume by an amount equal to the divergence of the $\vec{\alpha }$ field. The hypothesis was that the local density variation as a function of inhaled tidal volume, and consequently $\vec{\alpha }$, would remain consistent with time (days or weeks) if the lungs were not affected by disease or treatment intervention such as radiation therapy.

Measuring the local density change directly from CT scans acquired during free breathing would normally be challenging due to the complex hysteresis motion during respiration. However, with the approach proposed by Low et al.,¹ the position of the tissues at the individual free breathing CT scans could be correlated against the tidal volumes and airflows to generate the model parameters $\vec{\alpha }$ and $\vec{\beta }$. According to Eq. 6, the divergence of $\vec{\alpha }$ provided the relative density variation as though the patient had breathed infinitely slowly (consistent with the constant airflow restriction) so that hysteresis effects were not present.

While Eq. 6 provided the potential for examining the lung density variations, a validation of the equation would provide a powerful validation of the breathing motion model and its consequences. The left side of Eq. 6 was integrated throughout the lungs so Gauss’ theorem could be used to compare that integral to a surface integral

$${\int }_V\vec{\nabla }\cdot \vec{\alpha }dV={\oint }_S\vec{\alpha }\cdot d\vec{S},$$ (7)

where the integral on the left of Eq. 7 would be conducted throughout the entire lung volume V through volume elements dV, and the surface integral on the right would be conducted on the lung surface $\vec{S}$ through surface area elements $d\vec{S}$, which represent an infinitesimal surface area element whose direction was normal to the lung surface.

The term on the right could be expressed as

$${\oint }_S\vec{\alpha }\cdot d\vec{S}=\oint \frac{\vec{X}\left(v,f:{\stackrel{⃑}{X}}_0\right)-{\vec{X}}_0-\vec{\beta }\left({\vec{X}}_0\right)f}{v}\cdot d\vec{S}.$$ (8)

At end of inhalation and exhalation, the airflow equals zero. At these two phases, Eq. 8 became

$$\oint \vec{\alpha }\cdot d\vec{S}=\frac{1}{v}\oint \left(\vec{X}\left(v,f=0:{\stackrel{⃑}{X}}_0\right)-{\vec{X}}_0\right)\cdot d\vec{S}.$$ (9)

$\vec{X}\left(v,f=0:{\stackrel{⃑}{X}}_0\right)-{\vec{X}}_0$ was the displacement vector of an infinitesimal surface element on the lung, its vector product with the surface area was the change in lung volume through the infinitesimal surface. The integral of the displacement over the whole lung boundary gave the total change in lung volume due to inspiration at end of inhalation. The ratio of lung volume change to the tidal volume had been established to be 1.11,² the ratio of room air to lung air densities. Therefore,

$$\oint \vec{\alpha }\cdot d\vec{S}=\mathrm{1.11.}$$ (10)

Using Gauss’ law, Eq. 10 became

$${\int }_V\vec{\nabla }\cdot \vec{\alpha }dV=\mathrm{1.11.}$$ (11)

Equation 11 provided a useful test metric for the motion model. It indicated that for every patient and every 4DCT scan session, the integral of the divergence of $\vec{\alpha }\left({\vec{X}}_0\right)$ must be 1.11.

The value of $\vec{\beta }\left({\vec{X}}_0\right)$ was tested in a similar way. $\vec{\beta }$ related motion to airflow, which in the breathing motion model was assumed to be proportional to internal pressure imbalances that occurred during the act of inhalation and exhalation. Similar to the analysis of Eq. 7 where the surface integral of $\vec{\alpha }$ described the inflation of the lungs, the surface integral of $\vec{\beta }$ also described lung inflation, this time due to hysteresis. Because lung inflation due to changes in tidal volume was modeled by $\vec{\alpha }$, the lung inflation due to hysteresis should have been negligible, but unlike Eq. 10, integrating the divergence of $\vec{\beta }$ did not provide a unitless quantity (it had units of time), so interpretation of the results would have been difficult. Instead, the ratio of surface integrals of $\vec{\beta }$ to $\vec{\alpha }$ was defined, multiplying each integral by the maximum airflow f_max and tidal volume v_max. The surface integrals described the integrated rate of inflation. Multiplying the rate of inflation by the appropriate variable would yield the total inflation. For example, $\vec{\alpha }$ had units of distance per tidal volume, so by multiplying the surface integral by tidal volume gave the expansion at the lung surface at the maximum tidal volume. Similarly, $\vec{\beta }$ had units of distance per airflow, so multiplying by the maximum airflow gave the amount of lung inflation due to hysteresis. The ratio, defined as R, compared the maximum volume expansion for these two components.

$$R\equiv \frac{f_{\text{max}}}{v_{\text{max}}}\frac{\oint \vec{\beta }\cdot d\vec{S}}{\oint \vec{\alpha }\cdot d\vec{S}}.$$ (12)

The motion model predicted that the influence of tidal volume and airflow mechanics were independent and that the inflation was predicted by the volume component, so the $\vec{\beta }$ component, and consequently the ratio R, should have been equal to zero. The ratio of v_max∕f_max can be found in Table 1 for all patients enrolled in this study. The surface integral in the denominator of Eq. 12 was provided in Eq. 10. Applying Gauss’ law to the numerator of Eq. 12,

$$R=\frac{{\int }_V\vec{\nabla }\cdot \vec{\beta }dV}{1.11\times \frac{v_{\text{max}}}{f_{\text{max}}}}.$$ (13)

Like Eq. 11, this provided a test of the model parameter, in this case $\vec{\beta }\left({\vec{X}}_0\right)$.

Table 1.

v_max∕f_max of all the patients.

	Lung patients			Nonlung patients
	vmax (l)	fmax (l∕s)	vmax∕fmax (s)	vmax (l)	fmax (l∕s)	vmax∕fmax (s)
1	497.9	556.9	0.89	587.3	521.1	1.13
2	480.0	626.0	0.77	982.4	412.2	2.38
3	271.4	412.1	0.66	630.9	513.7	1.23
4	358.8	372.3	0.96	472.1	288.3	1.64
5	256.4	315.6	0.81	463.3	461.9	1.00
6	630.5	653.2	0.97	615.9	281.2	2.19
7	317.1	556.9	0.57	528.2	432.5	1.22
8	411.4	359.1	1.15	541.5	508.3	1.07
9	399.1	367.0	1.09	633.7	550.9	1.15
10	449.0	461.9	0.97	398.2	318.7	1.25
11	318.3	472.3	0.67	404.4	305.6	1.32
12	408.0	332.4	1.23	308.8	302.8	1.02
13	409.1	416.9	0.98	1438.7	611.1	2.35
14	459.0	402.5	1.14	335.7	356.1	0.94
15	848.9	699.4	1.21	523.9	443.8	1.18
16	557.9	321.6	1.73	569.1	425.5	1.34
17	971.0	510.0	1.90	240.0	349.7	0.69
18	546.6	595.7	0.92
Mean			1.03			1.36
VAR			0.12			0.25
STD			0.34			0.49
Overall
Mean	1.19
VAR	0.20
STD	0.45

Evaluation method

Equations 11, 13 were evaluated using clinical data from 35 patients. These patients were scanned using a 16-slice CT (Philips Brilliance, Philips Medical Systems, Cleveland, OH) scanner operated in ciné mode (spatial resolution: 0.98×0.98×1.5 mm³) with 25 scans acquired contiguously at each 24 mm wide couch position. Two external respiratory measurements were simultaneously acquired: Tidal volume measured using a spirometer (VMM-400, Interface Associates, Aliso Viejo, CA) and a bellows pressure signal measured using a pneumatic belt system that was wrapped around the abdomen. The bellows pressure measurement was correlated with the spirometry measurement to provide the tidal volume and airflow at each scan. Lu et al.³ described this technique in detail.

The tissue positions were mapped for each scan using the normalized cross-correlation. The scan with tidal volume closest to 0 ml (defined as the fifth percentile tidal volume) was employed as the reference scan. The remaining scans were sorted by tidal volume and categorized into whether they were acquired during inhalation or exhalation. The position matching was performed in the inhalation and exhalation category separately, ordered by increasing tidal volume and using the reference scan as the initial guess for the first operation in each category. The result from each match was used as the initial guess for the next match in the tidal volume order.

After the positions were mapped, the values of $\vec{\alpha }$, $\vec{\beta }$, and ${\vec{X}}_0$ were fit by minimizing the least-squares difference of the predicted [Eq. 1] and measured positions. The integrals of the divergences in Eqs. 11, 13 were computed and the results were used to evaluate the model quality.

RESULTS

Of the 35 data sets, 18 were from lung cancer patients and 17 were from non-lung-cancer patients. Table 1 lists the maximum tidal volume and airflow. The mean ratio of maximum airflow to tidal volume was v_max∕f_max=1.19s±0.45s.

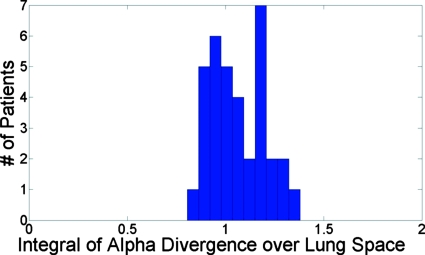
Tables 2, 3 list the results of Eqs. 11, 13 for each patient, respectively. According to Eq. 11, the prediction of ${\int }_V\vec{\nabla }\cdot \vec{\alpha }dV$ was 1.11 while the mean measured value was 1.06±0.14. Figure 1 shows a histogram of the values of ${\int }_V\vec{\nabla }\cdot \vec{\alpha }dV$ for the 35 patients. The predicted and mean measured values agreed within 5% and the spread of the results was relatively narrow.

Table 2.

Integral of ${\int }_V\vec{\nabla }\cdot \vec{\alpha }dV$ conducted over both lungs.

	Lung patient	Nonlung patient
1	1.189	1.076
2	1.203	1.160
3	1.276	0.968
4	0.928	0.888
5	1.217	1.100
6	1.026	1.239
7	1.082	1.081
8	1.208	1.007
9	0.941	1.107
10	0.911	0.918
11	1.274	1.202
12	0.942	1.160
13	1.045	0.806
14	1.381	1.015
15	0.922	1.031
16	0.869	1.172
17	0.899	0.965
18	1.005
Mean	1.073	1.053
VAR	0.159	0.119
STD	0.024	0.014
Overall
Mean	1.063
VAR	0.019
STD	0.139

Table 3.

Integral ${\int }_V\vec{\nabla }\cdot \vec{\beta }∕1.11\times v_{\text{max}}∕f_{\text{max}}dV$ conducted over both lungs.

	Lung patient	Nonlung patient
1	0.076	0.050
2	0.065	0.050
3	0.018	−0.003
4	−0.000	−0.018
5	0.024	−0.002
6	0.009	−0.000
7	0.035	0.003
8	0.043	−0.001
9	0.002	−0.004
10	0.083	0.012
11	0.052	0.032
12	0.003	−0.023
13	−0.014	−0.001
14	0.050	0.007
15	0.033	0.027
16	0.001	0.006
17	−0.003	−0.010
18	0.024
Mean	0.028	0.007
VAR	0.001	0.000
STD	0.029	0.021
Overall
Mean	0.018
VAR	0.001
STD	0.027

Figure 1.

Histogram of the integral of ${\int }_V\vec{\nabla }\cdot \vec{\alpha }dV$ for the 35 evaluated patient scans, predicted to be 1.11 according to Eq. 11.

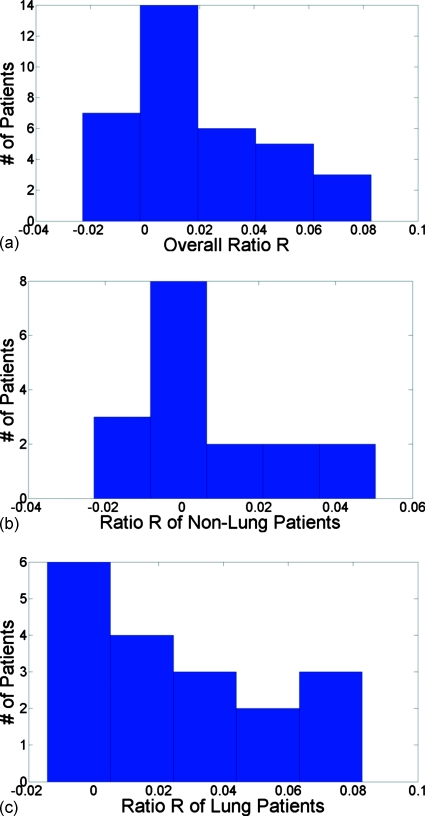
The prediction of R was 0. Figure 2a shows a histogram of the values of R for the 35 patients. The average value was 0.017±0.027. Figure 2b shows a histogram of the values of R for 17 non-lung-cancer patients with average value at 0.007±0.021. Figure 2c shows a histogram of the values of R for 18 lung cancer patients with an average value at 0.028±0.029. All the results were very close to the prediction of 0.

Figure 2.

(a) Histogram of $R={\int }_V\vec{\nabla }\cdot \vec{\beta }dV∕1.11\times v_{\text{max}}∕f_{\text{max}}$ for 35 patients. (b) Histogram of R in nonlung cancer patients. (c) Histogram of R in lung cancer patients.

DISCUSSION

Although Fig. 2 and Table 3 showed that the R ratios of both lung cancer and non-lung-cancer patients were very close to the prediction of 0, the results from non-lung-cancer patients, whose lungs were assumed to function more normally than lung cancer patients’, lay closer to the prediction, indicating that the motion model might be more robust for non-lung-cancer patients.

Both of the quantitative evaluations of the motion model showed that the predictions of the model agreed well with clinical data. The overall utility of the motion model will ultimately be tested by repeated testing in patients, but the data shown here have provided significant evidence to the model’s validity.

The reason that this analysis was possible was that the motion model used tidal volume and its time derivative airflow as the motion metrics and as independent variables. Most published breathing motion studies or models have used metrics such as abdomen height or a belt wrapped around the abdomen, neither of which provided a physiologic metric that could be used to provide independent verification of a motion model. The use of tidal volume and airflow allowed the model predictions to be validated, in this case using the continuity equation.