Abstract
Basic games, where each individual chooses between two strategies, illustrate several issues that immediately emerge from the standard approach that applies strategic reasoning, based on rational decisions, to predict population behavior where no rationality is assumed. These include how mutual cooperation (which corresponds to the best outcome from the population perspective) can evolve when the only individually rational choice is to defect, illustrated by the Prisoner's Dilemma (PD) game, and how individuals can randomize between two strategies when neither is individually rational, illustrated by the Battle of the Sexes (BS) game that models male-female conflict over parental investment in offspring. We examine these questions from an evolutionary perspective where the evolutionary dynamics includes an impulsive effect that models sudden changes in collective population behavior. For the PD game, we show analytically that cooperation can either coexist with defection or completely take over the population, depending on the strength of the impulse. By extending these results for the PD game, we also show that males and females each evolve to a single strategy in the BS game when the impulsive effect is strong and that weak impulses stabilize the randomized strategies of this game.
Introduction
A great deal of game-theoretic research has been devoted to explain the prevalence of cooperation in biological systems as well as in human society. One reason for the vast literature from members of the game theory community on this topic is that their methods do not work for the underlying stage game, the symmetric Prisoner's Dilemma, which pits cooperative behavior against its nemesis of defection. In particular, the only rational option in this PD stage game is to Defect since this strategy strictly dominates Cooperate (i.e. a player is better off defecting than cooperating no matter what the opponent does).
On the other hand, cooperation can be rational when the payoffs of the PD game are modified by assuming some relatedness between the players [1], [2], by them playing the game an uncertain number of times [3], or by extending the model to a multi-player (i.e. more than two) public goods game [4]. These predictions are often based on applying either static (e.g. evolutionarily stable strategy (ESS)) or dynamic (e.g. the replicator equation) methods from evolutionary game theory [5] that assumes a large population of agents paired at random to play the game. Population interactions that are structured either spatially (e.g. through nearest neighbors on a lattice) or socially (e.g. through adjacent nodes in a graph) also enhance the evolution of cooperation [6]–[11] as do the stochastic effects of finite populations [12].
To a lesser extent, the question of stability of mixed strategy equilibrium solutions (and their interpretation) has also created controversy in the game theory community [13], [14]. This is especially true of two-player non symmetric games due to the result that, at any evolutionarily stable state of such games, players must use pure strategies [15]. The controversy here is clearly demonstrated through typical payoffs used in the Battle of the Sexes game [5], [16], [17] introduced into biology by Dawkins [18] to model the conflict between males and females concerning their respective contributions to parental investment (see also the Buyer-Seller game [19] that has the same qualitative payoff structure). In the BS stage game, each player has two pure strategies and the only equilibrium solution is for both players to use a mixture of their strategies. Furthermore, the replicator equation applied to this game yields periodic solutions around this mixed strategy equilibrium pair even though Maynard Smith [17] (Chapter 11C) states that “I am unable to offer illustrative examples, or evidence that such cycles occur.”
In this article, we re-examine the PD and BS stage games from the dynamic perspective where, in addition to the continuous trajectories of evolutionary game theory, there are periodic jumps in the population size. In biological systems, these latter impulsive perturbations may be due to sudden changes in the physical environment (e.g. the effects of climate change or natural disaster) or to intrinsic diurnal/nocturnal and seasonal life history effects in the physiological and reproductive mechanisms of individuals in the population. Impulsive perturbations have also been used to model the effect on human behavior of sudden market corrections or of sudden shifts in the business cycle [20]. We assume that the impulsive “coefficient” for an individual depends only on its strategy and analyze the resultant dynamics. In particular, we give analytic conditions for the coefficients in the PD game for the successful initial invasion of Cooperators into a population of Defectors as well as conditions based on stronger impulsive effects for Cooperators to completely take over the system. We also show that these latter conditions applied to the BS game imply global convergence to a monomorphic system where all males use one pure strategy as well as all females. Moreover, when impulsive effects are weak in the BS game, a globally attracting polymorphic state emerges near the mixed equilibrium pair.
Analysis
Prisoner's Dilemma
The PD stage game is ubiquitous in the game theory literature and so needs no introduction. We follow the standard notation by taking its payoff matrix as
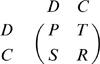 |
(1) |
where 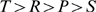 . The entries in this matrix give the payoff to the row player in a two-player interaction with the column player (e.g. if a player Defects against an opponent who Cooperates, his payoff is
. The entries in this matrix give the payoff to the row player in a two-player interaction with the column player (e.g. if a player Defects against an opponent who Cooperates, his payoff is 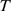 ). Since
). Since 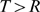 and
and 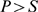 , Defect strictly dominates Cooperate and so it is the only rational outcome of this one shot game.
, Defect strictly dominates Cooperate and so it is the only rational outcome of this one shot game.
To illustrate how periodic impulses can be combined with an evolutionary dynamics, suppose that the replicator equation (see Eq.4a below) models behavioral evolution. From a biological perspective, these dynamics result from a direct correspondence between expected payoff and reproductive success [21]. Specifically, if 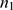 and
and 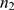 are the numbers of Defectors and Cooperators respectively in the population at time
are the numbers of Defectors and Cooperators respectively in the population at time  , then
, then
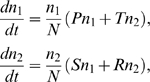 |
(2) |
where 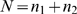 is the total population size. Here
is the total population size. Here 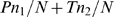 is the expected payoff to a Defector in a single interaction with a randomly chosen opponent assuming that population size is large. From Taylor and Jonker [21], the population dynamics (Eq.2) implies the frequency
is the expected payoff to a Defector in a single interaction with a randomly chosen opponent assuming that population size is large. From Taylor and Jonker [21], the population dynamics (Eq.2) implies the frequency 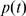 of Defectors in the population (i.e.
of Defectors in the population (i.e. 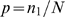 ) evolves according to the replicator equation (Eq.4a).
) evolves according to the replicator equation (Eq.4a).
Now suppose that individuals die at periodic intervals 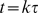 for
for 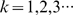 . That is, reproductive success (i.e. fitness) in Eq.2 refers only to births. Deaths cause a jump in the solution trajectories of Eq.2 of the form
. That is, reproductive success (i.e. fitness) in Eq.2 refers only to births. Deaths cause a jump in the solution trajectories of Eq.2 of the form 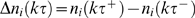 where
where 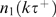 (respectively,
(respectively, 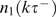 ) is the number of Defectors immediately after (respectively before) the jump. If the death rate of each strategy type is independent of population size, then
) is the number of Defectors immediately after (respectively before) the jump. If the death rate of each strategy type is independent of population size, then
| (3) |
for some 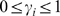 . The parameter
. The parameter 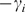 is called the “impulsive coefficient” for the i-th strategy. The dynamical system with periodic impulsive effects combines Eq.2 when
is called the “impulsive coefficient” for the i-th strategy. The dynamical system with periodic impulsive effects combines Eq.2 when 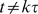 with Eq.3 when
with Eq.3 when 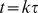 . In particular, for every nonnegative initial condition
. In particular, for every nonnegative initial condition 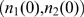 , this impulsive dynamical system has a unique nonnegative solution for all
, this impulsive dynamical system has a unique nonnegative solution for all  .
.
Evolutionary game theory is more concerned with the evolution of strategy frequencies than with how the absolute numbers of strategy users evolve over time. It is shown in File S1 (see also [22]) that
| (4a) |
| (4b) |
where 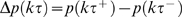 denotes the jump in
denotes the jump in 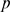 at moment
at moment 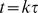 . That is,
. That is, 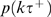 (respectively,
(respectively, 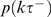 ) is the frequency of Defector immediately after (respectively before) the jump. For the analysis of this dynamical system, it is important to notice that the frequency dynamics Eq.4 is independent of population size
) is the frequency of Defector immediately after (respectively before) the jump. For the analysis of this dynamical system, it is important to notice that the frequency dynamics Eq.4 is independent of population size 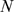 . When there are no impulsive effects, we have the standard replicator equation Eq.4a
[21]. For this reason, we call Eq.4 the replicator equation with periodic impulses.
. When there are no impulsive effects, we have the standard replicator equation Eq.4a
[21]. For this reason, we call Eq.4 the replicator equation with periodic impulses.
Remark
The replicator equation with periodic impulses developed above is based on continuous births throughout the season and deaths only at the end. One consequence of our assumptions is that birth and death rates are independent of population size. It can be shown [22] that dynamics Eq.4 also emerges when birth rates are altered by any strategy-independent background fitness (which is usually assumed to decrease as population size increases). This background fitness can be used to investigate the dynamics of total population size and not only the frequency dynamics as in the standard approach to evolutionary game theory [21]. The dynamics Eq.4 also models other periodic impulses in biological systems such as regular perturbations in the physical environment. It is well-documented [23]–[25] that humans (and other biological species) exhibit more cooperation in the face of natural disasters (also called the disaster syndrome). Such shifting of aggregate population behavior through individuals changing their strategy becomes a positive jump in the proportion of Cooperators. In fact, any impulsive coefficients in Eq.3 satisfying 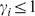 are suitable since
are suitable since 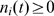 for all
for all  in this case. The interpretation of
in this case. The interpretation of 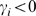 is that the impulse is then beneficial to the i-th strategy.
is that the impulse is then beneficial to the i-th strategy.
From Eq.4a, 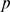 strictly increases during the season (i.e.
strictly increases during the season (i.e. 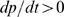 ) if
) if 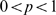 since
since 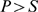 and
and 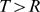 . Thus, if the Defector death rate is no higher than the Cooperator (i.e.
. Thus, if the Defector death rate is no higher than the Cooperator (i.e. 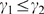 ), the population must evolve to all Defect since
), the population must evolve to all Defect since 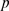 also increases at the end of each season. However, if the death rates benefit Cooperators (i.e. if
also increases at the end of each season. However, if the death rates benefit Cooperators (i.e. if 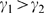 ), the effect of Defector deaths may offset their higher birth rates and so it is unclear which effect dominates (see Figure 1). In the extreme case where
), the effect of Defector deaths may offset their higher birth rates and so it is unclear which effect dominates (see Figure 1). In the extreme case where 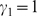 , all Defectors die at the end of the first season and the population is all Cooperate thereafter.
, all Defectors die at the end of the first season and the population is all Cooperate thereafter.
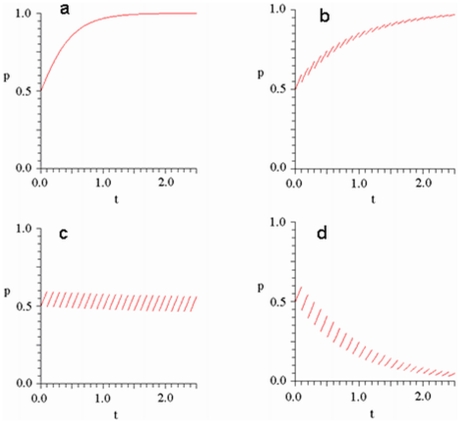
Figure 1. Trajectories for the replicator equation with periodic impulses (4) when payoffs 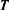 ,
, 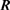 ,
, 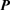 ,
, 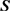 of the PD game are fixed at
of the PD game are fixed at 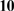 ,
,  ,
,  ,
, 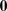 respectively and the initial frequency of Defect is
respectively and the initial frequency of Defect is 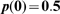 .
.
Here 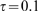 and the values taken for
and the values taken for 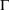 are (a)
are (a)  ; (b)
; (b) 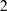 ; (c)
; (c) 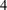 ; and (d)
; and (d)  .
.
For these reasons, we will assume that 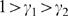 for the remainder of this section. The key to understanding the outcome in this scenario is to determine the stability of the boundary equilibria
for the remainder of this section. The key to understanding the outcome in this scenario is to determine the stability of the boundary equilibria 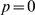 and
and 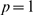 of Eq.4. Heuristically, when
of Eq.4. Heuristically, when 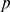 is near 0, the trajectory
is near 0, the trajectory 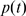 during the first season is approximated by
during the first season is approximated by 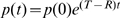 since, from Eq.4a,
since, from Eq.4a, 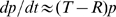 . Also, from Eq.4b, the jump at the end of this season is
. Also, from Eq.4b, the jump at the end of this season is 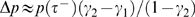 . For (asymptotic) stability of all Cooperate (i.e. for
. For (asymptotic) stability of all Cooperate (i.e. for 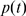 to converge to 0 if it is initially close to 0), we expect that
to converge to 0 if it is initially close to 0), we expect that 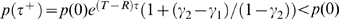 . This is true if and only if
. This is true if and only if
| (5) |
Notice that 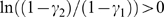 when
when 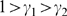 and so there are payoff matrices with
and so there are payoff matrices with 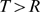 for which all Cooperate is stable.
for which all Cooperate is stable.
It is proved analytically in File S1 (see also [22]) that 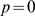 is stable if inequality Eq.5 is true and unstable (i.e.
is stable if inequality Eq.5 is true and unstable (i.e. 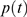 diverges from 0 if it is initially close) if this inequality is reversed (i.e.
diverges from 0 if it is initially close) if this inequality is reversed (i.e. 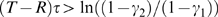 ). It is also shown there that all Defect is stable if
). It is also shown there that all Defect is stable if
| (6) |
and unstable if the inequality is reversed. In fact, the dynamic stability of the boundary equilibria for threshold parameters when Eq.5 or Eq.6 is an equality is also characterized there. Besides one exceptional case discussed in the final paragraph of this section when both Eq.5 and Eq.6 are equalities, there is a unique interior  -periodic trajectory (i.e. a
-periodic trajectory (i.e. a 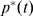 with
with 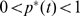 for all
for all 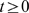 and
and 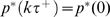 for all
for all 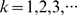 ) if and only if either both boundary equilibria are unstable or both are stable. In the first (respectively, second) case,
) if and only if either both boundary equilibria are unstable or both are stable. In the first (respectively, second) case, 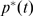 is globally stable (respectively, unstable). Finally, if exactly one boundary equilibrium is stable, then it is globally stable in that it attracts all interior trajectories.
is globally stable (respectively, unstable). Finally, if exactly one boundary equilibrium is stable, then it is globally stable in that it attracts all interior trajectories.
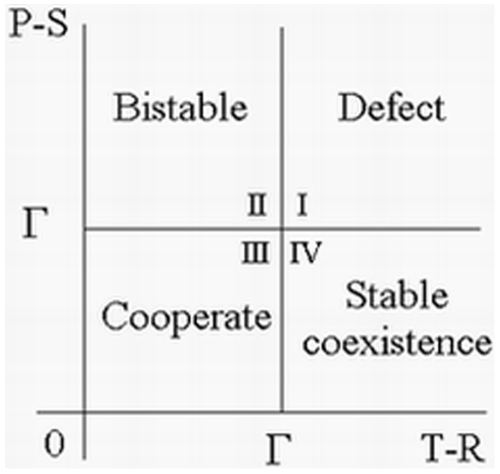
These analytic results from File S1, that are summarized in the preceding paragraph, are illustrated in Figures 1 and 2 for non threshold cases. In Figure 1, trajectories of Eq.4 are given for fixed payoff parameters and four different values of
| (7) |
In Figure 2, 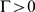 is fixed and the stability of boundary equilibria and interior
is fixed and the stability of boundary equilibria and interior  -periodic trajectories is characterized in different regions of the space with parameters
-periodic trajectories is characterized in different regions of the space with parameters  and
and 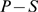 .
.
Figure 2. Regions of payoff parameter space determined by a fixed positive value of 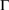 in Eq.7.
in Eq.7.
In region I, 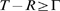 and
and 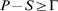 , and all Defect is globally stable; in region II,
, and all Defect is globally stable; in region II, 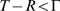 and
and 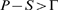 , both all Cooperate and all Defect are (locally) stable, and there exists an unstable
, both all Cooperate and all Defect are (locally) stable, and there exists an unstable  -periodic solution; in region III,
-periodic solution; in region III, 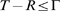 and
and 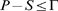 , and all Cooperate is globally stable; and in region IV,
, and all Cooperate is globally stable; and in region IV,  and
and 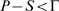 , both all Cooperate and all Defect are unstable, and there exists a globally stable
, both all Cooperate and all Defect are unstable, and there exists a globally stable  -periodic solution corresponding to a mixture of Cooperators and Defectors.
-periodic solution corresponding to a mixture of Cooperators and Defectors.
For small values of  , the population evolves to all Defect (Figs. 1a and 1b). An initial small population of Cooperators can successfully invade a population of Defectors once
, the population evolves to all Defect (Figs. 1a and 1b). An initial small population of Cooperators can successfully invade a population of Defectors once 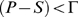 . Cooperators then completely take over the population if inequality
. Cooperators then completely take over the population if inequality 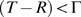 also holds (Fig. 1d and quadrant III in Fig. 2); otherwise the system approaches a globally stable
also holds (Fig. 1d and quadrant III in Fig. 2); otherwise the system approaches a globally stable  -periodic state consisting of a mixture of Cooperators and Defectors (Fig. 1c and quadrant IV in Fig. 2). If
-periodic state consisting of a mixture of Cooperators and Defectors (Fig. 1c and quadrant IV in Fig. 2). If 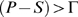 as in quadrants I and II of Figure 2, either all Defect completely takes over or we have a bistable situation where all Cooperate can persist if their initial frequency is sufficiently high.
as in quadrants I and II of Figure 2, either all Defect completely takes over or we have a bistable situation where all Cooperate can persist if their initial frequency is sufficiently high.
It is instructive to consider the case of small impulsive effects (i.e. when the impulsive coefficients 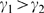 are both close to
are both close to 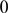 ). By Taylor's expansion,
). By Taylor's expansion, 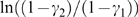 is approximately equal to
is approximately equal to 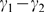 . Then Eq.7 becomes
. Then Eq.7 becomes
which represents the average impulsive effect over one season in favor of Cooperate. By inequalities Eq.5 and Eq.6, if the positive payoff advantage during the season to Defect over Cooperate is always less than this average impulsive effect (i.e. if 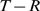 and
and  are both less than
are both less than  ), Cooperators invade and take over the population. This intuitive result can be generalized to all situations where impulsive effects are nearly equal (i.e.
), Cooperators invade and take over the population. This intuitive result can be generalized to all situations where impulsive effects are nearly equal (i.e. 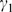 is close to
is close to 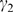 but they are not necessarily close to 0) (see also File S1). The central message here is that a small difference in the death rates of Cooperators and Defectors can have a major impact on the evolution of cooperation.
but they are not necessarily close to 0) (see also File S1). The central message here is that a small difference in the death rates of Cooperators and Defectors can have a major impact on the evolution of cooperation.
In fact, if we call  defined in Eq.7 the average impulsive effect over one season in favor of Cooperate for any choice of
defined in Eq.7 the average impulsive effect over one season in favor of Cooperate for any choice of 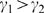 , the intuitive result of the previous paragraph remains true.
, the intuitive result of the previous paragraph remains true.
In the exceptional case where 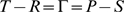 , the boundary equilibria are neutrally stable and every trajectory
, the boundary equilibria are neutrally stable and every trajectory 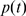 for any initial condition
for any initial condition 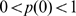 is
is  -periodic. Interestingly, the special payoffs for the PD game that satisfy
-periodic. Interestingly, the special payoffs for the PD game that satisfy 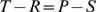 have attained prominence recently since this class includes the simplified PD games [1], [26] with payoff matrix
have attained prominence recently since this class includes the simplified PD games [1], [26] with payoff matrix
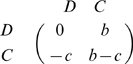 |
(8) |
Here 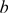 is the payoff benefit a player interacting with a Cooperator gains and
is the payoff benefit a player interacting with a Cooperator gains and  is the cost paid by Cooperators. Under the usual assumption that
is the cost paid by Cooperators. Under the usual assumption that 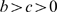 , the entries in this simplified payoff matrix have the same ordering as in Eq.1. From Eq.5 and Eq.6, if
, the entries in this simplified payoff matrix have the same ordering as in Eq.1. From Eq.5 and Eq.6, if 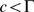 (respectively,
(respectively, 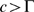 ), then all Cooperate (respectively, all Defect) is the final outcome. Unlike other studies on the simplified PD game [26] where the emergence of Cooperative behavior often depends on the cost-benefit ratio
), then all Cooperate (respectively, all Defect) is the final outcome. Unlike other studies on the simplified PD game [26] where the emergence of Cooperative behavior often depends on the cost-benefit ratio 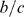 , here it depends only on the cost of Cooperation. The size of the payoff benefit has no impact on our results since neither the replicator equation Eq.4a nor the impulse Eq.4b depends on
, here it depends only on the cost of Cooperation. The size of the payoff benefit has no impact on our results since neither the replicator equation Eq.4a nor the impulse Eq.4b depends on 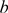 . In our model, it is the impulsive benefit
. In our model, it is the impulsive benefit  that replaces the payoff benefit
that replaces the payoff benefit 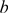 . In particular, Cooperation emerges if and only if the impulsive benefit to Cooperators is greater than the cost paid by Cooperators. That is, periodic impulses that favor cooperation provide a mechanism that promotes the evolution of cooperation.
. In particular, Cooperation emerges if and only if the impulsive benefit to Cooperators is greater than the cost paid by Cooperators. That is, periodic impulses that favor cooperation provide a mechanism that promotes the evolution of cooperation.
Battle of the Sexes
In the BS stage game, male strategies are either “faithful” or “philandering” and females are “coy” or “fast” [18]. In the following two paragraphs, we briefly summarize well-known facts about this game [5], [16], [17].
If parental investment costs  , the benefit gained from an offspring is
, the benefit gained from an offspring is 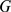 and the cost of a long engagement is
and the cost of a long engagement is 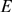 , then the payoffs to males and females are given in the following bimatrix (e.g. a philanderer receives the benefit
, then the payoffs to males and females are given in the following bimatrix (e.g. a philanderer receives the benefit 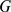 against a fast female whose net payoff is then
against a fast female whose net payoff is then  ).
).
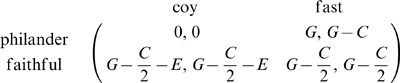 |
(9) |
With the usual assumptions that these payoffs satisfy 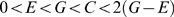 , the characteristic feature of the BS game is the cyclical character of male and female best responses. If females are coy, it pays males to be faithful; if males are faithful, it pays females to be fast; if females are fast, it pays males to philander; and if males philander, it pays females to be coy. This characteristic also leads to cycling in the standard evolutionary dynamics that is concerned with the evolution of strategy frequencies.
, the characteristic feature of the BS game is the cyclical character of male and female best responses. If females are coy, it pays males to be faithful; if males are faithful, it pays females to be fast; if females are fast, it pays males to philander; and if males philander, it pays females to be coy. This characteristic also leads to cycling in the standard evolutionary dynamics that is concerned with the evolution of strategy frequencies.
Let 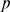 be the frequency of philanders in the male population and
be the frequency of philanders in the male population and 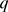 be the frequency of coy females in their population. The bimatrix replicator equation is then
be the frequency of coy females in their population. The bimatrix replicator equation is then
| (10a) |
| (10b) |
This two-dimensional dynamics on the unit square has the unique interior equilibrium 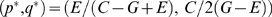 and all trajectories are periodic orbits surrounding
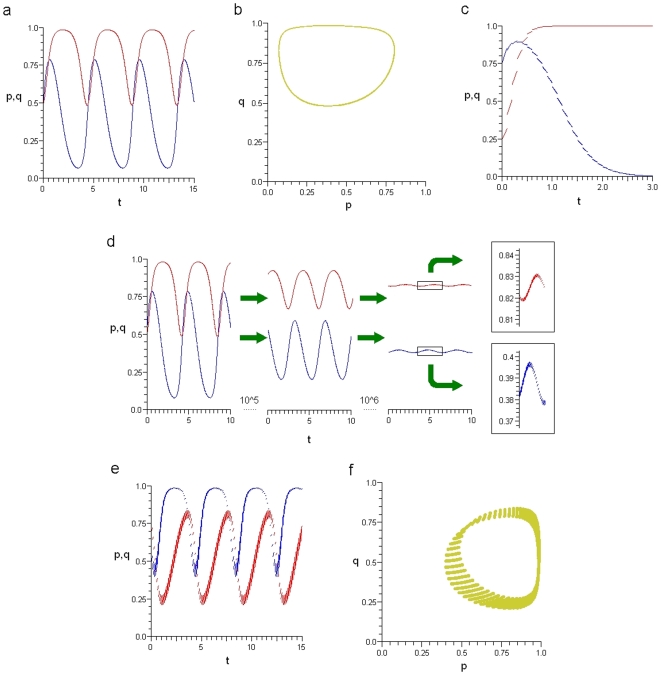
and all trajectories are periodic orbits surrounding 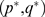 [5], [16], [17]. Figure 3a-b illustrates a typical trajectory of Eq.10 for the payoffs.
[5], [16], [17]. Figure 3a-b illustrates a typical trajectory of Eq.10 for the payoffs.
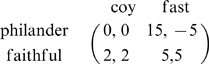 |
considered by Dawkins [18] that has 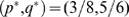 .
.
Figure 3. Trajectories for the bimatrix replicator equation with periodic impulses for the BS game in the 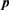 -
-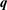 phase plane, where
phase plane, where 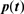 and
and 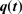 are represented by blue and red curves, respectively.
are represented by blue and red curves, respectively.
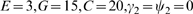 and
and 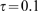 , i.e., the payoff matrix is
, i.e., the payoff matrix is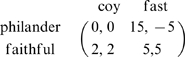 |
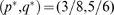 . The minimum period
. The minimum period 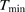 is about
is about 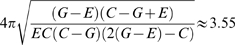 . In Figure 3a–b,
. In Figure 3a–b, 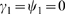 (no impulses) and the time step is from 1 to 15. All the interior trajectories are periodic orbits surrounding
(no impulses) and the time step is from 1 to 15. All the interior trajectories are periodic orbits surrounding 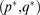 . In Figure 3c,
. In Figure 3c, 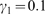 and
and 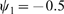 (strong impulses) and the time step is from 1 to 3. Since
(strong impulses) and the time step is from 1 to 3. Since 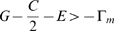 and
and 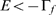 , from Table 1, boundary equilibrium
, from Table 1, boundary equilibrium 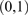 is stable and all the interior trajectories converge to
is stable and all the interior trajectories converge to 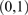 . In Figure 3d,
. In Figure 3d, 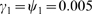 (weak impulses) and the time steps are respectively 1 to 10,
(weak impulses) and the time steps are respectively 1 to 10, 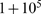 to
to 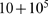 and
and 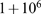 to
to 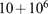 . All the interior trajectories converge to an attracting set within 0.015 of the interior equilibrium
. All the interior trajectories converge to an attracting set within 0.015 of the interior equilibrium 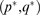 . In Figure 3e–f,
. In Figure 3e–f, 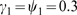 (intermediate impulses) and the time step is from 1 to 15. Clearly, interior trajectories do not always evolve to either a boundary equilibrium or to a set close to
(intermediate impulses) and the time step is from 1 to 15. Clearly, interior trajectories do not always evolve to either a boundary equilibrium or to a set close to  .
.We again assume that trajectories of the replicator equation are based on male and female births throughout the season and that there are jumps at 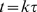 for
for 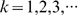 due to deaths at the end of the season. If the male (respectively, female) death rate is
due to deaths at the end of the season. If the male (respectively, female) death rate is 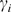 (respectively,
(respectively,  ) for their
) for their  -th strategy, these latter periodic impulses are
-th strategy, these latter periodic impulses are
| (11a) |
| (11b) |
at 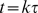 where
where 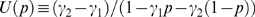 and
and 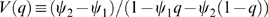 . The bimatrix replicator equation with periodic impulses combines Eq.10 at
. The bimatrix replicator equation with periodic impulses combines Eq.10 at 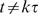 with Eq.11 at
with Eq.11 at 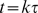 .
.
The analysis of this impulsive dynamical system is more difficult than the replicator equation with periodic impulses for the PD game. We will assume that 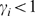 and
and 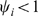 for
for 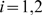 . Each edge of the unit square is then invariant (as is the interior of the square). For example, on the edge where
. Each edge of the unit square is then invariant (as is the interior of the square). For example, on the edge where 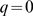 , we have
, we have
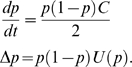 |
This impulsive dynamics is the same as that for the PD game with simplified payoffs Eq.8 given by 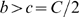 .
.
That is, on the edge where all females are fast, the game is one where males are playing a simplified PD game among themselves. Thus, all males will eventually be faithful if they have a lower death rate than philanderers (i.e., 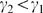 ) that satisfies
) that satisfies 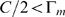 where
where 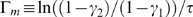 is the impulsive benefit for faithful males (cf. the discussion in the PD section about Eq.7). If
is the impulsive benefit for faithful males (cf. the discussion in the PD section about Eq.7). If 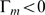 , it is an impulsive benefit for philandering males. On the other hand, philanderers will take over if their death rate is lower or if
, it is an impulsive benefit for philandering males. On the other hand, philanderers will take over if their death rate is lower or if 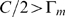 . In this section, we will not consider threshold parameter values where all trajectories on an edge are
. In this section, we will not consider threshold parameter values where all trajectories on an edge are  -periodic. Similarly, on the edge where all males are faithful, there is a simplified PD game among females (where
-periodic. Similarly, on the edge where all males are faithful, there is a simplified PD game among females (where  is now identified with
is now identified with 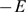 ). Let
). Let 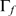 be the impulsive benefit for fast females (i.e.,
be the impulsive benefit for fast females (i.e.,  ). Thus, all females will eventually be fast (respectively, coy) if the cost of a long engagement is greater than (respectively, less than) the impulsive benefit for coy females, i.e.
). Thus, all females will eventually be fast (respectively, coy) if the cost of a long engagement is greater than (respectively, less than) the impulsive benefit for coy females, i.e. 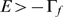 ) (respectively,
) (respectively, 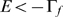 ).
).
In fact, 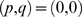 will be stable for the bimatrix replicator equation with periodic impulses (Eq.10 and Eq.11) on the unit square if males are eventually faithful on the first edge and females are eventually fast on the second edge. This result is indicated in the first row of Table 1 that summaries the stability of all four vertices of the unit square. The proof is in File S1 where it is also shown that, if one vertex is stable, then it is globally stable (i.e. all trajectories in the interior of the unit square converge to it). In particular, at most one vertex can be stable.
will be stable for the bimatrix replicator equation with periodic impulses (Eq.10 and Eq.11) on the unit square if males are eventually faithful on the first edge and females are eventually fast on the second edge. This result is indicated in the first row of Table 1 that summaries the stability of all four vertices of the unit square. The proof is in File S1 where it is also shown that, if one vertex is stable, then it is globally stable (i.e. all trajectories in the interior of the unit square converge to it). In particular, at most one vertex can be stable.
Table 1. Stability of Boundary Equilibria 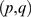 (
(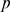 is the frequency of males who philander and
is the frequency of males who philander and 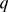 is the frequency of coy females).
is the frequency of coy females).
Boundary Equilibrium 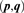
|
Conditions for Stability of Boundary Equilibrium |
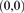
|
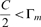 and and 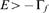
|
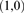
|
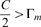 and and 
|
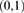
|
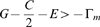 and and 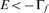
|
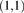
|
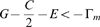 and and 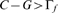
|
From Table 1, if impulsive effects are strong enough on any edge to reverse the flow of the replicator equation Eq.10 there (i.e., if any of the inequalities 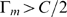 ,
, 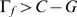 ,
, 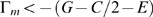 , or
, or 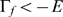 are true), then there is a globally stable pure strategy pair for males and females. In particular, these periodic impulses have removed the characteristic interior cycles of the BS game and replaced them with global stability at a vertex. Figure 3c illustrates a typical trajectory of Eq.10, Eq.11 when one of the stability conditions for the vertex (1,0) in Table 1 are satisfied.
are true), then there is a globally stable pure strategy pair for males and females. In particular, these periodic impulses have removed the characteristic interior cycles of the BS game and replaced them with global stability at a vertex. Figure 3c illustrates a typical trajectory of Eq.10, Eq.11 when one of the stability conditions for the vertex (1,0) in Table 1 are satisfied.
When impulses are not strong (i.e. when 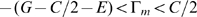 and
and 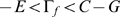 ), the limiting behavior of each trajectory on the boundary of the unit square is the same whether or not periodic impulses Eq.11 are combined with the bimatrix replicator dynamics; namely, all these trajectories evolve to the first vertex encountered in a counterclockwise direction. On the other hand, no interior trajectory evolves to a point on the boundary. Figure 3e–f illustrates a typical trajectory when impulses are of intermediate strength. Notice that this trajectory does not surround
), the limiting behavior of each trajectory on the boundary of the unit square is the same whether or not periodic impulses Eq.11 are combined with the bimatrix replicator dynamics; namely, all these trajectories evolve to the first vertex encountered in a counterclockwise direction. On the other hand, no interior trajectory evolves to a point on the boundary. Figure 3e–f illustrates a typical trajectory when impulses are of intermediate strength. Notice that this trajectory does not surround 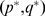 since the impulses occur before it has enough time to do so. In fact, through simulations (see File S1), it is apparent that the properties of such trajectories are quite complex with multiple
since the impulses occur before it has enough time to do so. In fact, through simulations (see File S1), it is apparent that the properties of such trajectories are quite complex with multiple  -periodic solutions possible. The number
-periodic solutions possible. The number 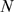 of these solutions appears to depend linearly on the ratio of
of these solutions appears to depend linearly on the ratio of  to the minimum period
to the minimum period 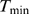 of interior periodic cycles of the bimatrix replicator dynamics Eq.10 in that it is approximated by
of interior periodic cycles of the bimatrix replicator dynamics Eq.10 in that it is approximated by 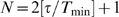 where [ ] is the integer part of a positive real number. Proofs of these conjectures suggested by simulations are beyond the current techniques available to analyze these impulsive systems. We are hopeful that game-theoretic intuition will extend these techniques in future research and, in the process, improve our understanding of how arbitrary periodic impulses affect the evolutionary dynamics, especially for non symmetric two-player games (such as the BS game) with a unique equilibrium in the interior of the strategy space.
where [ ] is the integer part of a positive real number. Proofs of these conjectures suggested by simulations are beyond the current techniques available to analyze these impulsive systems. We are hopeful that game-theoretic intuition will extend these techniques in future research and, in the process, improve our understanding of how arbitrary periodic impulses affect the evolutionary dynamics, especially for non symmetric two-player games (such as the BS game) with a unique equilibrium in the interior of the strategy space.
Finally, for weak impulses (i.e. for 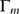 and
and 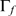 both close to 0 and at least one nonzero) with
both close to 0 and at least one nonzero) with 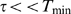 , simulations show that all interior trajectories evolve to a small neighborhood of
, simulations show that all interior trajectories evolve to a small neighborhood of 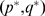 (see Figure 3d). Specifically, although the limiting behavior is not exactly the interior equilibrium, the large periodic cycles of the bimatrix replicator dynamics are replaced by orbits that become arbitrarily close to this equilibrium as the impulsive effect weakens. In fact, except for the one
(see Figure 3d). Specifically, although the limiting behavior is not exactly the interior equilibrium, the large periodic cycles of the bimatrix replicator dynamics are replaced by orbits that become arbitrarily close to this equilibrium as the impulsive effect weakens. In fact, except for the one  -periodic solution, it appears that all trajectories approach the single orbit in Figure 3d (which is not
-periodic solution, it appears that all trajectories approach the single orbit in Figure 3d (which is not  -periodic).
-periodic).
In summary, both strong and weak impulsive effects promote stability in BS games. Strong impulses imply the system has a globally stable outcome where all males adopt the same strategy as do all females (i.e. both sexes exhibit monomorphic behavior). On the other hand, weak impulses eliminate the wild fluctuations typical of the periodic cycles of the bimatrix replicator dynamics Eq.10 and replace them with an attracting set near its interior equilibrium that consists of a stable polymorphic population of males and females.
Results and Discussion
Our model combining periodic impulses with an evolutionary dynamics is based on several simplifying assumptions. First, population sizes are assumed to be sufficiently large that stochastic effects due to finite populations are ignored in the deterministic dynamics and fitness is given by expected payoff as in the original development of the replicator equation [21]. Our assumption that death rates depend only on strategy type then implies total population size does not influence the evolution of strategy frequencies given by our replicator equation with periodic impulses. Moreover, in the BS game, we have adopted the unstated common assumption of evolutionary game theory applied to asymmetric games with a bimatrix payoff matrix [5] that individual fitness is based on one random interaction per unit time between different types of individuals.
The analysis of the effects of periodic impulses becomes more complex when finite populations and/or unequal population sizes of different types in asymmetric games are included. In particular, the dynamics of total population size must then be taken into account. From this perspective, our analysis of the frequency effects of periodic impulses can be viewed as a base model against which these more complex systems can be compared, in much the same way that the replicator equation of evolutionary game theory has served as a means to gain an intuitive understanding of behavioral evolution. Our analytic results, that characterize when periodic impulses favoring cooperation in the PD game can overcome the selective advantage of defection and when both strong and weak impulses have a stabilizing effect in the BS game, can then be tested (perhaps numerically) to see if they continue to hold in more complicated models that do not satisfy our simplifying assumptions.
Supporting Information
Supporting information for “Stability and Cooperation through Periodic Impulses”.
(1.03 MB DOC)
Acknowledgments
The authors thank the anonymous referee for helpful suggestions on the original paper.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This research was supported by The National Basic Research Program (973) (No. 2007CB109107) of the People's Republic of China and by an Individual Discovery Grant from the Natural Sciences and Engineering Research Council of Canada. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Hamilton WD. The genetical evolution of social behavior. J Theor Biol. 1964;7:1–16. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
- 2.Taylor PD, Wild G, Gardner A. Direct fitness or inclusive fitness: how should we model kin selection. J Evol Biol. 2007;20:296–304. doi: 10.1111/j.1420-9101.2006.01196.x. [DOI] [PubMed] [Google Scholar]
- 3.Axelrod R. The Evolution of Cooperation. New York: Basic Books; 1984. [Google Scholar]
- 4.Sigmund K, Hauert C, Nowak MA. Reward and punishment. Proc Natl Acad Sci USA. 2001;98:10757–10762. doi: 10.1073/pnas.161155698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press; 1998. [Google Scholar]
- 6.Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
- 7.Nowak MA, May RM. The spatial dilemmas of evolution. Int J Bifur Chaos Appl Sci Eng. 1993;3:35–78. [Google Scholar]
- 8.Hauert C, Doebeli M. Spatial structure often inhibits the evolution of cooperation in the Snowdrift game. Nature. 2004;428:643–646. doi: 10.1038/nature02360. [DOI] [PubMed] [Google Scholar]
- 9.Nowak MA. Evolutionary Dynamics. Cambridge, MA: Harvard Univ. Press; 2006. [Google Scholar]
- 10.Nowak MA. Five rules for the evolution of cooperation. Science. 2006;314:1560–1563. doi: 10.1126/science.1133755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ohtsuki H, Hauert C, Lieberman E, Nowak MA. A simple rule for the evolution of cooperation on graphs and social networks. Nature. 2006;441:502–505. doi: 10.1038/nature04605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nowak MA, Sasaki A, Taylor C, Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature. 2004;428:646–650. doi: 10.1038/nature02414. [DOI] [PubMed] [Google Scholar]
- 13.Maynard Smith J. Can a mixed strategy be stable in a finite population? J Theor Biol. 1988;130:247–251. [Google Scholar]
- 14.Echenique F, Edlin A. Mixed equilibria are unstable in games of strategic complements. J Econ Theory. 2004;118:61–79. [Google Scholar]
- 15.Selten R. A note on evolutionarily stable strategies in asymmetric conflicts. J Theor Biol. 1980;84:93–101. doi: 10.1016/s0022-5193(80)81038-1. [DOI] [PubMed] [Google Scholar]
- 16.Schuster P, Sigmund K. Coyness, philandering and stable strategies. Anim Behav. 1981;29:186–192. [Google Scholar]
- 17.Maynard Smith J. Evolution and the Theory of Games. Cambridge: Cambridge University Press; 1982. [Google Scholar]
- 18.Dawkins R. The Selfish Gene. Oxford: Oxford University Press; 1976. [Google Scholar]
- 19.Cressman R. Evolutionary Dynamics and Extensive Form Games. Cambridge, MA: MIT Press; 2003. [Google Scholar]
- 20.Korn R. Some applications of impulse control in mathematical finance. Math. Meth Oper Res. 1999;50:493–518. [Google Scholar]
- 21.Taylor PD, Jonker L. Evolutionarily stable strategies and game dynamics. Math Biosciences. 1978;40:145–156. [Google Scholar]
- 22.Wang SC, Zhang BY, Li ZQ, Cressman R, Tao Y. Evolutionary game dynamics with impulsive effects. J Theor Biol. 2008;254:384–389. doi: 10.1016/j.jtbi.2008.05.016. [DOI] [PubMed] [Google Scholar]
- 23.Douty CM. Disasters and Charity: Some Aspects of Cooperative Economic Behavior. Am Econ Review. 1972;62:580–590. [Google Scholar]
- 24.De Alessi L. Toward an analysis of postdisaster cooperation. Am Econ Review. 1975;65:127–138. [Google Scholar]
- 25.Frey BS, Savage DA, Torgler B. Surviving the Titanic Disaster: Economic, Natural and Social Determinants. 2009. CESifo Working Paper Series No. 2551. Available at SSRN: http://ssrn.com/abstract=1347962.
- 26.Nowak MA, Sigmund K. Evolution of indirect reciprocity. Nature. 2005;437:1291–1298. doi: 10.1038/nature04131. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting information for “Stability and Cooperation through Periodic Impulses”.
(1.03 MB DOC)