Abstract
The use of the replica exchange (RE) molecular dynamics (MD) method for the efficient estimation of conformational populations of ligand-sized molecules in solution is investigated. We compare the computational efficiency of the traditional constant temperature MD technique to that of the parallel RE molecular dynamics method for a series of alkanes and rilpivirine (TMC278), an inhibitor against HIV-1 reverse transcriptase, with implicit solvation. We show that conformational populations are accurately estimated by both methods, however replica exchange estimates converge at a faster rate especially for rilpivirine which is characterized by multiple stable states separated by high free energy barriers. Furthermore convergence is enhanced when the weighted histogram analysis method (WHAM) is employed to estimate populations from the data collected from multiple RE temperature replicas. For small drug-like molecules with energetic barriers separating the stable states, the use of RE with WHAM is an efficient computational approach for estimating the contribution of ligand conformational reorganization to binding affinities.
I. INTRODUCTION
Constant temperature Molecular Dynamics (MD) conformational sampling of systems with rugged potential energy landscapes is problematic due to trapping in local minimum free-energy states. This is often manifested in poor coverage of conformational space and slow rates of convergence of thermodynamic quantities. Generalized ensemble conformational sampling algorithms [1–17] can circumvent these difficulties by adopting sampling distributions with more favorable characteristics than traditional methods. One of best known generalized ensemble algorithms is the temperature replica-exchange (RE) method [1, 2]. The RE method is a well-established and powerful technique to sample the rough energy landscapes of biomolecules, allowing rapid interconversion between conformations separated by high energy barriers.
In the most common implementations [18–20] several replicas of the system are run in parallel over a series of temperatures using constant temperature MD. Periodically exchanges of conformations are attempted between pairs of replicas, using a scheme designed to preserve canonical sampling at each temperature. Unlike conformational search techniques, temperature RE can be used to calculate thermodynamic quantities, such as conformational free energies, at each simulated temperature. Finally, the RE method is inherently a parallel algorithm well suited to take advantage of the large number of processors in modern computing clusters [21].
Although RE is a parallel simulation technique that is relatively straightforward to implement, there is still much to learn about how best to employ RE simulations in computational biophysics. In some circumstances questions have been raised about the efficiency of the algorithm relative to traditional constant temperature MD [22–24]. The efficiency of temperature replica exchange (RE) simulations hinges on their ability to enhance conformational sampling at physiological temperature by taking advantage of more rapid conformational interconversions at higher temperatures. Studies from our laboratory have pointed out that processes characterized by anti-Arrhenius kinetics behavior, such as protein folding, represent a challenge for temperature RE [25, 26]. Contrary to normal Arrhenius behavior, whereby the rates of kinetic processes increase with increasing temperature, anti-Arrhenius kinetics is characteristic of processes with smaller transition rates at higher temperatures. In these cases RE cannot take advantage of the normally faster kinetics at high temperatures to help convergence at low temperatures.
Additionally, RE incurs a higher computational cost than constant temperature MD if only data at one temperature is used to estimate populations at that temperature. This is because all of the samples from a constant temperature simulation can be directly employed to calculate physical quantities at the set temperature. On the other hand, a large fraction of the computational effort of RE is devoted to simulating the system at temperatures other than the temperature of interest, thereby producing mainly data which may or may not be useful in the estimation of physical quantities at the temperature of interest. Consequently, it is often unclear whether the enhancements of conformational sampling obtainable with RE are sufficient to offset the higher computational costs in order for RE to yield higher computationally efficiency than MD.
In this paper we present an analysis of the relative efficiency of temperature RE and constant temperature MD with respect to the computation of the conformational populations of a series of small molecules with implicit solvation. The study of the distribution of conformations of ligand-sized molecules in water is important for the estimation of the reorganization free energy component of the binding free energies of protein-ligand complexes. The phenomenon of conformational reorganization, sometimes referred to as conformational selection or induced fit [27], is recognized as a key factor to understand drug binding affinity, specificity and resistance. It generally refers to the free energy penalty incurred by the binding partners for reorganizing the distribution of conformations present in their unbound forms to those compatible with complexation.
The ligand component ΔF of the binding reorganization free energy is directly related to the population p in solution of the conformational state corresponding to the bound conformation by means of the equation
| (1) |
where kB is the Boltzmann constant. Thus, the estimation of ligand conformational free energies rests on the ability to obtain converged values of ligand conformational populations.
The systems we study in this work are a series of alkanes, and rilpivirine [28] (also known as TMC278, the name that will be used in the following), a potent inhibitor of reverse transcriptase enzyme of the human HIV virus. We perform MD and temperature RE simulations in vacuum and implicit solvation with the same total number of steps for these molecules and compare their computational efficiency defined in terms of the reduction of the statistical uncertainty of conformational populations at equal computational cost. We also test the applicability of the the temperature Weighted Histogram Analysis Method (T-WHAM) [29], a method that allows the utilization of data from multiple temperature replicas to improve the estimates of conformational populations at the temperature of interest. We find that RE, and especially RE in conjunction with WHAM, is more computationally efficient than constant temperature MD in converging the conformational populations of these small molecular systems. We rationalize this finding based on the relatively small number of degrees of freedom of these molecules limiting the rate of expansion of conformational space with increasing temperature which, for larger systems such as peptides and proteins, causes difficulties for RE sampling. In addition, the energetic, rather than entropic, nature of the free energy barriers between the stable states of these molecules allows more rapid conformational sampling at higher temperatures further enhancing the convergence rate. The WHAM method is found to be particularly helpful for estimating accurately small populations corresponding to high energy states which become more probable with increasing temperature.
In Section II computational details of the serial canonical MD simulations and the RE simulations are presented. Results and discussion are presented in Sec. III. Section IV is devoted to conclusions.
II. METHODS
We performed MD simulations of butane, pentane, and hexane in vacuum and TMC278 with AGBNP implicit solvation [30]. The numbers of dihedral angles excluding methyl groups rotations are one for butane, two for pentane, and three for hexane. The chemical structure of TMC278, which contains five rotatable bonds is shown in Fig. 1. The OPLS 2005 force field was used.[31] We employed the Nosé-Hoover thermostat,[32–34] whose equations of motion are
| (2) |
| (3) |
| (4) |
where ri, pi, mi, and Fi are coordinates, momentum, mass, and force of atom i, respectively. The variable ζ is a “viscosity” parameter for temperature control. The constant g is related to the number of atoms N as g = 3N − 6. The constant Q is the artificial “mass” for the thermostat. 𝒯 (t) and T0 are the instantaneous temperature and the set temperature, respectively. We integrated the equations of motion in Eqs. (2)–(4) by the time-reversible algorithm by Martyna et al. [35]. We used the relation Q = gkBT0τ2 for the Nosé-Hoover thermostat[36] with a relaxation time of τ = 10 fs. The MD time step was set to Δt = 0.5 fs.
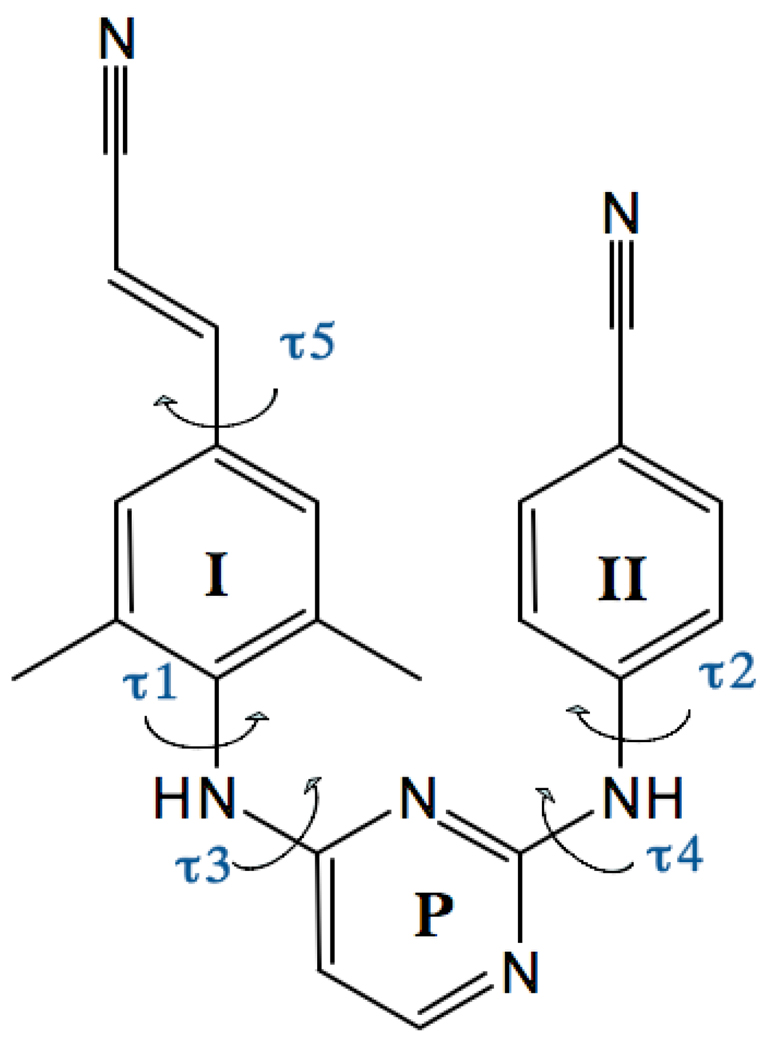
FIG. 1.
Chemical structure of TMC278. Wing I, wing II and pyrimidine rings labeled as I, II, and P respectively. Black arrows correspond to rotations associated with torsion angles τ1–τ5.
Serial molecular dynamics simulations were conducted at T0 = 300 K. We performed equilibration runs for 20 ns and then sampled conformations for 80 ns for the alkanes. For TMC 278, we performed an equilibration run for 50 ns and sampled conformations for 200 ns. Parallel replica exchange MD simulations were performed with four replicas at 300 K, 350 K, 400 K, and 450 K for the alkanes and with eight replicas at 300 K, 350 K, 400 K, 450 K, 500 K, 550 K, 600 K, and 650 K for TMC278. We performed REMD for 20 ns after 5 ns equilibration for the alkanes and for 25 ns after 6.25 ns equilibration runs for TMC278. The total sampling times are 80 ns for each alkane and 200 ns for TMC278. These sampling times are the same as for the corresponding serial MD simulations. Temperature exchanges were attempted 1 ps between adjacent temperatures and were accepted with probability
| (5) |
where βi = 1/kBTi and βj = 1/kBTi are the inverse temperature before the exchange and Ei and Ej are the potential energies of replica i and j, respectively.
Dihedral angle distributions at a particular temperature can be calculated by simply binning the data from only the corresponding replica. We also calculated the dihedral angle distributions using the temperature WHAM method [29, 37]:
| (6) |
| (7) |
where Pβ(ϕ) is the unnormalized angle distribution at inverse temperature β, M is the number of replicas, Ni(E, ϕ) is the histogram of potential energy, E, and dihedral angles ϕ = (ϕ1, ϕ2, …) at temperature Ti, and ni is the total number of samples at temperature Ti. Eqs. (6) and (7) are solved iteratively [29].
Dihedral angle distributions for the alkanes were also obtained by numerical grid integration of the corresponding partition functions. Let us suppose a model of an alkane with fixed bond lengths. This model has only internal degrees of freedom of dihedral angles ϕ0, ϕ1, … ϕn+1 and bond angles θ1, θ2,… θn+1, where the number of dihedral angles n is n = 1 for butane, n = 2 for pentane, and n = 3 for hexane. ϕ0 and ϕn+1 are the dihedral angles of the ends of the alkane chain, which include hydrogen atoms. Under these assumptions, the partition function Z of the molecule is given by
| (8) |
where the bold letters ϕ and θ denote the set of dihedral angles and bond angles, respectively. is the Jacobian for the ϕ and θ internal coordinates. The dihedral angle distribution P(ϕ1, … , ϕn) is calculated from the partition function Z by
| (9) |
The grid spacing of dihedral angles was set to 10°. Two grid points θeq and θeq + 4°, where θeq is the minimum energy bond angle, were employed for the bond angles integration (the potential energy of the cis conformation of butane is smallest for θ = θeq + 4°).
III. RESULTS AND DISCUSSION
A. Alkanes
The torsional potential of mean force of butane
| (10) |
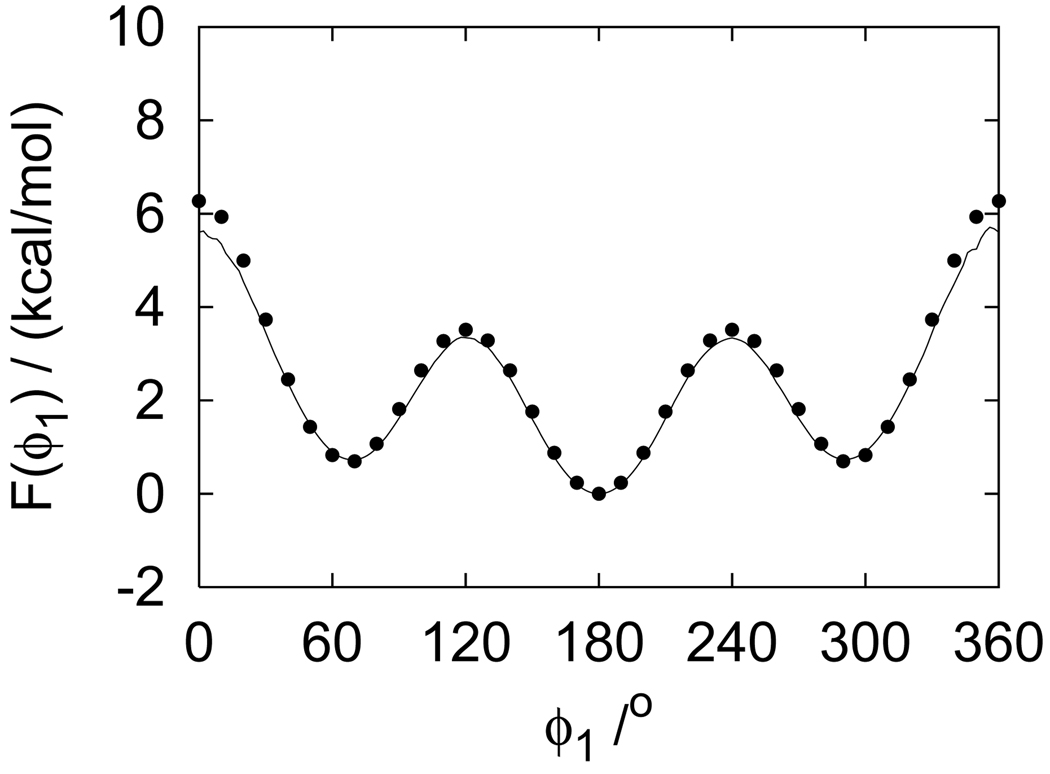
derived from the probability distribution P(ϕ1) computed from the REMD data and WHAM is shown in Fig. 2. Note that as defined F(ϕ1) is set to zero at ϕ1 = 180°. The torsional potential of mean force of butane shows (Fig. 2) the characteristic minima in correspondence with the trans (ϕ1 = 180°) and gauche (ϕ1 = −60, 60°) conformations.
FIG. 2.
Potential of mean force along the dihedral angle of butane obtained by replica exchange MD simulation with WHAM (line). The filled circles correspond to numerical integration results.
The probability of each state p was calculated by integrating the dihedral-angle distribution function. For example, the population pT of the trans state for butane is given by:
| (11) |
where this integral has been performed in the range of 0° ≤ ϕ1 < 120° for the G− state, in the range of 120° ≤ ϕ1 < 240° for the T state, and in the range of 240° ≤ ϕ1 < 360° for the G+ state. The computed populations for the stable states of butane, pentane, and hexane are listed in Table I, Table II, and Table III, respectively. The overall probability of the symmetry-related conformations are given in these tables, that is, the probability of the gauche structure of butane, for example, is the sum of the populations of the G+ and G− conformations.
TABLE I.
Populations of the conformational states of butane at T=300 K. The values in parenthesis indicate the uncertainty on the last digit.
| ϕ1 | MD | RE | RE+WHAM |
|---|---|---|---|
| Trans | 0.66(7) | 0.63(3) | 0.63(3) |
| Gauche | 0.34(7) | 0.37(3) | 0.37(3) |
TABLE II.
Populations of the conformational states of pentane at T=300 K. The values in parenthesis indicate the uncertainty on the last digit.
| ϕ1 | ϕ2 | MD | RE | RE+WHAM |
|---|---|---|---|---|
| Trans | Trans | 0.49(5) | 0.47(3) | 0.47(3) |
| Trans | Gauche+ | 0.45(5) | 0.47(3) | 0.48(2) |
| Gauche+ | Gauche+ | 0.050(13) | 0.050(6) | 0.051(4) |
| Gauche+ | Gauche− | 0.0073(16) | 0.0081(9) | 0.0084(6) |
TABLE III.
Populations of the conformational states of hexane at T=300 K. The values in parenthesis indicate the uncertainty on the last digit.
| ϕ1 | ϕ2 | ϕ3 | serial MD | RE | RE+WHAM |
|---|---|---|---|---|---|
| Trans | Trans | Trans | 0.350(43) | 0.360(28) | 0.356(22) |
| Trans | Trans | Gauche+ | 0.320(22) | 0.328(21) | 0.330(15) |
| Trans | Gauche+ | Trans | 0.158(26) | 0.139(17) | 0.145(13) |
| Trans | Gauche+ | Gauche+ | 0.072(16) | 0.071(9) | 0.067(6) |
| Gauche+ | Trans | Gauche+ | 0.042(17) | 0.041(9) | 0.041(8) |
| Gauche+ | Trans | Gauche− | 0.037(11) | 0.038(4) | 0.039(3) |
| Trans | Gauche+ | Gauche− | 0.0121(13) | 0.0115(20) | 0.0113(9) |
| Gauche+ | Gauche+ | Gauche+ | 0.0060(25) | 0.0100(17) | 0.0087(9) |
| Gauche+ | Gauche+ | Gauche− | 0.0023(7) | 0.0021(9) | 0.0022(3) |
| Gauche+ | Gauche− | Gauche+ | 0.00008(3) | 0.00010(10) | 0.000069(18) |
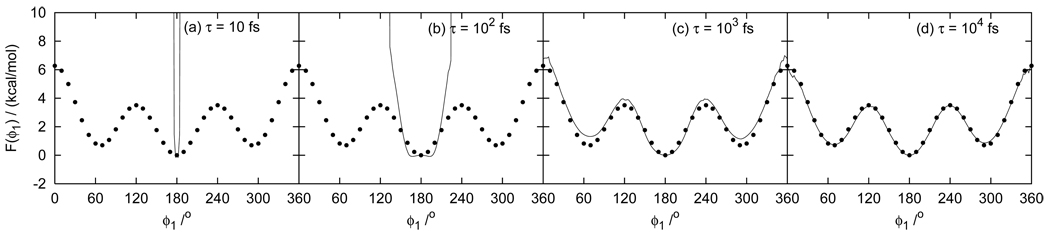
The distributions obtained from the simulations of the alkanes and the populations derived from them were found to be in agreement with numerical integration calculations to within 1% indicating that the Nosé-Hoover thermostat yields correct canonical conformational sampling for these small molecules. We found instead that the Berendsen thermostat [38, 39] (also known as the weak coupling thermostat) can introduce noticeable artifacts for these small molecules. As shown in Fig. 3 for butane, the Berendsen thermostat produces distributions which differ substantially from those obtained with the Nosé-Hoover thermostat and by numerical integration, especially for temperature relaxation times shorter than 100 fs. The same phenomenon was observed for the other alkanes and with both MD and REMD sampling. We observed that for these systems the Berendsen thermostat tends to cause trapping in minimum energy conformations accumulating kinetic energy in the vibration of bonds involving hydrogen atoms. Breakdown of the equipartition of kinetic energy with the Berendsen thermostat has been previously observed [40]. These problems with the Berendsen thermostat are alleviated by employing longer temperature relaxation times (see Fig. 3) at the expense of higher temperature fluctuations. These results indicate that the Berendsen thermostat is not suitable for the present application which requires accurate canonical conformational sampling of molecular systems with relatively few degrees of freedom.
FIG. 3.
Potential of mean force of the dihedral angle of butane by serial MD simulations with the Berendsen thermostat (line). The relaxation time τ is (a) 10 fs, (b) 102 fs, (c) 103 fs, and (d) 104 fs. The filled circles denote numerical integration results.
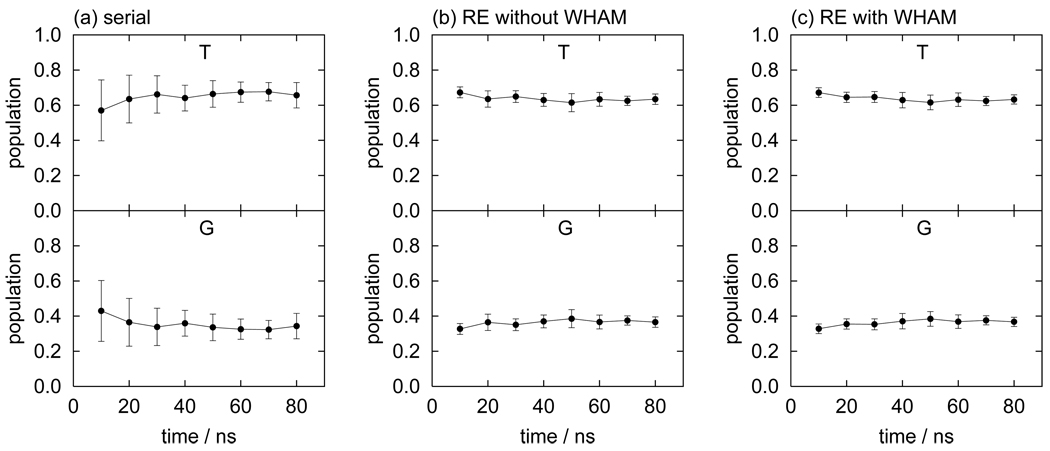
The computed population of the conformational states of butane consistently agree among serial MD, REMD without WHAM (denoted as RE in the following), and REMD with WHAM (RE+WHAM). However, differences in the values of the statistical uncertainties, which we take as a measure of computational efficiency, are noted. Fig. 4 shows the running averages of the population for each conformational state of butane with the corresponding error bars. In order to estimate statistical uncertainties, we divide the production run into five blocks and the uncertainties are estimated from the standard deviation of the five averages from each block. For example, the uncertainties of population at 10 ns were estimated by dividing the first 10 ns into five blocks of 2 ns each. The data listed in all Table I–Table III were obtained by dividing all 80 ns data into five segments of 16 ns each. Fig. 4 shows that the magnitude of the uncertainties follows the order (from smallest to largest): RE+WHAM, RE, and serial MD. The relative uncertainties (δp/p) of the G state, for example, are 7.1% for RE+WHAM, 8.1% for RE, and 21% for serial MD. In this case the RE uncertainty is approximately two times smaller than serial MD, despite the fact that the number of data points from the RE simulation (without WHAM) is only one fourth of the data from the serial canonical MD simulation (the length of the RE simulation with four replicas was set to one quarter of that of the MD simulation to compare the two at the same overall computational cost). The faster convergence observed with RE resides in its ability to overcome energy barriers more frequently than MD thereby reaching faster equilibrium between the conformational basins. The higher statistical efficiency of RE outweighs in this case the availability of fewer samples. The further enhancement of convergence achieved with RE+WHAM (the uncertainty is roughly three times smaller than with MD with the same computational cost) is interpreted as a consequence of the utilization, by means of WHAM, of additional data from the high temperature replicas.
FIG. 4.
Running averages of the populations for the trans (T) and gauche (G) states of butane obtained by (a) serial MD, (b) replica-exchange MD without WHAM, and (c) replica-exchange MD with WHAM.
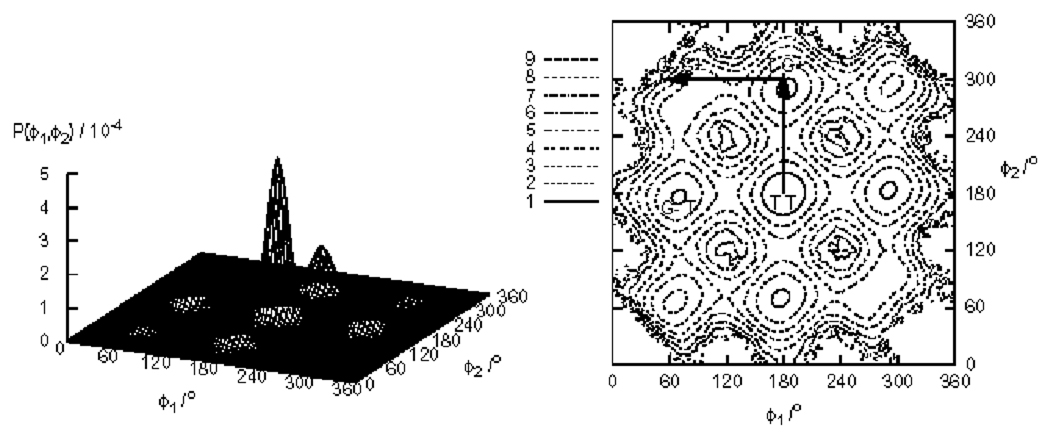
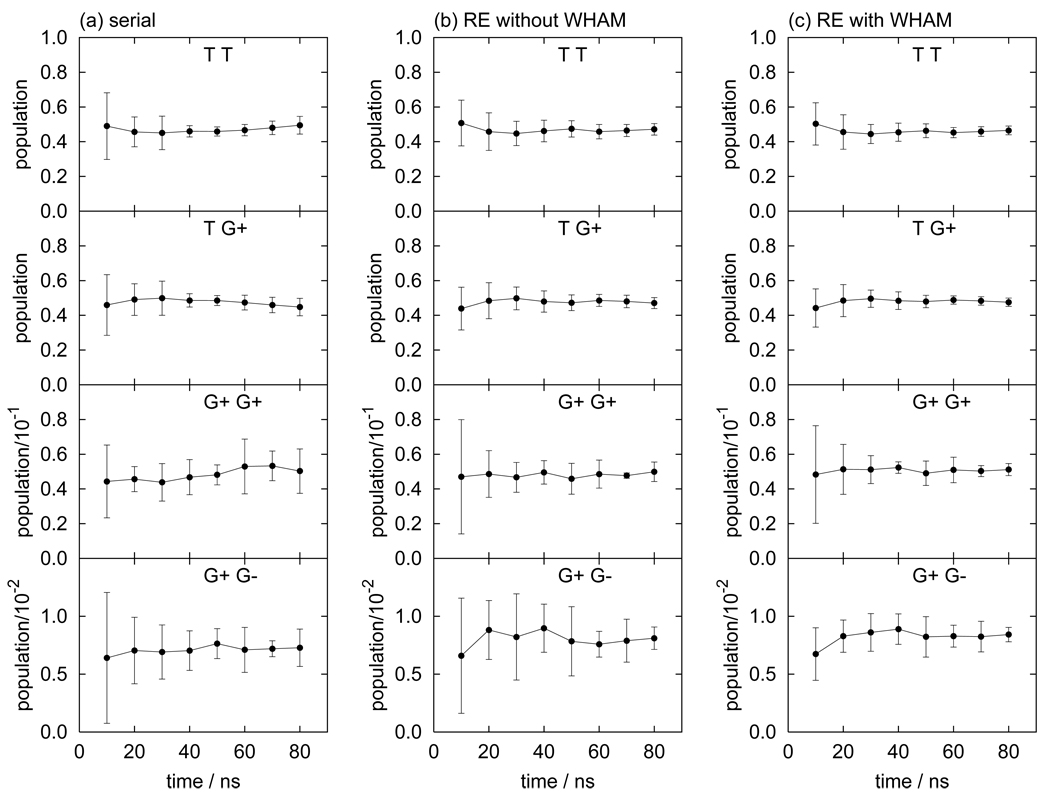
The dihedral angle distribution P(ϕ1, ϕ2) for pentane is shown in Fig. 5. Pentane has a total of nine stable rotamers but only four states are symmetrically independent: trans-trans (TT), trans-gauche+ (TG+), gauche+-gauche+ (G+G+), and gauche+-gauche− (G+G−). The populations of these states are listed in Table II. Fig. 6 shows that, similar to butane, RE yields faster convergence rates of the populations for all conformations. For example the relative population uncertainties for the G+G− state are 7.4% for RE+WHAM, 12% for RE, and 22% for serial MD.
FIG. 5.
Probability distribution P(ϕ1, ϕ2) of the dihedral angles of pentane (left) and the contour map (left) of the corresponding potential of mean force F(ϕ1, ϕ2) obtained by RE+WHAM. Arrows on the contour map indicate the route for the cut shown Fig. 12.
FIG. 6.
Running averages of the populations for the trans-trans (TT), trans-gauche+ (TG+), gauche+-gauche+ (G+G+), and gauche+-gauche− (G+G−) states of pentane obtained by (a) serial MD, (b) replica-exchange MD without WHAM, and (c) replica-exchange MD with WHAM.
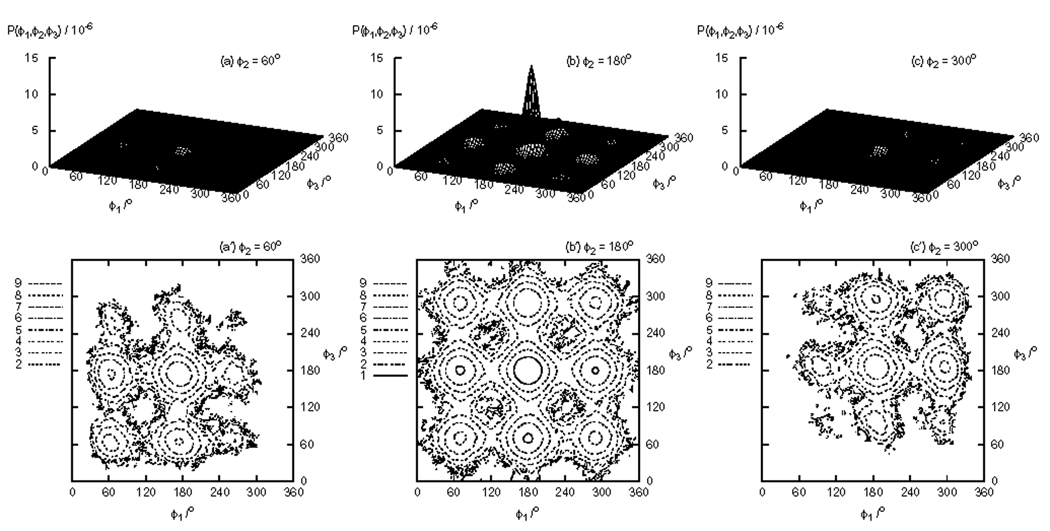
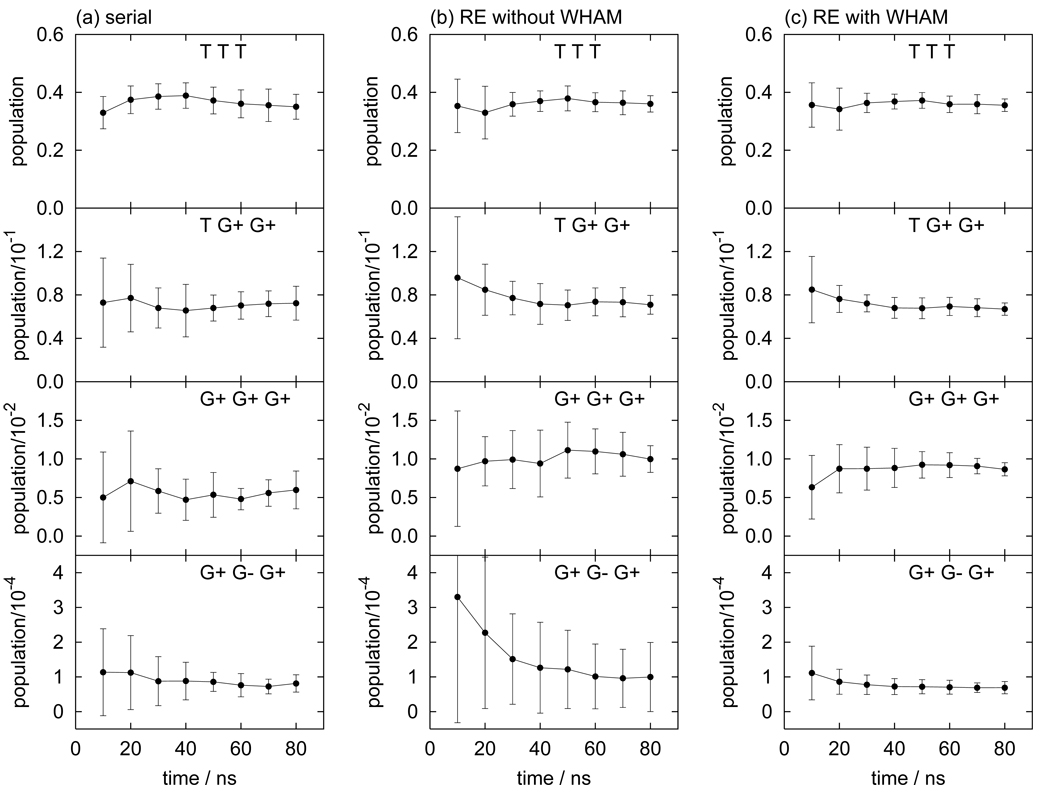
The distribution of dihedral angles P(ϕ1, ϕ2, ϕ3) for hexane is shown in Fig. 7. Because hexane has three dihedral angles, three 2-D distributions are shown at ϕ2 = 60° (G−), ϕ2 = 180° (T), and ϕ2 = 300° (G+). Hexane has a total of 27 stable rotamers of which ten are symmetrically independent, as listed in Table III. Running averages of the populations for the trans-trans-trans (TTT), trans-gauche+-gauche+ (TG+G+), gauche+-gauche+-gauche+ (G+G+G+), and gauche+-gauche−-gauche+ (G+G−G+) states out of the ten states are shown in Fig. 8. This set of states includes the most populated state (TTT) and the least populated state (G+G−G+). For the more populated states (TTT, TG+G+, and G+G+G+), the convergence rate of the populations follows the same order as for butane and pentane. However, for the least populated state (G+G−G+), the convergence rate of RE is worse than serial MD. The relative uncertainty of the population of the G+G−G+ state are 25% for RE+WHAM, 31% for serial MD, and 100% for RE. This indicates that for this particular conformational state the conformational sampling benefit provided by RE is outweighed by the fewer data points available when WHAM is not used. WHAM in this case yields a significant (4-fold) reduction in uncertainty. This is because, as the data listed in Table IV indicates, that the population of this minor state increases with increasing temperature. At T=450 K the computed (RE+WHAM) probability of the G+G−G+ state is more than 10 times larger than at 300 K. This suggests that the higher temperature replicas provide substantial statistics for this state that, when combined with WHAM, yields a significantly more precise estimate of the population. As has been previously discussed [29], temperature-WHAM is generally most useful for the estimation of the free energies of states that are sparsely populated at the temperature of interest and that become more populated at higher temperatures, as well as at lower temperatures [29]. This potential benefit of WHAM is in addition to the enhanced conformational sampling provided by RE, making the RE+WHAM a particularly suitable protocol to study the conformational flexibility of small molecules of this kind.
FIG. 7.
Cuts of the probability distribution P(ϕ1, ϕ2, ϕ3) of dihedral angles of hexane (above) and the contour map (below) of the corresponding potential of mean force F(ϕ1, ϕ2, ϕ3) obtained by RE+WHAM.
FIG. 8.
Running averages of the populations for the trans-trans-trans (TTT), trans-gauche+-gauche+ (TG+G+), gauche+-gauche+-gauche+ (G+G+G+), and gauche+-gauche−-gauche+ (G+G−G+) states of hexane obtained by (a) serial MD, (b) replica-exchange MD without WHAM, and (c) replica-exchange MD with WHAM.
TABLE IV.
Populations of the conformational states of hexane at T=450 K. The values in parenthesis indicate the uncertainty on the last digit.
| ϕ1 | ϕ2 | ϕ3 | RE+WHAM |
|---|---|---|---|
| Trans | Trans | Trans | 0.232(17) |
| Trans | Trans | Gauche+ | 0.328(11) |
| Trans | Gauche+ | Trans | 0.154(14) |
| Trans | Gauche+ | Gauche+ | 0.100(6) |
| Gauche+ | Trans | Gauche+ | 0.062(11) |
| Gauche+ | Trans | Gauche− | 0.060(7) |
| Trans | Gauche+ | Gauche− | 0.0341(12) |
| Gauche+ | Gauche+ | Gauche+ | 0.0190(24) |
| Gauche+ | Gauche+ | Gauche− | 0.0102(15) |
| Gauche+ | Gauche− | Gauche+ | 0.00075(16) |
B. TMC278
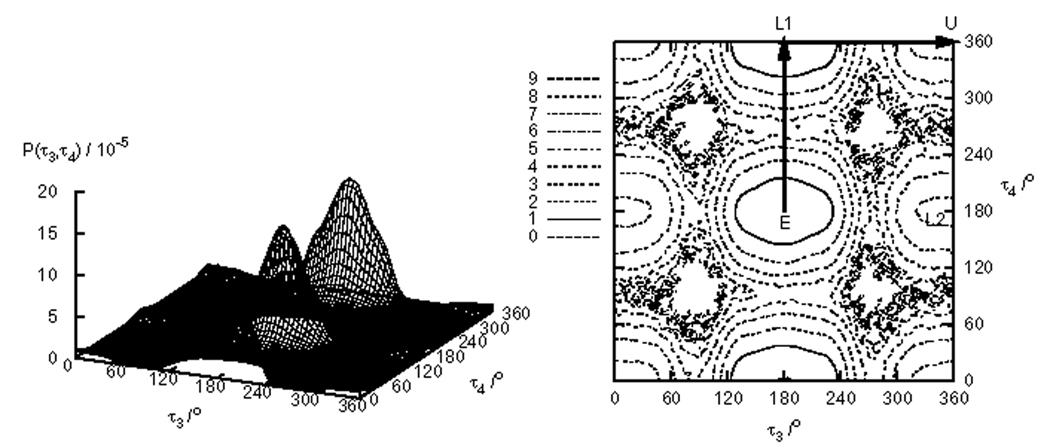
TMC278, shown in Fig. 1, has five rotatable bonds denoted by τ1– τ5. However τ1, τ2 and τ5 do not appreciably affect the overall shape of the molecule and it is sufficient in this case to take into account only the τ3 and τ4 dihedral angles [28]. The dihedral angle distribution P(τ3, τ4) of TMC278 in implicit water is shown in Fig. 9. There are four symmetrically independent states shown on Fig. 10 denoted by the labels E, L1, L2, and U [41]. The representative angle values for each state are (τ3, τ4) = (180°, 180°) for the E, (τ3,τ4) = (180°, 0°) for the L1, (τ3, τ4) = (0°, 180°) for the L2, and (τ3, τ4) = (0°,0°) for the U state. The labels are mnemonics for the shape of the molecule: E for Extended, L1 and L2 for L-shaped, and U for U-shaped (see Fig. 10). The U state corresponds to the conformation of TMC28 bound to HIV-RT [28].
FIG. 9.
Probability distribution P(τ3, τ4) of the τ3 and τ4 dihedral angles of TMC278 in implicit water (left) and the contour map of the corresponding potential of mean force F(τ3, τ4) obtained by RE+WHAM. Arrows on the contour map indicate the route of the cut shown in Fig. 12.
FIG. 10.
Representative conformations of TMC278 analyzed in this work. U conformation (τ3 and τ4 values between −90° and 90°); L1 conformation (−90° < τ4 < 90° and 90° < τ3 < −90°); L2 conformation (−90° < τ3 < 90° and 90° < τ4 > −90°); E conformation (τ3 > 90° and τ4 < −90°).
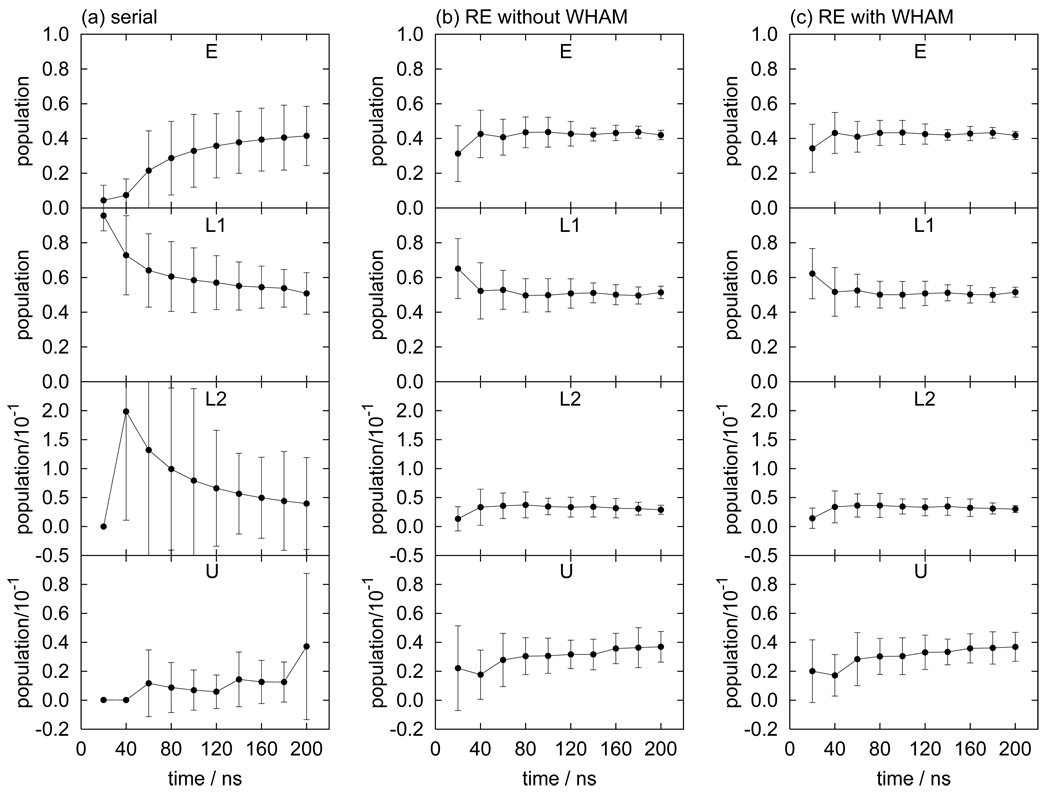
The computed populations of the E, L1, L2, and U states at 300 K are listed in Table V; Figure 11 shows the running averages of the corresponding populations. The magnitude of the uncertainties of the populations decreases in the following order: serial MD (largest), RE, and RE+WHAM (smallest). The relative uncertainty of the U state is 27% with RE+WHAM, 29% with RE, and 136% with serial MD. As for butane and pentane, RE (both with WHAM and without WHAM) converges much faster than serial MD, but the effect is quantitatively larger than for the alkanes; the uncertainties for the alkanes with RE+WHAM are one to three times smaller than serial MD at the same computational cost whereas RE+WHAM population uncertainties are at least five times smaller in the case of TMC278.
TABLE V.
Populations of the conformational states of TMC278 in solution at T=300 K. The values in parenthesis indicate the uncertainty on the last digit.
| State | MD | RE | RE+WHAM |
|---|---|---|---|
| E | 0.41(17) | 0.42(3) | 0.42(2) |
| L1 | 0.51(12) | 0.51(4) | 0.52(3) |
| L2 | 0.040(79) | 0.029(8) | 0.030(6) |
| U | 0.037(50) | 0.037(11) | 0.037(10) |
FIG. 11.
Running averages of the populations for the E, L1, L2, and U states of TMC278 in solution obtained by (a) serial MD, (b) replica-exchange MD without WHAM, and (c) replica-exchange MD with WHAM.
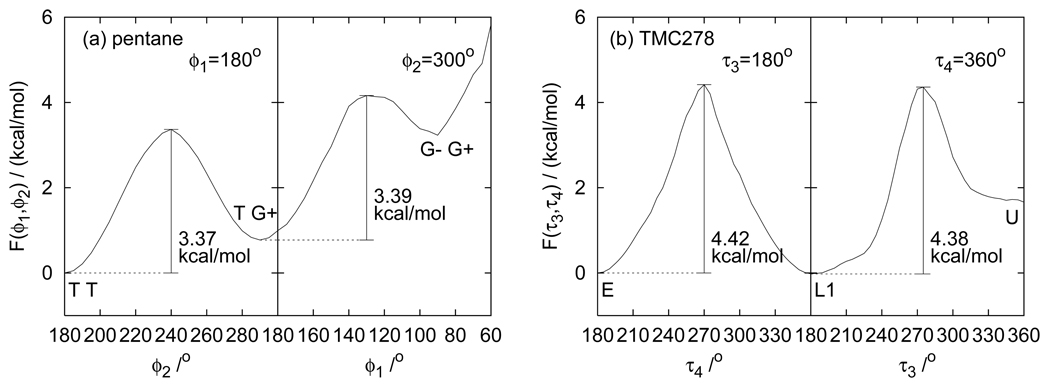
The much smaller uncertainties of TMC278 populations with RE sampling relative to serial MD can be understood in terms of the large free energy barriers between stable states which are crossed more frequently at higher temperatures than room temperature. The high free energy barriers are illustrated in Fig. 12. Fig. 12(a) shows the potential of mean force of pentane along a route from the TT state to TG+ state (from ϕ2 = 180° to 300° at fixed ϕ1 = 180°) plus that from the TG+ state to G−G+ state (from ϕ1 = 180° to 60° at fixed ϕ2 = 300°). Figure 12(b) shows the potential of mean force for TMC278 along a route from the E state to the L1 state (from τ4 = 180° to 360° at fixed τ3 = 180°) plus that from the L1 state to the U state (from τ3 = 180° to 360° at fixed τ4 = 360°). These routes are schematically shown in Fig. 5 and Fig. 9, respectively. The free energy barriers along these routes are 3.37 kcal/mol from the TT state to the TG+ state and 3.39 kcal/mol from the TG+ state to the G−G+ state of pentane. As shown in Fig. 12 the free energy barriers of TMC278 are significantly higher; 4.42 kcal/mol from the E state to the L1 state and 4.38 kcal/mol from the L1 state to the U state. The higher free energy barriers cause roughly a 10-fold reduction relative to the alkanes of the rate of interconversions between stable states at room temperature. By taking advantage of the more rapid interconversions at higher temperatures, RE is able to yield much faster convergence than MD for this system.
FIG. 12.
Potential of mean force F obtained by RE+WHAM (a) between TT, TG+, and G−G+ states of pentane, and (b) between E, L1, and U states of TMC278 in implicit water.
The reorganization free energy ΔF at 300 K for each conformational state of TMC278 is listed in Table VI as computed from Eq. (1) and the populations listed in Table V. The reorganization free energy of a state is defined as the free energy required to constrain the molecule in that state, thereby removing it from the thermodynamic equilibrium in which each state assumes its natural population in solution. One of the goals of the present study is to evaluate the ability of RE sampling to compute ligand binding reorganization free energies, that is the free energy penalties incurred by limiting the ligand conformational distribution in solution to the subset of conformations compatible with complexation. TMC278 binds HIV-RT only in the U conformation [28], therefore the ligand binding reorganization free energy for TMC278 binding to HIV-RT is predicted to be ΔF = 1.97 ± 0.16 kcal/mol, as computed by the population (3.7%) of the U state estimated by RE+WHAM. This a significant free energy contribution to the measured binding free energy (of the order of −10 kcal/mol) of this compound for HIV-RT. As shown in Table VI the uncertainty of the RE+WHAM estimate of the binding reorganization free energy (0.16 kcal/mol) is significantly smaller than that obtained from serial MD sampling (0.81 kcal/mol) at the same computational cost. This suggests RE sampling is a generally suitable method for computing ligand binding reorganization free energies of drug-like molecules with molecular weights similar to that of TMC278.
TABLE VI.
Reorganization free energies of the conformational states of TMC278 in solution at T=300 K.
| State | MD | RE | RE+WHAM |
|---|---|---|---|
| E | 0.52±0.25 | 0.52±0.04 | 0.52±0.03 |
| L1 | 0.40±0.14 | 0.40±0.04 | 0.40±0.03 |
| L2 | 1.92±1.19 | 2.11±0.16 | 2.09±0.12 |
| U | 1.96±0.81 | 1.97±0.17 | 1.97±0.16 |
IV. CONCLUSIONS
We have analyzed the relative efficiency of serial constant temperature MD and parallel replica exchange (RE) sampling for the calculation of conformational populations of a series of small molecules in vacuum and implicit solvent. The analysis focused on computational efficiency (as opposed to real time efficiency) measured as the level of convergence at equal CPU cost. Because RE employs multiple replicas of the system, we conducted proportionally shorter parallel RE simulations compared to serial MD in order to maintain the same computational cost. Conformational populations by RE sampling have been computed exclusively from the data of the room temperature RE replica, as well as from the data of all replicas using the temperature version of the weighted histogram analysis method (WHAM). Efficiency was measured in terms of the size of the statistical uncertainties of the populations estimated by block averaging.
We find that based on this measure RE is generally more computationally efficient than constant temperature MD despite the fact that, for the same computational cost, substantially fewer samples are directly available from RE at the temperature of interest. This finding is rationalized in terms of the higher statistical efficiency of RE trajectories characterized by more frequent interconversions between stable states compared to serial MD. This is a consequence of the relatively small number of degrees of freedom of these molecules which limit the increase in conformational space with increasing temperature which, for larger systems such as peptides and proteins, causes difficulties for RE sampling.[25, 26] Furthermore, the energetic, rather than entropic, nature of the free energy barriers between the stable states of these molecules, allows higher interconversion rates at higher temperatures thereby enhancing convergence. The WHAM method is found to help in the estimation of small populations corresponding to high energy states whose occupancies increase with increasing temperature. Noticeable benefits are observed for alkanes, which have relatively low energy barriers, and especially for TMC278, which is characterized by higher free energy barriers.
The RE method is a parallel algorithm which takes advantage of computational clusters which are nowadays commonly used in biocomputing research. In this work we have compared different sampling protocols in terms of their aggregate computational cost, which for RE is given by the length of the run multiplied by the number of replicas utilized in the simulation. We observe that based on this measure RE is three to five times more efficient than serial MD. The benefits of RE for this particular application would be further magnified if we had used for comparison real time efficiency, that is the actual time required to get the result regardless of the number of CPU’s involved in the calculation. This could be the case for example in situations in which low cost computational resources are readily available and the main concern is the wall clock time required to obtain the answer. Based on this measure we observe that the efficiency for RE is on the order of 10 to 20 times greater than that of serial MD.
This work paves the way for large-scale automated computations of the ligand binding reorganization free energies as done here for TMC278, an important inhibitor of HIV-1 reverse transcriptase (RT). For TMC278 we measure with the RE+WHAM protocol a binding reorganization free energy of approximately 2 kcal/mol (a substantial contribution to the total binding free energy) with less than 10% relative uncertainty. This constitutes a substantial contribution to the total binding free energy. Ligand reorganization free energies potentially play a significant role in modulating the affinities of inhibitors to their receptors. We plan to investigate with this method the binding reorganization free energies of a series of non-nucleoside inhibitors of HIV-1 RT as well as other pharmaceutically relevant systems. This work will be presented in future publications.
Acknowledgments
This work was supported in part by a National Institute of Health grant no. GM30580. The calculations reported in this work have been performed at the BioMaPS High Performance Computing Center at Rutgers University funded in part by the NIH shared instrumentation grant no. 1 S10 RR022375. We thank Prof. Eddy Arnold and Dr. Yulia Volovik Frenkel for discussions concerning HIV-RT inhibitors, and for providing the graphical representations of TMC278 used in this work.
References
- 1.Hukushima K, Nemoto K. J Phys Soc Jpn. 1996;65:1604. [Google Scholar]
- 2.Sugita Y, Okamoto Y. Chem Phys Lett. 1999;314:141. [Google Scholar]
- 3.Mitsutake A, Sugita Y, Okamoto Y. Biopolymers (Pept Sci) 2001;60:96. doi: 10.1002/1097-0282(2001)60:2<96::AID-BIP1007>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- 4.Berg BA. Comp Phys Commun. 2002;104:52. [Google Scholar]
- 5.Berg BA, Neuhaus T. Phys Lett B. 1991;267:249. [Google Scholar]
- 6.Berg BA, Neuhaus T. Phys Rev Lett. 1992;68:9. doi: 10.1103/PhysRevLett.68.9. [DOI] [PubMed] [Google Scholar]
- 7.Hansmann UHE, Okamoto Y, Eisenmenger F. Chem Phys Lett. 1996;259:321. [Google Scholar]
- 8.Nakajima N, Nakamura H, Kidera A. J Phys Chem B. 1997;101:817. [Google Scholar]
- 9.Okumura H, Okamoto Y. Chem Phys Lett. 2004;383:391. [Google Scholar]
- 10.Okumura H, Okamoto Y. Phys Rev E. 2004;70:026702. doi: 10.1103/PhysRevE.70.026702. [DOI] [PubMed] [Google Scholar]
- 11.Okumura H, Okamoto Y. Chem Phys Lett. 2004;391:248. [Google Scholar]
- 12.Okumura H, Okamoto Y. J Phys Soc Jpn. 2004;73:3304. [Google Scholar]
- 13.Okumura H, Okamoto Y. J Comput Chem. 2006;27:379. doi: 10.1002/jcc.20351. [DOI] [PubMed] [Google Scholar]
- 14.Okumura H, Okamoto Y. Bull Chem Soc Jpn. 2007;80:1114. [Google Scholar]
- 15.Morishita T, Mikami M. J Chem Phys. 2007;127:034104. doi: 10.1063/1.2747236. [DOI] [PubMed] [Google Scholar]
- 16.Okumura H, Okamoto Y. J Phys Chem B. 2008;112:12038. doi: 10.1021/jp712109q. [DOI] [PubMed] [Google Scholar]
- 17.Okumura H. J Chem Phys. 2008;129:124116. doi: 10.1063/1.2970883. [DOI] [PubMed] [Google Scholar]
- 18.Feig M, Karanicolas J, Brooks CL., III J Mol Graphics Modelling. 2004;22:377. doi: 10.1016/j.jmgm.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 19.Case DA, Cheatham TE, III, Darden T, Gohlke H, Luo R, Merz KM, Jr, Onufriev A, Simmerling C, Wang B, Woods RJ. J Comput Chem. 2005;26:1668. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Banks JL, Beard JS, Cao Y, Cho AE, Damm W, Farid R, Felts AK, Halgren TA, Mainz DT, Maple JR, Murphy R, Philipp DM, Repasky MP, Zhang LY, Berne BJ, Friesner RA, Gallicchio E, Levy RM. J Comput Chem. 2005;26:1752. doi: 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gallicchio E, Levy RM, Parashar M. J Comput Chem. 2008;29:788. doi: 10.1002/jcc.20839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Beck DAC, George WN, White GWN, Valerie Daggett V. J Struct Biol. 2007;157:514. doi: 10.1016/j.jsb.2006.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zuckerman DM, Lyman E. J Chem Theory Comput. 2006;2:1200. doi: 10.1021/ct600297q. [DOI] [PubMed] [Google Scholar]
- 24.Denschlag R, Lingenheil M, Tavan P. Chem Phys Lett. 2008;458:244. doi: 10.1021/ct8000365. [DOI] [PubMed] [Google Scholar]
- 25.Zheng W, Andrec M, Gallicchio E, Levy RM. Proc Natl Acad Sci USA. 2007;104:15340. doi: 10.1073/pnas.0704418104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zheng W, Andrec M, Gallicchio E, Levy RM. J Phys Chem B. 2008;112:6083. doi: 10.1021/jp076377+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ma B, Shatsky M, Wolfson HJ, Nussinov R. Protein Sci. 2002;11:184. doi: 10.1110/ps.21302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Das K, Bauman JD, Clark AD, Frenkel YV, Lewi PJ, Shatkin AJ, Hughes SH, Arnold E. Proc Natl Acad Sci USA. 2008;105:1466. doi: 10.1073/pnas.0711209105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gallicchio E, Andrec M, Felts AK, Levy RM. J Phys Chem B. 2005;109:6722. doi: 10.1021/jp045294f. [DOI] [PubMed] [Google Scholar]
- 30.Gallicchio E, Levy RM. J Comp Chem. 2004;79:479. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 31.Banks JL, Beard JS, Cao Y, Cho AE, Damm W, Farid R, Felts AK, Halgren TA, Mainz DT, Maple JR, Murphy R, Philipp DM, Repasky MP, Zhang LY, Berne BJ, Friesner RA, Gallicchio E, Levy RM. J Comput Chem. 2005;26:1752. doi: 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nosé S. Mol Phys. 1984;52:255. [Google Scholar]
- 33.Nosé S. J Chem Phys. 1984;81:511. [Google Scholar]
- 34.Hoover WG. Phys Rev A. 1985;31:1695. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 35.Martyna GJ, Tuckerman ME, Tobias DJ, Klein ML. Mol Phys. 1996;87:1117. [Google Scholar]
- 36.Evans DJ, Holian BL. J Chem Phys. 1985;83:4069. [Google Scholar]
- 37.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. J Comp Chem. 1992;13:1011. [Google Scholar]
- 38.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. J Chem Phys. 1984;81:3684. [Google Scholar]
- 39.Morishita T. J Chem Phys. 2000;113:2976. [Google Scholar]
- 40.Harvey SC, Tan RK-Z, Cheatham TM., III J Comp Chem. 1998;19:726. [Google Scholar]
- 41.Frenkel YV. PhD thesis. Rutgers University, Graduate Program in Biochemistry; 2009. The roles of structural variability and amphiphilicity of TMC278/rilpivirine and mechanisms of resistance avoidance and enhanced oral bioavailability. [Google Scholar]