Measuring Health: A Multivariate Approach

Abstract

We examined the health status of 171 countries by employing factor analysis on various national health indicators for the period 2000–2005 to construct two new measures on health. The first measure is based on the health of individuals and the second on (the quality of) the health services. Our measures differ substantially from indicators used in previous studies on health and also lead to different rankings of countries. As rankings are not that informative without further information, we analyzed the distance between each country and the sample mean. Differences between countries are much more pronounced for our measure on health services than for our measure on the health of individuals. Using cluster analysis, we classified the countries in six homogenous groups.

Introduction

Most studies that rank countries on the basis of their health status used the life expectancy or the mortality rate as indicator of the health status of a country, thereby implicitly assuming that health is a one-dimensional concept (cf. Charlton et al. 1983; Nolte and McKee 2003, 2008). However, this is not in line with the definition of health of the WHO, according to which health is “a state of complete physical, social and mental well-being, and not merely the absence of disease or infirmity. Health is a resource for everyday life, not the object of living, and is a positive concept emphasizing social and personal resources as well as physical capabilities” (WHO 1946). This definition suggests that health is a multi-faceted concept.

Nowadays, there is much information available on national health. How should all this information be combined? In other words, what is the appropriate conceptual framework for measuring health (Cutler et al. 1997)? What lessons can be learned from such a framework with respect to cross-country differences in health?

In our attempt to answer these questions, we applied factor analysis on various national health indicators for 171 countries over the period 2000–2005 to examine whether health has more than one dimension. Factor analysis is an excellent instrument to identify what different indicators of a latent construct (like health) have in common and to separate common factors from specific factors. We used the outcomes of the factor analysis to construct two new health measures. The first one refers to the health of individuals and the second captures the (quality of) health services.

Our measures differ substantially from indicators used in previous studies on health and also lead to different rankings of countries. As rankings are not that informative without further information, we analyzed the distance between each country and the sample mean. Differences between countries are much more pronounced for our measure on health services than for our measure on the health of individuals. Using cluster analysis, we classified the countries in six homogenous groups. Health differs substantially across these clusters.

The remainder of the paper is structured as follows. The next section explains factor analysis, while in Sect. 3 this method is applied to various indicators of health. Sect. 4 presents our rankings and a cluster analysis, while Sect. 5 offers a discussion of some of our findings. The final section presents our conclusions.

Methods

Model

Most previous studies on health employed an arbitrarily chosen one-dimensional indicator of health. The question is whether these indicators represent all dimensions of health. Furthermore, most indicators of health contain measurement errors that may lead to biased estimates (Klitgaard and Fedderke 1995). This is especially the case for samples including developing countries. To come up with a better measure for health and to determine whether health has a multidimensional character, we employed a so-called Explanatory Factor Analysis (EFA). The first step in this analysis is to check whether the data used is suitable for an EFA using the Kaiser–Meyer–Olkin measure of sampling adequacy testing whether the partial correlation among variables is low. A test statistic above 0.6 indicates that the data is suitable for an EFA (Kaiser 1970). An alternative test is Bartlett’s test of sphericity, that checks whether the correlation matrix is an identity matrix in which case the factor model is inappropriate (Lattin et al. 2003).

The objective of an EFA is to identify what different indicators of a latent variable (like health) have in common and to separate common factors from specific factors. Following Wansbeek and Meijer (2000) and Lattin et al. (2003), the EFA model can be written as:

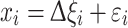1

where x _i is a vector containing the M indicators for observation i, i = 1…k (in our case the various indicators of health), ∆ is a vector of factor loadings of order M × k, and ξ is a vector of latent variables with mean zero and positive definite covariance. The random error term ε is assumed to be uncorrelated with the latent variables.1 Under these assumptions, the covariance matrix of x _i is:

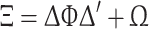2

where Ξ is the parameterised covariance matrix that can be decomposed in the covariance matrix of the factors Φ and the diagonal covariance matrix of error terms Ω. The model is estimated with the Maximum Likelihood (ML) method. By assuming that the factors and the disturbance term are normally distributed, it follows that the indicators are normally distributed. The log-likelihood function can be written as:

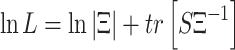3

where S represents the sample covariance matrix. Minimizing this fit function means choosing the values for the unknown parameters so that the implied covariance matrix comes as close as possible to the sample covariance matrix.

The next step is to decide on the number of factors to represent health on the basis of the scree plot, which plots the number of factors against the eigenvalues of the covariance matrix of the indicators. In general, there are two ways of interpreting the graph. According to Kaiser’s Rule, only factors with an eigenvalue exceeding unity should be retained (Kaiser and Dickman 1959). An alternative way is to look for an ‘elbow’ in the scree plot, i.e., the point after which the remaining factors decline in approximately a linear fashion, and to retain only the factors above the elbow.

After deciding on the number of factors, it is possible that the factors of the (standardized) solution of the model are difficult to interpret. In that case, rotating the factor loadings may yield a solution that is easier to interpret because the matrix has a simpler structure. Ideally, each indicator is correlated with as few factors as possible. The rotation technique that we used to interpret the factors is the Oblimin rotation, which allows for correlation among the factors and minimizes the correlation of the columns of the factor loadings matrix. As a result, a typical indicator will have high factor loadings on one factor, while it has low loadings on the other factors (Harris and Kaiser 1964).

All indicators received factor scores for the various dimensions (factors) identified. These factor scores were used to come up with the so-called Bartlett predictor, i.e., the best linear unbiased predictor of the factor scores:

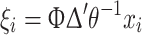4

These factor scores were used as indicator of the health status of a country.

Data

The selection of indicators of health is based on two rules. First, data should be widely available for a large number of countries. Here we faced a trade-off, as some indicators were only available for a limited number of countries. Second, to aggregate the data from micro level to macro level, the data should be gathered in a consistent way across countries and over time periods. We used data from the World Development Indicators of the World Bank and from the Statistical Information System of the World Health Organization.

We grouped our data on the health of individuals in three broad categories. Our first category contains various indicators on lifetime. It is quite common to proxy the health status of a country by the population’s life expectancy or mortality rate. In this category, we also included the number of healthy years that a person has and the prevalence of children with malnutrition measured by the share of children that is underweighted. Our second category refers to the prevalence of various communicable diseases. These include diseases that are transmitted from person to person or through insect bites and that can be fatale. Most diseases in this category can be epidemic and may form a serious treat for the health status of a country, especially in developing countries. Finally, our third category includes various non-communicable diseases. These are not caused by transmission, but by incident or by lifestyle. These diseases are more common in industrialized countries.

We applied factor analysis on 27 national indicators of the health of individuals. Table 1 presents the indicators used and their sources.

Table 1.

Indicators of the health of individuals

	Source
Lifetime
Healthy life expectancy	WHO (2007)
Life expectancy at birth	World Bank (2006)
Mortality rate adults	World Bank (2006)
Mortality rate under-5	World Bank (2006)
Mortality rate infants	World Bank (2006)
Years lost to communicable diseases	WHO (2007)
Years lost to non-communicable diseases	WHO (2007)
Years lost to injuries	WHO (2007)
Age standardized mortality rate: cardiovascular diseases	WHO (2007)
Age standardized mortality rate: cancer	WHO (2007)
Prevalence underweighted children	World Bank (2006)
Communicable diseases
Prevalence HIV	World Bank (2006)
Prevalence other sexual transmitted diseases	WHO (2007)
Prevalence tuberculosis	WHO (2007)
Prevalence ARI	WHO (2007)
Prevalence diarrhea	World Bank (2006)
Prevalence diphtheria	WHO (2007)
Prevalence measles	WHO (2007)
Prevalence tetanus	WHO (2007)
Prevalence malaria	WHO (2007)
Prevalence polio	WHO (2007)
Non-communicable diseases
Share of population with diabetes	WHO (2007)
Share of population with cardiovascular diseases	WHO (2007)
Share of population with asthma	WHO (2007)
Share of population with musculoskeletal diseases	WHO (2007)
Share of population with cancer	WHO (2007)
Share of population with mental and neuropsychiatric diseases	WHO (2007)

A different measure for the health status of a country is the quality of its health services. Therefore, we also applied factor analysis on 10 indicators of national health services. The indicators used and their sources are given in Table 2. Our first category includes indicators of the availability of health care. The more capacity there is, the earlier a patient will be seeing a doctor and get care. The second group of variables captures immunization. We argue that the immunization rate is a policy variable determined upon by the government (cf. Lake and Baum 2001).2

Table 2.

Indicators of health services

	Source
Staff
Number of dentists per 1,000 people	WHO (2007)
Number of nurses per 1,000 people	WHO (2007)
Number of physicians per 1,000 people	World Bank (2006)
Number of pharmacists per 1,000 people	WHO (2007)
Births attended by skilled staff (% of total)	World Bank (2006)
Hospital beds per 1,000 people	World Bank (2006)
Immunization rate
Immunization rate measles	WHO (2007)
Immunization rate DTP	WHO (2007)
Immunization rate hepatitis	WHO (2007)
Immunization rate tuberculosis	WHO (2007)

For both measures we used averages over the period 2000–2005 for a sample of 171 countries, giving 4,446 observations for the health of individuals and 1,710 observations for health services.3 For some countries one or two indicators were not available, yielding 214 missing observations for the health of individuals and 83 for health services, which is in both cases less than 5%. In order not to lose valuable information, we applied the EM algorithm to compute the missing observations. The EM algorithm was suggested by Dempster et al. (1977) to solve maximum likelihood problems with missing data. It is an iterative method, the expectation step involves forming a log-likelihood function for the latent data as if they were observed and taking its expectation, while in the maximization step the resulting expected log-likelihood is maximized.

Results

The Kaiser–Meyer–Olkin measure of sampling adequacy and Bartlett’s test of sphericity indicated that our data could be used for an Explorative Factor Analysis.

First, we analysed individual health. Because our data is measured on an interval or ratio scale and is normally distributed, Table 3 shows Pearson’s correlation coefficient. The results indicate that the correlations between the different indicators are often quite low, although generally significant. Therefore, we consider the different indicators of individual health as imperfect measures of health containing measurement errors (see also Pan American Health Organization 2001; Häkkinen and Joumard 2007; Klitgaard and Fedderke 1995).

Table 3.

Correlation matrix: indicators of the health of individuals

		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)	(13)	(14)
Healthy life expectancy	(1)	1.00	0.98**	−0.99**	−0.99**	−0.99**	−0.99**	0.92**	0.53**	−0.59**	−0.29**	−0.59**	−0.19**	−0.89**	−0.39**
Life expectancy at birth	(2)		1.00	−0.99**	−0.99**	−0.89**	−0.99**	0.90**	0.57**	−0.49**	−0.29**	−0.69**	−0.19**	−0.89**	−0.49**
Mortality rate adults	(3)			1.00	0.82**	0.80**	0.85**	−0.89**	−0.59**	0.41**	0.24**	0.80**	0.11*	0.82*	0.40*
Mortality rate under-5	(4)				1.00	0.99**	0.87**	−0.89**	−0.59**	0.48**	0.23**	0.41**	0.17**	0.79**	0.25**
Mortality rate infants	(5)					1.00	0.87**	−0.89**	−0.59**	0.53**	0.20**	0.40**	0.18**	0.79**	0.25*
Years lost to communicable diseases	(6)						1.00	−0.99**	−0.59**	0.36**	0.12**	0.54**	0.19*	0.82*	0.44**
Years lost to non-communicable diseases	(7)							1.00	0.42**	−0.39**	−0.19**	−0.59**	−0.29**	−0.89**	−0.49*
Years lost to injuries	(8)								1.00	−0.19**	−0.19**	−0.49**	−0.09*	−0.59**	−0.29**
Age standardized mortality rate: cardiovascular diseases	(9)									1.00	−0.09**	0.08**	0.08**	0.35*	0.03*
Age standardized mortality rate: cancer	(10)										1.00	0.13**	−0.09*	0.21**	0.04**
Prevalence HIV	(11)											1.00	0.01**	0.58**	0.34*
Prevalence other sexual transmitted diseases	(12)												1.00	0.18**	0.09**
Prevalence tuberculosis	(13)													1.00	0.39*
Prevalence ARI	(14)														1.00
Prevalence underweighted children	(15)
Prevalence diarrhea	(16)
Prevalence diphtheria	(17)
Prevalence measles	(18)
Prevalence tetanus	(19)
Prevalence malaria	(20)
Prevalence polio	(21)
Share of population with diabetes	(22)
Share of population with cardiovascular diseases	(23)
Share of population with asthma	(24)
Share of population with musculoskeletal diseases	(25)
Share of population with cancer	(26)
Share of population with mental and neuropsychiatric diseases	(27)

		(15)	(16)	(17)	(18)	(19)	(20)	(21)	(22)	(23)	(24)	(25)	(26)	(27)
Healthy life expectancy	(1)	−0.79**	−0.69**	−0.29**	0.11**	−0.29*	−0.39**	0.02**	0.04**	0.04**	0.00**	0.04**	0.10**	0.06**
Life expectancy at birth	(2)	−0.79**	−0.69**	−0.29**	0.09**	−0.29**	−0.39**	0.01**	0.05**	0.04**	0.01**	0.04**	0.06**	0.06**
Mortality rate adults	(3)	0.65*	0.51*	0.19**	−0.09**	0.19**	0.35**	0.04**	−0.06**	−0.06**	−0.06**	−0.06**	−0.06**	−0.06**
Mortality rate under-5	(4)	0.74**	0.70**	0.28*	−0.09*	0.29*	0.42*	−0.06**	−0.06**	−0.06**	0.00**	−0.06**	−0.06**	−0.06**
Mortality rate infants	(5)	0.77**	0.70**	0.25**	−0.09**	0.29**	0.37*	−0.06**	−0.06**	−0.06**	0.02**	−0.06**	−0.06**	−0.06**
Years lost to communicable diseases	(6)	0.76*	0.68*	0.22**	−0.19**	0.21**	0.36**	−0.16*	−0.06**	−0.06**	0.03**	−0.06**	−0.06**	−0.06**
Years lost to non-communicable diseases	(7)	−0.79**	−0.69**	−0.29*	0.09*	−0.29**	−0.39*	0.05*	0.03**	0.02**	−0.06**	0.04**	0.05**	0.02**
Years lost to injuries	(8)	−0.49**	−0.39**	−0.09**	0.10**	−0.09*	−0.29**	0.22*	0.11**	0.11**	0.06**	0.13**	0.13**	0.11**
Age standardized mortality rate: cardiovascular diseases	(9)	0.41**	0.25*	0.07**	−0.09**	0.08**	0.13**	0.23*	−0.06**	0.04**	−0.06**	−0.06**	−0.06**	−0.06**
Age standardized mortality rate: cancer	(10)	0.10*	0.15**	0.09**	0.04*	0.13**	0.14*	0.05**	−0.06*	−0.06*	−0.06*	−0.06*	0.02*	−0.06*
Prevalence HIV	(11)	0.33**	0.19**	0.02*	−0.09**	0.03**	0.12*	−0.06**	−0.06*	−0.06*	−0.06*	−0.06*	−0.06*	−0.06*
Prevalence other sexual transmitted diseases	(12)	0.12**	0.15*	0.44**	0.31**	0.07**	0.34*	0.04**	0.43*	0.40*	0.44*	0.51*	0.36*	0.65*
Prevalence tuberculosis	(13)	0.69*	0.53**	0.21**	−0.09*	0.17**	0.31**	−0.06**	0.01*	0.03*	0.04*	0.01*	−0.06*	0.02*
Prevalence ARI	(14)	0.29**	0.27**	0.02*	−0.09**	0.04**	0.07**	0.02*	0.00*	0.01*	0.04*	−0.06*	−0.06*	0.01*
Prevalence underweighted children	(15)	1.00	0.56*	0.13**	−0.09**	0.29*	0.24*	−0.06*	−0.06*	−0.06*	0.00*	−0.06*	−0.06*	−0.06*
Prevalence diarrhea	(16)		1.00	0.18**	−0.09*	0.18**	0.21*	−0.06*	−0.06*	−0.06*	0.02*	−0.06*	−0.06*	−0.06*
Prevalence diphtheria	(17)			1.00	0.90**	0.23*	0.77*	0.04**	0.44*	0.51*	0.55*	0.56*	0.54*	0.54*
Prevalence measles	(18)				1.00	−0.0 9*	−0.0 9*	0.14*	0.42*	0.50*	0.50*	0.54*	0.54*	0.51*
Prevalence tetanus	(19)					1.00	0.36**	−0.0 6*	−0.06*	−0.0 6*	0.02*	−0.0 6*	−0.0 6*	0.00*
Prevalence malaria	(20)						1.00	−0.0 6**	0.04*	0.04*	0.14*	0.06*	0.03*	0.06*
Prevalence polio	(21)							1.00	0.15*	0.46*	0.13*	0.22*	0.22*	0.16*
Share of population with diabetes	(22)								1.00	0.64**	0.64**	0.60**	0.54**	0.64**
Share of population with cardiovascular diseases	(23)									1.00	0.66**	0.64**	0.55**	0.64**
Share of population with asthma	(24)										1.00	0.61**	0.55**	0.65**
Share of population with musculoskeletal diseases	(25)											1.00	0.66**	0.64**
Share of population with cancer	(26)												1.00	0.64**
Share of population with mental and neuropsychiatric diseases	(27)													1.00

**/* indicates significance at 5 and 10% level

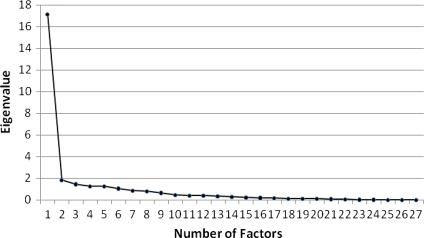
To extract the right number of factors out of the various indicators, we used the scree plot (see Fig. 1). According to the Kaiser rule, more than six factors should be identified. However, this is probably a so-called Heywood (1931) case where some solutions of the unique variances of the indicators are smaller than zero. If instead the elbow criterion is used, individual health can be represented as a one-dimensional construct. Both models were compared using a likelihood ratio test. In this case, the multiple-factor model does not fit the data significantly better than the one-factor model. The goodness-of-fit test statistic for the one-factor model is 2795.91, which is χ²(324) distributed, is highly significant (compared to a saturated model) at the five percent significance level, suggesting that the one-factor model is appropriate.

Fig. 1.

Scree plot of the eigenvalues and number of factors for indicators of health of individuals

Table 4 presents the factor loading of the various national indicators of the health of individuals and the variance of the indicators explained by the first factor. More than 60% of the variance is explained by the first factor and about 40% of the total variance is unique. The one-factor model can explain about 89% of the total variance of the mortality rate below 5 years, but less than 33% of the age standardized mortality of cancer.

Table 4.

Factor matrix health of individuals

Indicator	Factor loading	Variance explained
Healthy life expectancy	0.889	0.79
Life expectancy at birth	0.807	0.65
Mortality rate adults	−0.895	0.80
Mortality rate under-5	−0.943	0.89
Mortality rate infants	−0.880	0.77
Years lost to communicable diseases	−0.746	0.56
Years lost to non-communicable diseases	−0.700	0.49
Years lost to injuries	−0.921	0.85
Age standardized mortality rate: cardiovascular diseases	−0.623	0.39
Age standardized mortality rate: cancer	−0.741	0.55
Prevalence underweighted children	−0.588	0.35
Share of population with mental and neuropsychiatric diseases	−0.638	0.41
Prevalence other sexual transmitted diseases	−0.747	0.56
Prevalence tuberculosis	−0.934	0.87
Prevalence ARI	−0.766	0.59
Prevalence diarrhea	−0.771	0.59
Prevalence diphtheria	−0.591	0.35
Prevalence measles	−0.626	0.39
Prevalence tetanus	−0.668	0.45
Prevalence malaria	−0.781	0.61
Prevalence polio	−0.760	0.58
Share of population with diabetes	−0.622	0.39
Share of population with cardiovascular diseases	−0.757	0.57
Share of population with asthma	−0.654	0.43
Share of population with musculoskeletal diseases	−0.797	0.63
Share of population with cancer	−0.564	0.32

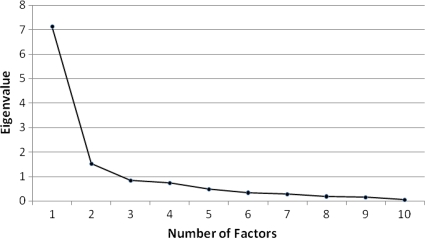
Next, we performed a factor analysis on the indicators of health services. Table 5 shows Pearson’s correlation coefficient. The results indicate that the correlations between the different indicators are often quite low, although generally significant. The scree plot is shown in Fig. 2. According to the Kaiser rule, two factors should be identified, while the elbow interpretation indicated only one factor. Both models were compared using a likelihood ratio test. The two-factors model does not fit the data significantly better than the one-factor model. The goodness-of-fit statistic of the one-factor model is 438.98 which is χ²(35) distributed and is highly significant at the five percent significance level, suggesting that the one-factor model is appropriate.

Table 5.

Correlation matrix: indicators of health services

Correlations		(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
Number of physicians per 1,000 people	(1)	1.00	0.77**	0.72**	0.54**	0.72**	0.74**	0.32**	0.58**	0.57**	−0.14**
Number of nurses per 1,000 people	(2)		1.00	0.60**	0.46**	0.64**	0.82**	0.27**	0.50**	0.48**	−0.14**
Number of dentists per 1,000 people	(3)			1.00	0.65**	0.63**	0.48**	0.28**	0.50**	0.52**	−0.11**
Number of pharmacists per 1,000 people	(4)				1.00	0.55	0.39**	0.12**	0.43**	0.40**	−0.09**
Births attended by skilled staff (% of total)	(5)					1.00	0.61**	0.38**	0.69**	0.72**	−0.05**
Hospital beds per 1,000 people	(6)						1.00	0.22**	0.45**	0.43**	−0.18**
Immunization rate hepatitis	(7)							1.00	0.55**	0.61**	0.13**
Immunization rate DTP	(8)								1.00	0.93**	0.12**
Immunization rate measles	(9)									1.00	0.14**
Immunization rate tuberculosis	(10)										1.00

** indicates significance at 5% level

Fig. 2.

Scree plot of the eigenvalues and factors of the indicators of health services

Table 6 presents the factor loadings of the various indicators and the variance of the indicators explained by the factor. About 60% of the variance is explained by the factor and about 40% of the total variance is unique.

Table 6.

Factor matrix health services

Indicator	Factor loading	Variance explained
Number of physicians per 1,000 people	0.865	0.75
Number of nurses per 1,000 people	0.790	0.62
Number of dentists per 1,000 people	0.767	0.59
Number of pharmacists per 1,000 people	0.716	0.51
Births attended by skilled staff (% of total)	0.848	0.72
Hospital beds per 1,000 people	0.844	0.71
Immunization rate hepatitis	0.548	0.30
Immunization rate DTP	0.758	0.58
Immunization rate measles	0.761	0.58
Immunization rate tuberculosis	0.512	0.26

Health Ranking and Cluster Analysis

We constructed new measures for the health of individuals and health services based on the factor scores as reported in Sect. 3. Table 10 in the “Appendix” shows the full list of the predicted factor scores and the implied ranking of the various countries.

Table 10.

Health measure

	Health of individuals		Health services		GDP per capita 2000–2005
	Rank	Score	Rank	Score	Rank	Score
Afghanistan	166	−2.015	169	−1.863	NA	NA
Albania	58	0.571	70	0.321	89	1,365
Algeria	87	0.318	92	−0.076	77	1,939
Antigua and Barbuda	53	0.668	57	0.568	36	9,080
Argentina	39	0.870	76	0.261	39	7,323
Armenia	67	0.544	50	0.745	107	848
Australia	10	1.289	18	1.367	19	22,025
Austria	18	1.208	12	1.473	11	24,663
Azerbaijan	107	0.000	34	1.035	106	858
Bahamas	72	0.457	49	0.753	24	16,187
Bahrain	43	0.728	66	0.466	29	13,069
Bangladesh	116	−0.298	147	−1.259	131	396
Barbados	44	0.786	47	0.798	NA	NA
Belarus	78	0.426	3	1.790	86	1,519
Belgium	23	1.186	2	1.861	17	23,165
Belize	79	0.370	90	−0.047	60	3,544
Benin	136	−1.099	124	−0.887	140	322
Bhutan	117	−0.337	136	−1.095	104	879
Bolivia	111	−0.110	17	1.372	99	1,024
Bosnia and Herzegovina	42	0.760	85	0.098	87	1,461
Botswana	164	−1.886	102	−0.192	57	4,035
Brazil	91	0.292	61	0.500	61	3,499
Brunei Darussalam	40	0.713	58	0.551	28	13,109
Bulgaria	49	0.742	20	1.330	80	1,805
Burkina Faso	156	−1.787	137	−1.102	148	242
Burundi	167	−1.846	149	−1.287	162	108
Cambodia	134	−0.910	154	−1.393	137	334
Cameroon	143	−1.353	135	−1.082	112	713
Canada	5	1.154	38	0.957	14	24,055
Cape Verde	95	0.273	116	−0.589	93	1,249
Central African Republic	162	−1.702	164	−1.694	149	238
Chad	145	−1.479	170	−1.890	153	212
Chile	31	0.940	75	0.267	45	5,206
China	69	0.530	107	−0.263	96	1,176
Colombia	70	0.525	86	0.088	75	2,046
Comoros	119	−0.341	125	−0.894	133	381
Congo	135	−1.012	153	−1.381	101	951
Costa Rica	30	0.952	83	0.127	52	4,195
Côte d’Ivoire	153	−1.609	143	−1.217	117	592
Croatia	37	0.848	43	0.889	49	4,670
Cuba	26	0.993	5	1.767	NA	NA
Cyprus	27	0.999	52	0.684	27	13,607
Czech Republic	32	0.942	11	1.479	41	5,987
Dem. Rep. Congo	161	−1.759	159	−1.426	163	86
Denmark	24	1.028	24	1.281	7	30,480
Djibouti	151	−1.475	141	−1.153	111	781
Dominican Republic	101	0.143	80	0.154	66	2,475
DPR of Korea	105	0.010	60	0.523	NA	NA
Ecuador	76	0.396	88	0.006	88	1,414
Egypt	86	0.311	104	−0.240	85	1,543
El Salvador	94	0.285	95	−0.105	73	2,102
Equatorial Guinea	137	−1.093	148	−1.277	62	3,454
Eritrea	133	−0.954	130	−1.039	156	179
Estonia	57	0.656	7	1.665	47	4,830
Ethiopia	154	−1.563	168	−1.789	161	128
Fiji	83	0.352	84	0.105	72	2,118
Finland	11	1.094	19	1.353	13	24,359
France	8	1.219	27	1.203	18	23,023
Gabon	127	−0.689	121	−0.817	59	3,869
Gambia	131	−0.808	118	−0.732	139	323
Georgia	63	0.600	67	0.412	110	790
Germany	12	1.208	16	1.391	16	23,443
Ghana	128	−0.711	127	−0.912	143	266
Greece	9	1.172	22	1.310	31	11,659
Guatemala	106	0.000	115	−0.518	83	1,725
Guinea	141	−1.236	162	−1.641	160	142
Guinea-Bissau	149	−1.598	160	−1.484	134	379
Guyana	113	−0.204	101	−0.187	100	979
Haiti	139	−1.178	163	−1.658	124	452
Honduras	103	0.089	111	−0.443	102	947
Hungary	51	0.702	33	1.040	46	5,140
Iceland	3	1.198	1	2.126	6	32,232
India	115	−0.292	131	−1.042	122	508
Indonesia	102	0.139	128	−0.956	105	864
Iran	88	0.289	98	−0.161	82	1,766
Iraq	120	−0.482	108	−0.313	NA	NA
Ireland	22	1.057	13	1.402	9	27,769
Israel	7	1.192	31	1.115	23	17,837
Italy	4	1.203	23	1.283	21	19,460
Jamaica	46	0.729	97	−0.134	63	3,192
Japan	2	1.321	8	1.541	3	37,406
Jordan	75	0.444	25	1.263	79	1,888
Kazakhstan	109	−0.072	40	0.918	84	1,605
Kenya	144	−1.355	133	−1.065	127	423
Kuwait	34	0.923	68	0.411	22	18,342
Kyrgyzstan	110	−0.078	55	0.585	141	301
Lao PDR	129	−0.816	165	−1.733	136	360
Latvia	62	0.588	32	1.107	54	4,077
Lebanon	73	0.480	41	0.901	44	5,339
Lesotho	170	−1.920	134	−1.065	120	517
Liberia	158	−1.779	156	−1.407	157	158
Libyan	65	0.590	59	0.549	40	7,008
Lithuania	55	0.679	10	1.497	58	4,005
Luxembourg	17	1.163	28	1.200	1	48,946
Madagascar	130	−0.844	151	−1.371	151	230
Malawi	168	−2.110	126	−0.898	159	148
Malaysia	60	0.620	94	−0.102	53	4,089
Maldives	104	0.060	93	−0.092	67	2,309
Mali	159	−1.832	157	−1.413	150	230
Malta	20	1.114	46	0.829	34	9,745
Mauritania	138	−1.101	139	−1.129	130	413
Mauritius	56	0.573	77	0.232	55	4,073
Mexico	54	0.724	73	0.291	42	5,959
Mongolia	108	−0.052	44	0.844	126	427
Morocco	90	0.287	112	−0.445	92	1,297
Mozambique	160	−1.837	140	−1.145	145	254
Myanmar	122	−0.536	129	−1.010	NA	NA
Namibia	148	−1.474	117	−0.620	78	1,929
Nepal	121	−0.484	155	−1.395	152	230
Netherlands	16	1.138	9	1.506	12	24,386
New Zealand	21	1.102	35	1.032	26	14,594
Nicaragua	93	0.284	113	−0.447	108	832
Niger	155	−1.790	171	−1.921	158	157
Nigeria	147	−1.413	166	−1.737	128	416
Norway	14	1.148	4	1.781	2	38,514
Oman	47	0.691	71	0.311	37	8,645
Pakistan	118	−0.346	150	−1.358	118	550
Panama	50	0.724	69	0.393	56	4,057
Papua New Guinea	123	−0.619	145	−1.220	114	640
Paraguay	77	0.385	105	−0.256	91	1,328
Peru	85	0.325	87	0.017	71	2,148
Philippines	98	0.214	119	−0.793	98	1,046
Poland	35	0.861	48	0.796	48	4,765
Portugal	29	0.975	37	1.006	32	11,062
Qatar	38	0.762	54	0.605	NA	NA
Republic of Korea	33	0.873	56	0.579	30	12,043
Republic of Macedonia	48	0.740	53	0.671	81	1,776
Republic of Moldova	84	0.328	51	0.721	135	362
Romania	68	0.574	63	0.479	76	1,954
Russian Federation	97	0.249	14	1.399	74	2,078
Rwanda	157	−1.894	132	−1.065	147	243
Saudi Arabia	66	0.537	79	0.169	35	9,265
Senegal	132	−0.937	152	−1.373	125	444
Serbia and Montenegro	52	0.687	65	0.473	94	1,202
Sierra Leone	171	−2.241	161	−1.528	155	188
Singapore	15	1.101	72	0.303	15	23,585
Slovakia	36	0.848	36	1.013	51	4,209
Slovenia	25	1.046	45	0.829	33	10,490
Solomon Islands	99	0.163	114	−0.509	113	653
Somalia	152	−1.744	167	−1.738	NA	NA
South Africa	140	−1.256	99	−0.173	64	3,177
Spain	13	1.207	26	1.206	25	15,041
Sri Lanka	64	0.557	91	−0.057	103	911
Sudan	126	−0.658	144	−1.219	129	416
Suriname	92	0.291	110	−0.429	68	2,275
Swaziland	165	−1.951	109	−0.356	90	1,344
Sweden	1	1.342	21	1.328	8	28,382
Switzerland	6	1.246	6	1.716	5	34,314
Syrian Arab Republic	71	0.512	78	0.171	97	1,135
Tajikistan	112	−0.183	82	0.129	154	197
Tanzania	150	−1.563	123	−0.882	142	294
Thailand	89	0.281	89	−0.005	70	2,194
Timor-Leste	124	−0.628	158	−1.419	132	392
Togo	142	−1.186	146	−1.248	146	244
Trinidad and Tobago	74	0.484	64	0.477	38	7,608
Tunisia	61	0.606	81	0.149	69	2,206
Turkey	82	0.372	100	−0.177	65	3,020
Turkmenistan	114	−0.200	103	−0.238	115	634
Uganda	146	−1.509	142	−1.195	144	256
Ukraine	81	0.357	30	1.136	109	799
United Arab Emirates	45	0.749	62	0.481	20	21,879
United Kingdom	19	1.048	39	0.936	10	25,611
United States of America	28	1.076	15	1.395	4	35,464
Uruguay	41	0.850	29	1.165	43	5,804
Uzbekistan	100	0.161	42	0.895	116	610
Vanuatu	96	0.235	106	−0.260	95	1,184
Venezuela	59	0.660	74	0.286	50	4,598
Viet Nam	80	0.369	96	−0.132	123	462
Yemen	125	−0.607	138	−1.121	119	533
Zambia	169	−2.078	122	−0.840	138	324
Zimbabwe	163	−1.912	120	−0.815	121	510

Based on the factor scores, which are taken in logarithms

The rankings lead to a number of conclusions. First, not surprisingly, western countries and Japan dominate the top of the rankings, while mostly African countries take the positions at the bottom. Second, in the ranking based on health services Cuba and Belarus score remarkably high. Third, the ranking differs substantially from the most recent ranking on health over almost the same period by Nolte and McKee (2008) for OECD countries (see Table 7). According to the results of Nolte and McKee (2008), France outranks all other countries in the OECD area. However, in our ranking France is at place eight in the ranking based on the health of individuals and is even number 14 in the ranking based on health services. Another example is Spain that takes the third place in the ranking of Nolte and McKee (2008), but is on place 13 in our ranking of health services.

Table 7.

Health ranking of OECD countries

	Health of individuals				Health services				Health measure Nolte and McKee (2008)
	World ranking	OECD ranking	Factor score	Difference with mean (%)	World ranking	OECD ranking	Factor score	Difference with mean (%)	OECD ranking	Mortality score	Difference with mean (%)
Australia	6	4	1.237	6.78	18	8	1.367	4.35	3	71.32	17.60
Austria	14	10	1.167	−0.44	12	4	1.473	16.02	11	84.48	2.40
Canada	8	7	1.200	2.90	38	18	0.957	−30.75	6	76.83	11.24
Denmark	23	16	1.087	−8.09	24	13	1.281	−4.25	15	100.84	−16.50
Finland	20	14	1.143	−2.80	19	9	1.353	2.90	13	93.34	−7.84
France	10	8	1.196	2.49	27	15	1.203	−11.43	1	64.79	25.15
Germany	11	9	1.178	0.66	16	7	1.391	6.89	12	90.13	−4.13
Greece	18	13	1.147	−2.41	22	11	1.31	−1.43	10	84.31	2.59
Ireland	24	17	1.075	−9.19	13	5	1.402	8.07	17	103.42	−19.49
Italy	5	3	1.252	8.39	23	12	1.283	−4.05	5	74.00	14.50
Japan	1	1	1.357	20.40	8	2	1.541	24.19	2	71.17	17.77
Netherlands	16	12	1.151	−2.02	9	3	1.506	19.91	8	81.86	5.42
New Zealand	15	11	1.155	−1.63	35	16	1.032	−25.35	14	95.57	−10.42
Norway	9	6	1.207	3.63	4	1	1.781	57.87	7	79.79	7.82
Portugal	28	19	0.998	−15.92	37	17	1.006	−27.27	18	104.31	−20.51
Spain	7	5	1.224	5.40	26	14	1.206	−11.17	4	73.83	14.70
Sweden	2	2	1.280	11.47	21	10	1.328	0.36	9	82.09	5.16
United Kingdom	21	15	1.101	−6.80	39	19	0.936	−32.19	16	102.81	−18.78
United States of America	25	18	1.034	−12.84	15	6	1.395	7.32	19	109.65	−26.68
Standard deviation			0.087				0.217			0.154

Note: Because our factor scores are in logarithms we subtracted the value of a country from that of the value for country with the highest score to obtain the difference in percentage. The factor score are computed in logarithms

As rankings are not that informative without further information, Table 7 also presents the distance between each OECD country and the OECD mean.4 This measure gives a much better impression about health differences between countries. The results show that there is a large difference between both health measures. While France scores about 2.5% higher in our measure on individual health, it scores about 11% below the mean on our health services measure. Nolte and McKee (2008) report that the United States scores about 27% below the mean. However, according to our measure of individual health, the United States scores only about 13% below the mean, while it scores above the mean according to our measure for health services. In general, Nolte and McKee (2008) report more dispersion compared to our measure on the health of individuals. However, the variance among the countries in our sample for our measure on health services is much higher than that of Nolte and McKee (2008). These results are confirmed if we take the standard deviation of the various measures divided by their mean.

Furthermore, if we expand our sample including not only the OECD countries, we find a similar, but even more pronounced, pattern. The data show that the differences between a country’s score and the sample mean are much higher for the measure for health services than they are for the measure for the health of individuals. The variance of the individual health measure is 1.1, while for the health services measure the variance is 2.4.

To sum up, our results indicate that there exist significant differences between our measures. The ranking based on the health of individuals is less dispersed than the ranking based on the quality of health services. This strengthens our conclusions that both measures are capturing different dimensions of a country’s health. So in contrast to Nolte and McKee (2008), we pose that cross-country comparisons of health should not be based on only one (arbitrarily chosen) variable.

To get a better view of health differences across countries, we categorized the countries in our sample on the basis of their similarities and differences using cluster analysis. Cluster analysis is recognized as a useful technique for this purpose and has been employed extensively in social and economic sciences (Punj and Stewart 1983; Hair et al. 1998).

For the cluster analysis we used our two health measures as identified by the factor analysis. We also included some additional health related variables: public health expenditure as a percentage of GDP, the percentage of the population having access to improved sanitation, the percentage of the population having access to improved water resources, and GDP per capita.5

The first step is to detect outliers and check for multicollinearity. Outliers distort the true structure of the data and make the derived clusters unrepresentative of the population structure. To test whether an observation is an outlier we used the Mahalanobis D² (Hair et al. 1998). The Mahalanobis D² estimates the standard deviation of the distances of the sample points from the centre of mass. If the distance between the test point and the centre of mass is more than one standard deviation, it is highly probable that the test point does not belong to the set and can be classified as an outlier. The Mahalanobis D² measure indicated that less than 2% of the observations are outliers. A scatter matrix (not shown, but available on request) confirmed that our dataset contains only a limited number of outliers. As a robustness check, we estimated the cluster analysis with and without the outliers. However, the outliers did not affect our results and these observations were therefore not deleted.

Also multicollinearity can be a problem in cluster analysis because it distorts the weighting of variables in the different clusters. We used as rule of thumb that the correlation between the variables should not exceed 0.8 (Green 2003). The correlation of two variables was higher: the share of people having access to improved water and the share of people having access to improved sanitation (see Table 11 in the “Appendix”). We therefore dropped the latter variable.6

Table 11.

Correlation matrix cluster variables

		(1)	(2)	(3)	(4)	(5)
Health individuals	(1)	1.00
Health services	(2)	0.61	1.00
GDP per capita	(3)	0.52	0.67	1.00
Improved sanitation	(4)	0.58	0.58	0.65	1.00
Improved water	(5)	0.61	0.56	0.57	0.82	1.00

The next step is to determine inter-object similarity, which is based on the distance between the objects. As a proxy we used the squared Euclidean distance, which is the square of the length of a straight line drawn between two objects (Hair et al. 1998). A higher value denotes less similarity. Because all variables are measured on a different scale, we first standardized the data by computing for each variable the standard scores (also known as Z scores) by subtracting the mean and dividing by the standard deviation of each variable.

Next, we used Ward’s linkage method to cluster countries (Hair et al. 1998). This method seeks to join the two clusters whose merger leads to the smallest within cluster sum of squares instead of joining the two closest clusters. An advantage of this method compared to others (like single linkage or complete linkage) is that Ward’s method is not sensitive to small distortions in the data.

There is no general rule on determining the number of clusters after the hierarchical clustering procedure. However, there are some rules of thumb. One of these rules is based on the so-called agglomeration coefficient. The agglomeration coefficient is the within-cluster sum of squares and measures the differences within a cluster. Joining two very different clusters results in a large agglomeration coefficient (or a large percentage change in the coefficient). One drawback of this method is that it has the tendency to indicate too few clusters (Hair et al. 1998). The agglomeration coefficients in Table 8 indicate that the largest percentage increase occurs if the number of clusters increases from one to two. After seven clusters, the agglomeration coefficient hardly changes.

Table 8.

Optimal clusters solution tests

Clusters	Agglomeration coefficient	Caliński-Harabasz F-index	Dunda-Hart pseudo T-index
2	452.12	301.80	202.58
3	285.57	398.92	146.41
4	214.94	372.45	93.77
5	191.88	367.89	69.37
6	173.31	409.56	23.78
7	154.74	368.09	19.99
8	140.87	349.46	33.54
9	129.83	345.47	32.76
10	117.51	343.78	44.76

An alternative rule is to compute the Caliński-Harabasz pseudo-F-index or the Duda-Hart pseudo-T-square (Milligan and Cooper 1985). A large pseudo-F-index and a small T-square indicate homogenous clustering. The results in the second part of Table 8 show that the six-clusters solution has the largest Caliński-Harabasz pseudo-F-index (409.56). The smallest pseudo-T-squared value is 19.99 for the 5-clusters solution, but notice that the pseudo-T-square value for the 6-clusters solution is also low (23.78).

A more formal test on the number of clusters is given by the Mojena test statistics (Mojena 1977). Mojena test I assumes that the distances of the agglomeration schedule are normally distributed up to a certain step of the fusion process. At each step it is tested whether the distance increase belongs to the assumed normal distribution. Mojena test II verifies whether the distance in a certain step can be predicted with a regression line that is estimated using the distances from the previous steps. If the distance lies outside the 95% confidence interval, a significant increase in the distance is found and the respective step of the fusion process is used as the optimal number of clusters.

In the present analysis, the two Mojena tests give the same results. According to test statistic I, the level of significance exceeds from seven to six clusters, whereas test statistic II suggests an optimal number of six clusters. This solution is in line with the results on the agglomeration coefficient, the Caliński and Harabasz pseudo-F-index, and the Hart pseudo-T-square. Therefore, we identified six clusters.

The six-clusters solution is also in line with the dendrogram. The dendrogram is a graphical representation of the results of a hierarchical procedure in which each object is arrayed on one axis and the other axis portrays the steps in the hierarchical procedure. The dendrogram shows how the clusters are combined in each step of the procedure until all are contained in a single cluster. (Because the dendrogram was too large to include in the paper, we only summarize it in Table 12 in the “Appendix”. However, the dendrogram is available upon request). The dendrogram table indicates that the first cluster solution based on the minimal distance shows 171 clusters with only one country, the second cluster solution indicates that countries can be categorized in 6 clusters.

Table 12.

Dendrogram table

Minimum distance between clusters	Number of clusters
1	171
2	6
3	5
4	5
5	3
10	2
15	2
20	2

Finally, we profiled these six clusters. Table 9 shows the P-value of the F-test that the clusters differ significantly with respect to the health variables (P < 0.05). It is clear that the clusters differ significantly from one another. There are two clusters with poor health, i.e., cluster four and cluster two. In cluster four, on average less than fifty percent of the population has access to improved water facilities and the government is only spending about two percent of (low) GDP on health. Compared to cluster four, cluster two includes countries with a population that has somewhat better access to improved water facilities, a somewhat higher level of government health spending, while the average GDP per capita is about twice as high as GDP per capita in cluster four.

Table 9.

Cluster characteristics

	F-test P-value	Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5	Cluster 6
Cluster variables
Individual health	0.000	1.18	−1.38	−0.03	−1.46	0.52	0.83
Health services	0.000	1.73	−1.01	−0.55	−1.13	0.31	0.87
Public health expenditure (% GDP)	0.000	6.41	3.21	2.30	2.01	2.53	5.39
Access to improved water	0.000	100.00	73.52	77.76	49.35	93.95	97.70
GDP per capita	0.000	28,277	808	1,049	428	4,805	5,515
Demographic and economic variables
Agriculture value added % of GDP		2.30	25.77	21.02	35.08	11.04	7.59
Gross savings as % of GDP		20.18	21.59	21.59	20.31	22.62	21.34
Gini coefficient		31.96	43.86	41.52	42.71	42.17	37.36
Unemployment rate		5.83	14.65	9.12	7.37	9.56	10.88
School enrolment rate: secondary		111.67	35.76	59.65	24.17	83.57	92.71
School enrolment rate: primary		102.96	92.37	104.28	85.34	104.50	105.33
Population growth		0.71	2.09	1.59	2.58	1.22	0.44
Fertility rate		1.73	4.89	3.25	5.80	2.17	1.78
Population ages 0–14		18.68	42.31	35.68	44.77	27.31	21.48
Population ages 15–64		66.48	54.40	59.76	52.20	65.58	66.85
Population ages 65 and above		14.84	3.29	4.56	3.03	7.10	11.67
Geographic variables
% North America		10.00	0.00	0.00	0.00	0.00	0.00
% Central America		0.00	0.00	8.80	3.80	17.50	17.40
% Latin America		0.00	0.00	8.80	0.00	15.00	13.00
% Africa		0.00	90.50	20.60	80.80	20.00	8.70
% Europe		80.00	0.00	2.90	0.00	15.00	56.50
% Asia		5.00	9.50	50.00	11.50	32.50	0.00
% Australia and Oceania		5.00	0.00	8.80	3.80	0.00	4.30
% of all observations		12.20	12.80	20.73	15.85	24.39	14.02

Clusters one and six have good and very good health outcomes. In these clusters almost the total population has access to improved water facilities and public health spending is more than five percent of GDP. Finally, the remaining two clusters are intermediate but differ in their health outcomes and income.

Table 9 shows that the clusters not only differ with respect to health, they also have different economic and demographic characteristics. Countries in clusters two and four are mostly countries with a low income, low school enrolment rate, and a high population growth. Countries in clusters one and six are high-income countries with a high school enrolment rate. Also the geographical dimension differs across clusters. African countries are mainly in clusters two and four, while most European countries can be found in clusters one and six. Table 13 in the “Appendix” shows the composition of the clusters.

Table 13.

Cluster membership

Cluster 1	Cluster 2	Cluster 3	Cluster 4	Cluster 5	Cluster 6
Ireland	Botswana	Guatemala	Cameroon	Slovakia	Greece
Italy	South Africa	Pakistan	Liberia	Lebanon	New Zealand
Luxembourg	Namibia	Nepal	Burkina Faso	Singapore	Poland
Norway	Côte d’Ivoire	Gabon	Kenya	United Arab Emirates	Portugal
Japan	Gambia	Honduras	Uganda	Cyprus	Belarus
United States of America	Zimbabwe	India	Guinea	Mauritius	Croatia
Iceland	Burundi	Comoros	Zambia	Latvia	Czech Republic
Switzerland	Lesotho	Paraguay	Congo	Malaysia	Estonia
Germany	Senegal	Viet Nam	Sierra Leone	Thailand	Malta
Denmark	Central African Republic	Philippines	Haiti	Egypt	Uruguay
Sweden	Ghana	Algeria	Mauritania	Libyan Arab Jamahiriya	Spain
United Kingdom	Rwanda	El Salvador	Lao People’s Democratic Republic	Russian Federation	Bulgaria
Belgium	Malawi	Maldives	Mali	Bahamas	Hungary
Canada	Djibouti	Guyana	Guinea-Bissau	Mexico	Brunei Darussalam
France	Benin	Peru	Nigeria	Ukraine	Costa Rica
Netherlands	Swaziland	Morocco	Democratic Republic of the Congo	Argentina	Jordan
Finland	United Republic of Tanzania	Cape Verde	Madagascar	Turkey	Bosnia and Herzegovina
Austria	Bhutan	Nicaragua	Niger	Albania	Colombia
Australia	Eritrea	Sri Lanka	Equatorial Guinea	Chile	The former state union Serbia and Montenegro
Israel	Timor-Leste	Indonesia	Mozambique	Dominican Republic	Suriname
	Togo	Kyrgyzstan	Chad	Ecuador	Panama
		China	Cambodia	Iran (Islamic Republic of)
		Bangladesh	Papua New Guinea	Jamaica
		Turkmenistan	Ethiopia	Tunisia
		Sudan		Syrian Arab Republic
		Solomon Islands		Republic of Moldova
		Yemen		Armenia
		Mongolia		Republic of Korea
		Vanuatu		Trinidad and Tobago
		Tajikistan		Belize
		Romania		Antigua and Barbuda
		Fiji		Brazil
				Kazakhstan
				Bolivia
				Venezuela (Bolivarian Republic of)
				Georgia
				Uzbekistan
				Azerbaijan

Discussion

On the basis of factor analysis and cluster analysis, this paper tried to offer a better view on cross-country differences in health. Because health is not directly observable and there are many different health indicators available, we used factor analysis to examine the dimensions of health and to come up with better measures for health. Because rankings of countries based on these measures (or any other indicator) do not give information about distances between countries, we focused upon the difference between a country’s health vis-à-vis the sample mean.

However, like any study, the present study has weaknesses. The main weakness is the availability of the data. One limitation of studies on cross-country differences in health is the limited availability of indicators for a long-term period. Even though we included twenty-seven indicators of the health of individuals and ten indicators of health services, this may not suffice to fully capture the concept of health. Unfortunately, other indicators are only available for a small number of (mostly industrialized) countries or are not constructed in a consistent way. Due to this limitation, it is possible that when more indicators become available for a larger set of countries and longer periods, our two measures of health may turn out to be multi-dimensional instead of one-dimensional. In other words, different data could lead to different results and conclusions.

Furthermore, we aggregated the micro level health data to the macro level. Therefore, we cannot take into account the individual (respondent) differences in our cluster analysis. We can only relate the (macro) health outcomes to country averages.

Another problem in research on cross-country health differences is the quality of the data, especially for developing countries. Some variables for these countries show large and unrealistic swings and gaps. Also the data dispersion within in a country cannot be addressed in this study because we focus on country level data.

The final weakness is that our two-one-dimensional health measures explain on average only between 60 and 70% of the total variance. This means that about one-third of the variance remains unexplained. However, extracting more factors did not give us a more insights and worsened the interpretation of the results.

Conclusions

One of the major problems in the economic and social science literature is the measurement of latent constructs. This certainly holds true for cross-country analyses of health. Most previous studies that ranked countries on the basis of their health status used arbitrarily chosen indicators of the health status of a country (cf. the life expectancy or the mortality rate), thereby implicitly assuming that health is a one-dimensional concept. Furthermore, most indicators of health contain some measurement error, which may lead to biased estimates. To come up with better measures for health and to determine whether health has a multidimensional character, a so-called Explanatory Factor Analysis (EFA) was employed on various national health indicators for 171 countries over the period 2000–2005. We used the outcomes of the factor analysis to construct two new national health measures. The first one refers to the health of individuals and the second captures health services.

Our new health measures differ substantially from those reported in earlier studies ranking countries on the basis of their health status. As rankings are not that informative without further information, we focused upon the difference between a country’s health vis-à-vis the sample mean. We found that the cross-country variance of our measure for health services is much higher than that of our measure for the health of individuals.

Furthermore, we found that health depends mostly on geography and development. The dispersion of the two health measures within OECD countries is much lower than in the full sample of countries. This strengthens our conclusion that both measures capture different dimensions of health and that cross-country comparisons of health should not be based on only one (arbitrarily chosen) variable.

Further analysis showed that there are six clusters of countries, ranging from countries with very good health to very bad health. The clusters not only differ with respect to health, they also have different economic and demographic characteristics.

Appendix

See Tables 10, 11, 12, and 13.