Multivariate evaluation of pharmacological responses in early clinical trials – a study of rIL-21 in the treatment of patients with metastatic melanoma

Abstract

AIMS

Evaluation of the utility of multivariate data analysis in early clinical drug development.

METHODS

A multivariate chemometric approach was developed and applied for evaluating clinical laboratory parameters and biomarkers obtained from two clinical trials investigating recombinant human interleukin-21 (rIL-21) in the treatment of patients with malignant melanoma. The Phase I trial was an open-label, first-human dose escalation safety and tolerability trial with two separate dosing regimens; six cycles of thrice weekly (3/w) vs. three cycles of daily dosing for 5 days followed by 9 days of rest (5+9) in a total of 29 patients. The Phase II trial investigated efficacy and safety of the ‘5+9’ regimen in 24 patients.

RESULTS

From the Phase I trial, separate pharmacological patterns were observed for each regimen, clearly reflecting distinct properties of the two regimens. Relations between individual laboratory parameters were visualized and shown to be responsive to rIL-21 dosing. In particular, novel systematic pharmacological effects on liver function parameters as well as a bell-shaped dose–response relationship of the overall pharmacological effects were depicted. In validation of the method, multivariate pharmacological patterns discovered in the Phase I trial could be reproduced by the dataset from the Phase II trial, but not from univariate exploration of the Phase I trial.

CONCLUSIONS

The new data analytical approach visualized novel correlations between laboratory parameters that points to specific pharmacological properties. This multivariate chemometric data analysis offers a novel robust, comprehensive and intuitive tool to reveal early pharmacological responses and guide selection of dose regimens.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Analysis of data from clinical trials is often performed using univariate statistics.

• In early phases of clinical drug development, interpretation of rare clinical events can be difficult by univariate methods.

• Principal component analysis has proven successful within related scientific areas such as, for example, genomics and metabonomics, where compression of data and extraction of maximum information are of utmost importance.

WHAT THIS STUDY ADDS

• This study reveals that multivariate chemometric methods coupled with visualization gives a comprehensive overview of early clinical trial data to guide dose and regimen selection and provides additional findings overlooked by traditional univariate methods.

• This method revealed novel pharmacological patterns in the treatment of metastatic melanoma with recombinant interleukin-21.

Introduction

Clinical drug development is a stepwise, time-consuming and complex process during which an increasing amount of data is collected across numerous trials with different end-points and aims. In controlled clinical trials, subjects are carefully evaluated with respect to predefined clinical and laboratory end-points and closely monitored with respect to unexpected effects. In clinical drug development it is important to extract as much information as early as possible to establish the foundation for the selection of regimen, dose, and patient population for subsequent large-scale clinical trials. Traditional analysis of clinical data is often univariate in nature. Multivariate analysis is capable of finding patterns that are only revealed by relations between variables. Chemometric data analysis tools coupled with visualization provide an opportunity for a rapid and comprehensive overview of a given biological experiment such as a clinical trial. For example, principal component analysis (PCA) allows visualization of a multivariate dataset through so-called principal components. The principal components are variables that are weighted averages of the original variables and found in such a way that they optimally (in a least squares sense) represent the major part of the variation in the data in as few components as possible. Each component can be considered as a descriptive fingerprint of the intrinsic underlying latent variations of the data in the sense that it contains information from all variables simultaneously (for review, refer to Wold et al. [1] and Christie [2]). Unlike more deductive approaches that typically need verified or hypothesized relevant measurements [3], PCA makes it possible to perform an exploratory analysis including many variables, even those that are not a priori known to be relevant. The exploratory analysis can then provide means for assessing to which degree such variables are indeed relevant. Chemometric methods have historically been developed for chemical analysis, but have in recent years proven valuable in other areas, such as genomics and metabonomics [4–7].

In the present study we applied PCA in early clinical pharmacology trials investigating recombinant human interleukin-21 (rIL-21) in the treatment of malignant melanoma. IL-21 is a cytokine with pronounced antineoplastic properties, primarily exerted by stimulation of natural killer (NK) cells and cytotoxic T-cell subsets to kill tumour cells (for review, see Skak et al. [8]). Currently, rIL-21 is in the development for the treatment of various neoplastic conditions, including malignant melanoma. Early clinical investigations have revealed that rIL-21 was generally well tolerated with signs of antineoplastic effects in a subset of patients [9, 10].

The most common adverse events encountered in the first-human dose trial were fatigue, fever, nausea, and headache and the maximal tolerable dose was declared to be 30 µg kg⁻¹[9]. Moreover, serum levels of soluble CD25 (sCD25) were shown to reflect rIL-21-mediated systemic immune activation and distinct pharmacodynamic responses of individual dosing regimens [9, 11]. In addition, several other molecular biomarkers of NK and T-cell activation have been investigated, including mRNA expression of the effector molecules granzyme B and perforin in CD56+ NK cells and CD8+ T cells [9, 12].

Here we propose a multivariate approach to analyse clinical laboratory parameters that can provide valuable information on pharmacological responses complementary to univariate methods when applied in early clinical pharmacology trials.

Methods

Data material

The present study is based on an early clinical development programme including a Phase I and Phase II trial. The Phase I data are from an open-label, two-armed dose escalation study, investigating the safety and tolerability, biomarkers, pharmacokinetics, and efficacy of increasing doses of rIL-21 administrated as an intravenous (i.v.) bolus injection in two different dose regimens: dosing at three times weekly (3/w) (Monday, Wednesday and Friday) in a period of 6 weeks (a total of 18 doses across six cycles) with four different dose levels (1, 3, 10 and 30 µg kg⁻¹) and daily dosing for 5 days followed by 9 days without treatment (5+9) in a period of 6 weeks (a total of 15 doses across three cycles) with six different dose levels (1, 3, 10, 30, 50 and 100 µg kg⁻¹). In the Phase I trial, a total of 29 patients with histologically confirmed surgically incurable metastatic stage IV malignant melanoma were enrolled [9]. The Phase II trial was an open-label, single-armed, fixed-dose study investigating the efficacy, safety and biomarkers of 30 µg kg⁻¹ rIL-21 administered as i.v. bolus injection in the ‘5+9’ dose regimen for a period 6 weeks. A total of 24 patients were enrolled and 12 patients were continued on extension treatment for assessment of progression-free survival [10]. According to the Phase I and Phase II protocols, a total of 43 variables encompassing clinical laboratory parameters and biomarkers were assessed in both trials. The half-life of rIL-21 is approximately 1–4 h [9]. The plasma levels of rIL-21 were hence not detectable at the time points when the majority of samples for laboratory parameters and biomarkers were collected, and pharmacokinetic data were therefore not included in the present analysis.

All patients were treated at the Austin Hospital, the Peter MacCallum Cancer Centre, the Royal Melbourne Hospital, Cabrini Health (all in Melbourne, Australia), Westmead Hosital (Sydney, Australia) or Sir Charles Gairdner Hospital (Perth, Australia). All patients provided written informed consent before any study-specific procedures. The trial protocols were approved by the Human Research Ethics Committees of the participating hospitals and were implemented under the Australian Therapeutic Goods Administration Clinical Trials Notification scheme. The clinical trials were sponsored by Novo Nordisk A/S.

Data analysis

The data were analysed using a modified version of PCA. PCA is a model where the multivariate dataset is compressed into a few orthogonal/uncorrelated principal components (PC) holding the systematic variation of the dataset. Each component is simply a new variable computed as a weighted average of all the original variables and can be considered a descriptive fingerprint in the sense that it contains information from all variables simultaneously. The weights are determined so that the first component explains as much as possible of all the variables. Subsequent components are determined similarly, explaining as much as possible of the yet unexplained part of the variation in data. Results from PCA are presented as components, each containing a score and a loading vector. Each loading vector has as many elements as variables and the elements are the weights for calculating the new variables – the scores. Hence, a numerically high weight implies that the specific variable is important for the component. The sample specific scores explain how the observation behaves with respect to the component. A high score value means that the specific observation has high values on the variables with high loading elements [1].

As expected from clinical trial data, the analysed datasets contain substantial variation across patients (data not shown). The influence of this variation is not of primary concern initially as the focus is on the overall treatment effect within each dose regimen. In order to focus on treatment effects in the PCA analysis, filtering is performed by removing the average level from each subject and each variable. This way, all individual patient data will have the same average level for every variable. Mathematically, removing patient-specific effects is done by orthogonalization and can be considered as a way to focus the analysis on the part of the data specific to treatment-related effects. As a consequence of this, no patient covariates was included in the analysis, as these effects would be removed in the orthogonalization step. Note that no use is made of treatment information in the orthogonalization, which is important in order to avoid spurious correlations (for details see Appendix).

The PCA solution is a least squares solution over all the variables and can therefore be overly influenced by individual variables that are given in numerically large numbers. The variables are hence scaled (and centred) to have equal variance prior to PCA. According to the protocol, not all laboratory or biomarker parameters were assessed on all trial visits. Values for such visits, i.e. for samples that were not obtained, are in PCA defined as ‘missing values’. These data are hence not deviating from the trial protocol but merely just collected as planned, i.e. at different time points compared with most other variables. Expectation maximization provides means for fitting the model without introducing biased estimates due to such ‘missing values’[13]. Using expectation maximization, the amount of missing values in the data is irrelevant, as these do not affect the resulting model. Only the amount of determined information present in the data is critical.

Outliers

Outliers are single measurements or samples identified as statistically irregular in the model, i.e. samples that influence the model in a way that is potentially detrimental to use of the model. The outliers are determined by model residuals (Q-residuals) and distance to model centre (Hotellings T²), and further examined for general pattern deviation and/or single variable measurement deviation [1]. One out of 212 data points was removed as an outlier from the Phase I ‘3/w’ dataset. A single extreme measurement was removed from the Phase I ‘5+9’ dataset. No outliers were removed from the Phase II dataset. The characteristics for the outliers are listed in Table 1. It is of utmost importance to emphasize that outliers are not necessarily wrong and hence should be medically evaluated for clinical relevance and eventually be examined properly by other methods. However, this is not described further as it is beyond the scope of the present paper.

Table 1.

Overview of removed outliers. If identifiable, the diverging measurements are listed

Patient ID	Removed data points	Outlier values	Number of recorded values (out of 43)	Clinical observations
105 –‘3/w’	All data points at day 2		2	No clinical observations observed
112 –‘5+9’	Band Abs at day 8	Band Abs – 0.8	12	No clinical observations observed

Model post-processing

The result of the first step is a PCA model of filtered data that contains a score and a loading vector for each component. The score vector has as many elements as there are time–patient points. The model can be further elaborated by re-arrangement of the scores into a matrix with as many rows as doses and as many columns as time points as written in step 4 of the Model description (Appendix, Model description). For each score vector a matrix is made where the average score for a given dose and time is given in the corresponding element. This matrix provides information on the time–dose information of that particular component and is analysed with a subsequent PCA model providing an even further condensed approximation of the variation in the data useful for understanding, e.g. the time-dependent variation. This will be exemplified in the Results section. An algorithm for the complete data analysis is described in the Appendix.

All calculations are conducted using in-house algorithms written in MATLAB® ver. 7.6.0.324. The function can be downloaded from http://www.models.life.ku.dk.

Results

Pharmacological responses of the ‘5+9’ dose regimen

By applying PCA to the ‘5+9’ datasets, two significant (P < 0.001) components appeared. For the ‘5+9’ regimen, components 1 and 2 describe 20.0% and 9.7%, respectively, of the total variation across all variables (Figure 1a,b). The structure of the pharmacological response described by the scores in the first component clearly reflected an underlying signature of the ‘5+9’ dose regimen (Figure 1a). During the course of 5 days of treatment, a pronounced decrease in score values was observed in each treatment cycle. This response was fully reverted during 9 days of treatment pause. The pattern described by the second component did not display a similar signature of the ‘5+9’ dose regimen. However, the score values increased to some extent during the course of three treatment cycles, indicating an accumulation of the pharmacological effect reflected by the variables expressed in this component (Figure 1b). Tentatively, and based on the shape of the curves, the two components describe the acute and the cumulative pharmacological effects, respectively. In order to illustrate dose-dependency of these distinct pharmacological responses, score values as function of day and dose were analysed with a subsequent one-component PCA as described in the Appendix (Figure 1c,d). For both components of this subsequent PCA model, a bell-shaped dependency of dose peaking at 30 µg kg⁻¹ was observed, indicating a maximal pharmacological response at this dose level. The observation of a bell-shaped pharmacology is novel and was not found in the original univariate analyses of these data [9].

Figure 1.

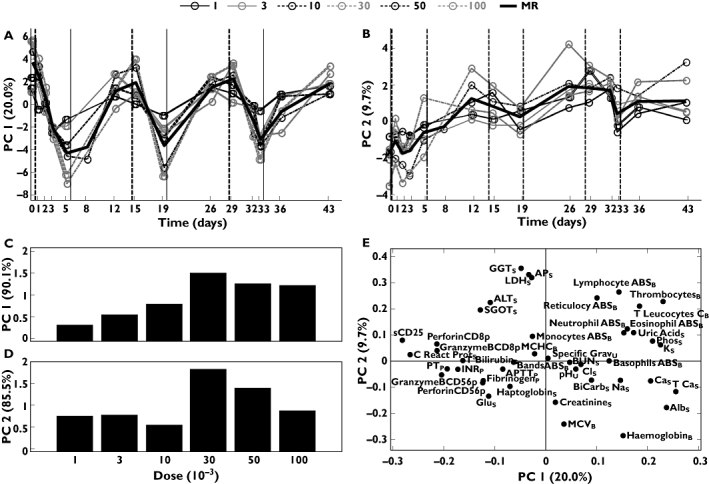
Results from two component models of data obtained from regimen ’5+9’. (a) Score values for component 1 plotted vs. day for each of the six doses (µg kg⁻¹) and the mean response (MR) of those. (b) Score values for component 2 plotted vs. day. (c) Scores from one-component principal component analysis (PCA) model of scores from component 1. (d) Scores from one-component PCA model of scores from component 2. (e) Loading plot of component 1 vs. component 2. Subscripts: B, blood; P, plasma; S, serum; U, urine

Potential relationships between the pharmacological responses of the individual laboratory parameters and biomarkers were assessed by a scatter plot of the first and second loading vector of the initial PCA model across all dose levels (Figure 1e). Based on the positions, the individual parameters could be divided into several categories. Parameters far from the origin are those most influential in the model and parameters close to each other are correlated with respect to the variation reflected by the components. One group of laboratory parameters (upper right quadrant) was composed of haematology parameters, e.g. peripheral blood lymphocyte counts (Lymphocyte ABS_B). These parameters showed high scores for both components and hence behaved as a combination of the two, i.e. decreased during the 5 days of treatment, increased during the 9 days of rest, and slightly accumulated during the 6 weeks of treatment. Opposite to this group (lower left quadrant) was a group composed of biomarkers of NK cell activation, e.g. perforin mRNA expression of purified peripheral blood CD56⁺ NK cells (PerforinCD56p). These parameters were negatively correlated to the group in the upper right quadrant and hence increased during treatment, decreased during rest, and slightly decreased during the 6 weeks of treatment, reflecting rIL-21-mediated effects on NK cell function. In general, variables with high positive or negative loading values for the first component, e.g. peripheral blood lymphocyte counts (Lymphocyte ABS_B) and sCD25, respectively, reflected the signature of the ‘5+9’ dose regimen and were thus qualified as biomarkers for the overall pharmacological effects. Pharmacological effects on these NK and T-cell activation biomarkers is an expected finding and was also described in the original reports of these data [9, 12]. However, the inverse relation between peripheral blood lymphocyte and T leucocyte counts vs. NK cell and T-cell activation markers that is clearly reflected in Figure 1e has not previously been described and supports rIL-21-mediated immune activation as the primary cause of changes in these blood cell counts.

Variables with high (positive or negative) loading values for the second component indicated an accumulation/decreasing pattern registered during the 6 weeks of treatment. Parameters with numerically low loading values for both components, e.g. mean corpuscular haemoglobin concentration (MCHC_B) did not match the overall pattern of the dataset and were hence inadequately described by this model. However, this does not imply absence of clinical relevance of such lab parameters, but merely indicated that the overall patterns observed in the two components were not reflected in these parameters.

Parameters with high loading values for the second component and low loading values for the first, such as the liver function parameters, e.g. gamma glutamyl transferase (GGT_S) behaved opposite to parameters with low second component and high first component loading values such as serum albumin (Alb_S). The finding that these and other liver function parameters systematically decreased and increased, respectively, during treatment cycles is novel and was not described in the original univariate analyses of this dataset [9]. Moreover, a subsequent PCA clearly reveals that this underlying pharmacological effect on liver function parameters is visible already at the third dose-level (10 µg kg⁻¹) tested during the dose-escalation part of the Phase I trial (Figure 2).

Figure 2.

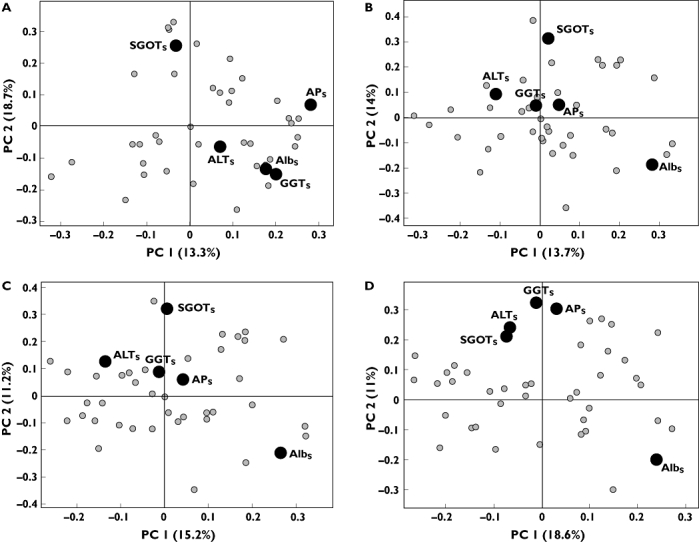
Loading plot of component 1 vs. component 2 from principal component analysis model from regimen ‘5+9’. (a) Dose level 1 µg kg⁻¹. (b) Dose level 1 and 3 µg kg⁻¹. (c) Dose level 1, 3 and 10 µg kg⁻¹. (d) Dose level 1, 3, 10 and 30 µg kg⁻¹. Only labels for liver functionality parameters are included. Subscript: S, serum

Pharmacological responses of the ‘3/w’ dose regimen

Components 1 and 2 of the ‘3/w’ regimen described 12.7% and 13.2% of the total variation, respectively (Figure 3a,b). In contrast to the cyclic signature of the ‘5+9’ dose regimen, a more continuous pharmacological effect was observed for the ‘3/w’ regimen. This difference in pharmacological effects between the regimens has previously only been described by univariate analysis of sCD25 and hence not as a general phenomenon across all assessed laboratory parameters [9]. In the ‘3/w’ regimen the first component showed large variability in the first few days of treatment, followed by a decrease to a constant yet fluctuating level from day 5 and onwards. Component 2 showed ascending score values for the first 2–3 weeks followed by a stable plateau for the rest of the treatment period, indicating that steady state was reached for the pattern of variables described in component 2. As for the ‘5+9’ regimen, maximal pharmacological responses were observed for the first component at 30 µg kg⁻¹ (Figure 3c). However, due to dose-limiting toxicities, dose levels >30 µg kg⁻¹ were not tested with the ‘3/w’ regimen [9]. For the second component the pharmacological effect was observed to peak at the 3 µg kg⁻¹ dose level (Figure 3d).

Figure 3.

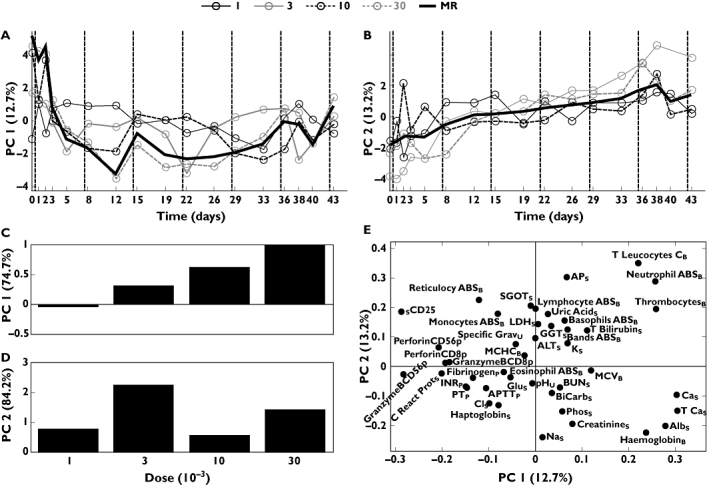
Results from two-component model of data obtained from regime ‘3/w’. (a) Score values for component 1 plotted vs. day for each of the four doses (µg kg⁻¹) and the mean response (MR) of those. (b) Score values for component 2 plotted vs. day. (c) Scores from one-component principal component analysis (PCA) model of scores from component 1. (d) Scores from one-component PCA model of scores from component 2. (e) Loading plot of component 1 vs. component 2. Subscripts: B, blood; P, plasma; S, serum; U, urine

Comparisons of pharmacological responses between dose regimens

For the ‘3/w’ dose regimen both differences from and similarities to the ‘5+9’ regimen were observed for the individual laboratory parameters and biomarkers when presented as a scatter plot of loading values corresponding to components 1 and 2 (Figure 3e). As for the ‘5+9’ regimen, the liver function parameters, e.g. GGT_S, clustered opposite to Alb_S in the direction of component 2, indicating an impact on the liver function for both regimens. However, for the ‘3/w’ regiment the distance between serum albumin and other liver parameters such as GGT and alkaline phosphatase (AP_S) was less pronounced, indicating similar but a more gradual effect on the liver function with the ‘3/w’ regimen compared with the ‘5+9’ regimen. For activation of NK cells, differences were observed between the two dose regimens. In the ‘3/w’ regimen, perforin mRNA expression of purified peripheral blood CD56⁺ NK-cells (PerforinCD56p) and lymphocyte ABS_B clustered in a single quadrant (Figure 3e, upper left). In the ‘5+9’ regimen, these parameters were clearly separated in opposite directions, indicating a more pronounced effect on NK cells compared with the ‘3/w’ regimen (Figure 1e). None of these pharmacological differences between the regimens was found by the univariate methods in the original reports of these data [9, 12].

Clinical efficacy and adverse events

During treatment, tumour size was registered as a secondary end-point for efficacy. In this trial, sporadic antitumour responses were observed in <10% of patients [9]. Analysis of change in tumour size vs. score values (for both components and regimens) did not reveal systematic variation in laboratory parameters and biomarkers that correlated with tumour shrinkage (data not shown). A similar analysis for the two most commonly reported adverse events, i.e. fatigue and pyrexia, revealed a positive correlation between score values for component 1 and number of fatigue events (P < 0.001) and pyrexia events (P= 0.02) for regimen ‘5+9’, indicating a rIL-21 treatment-related response (Figure 4 and Appendix, Analysis of adverse events).

Figure 4.

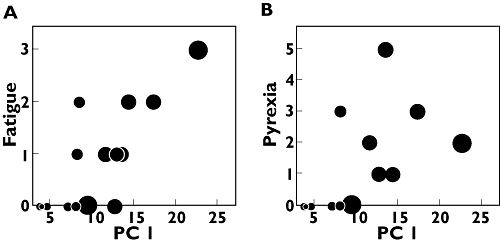
Number of adverse events vs. score values from a subsequent one-component model of initial principal component analysis results for regimen ‘5+9’. The size of the point reflects dose level for the respective patient. (a) Number of fatigue events. (b) Number of pyrexia events

Validation of the model in an independent clinical trial

A total of 43 variables were included in the ‘5+9’ regimen datasets from both the dose-escalation Phase I trial and the fixed-dose Phase II trial. A training model composed of the ‘5+9’ Phase I dataset and a validation model of the Phase II dataset was built. The training model from Phase I was analysed for the ability to predict score values from the Phase II data (Figure 5a,b). Although there were minor differences in magnitude of the pharmacological responses, with a trend towards higher responses in the Phase I trial, the pattern reflecting the signature of the ‘5+9’ regimen was clearly sustained for component 1 (Figure 5a) and to some extent also for the less descriptive second component (Figure 5b). Significant correlations were found between Phase I and II scores for each component (PC1, R²= 0.95, P < 0.0001; PC2, R²= 0.75, P= 0.02).1 Similarities between the Phase I and Phase II models were further verified by visual comparison of loading values from two independent PCA models (Figure 6). Mathematically, the loadings were rotated and superimposed in order to see if the two models capture the same variation. This revealed that most parameters clustered close together within the individual quadrants. Loading values for both components were found to be significantly correlated between the two trials (PC1, R²= 0.94, P < 0.0001; PC2, R²= 0.40, P= 0.008). However, some parameters shifted between the trials such as PerforinCD56p, GGT and albumin, indicating an effect of the dose-escalation vs. a fixed-dose trial.

Figure 5.

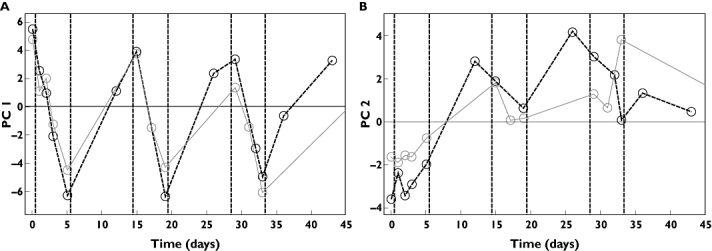
Validation and comparison of results from Phase I and Phase II dose regime ‘5+9’. Calibrated (Phase I) and validated (Phase II) score values for dose 30 µg kg⁻¹. (a) PC1. (b) PC2. (A) Phase I Expvar 20.0% (); Phase II Expvar 9.1% (); (B) Phase I Expvar 9.7% (); Phase II Expvar 3.9% ()

Figure 6.

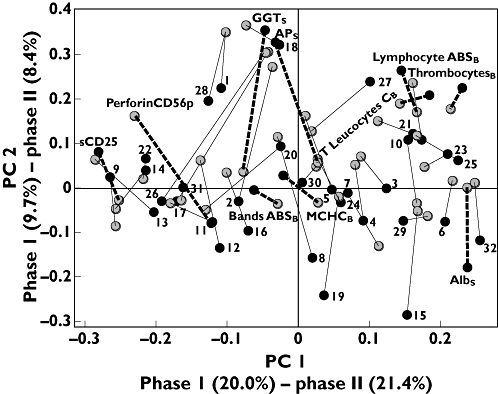
Validation and comparison of results from Phase I and Phase II dose regime ‘5+9’. Comparison of loading plots from two individual models from Phase I (•) and Phase II (), respectively. Matching variables are connected with lines. Only labels for discussed variables are shown with highlighted lines (‘––’). Subscripts: B, blood; P, plasma; S, serum; U, urine. The remaining variables are numbered, labels are listed in Appendix. Correlation between loadings are R²_{(PC 1)}= 0.94 and R²_{(PC 2)}= 0.40

Discussion

Analysis of individual laboratory parameters from a single or groups of trials can be an exhaustive process in which rare clinical events and/or unexpected pharmacological responses may not be clearly emphasized until relatively late in the development process. Moreover, such responses may be more clearly reflected in a pattern of several variables rather than individual ones. We hypothesized that multivariate chemometric data analysis coupled with visualization would provide an opportunity for a rapid and comprehensive overview of clinical trial data in revealing novel pharmacological findings. The nature of multivariate data analysis is to grasp the common variation of the data and hence the variation common across several variables. We developed a multivariate chemometric data analysis tool based on PCA for visual inspection of pharmacological responses in clinical pharmacology trials. The tool is an unsupervised data analysis tool, which in an assumption-free manner enables visualization of the main variation present in data. It combines methods for handling data collected at different time points as well as methods for focusing on variations relating to dose–time effects rather than interindividual effects. We utilized the tool to show distinct signatures of pharmacological responses of clinical laboratory and biomarker parameters in a Phase I and a Phase II trial investigating rIL-21 in the treatment of patients with malignant melanoma. The responses reflected acute (first component) and cumulative (second component) effects of two different dosing regimens. For both regimens, a maximal pharmacological response was for the first component observed at 30 µg kg⁻¹ and supports the notion that additional pharmacological effect cannot be achieved at doses >30 µg kg⁻¹. However, for the second component of the ‘3/w’ regimen the response was observed to peak at the 3 µg kg⁻¹ dose level (Figure 3d). Moreover, the response observed for this component gradually increased throughout the trial, indicating accumulation of some of the variables with the ‘3/w’ regimen (Figure 3b). Interestingly, dose-limiting toxicities were observed only at the 30 µg kg⁻¹ dose level with the ‘3/w’ regimen and not the ‘5+9’ regimen, suggesting different safety profiles of the two regimens [9]. Nevertheless, the 30 µg kg⁻¹ dose level was during dose escalation in the Phase I trial declared by clinical criteria as the maximal tolerable dose for both regimens, supporting the utility of chemometric approaches for selection of dose levels [9]. Moreover, the bell-shaped appearance of the pharmacological effects observed with the ‘5+9’ regimen (Figure 1c,d) has not previously been described and indicates that additional pharmacological activity may not be achievable at dose levels >30 µg kg⁻¹. However, whether doses >30 µg kg⁻¹ will be feasible is still under consideration [11].

In previous clinical investigations of rIL-21, serum levels of sCD25 have been shown to reflect rIL-21-mediated systemic immune activation and distinct pharmacodynamic responses of individual dosing regimens [9, 11]. These univariate sCD25 responses clearly resemble the observed multivariate patterns of acute (first component) responses across all the assessed laboratory and biomarker parameters and point to sCD25 as a robust surrogate for acute pharmacological responses to rIL-21 (Figures 1e and 3e). Other biomarkers also closely linked to the rIL-21 mechanism of action such as perforin mRNA expression of NK cells and numbers of peripheral blood lymphocytes have also previously been described by univariate methods [9, 12]. Here, we have shown more distinct responses between the two regimens for these biomarkers, indicating more pronounced effects with the ‘5+9’ regimen on NK cell activation. This difference between the two regimens is a novel finding that was not identified during the original analyses of the datasets based on univariate methods and supports the utility of the multivariate approach in regimen selection for subsequent late-stage clinical trials [9, 12]. However, these differences may at least in part also be related to different sample time points and inclusion of higher dose levels in the ‘5+9’ regimen.

In addition to mechanistic patterns of biomarker responses, the multivariate approach also revealed novel correlations between clinical laboratory parameters related to the safety of this novel compound. In particular, rIL-21 induced changes in liver function laboratory parameters that were clearly visualized by inverse clustering of Alb_s and liver enzymes [GGT_s, serum glutamic oxaloacetic transaminase (SGOT_s), serum alanine aminotransferase (ALT_s) and AP_s]. The observation that these liver function parameters systematically changed and inversely clustered is novel and was not detected during the original univariate analyses of these data. However, sporadic events of elevated liver enzymes were originally reported by univariate analysis in a subset of the patients [9]. By applying the multivariate approach it clearly becomes visible that these sporadic adverse events reflect a systematic and more general underlying pharmacological adverse effect on liver function parameters. Simultaneous analysis of available data as they are reported reveals that this trend, i.e. similar clustering of GGT_s, SGOT_s, ALT_s and AP_svs. Alb_s as illustrated in Figure 1e, becomes evident already at the third dose level (10 µg kg⁻¹) in the regimen ‘5+9’ of the dose-escalation Phase I trial (Figure 2c). This clearly supports the notion that the multivariate approach provides additional information to univariate methods and this at an earlier stage in the clinical development process. Moreover, differences between the dose regimens may indicate a more gradual effect on liver function with the ‘3/w’ regimen compared with the ‘5+9’ regimen. This important information was also not captured in the original univariate analyses of the data, further supporting the utility of multivariate approaches for regimen selection [9].

The systematic variation explained by the models is approximately 30% for both regimens in two components. There are 43 variables and hence if these were completely independent of each other (orthogonal) each component in a PCA would explain 2.33% of the variation. That 30% is explained in two components therefore directly implies that the variables have a large common underlying structure. It is also expected that the percentage of variance explained is well below 100%. Otherwise, the measured variables would have been completely redundant and all information could have been implicitly obtained from measuring just two variables rather than the present 43. Hence, there is additional information in these variables probably reflecting idiosyncratic phenomena that are not related to treatment.

Variables that do not correlate with the variation in the rest of the data material, i.e. data with low loading values for both component 1 and 2, are insufficiently described by the models. For example, the MCHC_B was inadequately described by the models. Evaluation of these types of variable should be supplemented by additional univariate statistical analysis in order to ascertain whether such variables have a different important clinical relevance.

According to the clinical trial protocols the individual laboratory and biomarker assessments were collected at different sample time points. For example, laboratory biochemistry and urinalysis were assessed on days 1, 2, 3 and 5 in the first week of dosing, whereas sCD25 was assessed on days 1, 2 and 5. In chemometric terms such sample collection schemes create ‘missing values’. In the model, such values are estimated by expectation maximization (see Methods). Consequently, variables with a high degree of ‘missing values’ are estimated with higher uncertainty. For this reason, pharmacokinetic data were not included in the present analysis. As for other cytokines, the half-life of rIL-21 is very short, i.e. approximately 1–4 h [9]. Hence, plasma levels of rIL-21 were undetectable at the time points when all other laboratory parameters were assessed. Future investigations of the proposed multivariate approach in clinical pharmacology trials investigating compounds with longer half-lives will reveal any potential value of integrating pharmacokinetic data into this model.

The robustness of the multivariate approach was tested by comparing a Phase I data model with an independent Phase II data model. This validation revealed that the pharmacological pattern depicted in the Phase I trial was strikingly reproducible and predictive of the response in a subsequent and independent trial. This finding further supports the utility of the multivariate approach in extracting additional information from early Phase I trials to facilitate decision making and planning for late-stage clinical development.

The presented multivariate models were not able to reveal correlations between laboratory variables and clinical end-points for efficacy using the present datasets. Also by univariate methods, parameters predictive of efficacy have not previously been reported and may at least in part be related to the fact that the overall proportion of patients that experienced measurable clinical antitumour responses in these early trials was <10% [9, 10]. In addition, these limited data were rather variable among the individual patients, and lack of association to the systematic PCA components is therefore not surprising. In other therapeutic areas such as diabetes, where clinical efficacy end-points are more frequently encountered, the multivariate model may have a higher potential in revealing correlations to efficacy. In support, the model did reveal significant correlations between the first component for the regimen ‘5+9’ and the more frequently encountered clinical safety end-points for fatigue and pyrexia, emphasizing that these events are related to the acute (component 1) treatment response. By univariate methods, increased levels of serum IL-10 have actually previously been reported in patients experiencing dose-limiting toxicities [14]. Since measurements of IL-10 and a large number of other serum biomarkers were not included in the Phase II trial, these data were not included in the present analysis. However, the lack of strong correlations to infrequently observed clinical end-points illustrates limitations in the utility of the presented multivariate model. This points to the notion that multivariate models should be applied only in conjunction with univariate methods in order to capture all relevant information. Future studies will reveal if multivariate models can be applied in other areas, e.g. in diabetes where the trial design, efficacy rates and safety measurements are very different from what is used in oncology. The presented findings warrant further investigations of the utility of multivariate chemometric approaches in early- and late-stage clinical drug development across therapeutic areas.

Conclusion

Multivariate chemometric data analysis offers a comprehensive and intuitive tool to reveal early pharmacological responses in clinical pharmacology trials. The multivariate nature of the method allows simultaneous analysis of many parameters and allows more detailed findings than traditional univariate approaches. The present study has revealed novel correlations between laboratory parameters related to liver function and biomarkers exploring the pharmacological properties of rIL-21. Furthermore, the presented multivariate approach can be used as guidance in dose and regimen selections for subsequent studies.

Appendix

Model description

In the following, the complete sequence of steps in our multivariate approach is explained in detail. The basis for the algorithm is a data matrix X of size I (rows) times J (columns). Each column holds the measurements of one variable and each row contains the data for one subject measured at one instance. Generically, the modelling is conducted as the following:

1. Missing individual observations (elements of X) are imputed using expectation maximization [13]. This means that the model is determined in a least squares sense given the observed data without any need to exclude either rows or columns, which would be wasteful and potentially critical given that only few subjects are usually available. Imputation works by iteratively fitting the model to complete data initialized with suitable numbers where missing data occur and then at each iteration replacing the elements that are missing with estimates of the data obtained from the model.

2. The data matrix X (I X J) is orthogonalized in order to remove systematic irrelevant variation, here due to subject-specific variation. Orthogonalization can be written formally as X_ort= (I−DD⁺)X where X_ort is the filtered data, I (I X I) is the identity matrix, and D (I X n_subj) is the design matrix with respect to subject. D⁺ refers to the pseudoinverse of D, n_subj refers to the total number of subjects/patients. The matrix D is a dummy matrix that contains ones in column n in the rows of subject n. This orthogonalization step removes any differences in level between subjects, i.e. similar to what can be termed the subject-effect in analysis of variance [15]. Orthogonalization is described in detail in the latter part of this Appendix. Removing this variation is essential in order to filter off subject variation that is not related to the effect of the treatment. Note that other types of irrelevant variation can also be removed using several orthogonalization steps if needed. Also, note that the residuals of the orthogonalization contain the subject-specific variation that, if needed, can be further scrutinized.

3. Having removed the subject-specific variation, a PCA model [16] is determined on the orthogonalized data. As opposed to traditional PCA, it is crucial to use the correct number of components, because the missing data imputation in step 1 depends on the number of components. In practice, several numbers of components are tested and evaluated using the explained variance vs. number of components plot as is usual in PCA [17], and number of iterations for determination of missing values. The statistical relevance of the model is tested by permutation testing using 1999 random permutations [18].

4. Post-processing is performed on the result of the PCA model in order to enhance the visualization. Specifically, the scores of the PCA model are averaged across day-dose. Hence, instead of presenting a score value for each subject, the scores are shown as averages for a specific day and dose.

The algorithm

According to the above, the formal algorithm can be written as follows.

1. Missing data elements are imputed with mean values of the respective variables.

2. Data are orthogonalized into; X_ort (matrix with information orthogonal to D) and X_rest (matrix with information linear correlated to D)

   
   

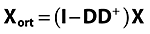
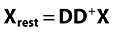
   where D⁺= (D′D)⁻¹D′

3. Data are autoscaled to equal variance [19].

4. PCA on orthogonalized and autoscaled data, decomposing X_ort into a score matrix (T), a loading matrix (P) and a residual matrix (E).

   

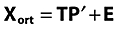
5. PCA data approximation calculated

   

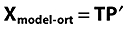
6. Approximation de-orthogonalized

   

7. Approximations backscaled

8. Missing data are imputed with backscaled approximations.

Step 2–8 is repeated until convergence of approximation results.

Orthogonalization

X(I X J) is a data matrix, D(I X k) is matrix (or vector) with external information such as patient id. The purpose of orthogonalization is to split X into a part linear related to D (X_D) and a part orthogonal/perpendicular to D (X_OD).

Examine the linear regression problem

where B is some regression matrix and E is the part of X not explained by D. From this B can be extracted as:

and X_D can be estimated to:

and X_OD to:

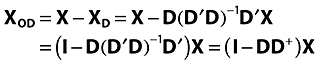with D⁺= (D′D)⁻¹D′ as the pseudo inverse of D.

Analysis of adverse events

The numbers obtained throughout the trial period of the most frequent adverse events (fatigue and pyrexia) were compared with score values from a one-component PCA model on the initial results. In Figure 4 data are shown for regimen ‘5+9’.

Abbreviations for Figure 6

1. ALT (alanine aminotransferase) serum

2. APTT (activated partial thromboplastin time) plasma

3. Basophils ABS blood

4. BiCarbonate serum

5. BUN (blood urea nitrogen) serum

6. Calcium serum

7. Chloride serum

8. Creatinine serum

9. C-reactive protein serum

10. Eosinophil ABS blood

11. Fibrinogen plasma

12. Glucose serum

13. GranzymeBCD56p

14. GranzymeBCD8p

15. Haemoglobin blood

16. Haptoglobin serum

17. INR (International Normalized Ratio) plasma

18. LDH (lactate dehydrogenase) serum

19. MCV (mean corpuscular volume) blood

20. Monocytes ABS blood

21. Neutrophil ABS blood

22. PerforinCD8p

23. Phosphorous serum

24. pH urine

25. Potassium serum

26. PT plasma

27. Reticulocyte ABS blood

28. SGOT (serum glutamic oxaloacetic transaminase) serum

29. Sodium serum

30. Specific Grav urine

31. T Bilirubin serum

32. T Calcium serum

33. Uric acid serum

Competing interests

M.C-J. and L.T.H. are employees of Novo Nordisk A/S.

Ulrik Mouritzen, Steen Hvass Ingerwersen and Per Knud Christensen are acknowledged for their scientific support and critical comments.