Abstract
Charting change in behavior as a function of age and investigating longitudinal relations among constructs are primary goals of developmental research. Traditionally, researchers rely on a single measure (e.g., scale score) for a given construct for each person at each occasion of measurement, assuming that measure reflects the same construct at each occasion. With multiple indicators of a latent construct at each time of measurement, the researcher can evaluate whether factorial invariance holds. If factorial invariance constraints are satisfied, latent variable scores at each time of measurement are on the same metric and stronger conclusions are warranted. In this paper we discuss factorial invariance in longitudinal studies, contrasting analytic approaches and highlighting strengths of the multiple-indicator approach to modeling developmental processes.
Keywords: Longitudinal designs, longitudinal models, growth curve models, factorial invariance
Longitudinal design is a sine qua non for assessing change and factors that influence change, which are principal goals of developmental science. In longitudinal investigations, participants are assessed at two or more points in time, corresponding to different chronological ages. From these longitudinal assessments, mean levels of behavior, change in behavior, and individual differences in change can be estimated and modeled. Over three decades ago, Wohlwill (1970, 1973) formalized these aims as the study of the function relating behavior (B) to chronological age (A), or B = f (A), and the investigation of variables that influence this function. These dual aims are so entwined with the nature of developmental science that few would question the importance of longitudinal investigations, despite attendant problems or confounds.
One of the more vexing problems in assessing development – and one that deserves greater attention – is the problem of measurement invariance. Researchers often use the same version of a scale for assessing a given construct at each time of measurement, so they can rest assured that the same construct is assessed, scale scores fall on the same metric, and thus change can be estimated unambiguously. But, just as often, researchers wonder whether to alter measuring instruments as participants get older, using developmentally appropriate measures so they can continue to assess “the same construct.” If levels of performance of participants change so much that notable ceiling or floor effects occur at older age levels, measuring devices must change to enable proper estimation of behavioral change (Embretson, 2006, 2007; May & Nicewander, 1998). More subtly, if the nature of the construct assessed by an instrument changes with age, an instrument might require alteration to ensure that the same underlying construct is still assessed (Widaman, 1991), although modeling such data requires dealing with changes in the scales, a topic for future investigations.
Investigating whether the same construct is assessed on the same metric across groups or occasions is discussed under the rubric of measurement invariance. Within structural equation modeling, measurement invariance is termed factorial invariance. First, we discuss how to evaluate factorial invariance in longitudinal designs using contemporary statistical models, outlining general analytic approaches and various levels of factorial invariance. Next, we describe how factorial invariance can be studied using one standard longitudinal technique, namely growth curve modeling. Then, after adding a caveat regarding implications of factorial invariance, we close with a summary of the importance of establishing invariance for research and theory in developmental science.
FACTORIAL INVARIANCE IN LONGITUDINAL CONTEXT
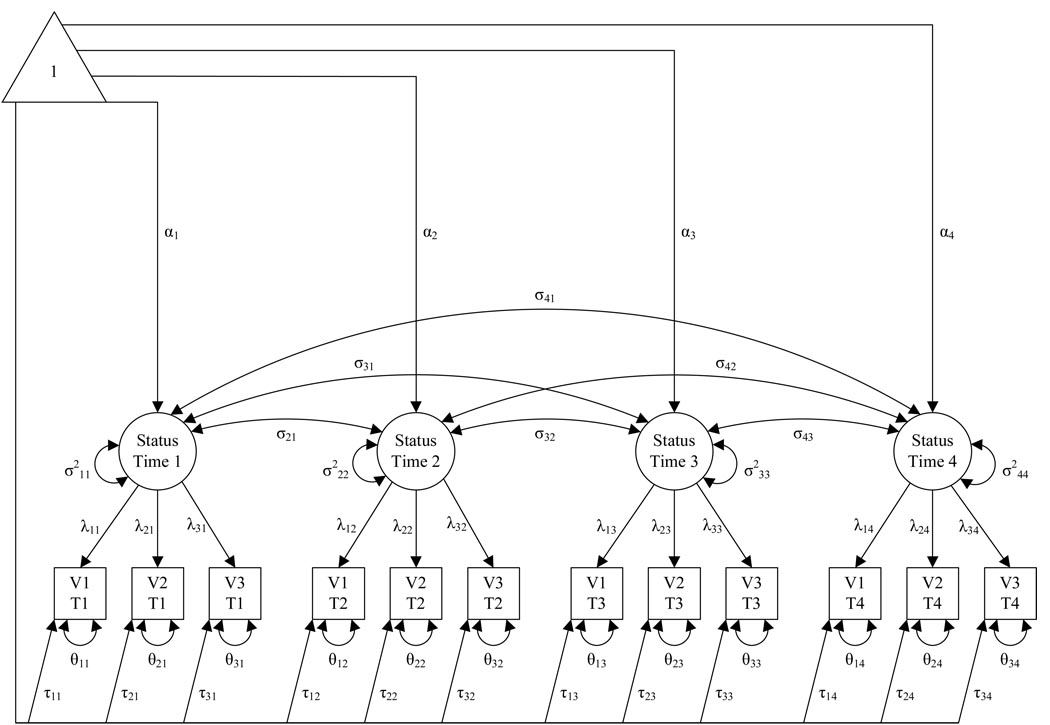
Investigating change in behavior across time (e.g., McArdle & Epstein, 1987; Meredith & Tisak, 1984, 1990) and interrelations across time among two or more processes (e.g., Cole & Maxwell, 2003; Curran & Bollen, 2001; Maxwell & Cole, 2007; McArdle, 2001; McArdle & Hamagami, 2001) are predicated on satisfying a key assumption: for each construct of interest, we are measuring the same thing in the same metric at each occasion. Rather than assuming this to be the case, we can formally test this hypothesis of factorial invariance, but only if multiple indicators of a construct are available at each occasion. A structural model satisfying this condition is shown in Figure 1, where 3 manifest variables (V1–V3) that are indicators of a construct are measured at each of four occasions (T1–T4). With this data structure, we can evaluate how well models with varying levels of factorial invariance fit the data and thereby test assumptions regarding factorial structure across time. In our figures, we use standard figural notation for path diagrams: (a) a triangle represents the unit constant that is used to estimate mean levels; (b) rectangles represent manifest variables; (c) circles represent latent variables; (d) one-headed arrows depict unidirectional, directed effects of one variable on another, associated with parameters such as regression weights or means; and (e) double-headed arrows designate non-directional relations between variables, reflecting variances or covariances. Specifically, a double-headed arrow from a variable to itself represents a residual variance, controlling statistically for unidirectional effects on the variable.
Figure 1.
Longitudinal confirmatory factor model for 12 manifest variables, consisting of three manifest variables (V1 through V3) assessed at each of four times of measurement (T1 through T4).
Measurement Models and Factorial Invariance
The model in Figure 1 is consistent with the following measurement equation for each manifest variable:
| (1) |
where Yijt is the score of person i (i = 1, …, N) on manifest variable j (j = 1, …, J) at time t (t = 1, …, T), τjt is the intercept for manifest variable j at time t, λjt is the factor loading for manifest variable j at time t, ηit is the latent variable score for person i at time t, and εijt is the unique factor score for person i on manifest variable j at time t. Intercepts τjt and factor loadings λjt can be estimated directly, but individual’s scores on the latent and unique factors are latent or implied entities and cannot be estimated directly. Instead, only the mean (αt) and variance (σ2 t) of scores on latent variable ηt and the variance (θjt) of scores on each unique factor εjt can be estimated (note, unique factor means are typically assumed to be zero).
Put simply, factorial invariance in longitudinal models concerns whether relations between latent variables and their manifest indicators are invariant across occasions. Stated differently, the expected value of a person’s score on manifest variable j at time t should be a function of her score on the latent variable and the associated unique factor at time t, and should not additionally depend on time of measurement (cf. Meredith, 1993). The key parameters involved in establishing factorial invariance are shown at the bottom of Figure 1. These parameters are (a) intercepts τjt, (b) factor loadings λjt, and (c) unique factor variances θjt that reflect the relations of the four latent factors (Status Time 1 — Status Time 4) with the manifest indicators.
Synthesizing prior work by Meredith (1964a, 1964b, 1993), Horn, McArdle, and Mason (1983), Jöreskog (1971), and others, Widaman and Reise (1997) identified four levels of factorial invariance and described how to test factorial invariance across groups. The Widaman and Reise approach is readily adapted to evaluating factorial invariance in longitudinal contexts, yielding:
configural invariance: the same pattern of fixed and free factor loadings across time;
weak factorial invariance: invariant factor loadings across time;
strong factorial invariance: invariant factor loadings and intercepts across time; and
strict factorial invariance: invariant factor loadings, intercepts, and unique factor variances across time.
Other researchers have discussed testing and evaluating factorial invariance informatively (e.g., Byrne, Shavelson, & Muthén, 1989; Chen, Sousa, & West, 2005; Cheung & Rensvold, 1999; Ferrer, Balluerka, & Widaman, 2008; Hancock, 2001; Little, 1997; McArdle, 1988; Meredith & Horn, 2001; Millsap & Meredith, 2007; Nesselroade, 1983; Rensvold & Cheung, 1998), but we use the Widaman and Reise terminology of levels of invariance to maintain consistency with key elements of the fundamental work by Meredith (1993).
Evaluating Factorial Invariance
Series of models with increasing invariance
An optimal approach to longitudinal evaluation of factorial invariance involves adapting the two-step procedure proposed by Anderson and Gerbing (1987). The first general step includes comparisons among a series of four models corresponding to the levels of factorial invariance listed in the preceding paragraph. First, a researcher should fit a longitudinal factor analysis model with configural invariance and minimal identification constraints. An identification strategy that leads to rather simple interpretation of parameter estimates is the following (refer to Figure 1): (a) fix α1 to 0.0 and σ2 11 to 1.0, so that latent variable scores at Time 1 have standardized metric (M = 0, SD = 1.0); (b) estimate the first loading, but constrain corresponding first loadings to be invariant across time (λ11 = λ12 = λ13 = λ14); (c) estimate the first intercept τ11, but constrain corresponding first intercepts to be invariant across time(τ11 = τ12 = τ13 = ô14); and (d) freely estimate all remaining parameters shown in Figure 1. In this model, one would specify free means on latent variables (α2 through α4) and free variances on (σ2 22 through σ2 44) and covariances among latent variables (σ21 through σ43), as shown in Figure 1. Additional parameter estimates could be added to this model, particularly covariances among unique factors for the same indicator across times of measurement (e.g., covariances among unique factors for V1 at times T1 through T4; these are not shown in Figure 1 to simplify the figural presentation).
Second, the researcher should fit the weak factorial invariance model, which adds across-time invariance constraints on the remaining loadings, or λ21 = λ22 = λ23 = λ24 and λ31 = λ32 = λ33 = λ34. Third, the strong factorial invariance model is fit, in which across-time invariance constraints are placed on the remaining intercepts, or τ21 = τ22 = τ23 = τ24 and τ31 = τ32 = τ33 = τ34. Finally, the researcher can fit the strict factorial invariance model to the data, a model in which across-time invariance constraints are placed on unique variances, or θ11 = θ12 = θ13 = θ14, θ21 = θ22 = θ23 = θ24, and θ31 = θ32 = θ33 = θ34. Our examples here have four times of measurement, but invariance testing would follow these steps regardless of the number of occasions.
Once a model with strong or strict invariance constraints and adequate fit to the data has been obtained, the second general step of the Anderson and Gerbing (1987) procedure can commence. Under this second step, the invariance model with optimal fit is used as a baseline model, and further models are evaluated to test alternative conjectures. These additional model comparisons can be pursued in many forms, including cross-lagged regression models (e.g., Cole & Maxwell, 2003), growth curve models (e.g., McArdle & Epstein, 1987), or latent difference score models (e.g. McArdle & Hamagami, 2001).
Comparing model fit
The preceding sequence of models – from configural invariance to strict factorial invariance – represents a series of increasingly restricted models. In comparing fit across models, likelihood ratio chi-square difference tests can be used because each successive model is nested within the previous one (Bentler & Bonett, 1980). But, because likelihood ratio tests become extremely powerful when sample size is large, differences in model fit should also be evaluated using differences in practical fit indices such as the Tucker-Lewis index (Tucker & Lewis, 1973), the comparative fit index (Bentler, 1990; McDonald & Marsh, 1990), and the root mean squared error of approximation (Steiger & Lind, 1980; Browne & Cudeck, 1993). If sample size is large and a set of invariance constraints leads to a statistically significant worsening of fit but no appreciable change in practical fit indices, the researcher might opt to accept the more restricted model due to its superior interpretive value, despite its significantly poorer statistical fit. Widaman and Thompson (2003) provide an accessible review of comparisons involving practical fit indices, particularly in longitudinal contexts.
Invariance of Latent Variables and Growth Estimates
To identify the same latent construct longitudinally, strong or strict factorial invariance must hold across times of measurement; configural and weak factorial invariance are insufficient. Configural invariance for a model like that in Figure 1 involves selecting one manifest indicator of a latent variable as the reference indicator and then placing certain constraints on factor loading and intercept estimates associated with the reference indicator; we provided one set of configural invariance constraints above. These minimal identification restrictions allow estimation of the model but cannot be used to argue that the same latent construct has been isolated. Ferrer et al. (2008) showed that, if either configural or weak factorial invariance is specified for a set of data, the nature of the latent variable, its relations with other variables, and estimated growth on the latent variable may vary widely as a function of which manifest variable is selected as reference indicator, a selection that can be arbitrary. But, if strong or strict factorial invariance restrictions are invoked, relations among latent variables and estimated growth parameters are invariant regardless of which manifest variable is selected as the reference indicator for the latent variable (Ferrer et al., 2008).
Full Versus Partial Factorial Invariance
In preceding sections, we discussed imposing invariance constraints on different sets of parameters – factor loadings, intercepts, and unique variances – assuming that invariance constraints on all estimates within each set were invoked. Occasionally, one or more estimates appear not to satisfy this pattern of invariance. For example, suppose that factor loadings for V1 and V2 in Figure 1 easily satisfy invariance constraints across all 4 times of measurement; however, the factor loading for V3, although invariant across Times 1 through 3, is rather different for Time 4, and imposing invariance of the loading at Time 4 leads to a very large worsening of fit. Allowing this one factor loading to violate full invariance is one example of what is termed partial measurement invariance (Byrne et al., 1989; McArdle & Cattell, 1994).
Few guidelines have been developed for comparing and interpreting models that have partial measurement invariance, even though partial invariance is not unexpected. We have the following suggestion: Assume that a researcher has a full strong factorial invariance model that has adequate fit to the data, but a partial strong factorial invariance model that relaxes invariance constraints on one or two factor loadings and/or intercepts leads to much better fit. The researcher could do the following: (a) use the full strong invariance model as baseline model and devise a number of model comparisons that test important theoretical questions, and (b) use the partial strong invariance model as baseline model and perform the same set of model comparisons. If model comparisons under the partial strong invariance model exhibit the same patterns of significance and the same magnitudes of effects as do model comparisons under full strong invariance, then the issue of full versus partial invariance is moot – the same conclusions are supported under each baseline model, so the choice of baseline model is not a crucial matter. Of course, if model comparisons under partial invariance support substantially different conclusions than under full invariance, the researcher would have to argue for one of the two invariance models as the better baseline model and interpret model comparisons under this model. Refer to Parke et al. (2004) for an implementation of this analytic strategy.
Multiple Indicators
As described previously, multiple indicators of a latent variable are needed to test factorial invariance, and these multiple indicators can be obtained in many ways. Careful planning of a test battery could ensure three or more separate tests or scales for each latent variable. Alternatively, many personality or behavioral scales are made up of multiple items that can be split up into parcels of items, where each parcel is the sum of a subset of scale items and each item from the scale is assigned to one of the parcels (Kishton & Widaman, 1994; Bandalos, 2002; Bandalos & Finney, 2001). Although use of parcels is a subject of some controversy (e.g., Little, Cunningham, Shahar, & Widaman, 2002), parcels provide a more stable set of manifest variables on which to base structural models than do the individual items comprising scales. Regardless of the method of their construction, multiple indicators are needed to test factorial invariance and provide assurance that the same underlying construct is assessed at each occasion.
MODELING GROWTH IN BEHAVIOR
Traditional Approaches to Assessing Growth and Change
Evaluating change as a function of age was traditionally handled with standard parametric statistics, such as t-tests or analysis of variance (ANOVA). For example, Bell (1953, 1954) described how to include multiple cohorts of participants in a crossed, accelerated design, and Schaie (1965, 1977) extended this approach to the consideration of age, cohort, and time of measurement. ANOVA approaches for examining change across age share three key characteristics: First, data consist of a single score for each person at each time of measurement for a given dependent variable. Second, chronological age is used as an independent categorical (i.e., group) variable. Third, the analytic goal is to analyze mean changes across individuals as a function of chronological age, with little attention to individual differences. Indeed, individual differences in change are relegated to error terms used to test trends in mean change.
Although ANOVA-based approaches provided useful descriptive information on mean trends, developmental science has long had a keen theoretical interest in individual patterns of development (e.g., Bayley, 1956). Given this interest, researchers turned to statistical methods that exploited individual differences in change, but contributions during the 1960s and 1970s suggested that change scores were too unreliable to use as outcome variables (e.g., Bereiter, 1963; Cronbach & Furby, 1970). The field seemed caught between Scylla and Charybdis, desiring methods for the study of individual differences in development, but being told that measures of change were too unreliable for use.
Modern Approaches to Growth Modeling
As noted earlier, Wohlwill (1970) argued that chronological age should not be used as an independent variable, as in ANOVA models. Rather, chronological age should be incorporated into the definition of the dependent variable, so that change in behavior as a function of age becomes the outcome variable. Embodying this focus, Meredith and Tisak (1984, 1990) extended earlier work by Tucker (1958) and Rao (1958), formalizing the latent growth model as a special form of the general structural equation model. McArdle and colleagues (McArdle & Epstein, 1987; McArdle & Aber, 1990; McArdle & Anderson, 1990) showed how to use growth curve models to test developmental hypotheses, and recent introductions were provided by Bollen and Curran (2006) and Duncan, Duncan, and Stryker (2006).
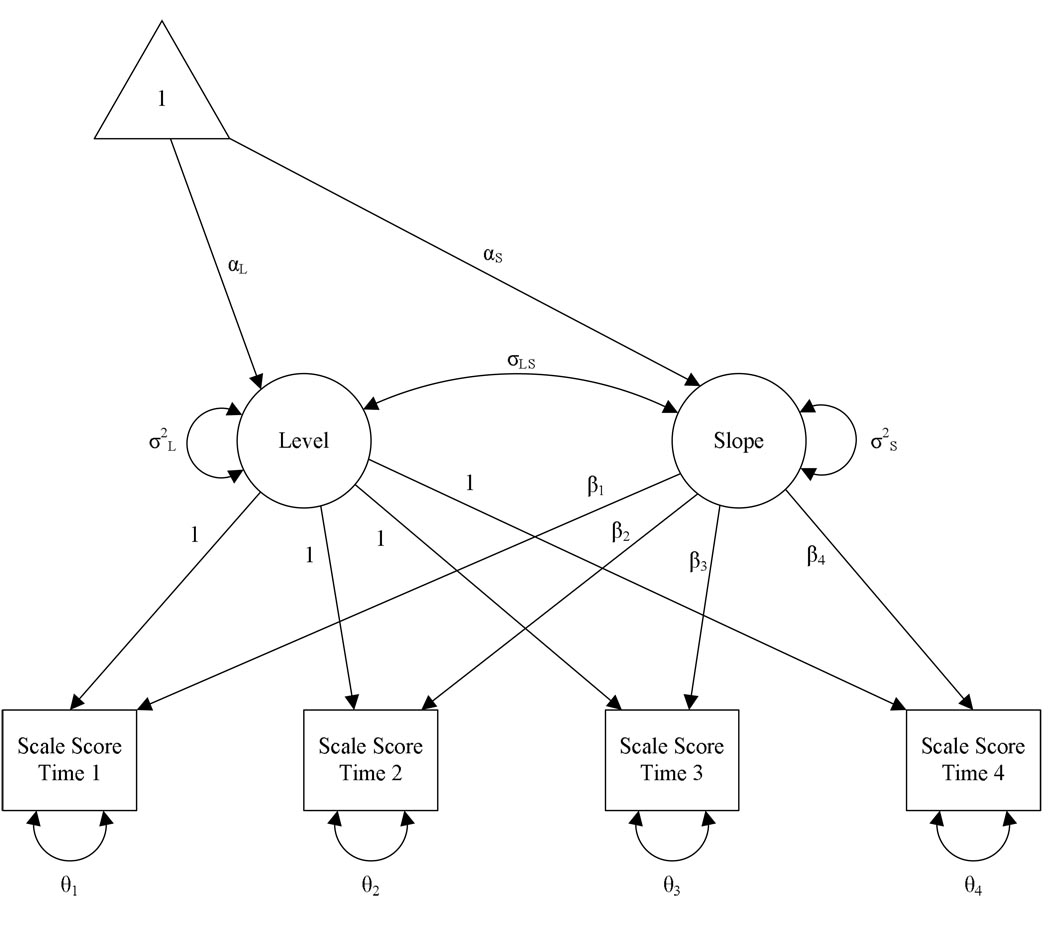
One depiction of a typical latent growth model is shown in Figure 2, which shows four manifest variables – Scale Score Time 1 through Scale Score Time 4 – which were placed in boxes to denote them as manifest or measured variables. These four variables represent scores on a particular scale for individuals in a longitudinal investigation with four equally spaced times of measurement (e.g., annual measurements). In Figure 2, two latent variables are shown in circles – Level and Slope. The Level latent variable has a path to each manifest variable, and these path coefficients are all fixed at 1.0. The Slope latent variable also has paths to the four manifest variables, with coefficients labeled β1 through β4. At least two of the paths β1 through β4 must be fixed to identify the model, and all four paths can be fixed. Often, paths β1 through β4 are fixed to 0, 1, 2, and 3, respectively, resulting in a Level latent variable that represents each person’s estimated level at Time 1, and a Slope latent variable that reflects estimated linear growth or change for each person after Time 1. Different alternatives for coding the coefficients of the Slope latent variable, with attendant utility in interpreting developmental trends, were described recently by Biesanz, Deeb-Sossa, Papadakis, Bollen, and Curran (2004).
Figure 2.
First-order latent growth model specified for four manifest variables, consisting of one manifest variable at each of four times of measurement.
The latent growth curve model is a distinct advance beyond ANOVA models in several important ways. First, it retains information on mean change over time, captured by the mean of the Slope latent variable, αS. Similar to ANOVA, it can include additional terms (e.g., quadratic or cubic trends) or relax constraints on β1 through β4 to model nonlinear growth or change. Second, it contains information regarding individual differences in change, reflected in σ2 S, which estimates variance across individuals in rate of growth. Third, it yields estimates of mean level of performance at a given point in time, embodied by αL, together with individual differences in this level, represented by σ2 L. Fourth, all of these estimates of developmental level and change are estimated at a latent level (i.e., with error variance removed) because estimates of residual variance in manifest variables are provided by parameters θ1 through θ4.
One signal shortcoming of the latent growth model shown in Figure 2 results from the use of a single score for each person at each occasion, a shortcoming shared with ANOVA. With only a single score at each occasion, the model begs questions regarding factorial invariance, relying instead on assumptions. That is, we must assume that the same construct is assessed in the same metric at each occasion, but this assumption cannot be tested. If the assumption were invalid, the entire modeling enterprise is for naught, as the purported indices of change across time in a given construct might represent a mish-mash of differences that have more to do with change in the nature of the construct than with change on a construct that maintains its identity across time.
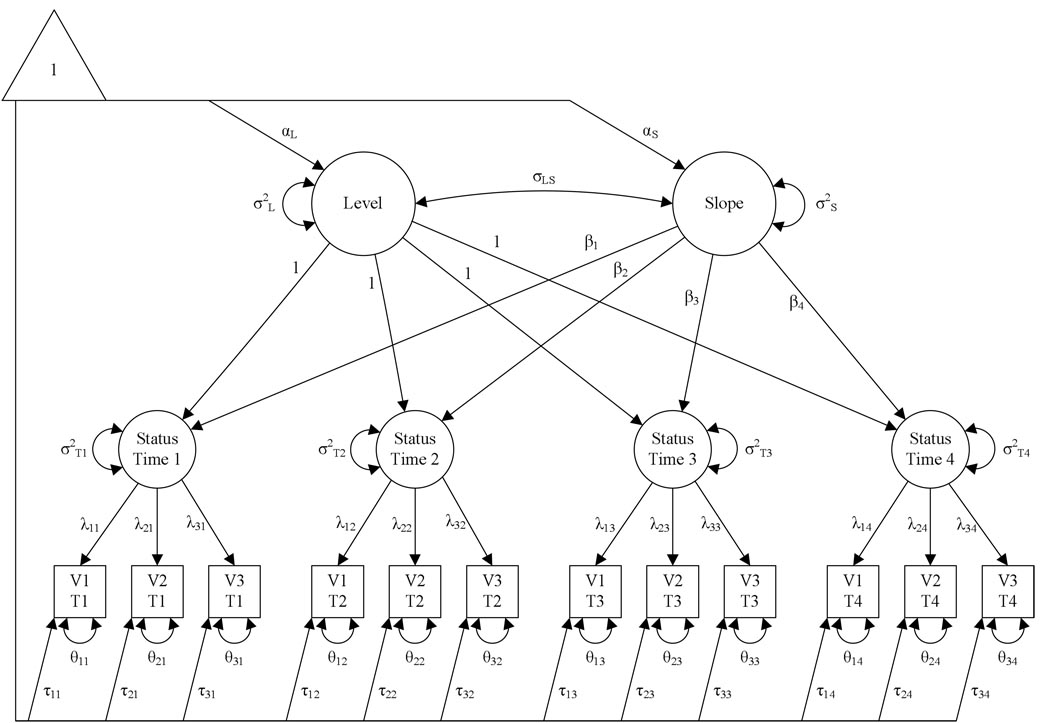
One solution to this dilemma is to use a model such as that shown in Figure 3, in which four first-order factors (Status Time 1 through Status Time 4) have loadings on multiple manifest indicators at each time of measurement. The Level and Slope latent variables in Figure 3 are second-order factors, meaning they have direct effects on first-order factors, not directly on manifest variables. With such a model, a researcher could assess levels of factorial invariance of the first-order factors as described in previous sections. If strong or strict factorial invariance held, growth processes represented by the Level and Slope latent variables reflect quantitative growth in a latent construct that retains its qualitative nature, and thus a constant interpretation, across time. For further treatments of such models, see McArdle (1988), Chan (1998), Sayer & Cumsille (2001), Ferrer et al. (2008), and Leite (2007).1
Figure 3.
Second-order latent growth model specified for 12 manifest variables, consisting of three manifest variables (V1 through V3) obtained at each of four times of measurement (T1 through T4).
If strong factorial invariance does not hold, the first-order construct is not invariant and the second-order growth model has no clear interpretation. However, change in factorial structure is an indicator that the nature of the construct is changing across occasions, and this is an important developmental phenomenon in its own right (Buss, 1974a, 1974B; Buss & Royce, 1975).
A FINAL CAVEAT
Assessing factorial invariance across time should be a more common aspect of developmental investigations, but a caveat is in order. Factorial invariance provides evidence at one level – the relation of latent variable to its indicators – that we are assessing the “same” construct at different ages. But, consider the following: In several studies, Widaman and colleagues (e.g., Widaman, Little, Geary, & Cormier, 1992) investigated development of numerical facility in participants from second grade through college. A Numerical Facility factor showed invariant loadings across all grade levels using paper-and-pencil tests of simple addition, complex addition, and subtraction as the three manifest indicators. Thus, conceiving of Numerical Facility as “speed and accuracy of solving simple number problems,” the same construct was assessed at each grade level. However, modeling participants’ reaction times to addition problems provided strong evidence that almost all second graders use reconstructive, counting strategies to solve problems, whereas virtually all college students use memory retrieval strategies. Thus, at the level of cognitive processes used to solve problems – which is central to understanding what we are modeling, a clear transition had been made such that the nature of the processing stages differed in a fundamental fashion between second grade and college. This occurred despite the fact that strict factorial invariance held for the multiple-indicator factor model. Thus, when evaluating outcomes of statistical modeling, we must take great care to delineate precisely what we mean by the constructs we investigate and what sophisticated statistical procedures can deliver (cf. Widaman, 1991).
SUMMARY
Assessing change in behaviors as a function of age is a principal goal of developmental research. To ensure that we are modeling change in the same theoretical construct across occasions, modern psychometric procedures should be used. For example, preliminary analyses using item response theory (IRT) procedures (see Millsap et al., this issue) can provide estimates of each person’s status on a latent variable that is on the same scale at each time of measurement. Using such estimates as single indicators in a latent growth model such as that in Figure 2 provides assurance that the same construct is assessed by each manifest variable score because the IRT modeling supports this inference. However, if multiple indicators of a latent construct are available at each time of measurement, invoking constraints associated with factorial invariance is a state-of-the-art approach that can and should be used to help ensure one is assessing change in the same construct over time.
Acknowledgments
This research was partially supported by grants from the National Institute of Child Health and Human Development, the National Institute on Drug Abuse, and the National Institute of Mental Health (HD047573, HD051746, MH051361, and DA017092) (Rand Conger, PI) and by grants from the National Science Foundation (BCS-05-27766) and from NIH-NINDS (R01 NS057146-01) (Emilio Ferrer, PI).
Footnotes
In addition to the publications cited, the Mplus user’s guide, available at http://www.statmodel.com/ugexcerpts.shtml, has several examples of fitting typical first-order latent growth models and second-order growth models (see especially Chapter 6, Section 14)
Contributor Information
Keith F. Widaman, Department of Psychology, University of California at Davis
Emilio Ferrer, Department of Psychology, University of California at Davis.
Rand D. Conger, Department of Human and Community Development, University of California at Davis
References
- Anderson JC, Gerbing DW. Structural equation modeling in practice: A review and recommended two-step approach. Psychological Bulletin. 1987;103:411–423. [Google Scholar]
- Bandalos DL. The effects of item parceling on goodness-of-fit and parameter estimate bias in structural equation modeling. Structural Equation Modeling. 2002;9:78–102. [Google Scholar]
- Bandalos DL, Finney SJ. Item parceling issues in structural equation modeling. In: Marcoulides GA, Schumacker RE, editors. New developments and techniques in structural equation modeling. Mahwah, NJ: Erlbaum; 2001. pp. 269–296. [Google Scholar]
- Bayley N. Individual patterns of development. Child Development. 1956;27:45–74. doi: 10.1111/j.1467-8624.1956.tb04793.x. [DOI] [PubMed] [Google Scholar]
- Bell RQ. Convergence: An accelerated longitudinal approach. Child Development. 1953;24:145–152. [PubMed] [Google Scholar]
- Bell RQ. An experimental test of the accelerated longitudinal approach. Child Development. 1954;25:281–286. [PubMed] [Google Scholar]
- Bentler PM. Comparative fit indexes in structural models. Psychological Bulletin. 1990;107:238–246. doi: 10.1037/0033-2909.107.2.238. [DOI] [PubMed] [Google Scholar]
- Bentler PM, Bonett DG. Significance tests and goodness of fit in the analysis of covariance structures. Psychological Bulletin. 1980;88:588–606. [Google Scholar]
- Bereiter C. Some persisting dilemmas in the measurement of change. In: Harris C, editor. Problems in the measurement of change. Madison, WI: University of Wisconsin Press; 1963. pp. 3–20. [Google Scholar]
- Biesanz JC, Deeb-Sossa N, Papadakis AA, Bollen KA, Curran PJ. The role of coding time in estimating and interpreting growth curve models. Psychological Methods. 2004;9:30–52. doi: 10.1037/1082-989X.9.1.30. [DOI] [PubMed] [Google Scholar]
- Bollen KA, Curran PJ. Latent curve models: A structural equation perspective. New York: Wiley; 2006. [Google Scholar]
- Browne MW, Cudeck R. Alternative ways of assessing model fit. In: Bollen KA, Long JS, editors. Testing structural equation models. Newbury Park, CA: Sage; 1993. [Google Scholar]
- Buss AR. A general developmental model for interindividual differences intraindividual differences, and intraindividual changes. Developmental Psychology. 1974a;10:70–78. [Google Scholar]
- Buss AR. Multivariate model of quantitative, structural, and quantistructural ontogenetic change. Developmental Psychology. 1974b;10:190–203. [Google Scholar]
- Buss AR, Royce JR. Ontogenetic changes in cognitive structure from a multivariate perspective. Developmental Psychology. 1975;11:87–101. [Google Scholar]
- Byrne BM, Shavelson RJ, Muthén B. Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychological Bulletin. 1989;105:456–466. [Google Scholar]
- Chan D. The conceptualization and analysis of change over time: An integrative approach incorporating longitudinal mean and covariance structures analysis (LMACS) and multiple indicator latent growth modeling (MLGM) Organizational Research Methods. 1998;1:421–483. [Google Scholar]
- Chen FF, Sousa KH, West SG. Testing measurement invariance of second-order factor models. Structural Equation Modeling. 2005;14:471–492. [Google Scholar]
- Cheung GW, Rensvold RB. Testing factorial invariance across groups: A reconceptualization and proposed new method. Journal of Management. 1999;25:1–27. [Google Scholar]
- Cole DA, Maxwell SE. Testing meditational models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Cronbach LJ, Furby L. How should we measure “change” – or should we? Psychological Bulletin. 1970;74:68–80. [Google Scholar]
- Curran PJ, Bollen KA. The best of both worlds: Combining autoregressive and latent curve models. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 107–135. [Google Scholar]
- Duncan TE, Duncan SC, Stryker LA. An introduction to latent variable growth curve modeling: Concepts, issues, and applications. 2nd ed. Mahwah, NJ: Erlbaum; 2006. [Google Scholar]
- Embretson SE. The continued search for nonarbitrary metrics in psychology. American Psychologist. 2006;61:50–55. doi: 10.1037/0003-066X.61.1.50. [DOI] [PubMed] [Google Scholar]
- Embretson SE. Impact of measurement scale in modeling developmental processes and ecological factors. In: Little TD, Bovaird JA, Card NA, editors. Modeling contextual effects in longitudinal studies. Mahwah, NJ: Erlbaum; 2007. pp. 63–87. [Google Scholar]
- Ferrer E, Balluerka N, Widaman KF. Factorial invariance and the specification of second-order latent growth models. Methodology. 2008;4:22–36. doi: 10.1027/1614-2241.4.1.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock GR, Kuo W-L, Lawrence FR. An illustration of second-order latent growth models. Structural Equation Modeling. 2001;8:470–489. [Google Scholar]
- Horn JL, McArdle JJ, Mason R. When is invariance not invariant: A practical scientist’s look at the ethereal concept of factorial invariance. Southern Psychologist. 1983;1:179–188. [Google Scholar]
- Jöreskog KJ. Simultaneous factor analysis in several populations. Psychometrika. 1971;36:409–426. [Google Scholar]
- Kishton JM, Widaman KF. Unidimensional versus domain representative parceling of questionnaire items: An empirical example. Educational and Psychological Measurement. 1994;54:757–765. [Google Scholar]
- Leite W. A comparison of latent growth models for constructs measured by multiple items. Structural Equation Modeling. 2007;14:581–610. [Google Scholar]
- Little TD. Mean and covariance structures (MACS) analyses of cross-cultural data: Practical and theoretical issues. Multivariate Behavioral Research. 1997;32:53–76. doi: 10.1207/s15327906mbr3201_3. [DOI] [PubMed] [Google Scholar]
- Little TD, Cunningham WA, Shahar G, Widaman KF. To parcel or not to parcel: Exploring the question, weighing the merits. Structural Equation Modeling. 2002;9:151–173. [Google Scholar]
- Maxwell SE, Cole DA. Bias in cross-sectional analysis of longitudinal mediation. Psychological Methods. 2007;12:23–44. doi: 10.1037/1082-989X.12.1.23. [DOI] [PubMed] [Google Scholar]
- May K, Nicewander WA. Measuring change conventionally and adaptively. Educational and Psychological Measurement. 1998;58:882–897. [Google Scholar]
- McArdle JJ. Dynamic but structural equation modeling of repeated measures data. In: Nesselroade JR, Cattell RB, editors. Handbook of multivariate experimental psychology. 2nd ed. New York: Plenum; 1988. pp. 561–614. [Google Scholar]
- McArdle JJ. A latent difference score approach to longitudinal dynamic structural analyses. In: Cudeck R, du Toit S, Sörbom D, editors. Structural equation modeling: Present and future. Lincolnwood, IL: Scientific Software International; 2001. pp. 342–380. [Google Scholar]
- McArdle JJ, Aber MS. Patterns of change within latent variable structural equation models. In: von Eye A, editor. Statistical methods in longitudinal research: Principles and methods of structuring change. New York: Academic; 1990. pp. 151–223. [Google Scholar]
- McArdle JJ, Anderson E. Latent variable growth models for research on aging. In: Birren JE, Schaie KW, editors. Handbook of the psychology of aging. 3rd ed. New York: Academic; 1990. pp. 21–44. [Google Scholar]
- McArdle JJ, Cattell RB. Structural equation models of factorial invariance in parallel proportional profiles and oblique confactor problems. Multivariate Behavioral Research. 1994;29:63–113. doi: 10.1207/s15327906mbr2901_3. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Epstein D. Latent growth curves within developmental structural equation models. Child Development. 1987;58:110–113. [PubMed] [Google Scholar]
- McArdle JJ, Hamagami A. Latent difference scores structural models for linear dynamic analyses with incomplete longitudinal data. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 139–175. [Google Scholar]
- McDonald RP, Marsh HW. Choosing a multivariate model: Noncentrality and goodness of fit. Psychological Bulletin. 1990;107:247–255. [Google Scholar]
- Meredith W. Notes on factorial invariance. Psychometrika. 1964a;29:199–185. [Google Scholar]
- Meredith W. Rotation to achieve factorial invariance. Psychometrika. 1964b;29:187–206. [Google Scholar]
- Meredith WM. Measurement invariance, factor analysis and factorial invariance. Psychometrika. 1993;58:525–543. [Google Scholar]
- Meredith W, Horn J. The role of factorial invariance in modeling growth and change. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 203–240. [Google Scholar]
- Meredith W, Tisak J. Statistical considerations in Tuckerizing curves with emphasis on growth curves and cohort sequential analysis; Paper presented at the annual meeting of the Psychometric Society; Santa Barbara, CA. 1984. Jun, [Google Scholar]
- Meredith W, Tisak J. Latent curve analysis. Psychometrika. 1990;55:107–122. [Google Scholar]
- Millsap RE, Meredith W. Factorial invariance: Historical perspectives and new problems. In: Cudeck R, MacCallum RC, editors. Factor analysis at 100: Historical developments and new directions. Mahwah, NJ: Erlbaum; 2007. pp. 131–152. [Google Scholar]
- Nesselroade JR. Temporal selection and factor invariance in the study of development and change. In: Baltes PB, Brim OG Jr, editors. Life-span development and behavior. Vol. 5. New York: Academic Press; 1983. pp. 59–87. [Google Scholar]
- Parke RD, Coltrane S, Duffy S, Buriel R, Dennis J, Powers J, Widaman KF. Economic stress, parenting, and child adjustment in Mexican American and European American families. Child Development. 2004;75:1632–1656. doi: 10.1111/j.1467-8624.2004.00807.x. [DOI] [PubMed] [Google Scholar]
- Rao CR. Some statistical methods for the comparison of growth curves. Biometrics. 1958;14:1–17. [Google Scholar]
- Rensvold RB, Cheung GW. Testing measurement model for factorial invariance: A systematic approach. Educational and Psychological Measurement. 1998;58:1017–1034. [Google Scholar]
- Sayer AG, Cumsille PE. Second-order latent growth models. In: Collins LM, Sayer AG, editors. New methods for the analysis of change. Washington, DC: American Psychological Association; 2001. pp. 179–200. [Google Scholar]
- Schaie KW. A general model for the study of developmental problems. Psychological Bulletin. 1965;64:62–107. doi: 10.1037/h0022371. [DOI] [PubMed] [Google Scholar]
- Schaie KW. Quasi-experimental designs in the psychology of aging. In: Birren JE, Schaie KW, editors. Handbook of the psychology of aging. New York: Van Nostrand Reinhold; 1977. pp. 39–58. [Google Scholar]
- Steiger JH, Lind JM. Statistically-based tests for the number of common factors; Paper presented at the meeting of the Psychometric Society; Iowa City, IA. 1980. May, [Google Scholar]
- Tucker LR. Determination of parameters of a functional relation by factor analysis. Psychometrika. 1958;23:19–23. [Google Scholar]
- Tucker LR, Lewis C. A reliability coefficient for maximum likelihood factor analysis. Psychometrika. 1973;38:1–10. [Google Scholar]
- Widaman KF. Qualitative transitions amid quantitative development: A challenge for measuring and representing change. In: Collins LM, Horn JL, editors. Best methods for the analysis of change: Recent advances, unanswered questions, future directions. Washington, DC: American Psychological Association; 1991. pp. 204–217. [Google Scholar]
- Widaman KF, Little TD, Geary DC, Cormier P. Individual differences in the development of skill in mental addition: Internal and external validation of chronometric models. Learning and Individual Differences. 1992;4:167–213. [Google Scholar]
- Widaman KF, Reise SP. Exploring the measurement invariance of psychological instruments: Applications in the substance use domain. In: Bryant KJ, Windle M, West SG, editors. The science of prevention: Methodological advances from alcohol and substance abuse research. Washington, DC: American Psychological Assocation; 1997. pp. 281–324. [Google Scholar]
- Widaman KF, Thompson JS. On specifying the null model for incremental fit indices in structural equation modeling. Psychological Methods. 2003;8:16–37. doi: 10.1037/1082-989x.8.1.16. [DOI] [PubMed] [Google Scholar]
- Wohlwill JF. The age variable in psychological research. Psychological Review. 1970;77:49–64. [Google Scholar]
- Wohlwill JF. The study of behavioral development. New York: Academic; 1973. [Google Scholar]