Integrin Conformational Regulation: Uncoupling Extension/Tail Separation from Changes in the Head Region by a Multiresolution Approach

SUMMARY

Integrin-dependent adhesion and signaling are regulated by conformational changes whose details remain controversial. Crystallography revealed bent shapes for resting and primed integrin ectodomains, whereas large, ligand-induced rearrangements in other constructs suggested extension, “opening,” and tail separation. We have used experimental/computed hydrodynamics to discriminate among different α_vβ₃ and α_IIbβ₃ atomic models built on X-ray, NMR, and EM data. In contrast with X-ray structures and EM maps, hydrodynamics indicate that resting integrins are already extended. Further-more, the hydrodynamics of an α_vβ₃ ectodomain-fibronectin fragment complex support opening via additional head region conformational changes (hybrid domain swing-out), but without tail separation. Likewise, frictional changes induced by priming agents in full-length α_IIbβ₃ correlate well with the swing-out coupled to a simple transmembrane helix shift in an extended, electron tomography-based model. Extension and immediate tail separation are then uncoupled from head region rearrangements following activation, thus underscoring integrins’ delicate, finely tuned plasticity.

INTRODUCTION

Integrins comprise a family of cell-surface receptors that transduce both intra- and extracellular signals and that regulate cellular adhesion, motility, and progression through the cell cycle (Hynes, 2002). They exist as transmembrane heterodimers consisting of an α and a β subunit; in mammals, 18 α subunits can associate with 8 β subunits to form 24 distinct integrins (Hynes, 2002). Each subunit has a large multidomain extracellular portion (together forming the “ectodomain”), a single transmembrane (TM) helix, and a small cytoplasmic domain. The domain/modular structure of a prototypical integrin, the platelets’ fibrinogen receptor α_IIbβ₃, is shown color-coded in Figure 1A.

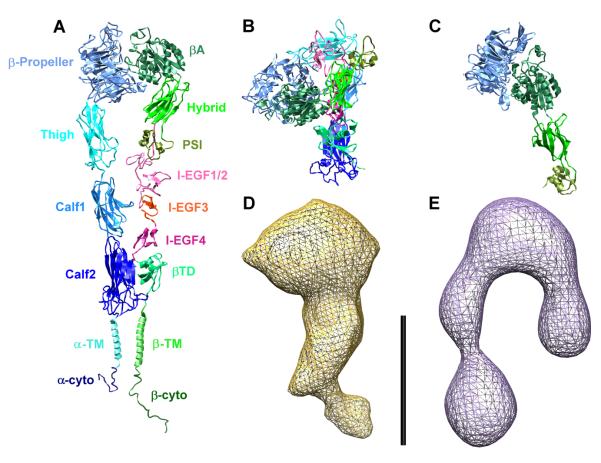
Figure 1. Integrin Domain Structure and Conformations.

(A) Fully extended model of integrin α_IIbβ₃, showing and color-coding all the modules (the α subunit in shades of blue, the β subunit in shades of green and red). The model was generated by homology modeling on the α_vβ₃ ectodomain (Xiong et al., 2001, 2002) and on the β₂ PSI/hybrid/I-EGF1-3 construct (Shi et al., 2007) crystal structures, with the addition of computer models of the TM helices (Gottschalk, 2005; Gottschalk and Kessler, 2004) and NMR structures of the cytoplasmic (cyto) domains (Vinogradova et al., 2000, 2004; Ulmer et al., 2001).

(B) Crystal structure of the α_vβ₃ ectodomain (Xiong et al., 2001, 2002), completed with the homology models of the EGF modules and with other missing portions (see the Supplemental Data; color-coding as in [A]).

(C) Crystal structure of the α_IIbβ₃ β-propeller/PSI/hybrid/βA construct in the high-affinity conformation, with the swung-out hybrid domain (Xiao et al., 2004; color-coding as in [A]).

(D and E) Electron density maps derived from cryo-EM (Adair and Yeager, 2002) and ET (Iwasaki et al., 2005) of full-length, solubilized α_IIbβ₃ resting and primed, respectively. All structures and maps are shown at the same scale (bar = 10 nm).

The ability of the integrin’s ectodomain to interact with macromolecular ligands depends on a signal transduced through the cytoplasmic domains, which converts the integrin from a low-affinity (resting) state to a high-affinity (activated) state. The primary binding site for extracellular ligands is at the interface between the β-propeller and the βA modules (Xiong et al., 2002). The active state can also be induced (“priming”) by certain divalent cations such as Mn²⁺, and, in integrins recognizing the Arg-Gly-Asp (RGD) motif, by the binding of small, RGD-containing ligands (Hynes, 2002).

The importance of integrins in mediating adhesion and cell-cell signaling has led to extensive structural characterization of their conformation and activation mechanisms (Xiong et al., 2001, 2002, 2004; Xiao et al., 2004; Shi et al., 2005, 2007; Beglova et al., 2002; Vinogradova et al., 2000, 2002, 2004; Ulmer et al., 2001; Li et al., 2001, 2005; Weljie et al., 2002; Takagi et al., 2002, 2003; Litvinov et al., 2004). However, the difficulties inherent to studying large, glycosylated integral membrane proteins and the different constructs and methods used in these studies have led to conflicting views about the resting and primed conformations of integrins and the structural changes that effect activation. For example, in contrast with early electron microscopy (EM) studies of α_IIbβ₃ and α₅β₁ that suggested an extended structure (such as the one shown in Figure 1A ; Carrell et al., 1985; Nermut et al., 1988), X-ray crystallography (Xiong et al., 2001, 2002) of the α_vβ₃ ectodomain showed a bent structure (Figure 1B), later confirmed by transmission electron microscopy (TEM) studies (Adair et al., 2005). Additionally, cryo-EM (Adair and Yeager, 2002) and electron tomography (ET) (Iwasaki et al., 2005) analyses of detergent-solubilized, full-length α_IIbβ₃ have produced electron density maps suggesting alternative conformations, from partially bent to almost fully extended (Figures 1D and 1E).

Currently, the most broadly supported integrin activation hypothesis identifies three predominant conformations (reviewed in Arnaout et al., 2005 and Luo et al., 2007). The resting state is associated with the bent conformation in which the cytoplasmic tails of the α and β subunits interact. The active state is associated with an extended conformation in which, additionally, the hybrid domain has swung outward from its position in the bent state (“open” conformation; Figure 1C) and the cytoplasmic tails of the subunits have separated and do not interact. A second low-affinity state, which is extended but in which the hybrid domain has not swung outward, has also been hypothesized (Luo et al., 2007). Thus, the position of the hybrid domain is proposed to be the major indicator of integrin ligand affinity. However, similar TEM density maps of the activated α_vβ₃ ectodomain, free or bound to a fibronectin (FN) fragment (Adair et al., 2005), and shape reconstruction from SAXS data of the α₅β₁ headpiece (Mould et al., 2003) suggested instead that activation and ligand binding can occur with no major shape changes. Further complicating interpretation of these data is the fact that although the integrin TM and cytoplasmic domains appear to interact in the resting state (Vinogradova et al., 2002, 2004; Weljie et al., 2002), many of the aforementioned studies have been restricted to analysis of the ectodomain alone or of smaller constructs. Hence, it is unclear to what extent interactions between the α and β subunits’ TM and cytoplasmic domains contribute to the hybrid domain swing-out angle, which has been observed to vary from 10° (Adair et al., 2005) to 60°–80° (Xiao et al., 2004; Takagi et al., 2003). Moreover, it is not clear whether separation of the TM and cytoplasmic regions is a consequence of priming.

Although integrins are membrane proteins, solution data on soluble constructs and solubilized full-length integrins provide structural information that complements higher resolution data. In particular, our group has extensively measured the hydrodynamic properties of α_IIbβ₃ solubilized in octylglucoside (OG) in the absence and presence of a series of low-molecular-weight integrin priming agents (Hantgan et al., 1993, 1999, 2001, 2002, 2003). Supported by low-resolution hydrodynamic modeling, these data were consistent with an elongated shape for the resting integrin and captured conformational changes when different priming agents were added (Hantgan et al., 1999, 2001, 2002, 2003). The hydrodynamics (Stokes radius, R_s) of the α_vβ₃ ectodomain resting, primed, and bound to an FN fragment have been also measured (Takagi et al., 2002; Adair et al., 2005).

In this work, we present a comprehensive multiresolution modeling study, constraining structural models with hydrodynamic data. Complete atomic models of the α_vβ₃ ectodomain and full-length α_IIbβ₃ were developed from the available crystal and NMR structures, complemented with carbohydrates and, when appropriate, detergent molecules and computer models of the TM helices (Gottschalk and Kessler, 2004; Gottschalk, 2005). Additional models were generated by fitting the structures into low-resolution EM/ET maps and were also compared with our own 2D-averaged EM images. Conformational transitions were not based solely on crystallography data; normal modes analysis (NMA) (Suhre and Sanejouand, 2004) was used to identify points of flexibility. Our study suggests that full-length integrins are extended already in the resting state and may collapse to fully or partially bent conformations under certain conditions, thus reconciling many apparently contrasting data present in the literature. In the high-affinity form, the hybrid domain swing-out is linked to a rearrangement of the transmembrane helices not leading to their immediate separation and clustering. At the biological level, this implies a finely tuned, stepwise mechanism that utilizes integrin’s plasticity to link bidirectional signaling with reversible mechanical actions.

RESULTS

Fully Bent α_vβ₃ Ectodomain Models Are at Odds with the Hydrodynamics of the Resting State

The X-ray structure of the α_vβ₃ ectodomain in the presence of Ca²⁺ revealed an unexpected compact, bent shape (Xiong et al., 2001, 2002). As described in the Supplemental Data available with this article online, a basic full atom model of this ectodomain was generated (model Av-1; residues α_v1-956, β₃1-692; data not shown), and then complemented with high-mannose carbohydrate groups (model Av-2, not shown). Subsequently, the model was further refined using the recently published (Shi et al., 2007) crystal structures of the PSI/hybrid/I-EGF1-3 modules from β₂ (Supplemental Data; model Av-3). However, we must point out that by inserting the corresponding homology models based on these structures, using the hybrid domain as the template, it is impossible to reconnect the chain with the I-EGF4/βTD domain (Figure S1). Therefore, the relative orientation of the modules had to be changed from that of the β₂ crystal structures (Supplemental Data). In any case, as can be seen in Table 1 the calculated R_s for these models (5.1-5.3 nm) are substantially lower than the 5.7 nm estimated for the α_vβ₃ ectodomain by size-exclusion chromatography (Takagi et al., 2002; Adair et al., 2005).

Table 1.

Comparison of Experimental and Computed R_s Values for the Resting α_vβ₃ Ectodomain

Experimental/Models	Rs, nm	% SD or % difference
αvβ3 Ectodomain, 1 mM Ca2+	5.7 ± 0.25	±4.3
Av-1 (basic model)	5.05	−11.4
Av-2 (basic model with carbohydrates)	5.33	−6.5
Av-3 (Av-2 + PSI-EGF1/3 β2 homology models)	5.34	−6.3
Av-4/S10 (Av-3 + 10° hybrid swing-out)	5.53	−3.0
Av-5/TEM (Av-4/S10 best fit in TEM map)	5.44	−4.6
Av-6/N20 (Av-4/S10 + 20° NMA opening)	5.70	0.0

See Adair et al., 2005.

To determine what extent of conformational rearrangements is required to match the experimental R_s, we have built a series of models that differ from the original crystal structure with respect to the relative positions of several domains. First, the Av-3 model was fit into the TEM-derived density map of the resting α_vβ₃ ectodomain (Adair et al., 2005) (kindly provided by B. Adair and M. Yeager, Scripps Research Institute, La Jolla, CA). This required (Adair et al., 2005) a 10° swing-out of the hybrid domain (model Av-4/S10) to provide a better fit. Although this improved the hydrodynamics to within experimental error (Table 1), the β₃ PSI/EGF1-2 modules are still clearly outside the map (Figures 2A and 2B). A subsequent model was generated to best fit the TEM map by a manual repositioning of these modules plus a ~1° opening between the head and the tails (model Av-5/TEM, Figures 2C and 2D); however, this worsened the agreement with the measured R_s (Table 1). Taken together, these initial models suggest that the X-ray and TEM conformations are more compact than the average solution conformation.

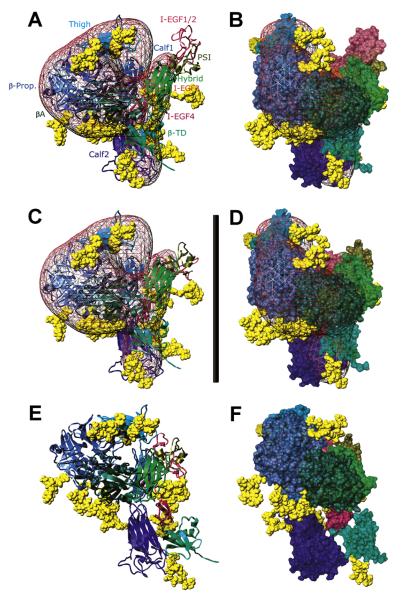
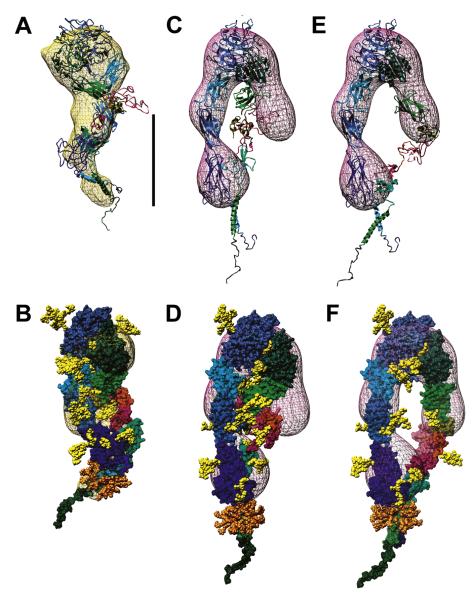
Figure 2. α_vβ₃ Ectodomain Resting Models.

(A and B) and (C and D) Two views, differing by a 35° rotation along the y-axis, of models Av-4/S10 (A and B) and Av-5/TEM (C and D) fitted inside the TEM map (Adair et al., 2005; pink mesh, contoured to 3.2 σ).

(E and F) Two views, differing by a 35° rotation along the y-axis, of model Av-6/N20 with the best hydrodynamics. In (A), (C), and (E), the subunits are shown as ribbons, with the modules (indicated in [A]) color-coded as in Figure 1. In (B), (D), and (F), surface representations of the chains are shown, with the same color-coding. In all panels, the carbohydrates are yellow VdW spheres. Scale bar = 13 nm.

The Resting α_vβ₃ Ectodomain Is in a Relatively Rigid, Partially Extended Conformation

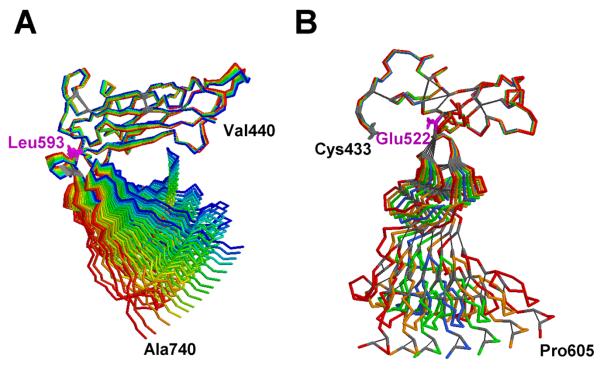
Because nearly all integrin activation schemes call for an extension from the bent crystal shape, we first investigated the effect of full flexibility on the hydrodynamics. Accordingly, we determined what unrestricted swing from and back to the bent conformation would be needed to match the experimental R_s (see Experimental Procedures). Reducing the number of beads used to compute the hydrodynamics led to a less than 1% change in the R_s of model Av-2 (5.37 vs. 5.33). A hinge-bending without restoring forces computation, using α_v Gly597 as the hinge point, indicates that a major ~70° wingspan “breathing” would be required for R_s = 5.7 nm. We then sought to find true molecular hinges in both subunits using NMA (Suhre and Sanejouand, 2004). Surprisingly, very little movement, even for large perturbations, was apparent in the full-sized α_vβ₃ ectodomain and isolated chains, likely because of inter- and intrasubunit contacts. By analyzing smaller fragments, we identified potential hinge regions between the thigh/calf1 modules in the α_v chain and the I-EGF2/I-EGF3 modules in the α₃ chain (Figure 3). However, their behavior clearly differs. The α_v hinge seems more extended, ranging from Leu593 up to Cys602, and the angle between the two modules widens (Figure 3A). In β₃, elastic deformation is severely constrained by the network of disulfide bridges, resulting in an oscillation around the starting position with a clear pivot at Glu522 (Figure 3B), that will not lead per se to a more extended conformation. Thus, the NMA results are in contrast with the previously hypothesized rapid interconversion between compact and extended forms (Takagi et al., 2002), indicating that a higher energy barrier has to be overcome. However, as suggested earlier (Beglova et al., 2002) and recently confirmed (Shi et al., 2007) by the β₂ structures comprising the PSI/hybrid/I-EGF1-2/3 modules, major conformational changes involving the reorientations between the I-EGF modules are clearly possible.

Figure 3. Selected NMA-Generated Structures, Shown as Backbone Traces, of α_vβ₃ Domains.

In each panel, the starting structure is blue and the ends of the perturbations, from −200 to +200 (amu^0.5 × Å) in steps of 10, are red. Cystine bridges are highlighted as gray sticks, and pivot residues are magenta.

(A) Thigh/calf1 modules of α_v (residues 440-740) after structural superposition of the thigh modules (mode 7; 15 structures).

(B) I-EGF1/4 domain of β₃, (residues 433-605), after structural superposition of the I-EGF1 modules (mode 7; 7 structures). Figure prepared with RasTop 1.3 (http://www.geneinfinity.org/rastop/).

An alternative model was then built (Av-6/N20, see the Supplemental Data for details), starting from model Av-4/S10, using a thigh/calf1 structure with a 20° unbending (Figures 2E and 2F). As Table 1 shows, this model perfectly matches the α_vβ₃ ectodomain experimental R_s. In substance, NMA and the hydrodynamics correlate better with a partially extended, relatively rigid shape in solution for the resting α_vβ₃ ectodomain. Moreover, it is more conceivable a reversion to the crystal/TEM shapes starting from this model than from a fully extended one.

The Hybrid Domain Swings-Out in Activated/Primed α_vβ₃ Ectodomains: No Further Extension, and the Tails Stay in Contact

Mn²⁺ is an activator of α_vβ₃, and it shifts (Takagi et al., 2002; Adair et al., 2005) the R_s of the ectodomain from 5.7 to 6.0 nm. This shift has been proposed to indicate a change in conformation of α_vβ₃ from bent to extended (Takagi et al., 2002), although it remains controversial (Adair et al., 2005; Arnaout et al., 2005). Upon addition of an RGD-containing peptide to either Mn²⁺- or Ca²⁺-complexed α_vβ₃ ectodomains, its R_s further increases (Takagi et al., 2002; Adair et al., 2005) to 6.4 nm, and this is taken to represent a primed state. Although fully extending the structure (model Av-7/ext) yields R_s = 6.24 nm, an intermediate value between the two conditions (Table 2) such a conformation is very far from the TEM evidence.

Table 2.

Comparison of Experimental and Computed R_s Values for the Primed and FNIII7-10+EDB-Bound α_vβ₃ Ectodomain

Experimental/Models	Rs, nm	% ± SD or % difference
αvβ3 Ectodomain, 0.2 mM Mn2+	6.0 ± 0.22	± 3.7
αvβ3 Ectodomain, 0.2 mM Mn2+ + RGD	6.4 ± 0.16	± 2.5
Av-7/ext (Av-2 fully extended)	6.24	+4.0 / −2.5
Av-8/S60-TC (Av-6/N20 + 60° swing-out, tails in contact)	6.20	+3.3 / −3.1
Av-9/S60-TS (Av-6/N20 + 60° swing-out, tails separated)	6.60	+10.0 / +3.1
FNIII7-10+EDB	4.0 ± 0.2	±5.0
FNs (straight)	3.93	−1.8
FNb (bent)	3.90	−2.5
αvβ3 Ectodomain, 0.2 mM Mn2++ FNIII7-10+EDB	7.3 ± 0.12	±1.6
Av-5/FNs (Av-5/TEM with FNs attached)	6.77	−7.3
Av-6/FNs (Av-6/N20 with FNs attached)	6.82	−6.6
Av-8/FNs (Av-8/S60-TC with FNs attached)	7.34	+0.5

See Adair et al., 2005.

We have instead developed models taking into account the crystal structure 1TY6 of the ligand-bound α_IIbβ₃ headgroup (Xiao et al., 2004), in which the hybrid domain has swung outward by 62°. Superimposing the βA modules, the swung-out hybrid domain was inserted into our best-matching model, Av-6/N20. When the C-terminal tails (α_v calf2 and β₃ βTD modules) were allowed to remain in contact, making small adjustments mainly at the I-EGF2/I-EGF3 junction, we obtained a calculated R_s of 6.2 nm (model Av-8/S60-TC). Conversely, when the tails were separated by ~10 nm, the calculated R_s was 6.6 nm (model Av-9/S60-TS). As Table 2 shows, although this second model is off the mark (and adopting the I-EGF2/I-EGF3 interface in the β₂ 2P28 crystal conformation [Shi et al., 2007] would push the β₃ subunit away from the plane of a hypothetical membrane), the first model lies within the experimental range for activated/primed ectodomains. Although many structural variants are possible, a smaller swing-out could, for instance, take place in the presence of Mn²⁺ only. Although these models are still at odds with the TEM 3D maps (Adair et al., 2005; data not shown), the swing-out’s reversibility might easily accommodate such a shape change. Overall, these data confirm that activation/priming induces the swing-out and suggest that it can take place with minimal (if any) tail separation.

The Primed α_vβ₃ Ectodomain Binds to a Fibronectin Fragment Without Further Shape Changes

The TEM density maps of the α_vβ₃ ectodomain bound to the 49.6 kDa FN fragment FNIII7-10+EDB show a fully bent conformation (Adair et al., 2005). This finding is inconsistent with the hypothesis of a fully extended and swung-out conformation for the primed (and presumably macromolecular ligand-bound) state (Arnaout et al., 2005; Luo et al., 2007), which was, for instance, very well documented in an EM study of a truncated integrin α₅β₁ construct bound to a FN fragment (Takagi et al., 2003). To resolve this issue, we have modeled the FN fragment bound to the previously created bent/resting and extended/primed models of the α_vβ₃ ectodomain and computed their R_s values. Models of the fragment (residues 1142-1600) were generated by inserting the 2FNB NMR structure (Fattorusso et al., 1999) of the EDB module between the FN-III7 and FN-III8-10 modules in the 1FNF structure (Leahy et al., 1996). Two versions were prepared: one straight (FNs), the other with a kink between the FNEDB and FN-III8 modules to simulate the effects of flexibility (FNb). As Table 2 shows, both models match very well with the R_s of 4.0 ± 0.2 nm, as estimated from Figure 1 in the study by Adair et al. (2005). The FNs model was attached to the α_vβ₃ ectodomain models using the RGD residues in the FN-III10 module with the 1L5G structure (Xiong et al., 2002) as a template. We find that the calculated R_s of 6.8–6.9 nm for the fully bent and partially extended α_vβ₃/FN fragment complex models without the swing-out (Av-5/FNs and Av-6/FNs, Table 2) are substantially lower than the experimentally observed value (Adair et al., 2005) of 7.3 nm. In contrast, the R_s calculated for the FN fragment bound to the partially extended, swung-out, tails-together integrin model Av-8/FNs (Figure 4) is in perfect agreement with the experimental results shown in Table 2. Models with full tail separation have much higher R_s values (data not shown) and would be even more at odds with the TEM evidence (Adair et al., 2005). These results are fully consistent with our model of the activated/primed α_vβ₃ ectodomain and show that little, if any, conformational changes take place in already primed integrins upon binding to a macromolecular ligand. In addition, they suggest that full tail separation is not immediately linked to binding events.

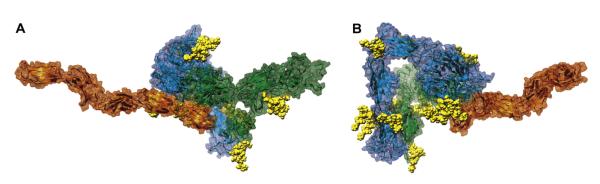
Figure 4. Model of the α_vβ₃ Ectodomain Bound to an FN Fragment.

(A and B) Two views, differing by a 110° rotation along the y-axis, of model Av-8/FNs, shown as ribbons inside a semitransparent surface. The α_v subunit is cyan/cornflower blue; the β₃ subunit is green/forest green; the FNIII7-10+EDB chain is orange/orange red; and the carbohydrates are yellow VdW spheres.

Hydrodynamic Data Suggest an Extended Conformation for Resting Full-Length α_IIbβ₃

We have previously generated preliminary all-atom models, including carbohydrates and an OG micelle, for the full-length α_IIbβ₃ integrin based on the α_vβ₃ crystal structure, and have demonstrated that experimentally and computationally derived hydrodynamic data of the resting integrin are inconsistent with a fully bent form (Hantgan et al., 2003, 2004). Here, we have remodeled α_IIbβ₃, starting from our new α_vβ₃ resting state model (Supplemental Data), and have generated additional models using the cryo-EM (Adair and Yeager, 2002) or ET (Iwasaki et al., 2005) envelopes as templates. A revised, more accurate set of hydrodynamic values derived from our previous analytical ultra-centrifugation (AUC) and dynamic light scattering (DLS) data (Supplemental Data) was used to discriminate between models having different degrees of extension and to investigate the role of the swing-out and of the C-terminal TM/cytoplasmic domain.

Crystallographic structures and TEM maps of the α_vβ₃ integrins were determined using constructs lacking TM and cytoplasmic domains, and the only experimental evidence regarding the orientation of the ectodomain relative to a hypothetical membrane is the cryo-EM study of full-length α_IIbβ₃ solubilized in OG (Adair and Yeager, 2002). We have first studied the impact of different orientations of the TM helices relative to the ectodomain on the calculated sedimentation and translational diffusion coefficients, $S_{(20,W)}^0$ and $D_{t(20,W)}^0$. Table 3 reports the data for partially extended β_IIbβ₃ integrins models based on the Av-6/N20 model, with TM helices oriented at 90° (model A2b-1/hb) or 140° (model A2b-2/hs) relative to the calf2 domain. Both models agree quite poorly with the resting integrin values, but model A2b-2/hs performs slightly better, showing that the angle of the TM helices has a relatively minor effect on the hydrodynamics.

Table 3.

Comparison of Experimental and Computed Hydrodynamic Parameters for Resting and Primed Solubilized α_IIbβ₃

Experimental/Models	${<S_{(20,W)}^0>}_W\left(\mathrm{S}\right)$	% ± SEM or % difference	${<D_{t(20,W)}^0>}_Z\left(\mathrm{F}\right)$	% ± SEM or % difference
αIIbβ3 Resting	8.18 ± 0.07a	±0.9	3.07 ± 0.08a	±2.6
A2b-1/hb (Av-6/N20 homology, helices bent)	8.95	+9.4	3.26	+6.2
A2b-2/hs (Av-6/N20 homology, helices straight)	8.85	+8.2	3.23	+5.2
A2b-3/CEM (A2b-1/hb best fit in cryo-EM map)	8.71	+6.5	3.18	+3.6
A2b-4/CEM/hs (A2b-3/CEM with helices straight)	8.59	+5.0	3.13	+2.0
A2b-5/ET (αIIb ectodomain and β3 βA/βTD fit in ET map)	8.22	+0.5	3.00	−2.3
αIIbβ3 Primed	7.65 ÷ 7.97b	−6.5 ÷ −2.6c	2.64 ÷ 2.99b	−14 ÷ −2.5c
A2b-3/S60-TC (A2b-3/CEM + 60° swing-out, tails in contact)	8.24	+0.7c	3.00	−2.3c
A2b-5/S60-TC (A2b-5/ET + 60° swing-out, tails in contact)	7.94	−3.0c	2.89	−5.9c
A2b-5/S60-TPS (A2b-5/ET + 60° swing out, tails partially separated)	7.77	−5.0c	2.83	−7.8c

Data in italic type were either obtained by DLS or were compared to DLS-derived data and were not used to discriminate between models because they could be affected by aggregates in the primed samples (see text for details).

^aData from Table S1.

^bLiterature (Hantgan et al., 1999, 2001, 2002) and Table S1 data.

^cWith respect to the experimental resting value.

In contrast to the highly bent α_vβ₃ (v-shape) crystal structure, the cryo-EM reconstruction of α_IIbβ₃ produced a partially extended, z-shape conformation (Adair and Yeager, 2002). Relatively major changes to the mutual orientation of several domains were required to reasonably fit (by manual fitting/inspection with the assistance of NMA [Suhre and Sanejouand, 2004] and SITUS [Chacón and Wriggers, 2002]) the α_IIbβ₃ homology model into the cryo-EM density map (kindly provided by B. Adair and M. Yeager). The final model (A2b-3/CEM) and map are shown in Figures 5A and 5B; as can be seen, the fit is not as good as that of the α_vβ₃ ectodomain in its map (Figures 2C and 2D; see also Movie S1). We found it very difficult to position the α_IIbβ₃ modules in the map while respecting biochemical and structural constraints, especially at the C termini, and this model is our best compromise. Furthermore, its hydrodynamics (Table 3) do not match the experimental values, and only straightening the helices (model A2b-4/CEM/hs; data not shown) can bring a partial agreement.

Figure 5. Models of α_IIbβ₃ Fitted in the Cryo-EM and ET Maps.

(A and B) Two views, differing by a 90° rotation along the y-axis, of model A2b-3/CEM fitted inside the cryo-EM map (Adair and Yeager, 2002; gold mesh, contoured to 3.2 s).

(C and D) and (E and F) Two views, differing by a 50° rotation along the y-axis, of models A2b-5/ET (C and D) and A2b-5/S60-TC (E and F), positioned inside the ET map (Iwasaki et al., 2005; plum mesh, contoured to a level of 1150). In (A), (C), and (E), the subunits are shown as ribbons, with the modules color-coded as in Figure 1. In (B), (D), and (F), surface representations of the chains are shown, with the same color coding. The carbohydrates and OG molecules are yellow and orange VdW spheres, respectively. Scale bar = 10 nm.

As an alternative, starting from this model we fitted the α_IIb subunit ectodomain and the β₃ βA domain inside the ET-derived map (Iwasaki et al., 2005; kindly provided by K. Iwasaki, Osaka University, Japan), although it was generated from primed α_IIbβ₃ solubilized in Triton. The relative locations of the PSI/I-EGF1-2 segment and the βTD module of the β₃ subunit were kept fixed, and the I-EGF3-4 segment was adapted to reconnect the chain (model A2b-5/ET; Figures 5C and 5D, and Movie S2). Strikingly, this model shows the best agreement with ${<S_{(20,W)}^0>}_W(+0.5\%)$, and the ${<D_{t(20,W)}^0>}_Z$ value is also very close (−2.3%) (Table 3). Thus, unlike the α_vβ₃ ectodomain, full-length, solubilized, resting α_IIbβ₃ seems to adopt a fully extended conformation, possibly induced and/or stabilized by the presence of the TM helices and cytoplasmic domains, although it cannot be excluded that different integrins may adopt different conformations.

The Hydrodynamics and the ET Map Support the Swing-Out Without Tail Separation in Primed, Full-Length α_IIbβ₃

Peptide and nonpeptide ligand-mimetics, such as RGDX (X = F, W, S), eptifibatide, and tirofiban, induce conformational changes in α_IIbβ₃ (priming) that can be monitored by changes (Hantgan et al., 1999, 2001, 2002) in s and D. Table 3 also reports these values (primed α_IIbβ₃), encompassing those identified from the reanalysis of our data as likely derived from “locked” primed conformers (see the Supplemental Data), together with percentage changes from the experimental resting value. Because DLS is more sensitive than AUC to aggregates/complexes possibly induced by the priming agents, we primarily used the ${<S_{(20,W)}^0>}_W$ values to evaluate the primed integrin models.

Models with the β₃ hybrid domain swing-out were developed from the α_IIbβ₃ resting models, as previously described for α_vβ₃. The “open” TM helices model described by Gottschalk (2005) was then inserted by superimposing the α_IIb TM helix, and the β₃ cytoplasmic domain was repositioned accordingly. The I-EGF3/I-EGF4/βTD region was moved to bridge the I-EGF2 module and the β₃ TM helix. In the cryo-EM-derived model A2b-3/S60-TC, an approximately −6.6% change from the ${<S_{(20,W)}^0>}_W$ value was obtained, but the absolute value is still higher than the experimental resting value (Table 3). Introducing similar changes in the ET-derived model (A2b-5/S60-TC, Figures 5E and 5F, and Movie S3) resulted instead in $S_{(20,W)}^0$ and $D_{t(20,W)}^0$ values at the upper limit and in the middle of the experimental range, respectively (Table 3). Keeping the same TM helices conformation but allowing the I-EGF3/I-EGF4/βTD region to slightly move away from the calf2 module brings the computed values closer to the lower experimental limits (Table 3, model A2b-5/S60-TPS; model not shown). Thus, a simple rearrangement of the TM helices coupled to the swing-out of the hybrid domain can account for the frictional changes induced in solution by many priming agents, and is fully compatible with the ET map. However, as in the α_vβ₃ partially extended structure, it was not possible to preserve the I-EGF2-3 interface observed in the β₂ PSI/hybrid/I-EGF1-3 crystal structure (Shi et al., 2007), which requires full tail separation.

Analysis of Resting and Echistatin-Primed α_IIbβ₃ EM Images Confirms the Hybrid Domain Swing-Out Without Tail Separation

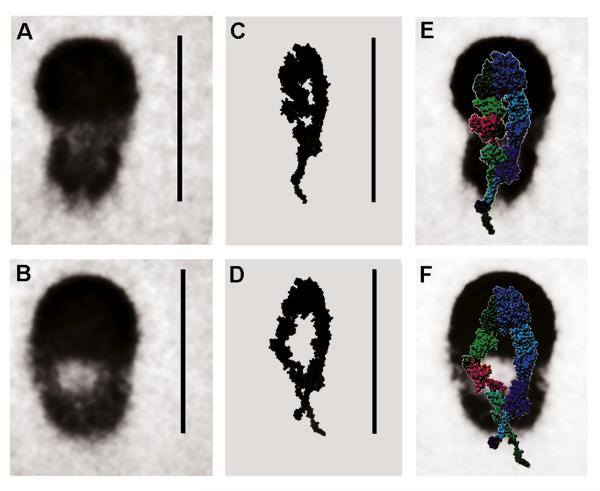
We have previously presented rotary-shadowed EM images of OG-solubilized α_IIbβ₃, resting and bound to the disintegrin echistatin (a 5.4 kDa snake venom polypeptide; Hantgan et al., 2004), showing a conformational change similar to that observed with small-molecule priming ligands. Figure 6 reports averaged EM images of resting (Figure 6A, 310 images) and echistatin-primed (Figure 6B, 414 images) α_IIbβ₃. The high-density, hemispherical regions are thought to represent the integrin headgroups. The decreased density observed for the stalk regions may result from averaging of conformational heterogeneity, possibly induced by interaction with the substrate. Notably, the EM image of primed, echistatin-bound α_IIbβ₃ shows an apparent enlargement of the central hole without a requirement of tail separation. Figures 6C and 6D show 2D projections of models A2b-5/ET and A2b-5/S60-TC, respectively, highlighting a possible structural interpretation of the EM images. Other features that are less well matched, such as the overall dimensions that are bigger in the averaged images, could either originate at the EM-level (metal coating, calibration, and surface-induced rearrangements, especially at the TM helices/OG micelle level) or could be due to inaccuracies in our modeling of this crucial region. To further aid their interpretation, in Figures 6E and 6F the two ET-based models are overlaid, after an ~15% rescaling to tentatively account for the metal layer, on the averaged images. As can be seen, the general agreement appears to be rather good and further supports the concept that priming does not immediately induce full tail separation.

Figure 6. Comparing Averaged EM Images with Projections of Resting and Primed α_IIbβ₃ Models.

SPIDER (Frank et al., 1996) averages of rotary-shadowed electron microscopy images (Hantgan et al., 2004) of α_IIbβ₃ solubilized in OG in resting conditions (A) and after priming with echistatin (B). (C and D) Chimera (Pettersen et al., 2004) solid rendition of SPIDER-generated (Frank et al., 1996) volumetric maps of models A2b-5/ET and A2b-5/S60-TC, respectively; the images were then blurred with Gaussian and median filter passes. (E and F) Surface representations, color coded as in Figure 1, of models A2b-5/ET and A2b-5/S60-TC overlaid on the averaged images of (A) and (B), after a 15% rescaling to account for the metal layer coating. Scale bars = 30 nm.

DISCUSSION

Integrins are complex, finely tuned macromolecular machines essential to cell adhesion and signaling (Hynes, 2002). Their deregulation or malfunction leads to serious disease, and their external control for therapeutic applications is a very active field of research, crucially depending on detailed knowledge of their structure and conformational changes. Notwithstanding the past few years’ spectacular progress (reviewed in Arnaout et al., 2005 and Luo et al., 2007), much remains to be learned, as complete high-resolution structures of full-length integrins in their various states are still lacking.

To bridge some of these critical gaps, we have employed a multiresolution approach, completing existing models, fitting them to the available EM evidence, and using experimental hydrodynamic data to validate the models and further refine them. By combining our results on two well-studied integrin systems, the α_vβ₃ ectodomain and the full-size, solubilized α_IIbβ₃, we can address some important lingering issues.

First, integrins appear to be more extended in solution than in the crystalline state or after being deposited on an EM grid. For the resting α_vβ₃ ectodomain, we demonstrate that moving from the crystal structure to a TEM map-fitting model, the hydrodynamics improve only from −11% to −5% with respect to the experimental data, while a 20° head-tail unbending is necessary to achieve a perfect match. Importantly, the hydrodynamic data were collected for the same samples used in the TEM studies (Adair et al., 2005) and likely identical to the previously crystallized material (Xiong et al., 2001, 2002). As the extracellular domain is naturally exposed to an aqueous environment, its solution behavior under near-physiological conditions should properly reflect its native state, barring conformational effects due to the absence of the TM helices and cytoplasmic domains (discussed below). In addition, we argue against the notion of fully flexible “knees” (Luo et al., 2007) because our NMA analysis revealed a major joint leading to more extended conformations only at the thigh/calf1 interface in the α_v subunit.

These findings are confirmed by the α_IIbβ₃ modeling. We show that a more extended conformation, even with respect to the already less bent cryo-EM model (Adair and Yeager, 2002), is also highly likely in this case (Movies S1 and S2). Furthermore, the excellent match obtained by fitting only the α_IIb ectodomain and the αA/βTD modules of the β₃ subunit in the ET map (Iwasaki et al., 2005) is remarkable, even though it was obtained from primed α_IIbβ₃ solubilized with Triton, which forms bigger micelles unsuitable for accurate hydrodynamic characterization. In contrast, studies with monoclonal antibodies (mAbs) raised against the β₂ subunit seem to support a bent resting integrin that extends upon activation (see, for example, Lu et al., 2001; reviewed in Luo et al., 2007). Although it cannot be excluded that different integrins may be differently regulated, this possibility seems unlikely given the degree of similarity between the subunits. The KIM127 and CBR LFA-1/2 mAb β₂ epitopes (Lu et al., 2001) can be mapped to the 514-518 and 543-554 zones, respectively, in the β₃ subunit, where they flank the Glu522 pivot. However, these regions seem already relatively exposed even in our starting α_IIbβ₃ model with the 20° opening (Movie S1). Thus, it could be the I-EGF region reorientation following the swing-out that is responsible for the differential mAbs binding (Movies S2 and S3).

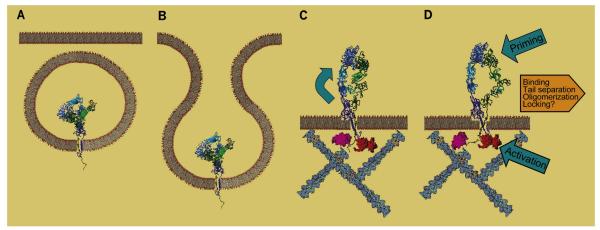
To summarize, although it has been much debated whether a transition to an extended conformation precedes or follows activation (Arnaout et al., 2005; Luo et al., 2007), integrins appear to be extended even in their resting state. However, they can revert to fully or partially bent forms under certain conditions that favor it, such as in crystals or adhesion to substrates in EM. Comparing the α_vβ₃ ectodomain with full-length α_IIbβ₃ suggests that the TM helices play a role in keeping a wider separation between head and tails, perhaps by stabilizing interactions at the C-terminal ends of the extracellular region. It is tempting to speculate that the fully bent form is a transport feature, used to export the protein on the outside of the cell, after which it opens like an umbrella, perhaps as a consequence of interactions with cytoskeletal components (Figures 7A, 7B, and 7C). Recent work on the biogenesis of α_IIbβ₃ provides evidence that the bent conformation is adopted early during assembly (Mitchell et al., 2007).

Figure 7. Simplified Schematic Representation of Proposed Integrin States.

(A and B) Integrins are synthesized and fold in the fully bent conformation in the ER; they are then segregated in vesicles that are exported to, and fuse with, the plasma membrane.

(C) Interaction with membrane/cytoskeletal components leads to a conformational change (extension) that could be aided/stabilized by disulfide rearrangements in the β subunit.

(D) Upon intracellular activation, the TM helices change conformation, inducing the swing-out that makes the heads competent to bind extracellular ligands; the event sequence is reversed following priming by small extracellular ligands. Binding of macromolecular ligands then stabilizes (and/or widens) the swing-out and facilitates TM separation and oligomerization; disulfide exchange in the β subunit may lock this activated conformation.

Our modeling fully supports the swing-out of the hybrid domain as the main conformational change following integrin priming/activation (Xiao et al., 2004; Takagi et al., 2003). Furthermore, its reversibility could easily explain the greater mismatch with the experimental data in the hydrodynamics of the crystal- and TEM-based models for α_vβ₃ primed and bound to a FN fragment. Again, crystal packing/surface interactions may favor the swung-in conformation, indicating that the energetics of this transition are relatively low, and implying a delicate mechanism transmitting the structural perturbations induced by ligand binding. Caution is needed in extending the very important results obtained on truncated constructs (see for example Xiao et al., 2004; Takagi et al., 2002, 2003; and Adair et al., 2005; reviewed in Arnaout et al., 2005; and Luo et al., 2007) to the mechanics of full-length integrins. In particular, the role of the TM helices and, perhaps, the cytoplasmic domains should not be underestimated.

Previous hydrodynamic analyses of full-length, solubilized α_IIbβ₃ indicated that stable conformers form after priming and that prolonged incubation is necessary to induce oligomerization (Hantgan et al., 1993, 1999, 2001, 2002, 2003). Although we can-not reject the possibility that the small OG micelle disfavors helix separation and delays their homomerization (Li et al., 2001, 2005), our modeling of the detergent-free α_vβ₃ ectodomain suggests that the calf2 and bTD modules are still in contact after ligand binding. Furthermore, we have shown that a simple rearrangement of the TM helices, as proposed by Gottschalk and Kessler (2004) and by Gottschalk (2005), leads to a model of the primed conformation that is quite compatible with the ET (Iwasaki et al., 2005), the hydrodynamics, and our averaged EM images (Figure 6; see also Figure 7D and Movie S3). Thus, full tail separation appears to be a consequence of, but not immediately coupled to, the swing-out induced by some macromolecular ligands (e.g., α_vβ₃-FN fragment, α_IIbβ₃-echistatin) and most priming agents. Interestingly, a recent work (Zhu et al., 2007) in which an engineered intersubunit disulfide bond blocked the TM helices separation in CHO-expressed mutant α_IIbβ₃ showed that, although clustering and outside-in signaling were abolished, ligand binding-induced conformational changes were still taking place.

Further in this respect, it has been assumed that the poor resolution of portions of the β subunit legs in either crystals (Xiong et al., 2001, 2002) or averaged EM images (Takagi et al., 2002) and ET maps (Iwasaki et al., 2005) results from their inherent flexibility and/or tail separation (Luo et al., 2007). Although the recent structures (Shi et al., 2007) of the PSI/hybrid/I-EGF1-2/3 from β₂ confirm that major conformational changes can indeed take place in this region, the β₃ subunit appears to be relatively rigid as a whole, constrained by the disulfide bridges network in the I-EGF1-4 modules. This rigidity seems to be reasonable, because mechanically transducing the hybrid swing-out movement down to the cytoplasmic tails would be difficult with a fully flexible lever. It is more likely that the fuzziness of the β subunit leg results from the presence of a few well-defined conformers, such as the ones revealed by our revised hydrodynamic analysis. Indeed, our data are consistent with the presence of two coexisting populations that are not in equilibrium, most likely corresponding to resting and “locked” primed conformations naturally present in the starting material (Supplemental Data). An intriguing possibility is that some conformational changes may be regulated or locked by disulfide exchange mechanisms in the β subunit. Although the presence of free sulfhydryls on integrins has been controversial, redox compounds and thiol-specific enzymes have been associated with platelet activation (reviewed in Essex and Li, 2006). If an external enzymatic action leads to disulfide isomerization in vivo, it may disappear in vitro, resulting in locked conformers.

To conclude, determining the structure and conformational changes of large multidomain proteins is a daunting task, calling for the application of many techniques. Furthermore, integrins’ transmembrane segments requiring solubilization present special complications. With a multiresolution approach, we have successfully used lower resolution solution data to constrain models derived from higher resolution techniques. The picture emerging is that of a relatively plastic structure with a delicate conformational balance that can be strongly influenced by external factors, whether physiological or nonphysiological. On the basis of our findings, we have presented in Figure 7 a new scheme of integrin states, revising some of the current concepts while operating within the same general frame. The new models that we have provided can be further tested experimentally, eventually leading to the complete elucidation of the mechanism of action of integrins.

EXPERIMENTAL PROCEDURES

Model Building

Visual inspection of the protein structure was performed using the programs O (Jones et al., 1991) and VMD (Humphrey et al., 1996). Most homology models were generated using the nest program of the Jackal package (Petrey et al., 2003) (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:Jackal), on a Pentium-II PC running under the Linux operating system, with no alignment tuning but refining all loops and secondary structure regions. The models were checked with WHATIF (Vriend, 1990) on a Web server (http://swift.cmbi.kun.nl/WIWWWI/). The Homology Modeling feature of WHATIF was also used in some cases. Although the atomic structures’ accuracy was not our primary concern, we idealized the stereochemical parameters of selected models with the program Refmac (Murshudov et al., 1997) so that about 95% of residues lie within the most favorable zone of the Rama-chandran plot and 2% lie in the additionally allowed areas. Atomic models were minimized by the conjugate gradients method using the Discover3 program of the Insight II suite (Accelrys/MSI, San Diego, CA). Energy minimization was performed using the AMBER forcefield (Weiner et al., 1984). Molecular graphics images and frames for movies were produced using the UCSF Chimera package (Pettersen et al., 2004) from the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIH P41 RR-01081) and with VMD. Morphing between two models was done with the Yale Morph Server (Krebs and Gerstein, 2000) (http://molmovdb.org/morph/), using adiabatic mapping (CNS-type). Movies were encoded with Quicktime Pro v. 7.2 (Apple Inc.) using the H.264 compressor, a 25 frames/sec frame rate, and a ≤950 kBit/sec bit rate. The neural network-based algorithm (Julenius et al., 2005) NetOGlyc 2.0 (http://www.cbs.dtu.dk/services/NetOGlyc/) was used to predict O-linked glycosylation sites on the α_IIb sequence retrieved from the SwissProt database (http://www.ebi.ac.uk/swissprot/) after removal of the signal peptide. While the server uses local thresholds to define Thr/Ser O-linked glycosylation sites, a few more were identified by using a cutoff potential >0.7.

Normal Modes Analysis (NMA) (Suhre and Sanejouand, 2004) was performed online using the ElNemo Web server (http://igs-server.cnrs-mrs.fr/elnemo/). Carbohydrates were removed from the structures before uploading. Only the ElNemo Web server was used, because low-frequency modes calculated with elastic network models are known to be robust (Nicolay and Sanejouand, 2006). Models were fitted inside EM maps using SITUS (Chacón and Wriggers, 2002) or Chimera (Pettersen et al., 2004).

Hydrodynamic Computations

To compute the hydrodynamic parameters, the high-resolution structures were converted into medium-resolution bead models with the program SOMO (Rai et al., 2005), with a 70% “popping” threshold and hierarchical overlap removal with outward translation for the exposed side-chain beads. One bead per peptide bond and one bead per side-chain were used for protein residues, and one bead per sugar unit was used for carbohydrate moieties (Rai et al., 2005). OG molecules were each represented with three beads. These settings resulted in ~3300 beads (~1980 exposed) for the α_vβ₃ ectodomain, ~4190 beads (~2620 exposed) for the α_vβ₃ ectodomain in complex with the FNIII7-10+EDB FN fragment, and ~3670 beads (~2890 exposed) for the α_IIbβ₃ plus 50 OG molecules complex. The hydrodynamic computations of rigid body bead models were performed by the SUPCW routine of BEAMS (Rai et al., 2005; Spotorno et al., 1997), excluding the buried beads. $S_{20,W}^0$ was computed for the α_vβ₃ ectodomain using molecular weights and partial specific volumes (${\stackrel{‒}{V}}_2$), calculated with PROMOLP (Spotorno et al., 1997), of 182,174 and 0.726 cm³/g without carbohydrates, 208,430 and 0.713 cm³/g with carbohydrates, and 257,871 and 0.716 cm³/g in complex with FNIII7-10+EDB. For α_IIbβ₃ with carbohydrates and 50 OG, those values were 240,324 and 0.723 cm³/g. For segmentally flexible models with a single hinge point, the FLEX routine of BEAMS (Spotorno et al., 1997) was used, with 7 degrees of freedom, hydrodynamic interaction between the subunits, and a step size of 2° with Cavalieri-Simpson integration, corresponding to 1° steps between conformations. To reduce the number of beads, we applied a cubic grid of 10 Å to the SOMO-generated, medium-resolution α_vβ₃ models using TRANS2VORONOI, an extended version of the program AtoB (Byron, 1997) developed by M. Nöllmann (University of California at Berkeley, CA), resulting in a total of 375 beads. Beads corresponding to the residues in the head (α_v 1-596, β₃1-518) and tail (α_v598-957, β₃519-692) regions were identified and grouped together, and a single bead representing α_vGly597 was used as the hinge point.

Electron Microscopy Image Analysis

Digitized images of electron micrographs of rotary-shadowed integrin samples (Hantgan et al., 2004), taken at an original nominal magnification of 60,000×, were subjected to particle selection, 2D alignment, and averaging using the SPIDER algorithms (Frank et al., 1996). A total of 310 individual particles of similar elongated morphology were selected from three micrographs of the ligand-free integrin, and 414 particles were selected from four micrographs of α_IIbβ₃ + echistatin. Windows (150 × 150 pixels) of each particle were created, their contrasts were inverted, and the particles were subjected to a reference-free alignment by a series of shifts and rotations. Then an average integrin image was created from each aligned group. We also selected and analyzed 68 particles with an approximately round morphology from the micrographs of ligand-free integrins. To facilitate direct comparison of these average integrin images and our models, SPIDER (Frank et al., 1996) was used to generate volume projections from their atomic coordinates. These projections were viewed and images prepared with Chimera (Pettersen et al., 2004).