Parabrachial nucleus neuronal responses to off-vertical axis rotation in macaques

Abstract

The caudal aspect of the parabrachial nucleus (PBN) contains neurons responsive to whole body, periodic rotational stimulation in alert monkeys. This study characterizes the angular and linear motion-sensitive response properties of PBN unit responses during off-vertical axis rotation (OVAR) and position trapezoid stimulation. The OVAR responses displayed a constant firing component which varied from the firing rate at rest. Nearly two-thirds of the units also modulated their discharges with respect to head orientation (re: gravity) during constant velocity OVAR stimulation. The modulated response magnitudes were equal during ipsilateral and contralateral OVARs, indicative of a one-dimensional accelerometer. These response orientations during OVAR divided the units into three spatially tuned populations, with peak modulation responses centered in the ipsilateral ear down, contralateral anterior semicircular canal down, and occiput down orientations. Because the orientation of the OVAR modulation response was opposite in polarity to the orientation of the static tilt component of responses to position trapezoids for the majority of units, the linear acceleration responses were divided into colinear dynamic linear and static tilt components. The orientations of these unit responses formed two distinct population response axes: (1) units with an interaural linear response axis and (2) units with an ipsilateral anterior semicircular canal-contralateral posterior semicircular canal plane linear response axis. The angular rotation sensitivity of these units is in a head-vertical plane that either contains the linear acceleration response axis or is perpendicular to the linear acceleration axis. Hence, these units behave like head-based (‘strap-down’) inertial guidance sensors. Because the PBN contributes to sensory and interoceptive processing, it is suggested that vestibulo-recipient caudal PBN units may detect potentially dangerous anomalies in control of postural stability during locomotion. In particular, these signals may contribute to the range of affective and emotional responses that include panic associated with falling, malaise associated with motion sickness and mal-de-debarquement, and comorbid balance and anxiety disorders.

Introduction

Vestibular sensation and the sense of illusory self-motion can elicit affective and emotional responses that range from disgust to panic (Balaban 1999; Mayo 1837). We have all experienced these phenomena. The malaise and disgust that accompany the development of motion sickness from the prodromal SOPITE syndrome builds up slowly in moving environments and under sensory conflict situations and can result in emesis (Graybiel and Knepton 1976; Money 1970; Money et al. 1996; Reason and Brand 1975; Tyler and Bard 1949). The emesis that is often associated with unilateral vestibular dysfunction is accompanied by similar affective changes. The panic that results from a perceived loss of balance control is a very different response. For example, we can all recall a scenario analogous to sitting stationary in a car at a traffic light on a hillside facing up. A large truck that is alongside the car inches forward slowly, in anticipation of the light changing from red to green. The unconscious interpretation of the situation is the perception of an uncontrolled, backward drift of your car down the hill. An urgent sense of panic accompanies a very forceful depression of the brake pedal, followed by a sense of relief with the realization that the loss of control was merely illusory. A third emotional response is the soothing, relaxing sense from rocking in a swing or hammock, in a rocking chair or on a boat on calm waters. Changes in homeostatic autonomic responses are integral components of this spectrum of emotional and affective responses associated with balance control.

The parabrachial nucleus (PBN) occupies a highly strategic position in central networks that mediate both the awareness of and the affective and emotional responses to intrinsic and extrinsic stimuli that alter the sense of the physiological well-being of the body (Craig 2002, 2003, 2009; Gauriau and Bernard 2002; Zylka 2005). Its connections suggest that it is an important circuitry link for processing emotional, affective influences on autonomic and homeostatic controls. Anatomical studies have shown that the PBN participates in ascending spino-parabrachio-thalamo-cortical/amygdala, spino-parabrachio-hypothalamic and spino-parabrachio-amygdala pain pathways (Bester et al. 1995; Feil and Herbert 1995; Herbert et al. 1990; Jasmin et al. 1997; Ma and Peschanski 1988; Moga et al. 1990), ascending gustatory and cardiovascular afferent pathways to the amygdala and cerebral cortex (Fulweiler and Saper 1984; Herbert et al. 1990; Norgren 1976; Norgren and Leonard 1973; Norgren and Pfaffmann 1975; Pritchard et al. 2000; Saper and Loewy 1980), and descending parabrachio-spinal and parabrachio-trigeminal pathways (Fulweiler and Saper 1984; Yoshida et al. 1997). PBN also receives descending projections from the cerebral cortex, hypothalamus, and central amygdaloid nucleus (Moga et al. 1990; Yasui et al. 1985). Chemical stimulation studies indicate that the descending projections of PBN neurons have the potential to influence cardiovascular (Chamberlin and Saper 1992; Hade et al. 1988; Hayward and Felder 1998; Saleh and Connell 1998) and respiratory (Chamberlin and Saper 1994) responses. The stimulus-evoked discharges of gustatory (Nishijo and Norgren 1997; Norgren and Pfaffmann 1975; Shimura et al. 1997), cardiovascular (Jhamandas et al. 1991), and nociceptive (Bernard and Besson 1990; Bester et al. 2000) PBN neurons under normal conditions are very similar to responses in the solitary nucleus or dorsal horn, respectively. However, the integration of respiratory-related, nociceptive, and other non-respiratory inputs by respiratory neurons in PBN has been described and discussed by Song et al. (Song et al. 2006). Thus, PBN appears to be an important link for relaying interoceptive information rostrally and for participating in descending control of respiratory and autonomic responses.

Studies employing lesions and chemical stimulation of the PBN support its hypothetical role in interoception, defined as any case when molar organic behavior is modified by visceral sensory activity, with or without sensory awareness (Cameron 2002). From this definition, it follows that the repeated demonstration, which lesions of the PBN abolish specifically taste- and odor-aversion learning (Grigson et al. 1998a, b; Reilly and Trifunovic 2000, 2001; Spector et al. 1992; Yamamoto et al. 1995), is a paradigmatic example of PBN involvement in interoception. Because the temporal properties of responses of gustatory PBN neurons are modified with conditioned behavioral responses (Shimura et al. 1997), these conditioned aversions suggest a role of PBN neurons in recognizing what Fanselow (1994) termed ‘innate danger stimuli’ and relaying those signals to the central amygdaloid nucleus.

The caudal PBN and Kölliker-Fuse nucleus are also a target of vestibular nucleus projections (Balaban 1996, 2004; Balaban et al. 2002; Porter and Balaban 1997) and are the source of more widespread projections back to the vestibular nuclei (Balaban 2004). Single units in the primate caudal PBN show responses to position trapezoid stimuli that are consistent with a convergence of both angular and linear acceleration signals (Balaban et al. 2002).

This study extends the analysis of these responses by comparison of unit behavior during off-vertical axis rotation (OVAR) and vertical position-trapezoid stimulation. Following the decay of horizontal semicircular canal responses to the yaw-axis angular velocity produced at the initiation of rotation, constant velocity OVAR produces a linear acceleration stimulus equivalent to the projection of the gravitational acceleration vector on the utricle. As is the case for vestibular nucleus responses (Reisine and Raphan 1992), the PBN units from these new experiments can display both a constant response component (a persistent increase or decrease in firing rate) and a modulation response (cosinusoidal modulation with head position relative to gravity) during OVAR. Combined with results from the position trapezoid stimuli, we report here that the responses of PBN neurons appear to represent a convergence of two linear acceleration components oriented along a single axis but with different response properties and opposite polarities, combined with an angular velocity response to vertical rotation either in the plane of the linear acceleration axis or around the linear acceleration axis. These responses can be conceived as head-based inertial guidance sensors, similar to strapdown sensors in inertial guidance systems.

Methods

Surgical procedures

All surgical procedures were conducted under aseptic conditions in an animal surgical suite at the Central Animal Facility of the University of Pittsburgh. Two female and one male macaque monkeys (Macaca nemestrina) were premedicated with atropine (0.05 mg/kg im) and ketamine (12 mg/kg im). After endotracheal intubation, anesthesia was maintained by inhalation of a 1–1.5% halothane–nitrous oxide–oxygen mixture. Three dental acrylic lugs were affixed to the skull for secure but painless head stabilization during recording sessions. One lug, positioned on the top of the skull, served as a pedestal for electrical connectors; the other two lugs were positioned behind the ears. At the site of the anterior lug, a 15–20 mm patch of skin and periosteum were removed, and small holes were drilled in the skull with a dental burr. Small stainless steel screws were tapped into these holes, and the lug was constructed by applying layers of dental acrylic around the screws to a height of approximately 9 mm. The two posterior lugs were similarly applied excepting that they were continuous with the acrylic base securing the recording chamber (below).

A search coil was implanted on the right eye to measure eye movements. The conjunctiva was cut at the limbus, and a preformed 16 mm diameter coil (three turns of Teflon-insulated stainless steel wire) was sutured to the sclera. Lead wires were passed subcutaneously to a connector on top of the skull. The conjunctiva was sutured with 7-0 vicryl to cover the coil.

A 20-mm diameter, 10-mm high stainless steel recording chamber was implanted over a hole trephined in the parietal bone to permit the chamber to contact the intact dura mater. The chamber was oriented toward a target centered 1 mm left of the midline and +1 mm anterior to the ear bars, but angled 15° posterior from vertical. This approach permitted complete exploration of the left PBN. Stainless steel screws were anchored within the surrounding bone through small burr holes, and dental acrylic applied to fix the chamber to the skull. The chamber was filled with antibiotic ointment and covered with a tightly fitting metal cap.

Recording sessions

The monkey was seated in a primate chair with its head fixed to the chair in the stereotaxic plane. The animal was placed in a two-axis rotation device enclosed in a soundproof, lightproof, shielded booth. Horizontal rotation about the yaw axis was driven by an 80 or a 300 ft-lb servo-controlled motor (Neurokinetics, Inc., Pittsburgh, PA), which reliably produced constant velocity rotations at user-defined rates. Vertical rotations about a pitch, roll, or vertical semicircular canal plane axis were driven by a second motor.

Eye movements were measured with the magnetic search coil technique (CNC Engineering, Seattle, WA). Because the transmitting coils for generating magnetic fields did not rotate with the animal, search-coil signals were demodulated with the “phase angle” method (Collewijn 1977).

Extracellular single-unit recordings were obtained with 0.005″ tungsten electrodes (Micro Probe, Potomac, MD) which were positioned with a Trent Wells X–Y stage attached to the implanted chamber and a Trent-Wells hydraulic microdrive. A 67–75 mm stainless steel guide tube (length depended upon the monkey) protected the electrode as it was lowered through the dura and tentorium cerebelli. Signals were amplified conventionally and filtered to remove 60 Hz noise. Unit and chair position data were recorded to digital tape (Cygnus CDAT16) at 24 kHz for off-line analysis.

To positively locate PBN units, the left abducens nucleus and left trochlear nerve root were identified as landmarks by noting their characteristic burst-tonic properties during eye movements. Single units were identified initially in the darkened booth during simultaneous ±10–20° amplitude, 0.7 Hz sinusoidal oscillation in the pitch plane, and 0.7 Hz sinusoidal oscillation in the yaw plane. Units with response modulation during the search stimulus were tested sequentially with ±9–20° position trapezoid stimuli in the darkened booth in (1) the pitch plane, (2) an approximate left anterior-right posterior semicircular canal plane (LARP, animal rotated 45° rightward re: pitch axis), (3) an approximate right anterior-left posterior semicircular canal plane (RALP, animal rotated 45° rightward re: pitch axis), (4) roll plane, and (5) yaw plane with head level. The position trapezoid stimulus comprises two static position segments and two transient rotation periods. The angular displacement of the static position about the central position was ±9–15° for animals L and K and ±20° for animal T, and the peak angular velocities of the rotation periods were 80 or 240 deg/s, respectively. The duration of static position periods was either 1.5 or 2.0 s; the durations of rotation periods were approximately 0.25 s for animals L and K and 0.5 s for animal T. For OVAR stimulation, the rotation superstructure was tilted 15° away from the earth-vertical axis so that the monkey was facing nose down. The monkey was then rotated at constant velocity about the tilted axis. Animals L and K were tested at velocities 25, 50, and 100 deg/s (equal to frequencies 0.07, 0.14, and 0.3 Hz). Animal T was tested on a different apparatus at constant velocities 20, 40, and 80 deg/s (equal to 0.06, 0.1, and 0.2 Hz). The initial nose down orientation of the monkey during OVAR orientation is referred to as “0°” or “±360°.”

Single unit data analysis

Single units were separated from background noise using an amplitude-based window discriminator with optional 60 Hz and spike width (duration of spike within the amplitude window) filters, written in LabView (National Instruments). Spike times were identified to 0.1 ms precision. In order to prevent aliasing in instantaneous rate records in trials with very few spikes, the spike rates for all responses were represented at each spike time as the average of the two instantaneous firing rate measures (i.e. the reciprocal of the interspike interval) calculated with respect to the preceding and following spikes.

The analyses for position trapezoid data are described in detail in a previous publication (Balaban et al. 2002). Briefly, least-squares methods were used to estimate the 64 bin averaged response to each stimulus as a weighted sum of (1) the mean response rate, (2) whole body angular velocity, (3) a leaky integration of angular velocity, and (4) angular position relative to gravity. The model fit was determined by sequential fitting of additive components in the following order. First, a model fit was determined for the mean firing rate plus angular velocity gain components, with both parameters free. Second, the gains for mean firing rate and angular velocity sensitivity were fixed, and the fit was optimized with the addition of the leaky integration of angular velocity (one free parameter). Third, the mean firing rate and the gains for the angular velocity sensitivity and leaky integration sensitivity from the previous fitting procedure were set as initial conditions and the values are optimized. Finally, the static position component was added, and a nested F test (described below) is used to determine if the inclusion of this component is warranted (α = 0.01).

The analysis of constant velocity OVAR responses was restricted to data collected at least 30 s after the initiation of OVAR, to permit decay of angular velocity responses due to horizontal semicircular canal stimulation (Reisine and Raphan 1992). Data from each OVAR stimulus cycle were apportioned into 64 equally spaced time bins, and average instantaneous firing rates in each bin were used to compute firing rates during an average stimulus cycle. Yaw-axis position data were obtained directly from the position feedback signals for the rotation device. Tilt angles for OVAR were obtained directly from an inclinometer mounted to the device.

Responses of units to individual OVAR stimulus conditions were described as a linear sum of two signals: (1) a mean firing rate and (2) a cosinusoidal modulation at the frequency of revolution of the linear acceleration stimulus component during OVAR. The cosinusoidal modulation was characterized by its magnitude and peak response location (the table position at which the peak response appeared, relative to the nose down orientation). Non-linear least-squares regression (Levenberg–Marquardt algorithm as provided in MatLab 6.1 (The Mathworks, Inc., Natick, MA)) was used to estimate unit responses during individual OVAR conditions as follows:

$$R=\text{max}(0,\mu +\rho \text{cos}(\omega t-\delta ))$$

where R is the total response of the cell in spike/s, μ the mean firing rate, ρ the magnitude of the modulation component of the response (equal to one-half of the peak-to-peak modulation amplitude), ω the frequency of revolution during OVAR, and δ the table position at peak response relative to nose down. Model outputs were constrained to a minimum value of zero because neurons cannot fire at negative rates.

A nested F test approach was used to determine whether the cosine model fit accounted for significantly more variance than the simple average rate. A regression-based nested F test was used here to assign a specific probability to the least-squares fit of the model with modulation magnitude ρ. This statistical procedure is an alternative to using analysis of power for determining the significance of power in a particular frequency range (Shumway and Stoffer 2006) or to adopting a ‘rule of thumb,’ such as requiring that the power of the fundamental be greater than 1.5 times the power of frequencies above the second harmonic (Schor et al. 1984) as a criterion for goodness of fit. The F test for comparing two nested models (one of which is a simplified version of, and has fewer free parameters than the other) is

$$F=\frac{(\mathrm{SSR}1-\mathrm{SSR}2)∕\mathrm{SSR}2}{(\mathrm{DF}1-\mathrm{DF}2)∕\mathrm{DF}2}$$

where SSR1 is the sum of squared residuals for the model R = μ, SSR2 the sum of squared residuals of the mean rate plus modulation model, and DF the degrees of freedom (DF = number of data points – number of free model parameters, in each equation). The only assumption of the nested F test is that the errors in the data be approximately normally distributed, and that both models are fitted to the same data. Responses for which the cosine fit did not account for significantly more variance than the mean were considered unmodulated (i.e., modulation was estimated as zero). Estimation of the parameters describing a unit's response from OVAR requires data from both CW and CCW OVAR at the same stimulus velocity. Therefore, units with OVAR data from only one direction at a particular frequency of revolution were not included in summary analyses.

A unit's phase for the OVAR modulation response (φ) was determined as the difference between the instantaneous table position (or head orientation) at the time of the peak modulation response and the table position (or head orientation) representing the direction of tilt corresponding to the unit's orientation vector (ξ). The stimulus direction at which the response peak occurs is then dependent on the direction of rotation of the table, with

$${\text{peak}}_{\mathrm{cw}}=\xi -\phi$$

and

$${\text{peak}}_{\mathrm{ccw}}=\xi +\phi .$$

The equation was then solved for ξ and φ:

$$\xi =({\text{peak}}_{\mathrm{cw}}+{\text{peak}}_{\mathrm{ccw}})∕2$$

and

$$\phi =({\text{peak}}_{\mathrm{ccw}}-{\text{peak}}_{\mathrm{cw}})∕2,$$

such that a positive phase value indicated a phase lead.

Statistical approaches for circular data

The analysis of directional data sets are the subject of a specialized area in statistics because they require parameter estimation for data (angles) distributed around circles or spheres rather than rectilinear axes. The properties and theory of circular distributions are discussed in detail in the literature on circular statistics (Mardia and Jupp 2000), along with the derivation of statistical tests that are cited in “Results”. A method for explicit modeling of mixed circular distribution functions for polymodal data is described below.

Statistical modeling of mixed circular distribution functions

Parameters for mixed circular distribution function fits to circular data were estimated by minimizing the error between the observed value of each ordered observation and its expected value from the model distribution function. This approach from order statistics uses the simple function (i – 0.5)/N for the cumulative probability value associated with the ith ordered observation from a sample of size N (David 1970) to interpolate the expected value of the observation from a calculated cumulative distribution function of the model. For two wrapped normal distributions, the model is (1 – q) X₁(μ₁, σ₁) + q X₂(μ₂, σ₂), where X₁ and X₂ are wrapped normal distributions with means μ₁ and μ₂ and standard deviations σ₁ and σ₂, respectively, and q ∈ [0,1] is the proportion of observations from distribution X₂. For three distributions, the model is (1 – q₁ – q₂) X₁(μ₁, σ₁) + q₁X₂ (μ₂, σ₂) + q₂ X₃(μ₃, σ₃), with constraints q₁, q₂ ∈ [0,1] and (q₁ + q₂) ≤ 1.

Statistical tests for axial distribution of circular data

The hypothesis that circular data are distributed along a mean axis is tested by determining if the distribution of the doubled angles is unimodal (Mardia and Jupp 2000); for example, by performing a Rayleigh test on the doubled angle data. If $\stackrel{‒}{\theta }$ is the mean of the doubled angles, then the mean axis is defined as the axis defined by $\stackrel{‒}{\theta }∕2$ and $\stackrel{‒}{\theta }∕2+180°$.

Results

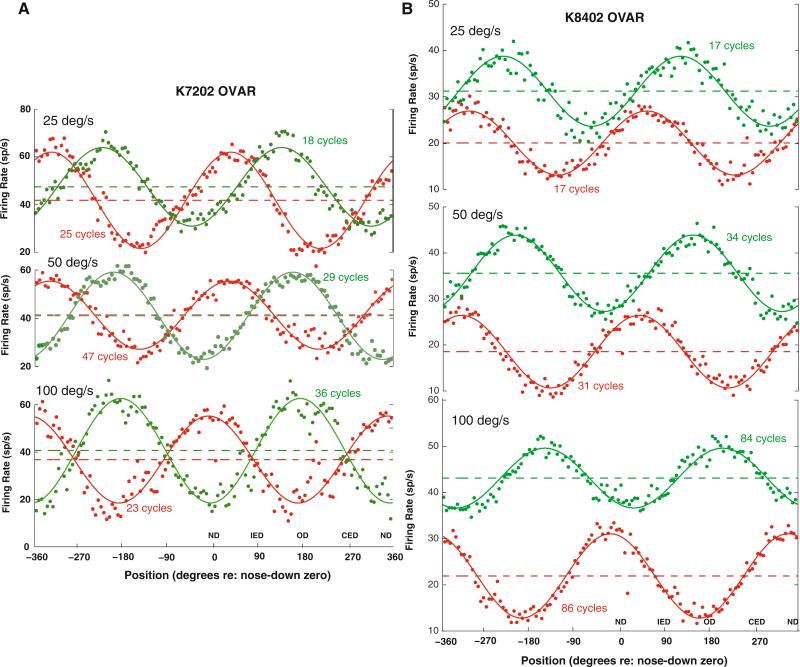
Units displayed either modulated or unmodulated responses during constant velocity OVAR. The most common unit response (65/103 units; 64%) was a per-stimulus firing rate modulation at the frequency of revolution, which could be superimposed on a change in mean firing rate from baseline activity (Figs. 1, 2a). The remaining units showed a shift in mean firing rate without significant modulation; an example is shown in Fig. 2b. The modulated units were defined on the basis of statistically significant modulation at the stimulus revolution frequency (using a nested F test, α = 0.05), a modulation magnitude parameter ρ ≥ 3 sp/s (i.e., peak-to-peak modulation ≥ 6 sp/s) and a goodness of fit of the response to a cosine at the stimulus frequency of revolution that accounted for at least 40% of the total variance of the unit response (i.e., product–moment correlation coefficient ≥ 0.63). The empirical cumulative distribution function of peak-to-peak modulation (2ρ) had a 10th percentile of 7.6 sp/s, a 25th percentile of 10.4 sp/s, and a 50th percentile of 15.8 sp/s. The direction of the peak modulation responses varied across the units. For the unit in Fig. 1a (K7202), the peak modulation response direction was between the ipsilateral ear down and occiput down orientations (–136.4° at 25 deg/s, –157.8° at 50 deg/s, and –173.6° at 100 deg/s re: nose down) during ipsilateral OVAR and between the ipsilateral anterior semicircular canal down and nose down orientations (–34.1° at 25 deg/s, –30.3° at 50 deg/s, and 10.4° at 100 deg/s re: nose down) during contralateral OVAR. For the unit in Fig. 1b (K8402), the peak modulation response direction was between the contralateral posterior semicircular canal down and ipsilateral posterior semicircular canal down orientations (–132.4° at 25 deg/s, –145.7° at 50 deg/s, and 152.2° (= –207.8°) at 100 deg/s re: nose down zero) during ipsilateral OVAR and between the ipsilateral anterior semicircular canal down and nose down orientations (–52.5° at 25 deg/s, –37.7° at 50 deg/s, and 19.8° at 100 deg/s re: nose down) during contralateral OVAR. For the unit in Fig. 2a, the peak modulation response direction was near the contralateral ear down orientation (85.4° at 25 deg/s, 76.3° at 50 deg/s, and 86.3° at 100 deg/s re: nose down) during ipsilateral OVAR and between the contralateral anterior semicircular canal down and nose down orientations (39.5° at 25 deg/s, 14.3° at 50 deg/s, and 17.3° at 100 deg/s re: nose down) during contralateral OVAR. The unit in Fig. 2b is representative of the 36% of the units that were unmodulated during constant velocity OVAR stimulation. However, these units showed shifts in their mean (background) activity with the direction and velocity of constant velocity off-axis rotation. Independent of the presence of an OVAR modulation response, the units showed velocity, integrated velocity, and position responses to position trapezoids that were consistent with our previous results (Balaban et al. 2002).

Fig. 1.

Examples of responses of two PBN units during constant velocity OVAR. The green trace shows responses during rotation toward the recorded side (ipsilateral rotation), while the red trace shows responses during rotation in the contralateral direction. The data are averaged across a window spanning two cycles of rotation. The head orientation relative to gravity is labeled relative to nose down (ND) as 0° and occiput down (OD) as 180°. The ipsilateral ear down (IED, +90°) and contralateral ear down (CED, –90°) orientations are also labeled. The constant speed of OVAR is listed for each pair of traces. The points indicate the average instantaneous spike rate and the solid line indicates the best least-squares fit of a constant baseline plus cosine modulation model to the data for the indicated number of steady state cycles of rotation (see text). The dashed line shows the baseline level for each unit in each stimulus condition, and the solid black line shows the background mean discharge rate. a The behavior of a PBN unit with a modulation response component and a baseline response component that are insensitive to a fourfold change in OVAR speed. b An example of a PBN unit with a significant modulation response component and with a baseline component that varies with the direction of rotation

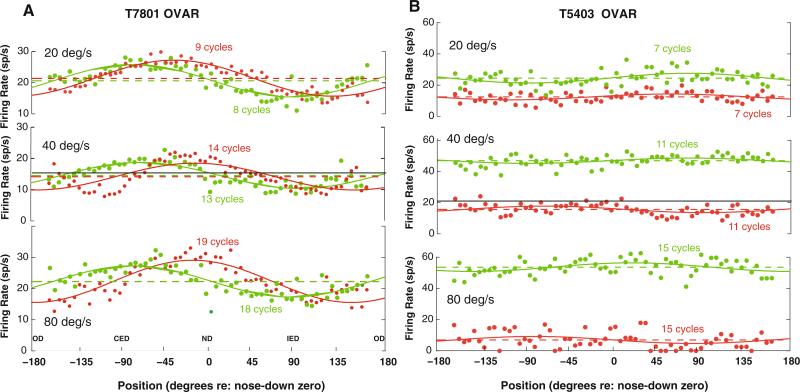
Fig. 2.

Two additional examples of the discharge rates of PBN units during constant velocity OVAR stimulation. The green trace shows responses during rotation toward the recorded side (ipsilateral rotation), while the red trace shows responses during rotation in the contralateral direction. The data are averaged across a window spanning one cycle of rotation. The head orientation relative to gravity is labeled in radians relative to nose down (ND) as zero and occiput down (OD) as ±180°. The ipsilateral ear down (IED) and contralateral ear down (CED) orientations are also labeled. The constant speed of OVAR is listed for each pair of traces. The points indicate the average instantaneous spike rate and the solid line indicates the best least-squares fit of a constant baseline plus cosine modulation model to the data (see text). The dashed line shows the baseline level for each unit in each stimulus condition, and the solid black line shows the background mean discharge rate. a The behavior of a PBN unit from another monkey with a small modulation response component and a baseline response component that did not change across OVAR stimulus velocities. b An example of a PBN unit with no significant modulation response during OVAR, but with a baseline component that varies with both the velocity and the direction of rotation

Unmodulated response component during OVAR

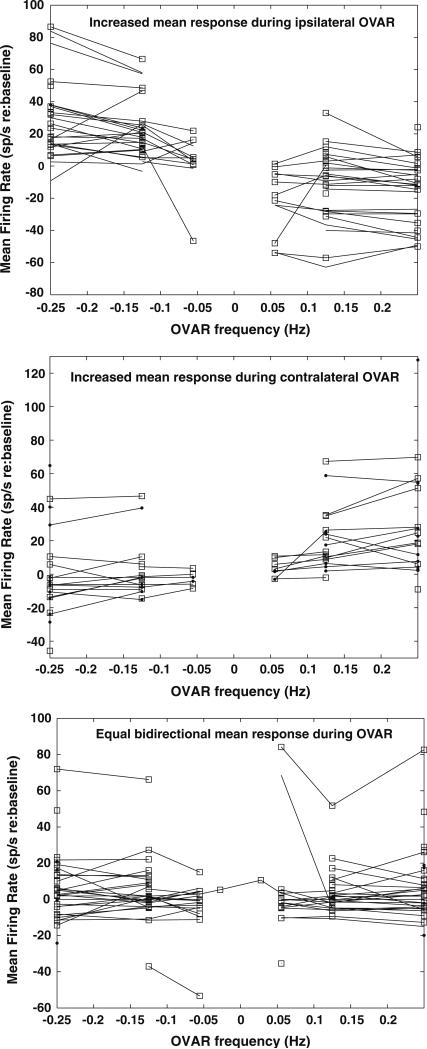
After subtraction of baseline firing rates, the response patterns of the units showing no modulation during OVAR and the mean firing rate components of the OVAR-modulated units’ responses could be classified into one of three groups. One group of units displayed a greater response during constant velocity OVAR in the direction ipsilateral to the recording site (Fig. 3, upper panel); examples of these unit responses are shown in Figs. 1b and 2b. The baseline firing rates of these neurons in the absence of rotation was 32.6 ± 3.7 sp/s. Note that the changes in mean response rates from baseline did not vary with the OVAR speed for each rotation direction. The mean response (re: baseline) of this group of units was 23.7 ± 7.0 sp/s during ipsilateral rotation and –12.3 ± 3.5 sp/s during contralateral rotation. The per-stimulus mean firing rate of individual units was 35.4 ± 3.6 sp/s greater during ipsilateral than contralateral rotation. A second group of units displayed a greater response during OVAR in the direction contralateral to the recording site (Fig. 3, middle panel). The baseline firing rates of these neurons in the absence of rotation was 18.8 ± 4.5 sp/s, which was significantly lower than the units with an increased mean response during ipsilateral rotation (P < 0.05, least-significant differences test). These units had a change in mean response of 0.4 ± 5.0 sp/s during ipsilateral rotation and 24.5 ± 6.0 sp/s during contralateral rotation. For individual units, the per-stimulus mean firing rate was 25.4 ± 4.3 sp/s greater during contralateral than ipsilateral OVAR. A third group of neurons (Fig. 3, lower panel) showed equal mean firing rate response components during rotation in either direction (difference, 0.7 ± 3.3 sp/s) and tended to have low mean rates during both ipsilateral (3.6 ± 2.7 sp/s) and contralateral rotations (4.3 ± 2.7 sp/s). The baseline firing rates of these neurons in the absence of rotation (24.5 ± 3.5 sp/s) did not differ significantly from the other two groups of units. Examples of these units are shown in Figs. 1a and 2a. This group also included 10 units with modulation responses that did not show any deviation in mean firing from baseline during OVAR. There was no difference in the behavior of the per-stimulus mean firing rates of units with unmodulated versus modulated OVAR responsiveness. Rather, the mean rate and modulation response components appear to be independent.

Fig. 3.

Mean firing rate patterns of PBN neurons during OVAR relative to baseline discharges. The baseline firing rate at rest was subtracted from the mean value of the response during OVAR. The upper panel shows the mean firing rates of units that showed an increasing mean discharge rate during ipsilaterally directed constant velocity OVAR and a decreasing rate during contralaterally directed OVAR. The middle panel shows the mean firing rates of units that showed a decreasing mean discharge rate during ipsilaterally directed constant velocity OVAR and an increasing rate during contralaterally directed OVAR. The lower panel shows the mean firing rates of units that showed an equal mean discharge rate during OVAR directed both ipsilaterally and contralaterally

The mean firing rate response component patterns were not correlated with the linear acceleration and angular velocity response properties of units. However, there was a tendency for different constant mean firing rate response patterns to be distributed differentially in the PBN. The units with an elevated mean response during contralateral OVAR tended to be located deeper and more laterally within PBN (medial and external medial PBN) than the other response patterns. This tendency was sufficient to produce a significant interaction effect (F(2,91) = 4.884, P = 0.01) by ANOVA (dependent variables for repeated measures: normalized depth and medio-lateral unit coordinates; between groups factor: response pattern).

Modulated responses to OVAR

Responses as a function of OVAR frequency of revolution

For each OVAR stimulus condition, the modulation magnitudes of each unit were symmetric for clockwise versus counterclockwise rotation (Table 1). When three statistical outliers were removed from the data for the analysis, the final regression slope (no constant term) was near unity and accounted for at least 85% of the variance in the data. Since these findings are consistent with the behavior of a one-dimensional linear accelerometer, the unit's response gain (sp/s/g) was estimated as the mean of the responses for both directions of rotation.

Table 1.

Regression results: OVAR modulation for contralaterally versus ipsilaterally directed rotation for each unit

OVAR velocity (deg/s)	Slope ± SE	Adjusted multiple R2
20–25	0.85 ± 0.05 (n = 24)	0.936
40–50	0.92 ± 0.05 (n = 51)	0.895
80–100	1.05 ± 0.06 (n = 47)	0.865

The estimated response gains and orientations during OVAR across the tested revolution frequency range are shown in Fig. 4. The response gains of the units were relatively constant across stimulus conditions. The majority of units showed little or no variation in estimated response orientation across stimulus conditions. However, the units were clearly differentiated into two main groups with orientations near either ipsilateral ear down or contralateral ear down tilt, with very few orientation estimates in the pitch plane. Eight other modulated units showed large differences in orientation estimates at the two highest stimulus frequencies (Fig. 4, lower panels), but retained symmetric modulation magnitudes (during ipsilaterally- and contralaterally directed OVARs) at each individual frequency of revolution.

Fig. 4.

The upper panels show the gain and orientation of the cosinusoidal modulation of unit responses during OVAR for majority of the cells, which were constant across the range of stimuli employed. The lower panels show the same properties for seven units with response orientations that varied with OVAR stimulus frequency of revolution

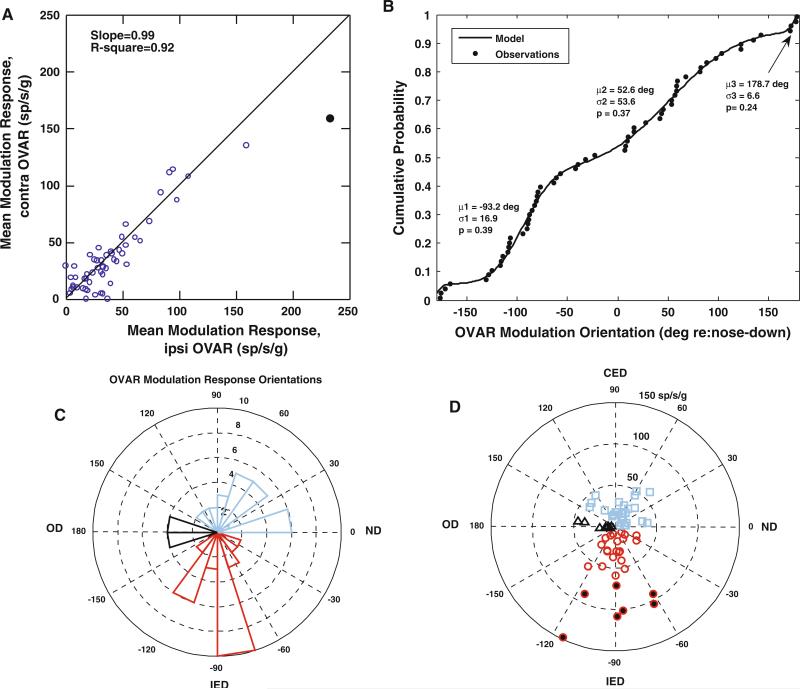
Because estimates of modulation response gain did not vary across OVAR frequencies, the grand mean of a unit's modulation magnitude across frequencies provides a robust estimate of its linear acceleration response gain. This estimate further underscores the behavior of the units as one-dimensional accelerometers. When three statistically identified outliers were excluded from the sample, linear regression analysis (with no constant coefficient) showed that the grand mean of the modulation response gains (i.e., across all tested frequencies) were nearly equal during clockwise and counterclockwise rotations (62 units, slope = 0.99 ± 0.04, adjusted multiple R² = 0.92; Fig. 5a). The regression analysis outcome was identical for the OVAR responses of the 54 modulated units with invariant response orientation estimates across frequencies.

Fig. 5.

OVAR modulation response properties of PBN units. a A scatter plot of the relationship between the mean modulation response gains of individual units during ipsilaterally- (ipsi) and contralaterally- (contra) directed constant velocity OVAR. The responses tend to be equal in both directions; a linear relationship with a slope of 0.99 (model with no constant term) accounts for 92% of the variance. b The empirical cumulative distribution function of the orientations of the OVAR modulation responses of the PBN units in the sample. The line shows a model fit for a mixture of three wrapped normal distributions (means μ1, μ2, and μ3; standard deviations σ1, σ2, and σ3; proportions of observations p1, p2, and p3). The details of the least-squared estimation procedure, based on an order statistics approach, are described in the text. c A polar histogram of orientations of the units and d a polar coordinate plot of the depth of modulation as a function of the best mean response orientation of the unit. By convention, 0° represents the nose down, 90° the contralateral ear down, –90° the ipsilateral ear down, and 180° the occiput down orientations. The units with peak modulation responses in the ipsilateral ear down orientation are shown in cyan bars in c and cyan squares in d. Units with peak modulation responses in the contralateral ear down orientation are designated by red bars in c and red circles in d, with circles filled in black indicating high sensitivity units. Finally, units with peak modulation responses in the occiput down orientation are shown by black bars in c and black triangles in d

Directional response populations

The summaries in Fig. 5b–d show that the units with a frequency-invariant orientation estimate for the OVAR modulation response may be subdivided into three spatially tuned populations. The modulation response orientation data are consistent with a mixture of three wrapped normal distributions that are centered (1) at the ipsilateral ear down orientation (mean –93.2 ± 16.9 (SD) deg re: nose down, 39% of observations), (2) near the occiput down orientation (mean 178.7° ± 6.6° (SD) re: nose down, 24% of observations), and (3) near the contralateral anterior semicircular canal down orientation (mean 56.2° ± 53.6° re: nose down, 37% of observations). The cumulative distribution functions of the data and mixture distribution model (Fig. 5b) conform closely and the orientation data for each component are shown in a histogram in polar coordinates in Fig. 5c. The gains of the modulation responses (Fig. 5d) for the ipsilateral ear down group of units are also greater than the gains in either of the other groups (Fisher's least-significant difference (LSD) test, P < 0.01), due to a small subset of seven high sensitivity units (symbols filled in black in Fig. 5d).

For the units with OVAR response orientations near ipsilateral ear down, the angular velocity sensitivity was oriented in a vertical plane containing the axis of the response orientation estimated from OVAR responses. A Rayleigh test of doubled angles (see “Methods”) indicated that the unit differences between the orientation of (position-trapezoid estimated) angular velocity azimuths and the OVAR-estimated peak linear acceleration response orientation are distributed along an axis between –3.3° and 176.7° (R statistic = 6.72, P < 0.05), implying that there are many units with linear acceleration and angular velocity azimuth sensitivities of the same or opposite polarity along a single axis. This relationship did not depend on the elevation component of the angular velocity response. The angular velocity azimuth data were consistent with a mixture of two wrapped normal components, one component (64% of observations) with a mean difference of –3.24° ± 25.1° (SD) and a second component (36% of observations) with a mean difference of –144.9° ± 61.9° (responses of the same and opposite polarity, respectively). Hence, the unit responses appear to reflect a convergence of inputs carrying information about linear translation/acceleration along the interaural axis and angular velocity in the roll plane, which may be of the same or opposite polarity (sign).

The spatial relationship between OVAR-estimated linear acceleration response orientation and azimuth of angular velocity responses differed markedly for the units with OVAR response orientations near occiput down. The relationships between the orientations of these components was unimodal (Rayleigh R statistic = 7.45, P < 0.05) and was distributed as single wrapped normal distribution with an angular difference of –89.1° ± 45.1° (SD). Hence, these units’ responses appear to reflect a convergence of linear translation/acceleration information along the naso-occipital axis and an orthogonal angular velocity component in the roll plane.

The spatial relationship (angular difference) between orientations of angular velocity responses and OVAR-estimated linear acceleration response orientations for units with OVAR response orientations near contralateral anterior semicircular canal down did not show a single preferred relative orientation (Rayleigh tests, not significant). Rather, the relationships were consistent with a mixture of two wrapped normal distributions, one component (78% of observations) with a mean difference of –148.5° ± 76.5° (SD) and a second component (22% of observations) with a mean difference of 56.7° ± 34.6°, indicating that OVAR modulation and angular velocity responses of different groups of neurons are aligned approximately 30° from opposite polarity and 30° from the orthogonal, respectively. These relationships did not depend on the elevation component of the angular velocity response. The orientations of vertical planes for angular velocity responses (azimuths) of these units had an axial distribution (Rayleigh test of doubled angles, R statistic = 9.32, P < 0.01) near the ipsilateral anterior semicircular canal-contralateral posterior semicircular canal plane (axis between –43.6° and 134.4° re: nose down zero). This distribution of angular velocity response orientations was consistent with a mixture of two wrapped normal components, one component (37% of observations) with a mean difference of –17.9° ± 12.3° (SD) and a second component (63% of observations) with a mean difference of 162.1° ± 47.4°, which lie between the pitch plane and ipsilateral anterior semicircular canal-contralateral posterior semicircular canal plane. Thus, the responses of units with OVAR-based orientation estimates near contralateral anterior semicircular canal down appear to reflect a convergence of linear acceleration signals in the direction of the contralateral anterior semicircular canal plane with signals reflecting angular velocity between the pitch plane and the ipsilateral anterior semicircular canal plane.

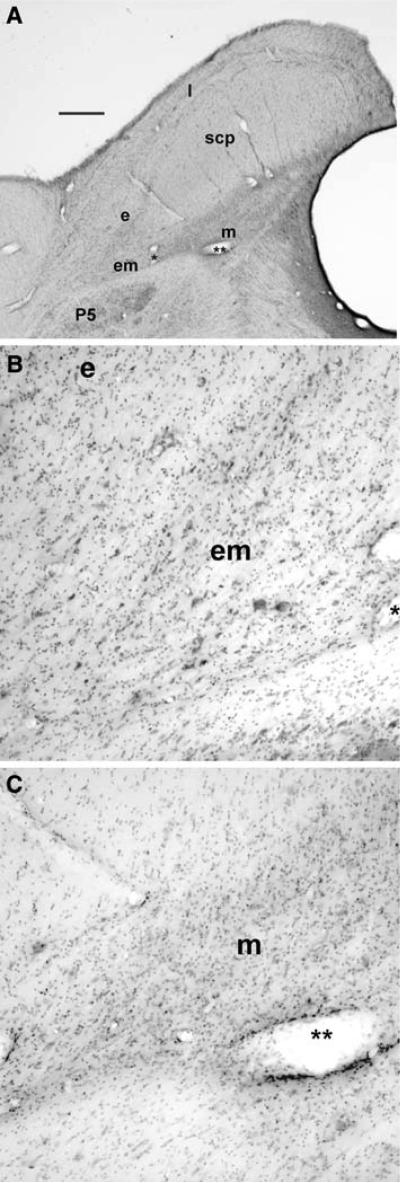
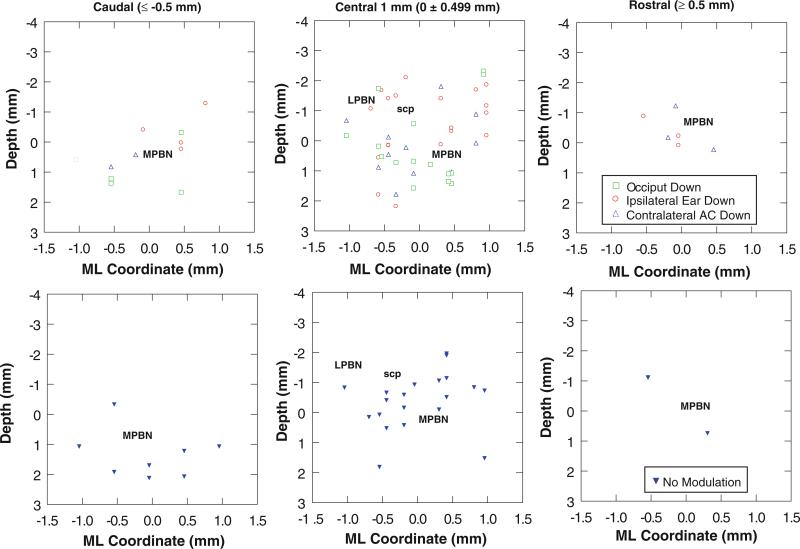
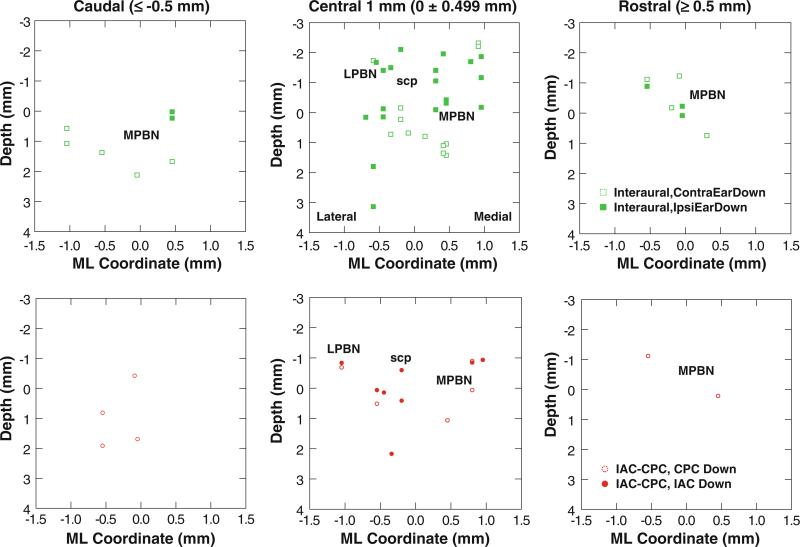
The area of PBN containing the responsive units is shown in photomicrographs (Fig. 6a). The region sampled by the electrode tracks included the cytoarchitectonically distinct lateral (l), external (e), external medial (em), and medial (m) subnuclei (Fig. 6b, c). The distribution of units with spatially tuned OVAR modulation responses is shown in Fig. 7. The differential distribution of the indicated response types is seen most clearly in the central 1 mm of the region responsive to OVAR and tilt stimuli. Units that lacked modulation responses tended to be located in the lateral PBN and the superficial (dorsal to dorsolateral) aspect of the medial PBN. One cluster of units responsive in the ipsilateral ear down orientation was located superficially in the lateral PBN and the dorsal third to half of the medial PBN. Units with OVAR-derived response orientation estimates near the contralateral ear down direction tended to be located deeper in the medial PBN, while the units with orientations near the occiput down direction tended to be located between these latter populations.

Fig. 6.

a A low magnification photomicrograph of a transverse section through PBN of a macaque. The PBN surrounds the superior cerebellar peduncle (scp): medial (m), external medial (em), external (e), and lateral (l) subnuclei of the PBN are labeled. Note the clear demarcation between the borders of the PBN and the principal sensory trigeminal nucleus (P5). b A higher magnification view of the external medial (em) and external subnuclei; the same blood vessel is marked by a single asterisk in a and b. c A higher magnification view of the medial parabrachial subnucleus (m); the two asterisks mark the same blood vessel in a and c. Calibration bar 1 mm in a; 200 μm in b and c

Fig. 7.

The distribution of PBN units is charted as a function of OVAR modulation response orientation for the caudal PBN (more than 0.5 mm caudal to the center of the responsive region), central 1 mm of PBN, and rostral PBN (more than 0.5 mm rostral to the center of the responsive region). The location of the medial region of the PBN (MPBN medial and external medial subnuclei), lateral region of the PBN (LPBN external and lateral subnuclei), and the superior cerebellar peduncle (scp) are indicated. The upper row illustrates the distribution of units with a significant OVAR modulation response. The lower row shows the distribution of units with no significant OVAR modulation

Phase of OVAR modulation responses

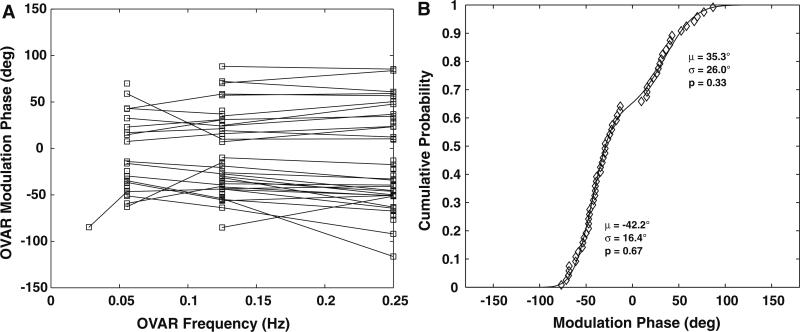
The response phase of the units with one dimensional OVAR modulation behavior was nearly invariant across the tested frequencies (Fig. 8a). The phases of these units tended to be clustered in two groups: one at approximately a 40° phase lead and the other at approximately a 40° phase lag. For units having OVAR-estimated linear acceleration responses with ipsilateral ear down or contralateral anterior semicircular canal down orientations, there were two clear populations (Fig. 8b): one with a phase lag of 42.2° ± 16.4° (SD) and the other with a phase lead of 35.3° ± 26° (SD).

Fig. 8.

The phase of OVAR modulation response of PBN units is plotted as a function of frequency of revolution in a. Individual units showed either a phase-leading or phase-lagging pattern that did not change across the frequencies tested. b The empirical cumulative distribution function of the mean phase responses of these units. The line shows a model fit for a mixture of two wrapped normal distributions with respective means (μ), standard deviations (σ), and proportions of observations (p), confirming the consistency of the data with two different response phase populations

Dynamic linear acceleration sensitivity: integrated analysis of OVAR and position trapezoid responses to linear acceleration

Spatial relationship between OVAR modulation and static tilt responses

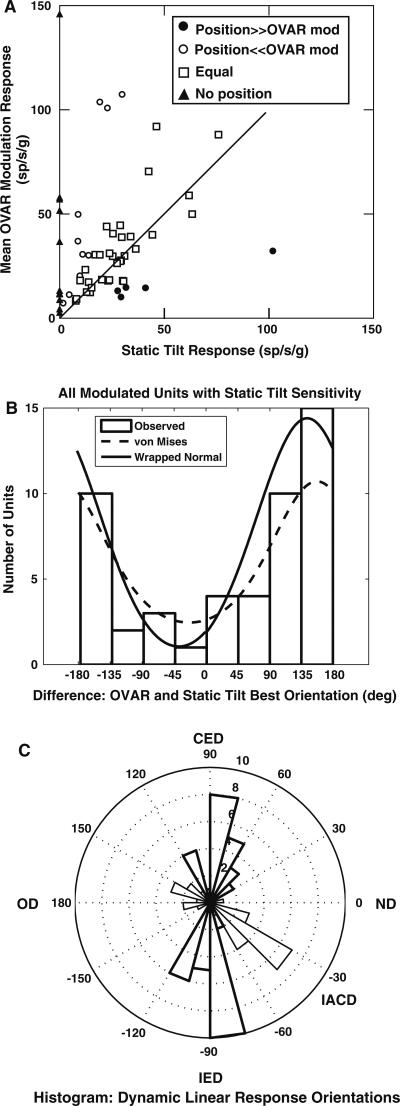
The modulation component of the constant velocity OVAR response is hypothesized to represent the net sum of dynamic and static linear acceleration responses. The relationship between each unit's OVAR response gain and the static tilt response is shown in Fig. 9a. The majority of the units (33/62) had approximately equal OVAR modulation and static tilt response gains, defined by a ratio of OVAR response gain to static tilt response of 0.5–2.0 (Wilson et al. 1986; Kasper et al. 1988). A smaller proportion (10/62) had greater OVAR modulation response gains (ratio greater than 2), while 5/62 units had greater static tilt response gains (ratio less than 0.5). In addition, 14/62 OVAR-modulated units had no static tilt sensitivity during position trapezoid stimulation. These data imply that PBN neurons receive different combinations of static and dynamic linear acceleration information.

Fig. 9.

Relationships between the gains and orientations of the OVAR modulation responses and the static tilt response estimates (from position trapezoid stimuli) for PBN units. a A scatter plot of the response gains of single units, estimated from OVAR and position trapezoids. Note that the majority of units have nearly equal gains under the two stimulus conditions. b A histogram of the difference between the best mean orientations of the OVAR responses and the orientations of the static tilt responses. The distribution indicates that the response orientations in dynamic (OVAR) and static (position trapezoid) testing conditions are of opposite polarity but along a single axis. c A polar histogram of the distribution of the best dynamic linear response orientations. The thick sectors indicate the interaural axis units, while the thin sectors indicate units with peak response orientations in the ipsilateral anterior-contralateral posterior semicircular canal plane

The static tilt responses of OVAR-modulated units tended to have orientations that were coplanar but opposite in sign compared to their OVAR-estimated response orientation. For all 49/62 modulated units with both significant static tilt responses and one-dimensional OVAR modulation responses, the angle between the orientations of static tilt and OVAR modulation responses was consistent with a single wrapped normal distribution, with a mean orientation difference of 142.5° ± 70.4° (SD). Alternatively, the angular differences are consistent with a von Mises distribution with location parameter (μ) of 156.2° and dispersion parameter (κ) of 42.2° (Fig. 9b). For the units with OVAR modulation response orientations near ipsilateral ear down, the angle between the orientation estimates from static tilt responses and OVAR modulation responses was 177.5° ± 75° (wrapped normal; von Mises: –178.2° ± 41.7°). For units with OVAR-based estimated response orientations near contralateral anterior semicircular canal down tilt, the angle between static tilt and OVAR modulation response orientations was 127.1° ± 43.1° (wrapped normal; von Mises: 139.2° ± 47.8°). For the units with OVAR-based estimated orientation near occiput down, the angle between static tilt and OVAR modulation response orientations was 166.1° ± 120.6° (wrapped normal; von Mises: 152.4° ± 15.8°). The angles for the ipsilateral ear down and contralateral anterior semicircular canal down units differ significantly (R statistic = 8.79, P < 0.05), further suggesting that they are distinct classes of units. However, the common features of the units suggest that the linear acceleration sensitivity of PBN neurons reflects a sum of approximately oppositely directed static and dynamic linear acceleration signals.

Defining dynamic linear acceleration response components

Because the modulation responses during OVAR of 62/65 modulated units were consistent with a one-dimensional accelerometer (Fig. 9a) and they behave as a sum of oppositely directed static and dynamic components (Fig. 9b), one can estimate the magnitude of the dynamic linear acceleration component as the vector difference between the OVAR modulation response and the static tilt response component during position trapezoid stimulation. Based on this approach, the 22 units with static tilt responses during position trapezoid stimulation but no OVAR modulation responses are regarded as having a dynamic linear acceleration response during OVAR of equal magnitude but opposite polarity to the static tilt response observed during position trapezoid stimulation. The distribution of the doubled best orientations of these estimates of dynamic linear sensitivity was bimodal, indicating that there are two axial distributions of angles (Mardia and Jupp 2000) in the sample. Fuzzy cluster c-means analysis (Bezdek 1981) of the unit vectors representing doubled orientation angles was used as a distribution-free (no assumptions about the statistical distribution of the data) method to identify two distinct response populations (Fig. 9c): (1) neurons with best linear acceleration axis orientations near the interaural axis (mean axis extends between –97.9° and 82.1° re: nose down) and (2) neurons with linear acceleration axis orientations near the ipsilateral anterior semicircular canal-contralateral posterior semicircular canal plane (mean axis extends between –34.7° and 148.3° re: nose down).

The spatial distribution of these units within PBN is shown in Fig. 10. Within the medial PBN region (medial and external medial subnuclei), the interaural response axis units tended to be medial and superficial to the units with best linear acceleration responses along the ipsilateral anterior semicircular canal-contralateral posterior canal axis. For the few units in the lateral PBN, the two units displaying ipsilateral anterior semicircular canal-contralateral posterior canal axis linear acceleration responses were lateral to the five units that displayed linear acceleration responses along the interaural axis.

Fig. 10.

The distribution of PBN units is charted as a function of the dynamic linear response orientation (OVAR modulation response minus static tilt response component during position trapezoid testing). Separate panels represent the caudal PBN (more than 0.5 mm caudal to the center of the responsive region), central 1 mm of PBN, and rostral PBN (more than 0.5 mm rostral to the center of the responsive region). The location of the medial aspect of the PBN (MPBN medial and external medial subnuclei), lateral aspect of the PBN (LPBN external and lateral subnuclei), and the superior cerebellar peduncle (scp) are indicated. The upper row illustrates the distribution of units with estimated dynamic linear acceleration sensitivity oriented along the interaural axis, with response polarity in either the ipsilateral ear down or contralateral ear down orientation. The lower row shows the distribution of units with estimated dynamic linear responses aligned with the ipsilateral anterior semicircular canal-contralateral posterior semicircular canal (IAC-CPC) axis, with response polarity in either the IAC down or the CPC down orientation

Spatial relationship between angular velocity and dynamic linear acceleration responses

The azimuths of the planes of the best angular velocity responses showed a distribution that was similar in character to the distribution of the orientations of linear acceleration responses. The distribution of the doubled angles was bimodal and was consistent with two response groups: (1) neurons with best angular velocity responses in a plane between pitch and the ipsilateral anterior semicircular canal-contralateral posterior semicircular canal planes (azimuths centered around an axis extending between –20.8° and 159.2° re: nose down) and (2) neurons with best angular velocity responses that have azimuths centered approximately around the roll plane (azimuths centered around an axis extending between –107.8° and 72.2° re: nose down). Only about 20% of the angular velocity responses showed a contralateral ear down polarity.

The angular velocity responses were expressed in coordinates rotated relative to the dynamic linear acceleration axis (represented in Cartesian coordinates as unit vectors) to explore the spatial relationships between angular velocity and linear acceleration responses. Two different analytical approaches yielded similar results. First, fuzzy cluster c-means analysis (Bezdek 1981) revealed three spatial relationships: (1) the azimuth of the angular velocity response was aligned with the dynamic linear acceleration responsiveness along a single axis (29.6% of units, mean difference of 12.2° ± 27.6°); (2) the azimuth of the angular velocity response was orthogonal to the unit's dynamic linear acceleration axis (35.2% of units, mean difference of –81.9° ± 30.3°); and (3) the azimuth of the angular velocity response was oriented 145.3° ± 39.6° from the unit's dynamic linear acceleration response axis (35.2% of units, components of approximately opposite polarity). Second, a least-squares approach based upon order statistics (see “Methods”) also modeled the cumulative distribution function as a sum of wrapped normal populations with orientations (mean ± standard deviation) of 5.2° ± 9.2°, –63.2° ± 4.3°, and 162.7° ± 103.0° relative to the dynamic linear acceleration axis. Hence, these groups of units have angular velocity responses that are either aligned with the axis of peak linear acceleration sensitivity or are most sensitive to rotations around an axis defined by the orientation of the linear acceleration sensitivity. The units with aligned angular velocity and linear acceleration sensitivity responses are potentially useful for distinguishing a tilt from a linear translation of the head in space. The units with an orthogonal relationship between the azimuth of the peak angular velocity response and the linear acceleration response axis are likely to facilitate the detection of angular deviations from linear motion trajectories during locomotion (as a rotation around the linear acceleration response axis), such as one may occur during a loss of balance.

Discussion

This study shows that PBN contains distinct groups of neurons that respond to linear accelerations imposed on the whole body. The responses of PBN units to OVAR are consistent with the behavior of a one-dimensional linear accelerometer. The magnitude and peak response direction components of the OVAR modulation responses of each unit are flat for frequencies over the range of 0.06–0.3 Hz and response magnitudes are equal for ipsilaterally and contralaterally directed rotations. Hence, bidirectional responses to OVAR provide an estimate of the orientation, gain, and phase of unit responses to linear acceleration. The orientation, gain, and phase of linear acceleration responses during OVAR are in most cases invariant across the revolution frequency range of 0.06–0.3 Hz.

There were also alterations in baseline discharges during constant velocity OVAR. One group of neurons showed augmented discharges during ipsilateral rotation and reduced or unchanged discharges during contralateral rotation. A second group of fewer units showed the opposite pattern: augmented discharges during contralateral rotation and reduced or unchanged discharges during ipsilateral rotation. A third group of units had discharges that increased equally during rotation in either direction. As has been reported for some vestibular nucleus neurons (Reisine and Raphan 1992), these response patterns were independent of response gain and orientation. The information conveyed by this response component is unclear.

Organization of linear acceleration and angular rotation response components

A more detailed analysis suggests that the linear acceleration responses of PBN neurons appear to represent a convergence of two components oriented along a single axis but with different response properties and polarities. The linear acceleration response parameters (estimated from OVAR) and the static tilt responses (estimated from the position trapezoids) tend to be of opposite polarity, suggesting that the total response of such units is a sum of oppositely directed static and dynamic linear acceleration components. This type of dynamic interaction in processing linear acceleration signals is not unprecedented. Schor et al. (1985) noted that a sum of an excitatory response and a high pass filtered (i.e., dynamic) inhibitory component accounted for responses of a major class of vestibular nucleus unit responses in canal-plugged cats. Their sample of units from the vestibular nuclei showed best responses for linear acceleration in the interaural to vertical canal plane azimuth orientations. In this regard, it is of interest to note that the linear acceleration responses of PBN neurons are organized around two similar axes with respect to the head: (1) the interaural axis and (2) an axis near the ipsilateral anterior semicircular canal-contralateral posterior semicircular canal plane.

The representation of the linear acceleration responses of the units as a sum of oppositely directed dynamic and static linear acceleration responses provides an explanation for two aspects of the behavior of the units. First, it is a direct description of the observed data from units with a given OVAR modulation response orientation and an oppositely directed static tilt response orientation. Second, it provides an explanation for the behavior of 15 units with an OVAR modulation response but no measurable static tilt response from position trapezoid testing. Finally, the behavior of 19 units with a static tilt response to position trapezoids but no OVAR modulation response can be explained as a destructive sum of oppositely directed static and dynamic linear acceleration signals over the small frequency range of stimulation. The opposite orientation of linear acceleration sensitivity with rapid and slow dynamics may be useful for detecting rapid transient linear head translational movements (e.g., a sudden deceleration during locomotion).

Different populations of PBN units can further be defined functionally on the basis of the orientation of angular rotation sensitivity relative to the linear acceleration axis. Two populations of PBN units are sensitive to angular rotation in a head-referenced vertical plane (i.e., sum of anterior and posterior semicircular canal signals) containing the linear acceleration sensitivity axis, which correspond to a sensors of pitch stability relative to the linear acceleration axis. Approximately, one-third of the units were excited by head down angular velocity in the same orientation as dynamic linear acceleration peak, such as one would encounter with a dynamic downward head rotation in the direction of the dynamic linear acceleration signal (e.g., while falling). Approximately another one-third of the units were excited by head down angular rotational velocity opposite to the direction of best dynamic linear acceleration sensitivity, such as one would encounter from backward inertial head rotation relative to dynamic linear acceleration (e.g., during translational movement). Finally, another one-third of the units were excited by head down angular rotational velocity around the axis of best dynamic linear acceleration sensitivity, which corresponds to a dynamic roll signal relative to the linear accelerometer axis. These responses would signal an accelerating spiralling or spinning trajectory, which would be an obvious indication of a loss of balance (or inertial guidance control relative to gravity) when the head is in closely regulated orientation (re: gravity) during locomotion and airborne leaps (Dunbar and Badam 1998; Dunbar et al. 2004).

The response properties of PBN units are strongly reminiscent of single axis sensor components of a head-referenced, strapdown inertial guidance system (Schroer 1984). Because the head rotates relative to the torso during activities, the head-referenced PBN unit responses during locomotion will depend upon the instantaneous head orientation relative to the body trajectory in space.

During normal activities, multiple postural control mechanisms, including vestibulospinal and vestibulocollic pathways (e.g., motor-related outputs of the vestibular nuclei), maintain head orientations (and movement velocities) during within a relatively limited range with respect to upright stance. These mechanisms stabilize the mean head position in macaques (Dunbar and Badam 1998; Dunbar et al. 2004) and humans (Grossman et al. 1988; Mulavara et al. 2002; Pozzo et al. 1990, 1995), such that the utricular macula and the horizontal semicircular canals are near an earth horizontal orientation, even during locomotion. Horizontal head rotations have been reported to be ±6° (re: torso) for humans walking and running in place under laboratory conditions (Grossman et al. 1988), with an amplitude range of ±50° during vigorous head shakes while standing. The velocity range of these head movements (Dunbar et al. 2004; Grossman et al. 1988) is also constrained and remains well within the range for linear performance of vestibuloocular reflexes. Humans and monkeys also perform voluntary horizontal head–eye gaze shifts during locomotion to look at objects of interest.

The head-referenced orientation of linear acceleration sensitivity of PBN units can be conceptualized as a design feature to provide inertial guidance information throughout the normal range of motion of the head during relative to locomotion or static postural control. Because both the linear and angular motion responses of PBN units have cosine spatial tuning, the populations of units in each PBN will have appreciable sensitivity (gain of at least 0.7 re: peak sensitivity) for inertial sensing across a range of head-on-torso orientations from nose forward to the full horizontal rotation range of approximately 85° (Mayer et al. 1993). This information is potentially available, via the strictly ipsilateral projections of PBN, to structures such as the central amygdaloid nucleus and several thalamic and hypothalamic nuclei (Bernard et al. 1993; Pritchard et al. 2000). The bilateral projections to some thalamic and hypothalamic nuclei, nucleus accumbens, substantia nigra and ventral tegmental area also raise the possibility that combinations of these signals could be used to enhance sensitivity along the naso-occipital axis. The PBN projections to the vestibular nuclei, medulla, and spinal cord could also be a mediator of vestibular contributions to sympathetic autonomic responses within the context of postural shifts.

Comparison with vestibular nucleus unit responses

The ‘vestibular-only’ units in the vestibular nuclei are the most comparable cell class for PBN units because (1) the vestibular nuclei project bilaterally to the location of units in caudal PBN (Balaban et al. 2002), (2) neither unit population displays eye movement-related activity, and (3) vestibular nucleus vestibular-only units and PBN units both can display linear acceleration and angular rotation sensitivity (Angelaki and Dickman 2000; Dickman and Angelaki 2002; Musallam and Tomlinson 2002; Reisine and Raphan 1992; Zhou et al. 2006). The orientations of the best linear acceleration response vectors of caudal PBN units were much similar to the reported orientations for vestibular-only units in the vestibular nuclei (Angelaki and Dickman 2000; Dickman and Angelaki 2002; Zhou et al. 2006). In particular, there are relatively few units with a best linear acceleration response orientation within 30° of the naso-occipital axis. Although all PBN units showed evidence of both canal- and otolith-related sensitivity, only half of vestibular-only units were reported to have both angular and linear motion sensitivities (Dickman and Angelaki 2002). The relationship between the best orientations of linear acceleration and angular rotation responses of the latter vestibular-only units (Dickman and Angelaki 2002) and PBN units appears to be quite similar. However, the linear acceleration response dynamics of caudal PBN units appear to differ markedly from discharges that have been reported for vestibular-only units in the vestibular nuclei. Although vestibular-only units could show high pass, low pass (high and low sensitivity), and flat linear acceleration frequency response characteristics (Dickman and Angelaki 2002), the OVAR frequency characteristics of PBN showed flat gains (0.06–0.3 Hz range) and phase characteristics that differed markedly from the vestibular nucleus units. These differences in response dynamics with vestibular nucleus units contrast with reports regarding the marked similarity between patterns of gustatory (Nishijo and Norgren 1997; Norgren and Pfaffmann 1975; Shimura et al. 1997), cardiovascular (Jhamandas et al. 1991) and nociceptive (Bernard and Besson 1990; Bester et al. 2000) evoked responses of units in other PBN regions to responses in the solitary nucleus or dorsal horn, respectively.

Functional considerations

The primary finding of this study is that the basic organization of whole body motion responses of caudal PBN units is equivalent to components of a head-referenced (strapdown) inertial sensor system. The PBN unit responses are organized as a one-dimensional linear accelerometer with angular velocity sensitivity for vertical semicircular canal-referenced rotations either in the plane of the peak linear acceleration axis or around the peak linear acceleration axis. The best linear acceleration axis orientations for different groups of these PBN unit responses are either near the interaural axis or near the ipsilateral anterior semicircular canal-contralateral posterior semicircular canal plane (i.e., a head-based coordinate frame). The head-based reference for these units is stabilized normally by robust vestibular reflexes and postural control systems that control instantaneous stance relative to gravity. For example, the mean head position is stabilized in macaques to align the horizontal semicircular canals near earth horizontal, even during locomotion, while head pitch velocity remains below saturation values for vestibulo-ocular reflexes (Dunbar and Badam 1998; Dunbar et al. 2004). In this context, the response properties of PBN units are appropriate for a sensory signal to detect anomalies in head stability control during daily activities, most commonly as a consequence of loss of body postural control relative to gravity. For example, head-based inertial guidance information from PBN units could may be particularly important to detect gyration during the airborne phase of leaps, when macaques hold their heads in a particularly rigid posture, possibly as a strategy to minimize the initiation of “unwanted and dangerous whole-body rotations” (Dunbar and Badam 1998). Human head control has similar characteristics (Mulavara et al. 2002; Pozzo et al. 1990, 1995). It is suggested, therefore, that PBN units may assist in detecting potentially dangerous departures from normal stabilized movement trajectories. As a sensory signal, this type of inertial guidance monitoring may provide interoceptive drive to ascending pathways from PBN, via projections to the thalamus, central amygdaloid nucleus, and insula. On the other hand, the ability to use vestibular information to discriminate signals reflecting whole body trajectory changes may also contribute to control of either postural control or adaptive cardiovascular (e.g., vestibulo-sympathetic) responses through descending PBN connections to the vestibular nuclei, medulla, and spinal cord.

These specific and spatially organized vestibular responses are of interest in light of the suggested role of the caudal aspect of PBN in central interoceptive pathways that include pain processing and influence emotional expression. Studies of spinal cord lamina 1 nociceptors resulted in the intriguing suggestion that nociceptive pathways though PBN mediates the autonomic, affective, emotional aspects of pain (Bernard et al. 1996; Craig 2002; Gauriau and Bernard 2002). Craig's (2002) opinion piece in Nature Reviews Neuroscience proposed that interoception (the determination of how we feel about our internal state) is mediated by a thalamic-level integration in the ventromedial thalamic nucleus of (1) lamina 1 spinothalamic afferents, (2) fine autonomic/sympathetic sensory afferent information from the nucleus of the solitary tract, and (3) a PBN integration of those spinothalamic and autonomic afferent channels. The pain component was proposed to be a homeostatic emotion (Craig 2003). These concepts were remarkably parallel to our contemporaneous published views on the convergence of interoceptive, somatic, vestibular information in the parabrachial pathway and its role in determinations of interoceptive well-being (Balaban 1999; Balaban and Thayer 2001). The linear acceleration and angular velocity responses of PBN neurons, then, may provide a portal for whole body motion relative to a gravitational-based inertial frame to influence affect, emotion, and perceived well-being in the same manner as nociceptive signals through more rostral regions of PBN. It is suggested that these signals may contribute to the range of affective and emotional responses that include panic associated with falling, malaise associated with motion sickness and mal-de-debarquement, and comorbid balance and anxiety disorders.