Electromechanical properties of tetragonal Pb(In_1∕2Nb_1∕2)O₃−Pb(Mg_1∕3Nb_2∕3)O₃−PbTiO₃ ferroelectric crystals

Abstract

The ferroelectric, dielectric, elastic, piezoelectric, and electromechanical properties of tetragonal Pb(In_1∕2Nb_1∕2)O₃−Pb(Mg_1∕3Nb_2∕3)O₃−PbTiO₃ (PIN–PMN–PT) crystals were investigated. The single domain piezoelectric coefficients d₃₃, d₁₅, and d₃₁ were found to be 530, 2350, and −200 pC∕N, respectively, with electromechanical coupling factors k₃₃, k₁₅, and k₃₁ being on the order of 0.84, 0.85, and 0.58. The mechanical quality factor Q for longitudinal mode was found to be >700, with high coercive field (E_c) being on the order of 10 kV∕cm. The temperature and dc bias electric-field characteristics of single domain tetragonal PIN–PMN–PT crystals were also investigated. In contrast to [001] oriented domain engineered rhombohedral crystals, tetragonal PIN–PMN–PT crystals exhibited broader temperature usage range and higher thermal∕electric field stability, with improved coercive field and mechanical quality factor.

INTRODUCTION

Relaxor based ferroelectric single crystals, such as Pb(Zn_1∕3Nb_2∕3)O₃−PbTiO₃ (PZN–PT) and Pb(Mg_1∕3Nb_2∕3)O₃−PbTiO₃ (PMN–PT), have attracted attentions due to their high piezoelectric response and electromechanical coupling factors.^{1, 2, 3, 4, 5} To date, investigations have been focused on relaxor based crystals with the [001] oriented rhombohedral phase, where through the domain engineering, ultrahigh piezoelectric coefficients (d₃₃>2000 pC∕N) and coupling factors (k₃₃>0.9) can be achieved, making these crystals promising candidates for ultrasonic transducers, actuators, and other various electromechanical devices. However, a drawback of these crystal systems is their relative low temperature usage range, limited by their low Curie temperature, further limited by the ferroelectric–ferroelectric phase transition temperature T_R-T, being on the order of 60∼95 °C, a consequence of a strongly curved morphotropic phase boundary (MPB).⁶

To broader the temperature usage range of relaxor-PT based crystals, two approaches have been adopted. One approach has been to identify new compositional systems which exhibit high Curie and ferroelectric–ferroelectric phase transition temperatures. Over the last few years, crystals in the binary systems Pb(Sc_0.5Nb_0.5)O₃−PbTiO₃,⁷ Pb(In_0.5Nb_0.5)O₃−PbTiO₃,^{8, 9} Pb(Yb_0.5Nb_0.5)O₃−PbTiO₃,¹⁰ and ternary system Pb(In_1∕2Nb_1∕2)O₃−Pb(Mg_1∕3Nb_2∕3)O₃−PbTiO₃ (PIN–PMN–PT) (Refs. ^{11, 12, 13}) have been grown and studied. Based on reported results, crystals in the PIN–PMN–PT ternary system, which can be readily grown by the Bridgman method, exhibit T_R-T∼130 °C, broadening the temperature usage range about 30 °C higher than that of commercial PMN–PT crystals.^{13, 14, 15} A second approach has been to utilize tetragonal crystals, in which no ferroelectric–ferroelectric phase transition occurs prior to the Curie temperature, thus expanding the usage temperature range to its Curie temperature.^{16, 17}

In this work, both approaches were proposed with tetragonal crystals in the ternary PIN–PMN–PT system, with a T_c>200 °C and no ferroelectric–ferroelectric phase transition between room temperature and Curie temperature. It is important to note that the single domain crystals were readily achieved in PIN–PMN–PT crystals, whereas it is hard to obtain in relatively low T_c crystals, including BaTiO₃, PZN–PT, and PMN–PT.

The full data set of properties, including dielectric, piezoelectric, elastic, and coupling factors of single domain tetragonal PIN–PMN–PT crystals were determined. The high field properties, including polarization versus electric field (P–E) and strain versus electric field (S–E) behaviors were studied. Finally, the temperature dependence of coupling factor k₃₃ at various dc bias electric fields were also investigated for [001] poled tetragonal PIN–PMN–PT samples.

EXPERIMENTAL

PIN–PMN–PT single crystals with nominal composition of xPIN−(1−x−y)PMN−yPT, where x>0.25–0.35 and y>0.30–0.34, were grown using the modified Bridgman technique.¹³ Analogous to binary PMNT crystals, the composition along the growth directions varies due to the large segregation of Ti. Hence, the crystal structure and phase changed along the growth direction. As shown in Fig. 1, approximately 60% of the as-grown crystal boule was in rhombohedral phase,¹³ with 25% of the boule located on the top being tetragonal. According to the segregation coefficients of Ti⁴⁺, Mg²⁺, and In³⁺, the PT content of the investigated tetragonal part was found to be on the order of 38%∼42%. The crystal portion in part I was small in size and with large piezoelectric∕dielectric variations, owing to the proximity to the mixed-phase region of the boule. The crystal portion in part III, with the lowest electromechanical properties, was prone to cracking during the poling process due to the relatively larger c∕a lattice ratio (∼1.016). The general properties of the tetragonal portion of the PIN–PMN–PT crystal boule are given in Table 1, where parts I, II, and III correspond to the portions depicted in the inset shown in Fig. 1. As expected, the dielectric and piezoelectric properties were found to decrease with PT content increasing, while the coercive field and tetragonality (c∕a ratio) were found to increase, showing a similar trend as observed in PMN–PT system.¹⁸ Therefore, crystal portion in part II was selected for investigation in this paper.

Figure 1.

Schematic diagram of the as-grown crystal.

Table 1.

Properties of [001] poled PIN–PMN–PT crystals, where parts I, II, and III correspond to the crystals in the inset of Fig. 1.

Material	PT content (%)	c∕a	Tc (°C)	TR-T (°C)	Ec (kV∕cm)	Pr (C∕m2)	${\epsilon }_{33}^T∕{\epsilon }_0$	d33 (pC∕N)	k33
Part I	38	1.009	210	−10–0	7	0.45	1800	1000	0.88
Part II	39–41	1.011	215–220	−50–(−30)	10	0.43	1100	500–600	0.84
Part III	42	1.016	220–225	−70–(−60)	12	0.42	800	350–400	0.83

The tetragonal crystals were oriented by real-time Laue x-ray and cut to obtain longitudinal rods (33-rod, for k₃₃), transverse bars [k₃₁ and k₃₁(45°)], shear-mode plates (k₁₅) and thickness-mode plates (k_t), with the aspect ratio following IEEE standard.¹⁹ Vacuum sputtered gold was applied to the polished surface as the electrodes for all the samples. The [001] oriented samples were poled by applying a 10 kV∕cm dc electric field at 120 °C, and field cooled down to room temperature, to avoid cracking. The stability of single domain state was checked using the S–E loop. For [001] poled tetragonal PIN–PMN–PT crystals, the S–E loop will be linear and hysteresis-free if the single domain state is stable, however, the S–E loop will exhibit nonlinear and hysteretic behavior for unstable single domain state, since the domain switching (domain wall motion) is an irreversible and nonlinear process with respect to applied electric field. The resonance and antiresonance frequencies for different vibration modes were determined using an HP4194A impedance analyzer. From the five different sample geometries, 11 independent electroelastic constants, including six elastic, three piezoelectric, and two dielectric constants could be determined.^{19, 20} High field polarization and strain behavior were determined using a modified Sawyer–Tower circuit and linear variable differential transducer driven by a lock-in amplifier (Stanford research system, model SR830). The temperature dependence of the dielectric permittivity was determined using an LCR meter (HP4284A) being connected to a computer controlled temperature chamber. The temperature dependent electromechanical properties were obtained from an impedance analyzer (HP4194A) connected to a temperature chamber. The dc bias field dependence of the electromechanical coupling factor k₃₃ was measured by the same impedance analyzer, meanwhile a high voltage source (Trek 609C-6) was used to apply dc bias on the samples, where a protective blocking circuit was placed between the voltage source and impedance analyzer.

RESULTS AND DISCUSSION

Temperature dependence of dielectric properties for [001] poled tetragonal PIN–PMN–PT crystals

Figure 2 shows the dielectric behavior as a function of temperature for [001] poled tetragonal PIN–PMN–PT crystal (part II, shown in Fig. 1), from which the Curie temperature T_c was found to occur at 220 °C, with no ferroelectric phase transition observed prior to T_c and above room temperature. The room temperature dielectric permittivity and dielectric loss were found to be 1090 and 0.4% at 1 kHz, respectively. Of particular significance was the flat dielectric behavior over the temperature range from 0 to 150 °C, with dielectric temperature coefficient being only <0.1%∕°C, significantly lower when compared to the [001] domain engineered rhombohedral PIN–PMN–PT crystals [∼7%∕°C in the temperature range of 25–125 °C∕T_R-T]. Interestingly, a dielectric anomaly was observed at −30–(−50) °C, far below room temperature, corresponding to the tetragonal to monoclinic∕rhombohedral phase transition temperature, the result of the curvature of MPB.

Figure 2.

Temperature dependence of dielectric permittivity (solid line) and dielectric loss (dotted line) for tetragonal PIN–PMN–PT single crystals.

Low field properties of [001] poled tetragonal PIN–PMN–PT crystals

The complete set of dielectric, piezoelectric, and elastic constants for [001] poled tetragonal PIN–PMN–PT crystals is summarized in Table 2, including the data of [001] poled PZN–12PT (Ref. ²¹) and PMN–42PT (Ref. ¹⁶) crystals for comparison. As will be discussed in Sec. 3C, single domain state in tetragonal PZN–12PT and PMN–42PT crystals is not stable, whereas the [001] poled PIN–PMN–PT crystals were found to possess a stable single domain structure. Table 2 represents the properties of single domain tetragonal PIN–PMN–PT crystals. The dielectric permittivities ${\epsilon }_{33}^T$ and ${\epsilon }_{11}^T$ were found to be on the order of 1090 and 15 000 at room temperature, respectively, much higher than those values of [001] poled PMN–42PT and PZN–12PT tetragonal crystals. The piezoelectric coefficient d₃₃ and electromechanical coupling k₃₃ of tetragonal PIN–PMN–PT were found to be 530 pC∕N and 0.84, respectively, larger than those observed for PMN–42PT crystals. A relative high thickness coupling k_t (∼0.61) was observed for tetragonal PIN–PMN–PT when compared to [001] poled domain engineered rhombohedral PIN–PMN–PT (k_t∼0.56) (Ref. ¹³) crystals. Of particular interest of this work was the high shear mode piezoelectric response of tetragonal PIN–PMN–PT, where the piezoelectric coefficient d₁₅ was found to be on the order of 2350 pC∕N, almost double that observed for PMN–42PT and PZN–12PT crystals. The high d₁₅ in tetragonal PIN–PMN–PT crystals is believed to be associated with the high dielectric permittivity ${\epsilon }_{11}^T$ and elastic compliance $s_{44}^E$ of compositions close to the MPB. As discussed by Budimir et al.,^{22, 23} the dielectric permittivity ε₁₁ and shear mode piezoelectric coefficients increase as the composition approaching the MPB in perovskite systems.

Table 2.

Measured and calculated materials properties of tetragonal PIN–PMN–PT crystals poled along [001] direction. The data of PMN–42PT and PZN–12PT crystals were obtained from the Refs. ¹⁶, ²¹ for comparison.

	Dielectric constants					Electromechanical coupling factor
Materials	${\epsilon }_{33}^{\text{T}}$	${\epsilon }_{33}^{\text{S}}$		${\epsilon }_{11}^{\text{T}}$	${\epsilon }_{11}^{\text{S}}$	k31(45°)	k31	k33		k15		kt
PIMNTa	1090	310		15 000	4800	0.58	0.50	0.84		0.85		0.61
PMN–42PTb	660	260		8600	3100		0.39	0.78		0.8		0.62
PZN–12PTc	870	210		12 000a	5100a	0.58	0.52	0.87		0.78a		0.55
Piezoelectric constants
	dij (pC∕N)			eij (C∕m2)			hij (×108 N∕C)			gij (×10−3 m2∕C)
Materials	d31	d33	d15	e31	e33	e15	h31	h33	h15	g31	g33	g15
PIMNTa	−200	530	2350	−4.2	9.5	46.4	−16.5	34.9	10.8	−20.6	55.0	16.4
PMN–42PTb	−91	260	1310	−2.1	12.2	37.5	−9.2	53.2	15.9	−15.6	44.5	13.9
PZN–12PTc	−200	560	1450a	−2.2	8.5	41.3a	−12.0	45.9	9.1a	−26	75.1	13.6a
Elastic constants sij (×10−12 m2∕N)
Materials	${\text{s}}_{11}^{\text{E}}$	${\text{s}}_{12}^{\text{E}}$	${\text{s}}_{13}^{\text{E}}$	${\text{s}}_{33}^{\text{E}}$	${\text{s}}_{44}^{\text{E}}$	${\text{s}}_{66}^{\text{E}}$	${\text{s}}_{11}^{\text{D}}$	${\text{s}}_{12}^{\text{D}}$	${\text{s}}_{13}^{\text{D}}$	${\text{s}}_{33}^{\text{D}}$	${\text{s}}_{44}^{\text{D}}$	${\text{s}}_{66}^{\text{D}}$
PIMNTa	17.1	−3.3	−14.2	41	55.0	25.0	12.3	−7.1	−2.5	12.1	15.1	25.0
PMN–42PTb	9.4	−1.7	−6.2	19.2	35.0	12.5	8.0	−3.1	−2.1	7.6	12.4	12.5
PZN–12PTc	22.4	−3.5	−20.9	58.0	38.1a	27.9	16.3	−9.7	−4.8	14.9	15.4a	27.9
Elastic constants cij (×1010 N∕m2)
Materials	${\text{c}}_{11}^{\text{E}}$	${\text{c}}_{12}^{\text{E}}$	${\text{c}}_{13}^{\text{E}}$	${\text{c}}_{33}^{\text{E}}$	${\text{c}}_{44}^{\text{E}}$	${\text{c}}_{66}^{\text{E}}$	${\text{c}}_{11}^{\text{D}}$	${\text{c}}_{12}^{\text{D}}$	${\text{c}}_{13}^{\text{D}}$	${\text{c}}_{33}^{\text{D}}$	${\text{c}}_{44}^{\text{D}}$	${\text{c}}_{66}^{\text{D}}$
PIMNTa	20.6	15.5	12.5	12.5	1.8	4.5	21.3	16.3	10.9	19.4	6.8	4.5
PMN–42PTb	17.5	8.5	8.3	10.5	2.9	8.0	17.7	8.7	7.2	17.0	8.1	8.0
PZN–12PTc	15.2	11.4	9.7	8.72	2.9a	3.6	15.4	11.6	8.9	12.5	7.3a	3.6

^aPresent work.

^bReference ¹⁶.

^cReference ²¹.

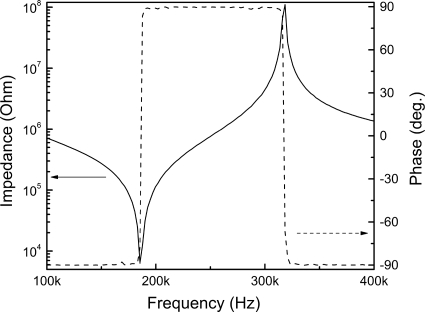
Figure 3 shows the resonance and antiresonance frequency characteristics of impedance and phase for [001] poled PIN–PMN–PT tetragonal crystals in longitudinal mode, from which, the mechanical quality factor Q was calculated and found to be on the order of >700, being significantly higher than that observed for [001] poled domain engineered rhombohedral crystals (∼100), owing to the single domain state where no domain walls exist.²⁴

Figure 3.

Impedance and phase spectrum for [001] poled PIN–PMN–PT tetragonal crystal with k₃₃ mode.

High field properties of [001] oriented tetragonal PIN–PMN–PT crystals

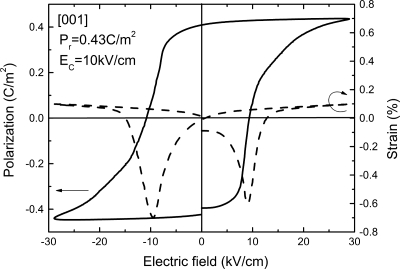
Figure 4 shows the bipolar polarization hysteresis for [001] oriented PIN–PMN–PT crystals. The remnant polarization (P_r) was found to be on the order of 0.43 C∕m², similar to the values observed in PMN–42PT and PZN–12PT crystals. On the other hand, the coercive field (E_c) was found to be on the order of 10 kV∕cm, significantly higher than that of PMN–42PT (∼6 kV∕cm) and PZN–12PT (∼8.5 kV∕cm) crystals, being related to the higher Curie temperature T_c. It was observed from Fig. 4 that the maximum strain at coercive field was about −0.7%, similar to the value as found in PZN–12PT (∼−0.7%) crystals. These high strain variations in tetragonal crystals were mainly the result of 90° domain switching, due to the [001] domains switching to [010] or [100] orientation in order to minimize the strain energy. In [001] oriented rhombohedral crystals, the strain at the coercive field is small, usually lower than −0.1%, which was only contributed by intrinsic piezoelectric response (lattice deformation), since the polarization vectors were equivalent along the [001] direction in the domain engineered configuration. Consequently, non-180° domain switching does not contribute to the strain along the [001] direction.

Figure 4.

Bipolar hysteresis loop and electric-field-induced strain for tetragonal PIN–PMN–PT crystals.

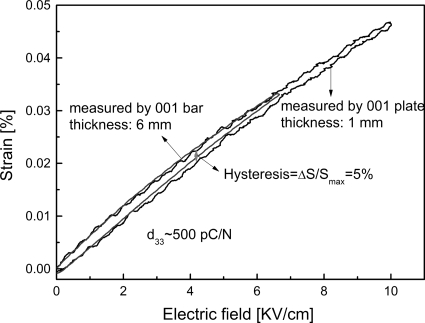
The unipolar strain as a function of electric field (S–E loop) for the [001] poled tetragonal PIN–PMN–PT crystals was measured on samples with different thicknesses, as presented in Fig. 5. It was reported that the S–E loop of tetragonal PZN–PT and PMN–PT crystals exhibited large hysteresis,^{25, 26} indicating that it is hard to obtain a stable single domain state in tetragonal PZN–PT and PMN–PT crystals. However, the S–E hysteresis of [001] poled tetragonal PIN–PMN–PT crystals was found to be less than 5%. The piezoelectric coefficient d₃₃ calculated from the S–E slope was found to be 500 pC∕N, similar to the value obtained from the resonance technique, indicating that extrinsic contributions (domain wall movement) to the piezoelectric response was minimal, again demonstrating a stable single domain state in PIN–PMN–PT crystals).

Figure 5.

Unipolar strain vs electric field for tetragonal PIN–PMN–PT single crystals poled along [001] direction.

Temperature and dc bias field dependent electromechanical coupling factor

To further investigate the domain stability over a wide temperature range for the tetragonal PIN–PMN–PT crystals, the temperature dependence of coupling k₃₃ was determined as a function of dc bias as shown in Fig. 6. The coupling factor k₃₃ showed no dc-bias-field dependence till temperature at 125 °C. At 200 °C, k₃₃ was found to be decreased from 0.84 to 0.81 with increasing dc bias field from zero to 7 kV∕cm. By studying the dc bias field dependence of electromechanical coupling factor in hard and soft lead zirconate titanate (PZT) ceramics,²⁷ it was found that the coupling factor of soft PZT (EC-76) decreased with increasing dc bias field. Therefore, the degradation of k₃₃ in tetragonal PIN–PMN–PT crystals with increasing dc bias fields can be attributed to a “softening” effect at elevated temperatures.

Figure 6.

Temperature and dc bias field dependence of k₃₃ for [001] poled tetragonal PIN–PMN–PT crystals.

In contrast to [001] poled rhombohedral crystals,^{13, 28} the bias field dependent electromechanical coupling k₃₃ of [001] poled tetragonal PIN–PMN–PT crystals was stable, since the dc bias electric field along [001] direction stabilizes the tetragonal phase.

CONCLUSION

Tetragonal crystals in the PIN–PMN–PT ternary system were grown using the modified Bridgman technique. The resulting crystals exhibited high T_c>200 °C, with no ferroelectric–ferroelectric phase transition observed prior to its Curie temperature and above room temperature, together with its near-zero temperature coefficient of dielectric permittivity, offering expanded temperature usage range. The complete set of dielectric, elastic, and piezoelectric coefficients for single domain tetragonal PIN–PMN–PT crystals was determined. The coercive field E_c was found to be on the order of 10 kV∕cm, higher than both rhombohedral PIN–PMN–PT and binary relaxor-PT crystals, due to its higher Curie temperature. High shear mode piezoelectric and electromechanical properties (d₁₅∼2350 pC∕N and k₁₅∼0.85) were observed in tetragonal PIN–PMN–PT crystals, demonstrating potential for shear mode piezoelectric applications. In addition, the electromechanical coupling k₃₃ exhibited a high dc-bias-electric-field stability when compared to its rhombohedral counterpart, demonstrating single domain tetragonal PIN–PMN–PT crystals are potential for using at elevated temperature and high dc bias field.

Investigations are currently underway, focusing on the growth of large tetragonal portion with high quality in the crystal boules. Furthermore, the orientation dependent properties for tetragonal PIN–PMN–PT crystals, together with the properties in domain engineered tetragonal crystals, will be studied in order to find the optimal cut directions of tetragonal PIN–PMN–PT crystals for various applications.