Analysis of Cross-Sectional Univariate Measurements for Family Dyads Using Linear Mixed Modeling

Abstract

Outcome measurements from members of the same family are likely correlated. Such intrafamilial correlation (IFC) is an important dimension of the family as a unit but is not always accounted for in analyses of family data. This article demonstrates the use of linear mixed modeling to account for IFC in the important special case of univariate measurements for family dyads collected at a single point in time. Example analyses of data from partnered parents having a child with a chronic condition on their child's adaptation to the condition and on the family's general functioning and management of the condition are provided. Analyses of this kind are reasonably straightforward to generate with popular statistical tools. Thus, it is recommended that IFC be reported as standard practice reflecting the fact that a family dyad is more than just the aggregate of two individuals. Moreover, not accounting for IFC can affect the conclusions.

The analysis of data from multiple family members poses unique challenges requiring special statistical techniques. One key analytic issue for family researchers is the nonindependence of data collected from different members of the same families. Measurements for members of the same family are likely to be correlated, and so their analysis requires statistical techniques that account for intrafamilial correlation (IFC) between pairs of within-family measurements. Statistical methods are available for analyzing family data that account for IFC, including structural equation modeling (Cook, 1994; Thomson & Williams, 1982) and hierarchical linear modeling (Raudenbush & Bryk, 2002), also called multilevel modeling (Singer, 1998). These methods also have been used to estimate specific types of models for family data, including the actor-partner independence model and the social relations model (Campbell & Kashy, 2002; Cook & Kenny, 2005; Kenny, Kashy, & Cook, 2006; Kenny & La Voie, 1984; Rayens & Svavarsdottir, 2003).

In this article, we demonstrate the use of linear mixed modeling (Brown & Prescott, 1999) for analyzing family data through example analyses of data from a cross-sectional study of families having a child with a chronic condition (National Institute of Nursing Research Grant R01 NR08048). The example analyses address assessments by parents in two-parent families of the relationship of family functioning and family management to the adaptation of children with a chronic condition. They demonstrate the use of linear mixed modeling for estimating model parameters across family member types (e.g., fathers and mothers), for adjusting for predictor (independent, explanatory) variables, and for assessing mediation of impacts of such predictors. They address the important special case of cross-sectional univariate measurements for family dyads.

Accounting for IFC Using Linear Mixed Models

Accounting for IFC is an important aspect of any analysis of data for multiple family members. As Kashy and Snyder (1995) pointed out in the context of couples, a family dyad is more than the aggregate of its two members. The two family members together are more than two unrelated individuals, and the correlation between their respective measurements represents an important structural property of the dyad they form. Nonetheless, family researchers do not always take IFC into account in their analyses. Some researchers conduct separate analyses for each family member. For example, Barnett and Gareis (2007) collected a variety of measures on dual-earner families with children and analyzed data for parental measures separately for fathers and mothers. Other researchers collect data from family dyads and analyze the combined data for both types of family members without accounting for possible IFC. For example, Gilliard, Blanton, and Bartley (2007) collected measures of intimacy and individuation among dual-earner husbands and wives and conducted standard correlation and regression analyses of combined data for all participating spouses, thereby treating measurements for spouses in the same families as independent observations.

These kinds of analyses are problematic because they assume that within-family measurements are uncorrelated. Separate analyses account for family member effects on model parameters (e.g., means, standard deviations, intercepts, slopes) but ignore the IFC and are equivalent to analyses of the combined data for both family members that treat the IFC as equal to zero. Likewise, analyses of combined measurements from both family members using standard methods such as means, standard deviations, analysis of variance, and regression also involve an explicit assumption of zero IFC because these methods are based on the assumption of independence across all participants. Treating the IFC as zero in analyses of combined data can affect the conclusions. For example, Knafl, Knafl, and McCorkle (2005) reported a difference in how mean depressive symptoms changed over time after surgery for prostate cancer for family caregivers compared to family care receivers that was identified only when the model accounted for IFC. Mean depressive symptoms decreased over time from about the same level at baseline for care receivers and for caregivers, but at a significantly (p = .04 accounting for IFC; p = .11 with IFC = 0) faster rate for care receivers than for caregivers.

Linear mixed modeling provides a useful approach for accounting for IFC in general family data (Knafl et al., 2005). Moreover, in the common, simplest case of cross-sectional univariate measurements for family dyads, IFC can be addressed using straightforward linear mixed models supported by popular statistical software tools including the Statistical Package for the Social Sciences (SPSS) (SPSS Inc., Chicago) and the Statistical Analysis System (SAS) (SAS Institute Inc., Cary, NC). These models accommodate the usual situation for family data of partial sets of outcome measurements for some families (e.g., families with only one parent participating) without loss of data or imputation. The standard tools for analyzing repeated measurements in SPSS and SAS, on the other hand, delete data for families with outcome measurements for partial sets of family members unless measurements for the other family members are imputed.

Linear mixed models formulate two components for modeling multiple outcome measurements for different participants. The fixed component models the mean (or expected) values for outcome measurements; the random component models the standard deviations and correlations (or equivalently the covariance matrix) of outcome measurements for the same participant. For family data, the family is treated as the “participant” with its multiple measurements taken for some subset of its family members.

The Fixed Component

Modeling how the mean changes is usually of primary importance, for example, how it changes across different types of family members and across different types of families. Such issues are addressed in linear mixed models by the fixed component, which can be based on the general linear model. The analysis of variance case uses only factors (i.e., categorical variables with two or more values each), the regression case uses only predictors (i.e., continuous variables), and the analysis of covariance case uses both factors and predictors (called covariates). All cases can be represented by equivalent regression models, replacing factors by appropriate sets of indicator variables. All of these alternatives are needed in analyzing dyadic family data. For such data, the fixed component should account for a possible effect to type of family member. For example, when dyads consist of fathers and mothers, the slope for the indicator variable for being a father represents the change in mean value for fathers compared to mothers, whose mean value corresponds to the intercept of the fixed component. When some families have only one participating family member, indicator variables also should be included to account for possible differences in mean values for those families compared to families with two participating members. For example, the mean value may differ for mothers from families with participating fathers versus those without participating fathers. The fixed component may address other issues as well. For example, a predictor (e.g., parent's age or family functioning) may be included to assess its impact on the mean. Although the fixed component typically addresses fundamental research issues (e.g., a hypothesis related to some specific aim of a research study) and so may seem of more importance than the random component, conclusions about the fixed component can be questionable if the random component is too simplistic (e.g., treating within-family measurements as independent with zero correlations).

The Random Component

The random component of a linear mixed model specifies the variances for measurements within participants as well as the correlations between pairs of such measurements. A variety of alternatives can be used to model the random component. The simplest nonindependent alternative, commonly applied to repeated measurements, is called compound symmetry because it assumes constant standard deviations across within-subject measurements and constant correlations between pairs of different measurements. At the other extreme, the most complex alternative treats all within-subject standard deviations and correlations as distinct parameters. The covariance matrix has the most general possible form without any simplifying structure, and so is called unstructured. Many intermediate choices are possible as well depending on the data, but cross-sectional univariate measurements for family dyads are simpler. The family is the “participant,” having measurements for one or both of its family members. There is a single correlation, the IFC between measurements for the two members of the family dyad (e.g., mothers and fathers). There are also only two possibilities for the standard deviations; they are either the same for the two members of the family dyad or they are different. The example analyses of this article allow for the more general case with different standard deviations. In other words, they use a compound symmetry approach with heterogeneous standard deviations.

Parameter Estimation

Parameter estimation for linear mixed models is conducted using full information maximum likelihood (FIML) (Arminger & Sobel, 1990), treating within-subject measurements as multivariate normally distributed with associated mean vector (determined by the fixed component) and covariance matrix (determined by the random component). FIML uses likelihood terms for participants (in our case, the family) based on only available outcome measurements for those participants (in our case, for selected members within families). Partial sets of outcome measurements for participants are not lost, and missing outcome measurements do not need to be imputed. Thus, outcome measurements for any possible set of members within families can be included in analyses of family data. However, this does not apply to missing predictor values. FIML estimation of linear mixed models has the added advantage of being supported in popular statistical software tools including SAS and SPSS.

Example Cross-Sectional Dyadic Family Data

Example analyses presented below use data from parents of a child with a chronic condition surveyed as part of a cross-sectional instrument development study. Data are available for 324 two-parent families, with fathers and mothers participating for 145 families and only mothers for the remaining 179 families. Families with a child 2 to 18 years old having a chronic condition for at least 6 months were recruited from five states (Connecticut, Delaware, Illinois, Pennsylvania, and Vermont). Mothers had to be willing to participate. Fathers in two-parent families could choose to participate or not. Single mothers also participated in the study, but their data are not used in example analyses to limit the complexity of those analyses.

Variables used in example analyses include measures of child adaptation, general family functioning, and family management of the chronic condition. Child adaptation was measured in terms of parents’ ratings of the intensity of the child's conduct-disordered behaviors using the Intensity Scale of the Eyberg Child Behavior Inventory (Eyberg & Pincus, 1999; Eyberg & Robinson, 1983). This scale is computed by summing 36 items rated from 1 to 7 so that scores have a maximal range of 36 to 252. Larger values indicate poorer adaptation. General family functioning was measured by the General Functioning Scale of the McMaster Family Assessment Device (Epstein, Baldwin, & Bishop, 1983). This scale is computed by averaging 12 items rated from 1 to 4 so that scores have a maximal range of 1 to 4. Larger values indicate poorer family functioning. Family management was measured using two of the six scales of the Family Management Measure (FaMM)—the Family Life Difficulty and Parental Mutuality Scales. The Family Life Difficulty Scale is computed by summing 14 items rated from 1 to 5 so that scores have a maximal range of 14 to 70. The Parental Mutuality Scale is computed by summing eight items also rated from 1 to 5 so that scores have a maximal range of 8 to 40. Larger values indicate more difficulty and mutuality, respectively, in managing the child's chronic condition. Four other FaMM scales (the Child's Daily Life, Condition Management Ability, Condition Management Effort, and View of Condition Impact) are also available but are not included in example analyses because the purpose of those analyses is to demonstrate linear mixed modeling methods, not to provide a complete assessment of family management. Missing item values for each scale have been imputed using the mean of the nonmissing item values reported by the same participant for that scale, as long as there are less than 30% missing item values. Families with any missing scale values for a participating parent have been excluded from the data set (28 altogether, including 3 two-parent families for which only fathers could be interviewed). This way there are no missing predictor values for example analyses and no families with data for only fathers.

Example Analyses

The example analyses reported in this section use the childhood chronic condition data described above to demonstrate the use of linear mixed modeling for assessing common analysis issues for cross-sectional data from family dyads including summary statistics, regression, and mediation while accounting for IFC. Other kinds of analyses of such data can be handled similarly. All linear mixed models used in these example analyses have the same random component based on an IFC parameter representing the correlation between measurements for parents in the same family together with different standard deviations for those measurements (i.e., compound symmetry with heterogeneous standard deviations). This IFC parameter provides a measure of the strength of the relationship between measurements for parents of the same family, which is different from the amount of agreement between those measurements (Larsen & Olson, 1990). Linear mixed models were computed with PROC MIXED in SAS Version 9.1 (SAS Institute Inc., 2005).

Example Summary Statistics

Family researchers need to report summary statistics for variables collected for family member types. They also need to test for differences in means for those variables across family member types. The example analyses in this section demonstrate the use of linear mixed modeling for conducting such assessments. Specifically, for the childhood chronic condition data, summary statistics are reported for child adaptation, general family functioning, difficulty, and parental mutuality and tests conducted for effects to family member types that are adjusted for IFC (Table 1). Data are compared for mothers and fathers in the 145 families with both parents participating. In addition, data are also compared for mothers from those 145 families to mothers in the 179 families without participating fathers. These analyses are based on the same fixed component for each variable with three parameters—an intercept and two slopes. The intercept parameter represents the mean value for mothers from families with participating fathers. For example, estimated mean child adaptation for these mothers is 87.5. One of the slope parameters is for the indicator of the parent being a father and represents the change in intercept value, and so also the change in mean value, for fathers compared to mothers in two-respondent families. For example, estimated mean child adaptation changes from 87.5 to the adjusted value of 90.3 for fathers by 2.8, the estimate for the associated slope parameter with a p value of .16. The other slope parameter is for the indicator of families without participating fathers and represents the change in intercept value, and so also the change in mean value, for mothers without participating fathers compared to those with participating fathers. For example, estimated mean child adaptation changes from 87.5 to the adjusted value of 86.0 for mothers without participating fathers by –1.5, the estimate for the associated slope parameter with p value of .65. p values for these slope parameters provide tests for significant differences in mean values between family member types adjusted for IFC.

Table 1.

Summary Statistics

Fixed Component
		Mothers With Participating Fathers	Fathers			Mothers Without Participating Fathers
	Maximal Range		Change in Intercept		Adjusted Intercept	Change in Intercept		Adjusted Intercept
Scale		Intercept		p			p
Child adaptation	36–252	87.5	2.8	.16	90.3	–1.5	.65	86.0
General family functioning	1–4	1.58	–0.04	.31	1.54	0.02	.72	1.60
Difficulty	14–70	30.8	–0.4	.66	30.4	0.1	.97	30.9
Parental mutuality	8–40	33.8	1.1	.01	34.9	–0.9	.09	32.8

Random Component
	Mothers	Fathers	Intrafamilial Correlation
Scale	SD	SD	Value	p
Child adaptation	29.0	28.4	.65	< .01
General family functioning	0.45	0.39	.39	< .01
Difficulty	11.1	11.3	.58	< .01
Parental mutuality	5.4	4.4	.41	< .01

Note: Using data from 324 two-parent families, with fathers and mothers participating for 145 families and only mothers for the remaining 179 families.

Estimated mean child adaptation, general family functioning, and difficulty are each not significantly different for mothers and fathers in two-respondent families (p = .16, p = .31, and p = .66) and for mothers in families with and without participating fathers (p = .65, p = .72, and p = .97). On the other hand, estimated mean parental mutuality significantly increases in two-respondent families from 33.8 for mothers by 1.1 units to 34.9 for fathers (p = .01), whereas it is not significantly different for mothers with and without fathers participating (p = .09). In summary, the only significant effect for parent type is for parental mutuality with fathers of two-respondent families assessing mutuality higher than mothers of either one- or two-respondent families.

The fact that all the change-in-intercept parameters with this one exception are nonsignificant might be used to justify eliminating those nonsignificant parameters and their associated indicator variables in subsequent analyses, but there is a possibility that inclusion of other terms in models will strengthen the impact of such family type indicators. To be conservative, all family type indicator variables and associated slope parameters are included in all subsequent analyses, a practice that seems appropriate for analyses of dyadic family data in general.

Linear mixed modeling provides p values for hypothesis tests about parameters of the fixed component that generalize standard t tests to address dyadic family data by accounting for IFC. The test for a difference in mean values for mothers compared to fathers in two-respondent families generalizes the standard paired t test to take into account data from mothers in one-respondent families. The test for a difference for mothers with and without participating fathers generalizes the standard two-sample t test to take into account data from fathers in two-respondent families. These standard tests can be conducted but would be based on subsets of the data. The tests generated through linear mixed modeling, on the other hand, are based on the complete data and so are more powerful. For large data sets like this one, standard analyses are likely to produce similar conclusions, but for smaller data sets significant conclusions are more likely for analyses of the complete data. In any case, the more general analyses based on linear mixed modeling provide more definitive conclusions because they are based on the full set of available data. Moreover, those analyses also provide a more complete assessment of the family as a unit through estimated IFC values.

Table 1 also contains estimates of random component parameters. An inspection of estimated standard deviations indicates that parental mutuality and possibly also general family functioning appear less variable for fathers than for mothers. Fathers in different families tend to be in closer agreement in these areas than do mothers in different families. On the other hand, there is little difference between fathers and mothers in variability for child adaptation and difficulty. A constant standard deviation model can be appropriate for some cases, but that will not always hold, and so heterogeneous standard deviations seem the better, more conservative choice in general.

Estimates of IFC are .65 for child adaptation, .39 for general family functioning, .58 for difficulty, and .41 for parental mutuality. All of these are significantly different from zero (p < .01). Fathers’ and mothers’ assessment of child adaptation, general family functioning, difficulty, and parental mutuality are distinctly correlated within families of children with chronic conditions, as would often hold for evaluations of the same constructs from the perspectives of members of the same family. Thus, the IFC can represent a very important dimension of family data. Furthermore, if the IFC is set to zero for the analysis of parental mutuality reported in Table 1, the significant (p = .01) difference in means for fathers and mothers becomes nonsignifi-cant (p = .06). Not accounting for the IFC can affect the investigator's conclusions, as also reported by Knafl et al. (2005) for analyses of longitudinal family data.

The fixed component used in these analyses is simpler than what is needed for cross-sectional dyadic family data in general because data are available only for fathers when data are also available for mothers of the same families. In other studies of mothers and fathers, there may be data for only fathers in some families. This case should be accounted for in the fixed component by adding a third slope parameter for the indicator variable for only fathers participating. This slope parameter represents the change in intercept, and so also the change in mean value, for fathers without participating mothers compared to the mean value for mothers with participating fathers. An indicator variable with another associated slope parameter also can be added to distinguish between single versus partnered parents when appropriate. Fixed components for other types of family dyads are based on analogous sets of slope parameters and indicator variables. These fixed components are examples of regression models that are equivalent to analysis of variance models because the indicator variables of the model represent factors, each corresponding to a parent type with two values (e.g., mother or father). The associated linear mixed models differ from standard regression and analysis of variance models in also accounting for IFC and for heterogeneous standard deviations.

Example Regression Analyses

Family researchers often want to test hypotheses that family functioning has an impact on available variables measuring other properties of the family or its members. The example analyses in this section demonstrate the use of linear mixed modeling for conducting such assessments. Specifically, they address how child adaptation to the condition and family management of the condition depend on general family functioning. Table 2 contains results for linear mixed models investigating these issues. General family functioning has been added as a predictor to the models used previously to compute summary statistics for the other three variables. The extra slope parameter added to these models represents how much means for child adaptation, difficulty, and parental mutuality change with unit changes in general family functioning. The original parameters of the model represent the intercepts for these linear relationships in general family functioning, allowing those intercepts possibly to be different for mothers and fathers in two-respondent families and for mothers in families with versus without participating fathers. Differences in these intercepts represent how much of a shift there is in these linear relationships for associated parent types.

Table 2.

The Impact of General Family Functioning on Child Adaptation and on Family Management

Fixed Component
	General Family Functioning		Mothers With Participating Fathers	Fathers			Mothers Without Participating Fathers
				Change in Intercept		Adjusted Intercept	Change in Intercept		Adjusted Intercept
Scale	Slope	p	Intercept		p			p
Child adaptation	16.4	< .01	61.7	3.5	.08	65.2	–1.8	.57	59.9
Difficulty	9.0	< .01	16.7	0.0	.99	16.7	–0.1	.92	16.6
Parental mutuality	–7.8	< .01	46.1	0.8	.05	46.9	–0.9	.04	45.2

Random Component
	Mothers	Fathers	Intrafamilial Correlation
Scale	SD	SD	Value	p
Child adaptation	27.8	27.2	.63	< .01
Difficulty	10.2	10.4	.50	< .01
Parental mutuality	4.0	3.4	.13	.13

Note: Using data from 324 two-parent families, with fathers and mothers participating for 145 families and only mothers for the remaining 179 families.

Mean child adaptation is significantly related to general family functioning with estimated slope 16.4 (p < .01), and so poorer general family functioning (larger scores) corresponds to poorer child adaptation (larger scores) in terms of more conduct-disordered behavior. Mean difficulty is significantly related to general family functioning with estimated slope 9.0 (p < .01), and so poorer general family functioning corresponds to increased difficulty. Mean parental mutuality is significantly related to general family functioning with estimated slope –7.8 (p < .01), and so poorer general family functioning corresponds to reduced parental mutuality. These results are all as would be expected with poorer general family functioning corresponding to poorer child adaptation, increased difficulty, and reduced parental mutuality.

The linear relationships for child adaptation and difficulty in terms of general family functioning are not significantly shifted for mothers and fathers in two-respondent families (p = .08 and p = .99) or for mothers with and without participating fathers (p = .57 and p = .92). However, the linear relationship for parental mutuality is significantly shifted up in two-respondent families from 46.1 for mothers by 0.8 units to 46.9 for fathers (p = .05), in agreement with the corresponding results reported in Table 1. For fixed levels of general family functioning, fathers tend to rate parental mutuality higher than mothers. Furthermore, the linear relationship for parental mutuality is significantly shifted down from 46.1 for mothers with participating fathers by 0.9 units to 45.2 for mothers without participating fathers (p = .04), in contrast to the corresponding results reported in Table 1. For fixed levels of general family functioning, mothers in families without participating fathers tend to rate parental mutuality lower than mothers in families with participating fathers. In summary, controlling for general family functioning, fathers tend to consider the dyad to work together more effectively than their spouses do, whereas mothers tend to consider the dyad to work together more effectively when fathers participate in the study than when they do not.

Two of the six p values for changes in intercepts reported in Table 2 are distinctly smaller than associated values in Table 1 (p = .08 for child adaptation and the change for fathers, compared to p = .16 in Table 1; p = .04 for parental mutuality and the change for mothers without participating fathers, compared to p = .09 in Table 1). Also, the one significant Table 1 p value (parental mutuality for mothers versus fathers in two-respondent families) remains significant. Thus, incorporation of a significant predictor variable has distinctly strengthened the impact of associated change-in-intercept parameters for these two cases, with one of them becoming significant. This supports the earlier decision to account for such changes even though only one Table 1 change is significant. These results also suggest that differences in means across parent types should be addressed in analyses of general family data even though they may be nonsignificant in prior analyses of those data.

The addition of the significant predictor general family functioning also has reduced the standard deviation values in all cases. The variability in child adaptation and difficulty is still similar for mothers and fathers and the variability in parental mutuality is still lower for fathers than for mothers. IFC values remain strong and significantly nonzero for child adaptation and difficulty (p < .01), but the IFC for parental mutuality is no longer significant (p = .13). However, this would still be considered a distinct IFC under the guidelines of Kenny and Kashy (1991), who feel that the generous cutoff of p = .25 should be used in assessing independence within dyads.

These example analyses treat linear relationships in general family functioning as possibly shifted for different family types but consider them to change in the same way for all family types (i.e., with the same slope). The further issue of whether linear relationships change with family types often will be of interest but is not addressed in the example analyses for brevity. It can be addressed by introducing interactions (i.e., products) for predictor variables with indicator variables for family member types. For example, for the childhood chronic condition data, the interaction between the predictor general family functioning and the indicator variable for being a father could be introduced into the models of Table 2. This would provide an assessment of whether being a father or not moderates (Baron & Kenny, 1986) the impact of general family functioning on either child adaptation or family management. The p value for the slope associated with this interaction provides a test of whether or not the linear relationship in general family functioning changes differently for fathers compared to mothers in two-respondent families. It is possible for linear relationships to change for more than one family member type, but the inclusion of interactions for all possible family member types at once is likely to generate overly complicated models, masking effective interactions (i.e., interactions with significant slopes when considered separately becoming nonsignificant) because of the inclusion of ineffective interactions (i.e., interactions with nonsignificant slopes when considered separately as well as in combination with other interactions). The assessment of interactions across family member types may require an exploratory approach that systematically adjusts the model to include effective interactions or to remove ineffective ones, but that is an issue for future research.

Example Mediation Analyses

Mediation (Baron & Kenny, 1986) is as important an issue for family research as it is for other types of research, but its assessment is complicated for family data by the need to account for IFC. The example analyses in this section demonstrate the use of linear mixed modeling for conducting mediation assessments for family data. Specifically, they assess how much of the direct impact of general family functioning on child adaptation can be represented as an indirect effect through family management of the condition as an intervening variable. For the sake of simplicity, only the difficulty and parental mutuality dimensions of family management are considered in these analyses, rather than all six possible dimensions.

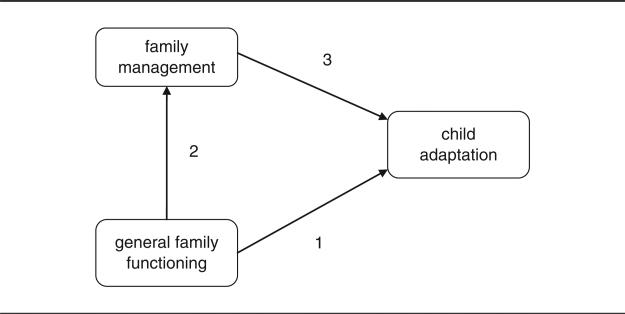
Example mediation analyses follow the standard approach of Baron and Kenny (1986), but using linear mixed models rather than standard regression models. Mediation analyses address the extent to which a mediator reduces the impact of a predictor on a dependent variable, in this case, how family management in terms of difficulty and/or parental mutuality mediates the impact of the predictor general family functioning on child adaptation (Figure 1). The predictor first must have significant impacts on both the dependent variable and the mediator (Paths 1 and 2 of Figure 1), which have been established for the example mediation analyses in the previous section (see Table 2). Mediation is then demonstrated by showing that the impact of the predictor on the dependent variable is reduced or fully explained by introduction of the mediator or mediators as an additional predictor or predictors (Path 3 of Figure 1). Table 3 contains results for this second step for the example mediation analyses.

Figure 1.

Mediation Model

Table 3.

Mediation of the Impact of General Family Functioning on Child Adaptation by Family Management

Fixed Component
Difficulty		Parental Mutuality		General Family Functioning		Mothers with Participating Fathers	Fathers			Mothers Without Participating Fathers
Slope	p	Slope	p	Slope	p	Intercept	Change in Intercept	p	Adjusted Intercept	Change in Intercept	p	Adjusted Intercept
0.7	< .01	–	–	10.5	< .01	49.6	3.5	.06	53.1	–1.8	.57	47.9
–	–	–1.0	< .01	9.5	.01	105.0	4.2	.03	109.2	–0.1	.39	102.3
0.6	< .01	–0.7	.02	6.1	.07	81.2	4.0	.03	85.2	–0.9	.44	78.9

Random Component
Mothers	Fathers	Intrafamilial Correlation
SD	SD	Value	p
27.0	25.9	.63	< .01
27.5	26.6	.63	< .01
26.8	25.7	.64	< .01

Note: Models include general family functioning along with difficulty alone, parental mutuality alone, or both together in that order. Using data from 324 two-parent families, with fathers and mothers participating for 145 families and only mothers for the remaining 179 families.

When the difficulty dimension of family management is introduced by itself into the model for child adaptation, it has a significant impact (p < .01), reducing the slope for general family functioning from 16.4 (Table 2) to 10.5, but this slope remains significant (p < .01). Similarly, when the parental mutuality dimension is introduced by itself into the model, it also has a significant impact (p < .01), reducing the slope for general family functioning even more to 9.5, but as for difficulty this slope remains significant (p = .01). Each of these two dimensions of family management addresses overlapping aspects of the impact of general family functioning on child adaptation, partially but not fully mediating that impact. On the other hand, the introduction of both the difficulty and parental mutuality dimensions reduces the slope for general family functioning to a nonsignificant value of 6.1 (p = .07). Thus, difficulty and parental mutuality together fully mediate the impact of general family functioning on child adaptation, and so its direct impact as represented by Path 1 of Figure 1 can be dropped leaving only its indirect impact through family management represented by the combined Paths 2 and 3 of Figure 1. These two dimensions of family management taken together are as effective as general family functioning in explaining child adaptation and have the added advantage of also providing specific information on how families manage childhood chronic conditions.

For fathers compared to mothers in two-respondent families, the linear relationship for mean child adaptation in terms of general family functioning is not significantly shifted with the inclusion of difficulty alone (p = .06) but is significantly shifted up for fathers by 4.2 units with the inclusion of parental mutuality alone (p = .03) and also by 4.0 units with the inclusion of both difficulty and parental mutuality (p = .03). On the other hand, for mothers without participating fathers compared to mothers with participating fathers, the linear relationship for mean child adaptation in terms of general family functioning is not significantly shifted with the inclusion of difficulty alone, parental mutuality alone, and both difficulty and parental mutuality (p = .57, p = .39, p = .44). Standard deviation and IFC estimates are similar for each of the three mediation models of Table 3. As in analyses of child adaptation reported in Tables 1 to 2, standard deviations are similar for fathers and mothers and IFCs are strong.

Discussion

The example analyses demonstrate the use of linear mixed modeling for analyzing cross-sectional univariate outcomes for family dyads while accounting for IFC. They address common analysis issues including summary statistics, regression, and mediation, providing interesting insights about family management of childhood chronic conditions. Fathers appear to rate mutuality in managing the condition higher than mothers, considering the dyad to work together more effectively than mothers. After controlling for the impact of general family functioning, mothers appear to rate the family as working together more effectively when fathers participate in the study than when they do not. Fathers’ participation in the study may be an indication that parents are more likely to function as a team in managing their child's condition. On the other hand, it is not clear that these statistically significant differences across parent types will prove to be clinically significant, but these results nonetheless suggest interesting questions for future investigation.

Also, the combined family management dimensions of difficulty and parental mutuality fully mediate the impact of general family functioning on child adaptation. These two family management dimensions taken together are as useful as general family functioning for explaining child adaptation and also provide important information on the specific nature of the family's response to the child's condition. Interventions for lowering the difficulty of managing these conditions and for increasing parental mutuality in managing them have the potential for improving child adaptation to chronic conditions. Despite the full mediating effect of family management on general family functioning, investigators might still want to collect measures of family functioning to investigate relationships between specific aspects of family functioning (e.g., problem solving, conflict) with child adaptation and family management. These mediation results have not accounted for the other possible dimensions of family management and so may not provide a complete assessment of the effects of family management. Furthermore, the example analyses treat relationships as linear. It is possible that different conclusions might be reached if the possibility of nonlinear relationships were considered in analyses. This would require nonstandard methods (e.g., as formulated by Knafl, Fennie, & O'Malley, 2006). More thorough analyses of the childhood chronic condition data are needed.

There are other issues of importance to the example data these analyses do not address, including the impact on child adaptation of child characteristics, especially the type of chronic condition, as well as interaction effects for possible moderator variables. Linear mixed modeling can be used to address such issues using approaches similar to those used in the example analyses. Also, the example data are not as general as possible. Some families of this study have only participating mothers but none only participating fathers and all have two parents. However, models can be extended to account for families with only fathers participating and/or for one-parent families. These kinds of models also can be adjusted readily to analyze cross-sectional univariate measurements for any type of dyad.

General linear mixed modeling is a complex statistical method that may appear challenging to some family researchers. A wide variety of covariance matrices is possible. Random effects and/or coefficients can be included as well as fixed effects and/or coefficients. However, the kinds of models needed for analyses for cross-sectional, univariate dyadic family data are reasonably straightforward to generate with popular statistical tools. Thus, it is no longer justifiable to conduct analyses for each family member separately. Moreover, not accounting for IFC can affect the investigator's conclusions. Consequently, it is recommended that IFC estimates should be reported as standard practice in analyses of dyadic family data, reflecting the fact that a family dyad is more than just the aggregate of two individuals (Kashy & Snyder, 1995). Also, a generous significance level should be used to conclude that the IFC is negligible (e.g., p = .25, Kenny & Kashy, 1991).

General family data can be much more complicated than the childhood chronic condition data analyzed in the example examples reported here. For example, measurements also may be taken over time and/or over more than two family members. More than one type of measurement (e.g., multiple family management dimensions in combination) may need to be considered in analyses. Linear mixed models also can be used in these situations (e.g., Knafl et al., 2005) but are not as straightforward as in the simpler case of cross-sectional measurements of a single type of measurement for family dyads. Even in this case, certain kinds of analyses are not conducted readily with linear mixed models. For example, the development of scales measuring parents’ perception of certain aspects of the family would be based on a cross-sectional survey of both mothers and fathers. Standard exploratory and confirmatory factor analysis models assume independence across participants, and so such factor analyses should be conducted using data for only one parent within families. This limitation can be circumvented by first developing family scales using responses for one type of family member (e.g., mothers) and then demonstrating that those scales are compatible with responses from other types of family members (e.g., fathers and/or children). However, it would be preferable to develop family scales using the combined responses for all available family members, but that would require development of factor analysis methods that account for IFC, an issue for future research.

Biography

George J. Knafl, PhD, is professor in the School of Nursing of the University of North Carolina at Chapel Hill, where he teaches statistics courses and provides biostatistical consultation. His research focuses on the development of adaptive statistical methods for exploratory analyses of health science data. His recent publications include “Mixed Models Incorporating Intra-Familial Correlation through Spatial Autoregressive Methods” in Research in Nursing and Health (2005, with K. Knafl & R. McCorkle) and “Parents’ Perceptions of Functioning in Families Having a Child with a Genetic Condition” in Journal of Genetic Counseling (2007, with K. Knafl, A. Gallo, & D. Angst).

Jane K. Dixon, PhD, is professor at the Yale University School of Nursing. Her program of research has specialized on problems of measurement, including the development and testing of new instruments so that they are meaningful and psychometrically sound. Her recent publications include “Instrument Translation Process: A Methods Review” in Journal of Advanced Nursing (2004, with W. Maneesriwongul), “The Guideline Implementability Appraisal (GLIA): Development and Validation of an Instrument to Identify Obstacles to Guideline Implementation” in BMC Medical Informatics and Decision-Making (2005, with R. Shiffman, C. Brandt, A. Essaihi, A. Hsiao, G. Michael, & R. O’Connell), and “Determining Content Validity of a Self-Report Instrument for Adolescents Using a Heterogeneous Expert Panel” in Nursing Research (2007, with L. Schilling, K. Knafl, M. Grey, B. Ives, & M. Lynn).

Jean P. O'Malley, MPH, is research associate in the Biostatistics and Design Program of the Oregon Clinical and Translational Research Institute of Oregon Health & Sciences University. Her research interests include the innovative application of statistical methods in the health sciences. Her recent publications include “Validation of a Care and Comfort Hypertonicity Questionnaire” in Developmental Medicine and Child Neurology (2006, with M. Nemer, P. Blasco, & B. Russman) and “Decreased Respiratory Compliance in Infants Less Than or Equal to 32 Weeks’ Gestation, Delivered More Than 7 Days after Antenatal Steroid Therapy” in Pediatrics (2008, with C. McEvoy, D. Schilling, P. Peters, & M. Durand).

Margaret Grey, RN, DrPH, FAAN, is Dean and Annie Goodrich Professor of Nursing at the Yale University School of Nursing. She has focused her program of research on the development and testing of interventions to improve outcomes for youth with type 1 diabetes and their parents. Her recent publications include “An Intervention for Multiethnic Overweight and Obese Parents and Their Overweight Children” in Applied Nursing Research (2007, with D. Berry, M. Savoye, & G. Melkus), “Coming Together, Keeping Together, Working Together: Transdisciplinary Research and Nursing, Past, Present, Future” in Nursing Outlook (2008, with C. Connolly), and “Short-Term Effects of Coping Skills Training in School Age Children with Type 1 Diabetes” in Pediatric Diabetes (2008, with J. Ambrosino, K. Fennie, R. Whittemore, & S. Jaser).

Janet A. Deatrick, RN, PhD, FAAN, is associate professor of nursing at the University of Pennsylvania School of Nursing. Her research focuses on potentially vulnerable populations at risk for health care disparities, addressing children with chronic conditions and cancer, family management styles, health-related decisions, advanced practice pediatric nursing, and qualitative research methods. She is currently conducting a study that explores family caregiving of adolescent and young adult survivors of childhood brain tumors. Her recent publications include “Further Refinement of the Family Management Style Framework” in Journal of Family Nursing (2003, with K. Knafl) and “Family Management Styles Framework: A New Tool with Potential to Assess Families Who Have Children with Brain Tumors” in Journal of Pediatric Oncology Nursing (2006, with A. Thibodeaux, K. Mooney, C. Schmus, R. Pollack, & B. Heib Davey).

Agatha M. Gallo, PhD, APN, CPNP, FAAN, is professor in the Department of Maternal-Child Nursing of the University of Illinois at Chicago College of Nursing. Her research has focused on family response to childhood chronic conditions and, more recently, for families where there is a child with a genetic condition. Her recent publications include “Parents’ Perceptions of Functioning in Families Having a Child with a Genetic Condition” in Journal of Genetic Counseling (2007, with K. Knafl, G. Knafl, & D. Angst) and “Parents’ Concerns about Issues Related to Their Child's Genetic Conditions” in Journal for Specialists in Pediatric Nursing (2008, with E. Hadley, D. Angst, K. Knafl, & C Smith).

Kathleen A. Knafl, PhD, FAAN, is Frances Hill Fox Distinguished Professor and associate dean for research at the School of Nursing of the University of North Carolina at Chapel Hill. Her program of research has focused on development of the family management style framework, a conceptualization of how families manage childhood chronic conditions and incorporate condition management into everyday life. Her recent publications include “Childhood Chronic Illness: A Comparison of Mothers’ and Fathers’ Experiences” in Journal of Family Nursing (2000, with L. Zoeller), “Further Refinement of the Family Management Style Framework” in Journal of Family Nursing (2003, with J. Deatrick), and “The Analysis and Interpretation of Cognitive Interviews for Instrument Development” in Research in Nursing and Health (2007, with J. Deatrick, A. Gallo, G. Holcomb, M. Bakitas, J. Dixon, & M. Grey).