Abstract
The kinetics for the assembly of viral proteins into a population of capsids can be measured in vitro with size exclusion chromatography or dynamic light scattering, but extracting mechanistic information from these studies is challenging. For example, it is not straightforward to determine the critical nucleus size or the elongation time (the time required for a nucleus to grow to completion). In this work, we study theoretical and computational models for capsid assembly to show that the critical nucleus size can be determined from the concentration dependence of the assembly half-life and that the elongation time is revealed by the length of the lag phase. Furthermore, we find that the system becomes kinetically trapped when nucleation becomes fast compared to elongation. Implications of this constraint for determining elongation mechanisms from experimental assembly data are discussed.
Introduction
The assembly of protein building blocks into a shell or capsid is essential for viral replication and thus understanding the mechanisms by which assembly proceeds could identify targets or opportunities for novel antiviral therapies. However, despite extraordinary progress in determining the structures of assembled capsids, assembly mechanisms for most viruses remain poorly understood because the structures of transient assembly intermediates have been inaccessible experimentally. The kinetics for spontaneous capsid assembly in vitro have been measured with size exclusion chromatography (SEC) and x-ray and light scattering (e.g., (1–7)), but extracting mechanistic information such as the critical nucleus size or the time to assemble an individual capsid has been challenging. In this article, we theoretically examine two models for capsid assembly kinetics to show that these properties can be determined from the concentration dependence of median assembly times and the lag phase.
Assembly kinetics in vitro has been measured for a number of icosahedral viruses (e.g., (1–7)) and demonstrates sigmoidal growth characterized by a lag phase, rapid growth, and finally saturation (see Figs. 1 and 2). Zlotnick and co-workers (2,8,9) showed that partial capsid intermediates assemble during the lag phase, but it has often been assumed that the duration of the lag phase corresponds to the time required for the concentration of critical nuclei to reach steady state, in analogy to models of actin nucleation. However, in this work we show that because light-scatter signal measures the mass-averaged molecular weight of assemblages (4) and SEC usually monitors complete capsids, the length of the lag phase is related to the elongation time, or the time required for a nucleated partial capsid to grow to completion. Similarly, the critical nucleus size cannot be reliably determined from the concentration dependence of initial or maximum growth rates (9), and a method to do so using the extent of assembly (9) is data-intensive. We demonstrate that the critical nucleus size can be identified in a straightforward manner from the concentration dependence of the median assembly time. Finally, we show that the system becomes kinetically trapped when the elongation time becomes long compared to the timescale for nucleation. It is important to note that we do not consider the effects of a slow transition between assembly-active and assembly-incompetent conformations of free subunits, recently suggested in Chen et al. (6).
Figure 1.
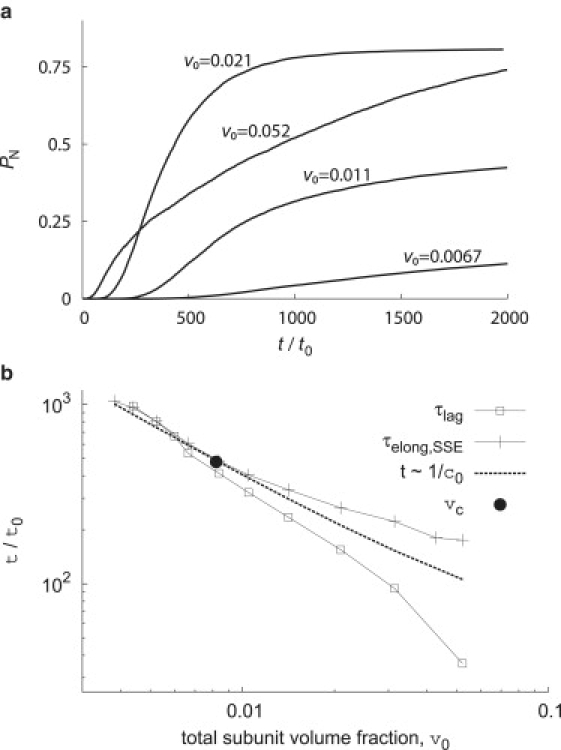
(a) The completion fraction PN in Brownian dynamics (BD) simulations (the NVT simulations) is shown as a function of time for indicated initial subunit volume fractions (v0). (b) Lag times τlag, elongation times τelong, and nucleation times τnucmin calculated from BD simulations are shown as functions of the initial subunit volume fraction. Lag times are calculated from canonical ensemble simulations as described in Fig. 3, whereas τelong is calculated from the steady-state ensemble as described in the text. The volume fraction vc corresponding to the crossover concentration is indicated by the •. The dashed line is a guide to the eye to demonstrate scaling inverse to subunit concentration. The scatter in the points at volume fractions below vc gives an indication of the statistical error at low concentrations.
Figure 2.
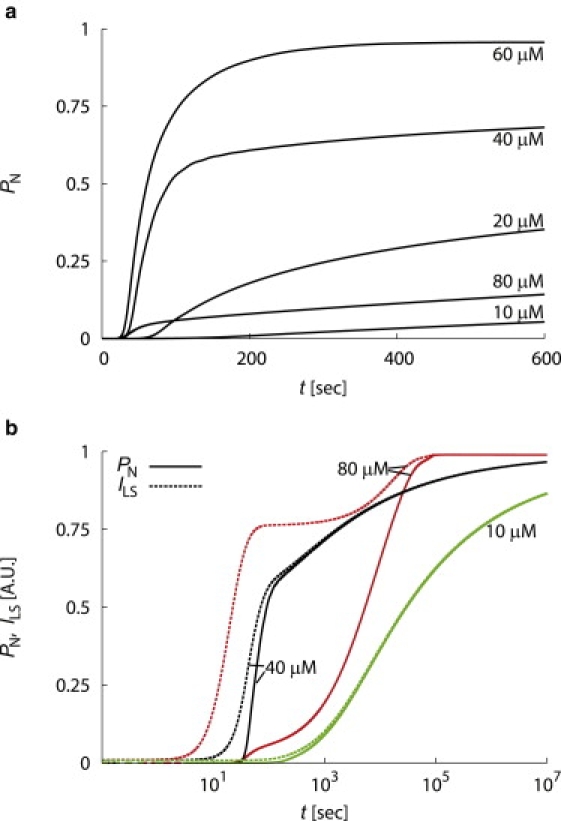
The time dependence of capsid assembly for the NG model varies with initial subunit concentration c0. (a) The completion fraction PN as a function of time for indicated initial subunit concentrations. (b) The calculated light scatter closely tracks completion fraction until kinetic trapping sets in. The calculated light scatter (dashed lines) and completion fraction (solid lines) are shown as a functions of time (on a logarithmic scale) for indicated initial subunit concentrations, with gnuc = – 7kBT, N = 120, and f = 105 M−1s−1.
While preparing this article, we became aware of a related study in which Morozov et al. (10) consider simplified capsid assembly models in which nucleation occurs via a single dimerization event, which enables a elegant analytic solution. They show that the early phase of assembly can be characterized as a shock front, and that for some conditions prohibitively long timescales are required to reach equilibrium. In this work, we consider nucleation as a multistep subunit addition process, with the objectives of understanding the concentration dependence of overall assembly times and inferring nucleation and capsid growth times from experimental light scatter measurements.
This article is organized as follows. In the next section, we use scaling laws for elongation and nucleation times as a function of subunit concentration in the context of a simplified assembly reaction. We then demonstrate that these estimates hold for a more realistic model by examining Brownian dynamics simulations for a model of assembly into icosahedral shells. We then further explore assembly timescales using a system of rate equations for the assembly of polyhedral shells and two models for capsid intermediate free energies. In Discussion and Outlook, we consider the implications of our findings for experimental measurements of capsid assembly dynamics. Additional simulation details, derivations, and further evaluation of approximations in the rate equation models are given in the Supporting Material.
Capsid Assembly Timescales
In this section, we develop scaling laws for the concentration dependence of the duration of lag phase and nucleation timescales. To facilitate the presentation, we first consider a systematic assembly process which is greatly simplified in comparison to capsid assembly. In the following sections and in the Supporting Material, however, we show that the conclusions of this section remain valid when the simplifications are eliminated.
We consider a system of capsid protein subunits with total concentration c0 that start assembling at the time t = 0 into capsids; the word subunit refers to the basic assembly unit, which could be a protein dimer or capsomer. Our simplified reaction is given by
| (1) |
where N is the number of subunits in a capsid, c1 is concentration of unassembled subunits, and bi is the dissociation rate constant (with i = {nuc, elong}), which is related to the forward rate constant by the equilibrium constant, bi = fexp(gi/kBT)/v0, with gi the subunit association free energy (arising from hydrophobic and electrostatic interactions (11,12)) and v0 the standard state volume. The nucleation and elongation phases are distinguished by the fact that association in the nucleation phase is not free-energetically favorable, c1 exp(–gnuc/kBT) < 1, whereas association in the elongation phase is favorable, c1 exp(–gelong/kBT) > 1. For the moment, we assume that there is an average nucleus size nnuc; identifying nnuc from assembly kinetics data is one of the objectives of our work. The physical origins of nucleation and the factors that determine nnuc are discussed in Rate Equation Models for Capsid Assembly.
We write the overall capsid assembly time τ as τ = τnuc + τelong, with τnuc and τelong the average times for nucleation and elongation, respectively. For all of the models considered in this work, we will see that when elongation is fast compared to nucleation, the duration of the lag phase is given by the mean elongation time for the first capsids to assemble: τlag = τelong(t = 0). Thus, for this model the lag time can be calculated from the mean first-passage time for a biased random walk with a reflecting boundary conditions at nnuc and absorbing boundary conditions at N, with forward and reverse hopping rates given by fc0 and belong = fexp(gelong)/v0, respectively. Mean first-passage times for these boundary conditions are derived in Bar-Haim and Klafter (13); inserting these forward and reverse hopping rates yields
| (2) |
with nelong = N – nnuc.
In the limit of , Eq. 2 can be approximated to give telong ≈ nelong/fc0, whereas for similar forward and reverse reaction rates, fc0 ≈ belong, it approaches the solution for an unbiased random walk telong ≈ /2fc0. We calculate elongation times for other models in the Appendix and measure them for a more realistic model in the next section.
Under conditions of constant free subunit concentration, we can derive the average nucleation time with an equation analogous to Eq. 2 (9,14),
| (3) |
with , and the interaction free energy for the pre-nucleus ( for this model). However, because free subunits are depleted by assembly, the net nucleation rate never reaches this value and asymptotically approaches zero as the reaction approaches equilibrium. Instead, treating the system as a two-state reaction with nnuc-th order kinetics (see the Supporting Material) yields an approximation for the median assembly time τ1/2, the time at which the reaction is 50% complete
| (4) |
with as the equilibrium fraction of subunits in complete capsids, which can be measured experimentally (11). The factor of N−1 in Eq. 4 accounts for the fact that N subunits are depleted by each assembled capsid.
For all models considered, we will see that when capsid growth times are negligible compared to nucleation times, τelong and Eq. 4, respectively, predict the duration of the lag phase and the overall median assembly time. However, as first noted by Zlotnick (8), the reaction becomes kinetically trapped if free subunits are depleted before most capsids finish assembling. It was recently suggested (10,14) that this trap occurs at binding free energies Gn and subunit concentrations c0 for which the rate of subunit depletion by nucleation (N/τnucmin) is equal to the elongation rate. We find that the relationships between τelong and assembly times begin to fail at a crossover concentration cc for which initial nucleation and elongation rates are equal, but the system becomes kinetically trapped at a larger concentration ckt defined by the point at which the median assembly time τ1/2 matches the elongation time. These concentrations are related to binding free energies and other parameters by
| (5) |
with and τ1/2, respectively, given by Eqs. 3 and 4.
Investigating The LAG Phase with Brownian Dynamics (BD) Simulations
There are a number of simplifications in the schematic assembly process of the previous section:
Malformed capsids are not considered (15–22);
Assembly proceeds along a single pathway (23–25);
Only single subunits can bind or unbind;
Transitions between intermediates are allowed through binding or unbinding of a single subunit; and
There is only one (average) forward rate constant f.
In this section, we show that our results are valid when applied to a computational model that does not make any of those simplifications. We specifically consider the conclusions about lag times because calculating median assembly times is computationally demanding at low concentrations; we examine nucleation times in the next section.
There are two observations about lag times made in this work to be checked:
The first, crucial, observation is that lag times correspond to the mean of the distribution of initial capsid elongation times below cc.
The second observation is that the mean elongation time varies inversely with free subunit concentration if elongation is primarily a first-order reaction; note that lag times will still correspond to mean elongation times even if elongation is not first-order.
We consider simulations of a model for the assembly of icosahedral shells (14,16,20), in which subunits are modeled as rigid bodies, where excluded volume interactions are modeled by spherically symmetric repulsive forces, and complementary subunit-subunit interactions that drive assembly are modeled by directional attractions. The lowest energy states in the model correspond to capsids, which consist of multiples of 30 subunits (each of which represents a protein dimer) in a shell with icosahedral symmetry. Because the spatial positions and orientations of all subunits are explicitly tracked, there are no assumptions about assembly pathways or the structures that emerge from assembly.
Simulation parameters
The parameters of the model are the energy associated with the attractive potential, ɛb, and the specificity of the directional attractions, which is controlled by the angular parameters θm and φm. Subunit positions and orientations are propagated according to overdamped Brownian dynamics, with the unit of time t0 = a2/D, where D is the subunit diffusion coefficient and a is the subunit diameter. Full details of the model are given in Hagan (14).We simulated systems with 2000 subunits in periodic boxes with side lengths ranging from 27 to 65, where all distances are measured in units of the subunit diameter a. These side lengths correspond to subunit volume fractions of v0 ∈ [0.052, 0.0038], corresponding to concentrations of c0 = 84 μM to 1 mM, with c0 = 6v0/(πa3NA) with the subunit diameter a = 5.2 nm and NA Avogadro's number. The interaction parameters were ɛb = 12.25 kBT, θm = 0.75, and φm = π. We consider the assembly of T = 1 capsids, so N = 30 dimer subunits.
NVT simulations
We consider two sets of simulations to evaluate the time dependence of capsid assembly. The first set corresponds to the in vitro empty-capsid experiments modeled throughout this work, and simulates capsid formation in the canonical (NVT) ensemble. Simulations are initialized by generating random positions and orientations for subunits, with subunit positions that lead to subunit-subunit overlap (positive potential energies in excess of 1 kBT) rejected, and dynamics are integrated until a prescribed time.
The fraction of subunits in complete capsids PN, which can be monitored by SEC, is shown as a function of time for several total subunit volume fractions in Fig. 1. In all cases there is a lag time, followed by the rapid appearance of complete capsids and then eventually saturation of growth. The rate of capsid formation is nonmonotonic with respect to initial subunit concentration; the highest subunit volume fraction (v0 = 0.052), which is above cc (Eq. 5), has the shortest lag time but a slow rise to saturation because the system becomes starved for free subunits or small oligomers and large oligomers rarely have geometries compatible with binding. Lag times are measured from simulation data using the procedure described in Fig. 3. Except at high concentrations, lag times roughly scale as τlag ∝ v0−1—indicative of a primarily first-order elongation reaction for these parameters, despite the fact that oligomer binding does occur for this model.
Figure 3.
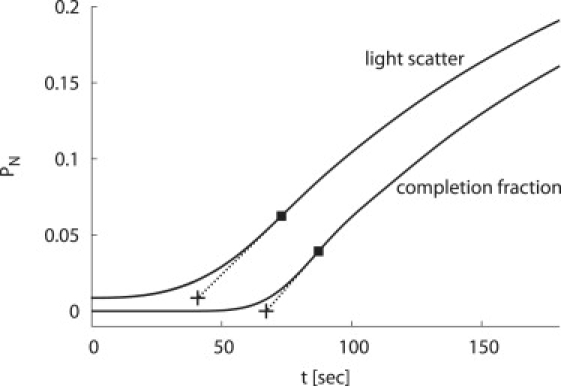
The end of the lag phase is measured by making a linear fit to the assembly kinetics trace at the point of maximal growth rate (■). The lag time (+) then corresponds to time at which the fit (dashed line) crosses the baseline. Plots are shown for the NG model with c0 = 20 μM.
Steady-state ensemble simulations
To evaluate the correspondence between lag times and initial elongation times, it is necessary to directly measure mean elongation times of growing capsids in the simulations. However, achieving statistical relevance and avoiding finite size effects for the measurement of initial elongation times is extremely challenging in the NVT simulations because, by definition, most capsids assemble later in the simulation when free subunits have been depleted. Therefore, we also consider simulations in a steady-state ensemble (26), in which the free subunit concentration becomes time-independent. Specifically, clusters that become complete capsids, defined as closed shells in which each subunit has its full complement of four bonds, and clusters that reach a size of 35 or more subunits, are removed from the system and their subunits are reinserted into the simulation box, subject to the same overlap criterion as the initial state. The simulations reach steady state in a time that closely corresponds to the lag time measured in the NVT simulations. Once steady state is achieved, we measure the distribution of elongation times and the average nucleation rate by tracking individual clusters. These simulations were run for the same sets of parameters as the NVT simulations.
At steady state in the steady-state ensemble simulations, the concentration of free subunits c1ss is equal to the total subunit concentration c0 minus the concentration of subunits in partially assembled capsids, which is dictated by the ratio of capsid production rates and free subunit consumption rates. Below cc, when elongation is fast compared to nucleation, the majority of subunits are free (or prenucleated) and c1ss is only slightly smaller than c0, but the ratio drops significantly with increasing c0, as shown in Fig. S7 in the Supporting Material.
The mean elongation times are shown as a function of the initial subunit volume fraction in Fig. 1. We see that for v0 ≤ 0.006 lag times measured from the NVT simulations and the mean elongation times in the steady-state ensemble agree to within error. Because the steady-state free subunit concentration c1ss closely corresponds to the initial free subunit concentration under these conditions (Fig. S7 in the Supporting Material), this finding supports the suggestion that lag times correspond to the initial mean elongation time. As the total subunit concentration increases above cc, the steady-state concentration becomes smaller than the initial concentration < c0 and thus the steady-state mean elongation times become longer than the lag times. We note, however, that above cc lag times increase faster than τlag ∝ 1/c0; similarly mean elongation times increase faster than τelong ∝ 1/. These results in part reflect the fact that binding of partial capsid intermediates becomes common above cc (see below). Furthermore, above cc, nucleation is no longer the rate-limiting step and lag times therefore correspond to the fastest members of the elongation time distribution, rather than the mean elongation time (i.e., when nucleation is rate-limiting, the first capsids to assemble have average elongation times, whereas those capsids with the shortest elongation times are the first to assemble when elongation is rate-limiting).
Rate Equation Models for Capsid Assembly
Because evaluating median assembly times is computationally demanding at low concentrations (see Fig. 4 a), we use rate equation models to explore the relationship between nucleation times and overall capsid assembly timescales. Zlotnick and co-workers (2,8,9) have developed a system of rate equations that describe the time evolution of concentrations of empty capsid intermediates as
| (6) |
where cn is the concentration of intermediates with n subunits, and fn and bn are, respectively, association and dissociation rate constants for intermediate n. There are several important assumptions, which are not present in the BD simulations: malformed capsids are not considered, only single subunits can bind or unbind, and only one fi and bi value is considered for each size i (averaged over averaged over all intermediates of that size). Despite these simplifications, rate equations of this form have shown good agreement with median assembly times of experimental assembly kinetics data (2,5). These simplifications should not affect our analysis of nucleation times, which involve a relatively small number of subunits and largely depend on the Boltzmann weights of pre-nuclei. Furthermore, we show that our results still hold when these simplifications are systematically eliminated in the Supporting Material.
Figure 4.
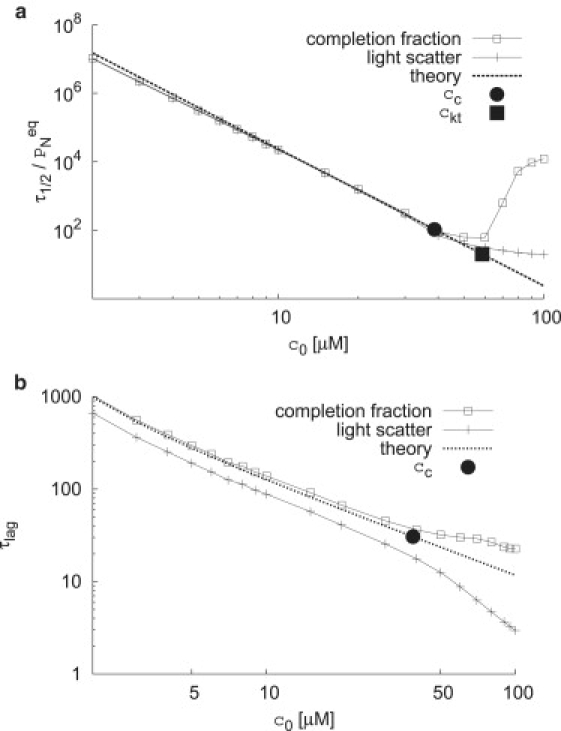
The median assembly times τ1/2 (a) and the lag times τlag (b) calculated from the completion fraction (PN) and calculated light scatter (ILS) are shown as functions of initial subunit concentration c0. The estimates for the nucleation time (Eq. 4 with nnuc = 5) and lag time Eq. 2 are shown as dashed lines, and the estimates for the crossover concentration cc and kinetic trap concentration ckt (Eq. 5) are shown as symbols on the estimated nucleation curve.
The association and dissociation rate constants are related by detailed balance bn = fexp(gn/kBT)/v0, with gn = Gn – Gn–1 the change in free energy due to association of a subunit. Association free energies gn, which can be fit to experimental data using the law of mass action (11,27,28), include hydrophobic and electrostatic interactions (12) and depend on pH and salt concentration (11). Specifying the assembly model requires defining the set of intermediates n and the transition rates fn, bn. To show that our conclusions are general, we consider two choices of these definitions.
The nucleation and growth (NG) model
Our first definition is based on the models of Zlotnick and co-workers (2,8,9), in which the subunit-subunit association free energy for intermediate i is proportional to the number of new subunit-subunit contacts nc,i formed by addition of a subunit to that intermediate. Note that this assumption neglects the fact that rotational entropy penalties are most likely not proportional to the number of contacts (see (35) for further discussion). Specifying {gi} thus requires defining the geometry of each intermediate. This usually begins with specifying the geometry of a capsid and its subunits in terms of a polyhedron (for example, see Fig. S6 in the Supporting Material or Fig. 1 in (9)), and assuming that assembly proceeds along a single path. The path can be comprised of the lowest energy intermediate for each size i (8) or correspond to an average pathway (9) in which all subunits, except during the initial and final stages of assembly, make the same average number of contacts. We choose the latter approach, as it is simpler and not obviously inferior in light of the other approximations in the rate equation models. Specifically, the association rate constant f is independent of intermediate size, and association free energies are given by gn = gnuc before nucleation (n < nnuc) and gn = gelong during elongation (nnuc ≤ n < N – 1), where nnuc is the critical nucleus size. Finally, inserting the last subunit makes the maximum number of possible contacts and thus enjoys the most favorable association free energy gN (see the Appendix for discussion of an irreversible final assembly step). Except for the last subunit, this model corresponds to Eq. 1.
Our NG model is quite similar to that of Zlotnick and co-workers (2,9), which reproduces experimental assembly kinetics for several viruses (2,5). Nucleation has been shown to correspond to completion of polygons (e.g., a pentamer of dimers for cowpea chlorotic mottle virus (3) or a trimer of dimers for turnip crinkle virus (30)), which can be understood by noting that the subunits assembling to form the first polygon make fewer contacts on average than later subunits. Furthermore, intertwining of flexible terminal arms and other subunit conformation changes can provide additional stabilization upon polygon formation. In Zlotnick and co-workers' formulation (2,9), the nucleation and elongation phases are distinguished by having different forward rate constants, with a slow rate constant before nucleation and a rate constant which is several orders-of-magnitude higher during growth. However, based on the fact that nucleation seems to correspond to the subunit stabilization that results from completion of polygons, we choose to distinguish the nucleation and growth phases with different subunit-subunit association free energies.
We find that our results concerning lag times and identification of the critical nucleus size are insensitive to parameter values. We will therefore present results in Numerical Results for one parameter set: nucleation size nnuc = 5 (a pentamer of dimers) and free energy parameters gnuc = 7 kBT, gelong = 2gnuc and gN = 2gelong, which imply that adding a subunit becomes, on average, twice as favorable after nucleation and four times as favorable for the final subunit. We note that the value of f corresponds to an average association rate, and not the association rate constant for a single subunit binding site. To clarify this point, we consider a model in the Supporting Material in which we relax the assumption that the association rate constant is independent of intermediate size.
The classical nucleation theory model
We also consider a definition of transition rates based on the classical nucleation theory (henceforth referred to as CNT) suggested by Zandi et al. (31), in which each partial-capsid intermediate is described as a sphere, with a missing spherical cap. The unfavorable free energy due to unsatisfied subunit-subunit interactions at the perimeter of the cap is represented by a line tension σ, and the binding free energy is
| (7) |
with the perimeter of the missing spherical cap given by
| (8) |
with gc the binding free energy per subunit (not per contact) in a complete capsid. Following Zandi et al. (31), we set the line tension to σ = –gc/2, which indicates that, on average, a subunit adding to the perimeter of the capsid satisfies half of its contacts. We find that Eq. 7 with σ = −gc/2 is a reasonable description during the growth phase in BD simulations, but fewer contacts are made by subunits associating to form the first polygon. Note that whereas Eq. 7 is derived under a continuum approximation, we use it to calculate free energies for intermediates with discrete sizes n when solving Eq. 6. We assume that the forward rate constant is proportional to the number of subunits on the perimeter, fn = f0ln, with f0 the association rate constant for a single binding site. From BD simulation trajectories (14,16,20), we know that this relation overpredicts the net forward rate constant, as only the subunit binding sites that lead to more than one subunit-subunit contact lead to productive assembly for parameters that give rise to effective assembly. However, we show in the Supporting Material that our conclusions are not affected by changing the proportionality constant. As for the NG model, our conclusions about lag times and identifying the critical nucleus are insensitive to parameter values.
The most significant difference between the CNT model and the nucleation and growth models is the size of the critical nucleus. For the NG model the critical nucleus size is nnuc, provided exp(gnuc/kBT) < c0v0 < exp(gelong/kBT). For the CNT model, the critical nucleus size varies with subunit concentration, and is given by the maximum in kBT log(c1v0)n + Gn, or (31)
| (9) |
with Γ = [gc – ln(c1v0)]/σ.
Numerical Results
We explore the concentration dependence of assembly kinetics by numerically integrating the system of rate equations (Eq. 6) with the initial condition c1 = c0 over a range of subunit concentrations. We start with the NG model, with representative parameters: the contact free energy gnuc = 7 kBT (≈ 4 kcal/mol) (11), capsid size N = 120 corresponding to 120 dimer subunits in hepatitis B virus (11), the critical nucleus size nnuc = 5, and the subunit association rate constant f = 105 M−1 s−1 (5). As is evident from Eqs. 2 and 4, assembly dynamics are insensitive to gelong and gN, provided that the forward reaction is favorable during elongation; we use gelong = 2gnuc and gN = 4gnuc (see Rate Equation Models for Capsid Assembly for further discussion).
As shown in Fig. 2, the fraction of subunits in complete capsids (PN(t)) obtained from the rate equations mirrors the results of the BD simulations (Fig. 1 a). In both cases, the kinetic trap point ckt roughly corresponds to the point at which the time to build the capsid becomes longer than the average nucleation time (Eq. 5). For the rate equation models, the kinetic trap concentration can be calculated as a function of our parameter values using Eqs. 2, 3, and 5 to give ckt ≈ 60, which corresponds well to the point at which assembly times increase with subunit concentration. Assembly eventually occurs above ckt as large partial capsids scavenge subunits from smaller intermediates.
We calculate light-scatter signal ILS from the mass-averaged molecular weight of assemblages (2). Because light-scatter units are arbitrary, we normalize calculated light scatter by N to give 1 if all subunits are in complete capsids (PN = 1). As shown in Fig. 2 b, the calculated light scatter closely tracks the completion fraction for initial subunit concentrations below cc ≈ 38 μM, as the majority of assembled subunits are found in complete capsids once the lag phase is complete.
The concentration-dependence of median assembly times and lag times
The median assembly times (reaction half-lives), and lag times numerically calculated for the nucleation and growth model, with respect to the completion fraction PN and calculated light scatter, are given in Fig. 4. As illustrated in Fig. 3, lag times are extracted from numerical solutions for each parameter set with a linear fit to the assembly trace at the point of maximal assembly rate (dPN/dt or dILS/dt). The lag time is given by the intersection of the linear fit with the baseline value, which is 0 for the completion fraction and roughly 1/N for calculated light scatter. Note that for initial subunit concentrations below cc, lag times for both the completion fraction and calculated light scatter are inversely proportional to c0, and the mean first-passage time estimate (Eq. 2) for the capsid elongation phase τelong closely predicts the lag time for completion fractions. The lag time for light scatter is shorter than for the completion fraction because signal is integrated over all assemblages, but demonstrates the same scaling. Hence, lag times measured for PN (SEC) or light scattering are associated with the elongation phase, or the time required to build a complete capsid. Note that our expressions for the lag time differ from the well-known expression for the time lag in nucleation theory (32), which gives the time for the concentration of nuclei to reach steady state.
The correspondence between light scatter and completion fraction lag times begins to break down at the crossover concentration cc (Eq. 5), when the concentration of free subunits is depleted before the first capsids finish assembling. Above this point, the molecular weight average growth rate becomes dominated by dimerization and hence varies inversely with the square of initial subunit concentration. The relationship between the lag time and the elongation phase of capsid assembly discovered here explains the observation of Endres and Zlotnick (9) that the duration of lag time is proportional to the elongation forward rate constant.
The reaction half-life (median assembly time) τ1/2 is given by PN(τ1/2) = 0.5 for the completion fraction, or the analogous relation for calculated light scatter. Below cc, half-lives measured with light scatter and completion fraction agree quantitatively, as anticipated from Fig. 2 b, and agree closely with the two-state nucleation kinetics estimate (Eq. 4). In Fig. 4 a, the numerical and theoretical half-lives are normalized by the equilibrium to emphasize that the scaling with concentration identifies the critical nucleus size:
The fact that assembly times can be predicted from nucleation kinetics alone can be understood by noting that assembly times are dominated by nucleation below cc. The close correspondence between the theoretical and numerical median assembly times below cc suggests that this quantity may provide a simple alternative to the critical nucleus estimator presented in the Appendix of Endres and Zlotnick (9).
As evident from Eq. 4, the critical nucleus size can also be identified by evaluating ln τ1/2/PN as a function of the subunit-subunit association free energy gnuc. We find that agreement between the theoretical predictions and numerical results is insensitive to gnuc and nnuc.
Maximum assembly rates
As noted by Endres and Zlotnick (9), it is not reliable to relate the critical nucleus size to initial assembly rates or the extent of assembly as a function of time due to the presence of the lag phase. At low concentrations, though, the maximum assembly rates approach the initial nucleation rate given in Eq. 3 (see Fig. S10 in the Supporting Material). However, because the maximum assembly rates deviate from the theoretical prediction well below the crossover concentration cc, it appears that median assembly times are a more robust predictor of the critical nucleus size.
The classical nucleation model
To evaluate whether our conclusions are model-dependent, we also consider the concentration dependence of assembly times and lag times for the CNT model. To facilitate comparisons between the models, we set gc = 13.8 kBT and f0 = 105/[2(N/π)1/2], so that and the average association rate constants are the same for both models. This choice enables the elongation time prediction of Eq. 2 to be directly compared with the numerically calculated lag time; as shown in Fig. 5, the numerical results and theoretical estimate agree. Furthermore, as for the NG models, the calculated light scatter closely tracks the completion fraction below the kinetic trap point. As noted in Rate Equation Models for Capsid Assembly, the most significant difference between the CNT and NG models is that the critical nucleus size in the classical nucleation model varies with subunit concentration (Eq. 9), with for the simulated range of initial subunit concentrations in this work. The reaction half-life, however, appears to scale roughly as τ1/2/PN ∝ because the effective critical nucleus size increases over the course of the reaction as free subunits are depleted.
Figure 5.
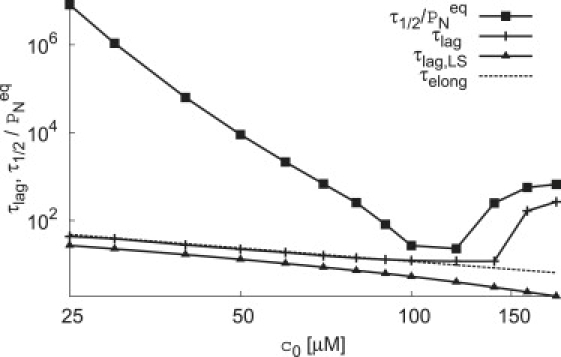
The median assembly time (■) and lag time (+) calculated from the completion time and the lag time for light scatter (▴) for the classical nucleation model are shown as functions of concentration. The theoretical prediction for lag time Eq. 2 is shown as a dashed line.
For all parameter sets we considered, the CNT model demonstrates a large effective critical nucleus size as the concentration is reduced below cc. Hence, analyzing the concentration dependence of experimental median assembly times could be one way to evaluate which of the CNT model or NG model better represents capsid assembly mechanisms.
The effect of binding between partial-capsid intermediates
Because binding between intermediates does occur in the BD simulations, their results validate the predictions we have just explored with rate equation models. This fact can be understood by noting that binding between partial capsid intermediates is most prevalent above cc, when many capsids are assembling at the same time. Although intermediate binding can, in principle, ameliorate the kinetic trapping predicted by the simple models above ckt, in practice the kinetic trap point is only slightly shifted because binding between large partial capsids is rarely compatible with their geometries. Although the time to assemble the first capsid continues to decrease with increasing subunit concentration for the BD simulations (Fig. 1), assembly of subsequent capsids is impeded at the highest subunit volume fractions (Fig. 1 a). Furthermore, malformed capsids become increasingly likely as concentrations increase and partial capsids interact (see (16,33) for further discussion of these points).
Binding between intermediates can also arise when the association rates or binding free energies are stronger along one subunit-subunit interface. For most viruses, in fact, the capsid protein rapidly dimerizes and exists primarily as a dimer in solution; the subunit considered in the NG and CNT models corresponds to a protein dimer, and the monomer is not explicitly considered. For systems in which rate constants are arranged so that hierarchical assembly and addition of individual subunits occur with comparable rates, as explored in Sweeney et al. (25), the correspondence between lag times and capsid elongation times will still hold, but the scaling of elongation times (and hence lag times) with subunit concentrations could differ. This possibility would be interesting to examine further.
The slow approach to equilibrium
We note that accurate estimation of is not necessary to obtain the critical nucleus size from τ1/2, as nucleation rates have such a dramatic concentration dependence even at subunit concentrations for which > 0.5. This observation could be important, as the median assembly times shown in Fig. 4 a and Fig. 5 extend beyond experimental feasibility at low concentrations (see Fig. S9 in the Supporting Material), particularly for the CNT model because of the large effective critical nucleus size. Furthermore, as noted by Zlotnick (8), capsid assembly approaches equilibrium asymptotically. Therefore, when estimating , it is important to plot PN(t) on a logarithmic scale to judge equilibration, and it may be necessary to extract the contact free energy gnuc or gc from fits to kinetic data over a series of concentrations (2,5). The slow approach to equilibrium due to nucleation barriers was noted from simulations in Hagan and Chandler (16), and is discussed for the classical nucleation model in Morozov et al. (10).
Discussion and Outlook
In this work, we examine simulations and two theoretical models for capsid assembly, for which we find that the duration of the lag phase measured by SEC or dynamic light scatter is related to the time for a nucleated capsid to grow to completion, and hence scales inversely with initial subunit concentration. When nucleation of new partial capsids is faster than this growth time, the system becomes kinetically trapped due to starvation of free subunits, meaning that capsid formation rates decreases with increasing initial subunit concentration. If there is a well-defined critical nucleus size, it can be identified from the scaling of the median assembly time with respect to initial subunit concentration.
These predictions have important implications for obtaining mechanistic information about capsid elongation (growth after nucleation) from bulk in vitro assembly kinetics experiments. The fact that overall reaction times are closely predicted by an expression based solely on nucleation kinetics (Eq. 4, Fig. 4) when assembly is most efficient, suggests that the lag phase contains the most information about elongation. In fact, the preceding analysis demonstrates that the average elongation time, and hence the average growth velocity during elongation, are directly related to the duration of the lag phase. Because Chen et al. (6) recently showed that time-resolved light scattering data can be obtained with millisecond resolution, it will be possible to measure lag times with high precision if the reaction is started in a controlled manner. Additional mechanistic information about the elongation process could be obtained if the distribution of growth times could be deconvolved from the distribution of nucleation times. The kinetic trap criterion, however, limits this possibility by constraining growth times, and hence causes the lag phase duration to be short compared to nucleation times.
This constraint could potentially be overcome in several ways. The distribution of elongation times can be directly measured in experiments that monitor the assembly of individual capsids, as the elongation and nucleation phases can be separated (34). For bulk assembly studies, recent theoretical studies (14,35) found that robust assembly is possible under conditions of fast heterogeneous nucleation if there is excess capsid protein. Thus, experimental systems in which capsid assembly is induced by nucleic acids (36), synthetic polymers (37,38), nanoparticles (39), and portal or scaffolding proteins (40–42) could be used to elucidate elongation mechanisms (although assembly mechanisms can be influenced by the heterogeneous component (14,36,43)).
Finally, we note that processes not considered in this work, such as transitions between assembly-active and assembly-inactive conformations of free subunits (6) or hierarchical assembly (44) would add additional complexity to analysis of the lag phase. In particular, if conformational transitions are slow compared to elongation times, the conformational transition timescale will be reflected in the duration of the lag phase. We plan to investigate that case further. In addition, a systematic comparison of model predictions with experimental assembly data over a wide range of concentrations could reveal additional features of complexity in assembly mechanisms and suggest model improvements.
Acknowledgments
We are grateful to Jane Kondev for a discussion that led us to investigate the origins of the lag phase and to Robert Jack for discussions about the steady-state ensemble.
M.F.H. and O.M.E. were supported by award No. R01AI080791 from the National Institute of Allergy and Infectious Diseases. M.F.H. also acknowledges support by the National Science Foundation through the Brandeis Materials Research Science and Engineering Center. The BD simulations were performed on the Brandeis High Performance Computing Cluster.
Appendix
We consider two additional cases for elongation times in this Appendix.
Elongation times with intermediate-dependent forward rate constants
The parameter f in Eq. 2 is the average forward rate constant for the elongation phase. For the CNT model, the forward rate constants are proportional to the perimeter of the partial capsid intermediate, fn = f0ln, with the perimeter ln given by Eq. 8. For we show in the Supporting Material that telong = 0.5(πN)1/2/(f0c1). In Fig. 5, we see that elongation times for the CNT model can be approximated with Eq. 2 by setting f = 2f0(N/π)1/2.
Irreversible elongation steps
It is evident from Eq. 2 that elongation times would be essentially the same if the final subunit insertion step was irreversible. In fact, as shown by Zlotnick (28), all features of assembly dynamics are the same in the case of a final irreversible assembly step except for times greater than the time for subunit dissociation from a complete capsid (bN). Subunit exchange from complete capsids has been seen experimentally (45), but over a timescale of days rather than the minutes or hours in which assembly takes place. This observation is captured by all of the models considered here, in which insertion of the final subunit is the most favorable free energy, and hence dissociation of a subunit from a complete capsid (bN ∝ exp(gN/kBT)) is slow. For the case of several irreversible steps during the elongation phase, elongation times could be calculated by breaking Eq. 2 into independent random walks in series, with one walk between each set of irreversible steps.
Supporting Material
References
- 1.Prevelige P.E., Jr., Thomas D., King J. Nucleation and growth phases in the polymerization of coat and scaffolding subunits into icosahedral procapsid shells. Biophys. J. 1993;64:824–835. doi: 10.1016/S0006-3495(93)81443-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zlotnick A., Johnson J.M., Endres D. A theoretical model successfully identifies features of hepatitis B virus capsid assembly. Biochemistry. 1999;38:14644–14652. doi: 10.1021/bi991611a. [DOI] [PubMed] [Google Scholar]
- 3.Zlotnick A., Aldrich R., Young M.J. Mechanism of capsid assembly for an icosahedral plant virus. Virology. 2000;277:450–456. doi: 10.1006/viro.2000.0619. [DOI] [PubMed] [Google Scholar]
- 4.Casini G.L., Graham D., Wu D.T. In vitro papillomavirus capsid assembly analyzed by light scattering. Virology. 2004;325:320–327. doi: 10.1016/j.virol.2004.04.034. [DOI] [PubMed] [Google Scholar]
- 5.Johnson J.M., Tang J.H., Zlotnick A. Regulating self-assembly of spherical oligomers. Nano Lett. 2005;5:765–770. doi: 10.1021/nl050274q. [DOI] [PubMed] [Google Scholar]
- 6.Chen C., Kao C.C., Dragnea B. Self-assembly of brome mosaic virus capsids: insights from shorter time-scale experiments. J. Phys. Chem. A. 2008;112:9405–9412. doi: 10.1021/jp802498z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Berthet-Colominas C., Cuillel M., Jacrot B. Kinetic-study of the self-assembly of brome mosaic-virus capsid. Eur. Biophys. J. Biophys. Lett. 1987;15:159–168. [Google Scholar]
- 8.Zlotnick A. To build a virus capsid. An equilibrium model of the self-assembly of polyhedral protein complexes. J. Mol. Biol. 1994;241:59–67. doi: 10.1006/jmbi.1994.1473. [DOI] [PubMed] [Google Scholar]
- 9.Endres D., Zlotnick A. Model-based analysis of assembly kinetics for virus capsids or other spherical polymers. Biophys. J. 2002;83:1217–1230. doi: 10.1016/S0006-3495(02)75245-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Morozov A.Y., Bruinsma R.F., Rudnick J. Assembly of viruses and the pseudo law of mass action. J. Chem. Phys. 2009;131:155101. doi: 10.1063/1.3212694. [DOI] [PubMed] [Google Scholar]
- 11.Ceres P., Zlotnick A. Weak protein-protein interactions are sufficient to drive assembly of hepatitis B virus capsids. Biochemistry. 2002;41:11525–11531. doi: 10.1021/bi0261645. [DOI] [PubMed] [Google Scholar]
- 12.Kegel W.K., Schoot Pv P. Competing hydrophobic and screened-Coulomb interactions in hepatitis B virus capsid assembly. Biophys. J. 2004;86:3905–3913. doi: 10.1529/biophysj.104.040055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bar-Haim A., Klafter J. On mean residence and first passage times in finite one-dimensional systems. J. Chem. Phys. 1998;109:5187–5193. [Google Scholar]
- 14.Hagan M.F. Controlling viral capsid assembly with templating. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;77:051904. doi: 10.1103/PhysRevE.77.051904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schwartz R., Shor P.W., Berger B. Local rules simulation of the kinetics of virus capsid self-assembly. Biophys. J. 1998;75:2626–2636. doi: 10.1016/S0006-3495(98)77708-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hagan M.F., Chandler D. Dynamic pathways for viral capsid assembly. Biophys. J. 2006;91:42–54. doi: 10.1529/biophysj.105.076851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nguyen H.D., Reddy V.S., Brooks C.L., 3rd Deciphering the kinetic mechanism of spontaneous self-assembly of icosahedral capsids. Nano Lett. 2007;7:338–344. doi: 10.1021/nl062449h. [DOI] [PubMed] [Google Scholar]
- 18.Wilber A.W., Doye J.P.K., Wong P. Reversible self-assembly of patchy particles into monodisperse icosahedral clusters. J. Chem. Phys. 2007;127:085106. doi: 10.1063/1.2759922. [DOI] [PubMed] [Google Scholar]
- 19.Hicks S.D., Henley C.L. Irreversible growth model for virus capsid assembly. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:031912. doi: 10.1103/PhysRevE.74.031912. [DOI] [PubMed] [Google Scholar]
- 20.Elrad O.M., Hagan M.F. Mechanisms of size control and polymorphism in viral capsid assembly. Nano Lett. 2008;8:3850–3857. doi: 10.1021/nl802269a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rapaport D.C. Role of reversibility in viral capsid growth: a paradigm for self-assembly. Phys. Rev. Lett. 2008;101:186101. doi: 10.1103/PhysRevLett.101.186101. [DOI] [PubMed] [Google Scholar]
- 22.Nguyen H.D., Reddy V.S., Brooks C.L. Invariant polymorphism in virus capsid assembly. J. Am. Chem. Soc. 2009;131:2606–2614. doi: 10.1021/ja807730x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Endres D., Miyahara M., Zlotnick A. A reaction landscape identifies the intermediates critical for self-assembly of virus capsids and other polyhedral structures. Protein Sci. 2005;14:1518–1525. doi: 10.1110/ps.041314405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhang T.Q., Schwartz R. Simulation study of the contribution of oligomer/oligomer binding to capsid assembly kinetics. Biophys. J. 2006;90:57–64. doi: 10.1529/biophysj.105.072207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sweeney B., Zhang T., Schwartz R. Exploring the parameter space of complex self-assembly through virus capsid models. Biophys. J. 2008;94:772–783. doi: 10.1529/biophysj.107.107284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maibaum L. Phase transformation near the classical limit of stability. Phys. Rev. Lett. 2008;101:256102. doi: 10.1103/PhysRevLett.101.256102. [DOI] [PubMed] [Google Scholar]
- 27.Ceres P., Stray S.J., Zlotnick A. Hepatitis B virus capsid assembly is enhanced by naturally occurring mutation F97L. J. Virol. 2004;78:9538–9543. doi: 10.1128/JVI.78.17.9538-9543.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zlotnick A. Distinguishing reversible from irreversible virus capsid assembly. J. Mol. Biol. 2007;366:14–18. doi: 10.1016/j.jmb.2006.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Reference deleted in proof.
- 30.Sorger P.K., Stockley P.G., Harrison S.C. Structure and assembly of turnip crinkle virus. II. Mechanism of reassembly in vitro. J. Mol. Biol. 1986;191:639–658. doi: 10.1016/0022-2836(86)90451-1. [DOI] [PubMed] [Google Scholar]
- 31.Zandi R., van der Schoot P., Reiss H. Classical nucleation theory of virus capsids. Biophys. J. 2006;90:1939–1948. doi: 10.1529/biophysj.105.072975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wu D.T. The time-lag in nucleation theory. J. Chem. Phys. 1992;97:2644–2650. [Google Scholar]
- 33.Whitelam S., Feng E.H., Geissler P.L. The role of collective motion in examples of coarsening and self-assembly. Soft Matter. 2009;5:1251–1262. doi: 10.1039/b810031d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jouvenet N., Bieniasz P.D., Simon S.M. Imaging the biogenesis of individual HIV-1 virions in live cells. Nature. 2008;454:236–240. doi: 10.1038/nature06998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hagan M.F. A theory for viral capsid assembly around electrostatic cores. J. Chem. Phys. 2009;130:114902. doi: 10.1063/1.3086041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Johnson J.M., Willits D.A., Zlotnick A. Interaction with capsid protein alters RNA structure and the pathway for in vitro assembly of cowpea chlorotic mottle virus. J. Mol. Biol. 2004;335:455–464. doi: 10.1016/j.jmb.2003.10.059. [DOI] [PubMed] [Google Scholar]
- 37.Sikkema F.D., Comellas-Aragonès M., Nolte R.J. Monodisperse polymer-virus hybrid nanoparticles. Org. Biomol. Chem. 2007;5:54–57. doi: 10.1039/b613890j. [DOI] [PubMed] [Google Scholar]
- 38.Hu Y., Zandi R., Gelbart W.M. Packaging of a polymer by a viral capsid: the interplay between polymer length and capsid size. Biophys. J. 2008;94:1428–1436. doi: 10.1529/biophysj.107.117473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sun J., DuFort C., Dragnea B. Core-controlled polymorphism in virus-like particles. Proc. Natl. Acad. Sci. USA. 2007;104:1354–1359. doi: 10.1073/pnas.0610542104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Parent K.N., Doyle S.M., Teschke C.M. Electrostatic interactions govern both nucleation and elongation during phage P22 procapsid assembly. Virology. 2005;340:33–45. doi: 10.1016/j.virol.2005.06.018. [DOI] [PubMed] [Google Scholar]
- 41.Parent K.N., Zlotnick A., Teschke C.M. Quantitative analysis of multi-component spherical virus assembly: scaffolding protein contributes to the global stability of phage P22 procapsids. J. Mol. Biol. 2006;359:1097–1106. doi: 10.1016/j.jmb.2006.03.068. [DOI] [PubMed] [Google Scholar]
- 42.Tuma R., Tsuruta H., Prevelige P.E. Detection of intermediates and kinetic control during assembly of bacteriophage P22 procapsid. J. Mol. Biol. 2008;381:1395–1406. doi: 10.1016/j.jmb.2008.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.McPherson A. Micelle formation and crystallization as paradigms for virus assembly. Bioessays. 2005;27:447–458. doi: 10.1002/bies.20196. [DOI] [PubMed] [Google Scholar]
- 44.Misra N., Lees D., Schwartz R. Pathway complexity of model virus capsid assembly systems. Comput. Math. Method Med. 2008;9:277–293. [Google Scholar]
- 45.Parent K.N., Suhanovsky M.M., Teschke C.M. Phage P22 procapsids equilibrate with free coat protein subunits. J. Mol. Biol. 2007;365:513–522. doi: 10.1016/j.jmb.2006.09.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


